Asymmetric Volatility Spillovers in Varying Market Conditions and Portfolio Performance Analysis of the South African Foreign Exchange Market
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Dynamic Time Warping Distance
- (i)
- and ;
- (ii)
- and and ;
- (iii)
- and .
3.2. Generalized Spillover and Measurement in a VAR Model
3.2.1. Variance Shares
3.2.2. Total Spillovers
3.2.3. Directional Spillovers
3.2.4. Net Spillovers
3.2.5. Net Pairwise Spillovers
3.3. Quantile Vector Autoregressive Model and Spillovers
3.4. Model Stability Test
3.5. Portfolio Optimization
3.5.1. Risk Parity Portfolio Optimization
3.5.2. Tangency Portfolio Optimization
3.5.3. Equally Weighted Portfolio
3.6. Portfolio Performance Measurement
3.7. Portfolio Backtest
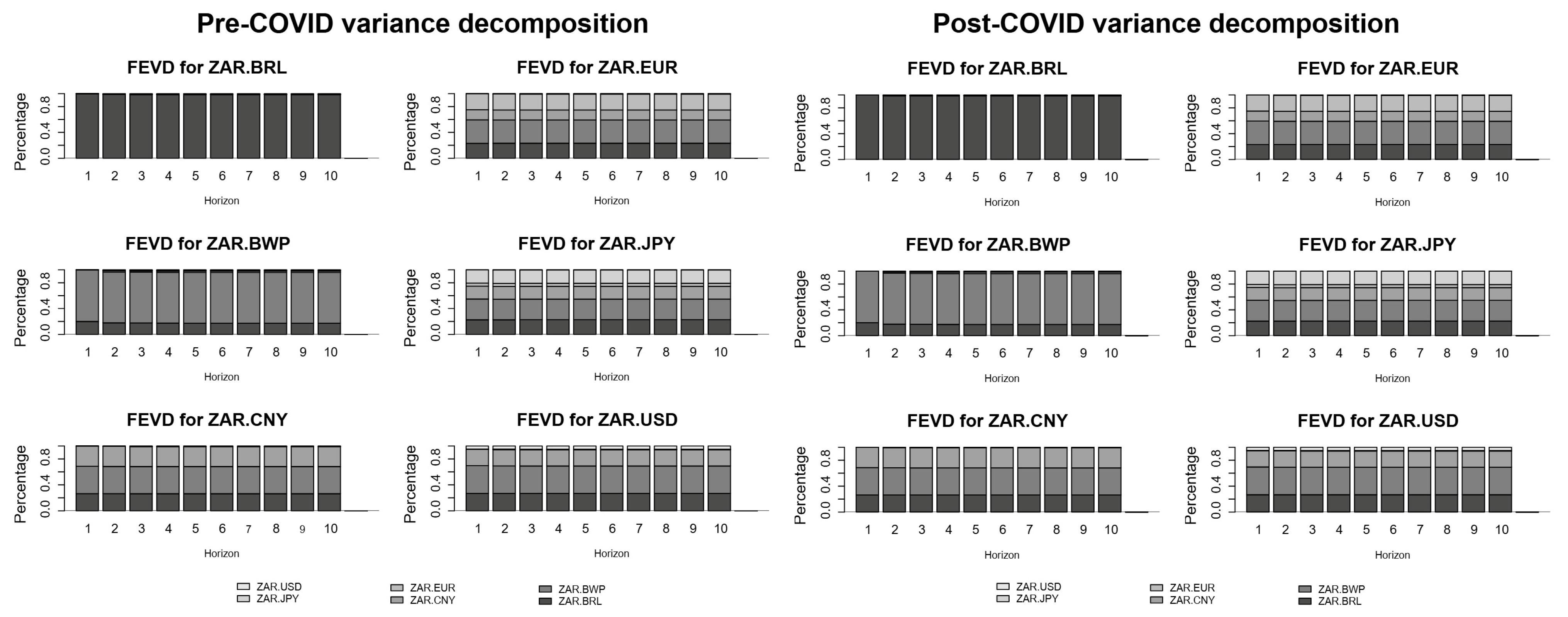
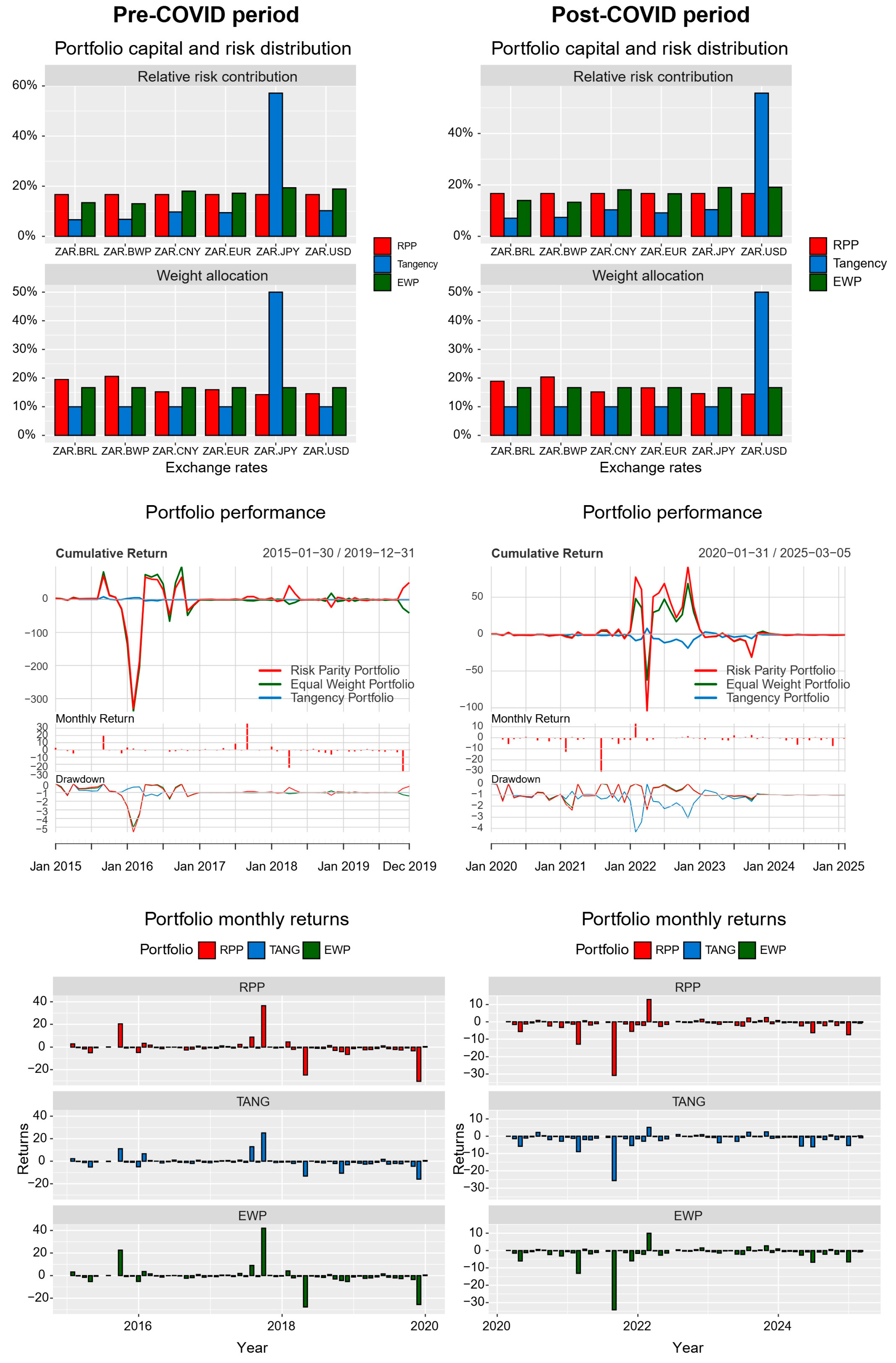
4. Empirical Findings
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Pre-COVID Period | |||||
|---|---|---|---|---|---|
| ZAR.BRL→ZAR.BWP | ZAR.BWP→ZAR.CNY | ZAR.CNY→ZAR.JPY | |||
| F | 2.833 * | F | 26.071 *** | F | 1.648 |
| ZAR.BWP→ZAR.BRL | ZAR.CNY→ZAR.BWP | ZAR.JPY→ZAR.CNY | |||
| F | 10.685 *** | F | 2.22 | F | 2.953 * |
| ZAR.BRL→ZAR.CNY | ZAR.BWP→ZAR.EUR | ZAR.CNY→ZAR.USD | |||
| F | 2.371 * | F | 27.887 *** | F | 0.579 |
| ZAR.CNY→ZAR.BRL | ZAR.EUR→ZAR.BWP | ZAR.USD→ZAR.CNY | |||
| F | 2.357 * | F | 0.416 | F | 1.242 |
| ZAR.BRL→ZAR.EUR | ZAR.BWP→ZAR.JPY | ZAR.EUR→ZAR.JPY | |||
| F | 1.42 | F | 14.003 *** | F | 2.29 |
| ZAR.EUR→ZAR.BRL | ZAR.JPY→ZAR.BWP | ZAR.JPY→ZAR.EUR | |||
| F | 3.598 ** | F | 0.38 | F | 3.505 ** |
| ZAR.BRL→ZAR.JPY | ZAR.BWP→ZAR.USD | ZAR.EUR→ZAR.USD | |||
| F | 0.262 | F | 28.089 *** | F | 0.693 |
| ZAR.JPY→ZAR.BRL | ZAR.USD→ZAR.BWP | ZAR.USD→ZAR.EUR | |||
| F | 4.18 ** | F | 1.504 | F | 0.696 |
| ZAR.BRL→ZAR.USD | ZAR.CNY→ZAR.EUR | ZAR.JPY→ZAR.USD | |||
| F | 3.44 ** | F | 0.953 | F | 3.418 ** |
| ZAR.USD→ZAR.BRL | ZAR.EUR→ZAR.CNY | ZAR.USD→ZAR.JPY | |||
| F | 2.291 | F | 0.38 | F | 1.73 |
| Post-COVID Period | |||||
| ZAR.BRL→ZAR.BWP | ZAR.BWP→ZAR.CNY | ZAR.CNY→ZAR.JPY | |||
| F | 3.232 ** | F | 5.533 | F | 3.334 ** |
| ZAR.BWP→ZAR.BRL | ZAR.CNY→ZAR.BWP | ZAR.JPY→ZAR.CNY | |||
| F | 2.019 | F | 0.123 | F | 1.278 |
| ZAR.BRL→ZAR.CNY | ZAR.BWP→ZAR.EUR | ZAR.CNY→ZAR.USD | |||
| F | 3.17 ** | F | 14.57 *** | F | 1.012 |
| ZAR.CNY→ZAR.BRL | ZAR.EUR→ZAR.BWP | ZAR.USD→ZAR.CNY | |||
| F | 0.332 | F | 0.083 | F | 0.734 |
| ZAR.BRL→ZAR.EUR | ZAR.BWP→ZAR.JPY | ZAR.EUR→ZAR.JPY | |||
| F | 2.643 * | F | 11.29 *** | F | 2.569 * |
| ZAR.EUR→ZAR.BRL | ZAR.JPY→ZAR.BWP | ZAR.JPY→ZAR.EUR | |||
| F | 0.682 | F | 0.216 | F | 0.568 |
| ZAR.BRL→ZAR.JPY | ZAR.BWP→ZAR.USD | ZAR.EUR→ZAR.USD | |||
| F | 2.696 * | F | 4.115 ** | F | 1.087 |
| ZAR.JPY→ZAR.BRL | ZAR.USD→ZAR.BWP | ZAR.USD→ZAR.EUR | |||
| F | 1.588 | F | 0.628 | F | 0.091 |
| ZAR.BRL→ZAR.USD | ZAR.CNY→ZAR.EUR | ZAR.JPY→ZAR.USD | |||
| F | 2.557 * | F | 1.088 | F | 0.615 |
| ZAR.USD→ZAR.BRL | ZAR.EUR→ZAR.CNY | ZAR.USD→ZAR.JPY | |||
| F | 0.423 | F | 0.441 | F | 1.433 |
| ZAR.BRL | ZAR.BWP | ZAR.CNY | ZAR.EUR | ZAR.JPY | ZAR.USD | FROM | ||
|---|---|---|---|---|---|---|---|---|
| ZAR.BRL | 45.49 | 9.25 | 12.13 | 10.54 | 10.31 | 12.29 | 28.34 | |
| ZAR.BWP | 5.34 | 29.15 | 17.9 | 15.31 | 14.18 | 18.12 | 61.33 | |
| ZAR.CNY | 6.14 | 15.12 | 22.96 | 17.01 | 17.11 | 21.67 | 94.66 | |
| VAR | ZAR.EUR | 5.84 | 14.13 | 18.38 | 24.84 | 18.13 | 18.67 | 80.04 |
| Pre-COVID | ZAR.JPY | 5.77 | 13.01 | 18.68 | 18.36 | 25.03 | 19.15 | 80.14 |
| ZAR.USD | 6.15 | 15.15 | 21.49 | 17.1 | 17.36 | 22.75 | 95.1 | |
| TO | 29.9 | 68.18 | 90.62 | 80.11 | 78.85 | 91.95 | 439.61 | |
| Inc.Own | 74.72 | 95.81 | 111.55 | 103.16 | 102.11 | 112.64 | TCI | |
| NET | 1.56 | 6.85 | −4.04 | 0.08 | −1.29 | −3.15 | 73.27 | |
| ZAR.BRL | 53.26 | 6.3 | 10.98 | 10.31 | 7.47 | 11.67 | 24.26 | |
| ZAR.BWP | 3.09 | 29.72 | 19.28 | 15.41 | 13.2 | 19.3 | 66.7 | |
| ZAR.CNY | 4.78 | 16.01 | 23.83 | 18.02 | 15.76 | 21.61 | 92.07 | |
| VAR | ZAR.EUR | 4.84 | 14.14 | 19.43 | 25.62 | 17.21 | 18.76 | 80.06 |
| Post-COVID | ZAR.JPY | 3.88 | 13.2 | 18.42 | 18.61 | 27.94 | 17.95 | 71.35 |
| ZAR.USD | 5.14 | 16.11 | 21.78 | 17.53 | 15.41 | 24.02 | 91.53 | |
| TO | 22.28 | 67.4 | 92.14 | 81.87 | 70.77 | 91.52 | 425.97 | |
| Inc.Own | 75 | 95.48 | 113.72 | 105.49 | 96.99 | 113.31 | TCI | |
| NET | −1.99 | 0.7 | 0.06 | 1.81 | −0.58 | −0.01 | 71 | |
| ZAR.BRL | 45.49 | 9.25 | 12.13 | 10.54 | 10.31 | 12.29 | 28.34 | |
| ZAR.BWP | 5.34 | 29.15 | 17.9 | 15.31 | 14.18 | 18.12 | 61.33 | |
| ZAR.CNY | 6.14 | 15.12 | 22.96 | 17.01 | 17.11 | 21.67 | 94.66 | |
| ZAR.EUR | 5.84 | 14.13 | 18.38 | 24.84 | 18.13 | 18.67 | 80.04 | |
| Pre-COVID | ZAR.JPY | 5.77 | 13.01 | 18.68 | 18.36 | 25.03 | 19.15 | 80.14 |
| ZAR.USD | 6.15 | 15.15 | 21.49 | 17.1 | 17.36 | 22.75 | 95.1 | |
| TO | 29.9 | 68.18 | 90.62 | 80.11 | 78.85 | 91.95 | 439.61 | |
| Inc.Own | 74.72 | 95.81 | 111.55 | 103.16 | 102.11 | 112.64 | TCI | |
| NET | 1.56 | 6.85 | −4.04 | 0.08 | −1.29 | −3.15 | 73.27 | |
| ZAR.BRL | 52.99 | 6.33 | 11.14 | 10.26 | 7.4 | 11.88 | 24.66 | |
| ZAR.BWP | 3.08 | 29.86 | 19.37 | 15.38 | 13.02 | 19.28 | 66.61 | |
| ZAR.CNY | 4.8 | 16.05 | 24.04 | 17.82 | 15.6 | 21.68 | 91.3 | |
| ZAR.EUR | 4.77 | 14.19 | 19.4 | 25.84 | 17.24 | 18.56 | 79.29 | |
| Post-COVID | ZAR.JPY | 3.79 | 13.17 | 18.38 | 18.63 | 28.15 | 17.88 | 71.1 |
| ZAR.USD | 5.18 | 16.13 | 21.85 | 17.31 | 15.36 | 24.17 | 91.16 | |
| TO | 22.11 | 67.34 | 92.12 | 81.15 | 70.14 | 91.26 | 424.11 | |
| Inc.Own | 74.62 | 95.75 | 114.17 | 105.24 | 96.77 | 113.46 | TCI | |
| NET | −2.55 | 0.73 | 0.83 | 1.86 | −0.96 | 0.1 | 70.69 | |
| ZAR.BRL | 45.49 | 9.25 | 12.13 | 10.54 | 10.31 | 12.29 | 28.34 | |
| ZAR.BWP | 5.34 | 29.15 | 17.9 | 15.31 | 14.18 | 18.12 | 61.33 | |
| ZAR.CNY | 6.14 | 15.12 | 22.96 | 17.01 | 17.11 | 21.67 | 94.66 | |
| ZAR.EUR | 5.84 | 14.13 | 18.38 | 24.84 | 18.13 | 18.67 | 80.04 | |
| Pre-COVID | ZAR.JPY | 5.77 | 13.01 | 18.68 | 18.36 | 25.03 | 19.15 | 80.14 |
| ZAR.USD | 6.15 | 15.15 | 21.49 | 17.1 | 17.36 | 22.75 | 95.1 | |
| TO | 29.9 | 68.18 | 90.62 | 80.11 | 78.85 | 91.95 | 439.61 | |
| Inc.Own | 74.72 | 95.81 | 111.55 | 103.16 | 102.11 | 112.64 | TCI | |
| NET | 1.56 | 6.85 | −4.04 | 0.08 | −1.29 | −3.15 | 73.27 | |
| ZAR.BRL | 22.54 | 14.81 | 15.81 | 15.7 | 14.96 | 16.17 | 72.88 | |
| ZAR.BWP | 12.83 | 19.74 | 17.45 | 16.58 | 15.91 | 17.49 | 89.17 | |
| ZAR.CNY | 13.15 | 16.65 | 18.7 | 17.18 | 16.24 | 18.08 | 97.29 | |
| ZAR.EUR | 13.31 | 16.18 | 17.43 | 19.01 | 16.81 | 17.27 | 93.52 | |
| Post-COVID | ZAR.JPY | 13.1 | 15.92 | 17.09 | 17.26 | 19.54 | 17.09 | 90.12 |
| ZAR.USD | 13.39 | 16.65 | 18.05 | 16.99 | 16.27 | 18.66 | 97.1 | |
| TO | 73.74 | 89.9 | 96.2 | 93.83 | 89.89 | 96.51 | 540.09 | |
| Inc.Own | 88.33 | 99.94 | 104.52 | 102.71 | 99.74 | 104.75 | TCI | |
| NET | 0.86 | 0.73 | −1.09 | 0.31 | −0.23 | −0.59 | 90.01 |
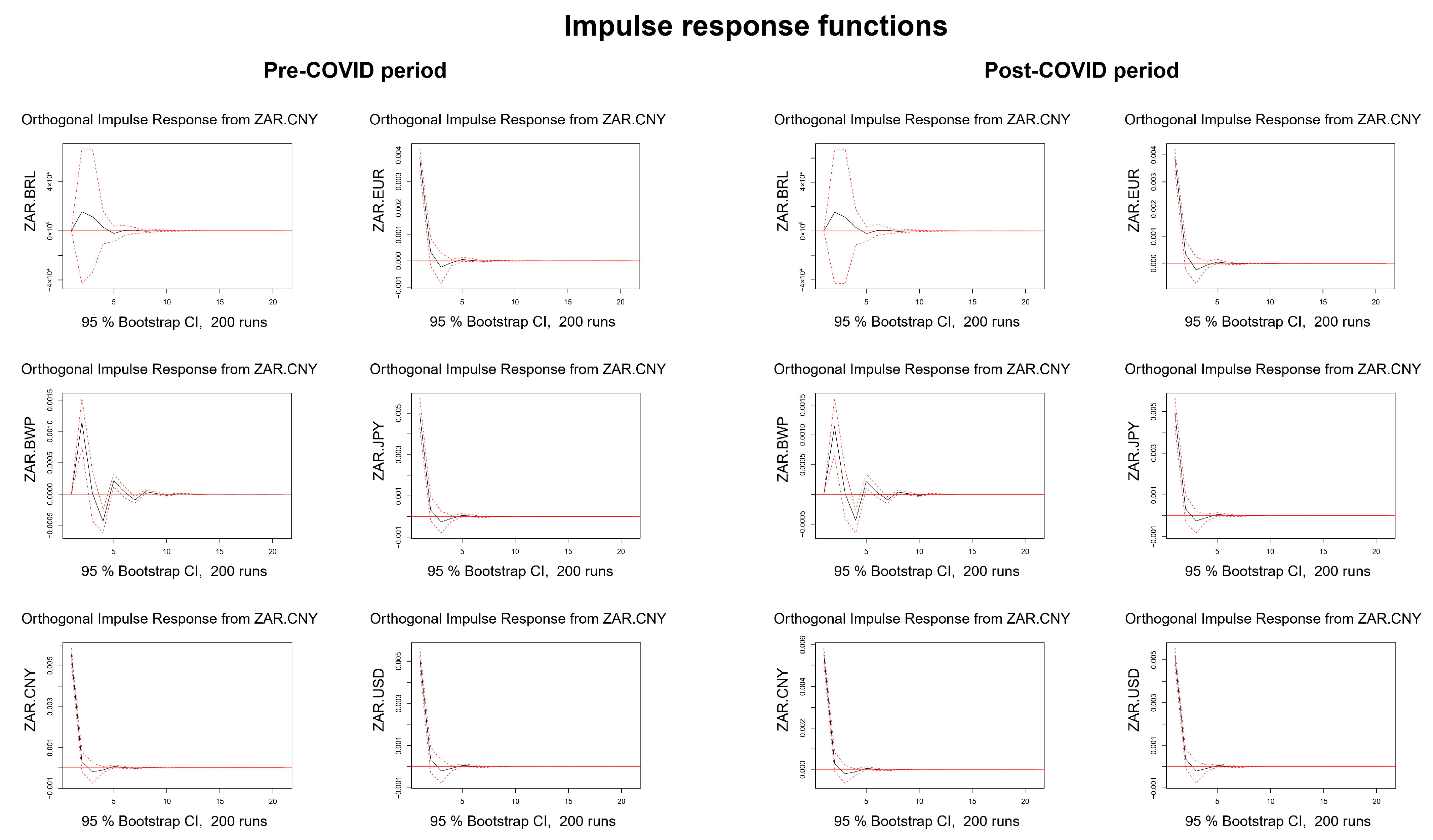
| 1 | In this study, terminologies such as stressed market conditions, distressed markets, crisis periods and turbulent market conditions have been used interchangeably to refer to market conditions characterized by increased downside risk. |
| 2 | In this study, exchange rates such as ZAR/BRL and ZAR.BRL have been used synonymously. |
References
- Adrian, T., Boyarchenko, N., & Giannone, D. (2019). Vulnerable growth. American Economic Review, 109(4), 1263–1289. [Google Scholar] [CrossRef]
- African Development Bank. (2021). African economic outlook 2021—From debt resolution to growth: The road ahead for Africa. African Development Bank. [Google Scholar]
- Aftab, M., Naeem, M., Tahir, M., & Ismail, I. (2024). Does uncertainty promote exchange rate volatility? Global evidence. Studies in Economics and Finance, 41(1), 177–191. [Google Scholar] [CrossRef]
- Aghabozorgi, S., Shirkhorshidi, A. S., & Wah, T. Y. (2015). Time-series clustering—A decade review. Information Systems, 53, 16–38. [Google Scholar] [CrossRef]
- Ando, T., Greenwood-Nimmo, M., & Shin, Y. (2022). Quantile connectedness: Modeling tail behavior in the topology of financial networks. Management Science, 68(4), 2401–2431. [Google Scholar] [CrossRef]
- Anyanwu, J. C., & Salami, A. O. (2021). The impact of COVID-19 on African economies: An introduction. African Development Review, 33, S1. [Google Scholar] [CrossRef]
- Badimo, D., & Yuhuan, Z. (2025). The effect of exchange rate (regime) on Botswana’s inbound leisure tourism demand. Environment, Development and Sustainability, 27(4), 8909–8934. [Google Scholar] [CrossRef]
- Baruník, J., & Křehlík, T. (2018). Measuring the frequency dynamics of financial connectedness and systemic risk. Journal of Financial Econometrics, 16(2), 271–296. [Google Scholar] [CrossRef]
- Bechis, L., Cerri, F., & Vulpiani, M. (2020). Machine learning portfolio optimization: Hierarchical risk parity and modern portfolio theory. LUISS Guido Carli. [Google Scholar]
- Begum, M., Masud, M. M., Alam, L., Mokhtar, M. B., & Amir, A. A. (2022). The impact of climate variables on marine fish production: An empirical evidence from Bangladesh based on autoregressive distributed lag (ARDL) approach. Environmental Science and Pollution Research, 29(58), 87923–87937. [Google Scholar] [CrossRef]
- Bekaert, G., & Harvey, C. R. (2003). Emerging markets finance. Journal of empirical finance, 10(1–2), 3–55. [Google Scholar] [CrossRef]
- Bernoth, K., & Herwartz, H. (2021). Exchange rates, foreign currency exposure and sovereign risk. Journal of International Money and Finance, 117, 102454. [Google Scholar] [CrossRef]
- Bishara, A. J., & Hittner, J. B. (2017). Confidence intervals for correlations when data are not normal. Behavior Research Methods, 49(1), 294–309. [Google Scholar] [CrossRef]
- Boakye, R. O., Mensah, L. K., Kang, S. H., & Osei, K. A. (2023). Foreign exchange market return spillovers and connectedness among African countries. International Review of Financial Analysis, 86, 102505. [Google Scholar] [CrossRef]
- Bureau for Economic Research. (2025). Economic prospects: Economic activity expected during 2025–2026. BER: Economic Prospects: Full Survey, 40(1), 1–40. [Google Scholar]
- Buthelezi, E. M. (2023). Exploring the relationship between exchange rate misalignment uncertainty and economic growth in South Africa. Cogent Economics & Finance, 11(2), 2267920. [Google Scholar] [CrossRef]
- Chang, H. W., Chang, T., & Wang, M. C. (2024). Revisit the impact of exchange rate on stock market returns during the pandemic period. The North American Journal of Economics and Finance, 70, 102068. [Google Scholar] [CrossRef]
- Chatziantoniou, I., Gabauer, D., & Stenfors, A. (2021). Interest rate swaps and the transmission mechanism of monetary policy: A quantile connectedness approach. Economics Letters, 204, 109891. [Google Scholar] [CrossRef]
- Chikwira, C., & Jahed, M. I. (2024). Analysis of exchange rate stability on the economic growth process of a developing country: The case of South Africa from 2000 to 2023. Economies, 12(11), 296. [Google Scholar] [CrossRef]
- Diebold, F. X., & Yilmaz, K. (2012). Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting, 28(1), 57–66. [Google Scholar] [CrossRef]
- Diebold, F. X., & Yilmaz, K. (2015). Financial and macroeconomic connectedness: A network approach to measurement and monitoring. Oxford University Press. [Google Scholar]
- Eichengreen, B., & Gupta, P. (2014). Tapering talk: The impact of expectations of reduced federal reserve security purchases on emerging markets (World Bank Policy Research Working Paper, No. 6754). World Bank. [Google Scholar]
- Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica, 50(4), 987–1007. [Google Scholar] [CrossRef]
- Forbes, K. J., & Warnock, F. E. (2012). Capital flow waves: Surges, stops, flight, and retrenchment. Journal of International Economics, 88(2), 235–251. [Google Scholar] [CrossRef]
- Fowkes, D., Radebe, T., & Nomdebevana, S. (2018). Crowding out: Diagnosing South Africa’s stubborn current account deficit. SARB Occasional Bulletin, 1, 27–32. [Google Scholar]
- Gabauer, D., & Gabauer, M. D. (2022). Package ‘ConnectednessApproach’ (Version 1.0.0). R package. Available online: https://CRAN.R-project.org/package=ConnectednessApproach (accessed on 11 June 2025).
- Goldstein, I., Koijen, R. S., & Mueller, H. M. (2021). COVID-19 and its impact on financial markets and the real economy. The Review of Financial Studies, 34(11), 5135–5148. [Google Scholar] [CrossRef]
- Gong, X. L., Zhao, M., Wu, Z. C., Jia, K. W., & Xiong, X. (2023). Research on tail risk contagion in international energy markets—The quantile time-frequency volatility spillover perspective. Energy Economics, 121, 106678. [Google Scholar] [CrossRef]
- Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3), 424–438. [Google Scholar] [CrossRef]
- Gudmundsson, T., Klyuev, V., Medina, L., Nandwa, B., Plotnikov, D., Schiffrer, F., & Yang, D. (2022). Emerging markets: Prospects and challenges. Journal of Policy Modeling, 44(4), 827–841. [Google Scholar] [CrossRef]
- Guijo-Rubio, D., Durán-Rosal, A. M., Gutiérrez, P. A., Troncoso, A., & Hervás-Martínez, C. (2018). Time series clustering based on the characterisation of segment typologies. arXiv, arXiv:1810.11624. [Google Scholar] [CrossRef]
- Gunjan, A., & Bhattacharyya, S. (2023). A brief review of portfolio optimization techniques. Artificial Intelligence Review, 56(5), 3847–3886. [Google Scholar] [CrossRef]
- Hartono, P. G., Robiyanto, R., Tinungki, G. M., Frensidy, B., Raya, M. Y., & Hidarto, A. (2024). Revisiting dividend policy and stock market reaction of Indonesian manufacturing enterprises amidst the COVID-19 crisis: A series of robustness checks. Scientific Papers of the University of Pardubice. Series D, Faculty of Economics & Administration, 32(1), 1–22. [Google Scholar]
- Huang, Z., & Zhang, W. (2024). Exploring the spillover effects of tail risk fluctuations in the RMB exchange rate—The time-frequency and quantile connectivity perspective. Research in International Business and Finance, 72, 102534. [Google Scholar] [CrossRef]
- IMF. (2020a). African dept, South Africa: Selected issues. IMF staff country reports, 2020(034), A002. Available online: https://www.elibrary.imf.org/view/journals/002/2020/034/article-A002-en.xml (accessed on 10 May 2025).
- IMF. (2020b). Toward an integrated policy framework. IMF policy paper. Available online: https://www.imf.org/en/Publications/Policy-Papers/Issues/2020/10/08/Toward-an-Integrated-Policy-Framework-49813 (accessed on 11 June 2025).
- IMF. (2023). South Africa. IMF staff country reports, 2023(194). Available online: https://www.elibrary.imf.org/view/journals/002/2023/194/article-A001-en.xml (accessed on 11 June 2025).
- Irfani, M. I., & Sudrajad, O. Y. (2023). Portfolio optimization using Markowitz model on Sri-Kehati index. International Journal of Current Science Research and Review, 6(8), 5778–5792. [Google Scholar] [CrossRef]
- Iyke, B. N., & Ho, S. Y. (2021). Exchange rate exposure in the South African stock market before and during the COVID-19 pandemic. Finance Research Letters, 43, 102000. [Google Scholar] [CrossRef]
- Jena, S. K., Tiwari, A. K., Abakah, E. J. A., & Hammoudeh, S. (2022). The connectedness in the world petroleum futures markets using a Quantile VAR approach. Journal of Commodity Markets, 27, 100222. [Google Scholar] [CrossRef]
- Khalfaoui, R., Hammoudeh, S., & Rehman, M. Z. (2023). Spillovers and connectedness among BRICS stock markets, cryptocurrencies, and uncertainty: Evidence from the quantile vector autoregression network. Emerging Markets Review, 54, 101002. [Google Scholar] [CrossRef]
- Koenker, R., & Xiao, Z. (2006). Quantile autoregression. Journal of the American Statistical Association, 101(475), 980–990. [Google Scholar] [CrossRef]
- Koop, G., Pesaran, M. H., & Potter, S. M. (1996). Impulse response analysis in nonlinear multivariate models. Journal of Econometrics, 74(1), 119–147. [Google Scholar] [CrossRef]
- Kyriazis, N., & Corbet, S. (2024). The role of international currency spillovers in shaping exchange rate dynamics in Latin America. The Quarterly Review of Economics and Finance, 94, 1–10. [Google Scholar] [CrossRef]
- Li, Y. Z., Yu, Y. H., Gao, W. S., Ray, S., & Dong, W. T. (2022). The impact of COVID-19 on UK and world financial markets. Jundishapur Journal of Microbiology, 15(1), 373–399. [Google Scholar]
- Liu, Y., Zhang, Y. A., Zeng, M., & Zhao, J. (2024). A novel distance measure based on dynamic time warping to improve time series classification. Information Sciences, 656, 119921. [Google Scholar] [CrossRef]
- Lütkepohl, H. (2005). New introduction to multiple time series analysis. Springer. [Google Scholar]
- Lütkepohl, H. (2013). Vector autoregressive models. In Handbook of research methods and applications in empirical macroeconomics (pp. 139–164). Edward Elgar Publishing. [Google Scholar]
- Maillard, S., Roncalli, T., & Teïletche, J. (2010). The properties of equally weighted risk contribution portfolios. Journal of Portfolio Management, 36(4), 60. [Google Scholar] [CrossRef]
- Maveé, N., Perrelli, R., & Schimmelpfennig, A. (2016). Surprise, surprise: What drives the rand/U.S. dollar exchange rate volatility? IMF Working Papers, 2016(205), A001. Available online: https://www.elibrary.imf.org/view/journals/001/2016/205/article-A001-en.xml (accessed on 10 June 2025).
- May, C., & Farrell, G. (2018). Modelling exchange rate volatility dynamics: Empirical evidence from South Africa. Studies in Economics and Econometrics, 42(3), 71–113. [Google Scholar] [CrossRef]
- McCloud, N., Delgado, M. S., & Jin, M. (2024). Foreign capital inflows, exchange rates, and government stability. Empirical Economics, 66(3), 945–977. [Google Scholar] [CrossRef]
- Merem, E. C., Twumasi, Y. A., Wesley, J., Olagbegi, D., Crisler, M., Romorno, C., Alsarari, M., Isokpehi, P., Alfarei, M., Ochai, G. S., & Nwagboso, E. (2021). The assessment of China’s scramble for natural resources extraction in Africa. World Environment, 11(1), 9–25. [Google Scholar] [CrossRef]
- Monamodi, N. E. (2024). The impact of current account balance on economic growth in South Africa. Economies, 12(2), 39. [Google Scholar] [CrossRef]
- Mpofu, T. R. (2021). The determinants of real exchange rate volatility in South Africa. The World Economy, 44(5), 1380–1401. [Google Scholar] [CrossRef]
- Ngondo, M., & Khobai, H. (2018). The impact of exchange rate on exports in South Africa. MPRA paper. Available online: https://mpra.ub.uni-muenchen.de/85079/ (accessed on 11 June 2025).
- Özdemir, H. (2024). Volatility spillover in the Turkish financial market: A QVAR analysis. İşletme Araştırmaları Dergisi, 16(1), 392–406. [Google Scholar] [CrossRef]
- Pav, S. E. (2021). The Sharpe ratio: Statistics and applications. Chapman and Hall/CRC. [Google Scholar]
- Pesaran, H. H., & Shin, Y. (1998). Generalized impulse response analysis in linear multivariate models. Economics Letters, 58(1), 17–29. [Google Scholar] [CrossRef]
- Pfaff, B., & Stigler, M. (2024). ‘VAR modelling’ in Package ‘vars’. CRAN, Version 1.6-1. Available online: https://cran.r-project.org/web/packages/vars/index.html (accessed on 11 June 2025).
- Pinto, S. P. (2020). Mining sector industry in Southern Africa. Иннoвации и инвестиции, 1, 75–79. [Google Scholar]
- Prasad, S. (2023). Measures of central tendencies. In Elementary statistical methods (pp. 37–96). Springer Nature Singapore. [Google Scholar]
- Rai, K., & Garg, B. (2022). Dynamic correlations and volatility spillovers between stock price and exchange rate in BRIICS economies: Evidence from the COVID-19 outbreak period. Applied Economics Letters, 29(8), 738–745. [Google Scholar] [CrossRef]
- Rakshit, B., & Neog, Y. (2022). Effects of the COVID-19 pandemic on stock market returns and volatilities: Evidence from selected emerging economies. Studies in Economics and Finance, 39(4), 549–571. [Google Scholar] [CrossRef]
- Rehman, M. Z., Tiwari, A. K., & Samontaray, D. P. (2022). Directional predictability in foreign exchange rates of emerging markets: New evidence using a cross-quantilogram approach. Borsa Istanbul Review, 22(1), 145–155. [Google Scholar] [CrossRef]
- Reinholtz, N., Fernbach, P. M., & De Langhe, B. (2021). Do people understand the benefit of diversification? Management Science, 67(12), 7322–7343. [Google Scholar] [CrossRef]
- Rey, H. (2013). Dilemma not trilemma: The global financial cycle and monetary policy independence. National Bureau of Economic Research. [Google Scholar]
- Roncalli, T. (2013). Introduction to risk parity and budgeting. CRC Press. [Google Scholar]
- Sarasa-Cabezuelo, A. (2023). Development of a backtesting web application for the definition of investment strategies. Knowledge, 3(3), 414–431. [Google Scholar] [CrossRef]
- Shabani, M., Ghanbari, H., & Mohammadi, E. (2024). Developing a new equally weighted portfolio strategy using different risk measures: An empirical evidence from S&P 500 index. Financial and Banking Strategic Studies, 2(1), 1–10. [Google Scholar]
- Sims, C. A. (1980). Macroeconomics and reality. Econometrica: Journal of the Econometric Society, 48(1), 1–48. [Google Scholar]
- South African Reserve Bank (SARB). (2020, April). Monetary policy review. Available online: https://www.resbank.co.za/content/dam/sarb/publications/reviews/monetary-policy-review/2020/9839/Monetary-Policy-Review---April-2020.pdf (accessed on 10 June 2025).
- South African Reserve Bank (SARB). (2023). Quarterly bulletin No. 308. Available online: https://www.resbank.co.za/en/home/publications/publication-detail-pages/quarterly-bulletins/quarterly-bulletin-publications/2023/FullQuarterlyBulletinNo308June2023?utm_source=chatgpt.com (accessed on 12 June 2025).
- South African Reserve Bank (SARB). (2024, April). South African reserve bank monetary policy review. Available online: https://www.resbank.co.za/content/dam/sarb/publications/monetary-policy-review/2024/Monetary%20Policy%20Review%20April%202024.pdf (accessed on 10 June 2025).
- Suris, F. N. A., Bakar, M. A. A., Ariff, N. M., Mohd Nadzir, M. S., & Ibrahim, K. (2022). Malaysia PM10 air quality time series clustering based on dynamic time warping. Atmosphere, 13(4), 503. [Google Scholar] [CrossRef]
- Surtee, T. G., & Alagidede, I. P. (2023). A novel approach to using modern portfolio theory. Borsa Istanbul Review, 23(3), 527–540. [Google Scholar] [CrossRef]
- Škrinjarić, T., Lovretin Golubić, Z., & Orlović, Z. (2020). Empirical analysis of dynamic spillovers between exchange rate return, return volatility and investor sentiment. Studies in Economics and Finance, 38(1), 86–113. [Google Scholar] [CrossRef]
- Taskinsoy, J. (2022). Stress testing financial systems: Macro and micro stress tests, Basel standards and value-at-risk as financial stability measures. Available online: https://ssrn.com/abstract=4032869 (accessed on 10 May 2025).
- Tsay, R. S. (2010). Analysis of financial time series (3rd ed.). Wiley. [Google Scholar]
- White, H., Kim, T. H., & Manganelli, S. (2015). VAR for VaR: Measuring tail dependence using multivariate regression quantiles. Journal of Econometrics, 187(1), 169–188. [Google Scholar] [CrossRef]
- Yeboah, M., & Takacs, A. (2019). Does exchange rate matter in profitability of listed companies in South Africa? An empirical approach. International Journal of Energy Economics and Policy, 9(6), 171–178. [Google Scholar] [CrossRef]
- Zaimovic, A., Omanovic, A., & Arnaut-Berilo, A. (2021). How many stocks are sufficient for equity portfolio diversification? A review of the literature. Journal of Risk and Financial Management, 14(11), 551. [Google Scholar] [CrossRef]
- Zhang, Q., & Wei, R. (2024). Carbon reduction attention and financial market stress: A network spillover analysis based on quantile VAR modeling. Journal of Environmental Management, 356, 120640. [Google Scholar] [CrossRef]

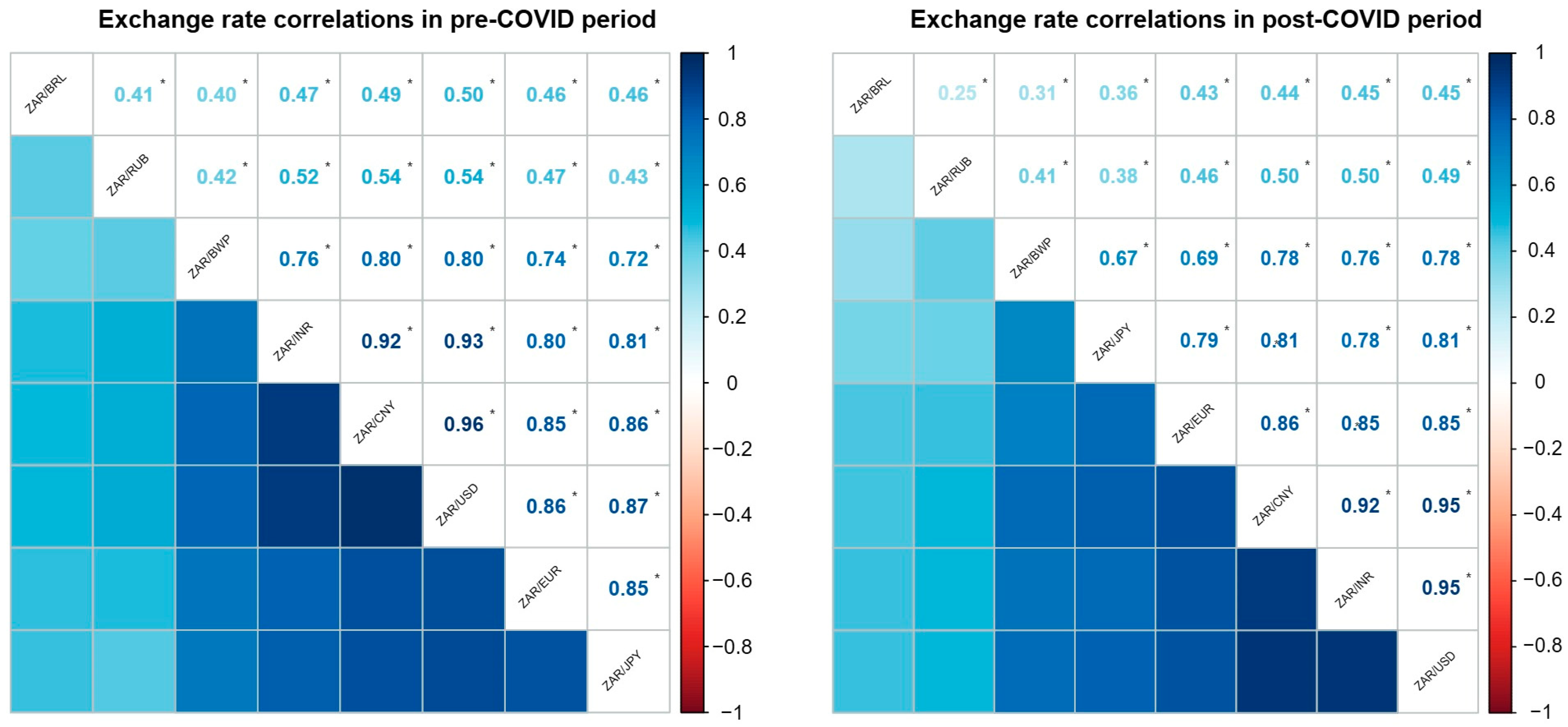
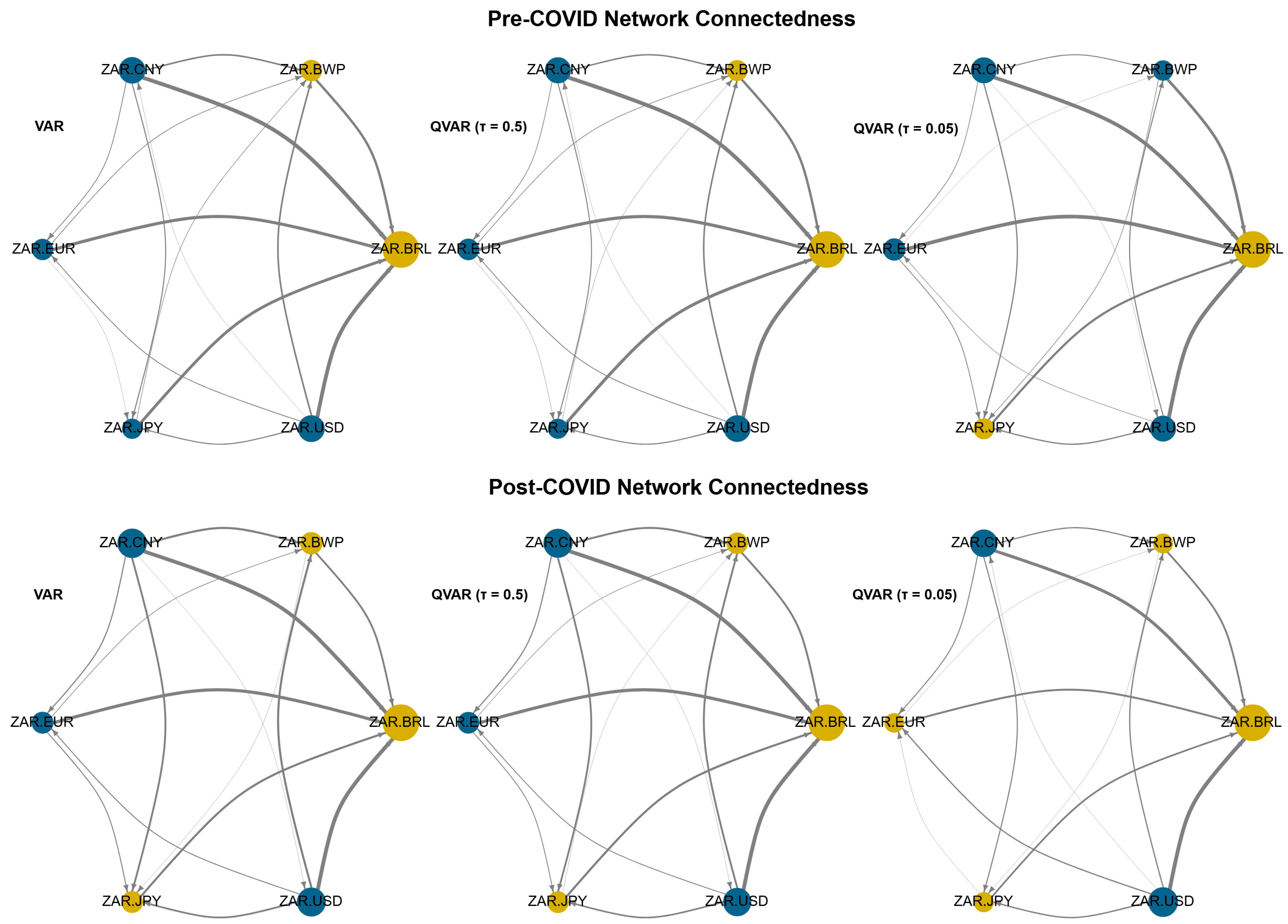
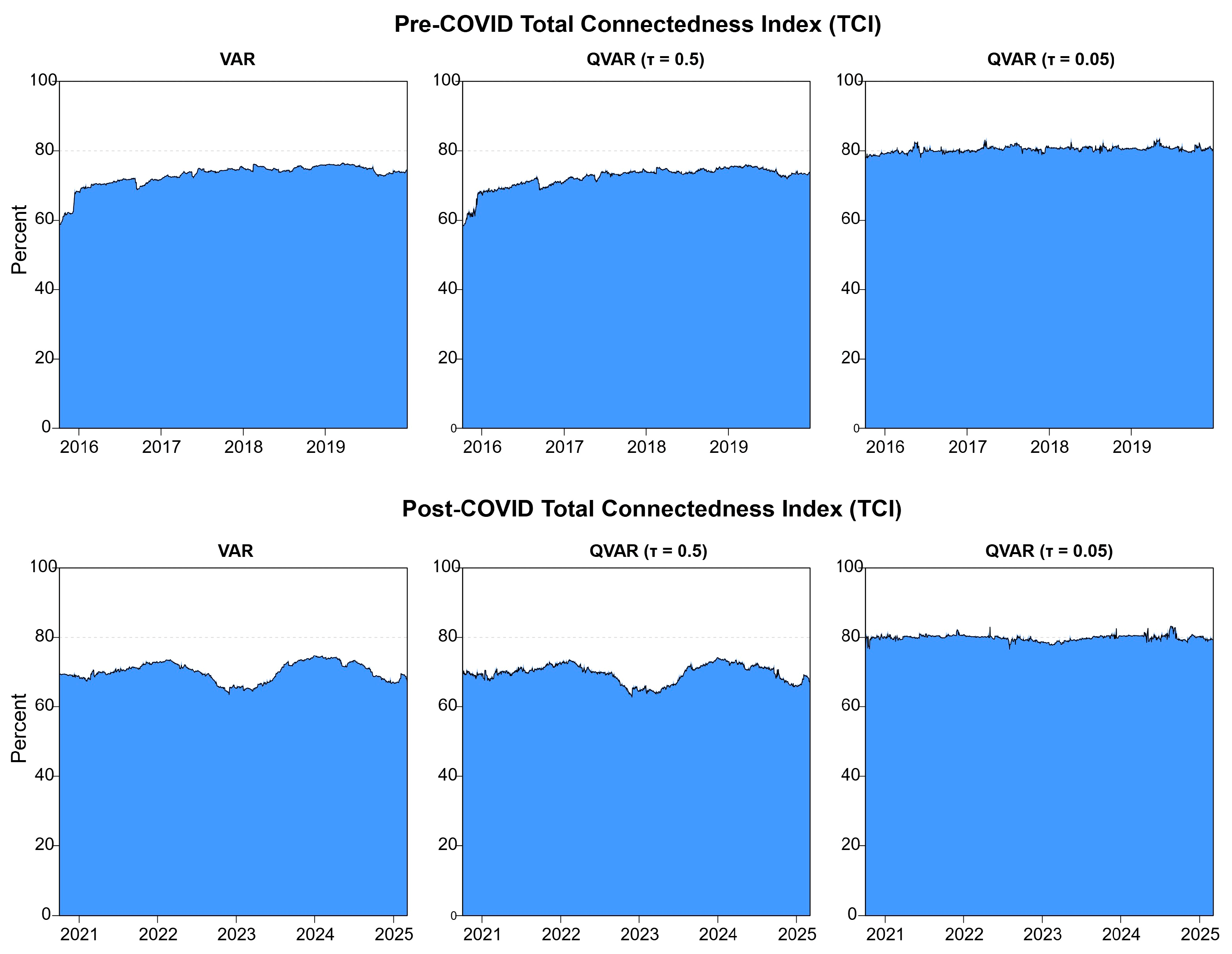




| Pre-COVID Period | ||||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Variance | Stdev | Skewness | Kurtosis | JB | ADF | LB | |
| ZAR.BRL | −0.0002 | 0.0001 | 0.0107 | 0.2550 | 2.3507 | 316.01 *** | −12.25 *** | 3.14 |
| ZAR.RUB | 0.0001 | 0.0001 | 0.0110 | −0.0952 | 2.9047 | 462.56 *** | −11.08 *** | 6.71 ** |
| ZAR.INR | 0.0000 | 0.0001 | 0.0095 | 0.1678 | 1.3869 | 111.50 *** | −11.84 *** | 0.67 |
| ZAR.CNY | 0.0000 | 0.0001 | 0.0099 | 0.1790 | 1.2221 | 88.86 *** | −12.05 *** | 1.29 |
| ZAR.EUR | 0.0001 | 0.0001 | 0.0099 | 0.2344 | 1.4165 | 121.85 *** | −11.39 *** | 2.84 |
| ZAR.JPY | 0.0002 | 0.0001 | 0.0111 | 0.4887 | 3.2923 | 643.43 *** | −11.68 *** | 0.37 |
| ZAR.USD | 0.0001 | 0.0001 | 0.0103 | 0.1907 | 1.2352 | 91.55 *** | −11.79 *** | 1.757 |
| ZAR.BWP | 0.0001 | 0.0001 | 0.0084 | 0.2683 | 2.1955 | 279.06 *** | −11.70 *** | 102.72 *** |
| Post-COVID Period | ||||||||
| ZAR.BRL | −0.0001 | 0.0001 | 0.0102 | −0.0065 | 0.7265 | 30.17 *** | −10.78 *** | 6.28 ** |
| ZAR.RUB | 0.0001 | 0.0004 | 0.0191 | −0.9900 | 21.6835 | 26,777 *** | −10.97 *** | 1.20 |
| ZAR.INR | 0.0001 | 0.0001 | 0.0085 | 0.3880 | 0.5812 | 53.34 *** | −10.72 *** | 1.54 |
| ZAR.CNY | 0.0002 | 0.0001 | 0.0086 | 0.3879 | 0.7491 | 66.02 *** | −10.61 *** | 4.06 |
| ZAR.EUR | 0.0002 | 0.0001 | 0.0082 | 0.6080 | 1.8775 | 283.38 *** | −10.42 *** | 5.29 * |
| ZAR.JPY | 0.0000 | 0.0001 | 0.0098 | 0.4492 | 2.7003 | 458.56 *** | −10.24 *** | 13.06 *** |
| ZAR.USD | 0.0002 | 0.0001 | 0.0091 | 0.2957 | 0.5955 | 40.06 *** | −10.10 *** | 1.23 |
| ZAR.BWP | 0.0000 | 0.0001 | 0.0074 | 0.2037 | 2.3254 | 315.83 *** | −11.43 *** | 105.78 *** |
| ZAR.BRL | ZAR.BWP | ZAR.CNY | ZAR.EUR | ZAR.INR | ZAR.JPY | ZAR.RUB | ZAR.USD | |
|---|---|---|---|---|---|---|---|---|
| ZAR.BRL | 0 | 4123.901 | 1019.624 | 37,280.62 | 7211.677 | 7434.839 | 7201.23 | 32,204.98 |
| ZAR.BWP | 5865.323 | 0 | 2375.65 | 42,639.27 | 2935.374 | 3161.105 | 2882.671 | 37,323.13 |
| ZAR.CNY | 3645.424 | 1497.752 | 0 | 39,505.97 | 5452.497 | 5682.827 | 5452.394 | 34,244.55 |
| ZAR.EUR | 26,752.26 | 33,250.56 | 31,291.1 | 0 | 45,811.71 | 46,032.4 | 45,777.19 | 952.4681 |
| ZAR.INR | 8822.11 | 2701.881 | 4475.34 | 36,148.07 | 0 | 151.8675 | 16.8235 | 40,442.37 |
| ZAR.JPY | 9046.757 | 2902.233 | 4690.733 | 36,343.62 | 148.3122 | 0 | 102.4296 | 40,663.56 |
| ZAR.RUB | 8795.101 | 2654.06 | 4440.329 | 36,092.31 | 10.7515 | 159.6142 | 0 | 40,435.68 |
| ZAR.USD | 22,183.47 | 29,035.06 | 27,020.84 | 1058.964 | 31,955.52 | 32,154.39 | 31,903.32 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ntare, H.B.; Muteba Mwamba, J.W.; Adekambi, F. Asymmetric Volatility Spillovers in Varying Market Conditions and Portfolio Performance Analysis of the South African Foreign Exchange Market. Economies 2025, 13, 232. https://doi.org/10.3390/economies13080232
Ntare HB, Muteba Mwamba JW, Adekambi F. Asymmetric Volatility Spillovers in Varying Market Conditions and Portfolio Performance Analysis of the South African Foreign Exchange Market. Economies. 2025; 13(8):232. https://doi.org/10.3390/economies13080232
Chicago/Turabian StyleNtare, Hamdan Bukenya, John Weirstrass Muteba Mwamba, and Franck Adekambi. 2025. "Asymmetric Volatility Spillovers in Varying Market Conditions and Portfolio Performance Analysis of the South African Foreign Exchange Market" Economies 13, no. 8: 232. https://doi.org/10.3390/economies13080232
APA StyleNtare, H. B., Muteba Mwamba, J. W., & Adekambi, F. (2025). Asymmetric Volatility Spillovers in Varying Market Conditions and Portfolio Performance Analysis of the South African Foreign Exchange Market. Economies, 13(8), 232. https://doi.org/10.3390/economies13080232






