Steadying the Ship: Can Export Proceeds Repatriation Policy Stabilize Indonesian Exchange Rates Amid Short-Term Capital Flow Fluctuations?
Abstract
1. Introduction
2. Literature Review
3. Data and Empirical Methodology
3.1. Data
3.2. TVP-VAR for Exchange Rate Volatility and Repatriated Export Proceeds
3.3. Stochastic Volatility with Mixture Sampling
4. Empirical Results and Analysis
4.1. Exchange Rate Volatilities
4.2. Estimation Results
4.3. Standard Deviation of Residuals
4.4. Forecast Error Variance Decomposition
4.5. Impulse Response Functions
5. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOAJ | Directory of open access journals |
| TVP-VAR | Time-varying parameter vector autoregression |
| IDR | Indonesian rupiah |
| IRD | Interest rate differential |
| IMF | International Monetary Fund |
| IV | Institutional View |
| IDX | Indonesian Stock Exchange |
| TV | Net trading volume of foreign exchange transaction |
| STCF | Short-term capital flows |
| EP | Repatriated export proceeds |
| ERV | Exchange rate volatility |
| OLS | Ordinary least square |
| MCMC | Markov Chain Monte Carlo |
| SML | Simulated maximum likelihood |
| GCD | Geweke Convergence Diagnostics |
Appendix A. Derivation of the Covariance Matrix V
Appendix B. Selection of the Mixing for Approximating the Distribution
| Component | |||
| 1 | 0.00730 | −10.12999 | 5.79596 |
| 2 | 0.10556 | −3.97281 | 2.61369 |
| 3 | 0.00002 | −8.56686 | 5.17950 |
| 4 | 0.04395 | 2.77786 | 0.16735 |
| 5 | 0.34001 | 0.61942 | 0.64009 |
| 6 | 0.24566 | 1.79518 | 0.34023 |
| 7 | 0.25750 | −1.08819 | 1.26261 |
Appendix C. Gibbs Sampler Algorithm
- 1.
- Initialize and .
- 2.
- Sample h from .
- 3.
- Sample s from .
- 4.
- Sample , from .
- 5.
- Sample from .
- 6.
- Sample from .
- 7.
- Go to 2.
Appendix D. The Algorithm to Obtain Posterior Draws of TVP-VAR Parameters
- 1.
- Initialize and s.
- 2.
- Draw from .
- 3.
- Draw from .
- 4.
- Draw from .
- 5.
- Go to 2.
Appendix E. The Impulse Response Functions of Crisis vs. Calm Periods in Longer Horizon


Appendix F. Robustness Tests Figures
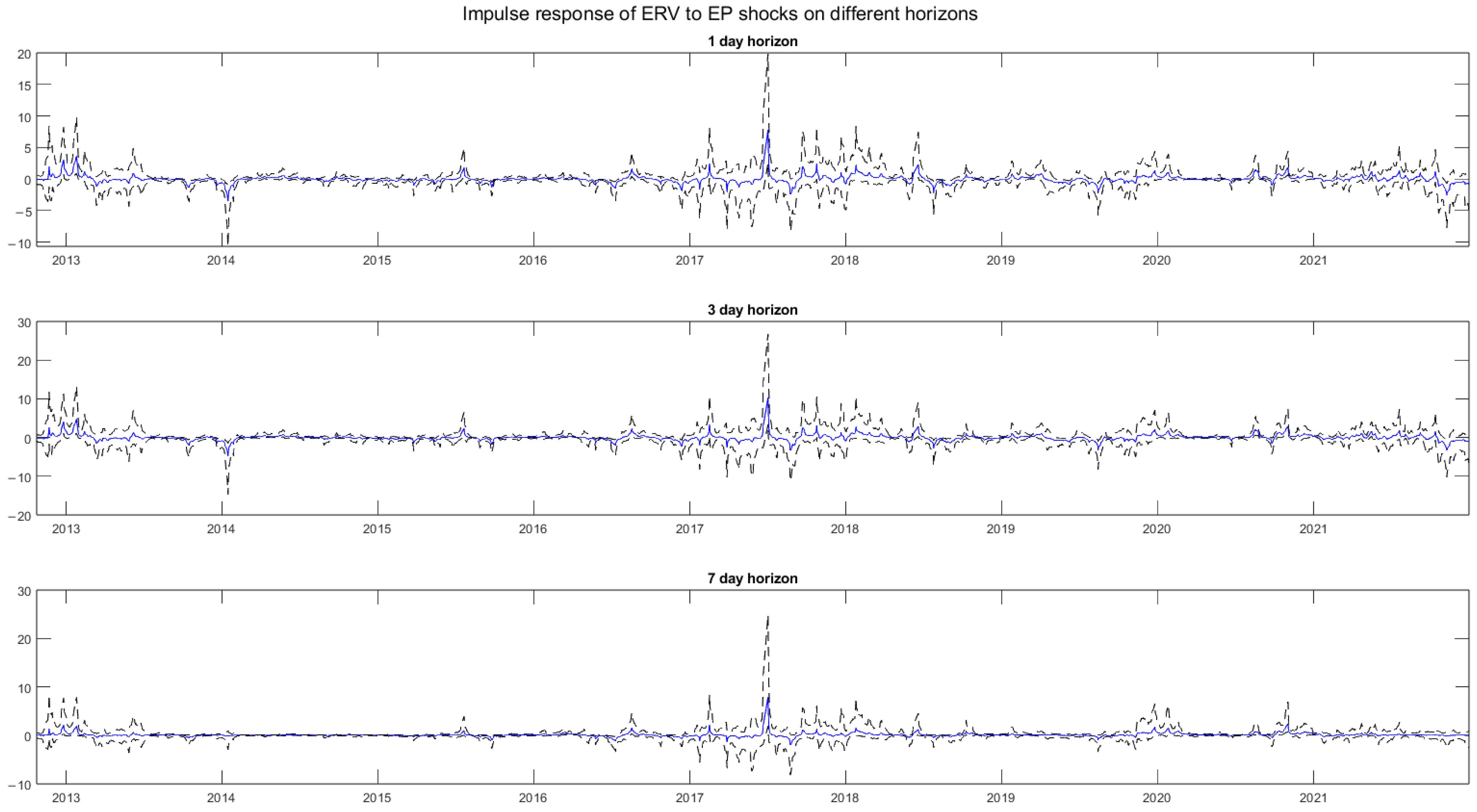
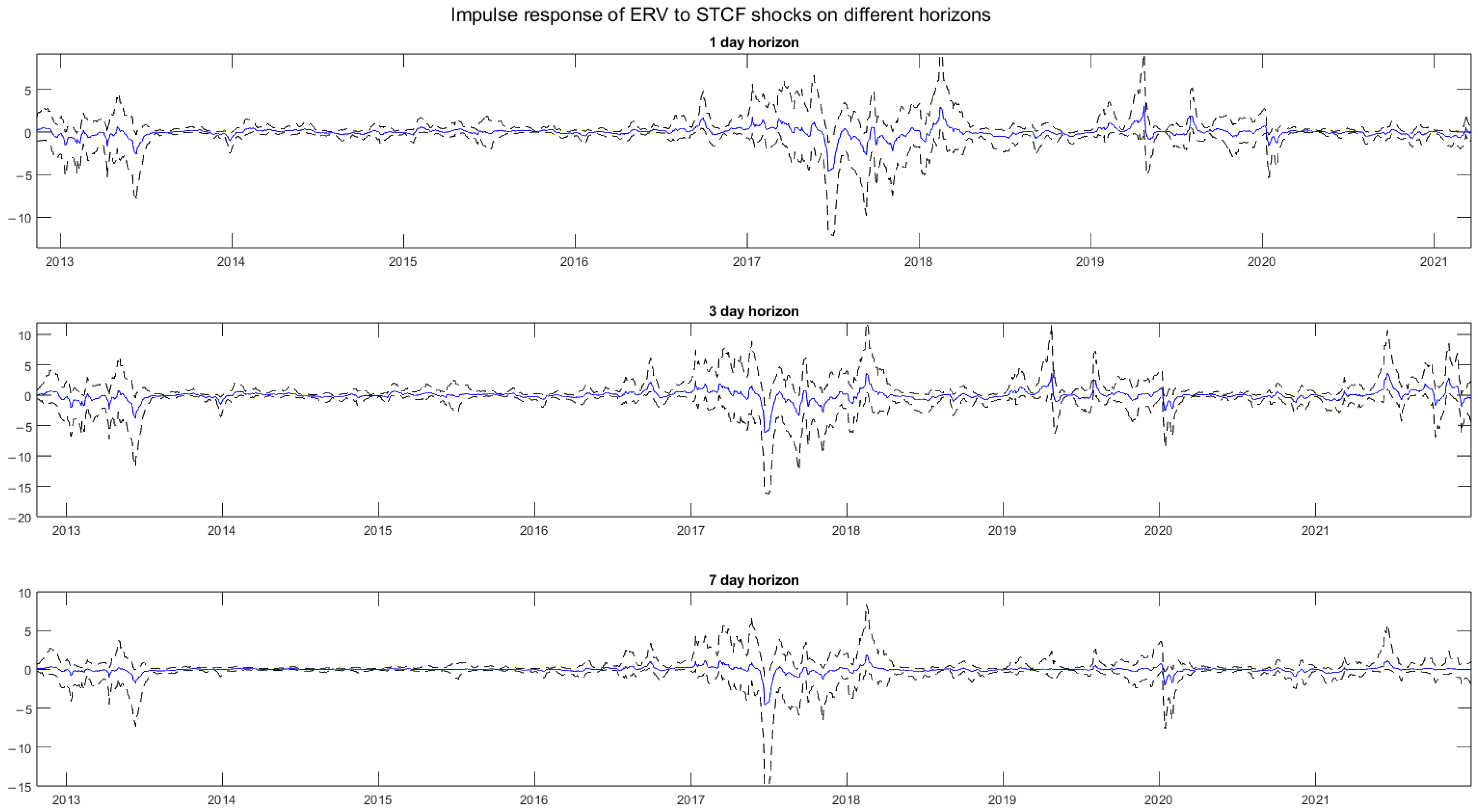

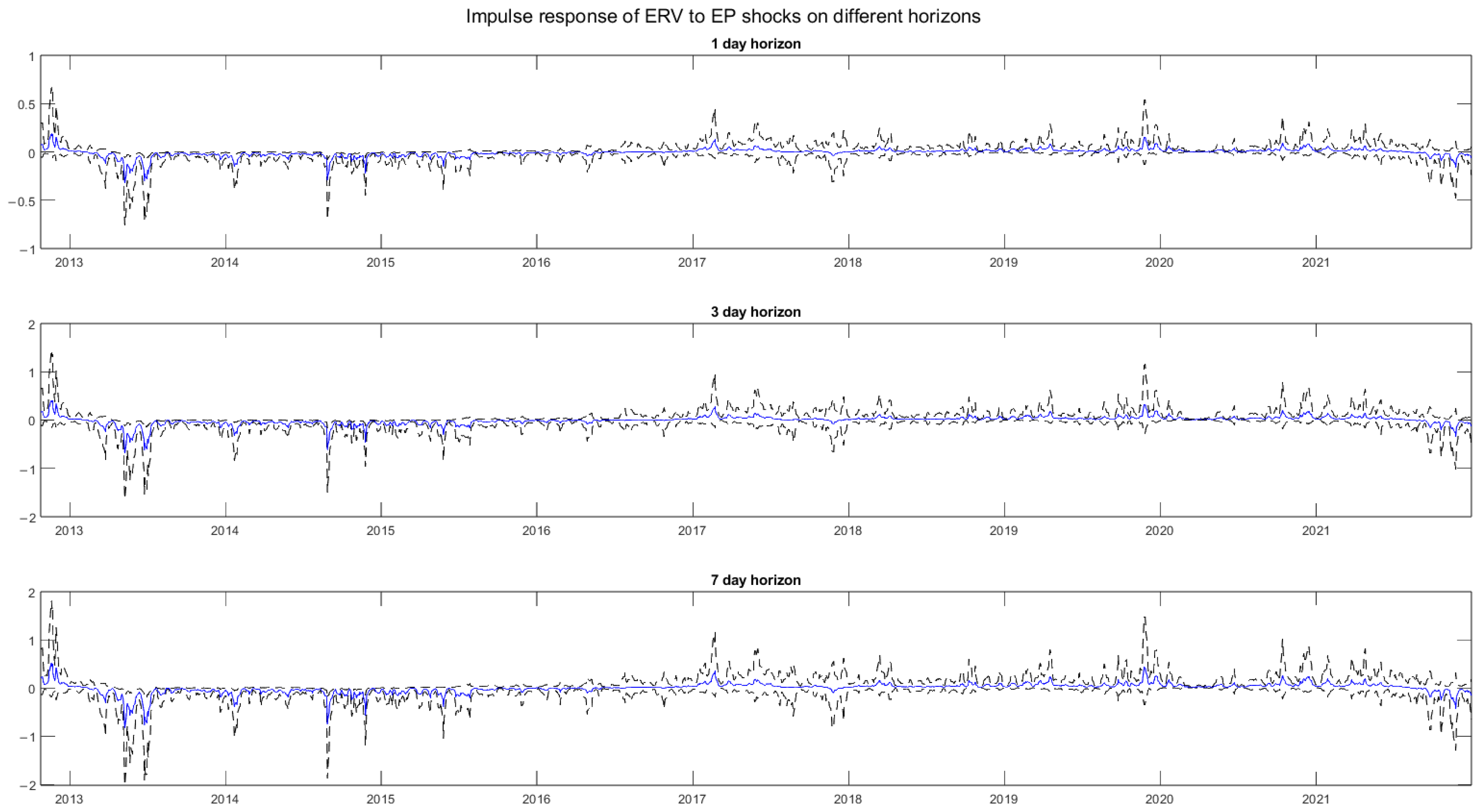


Appendix G. Types of Implementation of Export Proceeds Policy
| With Surrender and Conversion | With Surrender Only | No Other Obligations |
| 32 | 23 | 28 |
| 1 | In general, there are three types of repatriation policy: (i) repatriation with a time-limited surrender obligation to appointed parties and mandatory conversion to the local currency, (ii) repatriation with a time-limited surrender obligation to appointed parties without mandatory conversion to local currency, (iii) repatriation without any other obligations. Repatriation policy in Indonesia falls into the third category. The summary of the number of country that falls into each category is summarized in Appendix G. |
| 2 | Data source from The Annual Report on Exchange Arrangements and Exchange Restrictions by the IMF. |
References
- Aghion, P., Bacchetta, P., Rancière, R., & Rogoff, K. (2009). Exchange rate volatility and productivity growth: The role of financial development. Journal of Monetary Economics, 56(4), 494–513. [Google Scholar] [CrossRef]
- Alanya, W., & Rodríguez, G. (2018). Stochastic volatility in the Peruvian stock market and exchange rate returns: A bayesian approximation. Journal of Emerging Market Finance, 17(3), 354–385. [Google Scholar] [CrossRef]
- Asiedu, E., & Lien, D. (2004). Capital controls and foreign direct investment. World Development, 32, 479–490. [Google Scholar] [CrossRef]
- Aysun, U. (2024). Identifying the external and internal drivers of exchange rate volatility in small open economies. Emerging Markets Review, 58, 101085. [Google Scholar] [CrossRef]
- Baum, C. F., & Caglayan, M. (2010). On the sensitivity of the volume and volatility of bilateral trade flows to exchange rate uncertainty. Journal of International Money and Finance, 29(1), 79–93. [Google Scholar] [CrossRef]
- Bush, G., & López Noria, G. (2021). Uncertainty and exchange rate volatility: Evidence from Mexico. International Review of Economics and Finance, 75, 704–722. [Google Scholar] [CrossRef]
- Caporale, G. M., Ali, F. M., Spagnolo, F., & Spagnolo, N. (2017). International portfolio flows and exchange rate volatility in emerging Asian markets. Journal of International Money and Finance, 76, 1–15. [Google Scholar] [CrossRef]
- Carnero, M. A., Pena, D., & Ruiz, E. (2004). Persistence and kurtosis in GARCH and stochastic volatility models. Journal of Financial Econometrics, 2(2), 319–342. [Google Scholar] [CrossRef]
- Chan, J., Koop, G., Poirier, D. J., & Tobias, J. L. (2019). Time series models for volatility. In Bayesian econometric methods (pp. 391–410). Cambridge University Press. [Google Scholar] [CrossRef]
- Choudhri, E. U., & Hakura, D. S. (2006). Exchange rate pass-through to domestic prices: Does the inflationary environment matter? Journal of International Money and Finance, 25(4), 614–639. [Google Scholar] [CrossRef]
- Clarida, R., & Gali, J. (1994). Sources of real exchange-rate fluctuations: How important are nominal shocks? Carnegie-Rochester Confer. Series on Public Policy, 41, 1–56. [Google Scholar] [CrossRef]
- Daníelsson, J. (1998). Multivariate stochastic volatility models: Estimation and a comparison with VGARCH models. Journal of Empirical Finance, 5(2), 155–173. [Google Scholar] [CrossRef]
- De, K., & Sun, W. (2020). Is the exchange rate a shock absorber or a source of shocks? Evidence from the U.S. Economic Modelling, 89, 1–9. [Google Scholar] [CrossRef]
- Devereux, M. B., & Engel, C. (2002). Exchange rate pass-through, exchange rate volatility, and exchange rate disconnect. Journal of Monetary Economics, 49, 913–940. [Google Scholar] [CrossRef]
- Dominguez, K. M., & Frankel, J. A. (1993). Does foreign-exchange intervention matter? The portfolio effect. American Economic Review, 83(5), 1356–1369. [Google Scholar]
- Eichenbaum, M., & Evans, C. L. (1995). Some empirical evidence on the effects of shocks to monetary policy on exchange rates. The Quarterly Journal of Economics, 110(4), 975–1009. [Google Scholar] [CrossRef]
- Enders, W. (2015). Applied econometrics time series (4th ed., Vol. 19). John Wiley and Sons, Inc. [Google Scholar]
- Feldmann, H. (2011). The unemployment effect of exchange rate volatility in industrial countries. Economics Letters, 111(3), 268–271. [Google Scholar] [CrossRef]
- Flood, R. P., & Rose, A. K. (1999). Understanding exchange rate volatility without the contrivance of macroeconomics. The Economic Journal, 109(459), F660–F672. [Google Scholar] [CrossRef]
- Fuller, W. A. (1996). Introduction to statistical time series: Second edition. John Wiley and Sons, Incorporated. [Google Scholar] [CrossRef]
- Gabaix, X., & Maggiori, M. (2015). International liquidity and exchange rate dynamics. The Quarterly Journal of Economics, 130(3), 1369–1420. [Google Scholar] [CrossRef]
- Geweke, J. (1992). Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments. In J. M. Bernardo, J. Berger, P. Dawid, & A. F. M. Smith (Eds.), Bayesian statistics 4: Proceedings of the fourth Valencia international meeting, dedicated to the memory of Morris H. DeGroot, 1931–1989 (pp. 169–193). Oxford University Press. [Google Scholar] [CrossRef]
- Grier, R., & Grier, K. B. (2006). On the real effects of inflation and inflation uncertainty in Mexico. Journal of Development Economics, 80(2), 478–500. [Google Scholar] [CrossRef]
- Grossmann, A., & Orlov, A. G. (2014). A panel-regression investigation of exchange rate volatility. International Journal of Finance and Economics, 326, 303–326. [Google Scholar] [CrossRef]
- Guillaumont, P. (1980). The impact of declining terms of trade and inflation on the export proceeds and debt burden of developing countries. World Development, 8, 763–768. [Google Scholar] [CrossRef]
- Hafner, C. M., & Preminger, A. (2010). Deciding between GARCH and stochastic volatility via strong decision rules. Journal of Statistical Planning and Inference, 140(3), 791–805. [Google Scholar] [CrossRef]
- Jacquier, E., Polson, N. G., & Rossi, P. E. (1994). Bayesian analysis of stochastic volatility models. Journal of Business and Economic Statistics, 12(4), 69–87. [Google Scholar] [CrossRef]
- Kim, S., Shephard, N., & Chib, S. (1998). Stochastic volatility: Likelihood inference and comparison with ARCH models. Review of Economic Studies, 65(3), 361–393. [Google Scholar] [CrossRef]
- Krol, R. (2014). Economic policy uncertainty and exchange rate volatility. International Finance, 17(2), 241–256. [Google Scholar] [CrossRef]
- Lane, P. R. (2001). The new open economy macroeconomics: A survey. Journal of International Economics, 54(2), 235–266. [Google Scholar] [CrossRef]
- Lee-Lee, C., & Hui-Boon, T. (2007). Macroeconomic factors of exchange rate volatility: Evidence from four neighbouring ASEAN economies. Studies in Economics and Finance, 24(4), 266–285. [Google Scholar] [CrossRef]
- Macbean, A. I. (1962). Causes of excessive fluctuations in export proceeds of underdeveloped countries. Bulletin of the Oxford University Institute of Economics & Statistics, 27, 323–341. [Google Scholar] [CrossRef]
- Massell, B. F. (1964). Export concentration and fluctuations in export earnings: A cross-section analysis. The American Economic Review, 54, 47–63. [Google Scholar]
- Meese, R., & Rogoff, K. S. (1983). Empirical exchange rate models of the seventies: Do they fit out of sample? Journal of International Economics, 14(1–2), 3–24. [Google Scholar] [CrossRef]
- Morimune, K. (2007). Volatility models. Japanese Economic Review, 58(1), 1–23. [Google Scholar] [CrossRef]
- Nakajima, J. (2011). Time-varying parameter VAR model with stochastic volatility: An overview of methodology and empirical applications. Monetary and Economic Studies, 29, 107–142. [Google Scholar]
- Narayan, P. K. (2022). Understanding exchange rate shocks during COVID-19. Finance Research Letters, 45, 102181. [Google Scholar] [CrossRef] [PubMed]
- Negro, M. D., & Primiceri, G. E. (2015). Time varying structural vector autoregressions and monetary policy: A corrigendum. Review of Economic Studies, 82(4), 1342–1345. [Google Scholar] [CrossRef]
- Panggabean, S., Ekananda, M., Gitaharie, B. Y., & Djuranovik, L. (2025). Export proceeds repatriation policies: A shield against exchange rate volatility in emerging markets? arXiv, arXiv:2506.09168. [Google Scholar] [CrossRef]
- Pitt, M. K., & Shephard, N. (1999). Filtering via simulation: Auxiliary particle filters. Journal of the American Statistical Association, 94(446), 590–599. [Google Scholar] [CrossRef]
- Powell, A. A. (1959). Export receipts and expansion in the wool industry. Australian Journal of Agricultural Economics, 3, 64–74. [Google Scholar] [CrossRef]
- Prayoga, D. S., & Purnomo, D. (2024). The influence of foreign exchange policy from export proceeds, import payments, inflation rate, and rupiah exchange rate on foreign direct investment in Indonesia. Indonesian Interdisciplinary Journal of Sharia Economics (IIJSE), 7, 4875–4901. [Google Scholar]
- Primiceri, G. E. (2005). Time varying structural vector autoregressions and monetary policy. Review of Economic Studies, 72(3), 821–852. [Google Scholar] [CrossRef]
- Rafi, O. P. C. M., & Ramachandran, M. (2018). Capital flows and exchange rate volatility: Experience of emerging economies. Indian Economic Review, 53(1), 183–205. [Google Scholar] [CrossRef]
- Reinhart, C. M., & Reinhart, V. R. (2009). Capital flow bonanzas: An encompassing view of the past and present. NBER International Seminar on Macroeconomics, 5(1), 9–62. [Google Scholar] [CrossRef]
- Rossi, B. (2013). Exchange rate predictability. Journal of Economic Literature, 51, 1063–1119. [Google Scholar] [CrossRef]
- Ulm, M., & Hambuckers, J. (2022). Do interest rate differentials drive the volatility of exchange rates? Evidence from an extended stochastic volatility model. Journal of Empirical Finance, 65, 125–148. [Google Scholar] [CrossRef]
- Wallich, H. C. (1961). Stabilization of proceeds from raw material exports. In H. S. Ellis, & H. C. Wallich (Eds.), Economic development for latin america (pp. 342–365). Palgrave Macmillan UK. [Google Scholar] [CrossRef]


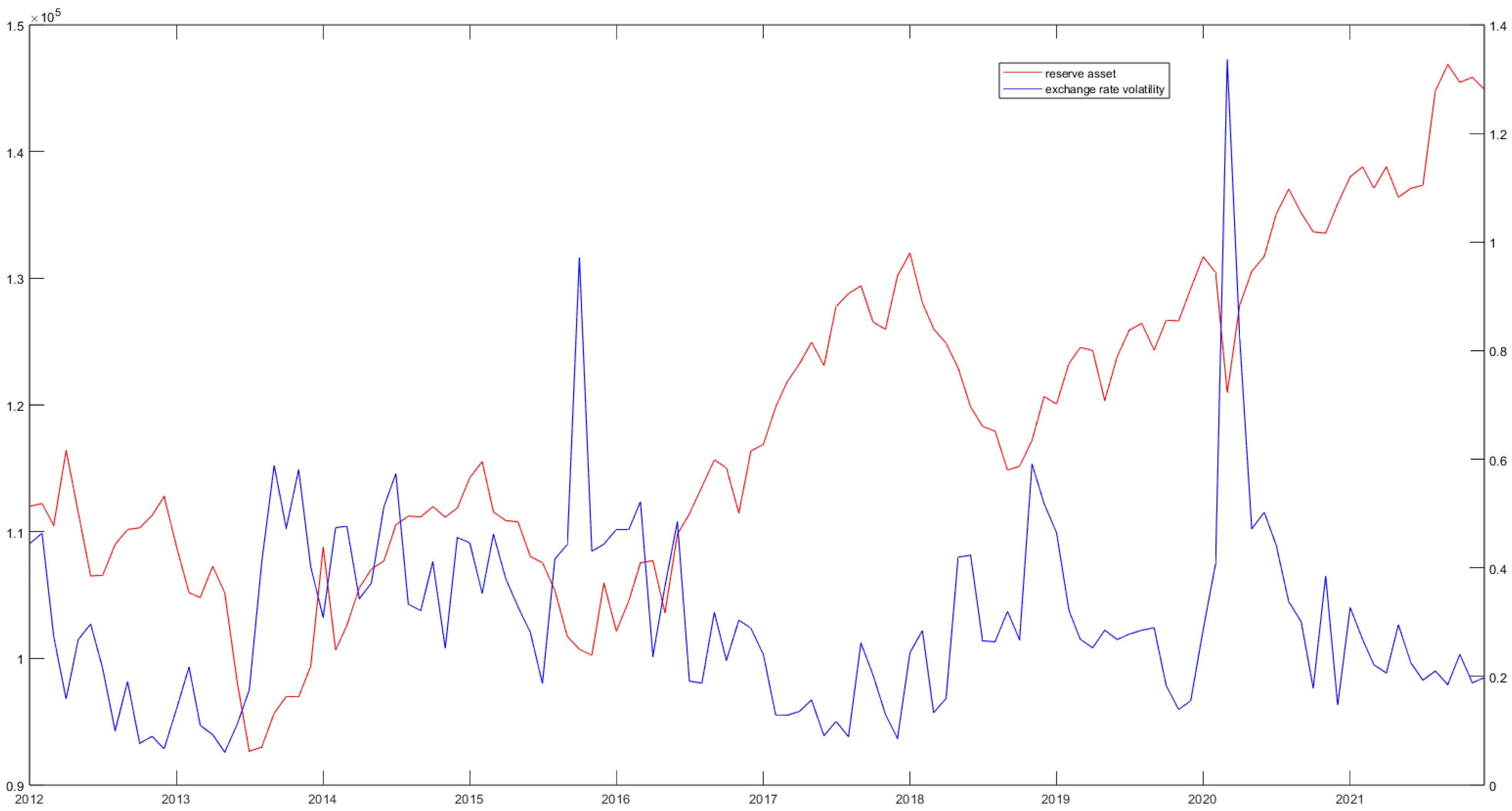
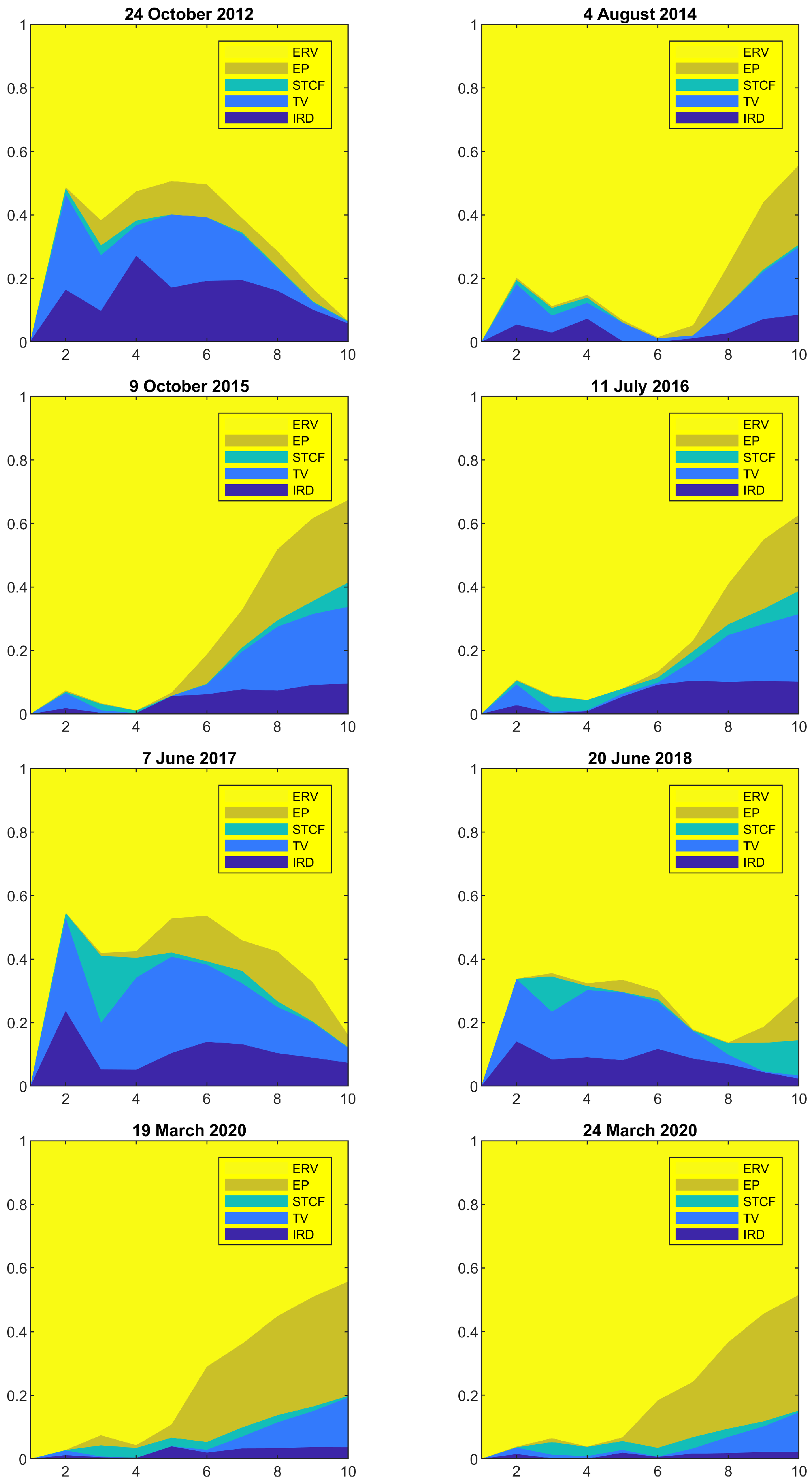








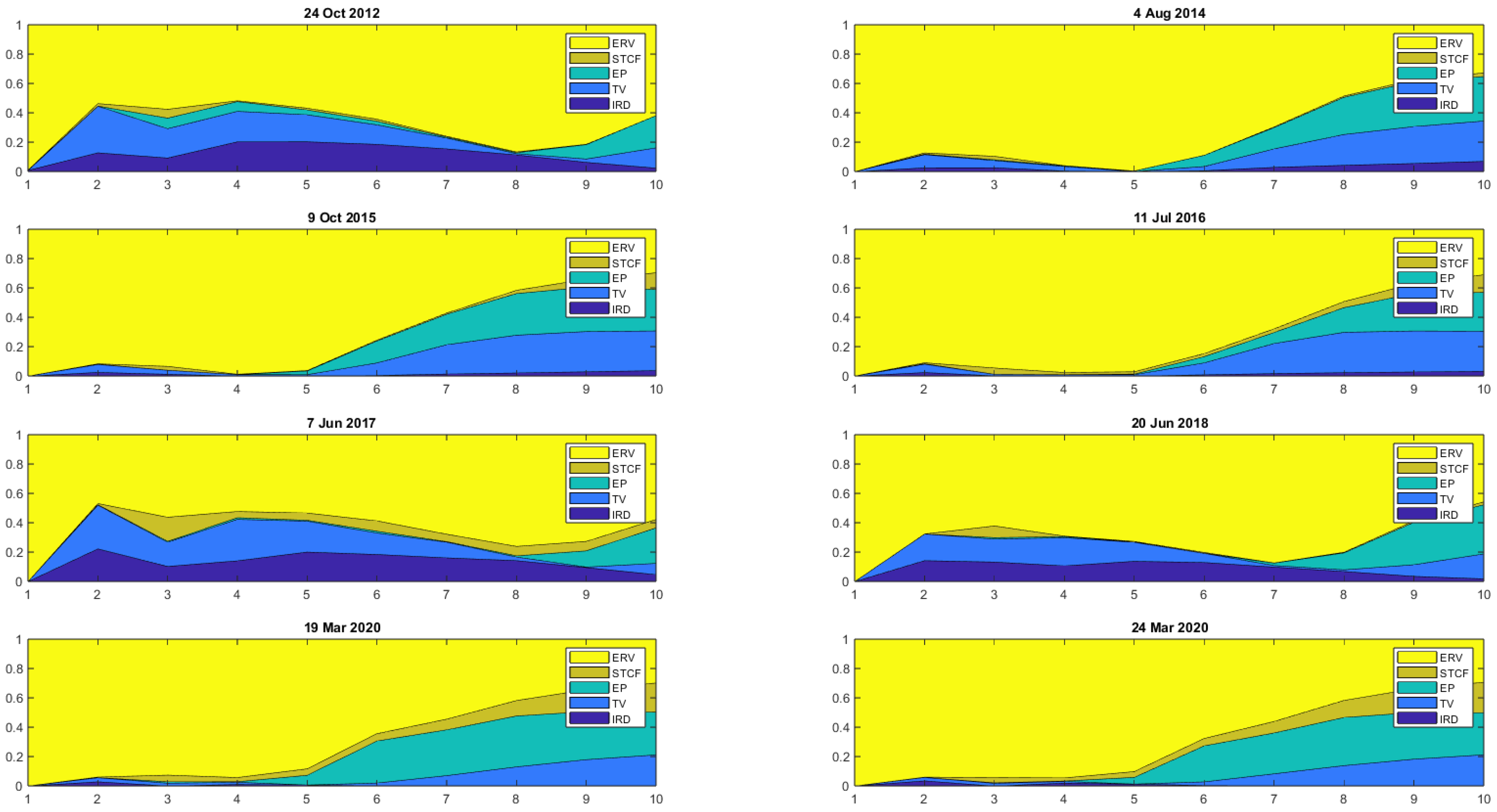
| Date | Stochastic Volatility | Volatility Category |
|---|---|---|
| 19 March 2020 | 2.1511 | High |
| 24 March 2020 | 1.7044 | High |
| 9 October 2015 | 1.6520 | High |
| 4 August 2014 | 0.5966 | Mid |
| 20 June 2018 | 0.4082 | Mid |
| 11 July 2016 | 0.2032 | Mid |
| 7 June 2017 | 0.0880 | Low |
| 24 October 2012 | 0.0748 | Low |
| Parameter | Mean | Stdev | 95 Percent Interval | GCD | Inefficiency |
|---|---|---|---|---|---|
| 0.000008 | 0.000001 | [0.000006, 0.000010] | 0.428 | 37.15 | |
| 0.000666 | 0.000092 | [0.000519, 0.000877] | 0.946 | 39.04 | |
| 0.004377 | 0.003770 | [0.001222, 0.015440] | 0.026 | 181.57 | |
| 0.005944 | 0.003887 | [0.001757, 0.016852] | 0.002 | 176.33 | |
| 0.576859 | 0.057139 | [0.472987, 0.697278] | 0.427 | 26.92 | |
| 0.078714 | 0.013666 | [0.054799, 0.108744] | 0.701 | 64.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panggabean, S.M.U.; Ekananda, M.; Gitaharie, B.Y.; Djuranovik, L. Steadying the Ship: Can Export Proceeds Repatriation Policy Stabilize Indonesian Exchange Rates Amid Short-Term Capital Flow Fluctuations? Economies 2025, 13, 180. https://doi.org/10.3390/economies13060180
Panggabean SMU, Ekananda M, Gitaharie BY, Djuranovik L. Steadying the Ship: Can Export Proceeds Repatriation Policy Stabilize Indonesian Exchange Rates Amid Short-Term Capital Flow Fluctuations? Economies. 2025; 13(6):180. https://doi.org/10.3390/economies13060180
Chicago/Turabian StylePanggabean, Sondang Marsinta Uli, Mahjus Ekananda, Beta Yulianita Gitaharie, and Leslie Djuranovik. 2025. "Steadying the Ship: Can Export Proceeds Repatriation Policy Stabilize Indonesian Exchange Rates Amid Short-Term Capital Flow Fluctuations?" Economies 13, no. 6: 180. https://doi.org/10.3390/economies13060180
APA StylePanggabean, S. M. U., Ekananda, M., Gitaharie, B. Y., & Djuranovik, L. (2025). Steadying the Ship: Can Export Proceeds Repatriation Policy Stabilize Indonesian Exchange Rates Amid Short-Term Capital Flow Fluctuations? Economies, 13(6), 180. https://doi.org/10.3390/economies13060180






