A Study on the Construction and Dynamic Evolution of a Chinese Science and Technology Finance Index

Abstract

This study addresses regional disparities and the dynamic evolution of China’s science and technology finance integration (STFI) by constructing a composite index system using the entropy method. Recognizing the limitations of subjective weighting in traditional assessment frameworks, the entropy approach was employed to objectively quantify the contribution weights of 23 indicators across four dimensions: capital investment intensity, market development level, technological innovation efficiency, and public service accessibility. Analysis of panel data from 31 provinces (2010–2020) reveals three key findings: (1) China’s overall STFI exhibits a declining trend, with market development and capital investment emerging as primary drivers; (2) regional disparities are widening, as evidenced by a 2.3-fold increase in the coefficient of variation, with northwestern provinces demonstrating the fastest growth, while southwestern regions lag significantly; and (3) public services and innovation contributions remain underdeveloped, accounting for only 15.6% of the composite index. The entropy-based assessment framework demonstrates superior discriminatory power compared to principal component analysis, particularly in capturing regional heterogeneity. Policy implications include calls for intergovernmental coordination mechanisms, national market unification, inclusive service diffusion strategies, and targeted innovation investments. This research contributes a novel quantifiable tool for evaluating technology–finance synergies while highlighting systemic inefficiencies in China’s innovation-driven development paradigm.

1. Introduction

The 2023 Central Financial Work Conference emphasized the need to effectively address the “five major tasks” of financial sector reform, including science and technology finance. As a policy agenda aligned with the development of China’s modern industrial system and the advancement of new forms of productive forces, science and technology finance traces its origins back to “technology loans” in 1985. Its policy value lies in establishing an efficient and smooth financing mechanism between financial capital and technological assets. The core principle is to ensure a reasonable and fair distribution of risks and returns throughout the technological innovation process, thereby stimulating innovation vitality, advancing scientific and technological progress, and promoting economic development. However, the coherence, diversity, and complexity of scientific and technological innovation activities, coupled with the broad applicability and flexibility of financial instruments, pose numerous challenges to the formulation and implementation of science and technology finance policies.

An index system for measuring the development level of science and technology finance can multi-dimensionally reflect the current characteristics and evolution trends of science and technology finance in a country or region. Scholars such as Fang (2015) have put forward a series of theoretical viewpoints and operational measures regarding the essential connotation and policy evolution of science and technology finance. They further point out that the essence of science and technology finance is a new economic paradigm that promotes the deep integration and aggregation of innovative elements such as technological capital, innovation capital, and entrepreneurial capital. It consists of three closely interconnected subsystems: technology–economy, finance–economy, and entrepreneurship–economy. They also propose a reciprocal relationship among the stages of economic development, R&D investment intensity, and R&D structure, providing a basis for measuring the demand for science and technology finance within a regional scope. Empirical research by Jie (2020) and Liu et al. (2020) indicate that science and technology finance significantly promotes regional high-quality development, but heterogeneous science and technology finance services have differentiated intermediary effects on high-quality development, with public science and technology finance exhibiting a complete intermediary effect, while market-based science and technology finance demonstrates an incomplete intermediary effect. Xu (2022) and Su (2024) argue that the allocation of science and technology financial resources significantly promotes high-quality economic development. Spatial interaction effects reveal that science and technology finance has a significant negative spatial spillover effect on total factor productivity (TFP). The allocation of science and technology financial resources, through the transformation of scientific and technological achievements, forces the adjustment of industrial structure, accelerates the industrialization process, optimizes the allocation of factor resources, and thus significantly enhances TFP. Geng et al. (2023) and Jiang (2023) emphasize the role of finance as a key force driving technological innovation and industrial development. To better facilitate technological innovation, it is essential to promote the mutual promotion and empowerment of science and technology and finance, thereby accelerating the formation of new forms of productive forces. Cao and Peng (2024) empirically investigate the innovation spillover effects of science and technology finance policies and their spillover channels. The results show that science and technology finance pilot programs significantly enhance the innovation level of suppliers in non-pilot regions through two channels: knowledge spillover and demand pull, transmitted from clients to suppliers.

In terms of index measurement, Z. J. Zhou et al. (2022), Corrado and Corrado (2017) employed the input–output method to evaluate regional science and technology finance efficiency, elucidating the characteristics of uneven development in China’s regional science and technology finance levels. Alam et al. (2019) and Wang et al. (2021) conducted an empirical analysis of financing behavior for R&D investment in emerging markets using the generalized method of moments, examining the impact of differences between allied and non-allied firms, as well as national financial systems, on corporate financing behavior. Chinese scholar Zou et al. (2025), based on the theory of financial intermediation and a multi-level science and technology financial service system, constructed a multi-dimensional comprehensive index system that includes public science and technology finance and market-based science and technology finance. Their measurement results indicate that China’s science and technology finance development index has shown a steady growth trend, with public and market-based science and technology finance advancing in tandem. The development index exhibits characteristics of a spiky, right-skewed, and heavy-tailed distribution with multiple peaks, a gradient decrease and diffusion pattern across eastern, central, and western regions, and an evolutionary pattern of “faster development in the south than in the north” along with uneven development towards higher levels. J. L. Li and Zhou (2024) adopted a combined approach of subjective and objective weighting to measure China’s science and technology finance development level index. The results revealed overall convergence, spatial agglomeration, and spatial heterogeneity in the development levels of China’s regional science and technology finance. Lei et al. (2024) developed a comprehensive evaluation index system comprising five dimensions—finance and innovation environment, science and technology finance input, financing environment for technology enterprises, regional science and technology output, and science and technology finance profitability—calculated via the entropy method. Hu and Liu (2022) measured science and technology finance efficiency using the super-efficiency SBM model, employed the Dagum Gini coefficient to dissect the spatial differences in science and technology finance efficiency, used Kernel density to examine spatial evolution trends, and revealed spatial correlation through the calculation of Moran’s I. K. Zhou and Guo (2019) used the composite entropy method to measure the basic index, input index, output index, and contribution index of science and technology finance in six central provinces and conducted a dynamic assessment of the regional distribution of these indices.

Overall, current academic studies on science-technology finance (STFI) primarily focus on macro-level systemic frameworks, integrating credit/capital/insurance markets through a traditional lens. However, data limitations constrain analytical depth, manifesting two key gaps: (1) Fragmented perspectives isolate financial development from broader socio-ecological contexts, with narrow policy-finance definitions obscuring ecosystemic interactions and yielding biased STFI assessments. (2) Existing metrics fail to capture the reciprocal evolution between financial innovation and technological progress, neglecting financial resource clustering effects and index internal coherence, thereby limiting analytical applicability. This study advocates for multidimensional frameworks bridging financial, technological, and societal dimensions to advance STFI theory and measurement.

This study investigates the reform of China’s science and technology finance (STFI) system in the context of developing new quality-driven productive forces. Building on the theoretical framework of “technology–economy–finance–entrepreneurship” symbiosis, we redefine STFI as an innovation-driven economic paradigm that systematically integrates technological, financial, and social capital through policy-institutional coordination across the “basic research–technology commercialization–industrial application” chain. This conceptualization extends beyond traditional financial instrument approaches by incorporating public service capabilities and institutional optimization as critical catalytic elements.

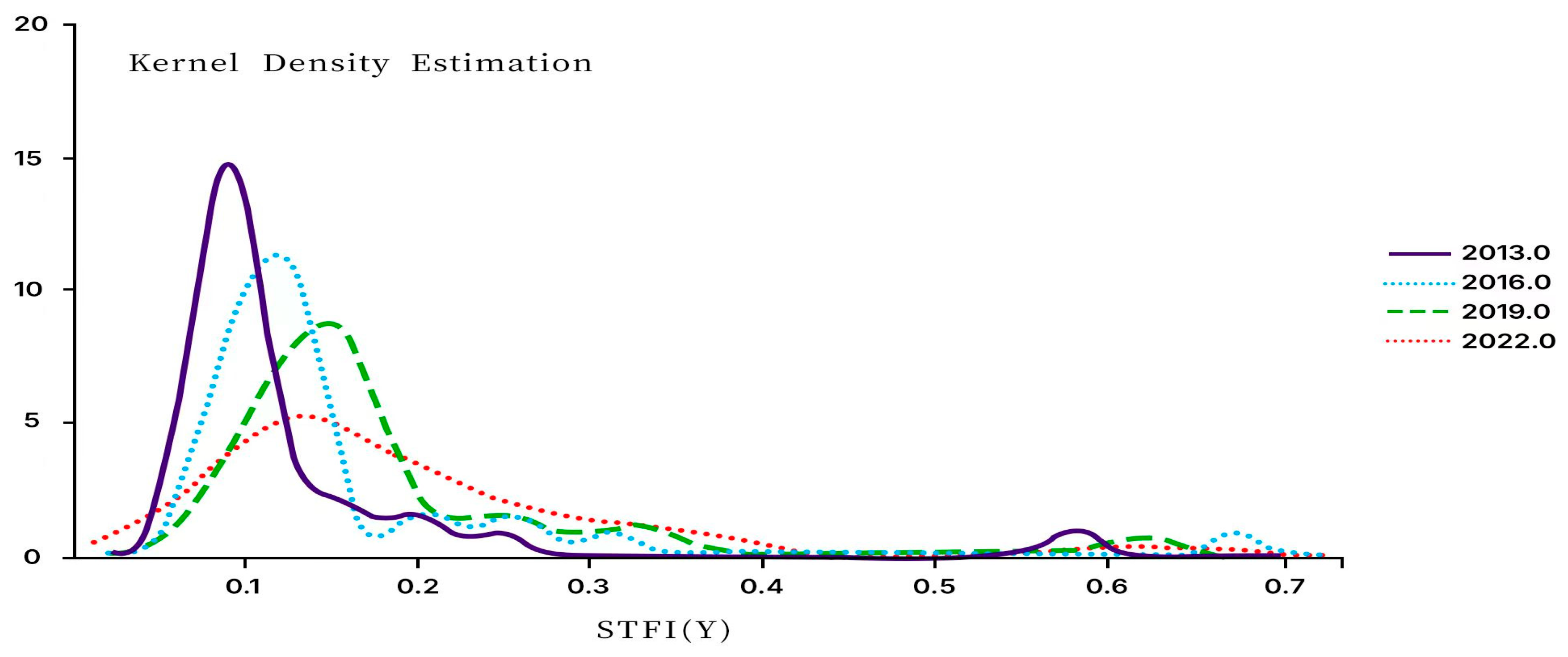
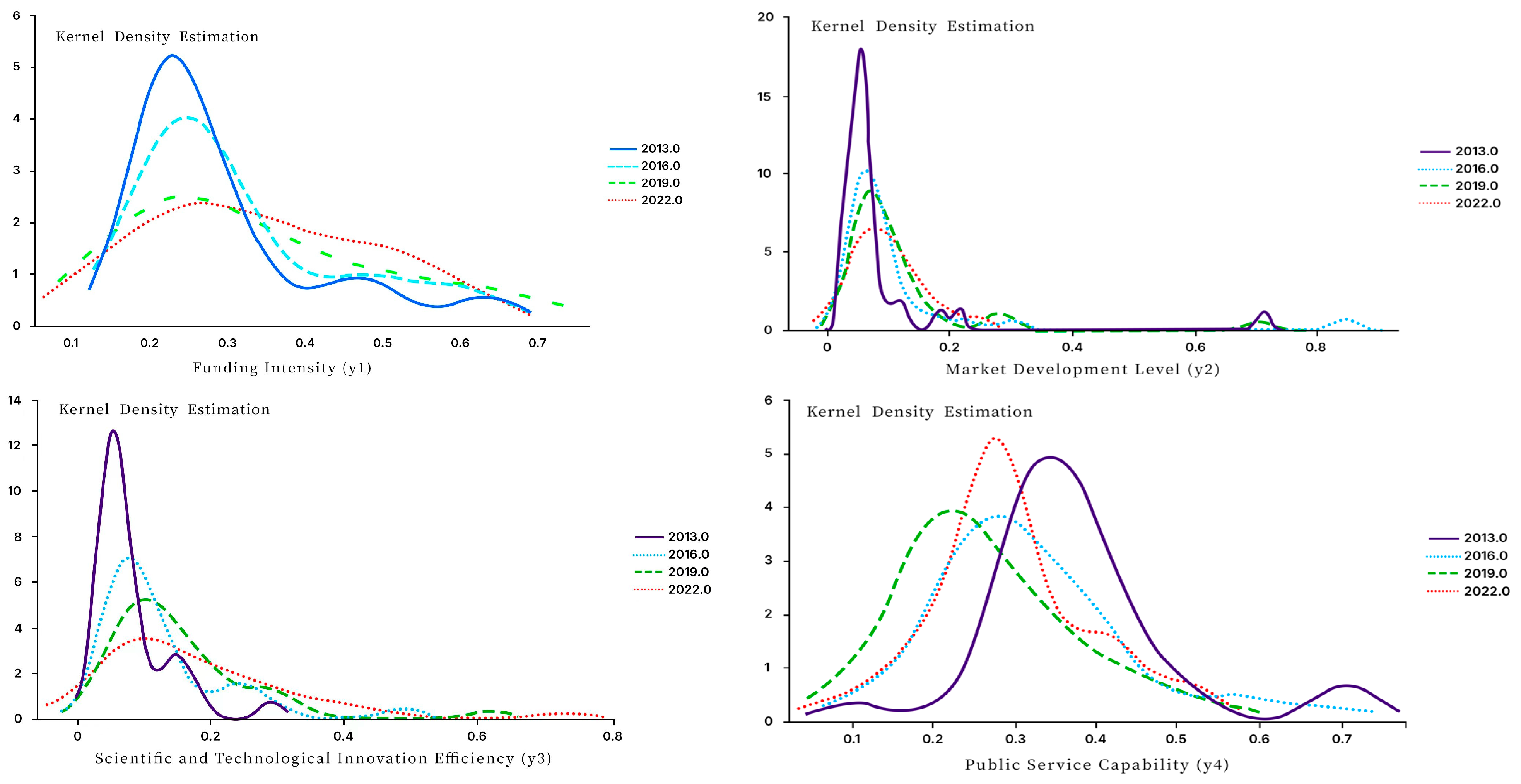
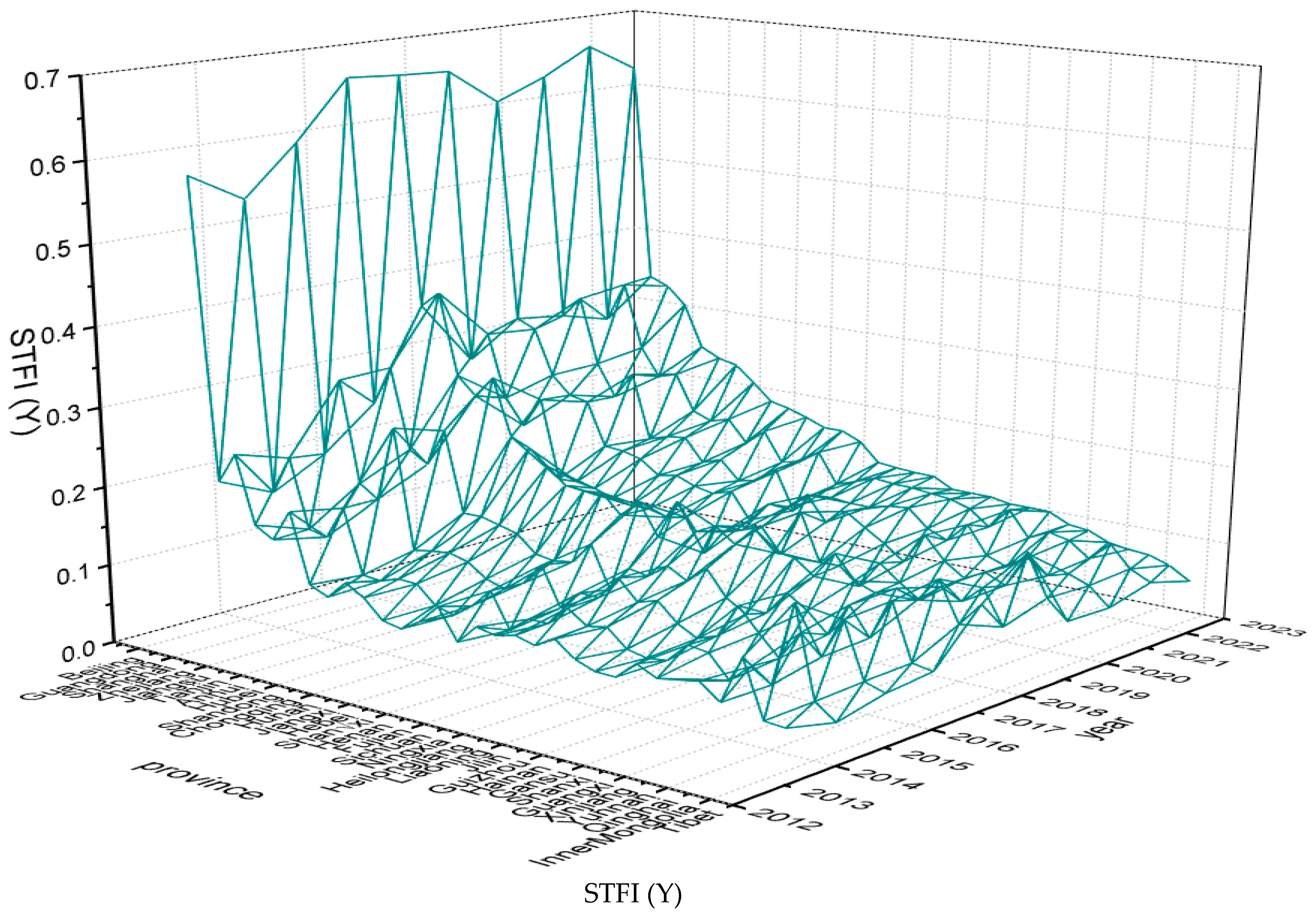
To address methodological shortcomings, this study introduces two key innovations: First, a multidimensional “finance–technology–society” index is constructed using hierarchical entropy weighting, with the innovative inclusion of regional public service capacity as a critical institutional dimension. This extends beyond traditional economic indicators, capturing systemic disparities across Chinese provinces. Second, analytical rigor is enhanced by integrating dynamic panel models with Dagum Gini decomposition to quantify spatiotemporal heterogeneity, while panel VAR modeling elucidates long-term innovation feedback loops. Theoretically, the study quantifies how institutional differentials mediate resource allocation efficiency within China’s innovation ecosystem. Methodologically, the shift from static cross-sectional analysis to dynamic evolutionary modeling with temporal-spatial interaction metrics provides superior explanatory power. Empirically, the findings reveal paradoxical trends between aggregate STFI growth and innovation output divergence, supporting differentiated governance strategies. However, several limitations remain: (1) Potential endogeneity concerns in entropy weighting calculations may bias the significance of dimensions; (2) Data availability constraints limited indicator selection, particularly excluding micro-level firm innovation dynamics and qualitative institutional factors, which could introduce omitted variable bias; (3) Provincial aggregation obscures significant sub-regional variations in technology adoption rates. Future research should incorporate mixed-methods approaches, combining big data analytics with qualitative case studies to fully capture the complexity of STFI evolution.

The remainder of this paper is structured as follows. Section 1 introduces the research context and policy significance, followed by a comprehensive literature review that synthesizes existing theories and empirical gaps in STFI studies. Section 2 details the entropy-based methodology for constructing the STFI, including indicator selection criteria and dimensional frameworks. 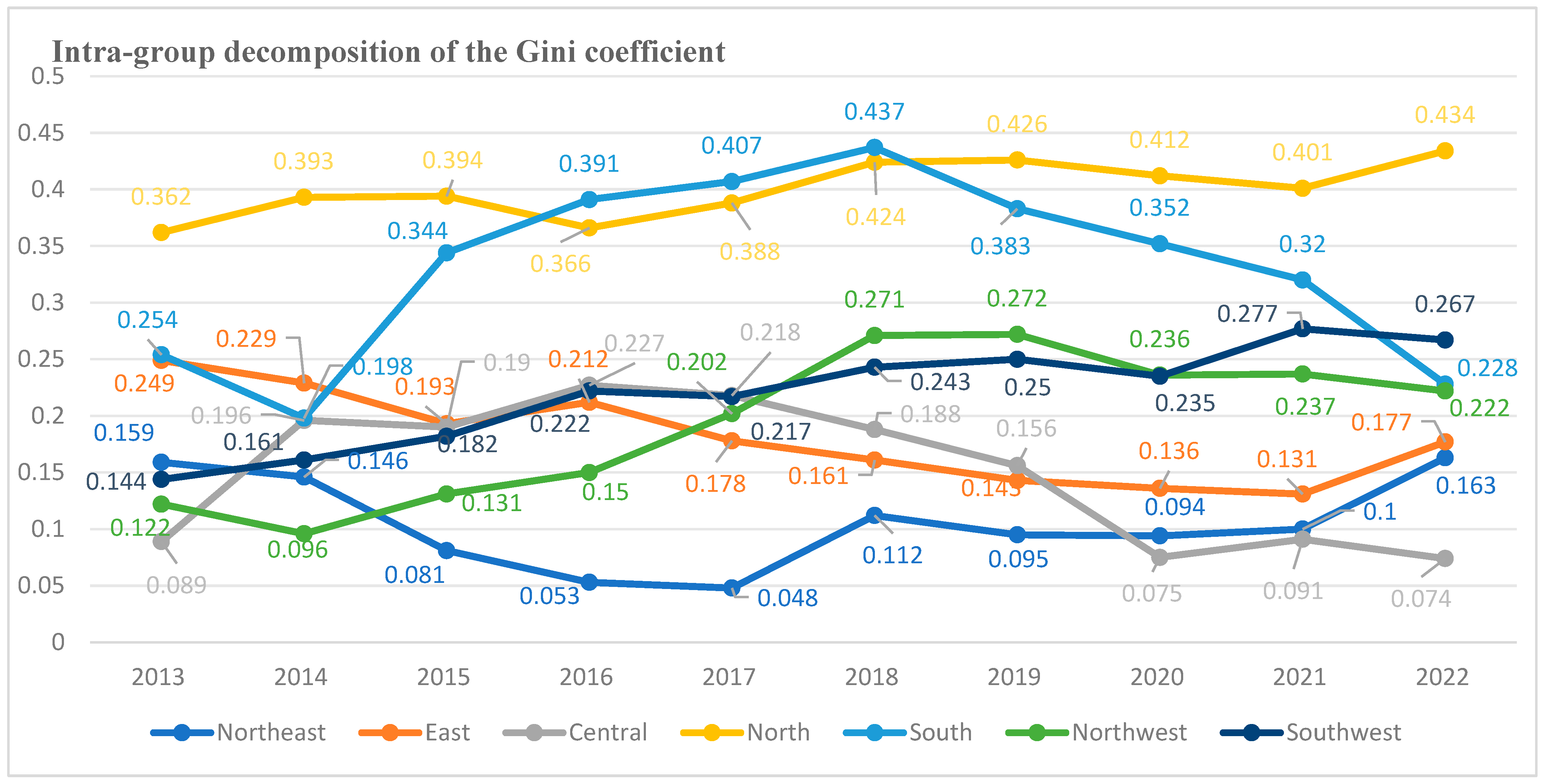Spatiotemporal trends and regional disparities of the composite index are analyzed in Section 3, while Section 4 employs the Dagum Gini coefficient to quantify inter-provincial heterogeneity. Section 5 explores causal mechanisms through fixed-effects regression and panel vector autoregression models, examining how capital investment intensity and market development drive innovation efficiency. Policy implications and recommendations are discussed in Section 6.

2. Mechanism of the Impact of Regional Public Service Disparities on Science and Technology Finance

As a crucial link in the synergy between government and market, the collaborative mechanism between public service capabilities and finance plays a decisive role in the allocation pattern and flow of innovation funds within a region, profoundly influencing enterprises’ funding shortages and the vibrancy of their investment decisions (Z. B. Li et al., 2022). It is generally believed that the supply conditions of regional public resources enhance the intensity and efficiency of science and technology finance investment by creating an external environment conducive to the aggregation of innovation elements and leveraging “generalized reciprocity” (Zhu et al., 2023). Specifically, advanced research facilities, high-quality educational resources, abundant data reserves, and efficient public services within a region can significantly attract key innovation elements such as innovative talents, funds, and technologies to cluster in specific areas, providing a sustained source of power for technological innovation and industrial upgrading and offering room for science and technology finance investment to exert its effects.

Meanwhile, optimized allocation strategies for public resources play a significant role in improving the utilization efficiency of innovation elements. By implementing refined resource allocation and sharing mechanisms, the maximized utilization of innovation elements within the region can be ensured, effectively avoiding resource waste and redundant construction. This reduces innovation costs while promoting deep collaboration and integration among innovation elements, forming a powerful synergistic force for innovation. Furthermore, sustained investment in and innovation upgrades of public resources are key factors in stimulating the vitality and creativity of innovation elements. The continuous improvement of regional infrastructure and hardware resources, the optimization of the policy environment, and the cultivation of an innovative culture lay a solid foundation for the sustained prosperity of innovation activities, contributing to the formation of a more open, inclusive, and dynamic innovation ecosystem.

The balanced distribution of public resources also has a significant impact on the balanced agglomeration of innovation elements. When resources are unevenly allocated across a region, innovation elements may become excessively concentrated in certain areas, leaving others relatively scarce. This uneven distribution is not conducive to the coordinated development of the regional economy and may hinder the smooth flow and cooperation of innovation elements. Therefore, the balanced allocation and distribution of public resources are intrinsic requirements for the balanced agglomeration and harmonious development of innovation elements within the region.

From the perspective of the layered network structure characteristics of technological innovation, newly added science and technology finance investments tend to establish connections with nodes that already have more connections within the network, exhibiting a behavior trait of “preferential attachment” (Pham et al., 2021). This manifests as key elements such as funds, resources, and technologies being more inclined to flow to regions or research institutions that already possess a good resource base, extensive cooperation networks, and significant influence. Due to their central position in the innovation network, these entities can often more effectively absorb and utilize new financial investments, promoting technological innovation, knowledge diffusion, and industrial upgrading. The “preferential attachment” of science and technology finance stems from the broader information channels and stronger information processing capabilities typically possessed by nodes with numerous established connections, enabling them to identify and seize new investment opportunities more quickly based on their information advantage and reduce information asymmetry and disperse investment risks through multi-partner collaborations.

As the number of new connections within the network grows, the value and influence of science and technology finance in the network also increase, thereby more effectively integrating internal and external resources, fostering cross-domain collaboration, attracting additional resource inflows and capital, and ultimately establishing a positive feedback loop. Nevertheless, the “preferential attachment” characteristic inherent in science and technology finance further intensifies the non-uniformity of capital distribution. This provides a theoretical foundation for optimizing the network environment, promoting equitable competition, and reinforcing policy support for underdeveloped regions.

3. Index Construction

To address the challenge of collinearity in indicator selection, this study adopts the entropy method over alternative approaches such as AHP and DEA due to its significant advantages in managing correlated variables. The entropy method calculates objective weights based on the information entropy principle, which quantifies the degree of disorder or variability within each indicator’s data distribution. This process inherently accounts for inter-indicator relationships by assigning higher weights to indicators with greater discriminatory power, thereby reducing redundancy caused by collinear variables. In contrast, AHP relies on subjective pairwise comparisons that may amplify collinearity effects through potentially biased judgment matrices, especially when evaluating multiple interrelated dimensions. While DEA avoids subjective weighting, it does not inherently address collinearity issues and may produce unstable efficiency frontiers when input/output variables exhibit strong correlations. The entropy method’s data-driven normalization process effectively mitigates these limitations by focusing on the relative information contribution of each indicator, ensuring robust composite index construction even in the presence of multicollinearity. This methodological choice aligns with best practices in composite indicator development, where collinearity diagnostics and objective weighting are crucial for valid empirical analysis.

3.1. Fundamental Principles

3.1.1. Diversification of Financial Investment

Technology finance exhibits a diverse nature to cater to the financing needs of heterogeneous innovation entities (Tian & Xu, 2024). In practical applications of technology finance, based on the differences in the attributes of investing entities, investment sources can be broadly categorized into three types: (i) Market-oriented capital investments, such as venture capital, technology loans, and technology insurance, which are dually regulated by the development levels of both the capital market and regional finance, and constitute the primary targets of government technology finance policies; (ii) Policy-based financial investments from the government, including various fiscal expenditures specific to technology, loans from policy-based financial institutions, and tax expenditures (Zhang, 2024). Government policy-based financial investments and market-oriented capital investments demonstrate certain differences and complementarities in their target entities and effectiveness (Xie & Cai, 2025), Isaksson et al. (2016). Additionally, in existing research on technology finance, relatively few scholars have focused on the third type of investment, namely, endogenous corporate funding based on free cash flow. Despite its limited scale, this type of funding can reduce corporate dependence on the external environment, enhance corporate risk resistance, mitigate internal incentive and moral hazard issues, thereby enabling companies to allocate funds more flexibly, increase investments in early-stage R&D, and form an organic connection with exogenous financing.

3.1.2. Innovation Efficiency Orientation

Innovation efficiency is a key indicator for measuring the effectiveness of technology finance development. Technology finance accelerates the process of technological innovation and promotes industrial upgrading and economic growth through financial means (Zhong et al., 2021). Emphasizing innovation efficiency orientation implies that indicator design should focus on how financial resources precisely and efficiently support technological innovation activities, ensuring that resources flow to areas with the greatest innovation potential and market prospects. Simultaneously, the efficiency-oriented principle helps reveal the rationality of resource allocation, identify potential resource allocation issues by assessing the input–output ratio of innovation activities, and provide a policy basis for optimizing resource allocation strategies. It is evident that innovation efficiency bridges effective communication between technology finance investment, government guidance policies, and corporate innovation willingness, serving as the foundation for “generalized reciprocity” among different entities in technology finance.

3.1.3. Combination of Market Drive and Public Service Provision

Although technology finance is often understood as a product defined within a policy context, its contingency character confirms that it cannot develop independently of the capital market. In other words, the driving force generated by the self-improvement and development of the capital market constitutes the primary impetus for the formation and development of technology finance, rather than the reverse. Therefore, constructing a capital market indicator system from a broader perspective aids in theoretically clarifying the drivers of technology finance, thereby providing a basis for seeking policy guidance intervention points. As China’s capital market integration deepens, the dynamic effects of regional financial markets exert a direct influence on technology finance, effectively linking government policy guidance with the capital market (Sheng et al., 2021). In the evolution of regional financial markets, public service provision offers spatial carriers and innovation element entities preferred by financial entities. Thus, this paper reinforces the integration concept of market drive and public service provision in indicator construction, ensuring that the indicators better align with the environmental behavioral characteristics of innovation activities.

3.2. Indicator Selection

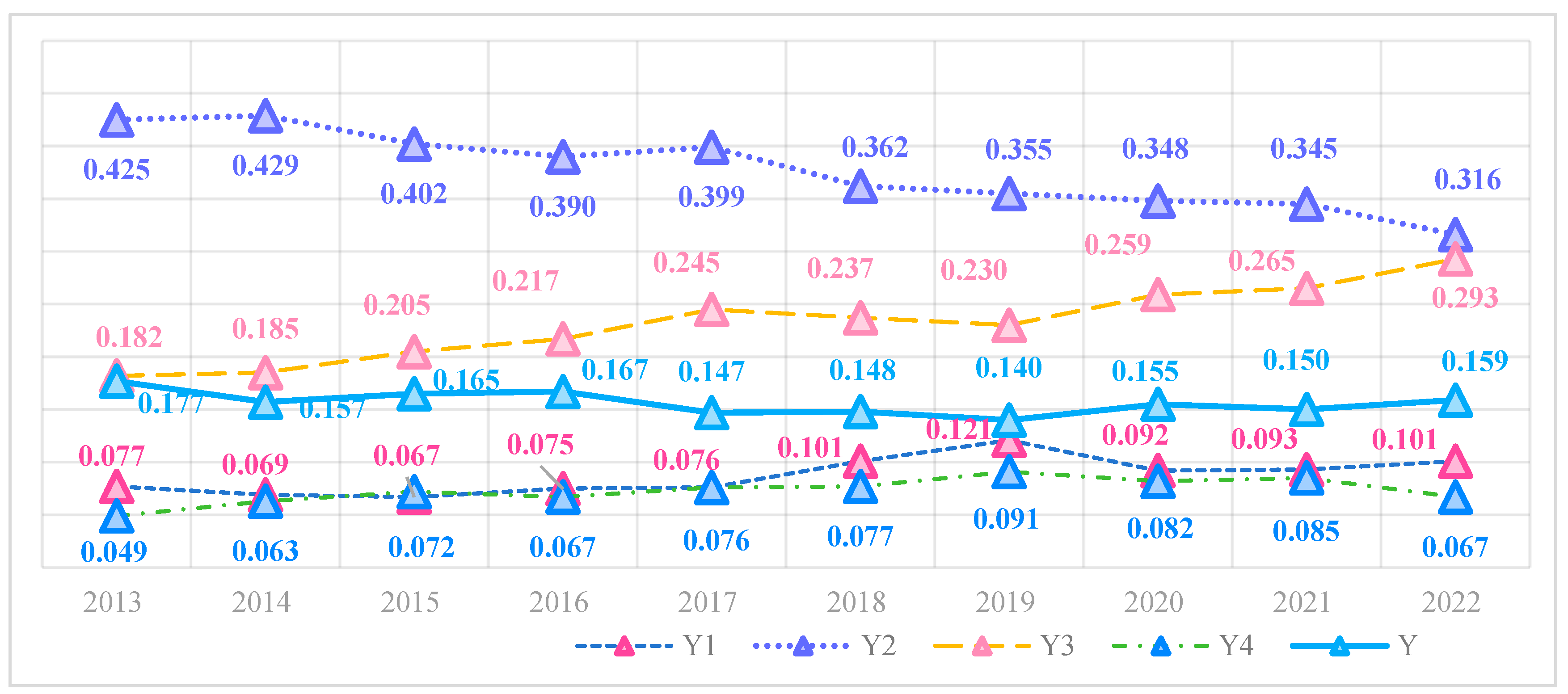
This paper constructs a technology finance index based on four dimensions: investment intensity, market development level, technological innovation efficiency, and social service capacity. Specifically:

• Investment Intensity (y1) is the foundation of technology finance development. Adequate funding supports technological innovation, promoting the research, development, and application of new technologies and products. The specific indicator design incorporates funding situations from multiple levels, including government, enterprises, financial institutions, and society, to reflect the funding supply conditions and liquidity of technology finance activities within a region.
• Market Development Level (y2) focuses on measuring the activity and maturity of technology finance. A mature and active market provides more financing channels and investment opportunities for technological innovation. The indicator design specifically includes the development status of six sub-markets: financial markets, insurance markets, bond markets, capital markets, venture capital markets, and technology markets.
• Technological Innovation Efficiency (y3) is the core driving force of technology finance development. Efficient technological innovation accelerates the application and popularization of new technologies and products, thereby enhancing the productivity and competitiveness of the entire society. In this study, technological innovation efficiency is assessed through five dimensions: output rate of innovation results, value conversion capability, corporate profitability, R&D activity level, and new product development rate.
• Social Service Capacity (y4) is designed based on the principles of “generalized reciprocity” and “preference attachment”, encompassing six aspects: regional macro tax burden level, public service level, education expenditure intensity, ecological environment development level, and energy consumption per unit of GDP. This indicator reflects the interactive impact between technology finance activities and economic-social development, as well as improvements in people’s livelihoods.

The specific indicator design is presented in

Table 1. Construction System of the STFI Indicators.

Secondary Indicator	Tertiary Indicator	Symbol	Calculation Method	Direction
Funding Intensity (y1)	Government Science and Technology Expenditure Intensity	x1	Local fiscal expenditure on science and technology/General public budget expenditure	+
	Enterprise R&D Expenditure Intensity	x2	R&D expenditure of enterprises above a certain size/Total assets	+
	Bank Loan Investment Intensity	x3	Balance of loans from financial institutions/GDP	+
	Social Financing Intensity	x4	Total new social financing/GDP	+
	Resident Deposit Intensity	x5	Resident deposit balance/GDP	+
	Enterprise Debt Intensity	x6	Total liabilities of enterprises above a certain size/Total assets of enterprises above a certain size	−
Market Development Level (y2)	Financial Market Development Level	x7	Financial sector GDP/Total GDP	+
	Insurance Market Development Level	x8	Insurance claims paid/GDP	+
	Bond Market Development Level	x9	Scale of corporate bonds/GDP	+
	Capital Market Development Level	x10	Market value of locally listed A-share companies/Total market value of A-shares	+
	Venture Capital Market Development Level	x11	Scale of private equity and venture capital fund investments/GDP	+
	Technology Market Development Level	x12	Transaction volume of the technology market/GDP	+
Scientific and Technological Innovation Efficiency (y3)	Outcome Output Rate	x13	Number of granted invention patents/Regional population	+
	Value Conversion Capability	x14	Sales revenue of high-tech enterprises/GDP	+
	Enterprise Profitability	x15	Profits of enterprises above a certain size/Owners’ equity	+
	R&D Activity Level	x16	Number of enterprises above a certain size engaged in R&D activities/Total number of enterprises above a certain size	+
	New Product Development Rate	x17	Expenditure on new product development by enterprises above a certain size/Sales revenue of new products	+
Social Service Capacity (y4)	Regional Macro Tax Burden Level	x18	Regional tax revenue/General public budget revenue	−
	Public Service Level	x19	Number of public buses and trams in operation/GDP	+
	Education Expenditure Intensity	x20	Local fiscal expenditure on education/General public budget expenditure	+
	Ecological Environment Development Level	x21	Green space ratio in urban built-up areas	+
	Energy Consumption per GDP	x22	Electricity consumption/GDP	+

Data Sources: Data on the balance of loans from financial institutions, total new social financing, total resident deposits, market value of locally listed A-share companies, total market value of A-shares, and scale of corporate bonds are sourced from the Wind database; data on the scale of private equity and venture capital fund investments are sourced from the iFinD database; sales revenue of high-tech enterprises is sourced from the China Torch Yearbook; profits and number of enterprises above a certain size engaged in R&D activities are sourced from the China Statistical Yearbook on Science and Technology; and all other data are sourced from the China Development Yearbook published by the National Bureau of Statistics. A balanced panel dataset comprising 310 observations from 31 provinces and municipalities in China (excluding Hong Kong, Macao, and Taiwan) was collected for the period 2013–2022. Missing data were supplemented using linear interpolation.

.

3.3. Index Fitting

In this paper, a hierarchical synthesis method is employed to fit the final index. Specifically, the tertiary indicators are first used to fit the secondary indicators, which are then used to fit the final index. The entropy method is utilized to determine the weight coefficients of the indicators during the synthesis process. The specific steps are as follows:

• Given that the units of measurement for various indicators across subsystems are not uniform, it is essential to eliminate these discrepancies prior to analysis by conducting interval or standardization processing on the data in order to address the homogeneity issue of the indicators. The initial data is standardized using the normalization method to unify the dimensions.

For positive indicators, the processing method is:

$${{\mathrm{x}}^{\prime }}_{ijk}={\displaystyle \frac{{\mathrm{x}}_{ijk}-\min ({\mathrm{x}}_{ik})}{\max ({\mathrm{x}}_{ik})-\min ({\mathrm{x}}_{ik})}}$$

For negative indicators, the processing method is:

$${{\mathrm{x}}^{\prime }}_{ijk}={\displaystyle \frac{\max ({\mathrm{x}}_{ik})-\min ({\mathrm{x}}_{ik})}{\max ({\mathrm{x}}_{ik})-{\mathrm{x}}_{ijk}}}$$

where i represents the province, j represents the year, and k represents the indicator code. ${\mathrm{x}}_{ijk}$ denotes the initial value of the kth indicator for province i in year j, denotes the standardized value after normalization, while $\min ({\mathrm{x}}_{ik})$ and $\max ({\mathrm{x}}_{ik})$ denote the minimum and maximum values of the kth indicator for province i over all years, respectively.

After the aforementioned processing, the initial data were standardized to the interval [0, 1]. The larger the positive indicators within this interval, the better, whereas the negative indicators behaved conversely.

• Calculate the proportion of the k indicator in Province i on an annual basis, respectively, get ${\mathrm{p}}_{ik}$.

  $${\mathrm{p}}_{ik}={\displaystyle \frac{{{\mathrm{x}}^{\prime }}_{ik}}{{\displaystyle \sum _{i=1}^{31}{\displaystyle \sum _{k=1}^{22}{{\mathrm{x}}^{\prime }}_{ik}}}}}$$
• The entropy value of the third-level indicators to the second-level indicators ${{\mathrm{x}}^{\prime }}_{ik}$ was calculated hierarchically by using the entropy value method in j years, get ${\mathrm{s}}_{ik}$.

  $${\mathrm{s}}_{ik}=-k{\displaystyle \sum _{i=1}^{31}{\displaystyle \sum _{k=1}^{22}{\mathrm{p}}_{ik}\ln ({\mathrm{p}}_{ik})}}$$

  where $k={\displaystyle \frac{1}{\ln (i\times k)}}\rangle 0$. In this study, i = 31, k = 10, and the range of the entropy weight coefficient is adjusted to lie within the interval (0, 1).
• The secondary indicators are constructed for each year j as follows:

  $${\mathrm{y}}_{it}={\displaystyle \sum _{i=1}^{31}{{\mathrm{x}}^{\prime }}_{ik}\times {\mathrm{s}}_{ik}}$$

  $${\mathrm{s}}_{it}={\displaystyle \sum _{i=1}^{31}{\mathrm{s}}_{ik}}$$

  with t ∈ {1,2,3,4} and when t = 1, k ∈ {1,2,3,4,5,6}; when t = 2, k ∈ {7,8,9,10,11,12}; when t = 3, k ∈ {13,14,15,16,17}; when t = 4, k ∈ {18,19,20,21,22}.
• Calculate the weight coefficient ${\mathrm{w}}_{it}$ of the secondary indicator ${\mathrm{y}}_{it}$ year by year.

  $${\mathrm{w}}_{it}={\displaystyle \frac{{\mathrm{d}}_{it}}{{\displaystyle \sum _{t=1}^4{d}_{it}}}}$$

  with the utility information ${\mathrm{d}}_{it}=1-{\mathrm{s}}_{it}$, ${\displaystyle \sum _{t=1}^4{\mathrm{w}}_{it}=1}$.
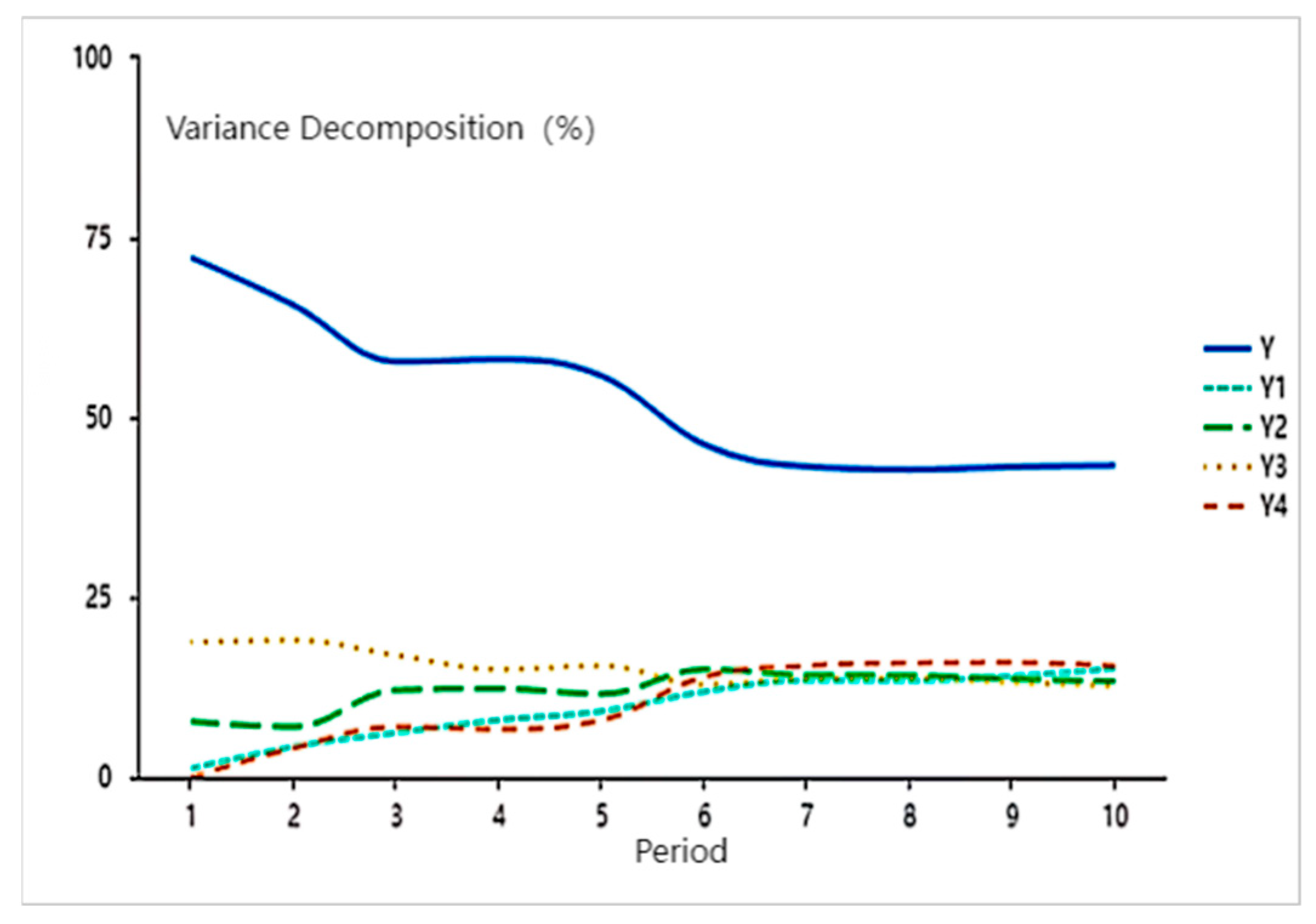
• The final STFI Y is calculated separately for each year j:

  $$Y={\mathrm{y}}_{it}\times {\mathrm{w}}_{it}$$

Compared with other studies, this paper adopts an objective assignment method for indicator synthesis, which can reduce the subjective bias that may arise from manual weighting.

4. Indicators Analysis

4.1. Overall Trend and Contribution

Based on the index fitting method described above, we measured the trends of China’s comprehensive STFI and the secondary indicators of the four dimensions from 2013 to 2022. The statistical analysis workflow was executed utilizing the SPASSau online platform, with critical procedural outputs—including weight coefficients and entropy values for variables—systematically documented in Appendix A. A final result as shown in Figure 1, the overall trend of China’s comprehensive STFI exhibits a decline, from 0.177 in 2013 to 0.159 in 2022, representing a decrease of 10.17%. The highest value appeared in 2016, with a peak value of 0.217, and the annual average was 0.1565. Among the secondary indicators, the growth rate of technological innovation efficiency is the most pronounced, increasing from 0.182 in 2013 to 0.293 in 2022, a growth of 60.99%. Compared to technological innovation efficiency, the growth rates of social service capacity and capital investment intensity are relatively slower, at 36.73% and 31.17%, respectively. Conversely, the market development level index shows a downward trend, with a decrease of 25.65%.

Figure 1 also reveals that among the four secondary indicator dimensions of science and technology finance, the market development level deviates the farthest from the comprehensive index, thus exerting the greatest positive pulling effect on the comprehensive STFI. However, its contribution is on a downward trend. Technological innovation efficiency also contributes positively to the comprehensive index, and its ability to drive the rise of science and technology finance continues to improve. In contrast, capital investment intensity and social service capacity have negative contributions to the overall STFI. After 2017, capital investment intensity showed a slow upward trend, but the improvement in social service capacity was not significant.

The Kendall kernel density plot in Figure 2 shows that the distribution pattern of China’s science and technology finance development index from 2013 to 2022 gradually shifted from a sharp-peaked right-skewed distribution to a flat-peaked, heavy-tailed right-skewed distribution. This shift indicates that over time, the kurtosis decreased, the number of provinces with low levels decreased, and the right tail thickened and moved to the right, suggesting an increase in inter-provincial disparities. The flat-peaked, heavy-tailed distribution pattern confirms the evolution of science and technology finance development from low-level equilibrium to high-level development.

Figure 3 presents the kernel density distributions of the secondary indicators. The trends for capital investment intensity, market development level, and technological innovation efficiency are similar to that of the STFI, all exhibiting sharp-peaked right-skewed distributions with long tails. This indicates a continuous improvement in the overall development levels of these three indicators across provinces, with a decrease in the number of provinces with low levels of capital investment intensity, market development level, and technological innovation efficiency. However, the peak of social service capacity did not change significantly and shifted slightly to the left, indicating that the changes in social service capacity among provinces were not significant. The peak value lies between 4 and 5, which is relatively high, and both the peak and the tail have shifted to the left, suggesting that regional differences are narrowing. This confirms that under the recent governance concept of equalization of general public services, China’s inter-provincial social service capacity has maintained a relatively high level of convergence.

4.2. Regional Heterogeneity

Figure 4 presents a surface plot of the comprehensive science, technology, and finance (STF) index and its secondary indices for various provinces and municipalities in China from 2013 to 2022. The results indicate significant variations in the comprehensive STF index among provinces, yet an overall upward trend is observed over the study period. As China’s financial hubs, Beijing, Guangdong, and Shanghai exhibit considerably higher levels of STF development compared to other regions. In 2013, there were 14 provinces with an STF index exceeding 0.1, including Qinghai, Shaanxi, Liaoning, Chongqing, Shandong, Anhui, Tianjin, Jiangsu, Zhejiang, Shanghai, Guangdong, and Beijing. By 2022, the number of provinces surpassing this threshold had surged to 26, marking an 85.71% increase. The highest value also rose from 0.579 in Beijing in 2013 to 0.635 in the same city in 2022. Six provinces—Hubei, Jiangxi, Hunan, Anhui, Hebei, and Henan—witnessed an index growth exceeding 100%, with growth rates of 151%, 150%, 147%, 145%, 109%, and 102%, respectively.

Regionally analysis shown in

Table 2. Statistics of regional STFI.2

Year	Northeast	North	East	South	Central	Northwest	Southwest
2013	0.095	0.205	0.135	0.120	0.081	0.109	0.083
2014	0.092	0.195	0.122	0.109	0.080	0.120	0.079
2015	0.105	0.227	0.153	0.126	0.095	0.129	0.089
2016	0.119	0.242	0.173	0.149	0.111	0.133	0.099
2017	0.152	0.269	0.248	0.206	0.173	0.155	0.144
2018	0.133	0.247	0.195	0.158	0.129	0.129	0.134
2019	0.145	0.243	0.212	0.180	0.154	0.146	0.121
2020	0.145	0.250	0.213	0.180	0.156	0.134	0.119
2021	0.147	0.257	0.224	0.183	0.172	0.142	0.129
2022	0.131	0.254	0.246	0.196	0.190	0.127	0.127
Average	0.126	0.239	0.192	0.161	0.134	0.132	0.112

, North China and East China exhibit higher levels of STF development, with annual average comprehensive indices reaching 0.239 and 0.192, respectively. This is primarily attributed to the presence of national financial centers such as Beijing and Shanghai within these regions. The overall STF levels in other regions are relatively similar. Within the study period, Central China experienced the fastest growth rate, with an increase of 135%, followed by East China and South China, with growth rates of 82% and 64%, respectively. Correspondingly, Northwest China saw the slowest growth in the STF index, with a mere 16% increase.

Further analysis was conducted using the Dagum Gini coefficient to examine inter-regional disparities. The overall Dagum Gini coefficient is composed of the within-group Gini coefficient (Gw), the between-group Gini coefficient (Gb), and the transvariation density Gini coefficient (Gt). The contribution rate refers to the proportion of the overall Gini coefficient attributed to Gw, Gb, or Gt. The results in

Table 3. Dagum Gini Coefficient and Contribution Rates.

Year	Gini Coefficient				Contribution Rate (%)
	Total	Gw	Gb	Gt	Gw	Gb	Gt
2013	0.347	0.041	0.239	0.066	11.747%	69.077%	19.176%
2014	0.346	0.040	0.237	0.069	11.672%	68.502%	19.826%
2015	0.338	0.038	0.210	0.089	11.352%	62.293%	26.355%
2016	0.365	0.041	0.239	0.085	11.142%	65.563%	23.295%
2017	0.365	0.039	0.230	0.096	10.761%	62.971%	26.267%
2018	0.387	0.040	0.237	0.110	10.443%	61.102%	28.455%
2019	0.395	0.037	0.269	0.088	9.497%	68.226%	22.277%
2020	0.382	0.035	0.270	0.078	9.114%	70.516%	20.370%
2021	0.369	0.034	0.265	0.069	9.296%	71.898%	18.806%
2022	0.390	0.036	0.284	0.069	9.363%	73.022%	17.615%
Average	0.3684	0.0381	0.248	0.0819	10.44%	67.32%	22.24%

reveal significant variations in the comprehensive science, technology, and finance (STF) index among regions, with an average overall Gini coefficient of 0.3684. The overall disparity showed little decrease from 2013 to 2022. The data indicate that the primary contributor to the overall disparity, with a contribution rate of 67.32%, is the large difference between regions. The second largest contributor is the transvariation density among regions, with a contribution rate of 22.24%. In contrast, within-region disparities are relatively small, accounting for only 10.44%. These findings suggest that the development of STF in China is characterized by inter-regional imbalance and relative intra-regional balance. From a dynamic perspective, the overall disparity in the STF index among different regions in China remained relatively stable from 2013 to 2022, with a slight increase of 12.39% over the decade.

The decomposition of the within-group Gini coefficient in Figure 5 shows that the Northeast region has a relatively low average within-group Gini coefficient, mostly below 0.1, indicating a relatively balanced development of STF among provinces in this region and good coordination within the region. In contrast, the North China and South China regions have higher within-group Gini coefficients, with averages above 0.4 and 0.3, respectively, suggesting significant disparities in STF development levels among provinces (municipalities) within these regions and poor coordination. For example, within North China, the average STF index for Beijing and Shanxi from 2013 to 2022 was 0.628 and 0.110, respectively, highlighting substantial intra-regional development differences. Furthermore, Figure 5 reveals that the within-group Gini coefficients for the Northeast, North China, Northwest, and Southwest regions exhibited a decreasing trend from 2013 to 2022, indicating a reduction in intra-regional imbalances in STF development. However, the within-group Gini coefficients for the East China, Central China, and South China regions showed an increasing trend, suggesting a rise in intra-regional imbalances in STF development.

5. Further Discussion

The “2023 China Patent Survey Report” reveals insufficient funding as one of the most critical factors hindering patent commercialization in China. A key policy objective of science and technology finance is to introduce resources, including funding, that are compatible with scientific and technological innovation activities. Capital, especially long-term and strategic investments, not only effectively alleviates the free cash flow constraints during the innovation process, enabling more decision-making projects to receive financial support, but also enhances the risk tolerance of enterprises in innovation activities through risk-sharing mechanisms, thereby indirectly improving innovation efficiency. Furthermore, the value orientation of science and technology finance enables it to demonstrate the ability to maintain a stable strategic direction when responding to economic fluctuations, thereby reducing enterprises’ sensitivity to market volatility and helping them adhere to established strategic paths, avoiding short-sighted decisions triggered by market fluctuations. This is also a crucial guarantee for improving enterprise innovation efficiency. In summary, investment in science and technology finance serves as a vital safeguard for enhancing the efficiency of scientific and technological innovation.

5.1. Fixed Effects Model

To investigate the impact of funding investment on the efficiency of scientific and technological innovation, the following regression model is established:

$${\mathrm{y}}_{\mathrm{it}}=\alpha +\beta {\mathrm{x}}_{it}+\theta +\varphi +\epsilon$$

(1)

where: α represents the constant term; ${\mathrm{y}}_{\mathrm{it}}$ denotes the efficiency of scientific and technological innovation in province i in year t, represented by the secondary indicator y3 value mentioned earlier; ${\mathrm{x}}_{\mathrm{it}}$ is a vector group, represented by the secondary indicators of funding investment intensity (y1), market development level (y2), and public service capacity (y4) mentioned earlier; and represent individual fixed effects, time fixed effects, and residuals, respectively. The step-by-step regression results are shown in

Table 4. Step-by-Step Regression Results for Model (1).

	−1	−2	−3	−4	−5	−6
	y3	y3	y3	y3	y3	y3
Constant	−0.075 ** (−7.594)	−0.026 (−1.700)	0.007 (0.161)	−0.066 ** (−3.780)	0.100 * (2.337)	0.152 ** (5.145)
y1	0.640 ** (22.723)	0.336 ** (10.457)	0.269 ** (4.533)	0.336 ** (11.229)	0.135 * (2.429)
y2		0.464 ** (15.271)	0.460 ** (4.757)	0.455 ** (16.023)	0.127 (1.266)
y4		−0.007(−0.250)	−0.246 ** (−3.816)	0.022 (0.809)	0.090 (1.062)
L. y1						0.320 ** (8.769)
L. y2						0.443 ** (12.931)
L. y4						0.183 (−3.556)
Individual Fixed Effects	-	-	Controlled	-	Controlled	Controlled
Time Fixed Effects	-	-	-	Controlled	Controlled	Controlled
Sample Size	310	310	310	310	310	279
Adjusted R2	0.625	0.786	0.826	0.816	0.862	0.076

t-values in parentheses. * indicates p < 0.1, ** indicates p < 0.05.

. The regression results indicate a significant positive correlation between science and technology finance investment and the efficiency of scientific and technological innovation. Increasing investment in scientific and technological innovation helps to improve its efficiency. Among the other variables, the impact of market development level y2 on technological innovation efficiency is significant in three out of four regression groups, generally proving its positive effect on technological innovation efficiency. However, the public service capacity indicator y4 fails to pass the significance test in most cases, indicating that public service capacity cannot influence the overall level of science and technology finance by improving the efficiency of scientific and technological innovation, and its specific path should be explored separately from the perspective of generalized reciprocity.

Using a panel model, the regression results are shown in

Table 5. Panel Model Regression Results.

	(1)	(2)	(3)	(4)	(5)	(6)
	y3	y3	y3	y3	y3	y3
	POOL Mode	FE Mode	RE Mode	POOL Mode	FE Mode	RE Mode
Intercept	−0.026 (−1.700)	0.070 * (2.281)	0.003 (0.140)	−0.075 ** (−7.594)	0.007 (0.346)	−0.035 * (−2.038)
y1	0.336 ** (10.457)	0.269 ** (4.533)	0.298 ** (7.227)	0.640 ** (22.723)	0.387 ** (6.314)	0.517 ** (11.252)
y2	0.464 ** (15.271)	0.460 ** (4.757)	0.480 ** (11.200)
y4	−0.007 (−0.250)	−0.246 ** (−3.816)	−0.066 (−1.732)
R2 (within)	0.219	0.259	0.237	0.071	0.125	0.111
Sample Size	310	310	310	310	310	310

t-values in parentheses. * indicates p < 0.1, ** indicates p < 0.05.

. Consistent with the conclusions in Table 4, a significant positive correlation is also observed between y3 and y1, indicating that the conclusions of the fixed effects model are robust.

5.2. VAR Model

The VAR model offers the advantage of not being theory-dependent and does not require prior constraints on variables. In this study, the SPSSau software was used to analyze five indicators: the comprehensive index of science and technology finance, funding investment intensity, market development level, efficiency of scientific and technological innovation, and social service capacity using the VAR model. To ensure the absence of collinearity among variables, we performed Granger causality tests and linearity assessments for each of the five indicators. The detailed test results are presented in Appendix B and Appendix C, which confirm the non-existence of collinearity among the variables. The automatic order determination principle is that the smaller the information criterion (such as AIC), the better. As shown in

Table 6. Automatic Lag Determination of the VAR.

Lag	AIC	BIC	FPE	HQIC
0	−27.303	−27.241	0.000	−27.278
1	−28.177	−27.801	0.000	−28.026
2	−28.715	−28.026	0.000	−28.439
3	−29.089	−28.086	0.000	−28.687
4	−29.385	−28.069	0.000	−28.858
5	−29.738	−28.109	0.000	−29.086
6	−30.222	−28.280 *	0.000	−29.444
7	−30.518	−28.263	0.000	−29.615
8	−30.747	−28.179	0.000	−29.718
9	−30.822	−27.941	0.000	−29.668
10	−31.112	−27.917	0.000	−29.832
11	−31.518	−28.009	0.000	−30.113
12	−31.592	−27.770	0.000	−30.061
13	−31.727	−27.592	0.000	−30.071
14	−32.147	−27.699	0.000	−30.365
15	−32.461	−27.700	0.000	−30.554
16	−32.616 *	−27.542	0.000 *	−30.584 *

* represents the order of the item.

, the AIC criterion suggests a 16th-order model, the BIC criterion suggests a 6th-order model, the FPE criterion suggests a 16th-order model, and the HQIC criterion suggests a 16th-order model. Among the four criteria, the minimum value is 6th order; therefore, SPSSau ultimately constructs the VAR model based on the 6th order. The forecast period is 12 periods. The results in

Table 7. VAR Model Results of Y3–Y1.

	Y3
Constant	0.295 ** (5.415)
L1 Y1	−0.332 ** (−3.757)
L2 Y1	−0.284 ** (−3.135)
L3 Y1	0.304 ** (3.374)
L4 Y1	−0.158 (−1.746)
L5 Y1	−0.246 ** (−2.707)
L6 Y1	−0.379 ** (−4.270)
nobs	304
llf	2608.395
AIC	−16.141
SC	−14.246
HQIC	−15.383

t-values in parentheses. ** indicates p < 0.05.

show that the regression coefficients between the changes in y1 (science and technology finance investment) and y3 (efficiency of scientific and technological innovation) have all passed the significance test. Moreover, the AR root plot in Figure 6 shows that all eigenvalues are within the unit circle, i.e., all points are inside the circle, indicating that the VAR model is stable.

In addition, a Granger causality test was conducted to examine the directional relationship between variables y1 and y3, as presented in

Table 8. Granger test result for Y3–Y1.

H0	F Value	p Value	df 1	df 2
‘y1’ is not the Granger cause of ‘y3’	5.028	0.000 **	6	291

** indicates that the result rejects H0 at the 1% significance level.

, indicates a p-value = 0.000 (<0.05). Therefore, the null hypothesis is rejected, which means that y3 is the Granger cause of y1.

The orthogonal impulse response function reflects the impact of a one-unit change in funding investment level on other variables. A larger absolute value implies a greater impact, while a value closer to 0 implies a smaller impact. According to the results in Figure 7, the orthogonal impulse response of funding investment level y1 on the efficiency of scientific and technological innovation y3 is positive for all but the 2nd order, indicating that changes in science and technology finance investment have a positive long-term effect on the efficiency of scientific and technological innovation. Figure 8 and Figure 9 show the variance decomposition results of funding investment level y1 and the efficiency of scientific and technological innovation y3, respectively. A larger variance decomposition value implies a greater influence proportion, while a value close to 0 implies minimal influence. According to the conclusions in Figure 8, the influence of funding investment level y1 on the efficiency of scientific and technological innovation y3 does not show a tendency to approach zero within the observed periods; instead, the variance decomposition value increases with the number of periods, indicating that the effect of funding investment intensity is long-lasting.

6. Conclusions and Policy Recommendations

6.1. Main Conclusions

The supply conditions of regional public resources enhance the intensity and efficiency of science and technology finance (STF) investment by creating an external environment conducive to the agglomeration of innovation elements and leveraging “preference attachment” formed through “generalized reciprocity”. Introducing the perspective of regional public service differences helps deepen the understanding of the dynamic evolution of the STF investment index. Further analysis, structuring the China STF index across four dimensions—funding intensity, market development level, technological innovation efficiency, and social service capacity—reveals that China’s overall STF composite index exhibits a declining trend with fluctuations, peaking in 2016. Among the two-dimensional indicators across the four dimensions, technological innovation efficiency stands out as the most significant contributor to the effectiveness of STF development. The flat-peaked and thick-tailed distribution observed in the kernel density test confirms the evolution trend of STF development from low-level equilibrium to high levels, albeit with an increase in inter-provincial disparities. The public service capacity among provinces remains relatively stable, with the peak and tail shifting leftward overall, indicating a narrowing gap between regions. Regionally, the STF composite index varies significantly, with higher levels of development in North and East China, the fastest growth rate in Central China, and the slowest growth in Northwest China. Further examination of the impact of funding investment on technological innovation efficiency, using both fixed-effects and VAR models, reveals a significant positive correlation, indicating that increased STF investment contributes to enhancing firms’ innovation efficiency.

6.2. Policy Recommendations

In light of the finding that technological innovation efficiency is the most influential component of the STF index, policy reforms should be further strengthened and policy coherence enhanced. The current output-oriented evaluation mechanism should be adjusted and shifted towards an application-oriented evaluation mechanism for technological innovation. The creation of high-value intellectual property (such as core patents, well-known trademarks, and quality copyrights) should be boosted, promoting the high-quality development of innovation-driven economies, brand economies, cultural industries, niche economies, and the digital economy, with various forms of intellectual property serving as core supports. The mechanism for the transformation and application of intellectual property should be strengthened to accelerate the conversion of innovation outcomes into real productivity, fostering powerful new drivers for the development of emerging productive forces.

(1)

To address the issue of increasing inter-provincial development imbalances, the mechanism for the flow of essential factors should be smoothed, facilitating the cross-regional flow of key production factors such as capital, talent, and technology, reducing administrative barriers and geographical restrictions, and ensuring that resources are efficiently allocated according to market laws. National fiscal investment in science and technology in Northwest China under the shared fiscal responsibilities should be increased. Regional collaboration should be strengthened to jointly promote the reform of the STF system and mechanisms, forming a favorable situation of complementary advantages and resource sharing.

(2)

Given the minimal changes in public service capacity, the public service system should be continuously optimized, combining universal and targeted services to enhance regional public service effectiveness. The construction of science and technology service institutions at all levels should be coordinated, standardization pilots should be promoted, and digital support should be strengthened. A national protection information platform should be established, enriching open data resources, supporting the construction of independent databases, and ensuring data security. A unified public service platform for small and medium-sized enterprises and startups should be built to enhance the platform’s information service capabilities. Efforts should be intensified to optimize university disciplines, focusing on cultivating high-level and international talents, and improving the talent evaluation and title appraisal mechanisms.

(3)

To align with regional heterogeneity in innovation ecosystems, policy tailoring should emphasize contextual adaptation across geographic strata. While our analysis confirms that funding investment positively impacts technological innovation efficiency, strategic deployment requires nuanced regional calibration. For example, coastal regions with mature venture capital markets may prioritize deepening private equity integration and intellectual property commercialization pathways, whereas inland provinces facing fiscal constraints would benefit from decentralized expenditure frameworks to empower local governance in targeting strategic sectors. Fiscal instruments should incentivize firms to enhance endogenous R&D capacity through progressive tax credits tied to pre-commercialization innovation stages, while simultaneously establishing risk-sharing mechanisms to catalyze early-stage equity participation. Long-term capital allocation must bridge regional divides via differentiated incentive structures: coastal areas could implement co-investment platforms aligning venture capital with industrial upgrade agendas, while inland regions require fiscal transfers targeting infrastructure gaps that limit technology diffusion.