Abstract
Shimer documents that the search-and-matching model driven by productivity shocks explains only a small share of the observed volatility of unemployment and vacancies, which is known as the Shimer puzzle. We revisit this evidence by replacing the representative firm’s optimization with a deep reinforcement learning (DRL) agent that learns its vacancy-posting policy through interaction in a Diamond–Mortensen–Pissarides (DMP) model. Comparing the learning economy with a conventional log-linearized DSGE solution under the same parameters, we find that while both frameworks preserve a downward-sloping Beveridge curve, learning-based economy produces much higher volatility in key labor market variables and returns to a steady state more slowly after shocks. These results point to bounded rationality and endogenous learning as mechanisms for labor market fluctuations and suggest that reinforcement learning can serve as a useful complement to standard macroeconomic analysis.
1. Introduction
1.1. Background
Macroeconomic modeling is the construction of models that characterize the behavior of the aggregate economy. Such models are used to forecast future dynamics, analyze relationships among key macro variables, and simulate the effects of policy or structural changes. Reinforcement learning (RL) develops systems that show intelligent behavior, including reasoning, learning, problem solving, and autonomous decisions, and is thus well suited to these tasks. RL can enhance the accuracy, flexibility, and adaptability of macro models, while macroeconomic environments provide disciplined testbeds for building and evaluating AI systems aimed at reproducing complex social and economic behavior.
With recent advances in neural networks, many surveys and applications combine DRL with macroeconomics, where agents and institutions interact dynamically (Atashbar & Shi, 2022; Evans & Ganesh, 2024; Maliar et al., 2021; Shi, 2023). In such settings, DRL can approximate policy functions without relying on linearity, potentially capturing nonlinear properties and learning dynamics that standard solution methods may overlook.
In standard search-and-matching frameworks such as the DMP model, a persistent quantitative tension is that model-implied fluctuations in labor market variables are far smaller than those observed in the data Shimer (2005), known as the “Shimer puzzle”. The existing literature typically modifies wage setting, shock processes, or calibration targets (Hall, 2005; Mortensen & Nagypal, 2007; Petrosky-Nadeau & Zhang, 2017). By contrast, we explore whether the solution method itself can produce more intense volatility when firms learn policies through interaction with the environment.
This leads to the central question of our paper: can the learning process of a firm, modeled via DRL, endogenously generate the observed volatility in labor market variables that standard expectations models fail to reproduce?
To investigate this question, we build a labor market framework that integrates a DMP model with endogenous firm size and a reinforcement learning agent. The agent begins without knowledge of the economy’s structure, preferences, or transition laws and learns vacancy posting and wage strategies through repeated interaction with the environment. After sufficient training, its behavior converges toward rational expectations benchmarks. Although the learning process is initially slow, since the agent must generate its own experience, the dynamics stabilize and become consistent over time. Through the simulation, we find that the RL-based system exhibits substantially greater volatility, suggesting that learning dynamics can amplify fluctuations in a way that better aligns with empirical observations. The current implementation remains deliberately parsimonious, focusing on productivity shocks and a simplified unemployment mechanism, but it provides a flexible prototype that can be extended to richer shock processes, heterogeneous agents, more realistic labor market frictions, and policy experiments.
This paper contributes by offering a learning-based interpretation of the Shimer puzzle and demonstrating that DRL can produce more realistic macroeconomic fluctuations. Methodologically, it introduces an interpretable framework that supports future policy analysis and strengthens the bridge between AI techniques and macroeconomic modeling. The remainder of the paper proceeds as follows: Section 1 reviews the related literature, with the topic of Shimer puzzle and RL in macroeconomics; Section 2 lays out the theoretical framework, a search-and-matching model with endogenous firm size; Section 3 explains the quantitative methods, including the benchmark DSGE model solved by log linearization and the design of the DRL agent; Section 4 reports the main results and compares the volatility and dynamic responses across the two approaches; Section 5 concludes with the main contribution, notes the limits of the study, and outlines directions for future work.
1.2. Related Works
1.2.1. Labor Markets as a Search-and-Matching Problem
The search-and-matching (DMP) view changed how we study unemployment, job creation, and wages. It states that workers and firms do not meet instantly. Because search takes time and effort, unemployment can arise in equilibrium. A full overview is given by Pissarides (2000).
In this framework, a simple matching function (often Cobb–Douglas) maps unemployment and vacancies into new hires. Market tightness is a key summary of conditions. It controls both job-finding for workers and vacancy-filling for firms. Wages are usually set by Nash bargaining, so they move with productivity and outside options (Pissarides, 2000).
Shimer (2005) shows that the baseline DMP model with Nash bargaining and standard calibration cannot match key business–cycle facts. In U.S. data, unemployment is strongly countercyclical, vacancies are strongly procyclical, and the two are tightly negatively correlated (a clear Beveridge curve). In contrast, when the model is hit by productivity shocks of realistic size, it produces only small movements in market tightness and unemployment.
The large gap between the model’s prediction and the observed volatility of vacancies and unemployment, widely known as the Shimer puzzle, has led to a search for amplification mechanisms. A prominent line of work stresses wage rigidity. Hall (2005) introduces a search-and-matching model with equilibrium wage stickiness, showing that when wages adjust slowly within the bargaining set, small productivity shocks can generate large fluctuations in vacancies and unemployment. Gertler and Trigari (2009) give a microfoundation with staggered multi-period wage contracts that generate smooth aggregate wages consistent with the data. The sufficiency of wage rigidity alone is contested. Mortensen and Nagypal (2007) review additional mechanisms, including strategic bargaining, realistic matching elasticities, turnover costs, and separation shocks, and suggest that several forces may be needed. Pissarides (2009) likewise questions whether wage stickiness by itself resolves the puzzle and emphasizes the role of the wage equation and parameter choices. A second line of work focuses on calibration and on solution methods. Hagedorn and Manovskii (2008) propose a surplus calibration in which a high value of nonmarket activity makes profits very sensitive to productivity, raising volatility. Petrosky-Nadeau and Zhang (2017) show that when one solves the model with accurate global methods rather than a local log-linear approximation, nonlinearities can produce much larger fluctuations and stronger impulse responses, which changes how earlier findings should be read.
To study a learning-based amplification mechanism, we start from a standard search-and-matching model with endogenous firm size, following Smith (1999). In this setup, concave production implies that a firm’s hiring decisions depend on its current size. Later work incorporates richer firm-level dynamics. Elsby and Michaels (2013) show that decisions at the “marginal job” within heterogeneous firms can amplify unemployment movements. Kaas and Kircher (2015) use a competitive search setting to connect firm growth and wage dynamics to business cycle facts. Kudoh et al. (2019) focus on adjustment margins in multi-worker firms and find that their model matches the cyclicality of hours. While these richer models offer important insights into structural amplification, we adopt a simple setup to clearly isolate the contribution of the DRL agent’s learning dynamics as a novel amplification mechanism.
Finally, the DMP framework is well-suited to learning-based methods. Because firms make sequential vacancy choices and receive informative feedback from matches and profits, reinforcement learning can allow them to learn effective hiring rules. We expand on this in the next section.
1.2.2. The Progress of RL and DRL
RL belongs to one of the three principal paradigms of machine learning, alongside supervised and unsupervised learning. While supervised learning relies on labeled data to learn mappings from inputs to outputs, and unsupervised learning focuses on discovering hidden structures in data, RL is fundamentally concerned with decision-making through sequential interaction with an environment. Its distinguishing feature is that the learner, called the agent, is not provided with explicit examples of correct behavior. Instead, it must discover effective strategies through trial and error, guided only by feedback in the form of rewards or penalties. This formulation makes RL particularly well suited for dynamic settings where agents must adapt to evolving circumstances—features that resonate with many problems studied in economics, such as investment, labor search, or firm competition.
RL has its intellectual roots in psychology and neuroscience, where concepts such as stimulus–response learning and reward prediction errors were originally developed (Lee et al., 2012). Formally, the RL framework can be cast as a Markov Decision Process (MDP), characterized by four elements: a set of states , representing all possible situations the agent might face; a set of actions , denoting the possible decisions available to the agent; a transition function , describing the stochastic evolution of the environment given current state s and action a; and a reward function , specifying the immediate feedback obtained when moving from state s to under action a (Puterman, 2014). Figure 1 provides a schematic overview of this interaction loop between the agent and its environment.
Figure 1.
The reinforcement learning framework. At each time step, the agent observes the current state and reward and selects an action, and the environment transitions to a new state with an updated reward.
The goal of the agent is to learn a policy , which specifies the mapping from states to actions, that maximizes the expected cumulative discounted reward over a finite or infinite horizon:
where denotes the reward at time t, is the discount factor reflecting time preference, and indicates the expectation with respect to the probability distribution induced by policy . This optimization problem is closely related to familiar concepts in economics, such as utility maximization under intertemporal preferences.
A wide range of algorithms has been proposed to solve the RL problem. Traditional reinforcement learning algorithms often rely on explicit tables or relatively simple mathematical functions to represent the mapping between states, actions, and values. Such approaches work well when the state and action spaces are small but quickly become infeasible in environments with many variables, continuous decision spaces, or complex nonlinear relationships—settings that are common in economics.
More recently, advances in deep learning have given rise to the field of DRL, where neural networks are employed as function approximators to handle high-dimensional state spaces and complex environments (Arulkumaran et al., 2017).
Deep learning provides a solution by using multi-layered neural networks, which are flexible mathematical models inspired loosely by the structure of the human brain. These networks are capable of automatically extracting and representing relevant patterns from raw data, without the need for hand-crafted feature design.
Among DRL algorithms, a particularly influential class is the family of actor–critic methods. These combine the strengths of value-based and policy-based approaches: the “actor” updates the policy directly, while the “critic” evaluates the quality of the policy by estimating value functions. The algorithm employed in this paper, Deep Deterministic Policy Gradient (DDPG) (Lillicrap et al., 2016), is a prominent example of this class. DDPG is designed for environments with continuous action spaces, where the agent’s decision variables are not discrete but rather take values from a continuum, much like the choices of consumption, investment, or wage offers in economic models.
1.2.3. RL in Economic Simulations
The application of RL in economics has developed from early theoretical explorations to modern deep RL implementations in macroeconomic and financial contexts. Early work at the intersection of RL and economics established the theoretical basis for using RL to model bounded rationality and adaptive expectations. Arthur (1991) and Barto and Singh (1991) explored computational approaches to economic decision-making, while Sargent (1993) emphasized the parallel between econometricians and economic agents in their learning processes. Subsequent contributions began to apply RL to specific economic problems, such as incomplete markets with liquidity constraints (Jirnyi & Lepetyuk, 2011).
A central strand of research employs DRL as a solution method for optimal policy design. For instance, Hinterlang and Tänzer (2021) demonstrated that deep RL can derive central bank interest rate rules that outperform traditional monetary policy benchmarks. Likewise, Castro et al. (2025) used policy gradient methods to optimize liquidity management in payment systems, and Curry et al. (2022) applied multi-agent deep RL to approximate equilibria in real business cycle models with heterogeneous agents. Other studies have investigated oligopolistic competition (Covarrubias, 2022) and algorithmic pricing (Calvano et al., 2020), showing the relevance of RL for industrial organization and market design.
RL has also been used to study bounded rationality and learning dynamics in macroeconomic models. M. Chen et al. (2021) applied the DDPG algorithm to analyze the convergence of rational expectations equilibria, while Ashwin et al. (2021) examined which equilibria are learnable when agents employ flexible neural networks. Extending these ideas, Hill et al. (2021) used deep RL to solve heterogeneous agent models, capturing precautionary saving behavior and macroeconomic responses to shocks.
Finally, multi-agent extensions of RL have opened new avenues for analyzing strategic interaction. Johnson et al. (2022) illustrated how production, consumption, and pricing patterns can emerge in spatial trading environments. Surveys such as that conducted by Hernandez-Leal et al. (2020) provide a comprehensive overview of opportunities and challenges in multi-agent RL for economics.
Despite these advances, the application of RL to labor market dynamics remains limited. One exception is R. Chen and Zhang (2025), who used multi-agent RL to examine how firms with different degrees of rationality adjust their policies and the resulting macroeconomic consequences. However, their analysis does not focus on market stability and volatility from an economic perspective. In contrast, the present paper applies mean-field theory to model competitive equilibrium in the labor market, analyzing how productivity shocks influence volatility and stability, and comparing these results with insights from classical economic approaches.
2. Model
The model follows the search-and-matching framework of Smith (1999) but abstracts from firm entry. Specifically, we consider a single representative firm with the total workforce normalized to one. This simplification suppresses the extensive margin of firm entry and allows us to focus on the intensive margin of employment dynamics within the firm.
The model is a discrete-time matching framework with a representative multi-worker firm. Since there is only one firm in the economy, firm entry is absent, and the total measure of workers is normalized to one. Workers are assumed to be homogeneous, so employment and unemployment satisfy .
The number of new matches in period t is given by
where denotes matching efficiency, measures the elasticity with respect to unemployment, is the unemployment rate, and is the vacancy rate. Market tightness is defined as
and the vacancy-filling probability is
Because , a decline in market tightness raises the probability that a posted vacancy is filled.
The representative firm chooses the number of vacancies to maximize the expected present value of profits:
where denotes the endogenous wage, c is the per-vacancy posting cost, and is the exogenous separation rate. The wage in period t is , which reflects the outcome of bargaining between workers and the firm. Wages are therefore not fixed parameters but depend on firm size and the bargaining power of workers.
Production is given by a concave technology
which implies that output increases with employment but marginal productivity declines as rises. denotes the level of total factor productivity (TFP).
At time t, the firm chooses vacancies to maximize expected firm value. The corresponding first-order condition is
The envelope condition is
We define the value functions for the workers. The value of being employed is the sum of the current wage and the discounted expected future value:
Similarly, the value of being unemployed, , consists of the unemployment benefit b and the discounted expected future value:
The wage is then set to split the total surplus of a match, which is derived from the firm’s value of a filled job and the worker’s net gain from employment. The derivation of the wage equation is detailed in Appendix A. Hence, the wage equation is
where governs the bargaining power of workers.
3. Method
3.1. Parameter Calibration
The model parameters are calibrated following standard practices in the search-and-matching literature. Table 1 reports the baseline parameter values used in our simulations. Our calibration strategy closely follows Kudoh et al. (2019), with targets chosen to match key empirical moments. The full set of steady-state equations used for the model’s calibration is listed in Appendix B.

Table 1.
Default experimental parameters.
We begin by setting parameters that can be determined from external evidence. Following Kudoh et al. (2019), the capital share parameter in the production function is set to , consistent with the labor share multiplier effect. The matching function is given by , where the elasticity is typically set between and . We adopt , as reported in Lin and Miyamoto (2014). By the Hosios (1990) condition, the worker’s bargaining power must equal the matching elasticity, so we set . This also satisfies .
The separation rate is taken from Miyamoto (2011), who estimate a monthly separation probability of . At quarterly frequency, this implies a total separation rate of . The quarterly real interest rate, r, is set to . The steady-state level of productivity, A, is normalized to 1. Finally, the TFP () process, evolving according to a first-order autoregressive process, , is calibrated following Kudoh et al. (2019), with a persistence of and a shock standard deviation of .
Next, we use empirical targets to pin down key variables in the model’s steady state. The central variable in the search-and-matching framework is labor market tightness, . We target the average vacancy–unemployment ratio of for Japan, as reported by Miyamoto (2011).
With determined, we can now identify the matching efficiency parameter, a. We follow the method of Lin and Miyamoto (2012), who report a monthly job-finding rate of . This implies a quarterly job-finding rate of . In the model, the job-finding rate is given by . Using our target for and the calibrated value for , we can solve for the matching efficiency .
Finally, the remaining parameters, the value of unemployment benefit b, and the vacancy cost c are calibrated to be consistent with the model’s steady-state equilibrium. Based on Nickell (1997), who reports a replacement rate of in Japan, we set the unemployment benefit to , where w is the steady-state wage. With all other parameters and steady-state values now determined, the vacancy cost, c, is chosen to ensure the model’s job creation condition holds in the steady state. This procedure yields a value of .
To facilitate direct comparison with the RL experiments, we ensure that both approaches use identical parameter values, shock processes, and initial conditions.
3.2. The Log-Linearization Approach
We first solve the model using the conventional method employed in the vast majority of the DSGE literature. This approach relies on creating a log-linearized approximation of the model, which we implement using the standard Dynare software package (version 6.4).
The core challenge in solving DSGE models is that their equilibrium conditions form a system of nonlinear difference equations that typically lacks a closed-form analytical solution. One solution is to approximate the model’s dynamics locally around its deterministic steady state through log-linearization, a technique that applies a first-order Taylor approximation to the logarithmic form of the model’s equations. The key advantage of this method is that it transforms the complex nonlinear system into a tractable set of linear equations where all variables are interpreted as percentage deviations from their steady-state values, well suited to business cycle analysis.
The implementation in Dynare follows the standard procedure of representing the model’s equilibrium conditions in a form suitable for numerical solution. Dynare computes the deterministic steady state of the system, which serves as the reference point for subsequent analysis. Around this steady state, the equilibrium conditions are log-linearized, reducing the original nonlinear system into a linear system of equations. This linearized system allows for efficient computation of impulse response functions and stochastic simulations under exogenous shocks.
In the experiment, productivity shocks are introduced as a persistent exogenous process, following the conventional autoregressive specification widely used in dynamic stochastic general equilibrium analysis. These shocks generate time variation in output and labor market variables. The Dynare implementation then simulates the dynamics of the model in response to these shocks, with all simulated variables expressed as deviations from their deterministic steady-state values.
3.3. The RL Approach
We formalize the search-and-matching framework as an RL environment. To set up an RL agent, it is sufficient to specify the state variables, the available actions, and the state transition dynamics. In each period, the agent observes the current state and selects an action accordingly. The baseline state variables consist of employment () and the unemployment rate (). For our experiment, we additionally incorporate a productivity shock, so productivity () is also included in the state space. The agent’s action corresponds to the number of vacancies () it chooses to create. The reward is defined as the firm’s income net of expenditures, which include wage payments and the costs of posting vacancies. A concise summary of the RL components, together with the corresponding transition functions, is provided in Table 2.

Table 2.
Components of RL.
The optimal policy for this RL environment is learned by the DDPG algorithm (Lillicrap et al., 2016), which maintains two parameterized networks: an actor and a critic.
- Actor Network: The policy function translates observed states into continuous control actions. It is implemented as a three-layer fully connected neural network with ReLU activations in the hidden layers and a final tanh transformation to ensure bounded outputs.
- Critic Network: The value estimator receives both the state and action as input and predicts their Q-value. It follows the same three-layer feedforward structure, with the state–action pair concatenated at the input layer.
Both networks use 256 hidden units per layer. The policy (actor) is optimized using the Adam optimizer with a step size of , while the value function (critic) is updated with a higher rate of . Target networks are updated by Polyak averaging with coefficient , and the discount factor is fixed at . Experience replay is handled by a buffer that stores up to transitions. During training, mini-batches of 256 samples are drawn to update the networks. Following the DDPG algorithm, updates alternate between critic and actor steps, with target networks softly adjusted at each iteration.
Training proceeds over 50 simulated episodes per iteration, each lasting 200 steps. As noted by Zhang and Chen (2025), a straightforward single-agent RL setup often drives the agent to act as a manipulator of its environment. To mitigate this issue, we adopt a mean-field game perspective and stabilize the system by fixing the value of within each run. After training, the system is restarted and executed for 400 steps to ensure convergence to equilibrium, followed by an additional 100 steps used solely for evaluation and analysis. For the results, all variables are reported in logs.
4. Simulation Result
Table 3 and Table 4 present the standard deviations and correlation patterns of the main labor market variables generated by the simulation in Dynare and by the RL framework.

Table 3.
Comparison of standard deviations: Dynare vs. RL.

Table 4.
Comparison of correlations: Dynare vs. RL.
First, the overall correlation structure is remarkably consistent across the two approaches. In particular, both models reproduce the negative relationship between unemployment and vacancies, with correlations of in Dynare and in RL. This result aligns with the empirically observed Beveridge curve and indicates that the RL-based simulation is not only theoretically coherent but also capable of reproducing one of the central stylized facts in labor market dynamics. The robustness of this negative association across methods provides reassurance that the RL framework remains grounded in the same theoretical mechanisms as the DSGE benchmark.
Second, there are significant differences in the magnitude of fluctuations. For unemployment rates, job vacancies, and labor market tightness, the standard deviation shown by the RL model is approximately several times that produced by the Dynare model. Since the job vacancy fill rate (q) and employment rate (Q) are mechanically linked to labor market tightness, their volatility is also enhanced in the RL framework. This increased variability provides a possible explanation for the Shimer puzzle. While the DSGE framework relies on rational expectations, RL agents introduce additional sources of noise and nonlinear adjustments in decision-making. Such mechanisms can generate larger fluctuations that may be closer to real-world labor market dynamics, where imperfect rationality, bounded information, and heterogeneous behaviors contribute to excess volatility that standard DSGE models fail to capture.
Third, employment rates remain at a relatively high level in both simulations, implying that their percentage deviations from the steady state are small. Since wages are primarily determined by the employment rate, their volatility also remains limited in both approaches, with only modest differences between Dynare and RL.
To examine the dynamic properties of our search and matching model, we also conduct impulse response analysis following a one-standard-deviation positive technology shock. We compare the responses generated by the linearized DSGE model with those obtained from the RL agent trained to optimize firm behavior in the same economic environment. The results are shown in Figure 2.
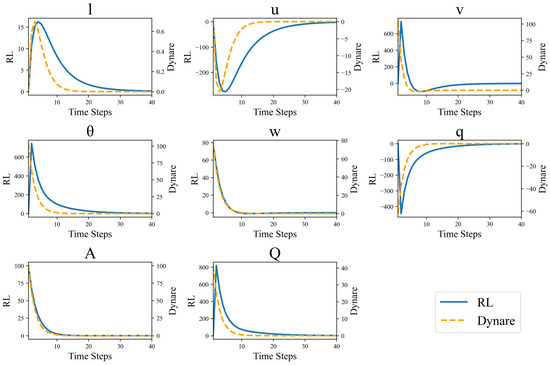
Figure 2.
System dynamics following an impulse shock to productivity. The orange dotted lines depict the responses generated by the linearized DSGE model in Dynare, while the blue solid lines represent the responses of the RL agent.
The impulse response functions are computed under identical initial conditions, with both approaches subjected to a technology shock of magnitude at period zero.
The DSGE approach relies on the log-linearized system of equations around the deterministic steady state, yielding responses that are inherently symmetric and proportional to the shock magnitude. In contrast, the RL framework employs agents that have learned optimal decision rules through interaction with the nonlinear economic environment, potentially capturing asymmetries and state-dependent responses that linear models cannot represent.
The difference between the two approaches is their convergence properties. The linearized DSGE model demonstrates rapid return to the steady state, with all variables converging to their long-run equilibrium within approximately 15 periods. In contrast, the RL-based simulation exhibits significantly slower convergence, requiring approximately 30 periods for the system to return to equilibrium. This extended adjustment period suggests that the nonlinear optimization behavior captured by the RL agents incorporates additional adjustment costs or strategic considerations not present in the linear approximation. Long-term convergence may reflect more realistic agent behavior, where adjustment decisions involve complex state-dependent trade-offs between current costs and future benefits.
The magnitude difference between the two methods is particularly striking. However, both methods exhibit similar qualitative directional responses—employment and labor market tightness increase while unemployment rates decline. The response magnitude generated by the RL framework is larger than that predicted by the linearized model. Specifically, the peak deviation in employment responses in RL simulations is approximately 25 times that when using Dynare, while the volatility of unemployment responses is approximately 10 times. Labor market tightness and job vacancy variables exhibit even more pronounced differences, with RL responses exceeding DSGE predictions by approximately 6 times and 20 times.
These differences reveal several important considerations. The consistency of directional responses under different methodological approaches provides validation for the economic mechanisms captured by the search-and-matching framework. Both methods correctly predicted that positive technological shocks would strengthen employment creation incentives, tighten the labor market, and reduce unemployment rates. The amplified responses in the RL framework suggest that linearization may significantly underestimate the true volatility of labor market variables following a technological shock. This finding has important implications for policy analysis as linear models may systematically underestimate the magnitude of labor market volatility and the time required for adjustment.
5. Conclusions
This paper develops a DRL implementation of a search-and-matching labor market and compares it to a linearized DSGE benchmark. A foundational result is that the DRL agent successfully generates a negative correlation between unemployment and vacancies (the Beveridge curve) and ensures that labor market tightness and job-finding rates move in parallel with productivity. This consistency provides an important validation, demonstrating that our DRL approach captures the fundamental economic mechanisms of the search-and-matching model. Building on this, our central finding is that the DRL model produces significantly greater fluctuations and converges more slowly than the linearized DSGE method. This suggests that the adaptive, state-dependent policies learned by the agent act as a powerful endogenous amplification mechanism, offering a complementary reading of the Shimer puzzle where plausible volatility arises from bounded rationality and learning dynamics.
However, our approach has several limitations. First, our model is stylized, featuring a representative firm and focusing solely on TFP shocks, thereby abstracting from the rich dynamics of agent heterogeneity and the extensive margin of entry and exit. A broader challenge is the interpretability of DRL agents. Unlike the structural parameters of DSGE models, the agent’s policy is embedded in a neural network, creating a “black box” that is difficult to map directly to economic theory. Furthermore, the RL paradigm is best suited for sequential decision problems and may be less appropriate for static equilibrium models or pure forecasting tasks where other methods excel. Finally, the computational intensity and hyperparameter sensitivity of DRL pose challenges for replication and robustness.
These limitations highlight promising avenues for future research. An immediate extension is to incorporate heterogeneous agents to analyze the distributional consequences of business cycles. To address the “black box” problem, future work could integrate techniques from explainable AI (XAI), such as SHAP value analysis, to provide clearer economic intuition for the agent’s learned policy (Lundberg & Lee, 2017; Milani et al., 2024). The framework is also well-suited for policy experiments, such as analyzing how firms learn to adapt to changes in unemployment insurance. Finally, moving to a multi-agent reinforcement learning (MARL) setting could open new avenues for studying strategic interaction and equilibrium formation in markets with learning agents, bridging the gap between macroeconomic modeling and game theory (Albrecht et al., 2024).
Funding
This research received no external funding.
Data Availability Statement
The raw data and code supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DDPG | Deep deterministic policy gradient |
| DMP | Diamond Mortensen Pissarides Model |
| DRL | Deep reinforcement learning |
| DSGE | Dynamic stochastic general equilibrium |
| MARL | Multi-agent reinforcement learning |
| RL | Reinforcement learning |
| TFP | Total factor productivity |
| XAI | Explainable AI |
Appendix A. Derivation of the Wage Equation
This appendix provides the derivation of the wage equation presented in Section 2. The derivation begins with the firm’s optimization problem and combines it with the Nash bargaining condition that splits the match surplus between the firm and the marginal worker.
First, we restate the firm’s value function and its key equilibrium conditions. The value of the firm is
The firm’s first-order condition (FOC) with respect to vacancies, , is
and the envelope condition is
The wage is determined by a generalized Nash bargaining process that splits the match surplus between the firm and the marginal worker. This is captured by the following condition, where is the worker’s bargaining power:
Here, represents the firm’s surplus from the marginal worker, and represents the worker’s surplus.
To solve for the wage, our first step is to find a non-recursive expression for the worker’s surplus. By subtracting the value of unemployment from the value of employment, we obtain a recursive expression for the surplus:
To solve this forward-looking equation, we need an expression for the future surplus, . We can find this by linking it to the firm’s future surplus, , using the Nash bargaining condition (Equation (A4)) for period :
The firm’s future surplus, can be found by rearranging its FOC for vacancy posting (Equation (A2)):
Substituting this into the expression for the future worker surplus gives
Finally, substituting this result back into our recursive equation (Equation (A5)) for the worker’s surplus yields a closed-form solution for the current surplus:
The final step is to substitute our expressions for the firm’s surplus (from the envelope condition, Equation (A3)) and the worker’s surplus (Equation (A9)) back into the original Nash bargaining condition (Equation (A4)). We arrive at the following first-order ordinary differential equation (ODE) for the wage function:
Solving this linear first-order ODE and applying the specific functional form for production (Equation (6)) yields the particular solution for the wage equation presented in the main text:
Appendix B. Steady-State Equations
This appendix presents the system of equations that pin down the deterministic steady state, the long-run values around which the model fluctuates.
In the steady state, the marginal cost of posting a vacancy equals the expected discounted marginal benefit of filling it. We obtain this by combining the firm’s first-order condition (Equation (A2)) with the envelope condition (Equation (A3)) and evaluating them at the steady state. This yields the general job creation condition:
Then, we substitute the specific functional forms for the production function (Equation (6)) and the bargained wage (Equation (11)) into the general job creation condition. This results in the following detailed equilibrium equation:
This equation forms a system of six equations in six unknowns together with the following five definitional and behavioral equations that close the model:
This system of nonlinear equations can be solved simultaneously for the steady-state values of the endogenous variables, which serve as the basis for the log-linearization and the initial state for the RL agent.
References
- Albrecht, S. V., Christianos, F., & Schäfer, L. (2024). Multi-agent reinforcement learning: Foundations and modern approaches. MIT Press. [Google Scholar]
- Arthur, W. B. (1991). Designing economic agents that act like human agents: A behavioral approach to bounded rationality. The American Economic Review, 81(2), 353–359. [Google Scholar]
- Arulkumaran, K., Deisenroth, M. P., Brundage, M., & Bharath, A. A. (2017). Deep reinforcement learning: A brief survey. IEEE Signal Processing Magazine, 34(6), 26–38. [Google Scholar] [CrossRef]
- Ashwin, J., Beaudry, P., & Ellison, M. (2021). The unattractiveness of indeterminate dynamic equilibria. Centre for Economic Policy Research. [Google Scholar]
- Atashbar, T., & Shi, R. A. (2022, December). Deep reinforcement learning: Emerging trends in macroeconomics and future prospects (IMF Working Papers No. 2022/259). International Monetary Fund. Available online: https://ideas.repec.org/p/imf/imfwpa/2022-259.html (accessed on 1 September 2025).
- Barto, A. G., & Singh, S. P. (1991). Reinforcement learning in artificial intelligence. Advances in Psychology, 121, 358–386. [Google Scholar]
- Calvano, E., Calzolari, G., Denicolo, V., & Pastorello, S. (2020). Artificial intelligence, algorithmic pricing, and collusion. American Economic Review, 110(10), 3267–3297. [Google Scholar] [CrossRef]
- Castro, P. S., Desai, A., Du, H., Garratt, R., & Rivadeneyra, F. (2025). Estimating policy functions in payment systems using reinforcement learning. ACM Transactions on Economics and Computation, 13(1), 1–31. [Google Scholar] [CrossRef]
- Chen, M., Joseph, A., Kumhof, M., Pan, X., Shi, R., & Zhou, X. (2021). Deep reinforcement learning in a monetary model. arXiv, arXiv:2104.09368v2. [Google Scholar]
- Chen, R., & Zhang, Z. (2025, March 17–20). Deep reinforcement learning in labor market simulations. 2025 IEEE Symposium on Computational Intelligence for Financial Engineering and Economics (CiFer) (pp. 1–7), Trondheim, Norway. [Google Scholar]
- Covarrubias, M. (2022). Dynamic oligopoly and monetary policy: A deep reinforcement learning approach. Available online: https://drive.google.com/file/d/1ivRIzPRzMr_Hlqrq6WsiQNlxxr1q0ZE_/view (accessed on 1 September 2025).
- Curry, M., Trott, A., Phade, S., Bai, Y., & Zheng, S. (2022). Finding general equilibria in many-agent economic simulations using deep reinforcement learning. arXiv, arXiv:2201.01163. [Google Scholar]
- Elsby, M. W. L., & Michaels, R. (2013). Marginal jobs, heterogeneous firms, and unemployment flows. American Economic Journal: Macroeconomics, 5(1), 1–48. [Google Scholar] [CrossRef]
- Evans, B. P., & Ganesh, S. (2024, May 6–10). Learning and calibrating heterogeneous bounded rational market behaviour with multi-agent reinforcement learning. 23rd International Conference on Autonomous Agents and Multiagent Systems (pp. 534–543), Auckland, New Zealand. [Google Scholar]
- Gertler, M., & Trigari, A. (2009). Unemployment fluctuations with staggered Nash wage bargaining. Journal of Political Economy, 117(1), 38–86. [Google Scholar] [CrossRef]
- Hagedorn, M., & Manovskii, I. (2008). The cyclical behavior of equilibrium unemployment and vacancies revisited. American Economic Review, 98(4), 1692–1706. [Google Scholar] [CrossRef]
- Hall, R. E. (2005). Employment fluctuations with equilibrium wage stickiness. American Economic Review, 95(1), 50–65. [Google Scholar] [CrossRef]
- Hernandez-Leal, P., Kartal, B., & Taylor, M. E. (2020, May 9–13). A very condensed survey and critique of multiagent deep reinforcement learning. 19th International Conference on Autonomous Agents and Multiagent Systems (pp. 2146–2148), Auckland, New Zealand. [Google Scholar]
- Hill, E., Bardoscia, M., & Turrell, A. (2021). Solving heterogeneous general equilibrium economic models with deep reinforcement learning. arXiv, arXiv:2103.16977. [Google Scholar] [CrossRef]
- Hinterlang, N., & Tänzer, A. (2021). Optimal monetary policy using reinforcement learning (Deutsche Bundesbank Discussion Paper). Deutsche Bundesbank. [Google Scholar]
- Hosios, A. J. (1990). On the efficiency of matching and related models of search and unemployment. The Review of Economic Studies, 57(2), 279–298. [Google Scholar] [CrossRef]
- Jirnyi, A., & Lepetyuk, V. (2011). A reinforcement learning approach to solving incomplete market models with aggregate uncertainty. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1832745 (accessed on 1 September 2025).
- Johnson, D., Chen, G., & Lu, Y. (2022). Multi-agent reinforcement learning for real-time dynamic production scheduling in a robot assembly cell. IEEE Robotics and Automation Letters, 7(3), 7684–7691. [Google Scholar] [CrossRef]
- Kaas, L., & Kircher, P. (2015). Efficient firm dynamics in a frictional labor market. American Economic Review, 105(10), 3030–3060. [Google Scholar] [CrossRef]
- Kudoh, N., Miyamoto, H., & Sasaki, M. (2019). Employment and hours over the business cycle in a model with search frictions. Review of Economic Dynamics, 31, 436–461. [Google Scholar] [CrossRef]
- Lee, D., Seo, H., & Jung, M. W. (2012). Neural basis of reinforcement learning and decision making. Annual Review of Neuroscience, 35(1), 287–308. [Google Scholar] [CrossRef]
- Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D., & Wierstra, D. (2016, May 2–4). Continuous control with deep reinforcement learning. 4th International Conference on Learning Representations, San Juan, Puerto Rico. [Google Scholar]
- Lin, C.-Y., & Miyamoto, H. (2012). Gross worker flows and unemployment dynamics in Japan. Journal of the Japanese and International Economies, 26(1), 44–61. [Google Scholar] [CrossRef]
- Lin, C.-Y., & Miyamoto, H. (2014). An estimated search and matching model of the Japanese labor market. Journal of the Japanese and International Economies, 32, 86–104. [Google Scholar] [CrossRef]
- Lundberg, S. M., & Lee, S.-I. (2017). A unified approach to interpreting model predictions. Advances in Neural Information Processing Systems, 30, 4768–4777. [Google Scholar]
- Maliar, L., Maliar, S., & Winant, P. (2021). Deep learning for solving dynamic economic models. Journal of Monetary Economics, 122, 76–101. [Google Scholar] [CrossRef]
- Milani, S., Topin, N., Veloso, M., & Fang, F. (2024). Explainable reinforcement learning: A survey and comparative review. ACM Computing Surveys, 56(7), 1–36. [Google Scholar] [CrossRef]
- Miyamoto, H. (2011). Cyclical behavior of unemployment and job vacancies in Japan. Japan and the World Economy, 23(3), 214–225. [Google Scholar] [CrossRef]
- Mortensen, D. T., & Nagypal, E. (2007). More on unemployment and vacancy fluctuations. Review of Economic Dynamics, 10(3), 327–347. [Google Scholar] [CrossRef]
- Nickell, S. (1997). Unemployment and labor market rigidities: Europe versus North America. Journal of Economic Perspectives, 11(3), 55–74. [Google Scholar] [CrossRef]
- Petrosky-Nadeau, N., & Zhang, L. (2017). Solving the diamond–mortensen–pissarides model accurately. Quantitative Economics, 8(2), 611–650. [Google Scholar] [CrossRef]
- Pissarides, C. A. (2000). Equilibrium unemployment theory (2nd ed.). The MIT Press. [Google Scholar]
- Pissarides, C. A. (2009). The unemployment volatility puzzle: Is wage stickiness the answer? Econometrica, 77(5), 1339–1369. [Google Scholar] [CrossRef]
- Puterman, M. L. (2014). Markov decision processes: Discrete stochastic dynamic programming. John Wiley & Sons. [Google Scholar]
- Sargent, T. (1993). Bounded rationality in macroeconomics. Oxford University Press. [Google Scholar]
- Shi, R. A. (2023). Deep reinforcement learning and macroeconomic modelling [Ph.D. thesis, University of Warwick]. [Google Scholar]
- Shimer, R. (2005). The cyclical behavior of equilibrium unemployment and vacancies. American Economic Review, 95(1), 25–49. [Google Scholar] [CrossRef]
- Smith, E. (1999). Search, concave production, and optimal firm size. Review of Economic Dynamics, 2(2), 456–471. [Google Scholar] [CrossRef]
- Zhang, Z., & Chen, R. (2025). From individual learning to market equilibrium: Correcting structural and parametric biases in RL simulations of economic models. arXiv, arXiv:2507.18229. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).