Abstract
This study presents a bibliometric and thematic analysis of economic convergence analysis from 1982 to 2025, based on a corpus of 2924 Scopus-indexed articles. Using VOSviewer and the bibliometrix R package, this research maps the field’s intellectual structure, identifying five main thematic clusters: (1) formal statistical models, (2) institutional-contextual approaches, (3) theoretical–statistical foundations, (4) nonlinear historical dynamics, and (5) normative and policy assessments. These reflect a shift from descriptive to explanatory and prescriptive frameworks, with growing integration of sustainability, spatial analysis, and institutional factors. The most productive journals include Journal of Econometrics (121 articles), Applied Economics (117), and Journal of Cleaner Production (81), while seminal contributions by Quah, Im et al., and Levin et al. anchor the co-citation network. International collaboration is significant, with 25.99% of publications involving cross-country co-authorship, particularly in European and North American networks. The field has grown at a compound annual rate of 14.4%, accelerating after 2000 and peaking in 2022–2024, indicating sustained academic interest. These findings highlight the maturation of convergence analysis as a multidisciplinary domain. Practically, this study underscores the value of composite indicators and spatial econometric models for monitoring regional, environmental, and technological convergence—offering policymakers tools for inclusive growth, climate resilience, and innovation strategies. Moreover, the emergence of clusters around sustainability and digital transformation reveals fertile ground for future research at the intersection of transitions in energy, digital, and institutional domains and sustainable development (a broader sense of structural change).
1. Introduction
The study of economic convergence has its theoretical foundations in the neoclassical growth model of Solow (1956) and the empirical frameworks developed by Barro and Sala-i-Martin (1992), which established the conditions under which poorer economies tend to grow faster than richer ones, closing income gaps over time. These foundational theories, centered on the concepts of absolute and conditional convergence, have shaped decades of research on structural adjustment and development dynamics. However, the field has since evolved beyond its original econometric and growth theory roots, expanding into institutional, spatial, technological, and sustainability-oriented domains—a transformation that has not yet been systematically mapped.
The economic convergence analysis has gained increasing importance today due to the profound structural, technological, social, and environmental transformations faced by economies and territories within a global context characterized by interdependence, technological disruption, pressure on natural resources, and new sustainable development challenges. Within this framework, convergence is not merely a technical–economic phenomenon but a critical category for evaluating the effectiveness of public policies, compliance with international commitments, and progress toward scenarios of greater equity, resilience, and regional integration (Agovino et al., 2021; M. Ahmad & Law, 2024; Akram et al., 2023; Maza & Villaverde, 2009a, 2009b, 2011).
Despite the extensive literature on convergence, a significant gap remains: most studies focus on isolated methodological approaches or specific thematic domains, lacking a comprehensive, integrative bibliometric and thematic mapping that captures the full intellectual structure and evolutionary trajectory of the field, particularly in the 2015–2025 period. Previous reviews have not systematically combined quantitative network analysis with qualitative content synthesis to identify emerging clusters, influential contributions, and underexplored research frontiers. This study addresses that gap by offering a holistic, up-to-date analysis that integrates bibliometric rigor with thematic depth, thereby providing a structured overview of how the field has evolved conceptually, methodologically, and geographically.
The theoretical body developed around convergence analysis during the 2015–2025 period draws upon classical frameworks such as those formulated by Barro and Sala-i-Martin (1992) and Sala-i-Martin (1994), as well as their subsequent developments (Sala-i-Martin, 1996, 2006), while also incorporating substantial methodological advancements. Contemporary studies, beyond examining the empirical existence of convergence, have expanded their scope to include the identification of structural and contingent mechanisms that determine it, as well as its interaction with institutional, spatial, institutional development, and sectoral integration.
This thematic breadth is accompanied by a richer conceptualization that distinguishes various forms of convergence: absolute, conditional, club-based or subgroup convergence, as well as spatial and temporal convergence. Moreover, the notion of convergence as an indicator of systemic efficiency has been introduced, interpreting it as a sign of collective improvement in the performance of analyzed systems, without necessarily assuming an equitable distribution of the benefits (Ab-Rahim et al., 2018; N. Ahmad et al., 2019; Akram et al., 2023; Alataş, 2023).
From an epistemological perspective, convergence analysis is framed within a relational and evolutionary approach. It is relational because it does not examine the attributes of a unit in absolute terms, but rather in terms of its comparative evolution relative to others. It is also evolutionary, as the focus is not solely on static levels, but on cumulative change processes and structural adaptation over time (Adeeko et al., 2023; Aghion & Jaravel, 2015).
Hence, convergence is closely linked to concepts such as organizational learning, technology transfer, institutional integration, regulatory harmonization, and territorial cohesion (Aaldering et al., 2019; M. Ahmad & Law, 2024). At a more abstract level, convergence can be understood as an emergent property of complex adaptive systems, in which multiple agents interact, learn, and adjust their behavior based on shared signals, thereby generating progressive patterns of alignment over time. Within this framework, the concept of convergence connects to dynamics such as coevolution, synchronization, systemic resilience, and adaptive feedback (Agovino et al., 2021; M. Ahmad & Law, 2024).
In this regard, economic convergence studies not only provide valuable insights for the academic understanding of structural adjustment processes but also offer a rigorous empirical foundation for the design of strategies aimed at reducing territorial or sectoral disparities (Hi, 2020; Hryhorkiv et al., 2017; Jadhav, 2023; Ud Din et al., 2023). The utility of convergence analysis lies precisely in its potential to generate actionable knowledge for decision-making in areas such as regional planning, public policy design, and the assessment of structural reforms.
Moreover, convergence analysis is vital for monitoring the distributive effects of contemporary structural transitions. In the context of the energy transition, digitalization, and the implementation of the Sustainable Development Goals (SDGs), convergence allows for the assessment of whether the benefits of these processes are being shared equitably or whether “multiple trajectories” are emerging, where only certain groups, regions, or sectors capture the gains from change (Agovino et al., 2021; Akhtar et al., 2024; Akram et al., 2024).
Convergence analysis acquires strategic value within the sustainability and resilience agenda. In a world marked by increasing asymmetries of power, technology access, and exposure to global risks, studying convergence enables the projection of future scenarios of cohesion or fragmentation, integration or polarization, and shared prosperity or exclusionary growth. Evaluating whether territories and sectors are approaching minimum desirable levels of well-being, efficiency, or sustainability is no longer merely a descriptive exercise but a prerequisite for designing inclusive, sustainable, and adaptive pathways (Dhaigude et al., 2025; M. Hu et al., 2025; Navarro Claro & Bayona Soto, 2025).
In terms of its current relevance, convergence analysis offers an appropriate framework to address critical questions regarding territorial justice, intertemporal equity, resilience to crises, and the distributive effectiveness of public policies. In the context of structural transitions such as digitalization, decarbonization, or the achievement of the SDGs, assessing the presence or absence of convergence becomes a normative criterion to judge the inclusive or exclusionary nature of these transformations (Eleftheriou et al., 2024; Goto & Sueyoshi, 2023).
Unlike previous reviews of convergence studies, this paper makes a distinctive contribution in three complementary dimensions. First, the temporal scope spans more than four decades (1982–2025), which allows us to trace both the foundational roots of the literature and the most recent developments related to sustainability, digitalization, and the energy transition. Second, the methodological integration combines advanced bibliometric tools (VOSviewer version 1.6.20, bibliometrix package in R version 4.4.3) with a systematic qualitative analysis of thematic clusters, ensuring not only the identification of citation patterns but also the substantive interpretation of underlying theoretical and methodological frameworks. Third, the study adopts an explicit orientation toward economic policy and sustainable development, showing how bibliometric findings translate into strategic implications for public policy design, territorial cohesion, and resilience to global crises.
This threefold contribution positions the article as an integrative effort that goes beyond the fragmentation of earlier reviews, by simultaneously providing a comprehensive map of intellectual evolution, a rigorous methodological characterization, and a normative connection to contemporary challenges of equity and sustainability. In this way, the research consolidates convergence analysis as a tool not only for academic inquiry but also for strategic policy formulation in the twenty-first century.
Against this backdrop, the present study aims to conduct a comprehensive and systematic analysis of recent literature on convergence analysis, with the goal of constructing a robust theoretical framework for understanding its foundations, applications, and current challenges. This review seeks to identify the main conceptual and methodological contributions in the field, as well as to detect underexplored areas requiring further attention. By integrating theoretical and empirical perspectives, the study intends to offer a meaningful contribution to the specialized literature, providing analytical inputs useful for both the development of new research and the design of evidence-based policies. Specifically, the objectives are: (1) to map the intellectual structure of the field through bibliometric analysis; (2) to identify dominant thematic clusters and their evolution; (3) to highlight the role of technological, institutional, and policy dimensions in shaping convergence research; and (4) to propose future research directions grounded in the identified gaps.
In this sense, understanding and managing convergence processes becomes an essential competence for designing effective responses to the challenges of the 21st century (Celati, 2023; F. Fan et al., 2025; Koutsougeras & Meo, 2018; T. Nguyen et al., 2024; Pattinson & Woodside, 2007).
The remainder of this paper is structured as follows. Section 2 presents a comprehensive literature review aligned with our first two research objectives. It examines the conceptual foundations of convergence analysis (Section 2.1), evaluates its relevance to structural transitions toward sustainability and equity (Section 2.2), analyzes methodological approaches and their applications (Section 2.3), and positions convergence as a strategic analytical category for policy design (Section 2.4). Building on this theoretical foundation, Section 3 outlines our mixed-methods bibliometric approach to mapping the intellectual structure of the field and identifying key thematic clusters. Section 4 presents empirical findings, while Section 5 discusses their implications and outlines future research directions. Finally, Section 6 offers concluding reflections that connect our methodological and theoretical contributions to the broader normative challenges of designing inclusive pathways in the twenty-first century. This structure supports our aim of bridging the gap between empirical insights and their strategic application to equity and sustainability.
2. Literature Review
Convergence analysis has emerged as a key tool for understanding adjustment dynamics among economies, sectors, or regions in their development trajectories. In general terms, convergence refers to the process through which units of analysis—whether countries, regions, industries, or other aggregates—tend to reduce disparities in income levels, productivity, infrastructure, or environmental indicators, moving toward a common steady state or a set of equilibria (Akram et al., 2023; Alataş, 2023). The relevance of the concept has transcended the traditional focus exclusively on per capita income, expanding into domains such as carbon emissions (Akram et al., 2024; Tang et al., 2025; Zhong et al., 2025), social public spending (Akram et al., 2023; Mishra et al., 2020; Onaran et al., 2022b), and energy efficiency (Alataş et al., 2021; D. Fan et al., 2024; Hou et al., 2024).
2.1. Conceptualizing Convergence Analysis
The concept of convergence has gained a central position in economic analysis—as well as in other social and environmental disciplines—as a theoretical and empirical framework for evaluating the evolution of disparities among heterogeneous units over time. Its most classical formulation originates in the field of economic growth, where it is posited that, under certain assumptions, economies with lower income levels will tend to grow faster than wealthier ones, thereby converging toward a common steady state (Alataş, 2023; Alemu et al., 2024). However, the concept has undergone substantial semantic and methodological expansion in recent decades, leading to its application in structural, social, technological, institutional, and environmental contexts (Agovino et al., 2021; M. Ahmad & Law, 2024; Akram & Ali, 2022).
In general terms, convergence can be defined as a dynamic process in which observed differences among units—whether countries, regions, sectors, organizations, or individuals—tend to diminish over time with respect to a specific attribute or set of attributes. This implies a trajectory of alignment toward a common reference pattern or a shared pathway (Ab-Rahim et al., 2018; Alataş, 2023). The notion requires a longitudinal and comparative perspective, whereby measuring the relative or absolute distance between units across multiple time periods allows for inferences about structural, institutional, or performance-based alignment trends. Convergence, in this sense, is not a static point but rather a behavioral tendency that may be total, partial, conditional, fragile, or even reversible, depending on the adjustment mechanisms involved (N. Ahmad et al., 2019; Akram et al., 2023).
From an epistemological perspective, convergence analysis is framed within a relational and evolutionary approach. It is relational because it does not examine the attributes of a unit in absolute terms, but rather in terms of its comparative evolution relative to others. It is also evolutionary, as the focus is not solely on static levels, but on cumulative change processes and structural adaptation over time (Adeeko et al., 2023; Aghion & Jaravel, 2015). Hence, convergence is closely linked to concepts such as organizational learning, technology transfer, institutional integration, regulatory harmonization, and territorial cohesion (Aaldering et al., 2019; M. Ahmad & Law, 2024).
Convergence analysis also draws on a plural conceptualization in terms of its forms and categories. Literature traditionally distinguishes between absolute (or unconditional) convergence and conditional convergence. Absolute convergence posits that all units will tend toward the same steady state regardless of their initial conditions, implying strong structural homogeneity among them.
In contrast, conditional convergence acknowledges that units may converge toward their own steady states if they share similar structural characteristics—such as savings rates, levels of human capital, or institutional quality—thus allowing for heterogeneity (Alataş, 2023; Alemu et al., 2024). This distinction not only enables the classification of evolution patterns but also supports theorizing about the structural determinants that facilitate or hinder convergence processes.
Moreover, the notion of convergence can be analyzed at different levels of aggregation. Sigma convergence (σ-convergence) refers to a reduction in the statistical dispersion (variance or standard deviation) among units over time, whereas beta convergence (β-convergence) assesses whether units with lower initial levels of a given attribute exhibit higher growth rates, as an expression of compensatory dynamics (N. Ahmad et al., 2019; Alataş, 2023). Although conceptually related, these two approaches are not equivalent: β-convergence is a necessary but not sufficient condition for σ-convergence, which suggests that adjustment mechanisms do not always lead to an effective narrowing of gaps (Ab-Rahim et al., 2018; Akram et al., 2024).
Another central component in contemporary conceptualization is the notion of club convergence, which posits that not all units converge toward a single equilibrium, but rather that there are subsets that share common adjustment trajectories toward differentiated equilibria. These patterns reflect similarities in productive structures, capital endowments, or institutional conditions (Aboal et al., 2023; Akram & Ali, 2022). This approach acknowledges the existence of multiple equilibria and development paths, thereby expanding the analytical scope of the classical paradigm and aligning with theories of path dependence and capability-driven growth.
To clarify the distinctions among these forms of convergence and their empirical applications, Table 1 synthesizes four principal types identified in the literature: absolute β-convergence, conditional β-convergence, σ-convergence, and club convergence, providing concise definitions, illustrative examples, and key references.

Table 1.
Types of Economic Convergence: Definitions, Examples, and Key References from Literature *.
At a more abstract level, convergence can be understood as an emergent property of complex adaptive systems, in which multiple agents interact, learn, and adjust their behavior based on shared signals, thereby generating progressive patterns of alignment over time. Within this framework, the concept of convergence connects to dynamics such as coevolution, synchronization, systemic resilience, and adaptive feedback (Agovino et al., 2021; M. Ahmad & Law, 2024). Incorporating this complex system’s perspective has led to an expansion of the notion of convergence beyond purely quantitative parameters toward qualitative dimensions such as institutional quality, governance, and shared values.
Convergence, as a concept, represents a versatile and expanding analytical category that enables the capture of directional adjustment processes across units in multiple domains. Its conceptual richness lies in its capacity to describe dynamics of alignment, integration, or synchronization over time, as well as in its cross-cutting applicability across different levels of analysis and types of systems. Consequently, its application requires not only conceptual clarity, but also methodological rigor and a well-defined problematization of the phenomenon under study.
2.2. Contemporary Relevance of Convergence Studies
The study of convergence analysis has gained increasing importance due to the profound structural, technological, social, and environmental transformations faced by economies and territories within a global context marked by interdependence, technological disruption, resource pressures, and sustainable development challenges. Within this framework, convergence is not merely a technical–economic phenomenon but a critical category for evaluating the effectiveness of public policies, compliance with international commitments, and progress toward greater equity, resilience, and regional integration (Agovino et al., 2021; M. Ahmad & Law, 2024; Akram et al., 2023).
A central justification for the current interest in convergence analysis lies in its capacity to detect persistent patterns of structural inequality—both between countries and across regions within the same state. While economic integration, trade liberalization, and technological diffusion are often expected to homogenize productive and institutional capacities, empirical evidence reveals a more complex reality: convergence is neither automatic nor universal. Studies show that gaps in income, human capital, productivity, and infrastructure often persist or even widen, challenging assumptions of automatic equalization (Alataş, 2023; Alemu et al., 2024). For instance, Padilla et al. (2024) document structural heterogeneity and divergence within the European Monetary Union, highlighting the fragility of convergence under asymmetric shocks. This diagnostic function is fundamental for designing cohesion policies, territorial redistribution, and balanced development strategies.
Moreover, convergence analysis is essential for monitoring the distributive effects of contemporary structural transitions. In the context of energy transition, digitalization, and the SDGs, it allows assessment of whether benefits are shared equitably or whether “multiple trajectories” emerge, where only certain groups, regions, or sectors capture the gains from change (Agovino et al., 2021; Akhtar et al., 2024; Akram et al., 2024). This introduces a normative dimension, enabling comparison between principles such as interregional justice, intergenerational equity, and international solidarity, and the actual dynamics observed in the data. At the same time, empirical findings reveal that convergence is often conditional and reversible: Jerzmanowski (2006) and Tyrowicz et al. (2025) show that growth trajectories can shift between regimes, with some economies stagnating in low-growth clubs while others advance rapidly.
Another key contribution of convergence analysis is its explanatory power in understanding differential performance during external shocks—such as financial crises, pandemics, or geopolitical disruptions. Units with similar structural characteristics often exhibit homogeneous responses, reinforcing club convergence patterns and limiting the effectiveness of uniform policy responses (M. Ahmad & Law, 2024; Alexakis et al., 2021). This highlights the need for differentiated strategies tailored to the specific structural gaps of each group, rather than one-size-fits-all interventions.
The contemporary scope of convergence studies has also expanded into diverse non-economic domains. Recent literature applies the concept to carbon emissions (Borozan, 2024; Liu et al., 2025; Zhong et al., 2025), social public spending (Akram et al., 2023; Mishra et al., 2020; Onaran et al., 2022b), energy and material productivity (Alataş et al., 2021; Balado-Naves et al., 2023; Sun et al., 2025), and sectoral efficiency in manufacturing (Adeeko et al., 2023; Lin et al., 2018; Stergiou & Kounetas, 2022). This thematic broadening demonstrates that convergence is no longer confined to per capita income but has become a cross-cutting tool to assess whether desired transformations reach all stakeholders or if exclusionary and lagging dynamics persist. The methodological sophistication of these studies enhances both the scientific relevance of the field and its practical applicability for decision-making.
Convergence analysis thus acquires strategic value within the sustainability and resilience agenda. In a world marked by asymmetries in power, technology access, and exposure to global risks, studying convergence enables the projection of future scenarios—of cohesion or fragmentation, integration or polarization, shared prosperity or exclusionary growth. Evaluating whether territories and sectors are approaching minimum desirable levels of well-being, efficiency, or sustainability is no longer merely descriptive but a prerequisite for designing inclusive, adaptive, and equitable pathways (Dhaigude et al., 2025; Z. Hu et al., 2025; Navarro Claro & Bayona Soto, 2025).
Today, convergence analyses constitute an indispensable approach for examining the equity, effectiveness, and sustainability of contemporary transformations. Their study helps unravel the logic of alignment or structural divergence among social, territorial, and economic units, providing key tools to guide public action toward more balanced, resilient, and inclusive development. However, as the evidence shows, convergence is not a foregone conclusion: it depends on institutional quality, policy design, and structural conditions. Recognizing both its potential and its limitations strengthens the analytical and normative value of the concept in a complex and unequal world.
2.3. Methodological Approach to Convergence Analysis and Its Applications
Convergence analysis has become a versatile methodological approach, grounded in well-established theoretical foundations and supported by a continuously expanding technical repertoire. Its application enables the evaluation of whether multiple units, be they territorial, institutional, sectoral, or functional, tend to reduce their differences regarding one or more variables over time. From a methodological standpoint, convergence analysis is based on the study of dynamic trajectories, the identification of structural adjustment patterns, and the detection of heterogeneous or clustered behaviors. To this end, a variety of quantitative techniques are available that respond to different assumptions, scales of analysis, and inferential objectives (M. Ahmad & Law, 2024; Akhtar et al., 2024; Akram et al., 2024).
Among the most widely used approaches are beta convergence (β-convergence) and sigma convergence (σ-convergence). The former is based on regression models that assess whether there is a negative relationship between the initial level of a variable (e.g., productivity, income, or efficiency) and its subsequent growth rate. A negative slope implies that units with lower initial levels tend to grow faster than more advanced ones, suggesting a tendency to close gaps (N. Ahmad et al., 2019; Alataş, 2023). This approach admits variants: absolute β-convergence assumes structural homogeneity among units, while conditional β-convergence allows for controlling structural factors (human capital, infrastructure, institutional quality), recognizing the existence of differentiated trajectories toward their own equilibria (Alemu et al., 2024; German-Soto & Brock, 2022; Navarro-Chávez et al., 2025).
Sigma convergence (σ-convergence), on the other hand, focuses on the evolution of dispersion among units over time. σ-convergence is considered to exist when the variance or coefficient of variation of a variable systematically decreases, indicating a process of progressive alignment. This approach captures the dynamics of aggregate concentration or dispersion, although it may not always reflect underlying processes if divergent trajectories exist within subsets (N. Ahmad et al., 2019; Rodríguez Benavides et al., 2022). Therefore, both methodologies are often used complementarily, as β-convergence is a necessary but not sufficient condition for σ-convergence.
In addition to these classical tools, more sophisticated methodologies have been developed, such as stochastic convergence, which examines the stationarity of the difference between trajectories of two or more units, typically through unit root and cointegration tests. This approach evaluates whether gaps tend to revert in the long term, even if temporary shocks occur, reflecting a statistically more robust form of convergence (Afzal & Sibbertsen, 2021; Apergis et al., 2025; N. U. P. Nguyen & Moehrle, 2023). It has been argued that this approach is more suitable when analyzing the persistence of adjustment, as it explicitly incorporates temporal dynamics and short-term effects. To illustrate the methodological evolution from classical to advanced approaches and highlight their respective strengths and limitations, Table 2 provides a comparative overview of key techniques in convergence analysis.

Table 2.
Classical vs. Advanced Methodological Approaches in Convergence Analysis *.
One of the most relevant methodological innovations is the use of the club convergence approach, formally proposed by Phillips and Sul (2007), which allows identifying subsets of units converging toward common trajectories without assuming global homogeneity. This technique is based on decomposing the series into deterministic and stochastic components and applying an iterative algorithm to classify units into groups exhibiting similar convergence patterns (Aboal et al., 2023; Akram & Ali, 2022; Akram et al., 2024). This perspective acknowledges the existence of multiple equilibria, which is especially useful in contexts with strong structural heterogeneity. Club convergence analysis enables the capture of partial convergence dynamics that would be invisible under traditional aggregate-level methods.
The choice of methodological approach depends on factors such as (i) the nature and quality of available data, (ii) the temporal and spatial scale of analysis, (iii) the characteristics of the units under study, and (iv) the type of underlying theoretical hypothesis (adjustment toward a single equilibrium, multiple trajectories, stochastic reversion, etc.) (N. Ahmad et al., 2019; Alataş, 2023; Alataş et al., 2021). Therefore, best methodological practices often involve combining multiple techniques to triangulate results and enhance the internal and external validity of inferences.
Regarding its theoretical applications, the convergence framework has been used to evaluate processes such as technological diffusion, productive efficiency, intersectoral learning, normative harmonization, institutional cohesion, environmental sustainability, and equity in the provision of public goods. From the endogenous growth theory perspective, convergence is interpreted as the result of knowledge externalities, technological spillovers, or heterogeneous absorptive capacities (Balado-Naves et al., 2023; Stergiou & Kounetas, 2022; Zhao et al., 2019). From the institutional economics standpoint, convergence is associated with the diffusion of norms, practices, and regulatory frameworks that induce similar behaviors among heterogeneous agents. Meanwhile, from the sustainable development perspective, it represents a criterion of intertemporal and territorial distributive justice, where all units are expected to reach minimally acceptable levels of economic, social, and ecological performance (Agovino et al., 2021; Ahouangbe & Turcu, 2024).
Convergence analysis constitutes a methodologically sophisticated and conceptually flexible field that enables the investigation of a broad range of theoretical questions concerning dynamic adjustment processes among structurally diverse units. The recent evolution of its techniques has expanded its applicability to environments characterized by high complexity, heterogeneity, and profound transitions, establishing it as a central instrument for comparative empirical analysis across multiple domains.
2.4. Convergence as a Strategic Analytical Category
Based on the preceding review, it can be affirmed that convergence analysis has consolidated itself as a strategic analytical category, whose conceptual evolution, contemporary relevance, and methodological sophistication make it a key tool to interpret processes of structural adjustment and differentiation in complex, changing, and heterogeneous contexts. Its theoretical richness lies in its ability to articulate a dynamic view of inequality, development, and integration, while providing solid foundations to evaluate the differential impact of policies, shocks, and global transformations.
Conceptually, convergence has moved beyond its original formulation limited to per capita income, becoming a transversal notion that encompasses multiple dimensions of development—economic, social, institutional, technological, and environmental—allowing the analysis of patterns of alignment or divergence among structurally differentiated units. This expansion has been accompanied by explicit recognition of heterogeneous trajectories, the existence of multiple equilibria, and the importance of conditioning factors that shape the speed, depth, and directionality of convergence processes (Ahouangbe & Turcu, 2024; Alataş, 2023).
In terms of its current relevance, convergence analysis offers an appropriate framework to address critical questions regarding territorial justice, intertemporal equity, resilience to crises, and the distributive effectiveness of public policies. In the context of structural transitions such as digitalization, decarbonization, or the achievement of the SDGs, assessing the presence or absence of convergence becomes a normative criterion to judge the inclusive or exclusionary nature of these transformations (Eleftheriou et al., 2024; Goto & Sueyoshi, 2023; Z. Hu et al., 2025; Lyulyov et al., 2024). It also enables empirical measurement of persistent asymmetries that limit the potential for integration and functional interdependence among economic, social, or institutional units.
Methodologically, the field has advanced toward a robust set of quantitative tools capable of capturing the dynamic, nonlinear, and fragmented nature of observed processes. Techniques such as β-convergence, σ-convergence, stochastic analysis, and convergence clubs provide different approaches which, when used integratively, allow for a nuanced understanding of development trajectories and their determinants. This methodological progress has strengthened the approach’s adaptability across various scales, domains, and empirical conditions, favoring its applicability in multiple fields of knowledge (M. Ahmad & Law, 2024; Akram et al., 2024).
However, this theoretical and methodological consolidation is not without challenges. Identifying convergence processes require consistent longitudinal data, which is not always available across certain thematic domains or units of analysis. Likewise, the interpretation of convergence must avoid deterministic simplifications: the existence of statistical patterns of convergence does not, by itself, imply structural improvement or social welfare, and may be influenced by regressive processes or regression to the mean effects. Therefore, it is essential to combine quantitative analysis with solid theoretical and contextual problematization to interpret findings within appropriate explanatory frameworks (Afzal & Sibbertsen, 2021; M. Ahmad & Law, 2024).
To ensure its strategic value, convergence analysis must be applied with careful attention to real-world policy contexts and potential misinterpretations. It has informed key initiatives such as the European Union’s Cohesion Policy, where diagnostics of income and productivity convergence guide the allocation of structural funds to lagging regions (Aboal et al., 2023; Padilla et al., 2024), and climate governance frameworks, where convergence in per capita emissions underpins equity-based burden-sharing agreements (Akram et al., 2024; Borozan, 2024).
However, these applications require critical awareness: β-convergence does not imply equitable development if growth occurs from a low base, and σ-convergence may mask a general decline rather than true improvement. Club convergence patterns, while empirically robust (Aboal et al., 2023; Tyrowicz et al., 2025), can reflect structural exclusion rather than successful adjustment. Moreover, spatial spillovers and omitted variables may generate spurious convergence signals (Balado-Naves et al., 2023; Zoltán & Imre, 2024). Therefore, while convergence remains a powerful analytical lens, its results must be interpreted alongside complementary indicators of sustainability, equity, and institutional quality to avoid policy pitfalls.
Ultimately, convergence analysis today represents a first-order analytical tool for applied social research, territorial diagnosis, and the design of structural policies. Its capacity to reveal patterns of adjustment or divergence across multiple dimensions and levels offers a powerful lens to understand contemporary transformations and their distributive effects. Consequently, its integration into comparative studies, policy evaluations, and planning strategies constitutes not only a methodological option but an epistemic imperative considering the growing need to build more equitable, resilient, and sustainable development trajectories.
3. Methodology
This study adopts a mixed-methods approach combining quantitative bibliometric analysis and qualitative thematic mapping, aimed at examining the conceptual evolution, emerging trends, and gaps in the academic literature on economic convergence analysis. The methodological strategy is structured following the recommendations of Donthu et al. (2021) and Öztürk et al. (2024), integrating automated scientific mining tools with interpretative procedures to ensure a comprehensive and systematic understanding of the field.
Data collection was conducted through the Scopus database, selected for its broad coverage of economic and social sciences as well as its capacity to incorporate standardized bibliometric indicators. The search strategy was designed using Boolean operators and specific filters to ensure thematic, disciplinary, documental, and linguistic relevance. The areas of interest were limited to the categories of Economics (ECON) and Business (BUSI), and only peer-reviewed articles published between 1982 and 2026, written in English, were included. Search terms were carefully selected to capture studies related to economic convergence analysis, growth, productivity, and econometric methods. Detailed search parameters are presented in Table 3.

Table 3.
Bibliographic Search Strategy.
The Scopus database was selected as the primary source for bibliographic data due to its extensive coverage of peer-reviewed literature in economics and business, its robust integration of citation metrics, and its advanced application programming interface (API) for automated data retrieval and analysis. Scopus offers broader inclusion of non-English journals and a more comprehensive representation of research output from emerging economies compared to Web of Science, making it particularly suitable for studies aiming to capture global scientific trends (Donthu et al., 2021; Öztürk et al., 2024). Furthermore, its consistent indexing of author affiliations and institutional data enhances the accuracy of collaboration and productivity analyses.
The resulting corpus was processed using specialized scientific analysis tools. VOSviewer software was employed to visualize co-citation networks, keyword co-occurrence, and thematic clustering maps. This tool enabled a graphical representation of the conceptual structure of the field and the detection of relevant scientific communities through modularity algorithms. Additionally, the R 4.4.2 programming language was used along with the bibliometrix, igraph, and tm packages to perform statistical analysis, text mining, and graphical representation of bibliometric indicators.
The analysis was conducted in three phases. First, automated filters were applied alongside a manual review based on a 20% random sample of the final dataset of 2924 peer-reviewed articles on economic convergence analysis to ensure the thematic relevance of the selected documents. Two researchers conducted cross-validation to confirm the consistency of the inclusion criteria. Second, a quantitative analysis was carried out to extract bibliometric indicators. Author, country, and institutional productivity were measured, along with cumulative citations (with an average of 34.06 per document) and collaboration dynamics, revealing that 25.99% of the documents involved international co-authorship. Thematic clusters were identified using community detection algorithms in VOSviewer, enabling a structural mapping of the field based on keyword co-occurrence and citation linkages.
Finally, a qualitative interpretation was conducted to label and characterize the algorithmically generated clusters. This process—referred to as “systematic coding” in the original description—consisted of analyzing the most frequent and central keywords, as well as the titles, abstracts, and theoretical frameworks of the most representative and highly cited documents within each cluster. Two researchers independently reviewed these elements to assign coherent thematic labels (e.g., “formal statistical models”, “institutional-contextual approaches”) based on recurring concepts, methodologies, and application domains. Discrepancies were resolved through discussion and consensus. This interpretive phase allowed for the integration of bibliometric results with thematic insights, reinforcing the identification of recurrent patterns, consolidated research lines, and emerging gaps, while ensuring transparency and replicability in the labeling process.
The validity of the process was ensured through cross-review between researchers and the use of automated tools that reduce human variability in data processing. To enhance the transparency and replicability of this study, a structured summary of the methodological approach is presented below (see Table 4).

Table 4.
Summary of the methodological approach *.
The methodological design of this study combines quantitative rigor with qualitative depth, allowing for a comprehensive exploration of the intellectual landscape surrounding economic convergence analysis. By integrating advanced bibliometric techniques with systematic content interpretation, the approach ensures both analytical robustness and thematic relevance. The following section presents the main empirical findings, organized around the structural patterns, emerging trends, and conceptual gaps identified in the literature.
4. Results
The findings presented below arise from a comprehensive analysis of the compiled bibliographic corpus, reflecting both the structural evolution of the field of economic convergence analysis and the thematic and collaborative dynamics that shape it. First, quantitative results obtained through bibliometric techniques are shown, followed by a qualitative interpretation of the identified patterns. This section offers insight not only into the intensity and distribution of the generated knowledge but also into the predominant conceptual frameworks and emerging theoretical gaps revealed by the analysis.
4.1. Temporal Evolution of Scientific Production
The annual progression of publications related to the subject under study reveals a pattern of steady growth in academic attention to the topic. Although the earliest records date back to 1982, production during the first two decades was sparse and sporadic, rarely exceeding 10 articles per year until the mid-1990s. From 1995 onwards, a more sustained upward trend is evident, with gradual increases in the number of publications annually. This growth intensifies from the year 2000, marking an inflection point that leads to continuous expansion. Between 1982 and 2024, the annual volume of publications grew at an approximate compound annual growth rate (CAGR) of 14.4%, reflecting the notable dynamism in the consolidation of the field (see Figure 1).
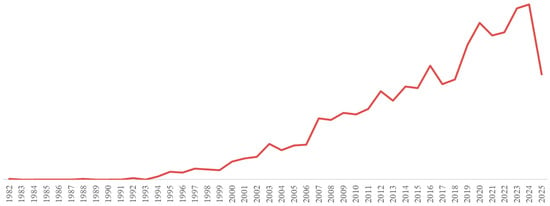
Figure 1.
Annual evolution of publications related to the subject of study (1982–2025). Scientific output on economic convergence has grown at a compound annual rate of 14.4% since 2000, signaling sustained consolidation and rising global interest in the field. Note: The drop in 2025 reflects the database cutoff date; data for the full year were not yet available at the time of analysis.
Between 2000 and 2010, scientific output multiplied, increasing from 23 articles in 2000 to 84 in 2010. This expansion continued into the following decade, reaching its highest point in the 2022–2024 period, with over 220 publications annually. Notably, 2024 recorded the highest number across the entire analyzed timeframe (226 articles), reflecting growing interest from the scientific community, driven by the consolidation of the field, advances in new analytical methodologies, and the intersection with emerging research topics. It is worth noting that although 2025 shows a decline compared to the previous year (136 articles), this drop can be attributed to the cutoff timing of the database used, as the current year had not yet concluded at the time of analysis. Overall, the data demonstrates a sustained consolidation of the topic as a significant area within international scientific production.
4.2. Journals with the Highest Publication Volume
The analysis of source journals reveals a high concentration of articles within a limited set of specialized journals, suggesting the existence of established scientific dissemination hubs centered on the study topic. In total, the ten most productive journals account for over 25% of the articles identified in the database, reflecting both thematic specialization and the field’s relevance within certain academic communities (see Table 5).

Table 5.
Top Ten Journals by Number of Publications on the Topic *.
Leading the list is the Journal of Econometrics with 121 publications, representing 4.14% of the total sample. It is followed by Applied Economics (4.00%) and Journal of Cleaner Production (2.77%), the latter reflects an interdisciplinary focus linking economics with sustainability and environmental issues. Applied-oriented journals such as Energy Economics (2.74%) and Applied Economics Letters (2.39%) also stand out, highlighting the growing interest in quantitative approaches to contemporary economic challenges. Meanwhile, publications like Technological Forecasting and Social Change and Knowledge-Based Systems demonstrate the field’s expansion toward prospective and computational intelligence-based perspectives. This diversity suggests an increasing convergence among economic, technological, and social disciplines in addressing the phenomena under study.
The Herfindahl-Hirschman Index (HHI), calculated based on the distribution of 2924 articles across 739 journals, yields a value of approximately 1250, indicating a low concentration level in scientific production. The top 10 journals account for 20.01% of all articles, while the top 30 journals represent 39.06%, suggesting moderate inequality in distribution. This pattern aligns with Lotka’s Law, characterized by a long tail where a few journals produce many articles and many journals publish only sporadically. Collectively, the analyses reveal a typical dynamic of complex bibliometric systems: a relatively small minority of journals dominate quantitatively, while the vast majority contribute marginally, evidencing a balance between specialization and diversification in scientific communication.
The dominance of journals such as Journal of Econometrics, Applied Economics, and Empirical Economics reflects the enduring centrality of rigorous econometric and panel data methodologies in convergence analysis, particularly in testing for β-convergence, club convergence, and stochastic stationarity. These journals serve as natural outlets for methodological innovation, which remains a core driver of the field’s evolution. At the same time, the strong presence of Journal of Cleaner Production, Energy Economics, and Technological Forecasting and Social Change signals a significant thematic shift: convergence research is increasingly embedded in sustainability science, energy transitions, and long-term socio-technical forecasting.
This expansion aligns with global policy agendas such as the SDGs and the European Green Deal, which incentivize research on equitable and environmentally sustainable development. Furthermore, the inclusion of journals focused on computational intelligence (Knowledge-Based Systems) and nonlinear dynamics (Nonlinear Analysis: Real World Applications) highlights the field’s embrace of advanced modeling techniques to capture complex, heterogeneous adjustment processes. Together, these patterns suggest that the journal ecosystem mirrors the intellectual trajectory of the field itself: from a narrow focus on income dynamics to a multidisciplinary domain where economic convergence is analyzed in tandem with environmental performance, technological diffusion, and institutional resilience.
4.3. Most Prolific Authors in Literature on the Topic
In terms of individual productivity, there is a significant concentration of publications within a small group of authors, indicating the presence of a well-established research community focused on the topic. For this analysis, only those authors who have published more than 10 articles on the subject were considered, focusing attention on those who have demonstrated sustained and relevant output. As shown in Table 6, the author Wang Y leads with a total of 33 articles, followed by Wang X (17), Phillips PCB (13), and a group of authors with between 11 and 12 publications, among whom Li Y, Wang Z, Zhang H, Li X, Zhang J, Zhang L, Zhang X, Zhang Y, Zhang Z, and Chen Y stand out.

Table 6.
Most prolific authors on the topic (more than 10 articles) *.
As shown in the table, the recurrence of certain surnames, particularly of Chinese origin, such as Wang, Zhang, and Li, suggests a strong presence of authors affiliated with Asian institutions, especially those based in China, in the scientific production on the topic. However, it should be noted that the presence of homonyms may affect the accuracy of the count, which is a common limitation in automated bibliometric analyses.
The pronounced presence of authors with Chinese surnames—particularly Wang, Zhang, and Li—reflects a broader trend of increasing scientific leadership from China in applied econometrics and regional development research. This geographic concentration is likely driven by national research priorities in economic restructuring, regional equity, and innovation-driven growth, which align closely with the core themes of convergence analysis. Institutions in China have heavily invested in studies of urban-rural disparities, energy efficiency convergence, and industry-university-research collaboration—topics that dominate recent publications.
At the same time, the sustained contribution of Western scholars like Phillips PCB highlights the continued influence of methodological innovation from established academic centers, particularly in the development of club convergence and distribution dynamics techniques. Together, these patterns suggest a dual engine of scientific production: one rooted in policy-driven research from emerging economies, and another in theoretical and statistical advancement from long-standing research hubs. This dynamic underscore the field’s evolution into a globally distributed, yet thematically cohesive, area of study.
4.4. Co-Citation Analysis Among Authors
The examined database records a total of 1000 authors organized into eight clusters generated using VOSviewer software (see Figure 2).
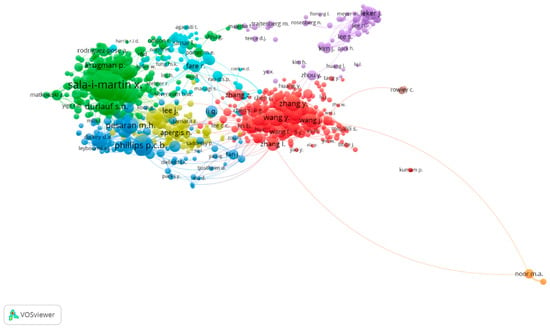
Figure 2.
Co-citation Map. Eight co-citation clusters reveal the field’s intellectual structure, with the two main clusters—centered on seminal works on panel unit roots and convergence clubs (Im et al., 2003; Quah, 1996)—accounting for 63.8% of authors and showing strong thematic polarization.
The distribution shows a high concentration within the first two clusters: Cluster 1 accounts for 33.6% of all authors, while Cluster 2 includes 30.2%. Together, these two groups encompass nearly two-thirds of all authors connected through co-citations, indicating a strong thematic or citation-based polarization. Clusters 3, 4, and 5 exhibit moderate participation, with proportions ranging between 8.6% and 10.5%, whereas Clusters 6, 7, and 8 represent distinctly minor cores; in particular, Clusters 7 and 8 each account for only 0.2%. This distribution suggests the presence of highly hierarchical structures in the analyzed field, with central communities of authors that are densely interconnected and a peripheral set characterized by lower relational density.
The analysis of the authors grouped in Cluster 1 (red) reveals a significant evolution in the theoretical and methodological approaches to the study of convergence, showing an increasingly broad and sophisticated scope. From a theoretical standpoint, convergence is conceived as a multidimensional phenomenon that transcends the classical focus on per capita income. Recent studies explore its manifestation in diverse domains such as energy productivity, ecological efficiency, technological innovation, institutional development, and sectoral integration. This thematic breadth is accompanied by a richer conceptualization that distinguishes various forms of convergence: absolute, conditional, club-based or subgroup convergence, as well as spatial and temporal convergence. Moreover, the notion of convergence as an indicator of systemic efficiency has been introduced, interpreting it as a sign of collective improvement in the performance of analyzed systems, without necessarily assuming an equitable distribution of the benefits.
In this context, the structural and dynamic determinants of convergence gain centrality, with emphasis on variables such as human capital, productive structure, institutional quality, technological intensity, and demographic configuration. Recent literature tends to integrate explanatory frameworks from endogenous growth theory, institutional theory, and resource economics, while highlighting the importance of externalities and spillover effects—technological, financial, and environmental. Of note is the emergence of the concept of institutional proximity, understood as a key mechanism in generating convergence between units with similar normative structures or governmental capacities, beyond their geographical proximity.
From a methodological perspective, the reviewed works stand out for a notable sophistication in econometric treatment. There is intensive use of nonlinear dynamic models and methods designed to address nonstationary time series, such as log-t estimators, cointegration models with structural breaks, semiparametric and nonparametric approaches, and estimators robust to misspecification errors or cross-sectional dependence. Spatial panel data techniques—such as spatial autoregressive models and Tobit models with regional effects—are frequently employed to capture patterns of heterogeneous convergence. In addition, the identification of convergence clubs through probabilistic classification methods or clustering techniques allows researchers to move beyond the global convergence hypothesis and recognize differentiated trajectories among homogeneous subsets.
Particular attention is devoted to the precise estimation of convergence rates, the development of asymptotic properties of estimators, and validation through Monte Carlo simulations. Several studies combine these tools with machine learning models, neural networks, and high-frequency estimation, enabling them to address empirical challenges stemming from noise, data asynchronicity, or high dimensionality. Finally, a distinctive feature of contemporary literature is the incorporation of spatiotemporal approaches, in which the dynamics of convergence are analyzed simultaneously over time and space using methods such as spatial Markov chains or evolving density kernels. Taken together, these contributions reflect a mature and diversified research agenda that addresses convergence from a comprehensive, flexible, and methodologically rigorous perspective.
The studies grouped within Cluster 3 (dark blue) represent an analytical strand focused on the rigorous formalization of the concept of convergence, with a strong emphasis on statistical consistency, identification of structural assumptions, and robust validation of econometric hypotheses. Unlike the approaches found in Clusters 1 and 2, which are more oriented toward empirical characterization of convergence patterns and contextual or institutional analysis of their determinants, this group is distinguished by a predominantly theoretical and methodological approach aimed at precisely delineating the statistical foundations of the convergence concept and the conditions under which its existence can be asserted.
Theoretically, these works adopt a narrower conceptual framework, defining convergence in terms of stochastic behavior, dynamic equilibrium, or long-term properties of economic processes. There is a clear emphasis on distinguishing between different notions of convergence (such as convergence in mean, in distribution, or in probability) and establishing strong links between these notions and underlying economic growth models. This orientation marks a significant departure from Cluster 1, where convergence was addressed across multiple thematic dimensions, and from Cluster 2, which prioritized contextual and institutional explanations of the phenomenon.
Methodologically, this cluster is characterized by a strong focus on rigorous statistical inference, with intensive use of formal convergence testing methods. Commonly employed techniques include unit root tests, stationarity tests, cointegration techniques, variance tests, and common components decomposition, among others. Many studies pay special attention to model assumption robustness, correction of estimation biases, and the sensitivity of results to different specifications. In contrast to Cluster 1, where applied dynamic models and simulations predominated, and Cluster 2, which leaned more toward adaptive techniques and contextual analyses, concentrates on methodological development per se, aiming to clarify the internal validity of metrics and criteria used to assert convergence.
A distinctive element of this cluster is the systematic attention given to error structure and cross-sectional dependence, as well as the treatment of issues such as non-stationarity and unobserved heterogeneity. This technical focus seeks to improve the quality of empirical inferences, even at the expense of thematic or interpretative diversity. Additionally, there is growing interest in the asymptotic properties of estimators, efficiency under various sampling conditions, and the identification of critical theoretical thresholds for test validity.
Overall, this cluster represents a specialized contribution within the convergence literature, primarily oriented toward strengthening methodological foundations and ensuring consistency in empirical claims through solid statistical architecture. Its divergence from the more applied, institutional, or contextual approaches positions it as a complementary line of work, essential for analytically underpinning the inferences made in other clusters but less focused on the substantive interpretation of the underlying economic and social processes driving convergence.
Cluster 4 (lime green) is characterized by a perspective focused on the interaction between convergence processes and long-term structural dynamics, with particular interest in the analysis of nonlinear trajectories, regime transitions, and endogenous transformations. Unlike Cluster 1, which centers on identifying multiple forms of convergence across different dimensions of development, and Cluster 2, which introduces a critical and institutional approach, this group stands out by linking convergence with historical processes of structural transformation, growth cycles, and technological or institutional transitions. The conceptual framework thus shifts from a static equilibrium view toward a more dynamic understanding, in which convergence is seen as a contingent outcome of evolutionary trajectories subject to ruptures, persistence, and reconfigurations.
From a theoretical standpoint, convergence is approached as a time-dependent, nonlinear, and potentially reversible phenomenon, calling into question the assumptions of stability and uniqueness of long-term equilibrium that predominate in other approaches. References to evolutionary theories, long-term structural transformations, and unbalanced growth are frequently incorporated, alongside notions drawn from comparative institutional economics and complexity theory. Unlike Cluster 3, which emphasizes the statistical formalization of the convergence concept under ideal conditions, Cluster 4 highlights the historicity and contingency of the process, recognizing that trajectories of approximation between units are subject to bifurcations, lock-ins, and path dependence generated by internal or exogenous factors.
Methodologically, this cluster exhibits a clear inclination toward approaches that detect structural breaks, identify multiple trajectories, and model discontinuous change processes. It employs regime-switching models (Markov-switching models), endogenous structural break tests, temporal segmentation techniques, nonlinear conditional convergence models, and local convergence analysis. These tools overcome the homogeneous view of the convergence process and acknowledge the coexistence of divergent dynamics within the same sample or period. In contrast to Cluster 1, which predominantly uses spatial panel models, or Cluster 2, which incorporates adaptive analyses with an institutional focus, this group favors detailed temporal analysis and evaluation of phase transitions without assuming continuity or symmetry in the processes.
Another distinctive characteristic of this cluster is its concern for the temporal validity of results, reflected in extensive use of period-specific sensitivity analyses, rolling estimations, and robust checks against structural shocks. Rather than seeking a global generalization of convergent patterns, it emphasizes the identification of episodes, windows of opportunity, and phases of temporal divergence. This approach captures more precisely the unstable nature of convergence processes, contrasting with the universal pattern search characteristic of Cluster 3.
Cluster 4 offers a unique contribution to the study of convergence by proposing an interpretation centered on structural dynamics, temporal heterogeneity, and the complexity of historical trajectories. In contrast to the more normative, formalist, or structuralist approaches of previous clusters, this group leans toward a processual and contingent understanding of convergence, where patterns of approximation are not an expected regularity, but a possibility conditioned by sectoral transformations and critical transitions over time.
Cluster 5 (purple) is characterized by a strong normative and practical orientation towards evaluating convergence processes, adopting a transversal approach that seeks to link technical analysis with interpretative frameworks in economic policy, sustainability, and inclusive development. Unlike the previous clusters—where agendas focused mainly on empirical estimation, institutional exploration, or statistical validation—this group of studies introduces a marked interest in the normative significance and socioeconomic implications of convergence, situating the analysis within broader debates on equity, welfare, and institutional design.
Theoretically, convergence is conceived not only as an empirical or dynamic property of economic systems but as a desirable goal connected to distributive justice and structural harmonization. This perspective departs from the more neutral or formal conceptualizations found in Clusters 3 and 4, if convergence may signal progress toward collective objectives such as cohesion, resilience, or sustainability. Within this framework, theoretical elements from political economy, development theory, and multilevel governance approaches are integrated, allowing convergence to be viewed as the outcome of both endogenous dynamics and deliberate institutional decisions.
Methodologically, this cluster is distinguished by a plurality of empirical approaches, with deliberate use of composite indicators, synthetic indices, and multidimensional metrics of convergence. Priority is given to incorporating indicators that capture structural and social aspects not directly observed in traditional economic accounting, such as institutional capacities, environmental performance, inclusion, and systemic resilience. Unlike Cluster 1, dominated by highly parameterized dynamic models, or Cluster 3, focused on statistical validity of tests, the works grouped here employ more flexible tools oriented toward comparability, such as normalized scales, multicriteria analysis, and aggregated distance measures. This approach facilitates the representation of complex trajectories across multiple dimensions without requiring rigid econometric structures.
A distinctive element of this cluster is the articulation between quantitative analysis and qualitative or normative interpretation. Empirical results are discussed regarding their relevance for public policy design, evaluation of regional or global targets, and monitoring of multilateral commitments. This contrasts with earlier clusters where the focus was primarily on endogenous system patterns or internal model dynamics. Here, convergence is assumed not only to be observed but also to be promoted, evaluated, and governed, introducing a prescriptive dimension that enriches academic debate while demanding more integrative theoretical frameworks.
Cluster 5 represents a research line that integrates empirical analysis, normative reflection, and strategic orientation, focusing on the practical value of the convergence concept as an evaluative tool and guide for action. In contrast to the more technical–formalist or structuralist orientations of previous clusters, this group proposes a more engaged reading, sensitive to development goals and open to constructing composite indicators that reflect the multiple meanings convergence can assume in contemporary contexts.
Taken together, the eight clusters illustrate complementary but distinct ways of advancing convergence theory. Cluster 1 expands the scope of convergence beyond income toward multidimensional domains, while Cluster 2 emphasizes institutional and contextual determinants, making them mutually reinforcing in linking structural factors with broader applications. In contrast, Cluster 3 narrows the lens to methodological rigor, ensuring the statistical validity of the empirical claims made in Clusters 1 and 2. Cluster 4 introduces a dynamic and historical dimension, highlighting nonlinear trajectories and structural breaks, thereby contrasting with the more equilibrium-oriented perspectives of Clusters 1–3.
Finally, Cluster 5 brings a normative and policy-oriented perspective, translating empirical findings into actionable insights for governance and sustainability. In this sense, the clusters collectively form a layered understanding: Clusters 1 and 2 provide breadth, Cluster 3 guarantees methodological depth, Cluster 4 stresses historical contingency, and Cluster 5 bridges academic analysis with real-world application.
Clusters 6, 7, and 8, although not discussed in depth, represent very small and peripheral author groups (together less than 1% of the network). Their marginal size and low relational density suggest that they do not substantially shape the core of convergence theory. However, they provide niche or emerging perspectives that enrich the intellectual map and may signal potential directions for future specialized inquiry.
4.5. Most Cited Documents at the Global Level
Table 7 presents the five articles that constitute an essential theoretical and methodological foundation for understanding the empirical and analytical evolution of the concept of economic convergence, as they have received the highest number of citations.

Table 7.
The five most cited articles *.
On the one hand, the works of Im et al. (2003) and Levin et al. (2002) provide robust econometric tools for panel time series analysis, which are fundamental for empirically testing the existence of unit roots—a necessary condition to evaluate the stationarity of income trajectories among countries or regions. On the other hand, the articles by Levine and Renelt (1992) and Quah (1996); Quah (1997) explore convergence from the perspective of economic growth, either by questioning the robustness of growth determinants or by proposing new analytical frameworks based on dynamic distributions. This thematic and methodological convergence toward a better understanding of economic convergence partly explains the high citation counts of these works, as they have been foundational both for empirical and theoretical researchers studying income evolution at national, regional, or global levels.
The work by Im et al. (2003) stands out for offering a flexible solution to the problem of heterogeneity in unit root testing for panel data. Their methodological proposal, the IPS test, allows for the analysis of whether time series with diverse individual structures converges toward a common trajectory, overcoming previous limitations that assumed homogeneity in individual dynamics. This tool is particularly useful in economic convergence studies where countries are expected to follow different growth patterns but eventually converge. The method’s high applicability and strong statistical foundation justify its elevated annual citation rate (420.26), making it one of the most widely used instruments to evaluate convergence hypotheses in macroeconomic contexts.
In the same methodological field, the article by Levin et al. (2002) presents an alternative unit root test for panels which, although it imposes homogeneity in temporal persistence, offers analytical advantages in terms of statistical power. Its contribution lies in providing a rigorous methodology to analyze income or per capita GDP series through panel data, a fundamental tool for research aiming to confirm or refute the convergence hypothesis among countries or regions. The LLC test has been widely used due to its ease of implementation and solid asymptotic framework, which explains its considerable number of citations (8160) and methodological influence on subsequent studies.
Meanwhile, Levine and Renelt (1992) adopt a critical approach toward the empirical literature on economic growth, questioning the stability of the determinants traditionally associated with long-term growth. Their sensitivity analysis introduces an essential dimension to the convergence debate: the robustness of correlations between structural variables (such as investment or international trade) and income growth. This work is crucial for understanding that evidence of convergence may depend on empirical model specifications and does not necessarily reflect strong structural relationships. Their approach has been fundamental in designing and evaluating policies aimed at development and convergence, especially in comparative cross-country studies.
Danny Quah’s (1996, 1997) two articles represent a conceptual shift in how economic convergence is approached, moving away from traditional regression models to focus on the dynamic distribution of income. Instead of studying whether growth rates negatively correlate with initial income levels (as in beta convergence), Quah analyzes the evolution of income distribution across countries, identifying patterns of polarization, stratification, and the formation of convergence clubs. His theoretical proposal introduces the concept of “twin peaks,” which describes the persistence of two differentiated groups of countries—rich and poor—thus challenging the global convergence hypothesis. These works have had a significant impact not only on economics but also on related disciplines interested in inequality and development, explaining their lasting academic influence.
The combined influence of these five articles extends beyond their individual contributions. Levine and Renelt (1992) permanently altered the standards of empirical research by introducing robustness checks as a prerequisite for any claim about convergence or growth determinants. Their work forced scholars to confront the fragility of cross-country regressions and created a lasting culture of methodological rigor that continues to guide applied economics today.
Quah’s (1996, 1997) contributions redirected the convergence debate from uniform trajectories to the dynamics of income distributions. His findings on polarization, stratification, and convergence clubs reshaped the analytical agenda, shifting attention toward the persistence of inequality and the conditions that generate heterogeneous growth paths. These insights have influenced not only macroeconomics but also development economics, labor economics, and inequality studies, where the “twin peaks” and club convergence frameworks remain central reference points.
The econometric advances of Levin et al. (2002) and Im et al. (2003) completed this transformation by providing tools capable of testing persistence and heterogeneity in panel data. The LLC and IPS tests became standard instruments in long-term macroeconomic analysis, enabling robust evaluation of hypotheses about convergence, purchasing power parity, and the effects of fiscal and monetary policy. Together, these methodological breakthroughs and conceptual innovations forged a new research paradigm. Current literature on convergence and inequality is built directly upon this legacy, asking not only whether convergence occurs but also how it evolves, which groups participate, and under what institutional or structural conditions it can be sustained.
To better illustrate the enduring influence of these foundational contributions, a timeline chart of their citation trajectories can be included. Such a visualization highlights not only the early reception of each article but also the persistence of their academic impact over time, making clear how methodological and theoretical innovations continue to shape current research agendas (see Figure 3).
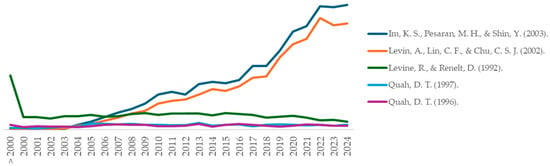
Figure 3.
Citation Trajectories of Foundational Works on Economic Convergence. Annual citation trends of the five most influential articles showing the lasting impact of their methodological and theoretical contributions to convergence research (Im et al., 2003; Levin et al., 2002; Levine & Renelt, 1992; Quah, 1996, 1997).
Together, these five articles have become pillars in economic convergence analysis, whether by refining econometric tools or through theoretical frameworks that allow for a more nuanced understanding of growth and global distribution. Their high citation rates respond not only to the technical quality of their contributions but also to their capacity to address key questions about the dynamics of economic development, the persistence of inequalities, and the conditions under which convergence among economies is possible—or not.
Figure 4 presents a co-occurrence map of keywords obtained through bibliometric analysis, aiming to visualize thematic relationships within the literature on convergence analysis. The map was generated using VOSviewer software, which enables the identification of conceptual clusters based on the frequency and association of key terms used in scientific publications in the field. Different colors represent thematic clusters grouping terms with high co-occurrence, facilitating the exploration of the main research lines and methodological approaches present in the discipline.
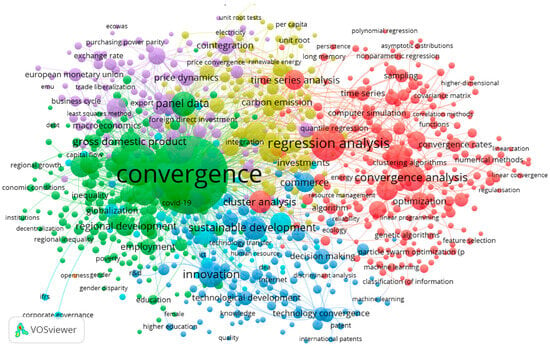
Figure 4.
Co-occurrence Map. Six thematic clusters structure the economic convergence literature, from formal models and institutional approaches to sustainability assessments, showing a field that combines methodological rigor with policy and environmental applications. In the figure, the clusters are identified by the following color coding and thematic focus: Cluster 1 (red)—Mathematical and computational foundations; Cluster 2 (green)—Economic and territorial dimensions; Cluster 3 (blue)—Digital transformation and innovation; Cluster 4 (yellow)—Environmental and energy sustainability; Cluster 5 (violet)—Applied econometric analysis; Cluster 6 (light blue)—Economic efficiency and governance.
Cluster 1, shown in red, is characterized by an intensive focus on the mathematical, statistical, and computational foundations of convergence analysis. This thematic group centers around a dense network of terms such as convergence analysis, convergence of numerical methods, optimization, regression analysis, stability, and parameter estimation, reflecting a rigorous methodological orientation aimed at the formalization, simulation, and validation of quantitative models.
Within this cluster, the importance of advanced numerical methods and computational algorithms—such as genetic algorithms, particle swarm optimization, simulated annealing, and machine learning—stands out as key tools for solving complex estimation, prediction, and optimization problems. These techniques are combined with regression, factor analysis, time series analysis, and probability theory to address both model stability and prediction accuracy. Additionally, concepts related to sampling, hypothesis testing, principal component analysis, and sensitivity analysis reinforce the emphasis on experimental design, statistical validation, and robustness of results.
A distinctive feature of this cluster is its interdisciplinary nature, merging applied statistics, econometrics, operations research, and computational science. This is evident in the presence of notions such as computational complexity, deep learning, support vector machines, and neural networks, alongside methods like Monte Carlo simulation and numerical experiments. Together, Cluster 1 represents a core methodological hub for the study of convergence, where formal precision, quantitative analysis, and the use of optimization algorithms are essential pillars for generating robust and replicable empirical evidence.
Cluster 2, shown in green, groups terms related to a structural economic and empirical view of convergence analysis, focusing primarily on territorial, social, and macroeconomic dynamics of development. Its central axis is the concept of convergence, accompanied by specific variants such as beta convergence, conditional convergence, income convergence, and regional convergence, highlighting an approach oriented toward studying patterns of economic and social homogenization across regions or countries.
This cluster integrates key variables of economic development—economic development, economic growth, productivity, employment, human capital, inequality, income distribution—with quantitative methodologies like panel data, spatial analysis, trend analysis, and decomposition analysis. Composite indicators and productivity measures, such as total factor productivity and the human development index, also play an important role, aligning with concerns about multidimensional measurement of economic and social progress.
A notable characteristic is the strong territorial dimension, evident in terms like regional development, regional economy, regional policy, urbanization, and spatial heterogeneity. These highlight a particular interest in spatial inequalities, agglomeration dynamics, and spillover effects, often analyzed at regional or subnational levels.
Contextual and institutional factors also appear, including governance approach, institutional framework, cohesion policy, and fiscal policy, linking convergence processes to structural factors and public policies. Contemporary issues such as COVID-19, pandemic, and crisis introduce a temporal and vulnerability dimension, broadening the analytical scope.
In summary, Cluster 2 reflects a branch of convergence analysis focused on socioeconomic, territorial, and institutional inequalities, backed by strong empirical foundations, a marked orientation toward longitudinal and spatial data analysis, and a concern for structural determinants of inclusive and sustainable growth.
Cluster 3, depicted in blue, revolves around the intersection of digital transformation, technological innovation, and industrial implications within convergence analysis. This group is marked by frequent terms like innovation, sustainable development, technological development, technology convergence, technology adoption, manufacturing, industrial performance, digitalization, ICT, and Industry 4.0. This suggests an orientation toward studies that approach convergence through the lens of productive processes, industrial sectors, and emerging technological frameworks.
Additionally, concepts such as patents, technology transfer, research and development, and entrepreneurship reflect a focus on the creation, diffusion, and use of technological knowledge, linked to business strategies and innovation policies. Terms like decision making, project management, knowledge management, and supply chain management emphasize the managerial and strategic nature of this research line, highlighting convergence as a driver of competitiveness and organizational efficiency.
Overall, this cluster represents a research line centered on technological–industrial convergence and its effects on sustainable development, business dynamics, and structural adaptation to the digital revolution. It connects convergence analysis with digital transformation, market-oriented innovation, and the transition toward more technological and sustainable economies.
Cluster 4, shown in yellow, groups a dense network of terms related to convergence in environmental, energy, and sustainability contexts. This cluster has a strong focus on carbon emissions, climate change, energy efficiency, and renewable energy adoption, reflecting research centered on the relationship between economic development and environmental pressure. Key terms include carbon dioxide emissions, carbon footprint, energy efficiency, energy consumption, renewable energy, environmental policy, and climate change, indicating an analytical approach that examines convergence patterns in ecological and energy indicators.
Simultaneously, analytical tools related to the study of these phenomena appear, such as stochastic convergence, panel data models, computable general equilibrium analysis, spatial econometrics, and club convergence, showing the use of advanced quantitative methods to explore differentiated trajectories among countries or regions. Themes connected to eco-efficiency, environmental management, energy policy, and environmental economics also emerge, underscoring concern about the impacts of growth on natural resources and long-term sustainability.
Together, this cluster embodies a robust research stream linking convergence analysis to global challenges of environmental sustainability, energy transition, and ecological governance, in dialogue with econometric approaches capable of capturing the spatial and temporal complexity of these processes.
Cluster 5, represented in violet, comprises an empirical and methodological thematic conglomerate applied to convergence analysis in economic, financial, and commercial contexts. It is characterized by the strong presence of terms such as cointegration, empirical analysis, econometrics, economic integration, numerical model, and price dynamics, revealing an intensive methodological orientation toward quantitative techniques focused on empirically validating hypotheses about structural, monetary, and commercial convergence.
Studies in this group explore price convergence (price convergence, law of one price, purchasing power parity), macroeconomic variables (inflation, interest rate, exchange rate, stock market), and sectoral structures (commodity market, energy market, housing market, agricultural economics), using methods such as cointegration analysis, error correction models, panel data, Granger causality, and vector autoregression. Terms like sectoral transformation, heterogeneity, asymmetry, and business cycle indicate attention to differentiated dynamics among countries or regions, acknowledging nonlinearity and structural shocks in convergence processes.
This cluster also reflects applied economics and public policy concerns, evident in concepts like monetary union, trade policy, development economics, market integration, and regulatory framework. The inclusion of specific geographic contexts (national economy, developing world, European monetary union) suggests a comparative outlook combining sectoral analyses with macroeconomic implications.
Overall, Cluster 5 represents a mature and robust research line combining technical rigor, thematic diversity, and empirical relevance, centered on the structural analysis of convergence processes and evaluation of their economic, monetary, and commercial determinants in global, regional, and national contexts.
Cluster 6, shown in light blue on the co-occurrence map, focuses on economic efficiency, financial analysis, and institutional governance within economic convergence processes. This thematic group is marked by intensive use of advanced quantitative tools, particularly Data Envelopment Analysis (DEA), technical efficiency, and cost–benefit analysis.
These approaches allow for evaluating the relative performance of economic units—be they firms, sectors, or countries—based on productivity and optimization criteria. Additionally, the cluster incorporates a strong financial dimension, reflected by terms such as finance, banking, capital market, financial system, and investment, indicating sustained interest in the link between financial development and economic efficiency, especially in emerging market contexts. The group also highlights institutional aspects, including corporate governance, regulation, policy making, and public sector, reflecting concern for efficient public policy design, state sector reform, and strategic stakeholder engagement.
Finally, terms like globalization, emerging markets, green economy, and technological change reveal a broad perspective connecting economic efficiency with global structural transformation, innovation, and sustainability. Collectively, this cluster presents a technical and applied approach aimed at understanding convergence dynamics at the intersection of economics, management, institutions, and public policies.
The temporal evolution analysis of the keywords presented in Figure 5 allows for the precise identification of academic attention cycles within the field of economic convergence.
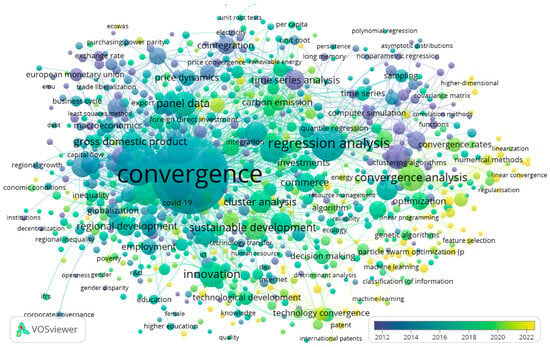
Figure 5.
Temporal Perspective of Keyword Co-occurrence. Thematic evolution of research shows a shift from theoretical–mathematical foundations (2002–2007) through empirical and econometric consolidation (2008–2015) to recent diversification into sustainability, AI, and spatiotemporal analysis (post-2020).
In the early years of the observed period (2002–2007), studies focused on theoretical and methodological foundations such as theorem proving, least squares approximations, and asymptotic stability, reflecting a strong orientation towards the development of formal mathematical models.
Between 2008 and 2011, there was an expansion towards empirical applications, with keywords like national economy, unit roots, exchange rate, and monetary policy evidencing growing interest in validating models within real macroeconomic contexts. The emergence of terms such as time series analysis (86 mentions in 2011) and modeling (40 mentions in 2011) marks the beginning of a methodologically intensive phase oriented towards applied research.
The period 2012–2015 represents a turning point characterized by thematic consolidation. Concepts like convergence of numerical methods (128 mentions in 2012), cointegration (70 mentions in 2013), economic convergence (62 mentions in 2013), and economic growth (376 mentions in 2015) gained prominence. Additionally, the intensified use of robust econometric tools (e.g., regression analysis, panel data, Monte Carlo methods) signals a maturation in the field’s technical sophistication.
In more recent years (2016–2023), there has been significant thematic diversification. Keywords such as sustainable development (118 mentions in 2019), spatial analysis (86 mentions in 2017), technology adoption (25 mentions in 2018), and machine learning (17 mentions in 2022) indicate a convergence between classical quantitative approaches and emerging global agendas, including sustainability, innovation, and digitalization. Similarly, terms like club convergence (49 mentions in 2021) and technological convergence (20 mentions in 2020) show a renewed focus on differentiated convergence patterns across groups of countries or sectors, reflecting growing concern for structural inequalities.
Finally, the appearance of recent terms such as artificial intelligence, spatiotemporal analysis, and systematic literature review from 2022 onward suggests a shift towards new computational analysis methods and comprehensive knowledge synthesis, which may redefine the research agenda on convergence in the coming decade.
To deepen this analysis, a correspondence analysis was conducted on the complete matrix of keywords against years. The first two dimensions jointly explained only 9.10% of the total inertia (4.55% each). This low percentage is common in correspondence analyses involving many categories and suggests that thematic variability is widely dispersed across multiple latent axes, with no small set of dimensions capturing most of the variance. In Dimension 1, the terms spatiotemporal analysis (4.92%) and least squares approximations (4.08%) emerge as the main contrasting drivers, while in Dimension 2, spatiotemporal analysis (5.63%) maintains a leading role alongside asymptotic stability (3.72%), indicating that these topics define both the primary axis of differentiation and secondary nuances in the scientific discourse. Regarding the years, 2022 made the most significant contribution to both dimensions (41.4% in Dim 1 and 47.3% in Dim 2), evidencing an increasing concentration of research on advanced methodologies in the latest temporal phase, surpassing earlier years such as 2020 (14.3% and 7.9%), 2018 (8.4% and 6.0%), 2015 (6.2% and 0.6%), and 2006 (7.0% and 4.5%).
The filtered biplot (see Figure 6) provides a clear depiction of the thematic evolution within the field of convergence.
Figure 6.
Biplot shows thematic evolution over the years. Recent research (2018–2022) shifts from traditional growth-focused approaches to spatiotemporal models and heuristic optimization, with 2022 showing the strongest influence.
In the early years, vectors such as “growth theory” and “least squares approximations” cluster in the left quadrant, reflecting an emphasis on classical analytical approaches. As time progresses toward the last decade, this trajectory gradually shifts to the upper-right quadrant, where terms like “particle swarm optimization” and “spatiotemporal analysis” emerge. This spatial sequence, reinforced by the continuous timeline of years, highlights a disciplinary shift toward computational methodologies and spatiotemporal analysis, indicating how the research community has progressively adopted more sophisticated techniques.
Simultaneously, the arrangement of the annual vectors along this path reveals a process of thematic diversification: the points corresponding to 2006 and 2010 show a concentration on traditional paradigms, whereas the vectors for 2018, 2020, and 2022 illustrate conceptual and methodological enrichment. The convergence of these poles within the factorial space not only marks a shift in focus—from growth theory and least squares methods toward heuristic optimizations and spatiotemporal models—but also underscores the ability of correspondence analysis to capture complex historical dynamics across large volumes of categories. This biplot enhances our understanding of the scientific discourse evolution, revealing how technological advances and new analytical tools have progressively reshaped the research landscape.
International scientific collaboration is a cornerstone for knowledge generation and dissemination in an increasingly interconnected world. The country collaboration map shown in Figure 7 reveals a dense network of global academic links, highlighting key hubs of intensive interaction such as the United States, China, and several European countries.
Figure 7.
Country Collaboration Map. International collaboration is structured around regional blocs, with the U.S., China, and Western Europe as central hubs shaping global knowledge flows. Darker blue shades indicate countries with higher scientific output and collaboration activity, while lighter shades represent lower activity. Grey indicates no recorded activity. Lines show international collaboration links.
This visual mapping not only highlights the centrality of certain key players in global scientific production but also illustrates the flows of knowledge established through co-authorship networks and institutional alliances. The strengthening of these networks reflects a trend toward convergence in research agendas, methodologies, and scientific priorities, serving as a necessary prelude to a more detailed examination of co-citation and co-authorship patterns—key indicators of integration and reciprocity within national science, technology, and innovation systems. In this context, convergence analysis gains relevance by providing tools to assess whether the scientific trajectories of different countries tend to align over time, both in terms of productivity and thematic orientation and cooperation.
The co-authorship analysis between countries, visualized through a map generated with VOSviewer, reveals a complex and densely interconnected structure composed of five main clusters differentiated by color, reflecting regional, linguistic, and geopolitical affinities (see Figure 8).
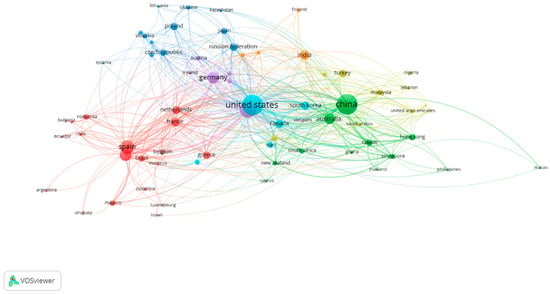
Figure 8.
Co-authorship map between countries. Five co-authorship clusters—Asia–Pacific, Ibero-Mediterranean, Eastern Europe–Central Asia, Middle East–Africa, and US–Nordic—reflect geopolitical and linguistic ties, highlighting strong regional cooperation. The green cluster (2) groups Asian and Pacific economies with growing scientific production; the red cluster (1) reflects the Ibero-American and Mediterranean network led by Spain; the blue cluster (3) represents regional cooperation in Eastern Europe and Central Asia; the yellow cluster (4) shows the progressive integration of Middle Eastern and African countries; and the light blue cluster (5) constitutes the highly connected core led by the United States and Northern Europe.
The green cluster (≈25.9% of countries) groups Asian and Pacific economies with growing prominence in scientific production, such as China, India, Malaysia, Singapore, Australia, and South Africa, reflecting a South-South cooperation network and strategic links with traditional centers. The red cluster (≈18.8%) revolves around Spain and its Latin American and Mediterranean influence network, including Mexico, Brazil, Colombia, Chile, Ecuador, and Morocco, suggesting a strong cultural and linguistic dimension in collaboration patterns.
The blue cluster (≈15.3%) consists of Eastern European and Central Asian countries such as Poland, the Czech Republic, Ukraine, Lithuania, and Kazakhstan, together with Japan and Finland, representing a more regionalized cooperation network, albeit connected to central nodes like Germany.
Meanwhile, the yellow cluster (≈12.9%) includes countries from the Middle East and Africa, such as Turkey, Egypt, Nigeria, the United Arab Emirates, and Pakistan, highlighting their progressive integration into the global scientific system.
Finally, the light blue cluster (≈11.8%) is led by the United States and Northern European countries such as Sweden, Norway, and Denmark, forming a highly connected core with cross-cutting influence over the other groups.
This distribution shows that, although asymmetries persist in global scientific production, co-authorship dynamics tend to create convergence spaces between traditionally distant regions, fostering processes of integration and knowledge transfer.
The country co-citation map analysis reveals the existence of twelve clearly differentiated clusters, each identified by a number and a characteristic color (see Figure 9).
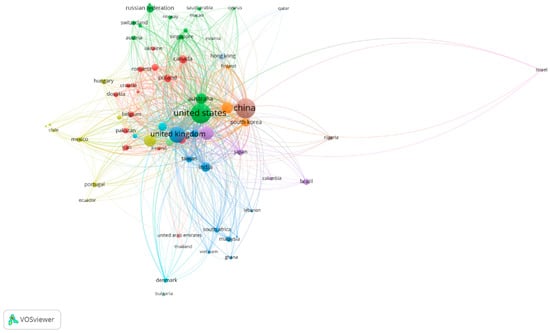
Figure 9.
Country co-citation map. Twelve co-citation clusters reveal that convergence research is dominated by the U.S. and Western Europe, with emerging economies gaining visibility in applied and regional studies across geo-economic and thematic blocs. The clusters are organized by color and thematic focus: red (1) links European and emerging economies; green (2) groups global economic powers; light blue (3) reflects postcolonial dynamics; yellow (4) connects Latin America with Mediterranean Europe; purple (5) examines South-North cooperation; cyan (6) analyzes welfare states; olive (7) specializes in digital innovation; orange (8) studies high-population markets; pink (9) addresses niche financial systems; while clusters 10–12 (salmon, pistachio, dark green) explore themes like financial hubs and small-state dynamics.
Cluster 1 (red) mainly groups countries from Western and Central Europe—Belgium, France, Poland, Romania, Slovakia, Croatia, and Hungary—along with some emerging Asian economies (Philippines, Pakistan, Iran) and Canada, suggesting a strong interrelation in the literature regarding mature markets and their interaction with developing regions.
Cluster 2 (green), with key nodes like the United States and Australia, includes Austria, Switzerland, Norway, Singapore, United Arab Emirates, Saudi Arabia, and Russia, reflecting a bloc of economic powers and global financial centers.
Cluster 3 (light blue), centered around India and the United Kingdom, also brings together former Commonwealth members (South Africa, Malaysia, Ghana, Lebanon, Turkey, Taiwan, Vietnam, and Tunisia), pointing to a coherent academic corpus focused on postcolonial dynamics and English-speaking trade networks.
In contrast, Cluster 4 (yellow) groups Latin American countries (Argentina, Chile, Ecuador, Mexico, Uruguay, Brazil, and Colombia) alongside Italy, Portugal, and Indonesia, indicating shared interest in regional development models and comparisons between Mediterranean Europe and Latin America.
Cluster 5 (purple), led by Japan and Spain, also includes Brazil and Morocco, highlighting studies on South–North cooperation and technology flows.
Cluster 6 (light blue) formed by Sweden, Denmark, the Netherlands, and Bulgaria, reflects research lines on social welfare and European integration policies.
Cluster 7 (olive), including Germany, Finland, and South Korea, focuses its co-citations on technological innovation and advanced digital economy.
Cluster 8 (orange), dominated by China and Nigeria, emphasizes attention to markets with large populations and emerging labor forces.
Cluster 9 (pink), composed of Israel and Luxembourg, suggests a focus on niche financial systems and high innovation.
Finally, Cluster 10 (salmon) groups Thailand and the United Arab Emirates, Cluster 11 (pistachio green) brings together Estonia and Greece, and Cluster 12 (dark green) includes Hong Kong and Qatar; all of these form subnetworks addressing urban–regionalism, financial hubs, and small-state dynamics in the global economy.
This multicolored network structure reveals how research lines are distributed among global powers, former Commonwealth colonies, European regional blocs, emerging Latin American countries, and highly specialized isolated nodes.
A thematic integration is presented through a factorial map obtained from a correspondence analysis (or term factor analysis). This map organizes the semantic field of the literature on convergence analysis along two latent dimensions, which can be interpreted as axes of “methodological rigor—regional and thematic application” (horizontal axis, F1) and “quantitative abstraction—orientation towards sustainability and the environment” (vertical axis, F2) (see Figure 10).
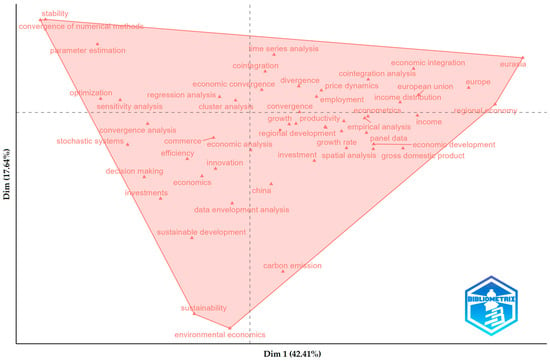
Figure 10.
Perceptual Map. Two latent axes—methodological rigor vs. regional application and quantitative abstraction vs. sustainability—form four quadrants, showing a field balancing rigor and sustainability with hybrid research at the center.
The factorial map is based on a correspondence analysis of keyword co-occurrence. Dimension 1 (horizontal axis) explains 42.41% of the total inertia and primarily contrasts methodological and theoretical studies with applied and regional analyses. Dimension 2 (vertical axis) accounts for 17.64% of the variance and distinguishes quantitative-abstract approaches from sustainability-oriented research. Together, these dimensions capture over 60% of the thematic structure, providing a robust visualization of the field’s intellectual organization.
On the F1 axis (horizontal), on the left side, there is a group of terms related to mathematical and numerical formalization—such as “stability,” “convergence of numerical methods,” “parameter estimation,” “optimization,” and “stochastic systems”—which indicate research lines focused on the theoretical robustness of models. Moving toward the right, more applied and empirical concepts appear, like “regional economy,” “gross domestic product,” “income distribution,” “economic development,” “European Union,” and “Eurasia,” reflecting studies centered on specific regions and macroeconomic indicators.
On the F2 axis (vertical), the upper part gathers advanced quantitative and econometric techniques, including “time series analysis,” “cointegration,” “price dynamics,” “econometrics,” and “empirical analysis.” In contrast, the lower area features terms such as “environmental economics,” “sustainability,” “sustainable development,” and “carbon emission,” pointing to a focus on ecological impact assessment and sustainable development policies.
The resulting quadrants allow the identification of four thematic poles:
- Quadrant I (F1 > 0, F2 > 0): Applied macro-regional research and economic convergence analysis (e.g., “regional development,” “growth rate,” “panel data,” “European Union”), where econometric methods intersect with studies on integration and productivity.
- Quadrant II (F1 < 0, F2 > 0): A strictly quantitative methodological core—stability models, numerical methods, parameter estimation—that underpins the technical base of the econometric studies in the upper central zone.
- Quadrant III (F1 < 0, F2 < 0): Research in environmental economics and sustainable development, with a strong emphasis on “environmental economics,” “sustainability,” and “sustainable development,” prioritizing reflection on ecological footprints and green policies.
- Quadrant IV (F1 > 0, F2 < 0): Points of contact between empirical applications and sustainability, for example “carbon emission” or “data envelopment analysis” applied to environmental efficiency, forming hybrid studies combining economic indicators and ecological criteria.
This map reveals a two-factor structure opposing, on one side, the rigor of mathematical–econometric developments, and on the other, concreteness in regional and environmental fields. This duality explains the coexistence of three major currents in the literature: pure methodology, macro-regional applied analysis, and sustainability orientation, all interconnected through intermediate nodes (“econometrics,” “cluster analysis,” “investment”) that serve as epistemological bridges between the extremes of the research space.
5. Discussion
The systematic analysis of the literature on economic convergence between 1982 and 2026 confirms that this field has consolidated as a highly relevant analytical strand, both theoretical and applied, to understand structural alignment processes in dynamic and heterogeneous economic contexts. However, this consolidation does not imply conceptual or methodological homogeneity. On the contrary, the results highlight an evolution toward increasingly sophisticated and multidimensional approaches, in which convergence is analyzed not only as an expected outcome of economic growth but as a phenomenon conditioned by institutional, spatial, technological, and normative factors (M. Ahmad & Law, 2024; Sharma & Sharma, 2023).
This study offers an integrative and up-to-date perspective on the field of economic convergence analysis, combining a rigorous bibliometric approach with thematic and temporal analyses to capture the multidimensionality and evolution of the area. Unlike previous reviews that focused on specific aspects or a single method, this work highlights the conceptual and methodological heterogeneity as well as the growing interconnection between mathematical, economic, institutional, and environmental domains. Furthermore, the identification of thematic clusters and the mapping of international collaboration provide a novel view of the knowledge structure and global scientific flows, thereby establishing a solid foundation for future interdisciplinary research.
In line with classical and recent literature, the study confirms the persistent distinction between β convergence and σ convergence, as well as the progressive incorporation of stochastic and club convergence analyses. This methodological diversification responds to the need to capture the complexity of adjustment processes among heterogeneous units, overcoming the restrictive assumptions of absolute convergence models (Afzal & Sibbertsen, 2021; Alataş, 2023). Significantly, the clusters identified in the bibliometric analysis show polarization between formal statistical approaches (cluster 3), contextual institutional perspectives (cluster 2), and strategic normative frameworks (cluster 5), reinforcing the idea that convergence analysis has ceased to be a univocal category and has transformed into an interdisciplinary field with multiple theoretical and applied lines.
Looking forward, emerging research directions also pose technical challenges, such as integrating complex hybrid models and dealing with data accessibility issues, particularly for real-time or high-frequency monitoring systems. Addressing these obstacles will be essential to fully harness the potential of advanced methodologies in capturing the dynamic and multifaceted nature of convergence processes.
The bibliometric patterns identified in this study offer actionable insights for policymakers and institutional planners. For example, the growing integration of sustainability indicators into convergence research, evident in the thematic prominence of journals like Journal of Cleaner Production and the focus on carbon and energy convergence, can inform the design of climate equity frameworks in international agreements. Regional development agencies could use these findings to prioritize funding in lagging regions not only based on income gaps but also on convergence trajectories in energy efficiency and green innovation.
Similarly, the methodological shift toward club convergence and nonlinear dynamics suggests that one-size-fits-all policy interventions may fail in heterogeneous contexts. For instance, the European Union’s cohesion policy could leverage these insights to move from uniform funding formulas to targeted, cluster-based strategies that address the distinct structural barriers of different regional blocks, such as the divergent paths observed in Southern vs. Northern Europe. By aligning policy design with the empirically observed fragmentation of convergence processes, decision-makers can enhance both the effectiveness and equity of development interventions.
5.1. Future Research Lines
Considering these findings, several future research lines emerge directly from the identified theoretical and methodological gaps:
- Integration of hybrid convergence models: Progress toward approaches combining dynamic models with institutional and structural elements remains incipient. The incorporation of integrated frameworks articulating spatial econometrics, institutional theory, and network analysis can enrich understanding of convergence dynamics under complex interdependencies (N. Ahmad et al., 2019; Akram et al., 2024; Maza & Villaverde, 2009a).
- Convergence in non-economic dimensions: Although literature has begun including variables such as energy efficiency, carbon emissions, and institutional performance, greater development of composite indicators integrating social, environmental, and technological dimensions is needed. This is especially relevant in the context of the SDGs (Akhtar et al., 2024; Eleftheriou et al., 2024; Goto & Sueyoshi, 2023; Z. Hu et al., 2025; Lyulyov et al., 2024).
- Exploration of reversible and bifurcated trajectories: Studies clustered in group 4 emphasize examining convergence as a nonlinear process subject to transitions, blockages, and breaks. Future research should focus on modeling these multiple regimes using tools such as Markov-switching, institutional shift analysis, and non-stationary time series (Boswijk et al., 2021; Cutrini & Mendez, 2023; Gabriel et al., 2025; Jerzmanowski, 2006; Tyrowicz et al., 2025).
- Comparative studies across regions and sectors: Most of the literature focuses on countries or national regions. However, analytical opportunities exist in studying sectoral, technological, or institutional convergence, especially in global value chains and transitioning economies (Aboal et al., 2023; Guan & Xu, 2021; Kordalska & Olczyk, 2023; Niu et al., 2025).
- Evaluation of convergence policy impacts: The normative dimension remains limited. Explicitly linking empirical results with policy evaluations aimed at promoting territorial cohesion and economic integration is essential, especially in regions with persistent structural gaps (Akram et al., 2023; Hansen & Herrmann, 2012; Onaran et al., 2022a).
- Development of adaptive and real-time metrics: Incorporating artificial intelligence, machine learning, and high-frequency analysis can enable continuous monitoring systems sensitive to contextual changes, exogenous shocks, and disruptive transformations. Emerging tools such as large language models (LLMs) and deep neural networks could further enhance the capacity to analyze unstructured policy texts, detect latent convergence patterns, and forecast structural transitions, opening new frontiers for real-time, data-driven convergence assessment (Li et al., 2022; Padilla et al., 2024; Wei et al., 2022; Xi et al., 2022; Xu et al., 2024).
Considering the above, economic convergence should be understood not as a linear or deterministic phenomenon but as an emergent property of dynamic and complex systems, where structural alignment trajectories depend on multiple contextual factors and strategic decisions. This study reinforces the need to adopt integrative methodological approaches sensitive to the diversity of historical, institutional, and territorial experiences that allow not only description but also guidance of convergence processes toward equity, resilience, and sustainability goals.
5.2. Limitations
This work presents several methodological limitations that should be considered when interpreting the results. First, the language restriction to articles written only in English may have excluded relevant contributions published in other languages, potentially introducing geographic and cultural biases. Second, the exclusive use of Scopus entails certain limitations. While it provides wide coverage, some high-impact journals indexed in Web of Science may not be fully represented in Scopus, and vice versa. The absence of a multi-database triangulation (e.g., combining Scopus with Web of Science or Dimensions) may result in the omission of relevant studies, particularly those published in niche or regionally focused journals. Additionally, relying on a single database increases the risk of systematic bias related to indexing policies and disciplinary emphasis. Future studies could address this limitation by conducting comparative bibliometric analyses across multiple platforms to ensure greater comprehensiveness and robustness of findings.
Third, the use of predefined search terms with Boolean operators could have constrained the identification of interdisciplinary approaches, particularly those related to sustainability or digital integration. Additionally, the recurrence of common author surnames (such as Wang, Zhang, and Li) may have led to inaccuracies in counting publications by individual authors, thus affecting the precision of productivity metrics. Finally, the dependence on longitudinal data, which is inconsistent or incomplete in some domains or regions, restricts the capacity to detect long-term convergence trends or structural breaks. Despite these constraints, the mixed-method approach and cross-review among researchers strengthen the internal validity of the study, offering a comprehensive and robust view of the state of the art in economic convergence analysis.
6. Conclusions
This study demonstrates that economic convergence analysis has evolved into a multidimensional and methodologically diverse field, capable of capturing complex structural adjustment dynamics across heterogeneous systems. By integrating quantitative, institutional, and normative perspectives, it provides a robust framework for understanding alignment processes in a global context marked by inequality and transformation.
However, convergence remains a contingent and non-linear phenomenon, shaped by disruptions and structural shifts. No single method can fully capture its complexity, underscoring the need for interdisciplinary integration, methodological innovation, and the inclusion of emerging dimensions such as digitalization and sustainability.
While this study offers a comprehensive mapping of the field, limitations related to database scope (Scopus only) and language bias (English-only) should be considered in future research. Nevertheless, the integrative approach developed here provides a solid foundation for advancing both theoretical and policy-relevant work on convergence in the 21st century.
In sum, the future of economic convergence analysis lies in its capacity to integrate advanced computational methods, expand into non-economic dimensions, and respond to pressing global challenges such as sustainability, equity, and technological disruption. Emerging tools like machine learning, spatiotemporal modeling, and large-scale data analytics offer promising avenues for real-time monitoring and adaptive policy design. By embracing this integrative and forward-looking approach, the field can move beyond descriptive analysis to become a proactive instrument for shaping inclusive and resilient development trajectories in an increasingly complex and interconnected world.
Author Contributions
Conceptualization, G.G.-V. (Geisel García-Vidal) and G.G.-V. (Gelmar García-Vidal); Methodology, G.G.-V. (Geisel García-Vidal) and N.A.L.-C.; Software, N.A.L.-C.; Validation, G.G.-V. (Geisel García-Vidal), N.A.L.-C. and R.P.-C.; Formal analysis, R.P.-C.; Investigation, G.G.-V. (Geisel García-Vidal) and R.P.-C.; Resources, G.G.-V. (Gelmar García-Vidal); Data curation, N.A.L.-C.; Writing—original draft, G.G.-V. (Geisel García-Vidal); Writing—review & editing, G.G.-V. (Gelmar García-Vidal); Visualization, R.P.-C.; Supervision, G.G.-V. (Gelmar García-Vidal); Project administration, G.G.-V. (Gelmar García-Vidal). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in this study are publicly available in Scopus and can be replicated by applying the search string provided in Table 3. It is important to note that the search has a cut-off date of July 2025. For further inquiries, please contact the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aaldering, L. J., Leker, J., & Song, C. H. (2019). Uncovering the dynamics of market convergence through M&A. Technological Forecasting and Social Change, 138, 95–114. [Google Scholar] [CrossRef]
- Aboal, D., Lanzilotta, B., Pereyra, M., & Queraltó, M. P. (2023). Regional development and convergence clubs in uruguay. Economia Aplicada, 27(3), 351–381. [Google Scholar] [CrossRef]
- Ab-Rahim, R., Selvarajan, S. K., Md-Nor, N. G., & Marikan, D. A. A. (2018). Convergence clubs of economic liberalization in ASEAN, China, and India. Jurnal Ekonomi Malaysia, 52(3), 137–151. [Google Scholar] [CrossRef]
- Adeeko, O., Sanusi, O. I., & Tabash, M. I. (2023). An assessment of efficiency and productivity analysis of manufacturing industries in Bangladesh. International Journal of Applied Economics, Finance and Accounting, 16(2), 248–263. [Google Scholar] [CrossRef]
- Afzal, A., & Sibbertsen, P. (2021). Modeling fractional cointegration between high and low stock prices in Asian countries. Empirical Economics, 60(2), 661–682. [Google Scholar] [CrossRef]
- Aghion, P., & Jaravel, X. (2015). Knowledge spillovers, innovation and growth. Economic Journal, 125(583), 533–573. [Google Scholar] [CrossRef]
- Agovino, M., Ferraro, A., & Musella, G. (2021). Does national environmental regulation promote convergence in separate waste collection? Evidence from Italy. Journal of Cleaner Production, 291, 125285. [Google Scholar] [CrossRef]
- Ahmad, M., & Law, S. H. (2024). Financial development, institutions, and economic growth nexus: A spatial econometrics analysis using geographical and institutional proximities. International Journal of Finance and Economics, 29(3), 2699–2721. [Google Scholar] [CrossRef]
- Ahmad, N., Naveed, A., & Naz, A. (2019). A hierarchical analysis of structural change and labour productivity convergence across regions, countries and industries within the EU. Labour and Industry, 29(2), 181–198. [Google Scholar] [CrossRef]
- Ahouangbe, V. L., & Turcu, C. (2024). How bilateral foreign direct investment influences environmental convergence. World Economy, 47(1), 37–95. [Google Scholar] [CrossRef]
- Akhtar, M. J., Rehman, H. U., & Abbas, Q. (2024). “The promissory note at COP-21 of sustainable energy for all” Is it converging toward economic development? Environment, Development and Sustainability, 26(10), 26557–26578. [Google Scholar] [CrossRef]
- Akram, V., & Ali, J. (2022). Do countries converge in natural resources rents? Evidence from club convergence analysis. Resources Policy, 77, 102743. [Google Scholar] [CrossRef]
- Akram, V., Rath, B. N., & Panda, B. (2023). Convergence analysis of social sector expenditure and its components: Evidence from the Indian states. Applied Economics, 55(33), 3850–3862. [Google Scholar] [CrossRef]
- Akram, V., Rath, B. N., & Sahoo, P. K. (2024). Club convergence in per capita carbon dioxide emissions across Indian states. Environment, Development and Sustainability, 26(8), 19907–19934. [Google Scholar] [CrossRef]
- Alataş, S. (2023). Revisiting the Solow growth model: New empirical evidence on the convergence debate. Journal of Economic and Administrative Sciences, 39(4), 801–817. [Google Scholar] [CrossRef]
- Alataş, S., Karakaya, E., & Sarı, E. (2021). The potential of material productivity alongside energy productivity in climate mitigation: Evidence from convergence tests in the EU28. Resources, Conservation and Recycling, 167, 105322. [Google Scholar] [CrossRef]
- Alemu, S., Udvari, B., & Kotosz, B. (2024). Income convergence in Central and Eastern Europe: Evidence from cross-country panel data analysis. Acta Oeconomica, 74(3), 329–357. [Google Scholar] [CrossRef]
- Alexakis, C., Kenourgios, D., Pappas, V., & Petropoulou, A. (2021). From dotcom to COVID-19: A convergence analysis of Islamic investments. Journal of International Financial Markets, Institutions and Money, 75, 101423. [Google Scholar] [CrossRef]
- Apergis, N., Delgado, F. J., & Suárez-Arbesú, C. (2025). Inequality and poverty in Spain: Insights from a regional convergence analysis. International Journal of Finance and Economics, 30(2), 1707–1723. [Google Scholar] [CrossRef]
- Balado-Naves, R., Baños-Pino, J. F., & Mayor, M. (2023). Spatial spillovers and world energy intensity convergence. Energy Economics, 124, 106807. [Google Scholar] [CrossRef]
- Barro, R. J., & Sala-i-Martin, X. (1992). Convergence. Journal of Political Economy, 100(2), 223–251. Available online: http://www.jstor.org/stable/2138606 (accessed on 15 June 2025). [CrossRef]
- Borozan, D. (2024). European institutional quality and carbon emissions: Convergence club analysis. Structural Change and Economic Dynamics, 71, 646–657. [Google Scholar] [CrossRef]
- Boswijk, H. P., Cavaliere, G., Georgiev, I., & Rahbek, A. (2021). Bootstrapping non-stationary stochastic volatility. Journal of Econometrics, 224(1), 161–180. [Google Scholar] [CrossRef]
- Celati, B. (2023). Managing complexity: The efficiency of administrative performance and the re-emergence of economic planning for the reconciliation of strategic interests of territories. P.A. Persona e Amministrazione, 12(1), 145–170. [Google Scholar] [CrossRef]
- Cutrini, E., & Mendez, C. (2023). Convergence clubs and spatial structural change in the European Union. Structural Change and Economic Dynamics, 67, 167–181. [Google Scholar] [CrossRef]
- Dhaigude, A. S., Verma, A., & Nayak, G. (2025). Sustainable production and consumption: A bibliometric analysis of SDG-12 literature through a financial management lens. Cogent Economics and Finance, 13(1), 2467882. [Google Scholar] [CrossRef]
- Donthu, N., Kumar, S., Mukherjee, D., Pandey, N., & Lim, W. M. (2021). How to conduct a bibliometric analysis: An overview and guidelines. Journal of Business Research, 133, 285–296. [Google Scholar] [CrossRef]
- Eleftheriou, K., Nijkamp, P., & Polemis, M. L. (2024). Club convergence of sustainable development: Fresh evidence from developing and developed countries. Economic Change and Restructuring, 57(2), 32. [Google Scholar] [CrossRef]
- Fan, D., Peng, B., Wu, J., & Zhang, Z. (2024). The convergence of total-factor energy efficiency across Chinese cities: A distribution dynamics approach. Structural Change and Economic Dynamics, 69, 406–416. [Google Scholar] [CrossRef]
- Fan, F., Yang, B., & Wang, S. (2025). The convergence mechanism and spatial spillover effects of urban industry-university-research collaborative innovation performance in China. Technology Analysis and Strategic Management, 37(5), 551–567. [Google Scholar] [CrossRef]
- Gabriel, L. F., Ribeiro, L. C. D. S., & Sousa Filho, J. F. (2025). Structural change and productive interdependence: An analysis for Brazil. Structural Change and Economic Dynamics, 72, 256–274. [Google Scholar] [CrossRef]
- German-Soto, V., & Brock, G. (2022). Overall US and census region β-convergence 1963–2015 controlling for spatial effects. Comparative Economic Studies, 64(1), 44–67. [Google Scholar] [CrossRef]
- Goto, M., & Sueyoshi, T. (2023). Sustainable development and convergence under energy sector transition in industrial nations: An application of DEA environmental assessment. Socio-Economic Planning Sciences, 87, 101316. [Google Scholar] [CrossRef]
- Guan, C., & Xu, Q. (2021). The boundary of supranational rules: Revisiting policy space conflicts in global trade politics. Journal of World Trade, 55(5), 853–880. [Google Scholar] [CrossRef]
- Hansen, H., & Herrmann, R. (2012). The two dimensions of policy impacts on economic cohesion: Concept and illustration for the CAP. Food Policy, 37(4), 483–491. [Google Scholar] [CrossRef]
- Hi, T. (2020). Is stability for regional disparities of unemployment rates truly mysterious? An analysis from statistical approach. Regional Science Inquiry, 12(1), 253–260. [Google Scholar]
- Hou, Y., Li, X., Wang, H., & Yunusova, R. (2024). Focusing on energy efficiency: The convergence of green financing, FinTech, financial inclusion, and natural resource rents for a greener Asia. Resources Policy, 93, 105052. [Google Scholar] [CrossRef]
- Hryhorkiv, V., Verstiak, A., Verstiak, O., & Hryhorkiv, M. (2017). Regional economic growth disparities in Ukraine: Input-output analysis approach. Scientific Annals of Economics and Business, 64(4), 447–457. [Google Scholar] [CrossRef]
- Hu, M., Song, H., Wu, J., & Yang, J. (2025). Inexact primal-dual active set iteration for optimal distribution control of stationary heat or cold source. Journal of Global Optimization, 91(1), 235–253. [Google Scholar] [CrossRef]
- Hu, Z., Wu, G., Wang, T., & Yuan, H. (2025). Convergence of sustainable development goals evolution and Five-Year Plans reform: Lessons from China. Socio-Economic Planning Sciences, 98, 102156. [Google Scholar] [CrossRef]
- Im, K. S., Pesaran, M. H., & Shin, Y. (2003). Testing for unit roots in heterogeneous panels. Journal of Econometrics, 115(1), 53–74. [Google Scholar] [CrossRef]
- Jadhav, V. (2023). Dynamics of national development and regional disparity: Evidence from 184 countries. Journal of Economic Studies, 50(5), 1048–1062. [Google Scholar] [CrossRef]
- Jerzmanowski, M. (2006). Empirics of hills, plateaus, mountains and plains: A Markov-switching approach to growth. Journal of Development Economics, 81(2), 357–385. [Google Scholar] [CrossRef]
- Kordalska, A., & Olczyk, M. (2023). Upgrading low value-added activities in global value chains: A functional specialisation approach. Economic Systems Research, 35(2), 265–291. [Google Scholar] [CrossRef]
- Koutsougeras, L. C., & Meo, C. (2018). An asymptotic analysis of strategic behavior for exchange economies. Economic Theory, 66(2), 301–325. [Google Scholar] [CrossRef]
- Levin, A., Lin, C. F., & Chu, C. S. J. (2002). Unit root tests in panel data: Asymptotic and finite-sample properties. Journal of Econometrics, 108(1), 1–24. [Google Scholar] [CrossRef]
- Levine, R., & Renelt, D. (1992). A sensitivity analysis of cross-country growth regressions. American Economic Review, 82(4), 942–963. [Google Scholar]
- Li, C., Xiong, G., Fu, X., Mohamed, A. W., Yuan, X., Al-Betar, M. A., & Suganthan, P. N. (2022). Takagi–Sugeno fuzzy based power system fault section diagnosis models via genetic learning adaptive GSK algorithm. Knowledge-Based Systems, 255, 109773. [Google Scholar] [CrossRef]
- Lin, S., Sun, J., Marinova, D., & Zhao, D. (2018). Evaluation of the green technology innovation efficiency of China’s manufacturing industries: DEA window analysis with ideal window width. Technology Analysis and Strategic Management, 30(10), 1166–1181. [Google Scholar] [CrossRef]
- Liu, C., Xie, R., & Ma, C. (2025). Convergence of Chinese urban carbon marginal abatement cost. Applied Economics, 57(5), 525–542. [Google Scholar] [CrossRef]
- Lyulyov, O., Pimonenko, T., Chen, Y., Kwilinski, A., & Yana, U. (2024). Countries’ green brands within the context of sustainable development goals. Journal of Innovation and Knowledge, 9(3), 100509. [Google Scholar] [CrossRef]
- Maza, A., & Villaverde, J. (2009a). Provincial wages in Spain: Convergence and flexibility. Urban Studies, 46(9), 1969–1993. [Google Scholar] [CrossRef]
- Maza, A., & Villaverde, J. (2009b). Spatial effects on provincial convergence and income distribution in Spain: 1985–2003. Tijdschrift voor Economische en Sociale Geografie, 100(3), 316–331. [Google Scholar] [CrossRef]
- Maza, A., & Villaverde, J. (2011). EU regional convergence and policy: Does the concept of region matter? Journal of Policy Modeling, 33(6), 889–900. [Google Scholar] [CrossRef]
- Mishra, P. K., Mishra, S. K., & Sarangi, M. K. (2020). Social sector development and economic growth in India, 1990–1991 to 2017–2018. Journal of Economic Development, 45(4), 49–68. [Google Scholar]
- Navarro-Chávez, C. L., Morán-Figueroa, J. C., & Ayvar-Campos, F. J. (2025). Conditional β-convergence in APEC economies, 1960–2020: Empirical evidence from the pooled mean group estimator. Econometrics, 13(1), 7. [Google Scholar] [CrossRef]
- Navarro Claro, G. T., & Bayona Soto, J. A. (2025). The impact of artificial intelligence on quality and sustainable development: A bibliometric analysis. Quality Innovation Prosperity, 29(1), 81–97. [Google Scholar] [CrossRef]
- Nguyen, N. U. P., & Moehrle, M. G. (2023). Combining the analysis of vertical and horizontal technology convergence: Insights from the case of urban innovation. IEEE Transactions on Engineering Management, 70(4), 1402–1415. [Google Scholar] [CrossRef]
- Nguyen, T., Nghiem, S., & Bhati, A. S. (2024). Risk-adjusted efficiency and innovation: An examination of systematic difference and convergence among BRIC banks. Economic Systems, 48(1), 101167. [Google Scholar] [CrossRef]
- Niu, M., Wang, Z., Zhang, Y., & Mao, Y. (2025). The chasing dragon: To what extent and how does China catch up with USA under global value chains? Applied Economics, 57(8), 839–852. [Google Scholar] [CrossRef]
- Onaran, Ö., Oyvat, C., & Fotopoulou, E. (2022a). Gendering macroeconomic analysis and development policy: A theoretical model. Feminist Economics, 28(3), 23–55. [Google Scholar] [CrossRef]
- Onaran, Ö., Oyvat, C., & Fotopoulou, E. (2022b). A macroeconomic analysis of the effects of gender inequality, wages, and public social infrastructure: The case of the UK. Feminist Economics, 28(2), 152–188. [Google Scholar] [CrossRef]
- Öztürk, O., Kocaman, R., & Kanbach, D. K. (2024). How to design bibliometric research: An overview and a framework proposal. Review of Managerial Science, 18(11), 3333–3361. [Google Scholar] [CrossRef]
- Padilla, L., Carrington, S. J., & Nicolalde, E. M. (2024). Fragile union: A machine learning analysis of structural heterogeneity and divergence within the EMU. Ekonomika, 103(4), 61–80. [Google Scholar] [CrossRef]
- Pattinson, H. M., & Woodside, A. G. (2007). Mapping strategic thought and action in developing disruptive software technology: Advanced case study research on how the firm crafts shared vision. Innovative Marketing, 3(4), 107–137. [Google Scholar]
- Phillips, P. C. B., & Sul, D. (2007). Transition modeling and econometric convergence tests. Econometrica, 75(6), 1771–1855. [Google Scholar] [CrossRef]
- Quah, D. T. (1996). Empirics for economic growth and convergence. European Economic Review, 40(6), 1353–1375. [Google Scholar] [CrossRef]
- Quah, D. T. (1997). Empirics for growth and distribution: Stratification, polarization, and convergence clubs. Journal of Economic Growth, 2(1), 27–59. [Google Scholar] [CrossRef]
- Rodríguez Benavides, D., Mendoza González, M. Á., & Muller Durán, N. (2022). Regional covergence in Mexico: A test of weak σ-convergence. Investigaciones Regionales, 2022(54), 29–49. [Google Scholar] [CrossRef]
- Sala-i-Martin, X. (1994). Cross-sectional regressions and the empirics of economic growth. European Economic Review, 38(3–4), 739–747. [Google Scholar] [CrossRef]
- Sala-i-Martin, X. (1996). The classical approach to convergence analysis. The Economic Journal, 106(437), 1019–1036. [Google Scholar] [CrossRef]
- Sala-i-Martin, X. (2006). The world distribution of income: Falling poverty and … convergence, period. The Quarterly Journal of Economics, 121(2), 351–397. [Google Scholar] [CrossRef]
- Sharma, P., & Sharma, N. (2023). Convergence hypothesis: A systematic literature review with bibliometric analysis. International Journal of Sustainable Economy, 15(4), 447–477. [Google Scholar] [CrossRef]
- Solow, R. M. (1956). A contribution to the theory of economic growth. The Quarterly Journal of Economics, 70(1), 65–94. [Google Scholar] [CrossRef]
- Stergiou, E., & Kounetas, K. (2022). Heterogeneity, spillovers and eco-efficiency of European industries under different pollutants’ scenarios. Is there a definite direction? Ecological Economics, 195, 107377. [Google Scholar] [CrossRef]
- Sun, Q., Li, C., & Ma, X. (2025). Regional equity in the energy transition: Assessing the role of productivity gaps and technology selection. Energy Economics, 147, 108531. [Google Scholar] [CrossRef]
- Tang, Z., Ma, S., Fu, M., Wang, Y., Xue, J., Yin, Y., & Xiao, Y. (2025). Carbon emissions induced by land use and land cover change amid rapid urbanization in Chengdu-Chongqing economic circle, China: Efficiency, transfer and process. Environment, Development and Sustainability, 27(2), 4403–4423. [Google Scholar] [CrossRef]
- Tyrowicz, J., Makarski, K., & Lutynski, J. (2025). Structural change and inequality in a general equilibrium model of a transition economy. Economics of Transition and Institutional Change, 33(3), 667–693. [Google Scholar] [CrossRef]
- Ud Din, M. A., Dar, M. H., & Haseen, S. (2023). Inter-state disparities in government health expenditure in India: A study of national rural health mission. International Journal of Health Governance, 28(1), 82–94. [Google Scholar] [CrossRef]
- Wei, L., Zhang, F., Chen, Z., Zhou, R., & Zhu, C. (2022). Subspace clustering via adaptive least square regression with smooth affinities. Knowledge-Based Systems, 239, 107950. [Google Scholar] [CrossRef]
- Xi, X., Shi, Z., Wang, X., Xing, C., & Li, S. (2022). Adaptive finite-time parameter estimation for grid-connected converter with LCL filter. Frontiers in Energy Research, 10, 964216. [Google Scholar] [CrossRef]
- Xu, J., Bao, C., & Xing, W. (2024). Convergence rates of training deep neural networks via alternating minimization methods. Optimization Letters, 18(4), 909–923. [Google Scholar] [CrossRef]
- Zhao, X., Zhang, Y., & Li, Y. (2019). The spillovers of foreign direct investment and the convergence of energy intensity. Journal of Cleaner Production, 206, 611–621. [Google Scholar] [CrossRef]
- Zhong, L., Lin, Y., Yang, M., He, Y., Liu, X., Yu, P., & Xie, Z. (2025). Spatiotemporal pattern of embodied carbon emissions from in-use steel stock in countries along the Belt and Road. Resources, Conservation and Recycling, 214, 108038. [Google Scholar] [CrossRef]
- Zoltán, E., & Imre, L. (2024). Spatial econometric analysis of convergence processes in East-Central European regions. Statisztikai Szemle, 102(8), 781–809. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).