A Note on Keynesian Models Used in Standard Textbooks

Abstract

This article shows that there is a methodological problem in the traditional IS-LM model. If production cannot be sufficiently adjusted downwards, there is no uniform interest rate that simultaneously clears the money and goods markets. An extension of the credit market in the tradition of the loanable funds theory resolves this contradiction and yields a coherent mechanism for crisis dynamics and policy transmission. In this expanded model, the interest rate is determined by the credit market whereby the total supply of credit results from household savings and the credit supply of banks and the demand for credit is due to investment demand and the demand for liquidity. This methodological approach facilitates the explanation of crisis dynamics, as involuntary inventory investment generates liquidity problems and disequilibria in the goods market lead to imbalances in the financial markets.

1. Introduction and Overview

The following paper argues that the explanatory approaches for analysing recessions and depressions are not adequately captured by standard Keynesian macro models.1 It is shown why these models quickly reach their limits. The IS-LM model developed by Hicks (1937) as well as the New Keynesian models are quite useful for many issues. However, if one wants to explain recessions and depressions, it has to be considered that production cannot be adjusted downwards at will. Taking this fact into account, new insights emerge. A uniform equilibrium interest rate for the goods market and the money market together no longer arises in the IS-LM model but can be re-established by the introduction of a broader credit market in the tradition of the loanable funds theory.

For the sake of simplicity, Section 2 of the paper draws on the traditional Keynesian concept of animal spirits.2 This simplification ensures that aggregate demand is solely determined by expectations; the interest rate plays no role in the short and medium term. With demand exclusively driven by (sales) expectations, the basic idea of the paper can be outlined through a relatively simple model. These expectations about aggregate demand determine the interest rate in the Keynesian models. However, we show that the traditional IS-LM model reaches its limits in explaining the interest rate and becomes inconsistent if production cannot be adjusted downwards without restriction. The equilibrium interest rate on the money market would then have to be higher than that on the goods market.

Taking this as the starting point, Section 3 shows that an interest rate that clears the goods market and the money (bond) market is still feasible, even if output adjustment is bounded downwards. This necessitates the modelling of a credit market with a broadly defined demand for and supply of loanable funds. The supply of credit results from household savings and the credit supply of banks and the demand for credit arises from investment demand and the demand for money. Such models were developed in the 1930s.3 Macroeconomic stabilisation crises are characterised by an underutilisation of production factors and an excess supply of goods. These problems in the real sector of an economy lead to liquidity and profitability problems for firms and banks and to financial crises. It is shown that in this context the interest rate can no longer be determined in the real sector alone. The standard Keynesian models represent only a special case of this more general loanable funds theory. The following explanations refer fundamentally to theoretical work by Vogt (2023), whose analyses have been supplemented by charts and empirical material.

2. Economic Fluctuations Due to Animal Spirits

In order to present the following ideas more precisely, we use a simple and standard production function, like in many textbooks (see, e.g., those mentioned in note 1). Let N and K be labour and capital input, respectively, and T the state of technology. Thus, T·N is the effective labour input, and the production function is given by Y = F(TN,K). Assume constant return to scale yields Y/K = f(TN/K), where Y/K is output per capital unit. Accordingly, T/K represents the level of technology per unit of capital. If an increase in the capital stock of each individual firm causes, in the aggregate, a positive external effect on the level of technology, T/K remains constant as the capital stock increases. If K increases, the level of technology T increases by the same amount, and the marginal product of capital, F_K, remains constant (Aghion & Howitt, 2025; Carlin & Soskice, 2006, p. 529 ff). This simplifies the following discussion considerably. On this basis, the following relationships arise for the production functions F(TN,K) and f(TN/K), as well as the marginal products of labour F_N and capital F_K:

$$Y=F\left(TN,K\right)\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}{\displaystyle \frac{Y}{K}}=f\left({\displaystyle \frac{TN}{K}}\right) and\hspace{0.33em}\hspace{0.33em}{f}^{\prime }\left({\displaystyle \frac{TN}{K}}\right)>0,{ f}^{″}\left({\displaystyle \frac{TN}{K}}\right)<0,$$

where

$${\displaystyle \frac{\partial Y}{\partial K}}=F_K=f\left({\displaystyle \frac{TN}{K}}\right)-{\displaystyle \frac{TN}{K}}{f}^{\prime }\left({\displaystyle \frac{TN}{K}}\right) and {\displaystyle \frac{\partial Y}{\partial N}}=F_N\hspace{0.33em}={\displaystyle \frac{T}{K}}{f}^{\prime }\left({\displaystyle \frac{TN}{K}}\right)K$$

(1)

$$\mathrm{i}\mathrm{f}\hspace{0.33em}\hspace{0.33em}\lambda ={\displaystyle \frac{T}{K}},\mathrm{we}\mathrm{obtain}{\displaystyle \frac{\partial Y}{\partial K}}=f\left(\lambda N\right)-\lambda N{f}^{\prime }\left(\lambda N\right) and {\displaystyle \frac{\partial Y}{\partial N}}=\hspace{0.33em}\lambda f^{\prime }\left(\lambda N\right)K.$$

On the labour market, the constant labour supply N₀ is supplied in a completely inelastic way and remunerated with the real wage rate w. Capital is remunerated at the real interest rate r. The real wage depends directly on the productivity parameter λ (=T/K) and increases with the growth rate of capital, given a constant labour supply N₀. The return on capital also depends on the productivity parameter λ. If the latter is constant, the real interest rate is constant, too.

With full employment income of Y₀, firms’ profits are given by Y₀ −wN₀ −rK. Profit maximisation or a minimum cost combination of production factors implies w/r = F_N/F_K. With the equilibrium factor price ratio w/r and a given capital stock, we obtain a fixed input ratio of capital to labour K/N, which cannot be changed in the short run. The firms therefore set up a sufficient number of jobs N₀ for a given capital stock. With the above production function, the marginal product of capital F_K is constant. If the market interest rate is below F_K, r < F_K, the firm’s profit G and the profit per unit of capital r_F are given by G = Y₀ − wN₀ – rK = Y₀ − (r/F_K)(F_NN₀ + F_KK). With constant returns to scale, we therefore obtain Y₀ = F_NN₀ + F_KK and G = (1 − r/F_K)Y₀ = (1 − r/F_K)f(TN₀/K)K. This equation is intuitively plausible. If the market interest rate r is below the marginal product of capital F_K, capital is not remunerated at its marginal product but only in the amount of F_K(r/F_K). Cost minimisation requires that labour is also remunerated with the same discount. Therefore, the real wage w = F_N(r/F_K). Actual production amounts to f(TN₀/K)K, of which the share (1 − r/F_K) goes to firms. Full employment results in a profit per capital of r_F = G/K = (1 − r/F_K)f(TN₀/K). In a neoclassical model, if r < F_K, investment demand would increase. This is not always the case in Keynesian models. Despite r < F_K, demand for investment will not increase when sales expectations are pessimistic. If expected demand Y^E is important for the investment decision, investment will not be stimulated, even if r < F_K, because losses can occur if the goods produced cannot be sold.4

The formation of expectations about the demand in the next period Y^E is very complex, as part of this demand is given by expected investment I^E, which in turn depends on expected aggregated demand in the period after the next one.

In order to produce the level of Y in line with this expected demand Y^E in equilibrium and with full employment N₀, the firms have to plan the capital stock K^E = Y^E/f(T^E N₀/K^E) for the next period, given the production function (1). In the current period, we have K = Y/f(TN₀/K). Due to the external effect, f(TN₀/K) = f(T^EN₀/K^E), and therefore investment is I = K^E − K=(Y^E − Y)/f(TN₀/K) = (Y(Y^E − Y)/Y)/f(TN₀/K) = Yy^E/f(TN₀/K), with y^E = (Y^E − Y)/Y as the expected growth rate of income. Because f(TN₀/K) = Y/K, we also obtain I/K = y^E. From this Keynesian perspective, the growth rate of the capital stock corresponds to the expected growth rate of income or production. As it can be seen from the system of Equation (2), the interest rate is determined by expectations of the growth of Y. These expectations determine investment demand and the competition among savers for profitable investment opportunities, in turn, determines the interest rate.

Full employment income Y₀ implies

$$s\left(r\right)Y_0=I, I={\displaystyle \frac{Y^E-Y_0}{f\left(\frac{T{N}_0}{K}\right)}}, s^{\prime }\left(r\right)>0, {\displaystyle \frac{\partial S}{\partial Y}}>0,$$

$$s\left(r\right)f\left({\displaystyle \frac{T{N}_0}{K}}\right)=y^E, y^E={\displaystyle \frac{Y^E-Y_0}{Y_0}}.$$

(2)

We assume that the firms enter into wage agreements, which enable full employment N₀, and thus an output of Y₀ is possible. Capital intensity K/N is planned ex ante and cannot be changed in the short term.

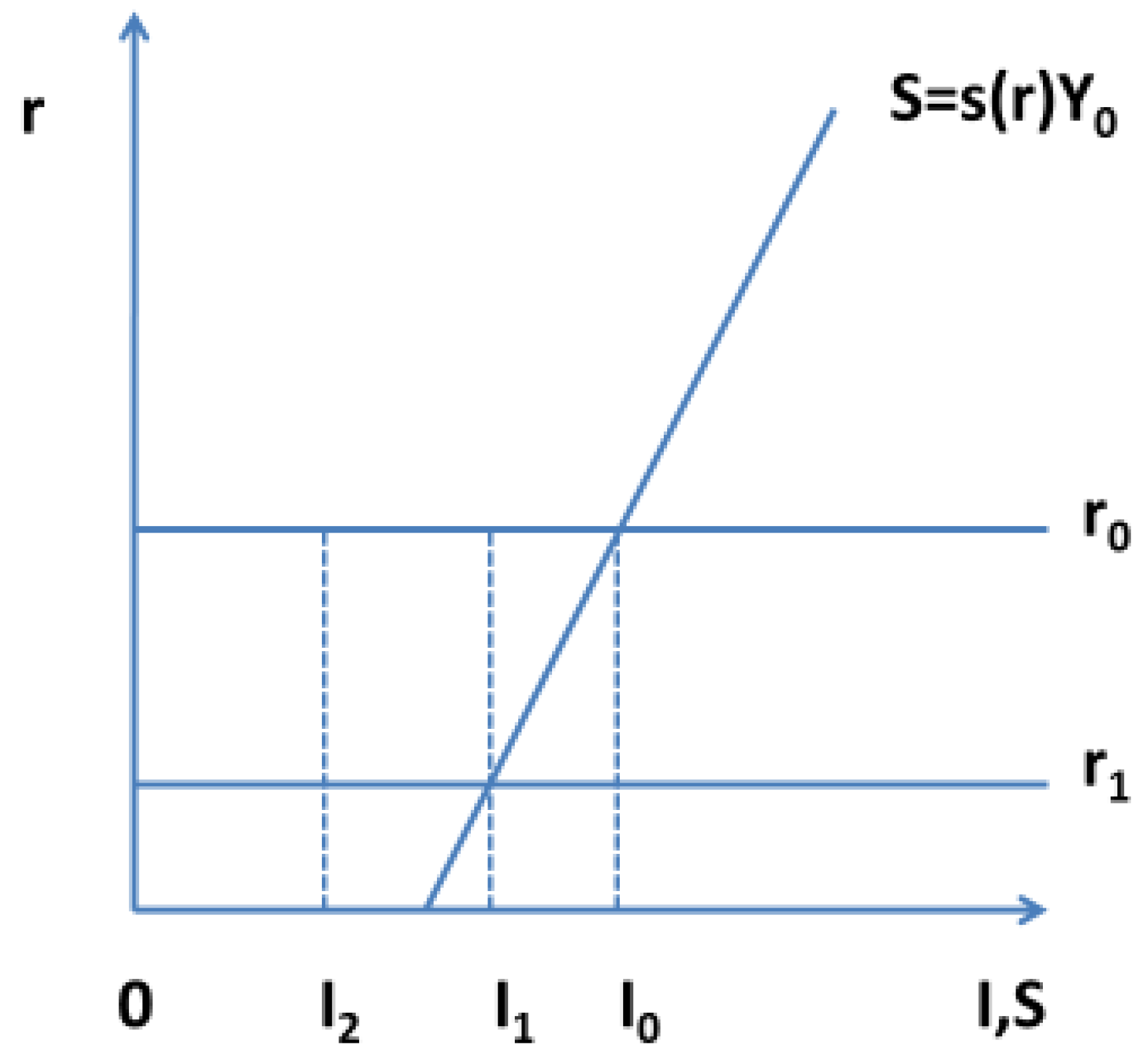
Wages are flexible. Sales expectations for the next period are sufficiently high so that planned investments are I₀ = K^E – K = (Y^E − Y₀)/f(TN₀/K). Capital market equilibrium is shown in Figure 1.

Investment I₀ depends on expected demand Y^E and is completely inelastic to interest rates. An equilibrium on the capital market at the interest rate r₀ is established via the adjustment of savings S = s(r₀)Y₀ to investment I₀, determined by expectations. The equilibrium at r₀ is stable, as r > r₀ leads to increased competition among savers for investment opportunities, which causes the interest rate to fall. In contrast, in the case of r < r₀, competition from firms for loans would drive up the interest rate. A market interest rate r₀ below the marginal productivity of capital would generate extra profits of G = (1 − r₀/F_K)Y₀. Despite these extra profits, firms do not demand more capital due to limited sales expectations. These extra profits would be reflected in the valuation of the firms but are disregarded in the model.

Figure 1 also illustrates that a deterioration in sales expectations and the associated lower investment I₁ does not necessarily lead to crises if the interest rate falls from r₀ to r₁. The slump in demand for capital goods would be compensated for by lower savings, i.e., increased consumer spending.

A deflationary gap, S > I, arises if, at a real interest rate of zero, savings exceed investment demand: I₂ < s(0)Y₀.5 However, firms can adjust production to a certain extent so that planned investment corresponds to planned savings. The planned N₀ jobs are not fully filled ex post, and capital is not fully utilised. Instead of Y₀, the firms now plan production Y = aY₀ with a < 1. Together with (1), we obtain Y = f(TaN₀/aK)aK = aY₀. Because current consumption depends on disposable income, aY < Y₀ implies aY = C + I = (1 − s(r))aY + I, which yields a goods market equilibrium of s(r)aY = I.6 For any given interest rate r, savings S fall when Y falls. In Figure 1, the curve S shifts to the left. From Equation (2), we obtain

$$s\left(r\right)af\left({\displaystyle \frac{T{N}_0}{K}}\right)=y^E, y^E={\displaystyle \frac{Y^E-Y_0}{Y_0}}.$$

(3)

At a capacity utilisation rate of a = I/sY₀, planned investments again equal voluntary savings.

However, this adjustment of savings to investment via a decline in production has its limits. Production is not sufficiently flexible downwards if the shutdown and resumption of production are associated with high costs. Therefore, it can be assumed that there is a minimum limit Y_min for the supply of goods, at least for a certain period of time and if only a temporary crisis period is expected.7 Consequently, production fluctuates among Y_min ≤ Y ≤ Y₀. If there is a minimum production level Y_min, projected production Y < Y_min is not possible, although aggregate demand Y^E < Y_min is expected. 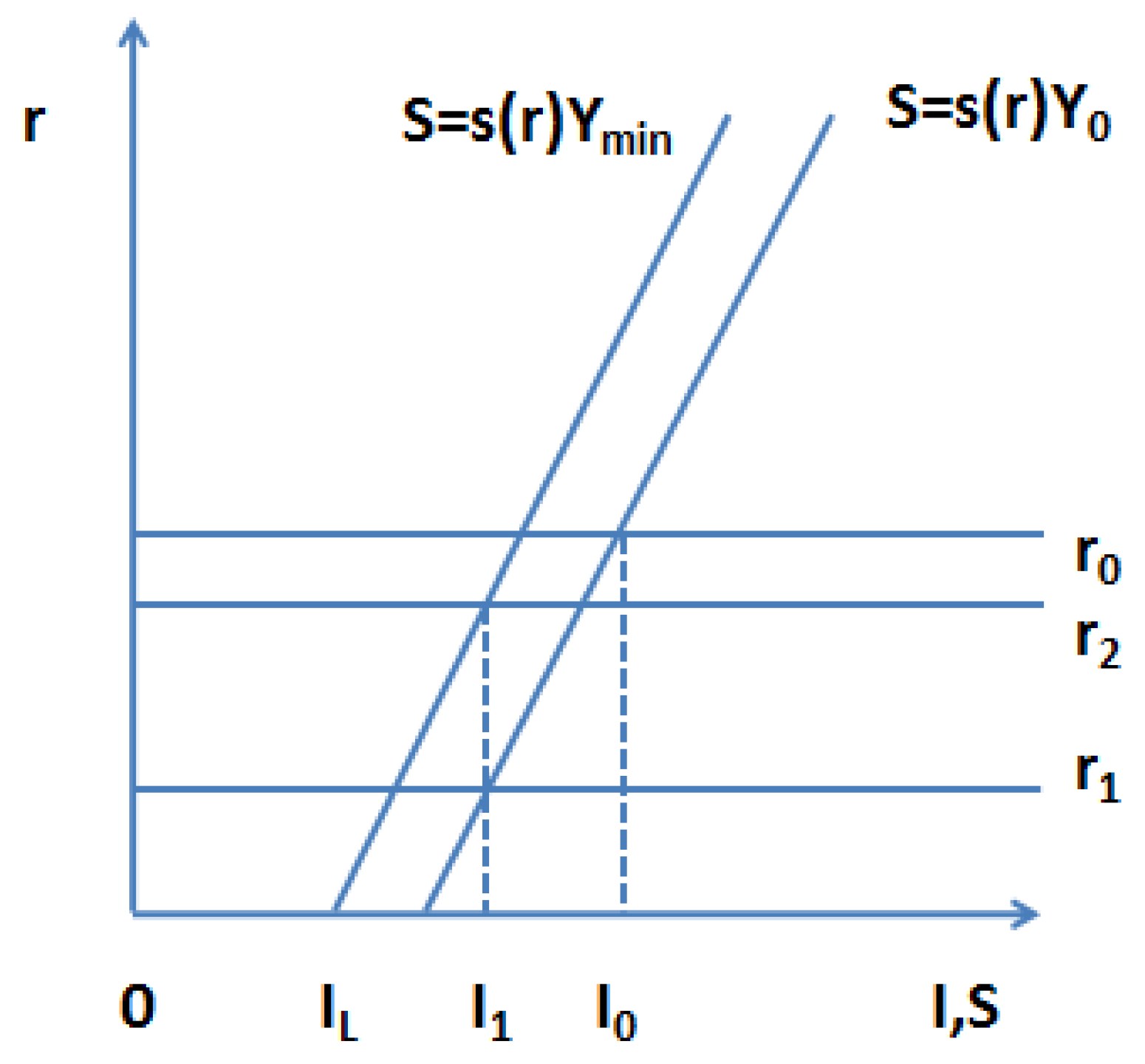These capital market disequilibria are shown in Figure 2.

The starting point is equilibrium at full employment r₀ − Y₀ with investment I₀ = (Y^E − Y₀)/f(TN₀/K). If investment falls from I₀ to I₁ due to deteriorating sales expectations and the interest rate does not fall from r₀ to r₁ but only to r₂, there would still be an equilibrium if savings adjust to investment via the reduction in income. However, if production cannot fall below a minimum level Y_min, this adjustment is impeded as I₁ = s(r₂)Y_min. A deflationary gap arises with I < I₁ and a constant real interest rate r₂. With r = 0 and I_L, a capital market equilibrium, I_L = s(0)Y_min, would just be possible. But a further deterioration in sales expectations in this situation, I < I_L, could no longer be offset by adjusting production. In this case, savings would exceed investment, S > I. The IS-LM model (as well as the three-equation New Keynesian model) cannot solve this problem either, as the following explanations show.8

Assume a traditional IS-LM model with the following money demand function L: L(Y, i) = m(i)Y. The demand for money increases when Y rises, as more money is needed for transactions; it falls when the nominal interest rate i rises, because holding money becomes relatively more expensive. The nominal interest rate i is the opportunity cost of holding money,9 as in the event of inflation π, the nominal interest rate adjusts to offset the loss in the value of money compared to real assets; the Fisher equation i = r + π holds. Because we are initially disregarding inflationary and deflationary processes, we set for simplicity π = 0 and thus i = r. The real money supply is given by M₀/P₀, where M₀ and P₀ are the nominal money supply and the price level, respectively. With savings S = s(r)Y and investment determined by expectations, money market equilibrium implies

$${\displaystyle \frac{M_0}{P_0}}=m\left(r\right)Y$$

(4)

and goods market equilibrium is given by

s(r)Y = I

(5)

The two equilibrium conditions (4) and (5) together determine income Y and the interest rate r for a given money supply and given investments. These two equilibrium values for Y and r simultaneously guarantee money (or financial) market and goods market equilibrium. In the case of interest-inelastic investments, the interest rate influences the goods market via savings (consumption).

Money market equilibrium implies Y = (M₀/P₀)/m(r), goods market equilibrium Y = I/s(r). Therefore, the equilibrium interest rate for an equilibrium Y solves m(r) = s(r)(M₀/P₀)/I. With full capacity utilisation Y₀ and investment I₀, the equilibrium interest rate is determined by s(r₀)Y₀ = I₀. The equilibrium condition for the interest rate, s(r)/m(r) = I/(M₀/P₀), reveals that in the IS-LM model the equilibrium interest rate falls when the real money supply increases and rises when investment increases. From the condition for goods market equilibrium, s(r)Y = I, it follows that for a given level of investment, the utilisation rate Y falls when the equilibrium interest rate rises.

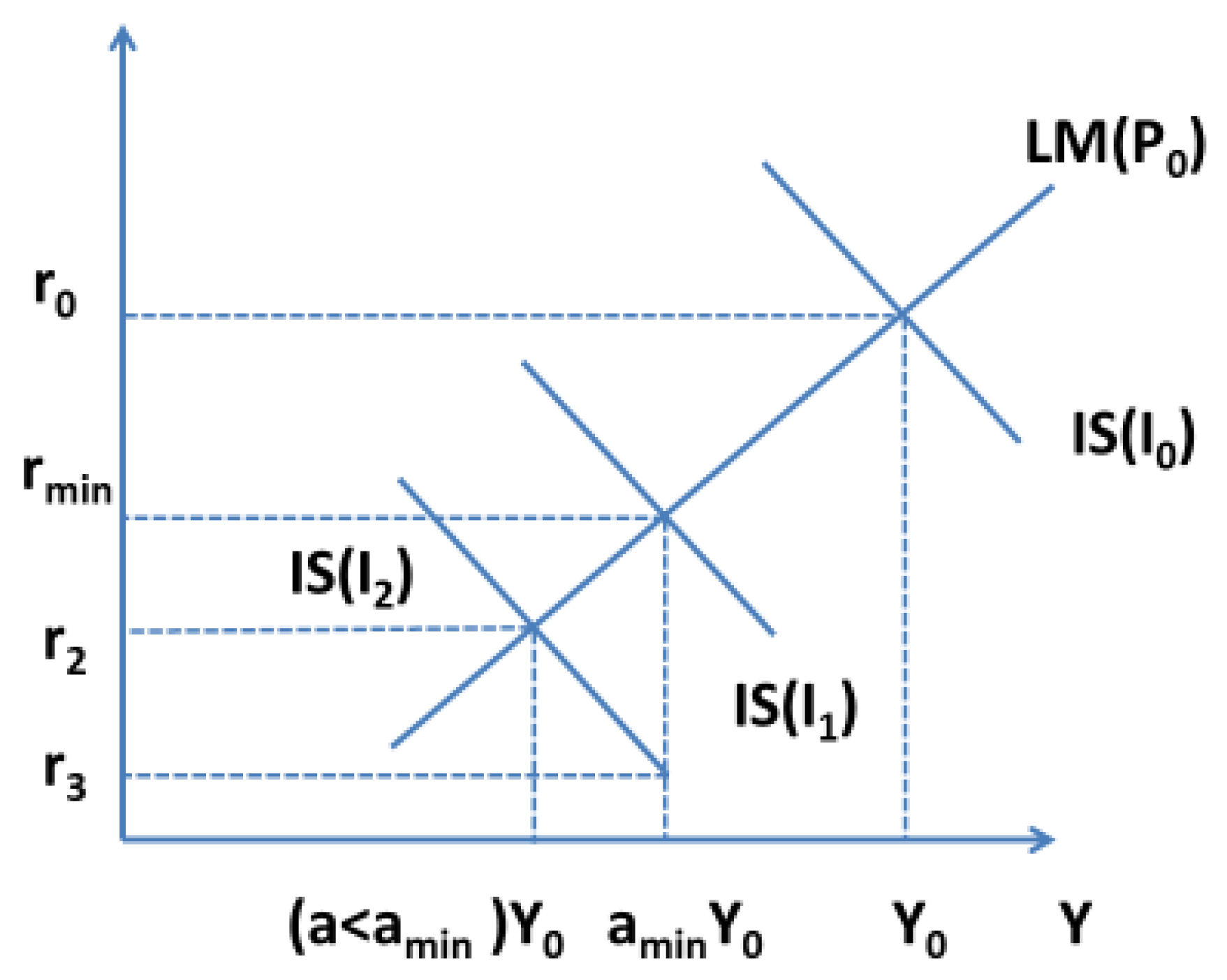
However, if a further downward adjustment of production Y is no longer possible because production is already at Y_min, the IS-LM model also reaches its limits. These relationships can be illustrated with Figure 3.

The shapes of the IS and LM curve are as usual. Prices are fixed in the short run. Figure 3 shows different goods market and money market equilibria for $a_{min}\le a\le 1$. The respective equilibrium interest rates are $r_2\le r_{min}\le r_0$. If the utilisation rate falls due to pessimistic expectations, the interest rate falls. If, however, investment continues to fall from I₁ to I₂ due to even worse sales expectations and the price level P₀ remains constant, goods and money market equilibrium would only be possible at the interest rate r₂ and income (a < a_min)Y₀. However, if production cannot fall below a minimum level, the current production is a_minY₀ > aY₀. This income is too high for goods market equilibrium, and savings exceed planned investment, S > I. With an output level of a_minY in Figure 3, the equilibrium interest rate for the goods market, I = S, would be the interest rate r₃ < r₂, as only in this case would savings be sufficiently low at the income a_minY. However, money market equilibrium requires an interest rate r_min > r₂ at a_minY. The money market is in disequilibrium, L > M.

Very pessimistic expectations, I₂ < I₁, lead to a deflationary gap S > I in the event of price rigidities because income cannot adjust any further. With completely flexible wages and prices, income Y₀ would not have to be adjusted. The resulting price reductions would shift the LM curve to the right, and the interest rate would fall due to the higher real money supply. There would be no problem with a lower limit for Y. Only the interest rate would be limited downwards. However, with wages and prices that are not fully flexible and with investment largely determined by expectations, the IS-LM model reaches its limits if fully flexible adjustment of Y is not possible. To analyse this situation, we assume below (medium-term) price rigidities in combination with downward quantity restrictions and introduce a broad market for loanable funds.

3. Credit Market Equilibrium: The Market for Loanable Funds

In the IS-LM model with expectations, the interest rate is determined by the interplay between the goods and the money market, but deflationary gaps with S > I and L > M cannot be captured in a satisfactory manner. This is particularly problematic because imbalances in goods markets have direct repercussions on financial markets. Let I and S be planned investment and savings at the beginning of the period and I_exp investment ex post at the end of the period. In the case of a deflationary gap, S = I_exp, i.e., ex post, investment adjusts to savings via changes in inventories (inventory investments). If firms have to increase unplanned inventories because S > I, they lose planned income. The unplanned increase in inventories leads to a liquidity problem for firms, and we have L > M.

In the following section, in the tradition of the most prominent representatives of the theory of loanable funds (Robertson, Ohlin, and Haberler) and of Keynes, the functioning of a more general credit market is formulated in which households, firms, and the banking sector operate. It will be shown that the IS-LM model is a special variant of this general model.

The agents in the market for loanable funds are private households, firms, and the banking sector, including the central bank. It is also considered that money creation is generally associated with lending. The money demand function is unchanged; L(Y, i) = m(i)Y, where i is the nominal interest rate. Credit supply corresponds to planned savings of households S = Y − C, and the money supply from the banking sector equals M₀/P₀. The demand for credit stems from the investment demand of firms I and the demand for money L.10 In addition, π = 0 and thus i = r applies again initially; Y^E is expected income. In total, this yields the following equilibrium on the market for loanable funds (see also Bofinger, 2020):

$${\displaystyle \frac{M_0}{P_0}}+s\left(r\right)Y=m\left(r\right)Y+I, \left(m\left(r\right)-s\left(r\right)\right)Y={\displaystyle \frac{M_0}{P_0}}-I,$$

$$I={\displaystyle \frac{Y^E-Y}{f\left(\frac{TN}{K}\right)}},\hspace{0.33em}i=r\hspace{0.33em}\mathrm{a}\mathrm{s}\hspace{0.33em}\pi =0,$$

(6)

$$L=m\left(r\right)Y,\hspace{0.33em}\hspace{0.33em}{m}^{\prime }\left(r\right)<0, {\displaystyle \frac{dL}{dY}}>0.$$

In this market for loanable funds, the interest rate is determined based on a broader credit market (market for loanable funds), where the demand for loans includes the demand for liquidity and the supply of loans also includes the supply of loans from the banking sector. If there is excess demand for loans M₀/P₀ + s(r)Y < m(r)Y + I, the interest rate will rise. If there is an excess supply of loans M₀/P₀ + s(r)Y > m(r)Y + I, the interest rate will fall. The loans market can be in equilibrium if the excess supply of savings over investment is compensated for by the excess demand for liquidity: s(r)Y − I = m(r)Y − M₀/P₀ > 0.

In the market for loanable funds, as in the Keynesian model, if the capital or goods market is in equilibrium, I = S, the money market is also in equilibrium, L = M₀/P₀. As long as current production Y can be flexibly adjusted, a_minY₀ ≤ Y ≤ Y₀, the IS-LM model can therefore be interpreted as a special case of the market for loanable funds.

Equilibrium on the market for loanable funds implies (m(r_LF) − s(r_LF))Y = M/P − I, where r_LF is the equilibrium interest rate on the market for loanable funds. Thus, for the empirically realistic assumption M/P > I11 and given M/P and I, an increase in Y is only compatible with equilibrium if the interest rate on the market for loanable funds, r_LF, rises, leading (m(r_LF) − s(r_LF)) to fall. If Y rises, savings increase together with the supply of credit. Due to the higher transaction demand for money, the demand for liquidity also increases, but disproportionately, as m(r) > s(r). This disproportionate increase must be compensated for by an increase in the interest rate, which causes savings to rise once again and the demand for money to fall.12

Following Haberler (1948, p. 180), these disequilibria S − I = L − M > 0 are analysed below in Figure 4 in the context of a market for loanable funds. We also explain why one cannot rely on the usual market mechanisms to return the economy to equilibrium relatively quickly. Various real interest rates are plotted on the vertical axis, whereas investment I, savings S = s(r)Y, the credit supply of the banking system M₀/P₀, and the demand for liquidity L = m(r)Y are shown on the horizontal axis.13

Rising sales expectations shift the investment curve to the right. A falling price level shifts the real money supply curve M₀/P₀ to the right. And, the savings curve S = s(r)Y shifts to the right when the capacity utilisation rate and thus Y increase. As a result, the demand for liquidity L = m(r)Y also increases at every interest rate (rightward shift). The total credit supply on the market for loanable funds is obtained by adding the corresponding individual curves S and M₀/P₀ horizontally. The total demand for loans is obtained by adding the corresponding individual curves I and L horizontally.

In Figure 4, (M₀/P₀ + S) represents the total supply of funds and (I₂ + L) the total demand for funds. In the loanable funds model, a lower demand for investment, e.g., I₂ < I₁, would lead to an adjustment of production Y, as in the traditional IS-LM model, and thus to a new equilibrium if the price level is constant. As already explained above, dr/dY > 0 applies. If production falls, the interest rate falls. However, the excess supply of credit is not absorbed by a reduction in interest rates alone. With the possibility of a flexible adjustment of production, the fall in Y also lets savings fall. The curve S shifts to the left. The demand for transaction balances falls, too; the curve L shifts to the left. In the new equilibrium, we obtain I = S and L = M₀/P₀. As in the IS-LM model, there is lower production, a lower interest rate, and all markets clear.

However, if Y has already been adjusted downwards to the minimum, Y = a_minY₀, then the market for loanable funds differs from the IS-LM model. The starting point for the following considerations is an equilibrium on the market for loanable funds from which Y can no longer be adjusted further (downwards) because Y = a_minY₀ has already been reached. This equilibrium in Figure 4 corresponds to the IS-LM equilibrium a_minY₀ − r_min in Figure 3. At r_min, we obtain I₁ = S with S = s(r_min) a_minY₀ and M₀/P₀ = L with L = m(r_min) a_minY₀. The total demand for loans I₁+L corresponds to the total supply of loans M₀/P₀ + S.

If investment falls from I₁ to I₂ in Figure 4, a new goods market equilibrium, I = S, can only be attained at an interest rate of r₃ (analogous to Figure 3). However, money market equilibrium would require an interest rate of r_min instead. In Figure 4, the savings function S and the demand function for liquidity L cannot shift to the left, because Y cannot fall below Y = a_minY₀. There are only movements along the curves S and L. However, as Figure 4 depicts a market for loanable funds, there exists an equilibrium interest rate, r_LF, which also brings the supply of and the demand for funds into equilibrium for S > I and L > M/P. This equilibrium interest rate r_LF is between r_min and r₃ and guarantees an equilibrium of loan supply and loan demand. The demand for credit falls when investment demand declines. In equilibrium, the supply of credit must also fall. The supply of credit falls when interest rates fall, as this reduces savings. However, because Y is constant, dY = 0, and the fall in the supply of credit must occur solely through the reduction in interest rates. For goods market equilibrium, I = S, the interest rate would have to fall very sharply, in Figure 4 to r₃. For an equilibrium of credit supply and credit demand, the interest rate does not have to fall as sharply, as the interest rate cut increases the demand for liquidity and the fall in credit demand is therefore less pronounced. In equilibrium, the net effect of the interest rate cut must just offset the fall in demand for credit due to lower investment.14

The advantage of the loanable funds model is that we consider the entire demand for credit and the entire supply of credit. This means that I = S and L = M do not have to apply throughout. For an intuitive understanding, let us take a look at a concrete example using Figure 4. We start at the point r_min with L = m(r_min)a_minY₀ = M₀/P₀ and I₁ = s(r_min)a_minY₀. If investment falls, dI = dS = s′(r)Ydr + s(r)dY would hold. For goods market equilibrium, I = S, it would be necessary for the interest rate and income to fall with lower investment. However, if income cannot fall any further, Y = a_minY₀, the interest rate must fall very sharply, in our example to r₃.

A constant money supply implies m′(r)Ydr + m(r)dY = 0. If income cannot fall any further, dY = 0, i.e., equilibrium is only compatible with dr = 0. This, in turn, contradicts the condition for goods market equilibrium. However, if there is no need for savings to fall to the same extent as investment because an excess supply of goods is compatible with an excess demand for liquidity on the market for loanable funds (the distance AB, the excess supply of loans, corresponds to the distance CD, the excess demand for liquidity), the interest rate does not have to fall to r₃; the interest rate r_LF is sufficient for an equilibrium on the market for loanable funds. On the goods market, there is a deflationary gap S > I₂, which is compensated for by the excess demand on the money market:

L − (M₀/P₀) = S − I₂ or m(r_LF)a_minY₀ − M₀/P₀ = s(r_LF)a_minY₀ − I₂.

It was an important insight of the proponents of the loanable funds theory that an economy cannot easily get out of this dilemma. The most important arguments are discussed below.

If there is a deflationary gap with underutilised capacity and therefore unemployment, real wages could fall due to falling nominal wages, and therefore employment could rise. Through competition for the lack of demand, firms will pass on these lower costs by lowering prices. The real wage remains constant, and the real money supply increases. In Figure 4, the curve M₀/P₀ would shift to the right and contribute to a reduction in the interest rate. This could reduce savings. However, in times of crisis, households often increase their savings anyway in order to make provisions for bad times. This was extremely pronounced during the COVID-19 pandemic. However, this precautionary saving appears to be an empirical regularity internationally in general (see, e.g., Levenko, 2020).15 If households save more for precautionary reasons at each interest rate, the savings curve in Figure 4 shifts to the right and an even lower interest rate would be necessary for a capital market equilibrium. The argument that falling prices would increase households’ financial assets and that this real balance effect would contribute to a revival in demand is not really convincing either. After all, the “money supply” is largely created by the granting of loans, meaning approximately that firms have borrowed M₀ from the banking system. Deflation would cause the real value of companies’ liabilities to rise, and firms’ investment demand would therefore tend to fall.

A deflationary gap can lead to higher credit demand. However, if firms reduce capacity to a_minY₀ ≤ Y ≤ Y₀, there is a profitability problem. Firms have lower revenues, Y = aY₀, and the capital stock is only utilised at aK given the costs rK. Labour costs fall because only N = aN₀ workers are employed or short-time work is introduced. The firm’s profit G is given by G = aY₀ − waN₀ − rK = aY₀ − (r/F_K)(F_NaN + aF_KK) − rK + (r/F_K)aF_KK = (1 − r/F_K)aY₀ − (1 − a)rK. The profit per capital unit (G/K = r_U) when resources are underutilised can therefore be written very simply as a function of r_U = ar_F − (1 − a), r where r_F describes the profit per capital unit at full employment, r_F = (1 − r/F_K)f(TN₀/K). If capacity utilisation decreases, the profit per unit of capital falls because fewer extra profits are generated per unit of capital (ar_F falls) and the proportion of unused capital stock, (1 − a), rises. If r_U becomes negative, the demand for credit increases for this reason. The underutilisation leads to liquidity bottlenecks and the demand for loans increases. If the market interest rate r rises as a result, r_U falls further. This profitability problem lets lenders (banks) become more cautious and grant fewer loans, especially to companies (credit rationing). This is also regularly observed in times of crisis. For example, Deutsche Bundesbank (2016) shows that in the course of the financial crisis of 2007/2008, banks in Germany and the euro area switched to a more restrictive lending policy, driven by factors on the banking side and a change in risk assessment.

The liquidity problem is exacerbated for firms if they have to make unplanned inventory investments during the crisis, S > I. The difference S − I represents a payment default, and the demand for liquidity increases by this amount, S − I = L − M > 0. Accordingly, there will be further demand for loans, and the interest rate could even rise during the crisis. Empirically, the latter is rarely observed, as banks tend to ration credit instead; see, for example, the literature on the credit channel (e.g., Bernanke & Gertler, 1995). Potential lenders, such as banks, therefore appear to be more likely to restrict their lending, and the M₀/P₀ curve in Figure 4 would move to the left. However, they may also (additionally) prefer to hold more liquidity during the crisis. In Figure 4, the curve L would then shift to the right, with more liquidity being demanded at each interest rate r.

Even in the very unrealistic case of completely flexible prices downwards and massive deflation, a stabilisation of the situation is not necessarily certain; on the one hand, the real money supply would increase, but, on the other hand, the demand for money depends on the nominal interest rate i = r + π^E, which falls if expected deflation π^E < 0 increases and thus stimulates the demand for liquidity.

A central bank can avoid the collapse of financial markets through an expansive monetary policy and is certainly also in a position to lower the (risk-free nominal) interest rate (up to the effective lower interest rate bound). However, this does not close any deflationary gap, as the central bank does not buy any goods. Commercial banks often use the additional loans from the central bank to increase their deposits at the central bank and do not pass the loans on to firms. This is precisely the behaviour that has been observed in recent crises in the euro area (financial crisis and Great Recession 2008/2009, euro and sovereign debt crisis, coronavirus pandemic). The banks’ excess reserves at the Eurosystem peaked at over EUR 4000 billion.

Banks are therefore extremely reluctant to finance investments, despite favourable conditions, as sales expectations are too negative. Low interest rates tend to lead to booming asset markets, such as equity and property markets. Share prices rise when market interest rates fall and households and firms try to invest their savings profitably (and risk-bearing) into the real estate and stock markets. The following Figure 5 shows the trend for these two markets for the period from 2009 to 2020 for Germany and the euro area.

The idea that a deflationary gap can lead to no money flowing from the money market to the capital or credit market is one of the central insights of the “old wise men” and can be illustrated very well with a market for loanable funds (see Keynes, 1973; Haberler, 1948).

Relying on the self-healing forces of the market in a deflationary gap is probably too optimistic. With S > I, there is only a way out of the crisis if the demand for goods increases. The traditional proposal of the “old wise men” was to increase government spending. At that time, however, government debt was still rather low.

4. Summary, Conclusions

This paper has shown that standard Keynesian macro models for explaining recessions and depressions reach their limits if production cannot be sufficiently adjusted downwards. In that case, the interest rate on the goods market would have to be lower than that on financial markets. This problem does not arise if the interest rate is determined via a credit market in which credit supply originates in the banking system and via savings and the demand for credit results from the demand for investment and liquidity. As in the tradition of loanable funds, an equilibrium interest rate for the credit market is obtained for a medium-term period in which a deflationary gap is also possible. The conventional IS-LM model is a special case of this model of a comprehensive credit market.

Integrating elements of the loanable funds theory in traditional macro models would help to achieve a more realistic and convincing understanding of macroeconomic crisis periods. Additionally, a more consistent picture of financial and real crises would emerge.