1. Introduction
Worldwide health care systems are facing persistent shortages of health care professionals (see e.g.,
OECD 2023). Shortages of health care personnel may stem from several different developments, varying from excessive growth in health care demand to a shrinking labour supply, both largely the result of demographic developments. Labour market developments, however, are not just the straightforward product of demand and supply figures, but are influenced by complex interactions between demographics, medical technical innovations, wages, technical substitution, product substitution, input substitution and so forth. It should also be noted that excessive growth in the demand for health care not only affects health care production itself, but also puts pressure on the whole economy, as shifts in labour force distribution towards health care may affect production in other sectors.
In this contribution, we will narrow our focus to the production side of health care. In particular, we will focus on the relationships between cost, health care demand, labour demand, wages and technical change. One way to deal with labour shortages is by increasing productivity, in particular labour productivity. Productivity can be enhanced by improving technical, allocative and scale efficiencies, but predominantly by speeding up technical change. Efficiencies refer to improvements in the current state of technology, whereas technical change refers to the introduction of new technologies. Technical change can be especially helpful in reducing labour market tensions if it helps save labour. In The Netherlands, for example, policymakers tried in 2006 to offer productivity incentives by fostering competition in the hospital and health insurance market. The central idea behind this was that productivity-enhancing technical changes would be particularly initiated in a competitive market.
A priori, one may question this policy, given the general struggle in the service industry, and in public services in particular, to increase productivity. It cannot be ruled out that this phenomenon, known as Baumol’s disease, also applies to the hospital industry and only exacerbates labour shortages.
This raises a relevant question: has productivity risen since the introduction of competition in the hospital industry in 2005, and how has it affected labour demand in the industry? We, therefore, present a simple model to provide insight into the developments in and correlations between several relevant variables. The model shows how inputs, and labour input in particular, have responded to changes in production levels, input prices and technology. The literature includes several studies estimating the Baumol effect, mainly inspired by the work of
Nordhaus (
2008). Central to these studies is the idea that wages in the stagnant sector follow wages in the progressive sector. In the presented model, we abandon this rigid assumption and control for relative wage growth. The results will show that this is a relevant adjustment. Furthermore, we derive our model from a cost function framework known from microeconomics. The model’s parameters can be estimated by conducting a regression on a set of time series variables, from which labour productivity can easily be derived. The raw data will also provide insight into how hospital labour wages correlate to wages in the economy as a whole. The model will be applied to Dutch hospital industry data for the period 2000–2021. The following research questions will be addressed:
- ⇨
Is the hospital industry suffering from Baumol’s cost disease?
- ⇨
Do hospital wages actually follow other wages in the economy?
- ⇨
Has there been a shift in the distribution of the labour force towards the hospital industry?
Following Baumol’s original view, we could hypothesize that since the hospital sector is a labour-intensive sector, productivity growth is low, long-run wages must be in line with the rest of the economy and the pressure from hospitals on the labour market must keep increasing.
In
Section 2, we will discuss a number of theoretical considerations regarding Baumol’s disease, the nature of technical change and the gap between wages and productivity.
Section 3 describes the institutional context of the Dutch hospital industry. In
Section 4 and
Section 5, we present the empirical model and the available data.
Section 6 presents the outcomes of the empirical model.
Section 7 concludes the paper.
2. Theoretical Considerations
Production is the result of the transformation of labour, capital, supplies and raw materials, and each combination of these inputs can produce a corresponding combination of products. This complex technical process can be expressed in formal mathematical expressions, such as the simple Cobb–Douglas production function (
Cobb and Douglas 1928). Microeconomic theory tells us that the inputs used and products delivered actually depend on various economic considerations, such as input and product prices. Based on behavioural assumptions such as profit maximisation, cost minimisation or revenue maximisation, amounts of inputs and products can be optimised, implying that the actual demand for labour is also a result of an optimisation process.
Naturally, the process of transformation described here is not static, but changes over time due to technological innovations, organisational changes and changes in legislation. This process is known as technical change and will, in principle, continue in perpetuity. Technical change is reflected in productivity change, which is defined as the relative change in the ratio between products and inputs. Strictly speaking, productivity changes may also be prompted by changes in efficiency, or the ability to produce more products with the same inputs at the current state of technology (or the same products with fewer inputs). Efficiency changes are finite and are exhausted when a company achieves its maximum productivity at the current state of technology.
Many studies on productivity have described technical change as a continuous constant phenomenon that affects the production process in a neutral way. This requires the implicit assumption that technical change is Hicks-neutral or disembodied (
Hicks 1932;
Ray 1982), and only pushes boundaries further over time. However, economic theory shows that technical change may have many appearances, as it may also, for example, affect the optimal allocation of inputs or products (
Jorgenson and Griliches 1967;
Nelson 1984;
Solow 1957). It may, for instance, become more capital-intensive. In a more recent study, it is argued that technical change can also be driven by changes in the composition of skilled and non-skilled labour, with far-reaching consequences for productivity and labour demand (
Hutter and Weber 2021).
In empirical studies, technical change is often implemented simply by adding a time trend variable to a cost or production equation, which implies that technical change is either a continuous process that transpires at a constant rate or, at least, a smooth process with a constantly changing growth rate.
Kopp and Smith (
1983) provided empirical evidence that time trends are poor proxies for the pace of innovations and new technologies. A more realistic assumption is, therefore, that innovations and new technologies are more discrete, shock-related occurrences that can take some time to be implemented.
Blank and Vogelaar (
2004) provide clear evidence that this is the case for Dutch hospitals. A similar result can be found with
Heshmati and Rashidghalam (
2020), who emphasize the role of technological shifters. As mentioned before, technical change may also be non-neutral, which can be specified by interaction terms between price variables and a time trend variable in a cost function.
Baumol (
1967,
1993) describes cost disease as a relative cost increase in sectors with low productivity growth. To compete for workers, companies are forced to pay competitive wages, in line with those in other sectors of the economy. Due to low productivity, the relative price of products in sectors affected by Baumol’s cost disease will constantly rise. According to Baumol, service industries in which the scope for productivity hikes is limited are particularly prone to this phenomenon. A famous example is that a Mozart quintet cannot be played any faster today than it could two centuries ago, nor with fewer musicians. Naturally, this phenomenon will also trigger a shift in the distribution of the labour force from high-productivity to low-productivity sectors, and the share of employees in low-productivity sectors will increase over time. The only thing that can prevent this from happening is an equivalent shift in consumer demand from goods and services in low-productivity sectors to high-productivity sectors. However, it is to be expected that the elasticity of demand for these public goods and services is low, because of their social relevance and irresponsiveness to market forces and the price mechanism.
The phenomenon of diverging wages is known as the wage premium. A wage premium is a higher wage rate for employees in a specific sector or for employees with specific skills. The differences may be due to differences in skills, level of education and the rarity of employees’ characteristics. Wage premiums may also indicate certain tensions in the labour market, as they are a way to help companies attract and retain scarce personnel. The wage premium phenomenon is highly relevant, as it clearly shows that wages do not automatically follow productivity change, but may deviate from it for all kinds of reasons. The difference between wages and productivity is also known as the wage gap. In the private sector, the wage gap normally causes a shift in the distribution of labour and capital income, whereas in the public sector, the tax-paying citizens and companies have to carry this weight.
3. Dutch Hospital Industry
Health care is the largest public sector in The Netherlands. In 2021, nearly 23% of public service workers worked in health care (432,000 FTEs), representing a substantial share of total Dutch employment (6.6% of all FTEs in The Netherlands). More than half of this workforce is engaged in hospital care (234,750 FTEs), including self-employed physicians. The associated wage costs amount to 4.6% of the total wage costs of the Dutch economy.
There are three types of hospitals in The Netherlands: general hospitals, academic hospitals and specialty hospitals. Most Dutch hospital staff, about two-thirds, work in general hospitals. General hospitals are medical specialist centres for outpatient treatment and inpatient care that do not focus on a specific population group and/or specific physical or mental diseases. In 2021, The Netherlands had 57 general hospitals spread across the country. Some of these hospitals are specialised in providing ‘top-level clinical care’: treatments such as organ transplants and radiotherapy, which need to be concentrated for the sake of optimal quality and efficiency.
In addition to general hospitals, there are also seven major university medical centres in The Netherlands, also known as academic hospitals. In 2021, these hospitals employed approximately 30% of the country’s total hospital workforce. Academic hospitals are medical specialist centres for outpatient treatment and inpatient care, with a focus on highly specialised care for patients with difficult-to-treat, rare or complex medical conditions (referral care). Additionally, they engage in scientific research and provide education for the medical faculty of the affiliated university.
The remaining portion of the Dutch hospital staff (4–5%) works in specialty or categorical hospitals. These are medical specialist centres for outpatient treatment and inpatient care that specialise in the treatment of specific diseases or conditions, such as eye hospitals and rehabilitation centres.
As elsewhere in the health care industry, hospitals are plagued by major staff shortages for a vast array of underlying reasons. The bottom line is that there is a mismatch between supply and demand in the labour market, which has been a problem for decades. To help resolve this mismatch, the Dutch government decided in 1999 to regulate the health care labour market, setting up the Advisory Committee on Medical Manpower Planning (ACMMP, Dutch: Capaciteitsorgaan). The ACMMP now plays an important role in regulating the health care labour market by issuing recommendations and publishing forecasts on the desired intake of the various medical profile training programmes and postgraduate medical training programmes (
ACMMP 2019). However, government regulation has not been able to eliminate the continuing mismatch between supply and demand due to the ongoing changes in workers’ preferences regarding part-time work and labour relations (self-employed or on payroll).
Since 2005, the Dutch hospital industry has undergone various important changes, starting with the introduction of a product classification system that classifies patients by diagnoses and treatments. This classification results in a product, known as a DTC (Diagnostic Treatment Combination), similar to the Diagnostic Related Groups (DRGs) used in the U.S. and in other European countries. From an economic perspective, there are two types of DTC: the A-segment, the price of which is regulated and set by the government, and the B-segment, the price of which is negotiated by hospitals and health insurers (
Blank et al. 2016;
Jeurissen and Maarse 2021).
The introduction of the DTC system was an important condition for the creation of regulated competition in the health care industries, with hospitals and other health care providers negotiating prices, treatment volumes and quality levels with health insurers. An important aim of this was to curb the ever-increasing costs of health care. However, after it became apparent that costs continued to rise at even faster rates, the Ministry of Health, all health care providers and all insurers agreed in 2011 on a voluntary ceiling for the annual growth of hospital and mental health care spending. When overall costs exceed that limit, the government has the power to control spending via generic budget cuts (
Jeurissen and Maarse 2021;
Varkevisser et al. 2023;
Wammes et al. 2020).
A special feature of the Dutch hospital system is the presence of two types of physicians in hospitals: physicians employed by the hospital and self-employed physicians contracted by hospitals. The vast majority of self-employed physicians work in general hospitals. In 2015, the remuneration of medical specialists was integrated into DTC prices (
Varkevisser et al. 2023), which means that self-employed specialists are paid by hospitals instead of an insurance company.
4. Methodology
A literature search shows that many attempts have been made to empirically test the validity of Baumol’s cost disease. A substantial part of the empirical research is based on the earlier work of
Colombier and Weber (
2010),
Nordhaus (
2008) and
Rossen and Faroque (
2016), who all present models that divide the economy into a progressive and a stagnant sector, in line with Baumol’s model of unbalanced growth (
Baumol 1967). For the sake of simplicity, these studies cast labour as the only factor of production. Labour productivity growth in the progressive sector is assumed to outstrip labour productivity growth in the stagnant sector by far, while wages in the stagnant sector are assumed to follow wages in the progressive sector. By means of several simple algebraic manipulations, they derive regression equations from which the Baumol effect can be estimated. The key element in their models is the nominal or adjusted Baumol variable, expressed as the difference between wage growth and productivity change. The term adjusted refers here to whether or not the Baumol variable is corrected for the share of the stagnant sector in the total economy.
In this paper, we follow a slightly different approach that has a sounder basis in microeconomic duality theory and sheds some more light on the underlying process. By providing more insight into underlying determinants, we intend to give policymakers more tools to control unbalanced growth.
We derive the empirical model from a cost function framework. A cost function assumes a relationship between cost, production, resource prices and technical change. An empirical cost function provides interesting insights into the quantitative contribution of each of the variables of production, input prices and technical change to cost. From the cost function, cost share equations can theoretically be derived that describe the demand for resources (
Shephard 1970). In other words, if we know the empirical cost function, we also know the corresponding demand function for labour (or any other input). Note that this theory originally focusses on the behaviour of the firm. In this case, the sector is the unit of analysis. A complete cost function framework has been applied earlier to the Dutch hospital sector (
Blank and Eggink 2014) and the judiciary (
Blank and Heezik 2020). If we are only interested in the demand for inputs, we can limit the analysis to the share equations only. We then know that there is some theoretically sound empirical model in the background describing the cost structure.
In our approach, we simplify the economy to an economy that produces hospital products and other products. Further, we make a similar distinction regarding the labour market, in which there is a demand for hospital labour and other labour. Both labour markets may have different wages and different patterns of technical change. Of course, this simplification may bias the results. For further insight into the complexity of the dynamics of the economy and labour market, we refer to other models (
Di Guilmi and Fujiwara 2022). Such an approach would go beyond our purpose here. Nevertheless, if we are able to find any meaningful outcomes in a statistical sense at this high level of aggregation, then we may derive some general conclusions. This may be a first step to a more refined model in which different sectors are included.
Hospital production is measured by physical quantities of products delivered, whereas other products are measured by their monetary value, indicated by other value added. We impose constant returns to scale, implying that 1% growth in all products leads to 1% growth in all inputs. General production growth, therefore, leaves cost shares unaltered. Since only changes in relative products can affect cost shares, they are included in the cost share function. In this case, we measure the hospital products relative to the other value added. The same holds true as input prices in hospital industry and other products economy change equally. Only changes in relative input prices can affect cost shares (there is no
money illusion). Based on these assumptions and using the cost function framework, we can write the model as
= cost share of the hospital industry in the total economy;
= production of hospital product 1;
= production of hospital product 2;
= production of other products;
= wages in the hospital industry;
= wages in the total economy;
= time trend;
= error term.
, , , and are parameters to be estimated.
In summary, Equation (1) says that the cost share of the hospital industry can be described as a function of relative hospital products, relative hospital wages and a time trend. Note here that we do not need any assumption about wages in one sector following wages in another sector. In Equation (1), we only factor in two hospital products for reasons of convenience, but this could easily be expanded to three or more. Furthermore, we have omitted the time suffix for reasons of readability. The right-hand variables in Equation (1)—with the exception of the time trend—are transformed into natural logarithms. This mathematical specification comes from applying Shephard’s lemma to the popular translog cost function (
Christensen et al. 1973). The specification in Equation (1) has the advantage of facilitating the interpretation of the parameters, which reflect the impact of a percentual change in a variable on the cost share. If, for instance, the estimated parameter for hospital product 1 equals 0.04, a 10% relative rise in product 1 will increase the cost share of the hospital sector by 0.4%.
The estimation method is an iterative Cochrane–Orcutt procedure with the modification that retains the first observation. What will these outcomes tell us? The estimated parameter reflects the relevance of the hospital industry in the total economy, expressed in terms of the labour cost share in the base year (in this case 2000).
The long-term trend of the labour cost share, expressed as the average annual autonomous change, is reflected in the estimated parameter . If this parameter is positive, it tells us that, over time, the hospital industry has taken up a larger proportion of the labour force, as dictated by the Baumol effect.
The estimated parameters and represent the relative importance of each hospital product. For example, growth in the number of admissions has a larger impact on demand for labour than an equal growth in the number of outpatient visits. Note that we measure hospital production by physical quantities instead of turnover, as is particularly helpful in sectors characterised by an absence of market prices due regulations and government funding. Alternative concepts such as added value are best avoided due to the risk of the circular reasoning fallacy.
The parameter
reveals how the hospital industry responds to diverging wages between the hospital industry and other industries in the economy. From this parameter, we can also derive how the hospital sector responds to wage raises by what is known as the own price elasticity of demand:
At negative values, the demand for hospital labour diminishes as wages rise, reflecting the situation that economic theory would lead us to expect.
Furthermore, the residuals may also contain some interesting information. Since residuals include all kinds of omitting variables and measurement errors, they may also include productivity changes that are not captured by the trend term or the substitution effect. In the theory section, we already argued that technical change may be erratic. Since we are only interested in long-term developments, the trend parameter may provide a rather accurate estimate. However, the year-by-year development may show some fluctuations and may be captured by the estimated residual.
5. Data
Data Collection
The empirical analyses performed for this study are based on a set of time series variables of the Dutch hospital sector. The data are derived from a unique, interactive and user-friendly publicly accessible database on public sector trends from 2000 to 2021, which also includes figures on productivity change (
https://www.trendsinpubliekesector.nl/Zorg/Ziekenhuizen, accessed on 15 August 2024). This database will be updated annually. This means that there are 22 observations.
Table 1 describes the data used in the analyses.
The production of other industries is measured by the GDP at constant prices minus the cost of the hospital industry at constant prices. The production of the hospital industry is measured by the number of admissions and third-party revenues at constant prices. Obviously, admissions are the most important driver of hospital costs. However, it should be noted that the number of activities not directly related to patient care, such as education and research, is growing steadily. The turnover of these activities is, therefore, included in the cost function as well. Other studies also include the number of outpatients, but the relevance in terms of cost is limited and, therefore, left out.
Van Hilten et al. (
2022) argue that using this type of variable might lead to an underestimate of the ‘true’ value of health production, since quality is not taken into account. They justify their statement by providing a number of examples that show that the effectiveness of various treatments has improved. The same reasoning also holds for the production of goods in other sectors of the economy: for example, as the processing power of computers improves, cars become safer and use less fuel. Although
Van Hilten et al. (
2022) make a clear point, in empirical work like this it is undoable to take quality developments into account. Since we use ratios between production in the hospital sector and other sectors of the economy, we implicitly assume that we have divided the quality dimension out of the equation.
Wages are measured in two different ways. The first way is to compute wages as personnel costs per hour worked, distinguishing between the hospital industry, on the one hand, and other sectors on the other. The second way is based on data derived by Statistics Netherlands from salary scales and other employment benefits outlined in collective labour agreements. Obviously, personnel costs per hour worked include various fringe benefits that are not reflected in contractual wages, such as training costs or promotions.
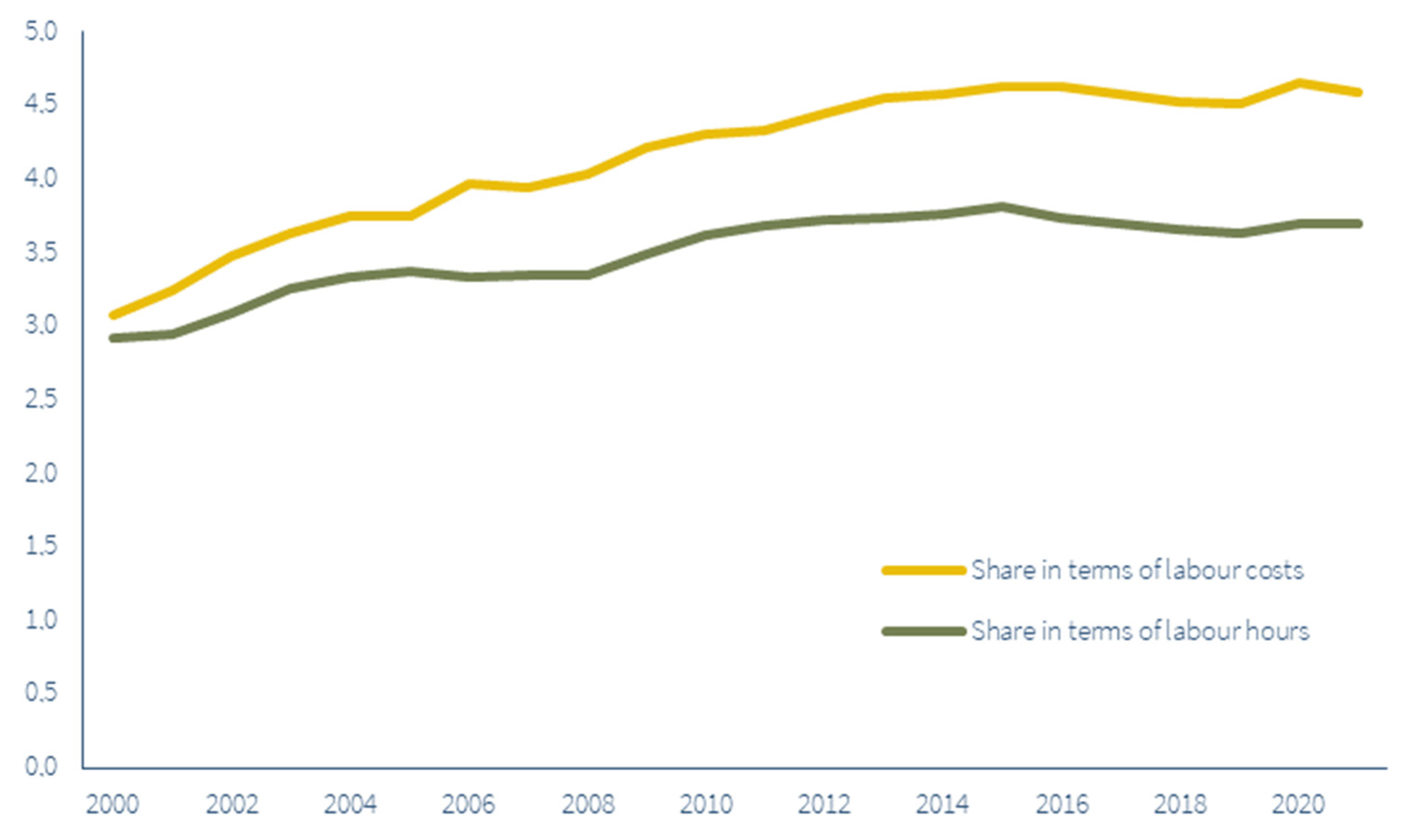
Figure 1 reflects the relative pressure of the hospital industry on the labour market, measured by the share of hospital employment in total employment. We can express this share in terms of labour hours or in terms of labour costs.
Figure 1 shows that the share of employment in the hospital industry in total employment in terms of labour costs grew from 3.1% to 4.6%. In terms of labour hours, it grew from 2.9% to 3.7%. The higher growth rate of the labour share in terms of costs may be due to a rise in the average quality of personnel, but nominal effects cannot be excluded. During the research period, the growth rate varied strongly between the first (2000–2012) and last period (2012–2021). Note that in this period, the labour force in The Netherlands grew by 14% due to a substantial increase in the retirement age and labour immigration.
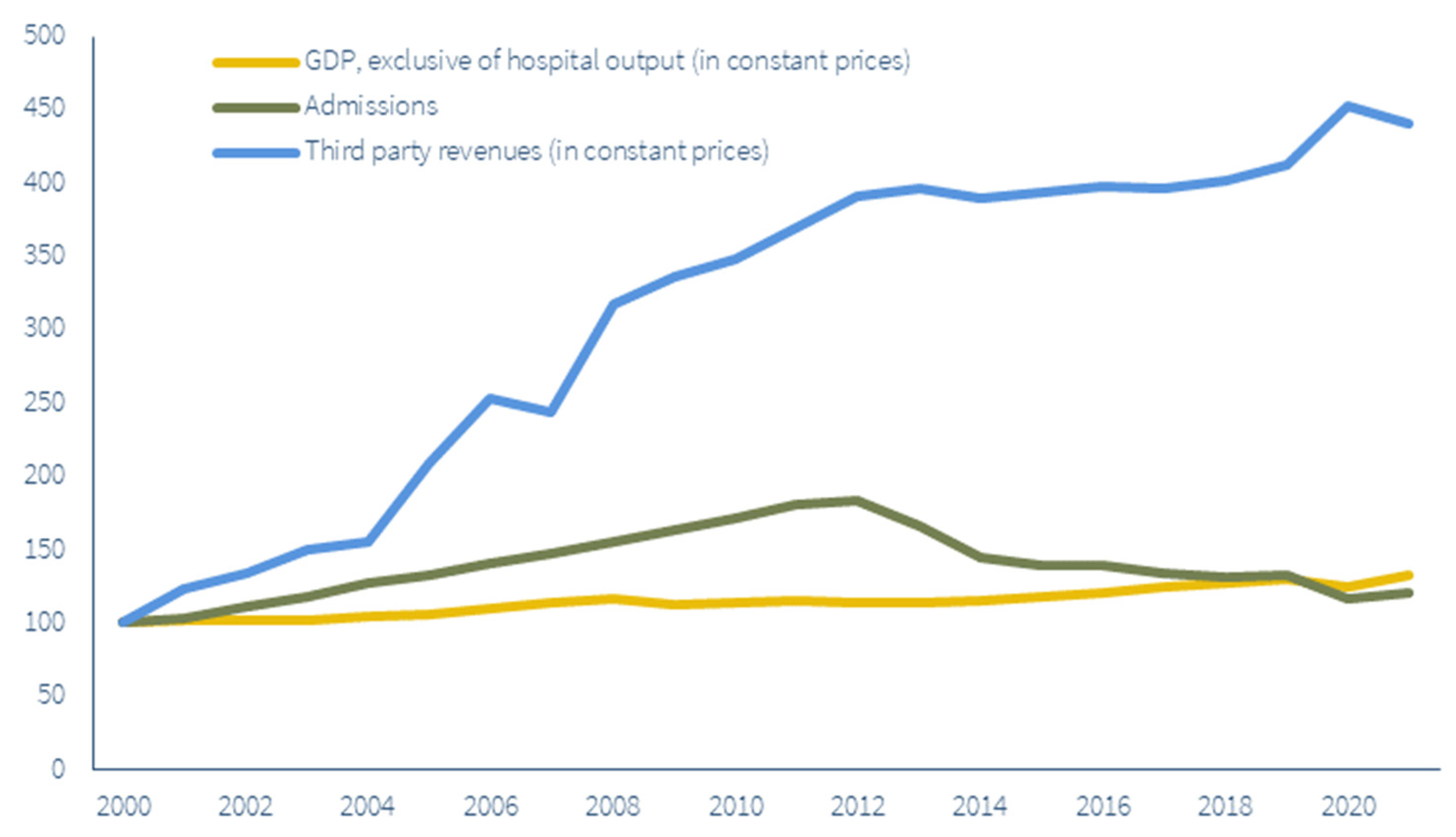
Figure 2 represents the development of the production variables during the period 2000–2021 in index numbers with base year 2000.
Figure 2 shows that, between 2000 and 2021, other industries saw production grow by 32%. During that time, the number of admissions in the hospital industry increased by 21%, while third-party revenues were up 340%. Note that in 2000, third-party revenues were rather modest compared to the costs in 2000. However, in time it became a substantial part of hospital production. Furthermore, the number of admissions shows a striking pattern: a strong increase between 2000 and 2012. This was followed by a strong decline between 2012 and 2014 due to the budget ceiling implemented in 2012. The idea behind this was to enhance the substitution of clinical treatments with outpatient treatments and treatment by general practitioners. Over the whole research period, the growth of total hospital production substantially exceeded growth in the other industries in the economy.
Since wages play a key role in Baumol’s theory, it is interesting to see whether the development of wages in the hospital industry diverges from or lags behind the development of wages in the other industries.
Figure 3 shows the development of wages between 2000 and 2021 in the hospital industry and other industries. We make a distinction between the development of contractual hourly wages and actual hourly wages measured as labour costs per working hour. The latter also includes the costs of fringe benefits, shifts in the quality of labour and effects of labour shortages or surpluses.
Figure 3 shows that between 2000 and 2021, contractual hourly wages in the hospital industry increased by 70%, 8 percentage points more than in other industries. This is a striking result, since we formulated the hypothesis that the hospital industry would be a stagnant industry with hourly wages that lagged behind other industries. For actual hourly wages, the difference was even more pronounced, with actual hourly wages in the hospital industry and other industries growing by 94% and 61%, respectively.
Heyma et al. (
2023) have recently presented similar results, noting that, in general, monetary wages in the public sector climbed faster than in the private sector between 2013 and 2022. Furthermore, they observe that secondary labour conditions in the public sector are generally better than in the private sector. Regarding health care, they also notice that wages improved much more for higher-educated personnel than lower-educated personnel. Since it is to be expected that the level of education of hospital personnel is higher than in other parts of health care, wages in hospitals outperformed those in other private sectors.
One of the reasons for this may be found in the composition of labour input, in particular in the share of physicians, whose remuneration can differ substantially from the wages earned by other workers. Therefore, we chose to also inspect the development of the share of physicians in the total hospital labour force.
Figure 4 shows that while the share of physicians in the total hospital labour force increased substantially from almost 5% to 8.5% from 2000 to 2021, the share itself was still very modest. Even if wage increases for physicians were to substantially differ from those for other hospital employees, then, the impact on the actual hourly wages presented in
Figure 3 would be modest. Unfortunately, since we have no data on the actual hourly wages of physicians, we cannot produce an accurate estimate. We also see an increase in the number of nurse practitioners and physician assistants, although both groups are still relatively small (
Dankers-de Mari et al. 2023). Since these workers should effectively take over tasks that would previously have been performed by a physician, the increase should have a downward effect on wages.
Even after correcting for composition, the remaining difference between actual hourly hospital wages and wages in other industries demands further explanation. One explanation could be that the hospital industry is not, in fact, a stagnant industry. A second explanation might be that labour market demand and supply conditions differ between the hospital industry and other industries. Note that many employees in the hospital industry are highly trained and have specialised skills, implying that labour substitution between these industries may be limited. We have already discussed the regulations on educational and training standards of medical doctors and nursing personnel, and with educational and training capacities also being regulated, the supply of these professionals responds slowly to changing demand. Consequently, wage developments in the hospital industry are also subject to these specific demand–supply conditions, and less so to general wage developments. There might be a special role for the systematic procedure of the governmental contribution to the labour cost development in health care (the so-called OVA-convenant in Dutch), which compensates for wage increases based on estimated wage developments in the market sector. This compensation is not corrected for productivity changes. So, productivity growth in the hospital sector creates room for extra wage increases.
A strong rise in the demand for hospital care may, therefore, spark labour market tensions in this industry and may lead to even higher wages than in other industries, resulting in an even worse scenario than the situation predicted by Baumol’s theory.
6. Results
Table 2 shows the parameter estimates, standard errors, T-values, explained variance and LM autocorrelation test of the cost share function.
The model estimates fit the data well, with an R2 of 98%. Except for the third-party revenues, the T-values exceed the threshold (2.10) at the 5% significance level and 18 degrees of freedom. The estimated autocorrelation parameter equals 0.67. Furthermore, the model meets requirements such as positive monotonicity in production parameters: a relative increase in hospital products leads to a higher cost share of hospital labour. The own price elasticity for labour demand—which can be derived from the wage parameter—equals −0.339 and meets the requirement that demand for hospital labour decreases as hospital wages increase.
In order to get an impression of the magnitude of the estimated effects during the research period, we calculated the contribution of each variable in 2021 to the expected value of the hospital labour share in total employment.
Table 2 shows that the estimated labour share in 2000 equalled about 3.1% (constant = 0.0311). A 233% increase in relative third-party production in 2021 led to an increase in the estimated hospital labour share of about 0.5 percentage points (=2.33 × 0.0022), whereas the contribution of admissions is null (=−0.085 × 0.0054). A 19% increase in the relative price of hospital labour in 2021 increased the estimated hospital labour share by 0.4 percentage points (=0.19 × 0.0225). The time variable, reflecting relative technical change, led to an increase of 0.8 percentage points (=21 × 0.0004) over the course of 21 years. In other words, due solely to the fact that productivity is lagging behind the other sectors of the economy, the pressure from hospitals on the labour market has increased. We can interpret this estimated parameter as an estimate of the Baumol effect. Adding up all these percentages gives a hospital labour share of approximately 4.6% in 2021.
Since the growth of total hospital production was limited, its effect on the hospital labour share was also limited. However, if demand grows due to the ageing of the population, the corresponding growth in the hospital labour share could become an issue in the near future.
A striking observation is the excessive growth of hospital wages relative to other sectors. One may expect the hospital sector to respond to this relative price increase by downsizing the input of labour, which is confirmed by the negative own price elasticity for labour demand.
The main reasons for this discrepancy are the differences in technical change between the hospital industry and other industries (Baumol effect), accounting for two-thirds of the total growth of the cost share of labour. The analysis shows that the hospital industry must be—in the words of Baumol—regarded as a stagnant industry, which is added to the fact that substitution between the hospital and other industries is limited and that the hospital labour market has its own dynamics. The scarcity of medical personnel may drive up wages and costs, making cost developments in hospitals even more problematic than labour developments.
We also conducted a sensitivity analysis, looking particularly at the definition of wages. We reran the regression analysis on a cost share function that included contractual wages instead of the unit cost of personnel and found that the impact of the production variables on the cost share only underwent modest change. The impact on the effect of the relative wages on the cost share, however, was substantial, with the effect almost zeroing out, probably due to a lack of variation in the wage variable. The impact on the effect of the technical change variable was also very modest. In sum, the definition of the wage variable does not affect the conclusions of our analysis.
We also ran the regression on different specifications of the production variables, for instance by also adding the number of outpatients as an independent variable. Due to a strong correlation between some of the product variables, parameters corresponding to the product variables were affected by the different specifications. However, the effect on the parameter of the trend variable was limited.
7. Conclusions and Recommendations
In this paper, we focus on the sustainability of hospital care in The Netherlands from a labour market perspective. The continued increase in the demand for hospital care and the subsequent growth in the demand for hospital labour can cause permanent shortages of medical and nursing personnel, but it can also affect labour conditions in other sectors of the economy, potentially culminating in the complete disruption of social welfare in The Netherlands.
The first signs of such a worrisome development can already be gleaned from recent observations in the Dutch hospital sector. Between 2000 and 2021, the demand for labour in the hospital sector grew substantially, even in relative terms. In the same timeframe, the cost share of labour in the total economy rose from 3.1% in 2000 to 4.6% in 2021.
Therefore, we analysed this development in more detail by splitting it into three components: production change, wage change and technical change. We then applied a regression analysis on the cost share of hospital personnel in the total economy, based on these three components.
From the raw data, we observed two striking developments. First, hospital production experienced modest growth over the whole research period, only just outgrowing other sectors of the economy. This ‘modest’ development is a direct consequence of the policy of macro-level budgetary constraints implemented in 2012. The growth in demand for hospital care before 2012 was directly followed by a decline in admissions after 2012. The second striking development is the explosive growth in wages, expressed in terms of labour costs per full-time equivalent, in particular when compared to wages in other sectors of the economy. The hypothesis that hospital wages follow wages in other sectors of the economy appears to be false. The opposite seems to be true, with hospital wages apparently developing independently from other sectors. The strong wage increase may be largely due to two re-enforcing factors. The first one is the restrictive capacity in schools for medical professionals, which creates a permanent situation of scarcity. The second one refers to the system of the governmental contribution to labour costs in health care, which compensates for wage increases based on present and expected wages in the private sector. Since this compensation is not corrected for productivity changes, productivity growth in the hospital sector creates room for extra wage increases.
The regression analysis shows that there are some substitution possibilities in inputs. Wage raises are almost proportionally transformed into increases in the share of hospital labour costs. Another worrisome result comes from the estimated Baumol parameter, which indicates that productivity in the hospital sector is lower than in other sectors of the economy. This implies that the hospital sector, aside from developments in the demand for hospital care and hospital wages, is causing a serious problem due to a low or negative productivity change.
At this rate, we will stumble into the situation that the pressure of hospitals on the Dutch labour force will be almost doubled in a few decades, due only to the Baumol effect. On top of this, the pressure on the labour market will further increase due to the growth in health care demand and the ongoing rise in wages. To avoid this situation, severe measures will need to be taken.
First of all, production growth needs to be restricted as much as possible, particularly with a view to the upcoming growth in demand for hospital care due to the ageing of the population. There is evidence that the macro-level budgetary measures introduced in 2012 have been effective. However, we need to bear in mind that part of hospital care has probably shifted to general practitioners.
The second type of measure to be taken is controlling the excessive growth in hospital labour costs per FTE. The training and educational capacity must be reconsidered to increase the supply of nursing and medical professionals in order to mitigate the structural lack of labour supply in this sector. Another suggestion is to adjust the current system of the governmental contribution to labour cost development by including a reduction factor for productivity growth. One may also consider changing the system in which physicians can be self-employed in favour of a system in which all physicians are hired as hospital employees.
The third type of measure is the introduction of more incentives to enhance productivity and stimulate labour and cost-saving innovations. Special attention must be paid to the possibility of downsizing the enormous administrative bureaucracy in hospitals related to quality systems, accountability requirements and complex budgeting systems. In an international comparison, The Netherlands has the next highest administrative costs after the U.S. (
Himmelstein et al. 2014). They found that administrative costs account for 19.8 percent of total Dutch hospital expenditures. Furthermore, data from Statistics Netherlands indicate that between 2013 and 2020, the share of hospital personnel unrelated to the primary process grew. Figures on health care over a longer period of time show an even more troublesome picture.
Obviously, the presented two-sector model is a far-reaching simplification of the complex relationships between labour demand, wages and productivity. The outcomes, therefore, come with great uncertainties. Nevertheless, it presents a worrisome picture that should incite policymakers to deal seriously with this issue.