Abstract
In this study, we compare the performance of stochastic processes, namely, the Vasicek, Cox–Ingersoll–Ross (CIR), and geometric Brownian motion (GBM) models, with that of machine learning algorithms, such as Random Forest, Support Vector Machine (SVM), and k-Nearest Neighbors (KNN), for predicting the trends of stock indices XLF (financial sector), XLK (technology sector), and XLV (healthcare sector). The results showed that stochastic processes achieved remarkable prediction performance, especially the CIR model. Additionally, this study demonstrated that the metrics of machine learning algorithms are relatively lower. However, it is important to note that stochastic processes use the actual current index value to predict tomorrow’s value, which may overestimate their performance. In contrast, machine learning algorithms offer a more flexible approach and are not as dependent on the current index value. Therefore, optimizing the hyperparameters of machine learning algorithms is crucial for further improving their performance.
1. Introduction
Modeling and predicting asset prices are essential elements for participants in financial markets, from individual investors to financial institutions. These predictions play a crucial role in making informed investment decisions, aiming to maximize returns while minimizing risks. Over the decades, various approaches have been developed to capture the complex dynamics of prices in financial markets. Traditionally, stochastic models have been widely used to model asset price fluctuations. Among these models, geometric Brownian motion Mensah et al. (2023), the Vasicek model Nadarajan and Nur-Firyal (2024), and the Cox–Ingersoll–Ross (CIR) model Bernaschi et al. (2007) have been pillars in modeling random processes. These models have been extensively employed in the past to predict price movements in financial markets, but they also have limitations, particularly in their ability to capture non-linearities and observed changes in volatility in these markets. Concurrently, the emergence of machine learning has opened new perspectives in predicting asset prices. Techniques such as Random Forest, KNN, and SVM have shown effectiveness in modeling complex relationships between variables and predicting price trends Ayyildiz and Iskenderoglu (2024). However, their application in the financial domain requires a thorough evaluation of their advantages and limitations compared to traditional stochastic approaches. In this dynamic research context, this study aims to compare the performance of traditional stochastic modeling approaches with that of machine learning algorithms in predicting asset prices. By utilizing real data representing ten years of daily observations from the XLF (Financial Select Sector SPDR ETF), XLK (Technology Select Sector SPDR ETF), and XLV (Healthcare Select Sector SPDR ETF) indices, we seek to identify the strengths and weaknesses of each approach, as well as opportunities to combine these methods to improve forecast accuracy. Additionally, considering three distinct sectors allows us to investigate whether there is a sector effect on prediction accuracy. This comparative analysis aims to provide valuable insights for professionals in the financial industry, enabling them to choose the most suitable methods for their asset price prediction needs.
This introduction establishes the context of our study by highlighting key players and recalling the history of models used in stock market prediction. It also clearly outlines the objectives of our research by focusing on understanding the advantages and limitations of stochastic approaches and machine learning algorithms.
2. Literature Review
Predicting asset prices has been a major subject of study for decades, employing various approaches ranging from traditional stochastic models to more recent machine learning techniques. Stochastic processes were among the earliest approaches applied in stock price prediction Li (2012). These models, based on assumptions of random price behavior, have been widely used to model fluctuations in financial asset prices. Among classical works, Louis Bachelier introduced the concept of geometric Brownian motion in the early 20th century, laying the groundwork for the use of stochastic processes in modern finance Be (1913). Subsequently, researchers such as Robert C. Merton and Fischer Black developed more sophisticated stochastic models, such as the Black–Scholes model for option pricing Shinde and Takale (2012). However, with the rise of information technology and the increasing availability of data, machine learning techniques have become increasingly popular in stock price prediction. These methods enable the identification of complex and nonlinear patterns in financial data, offering new perspectives for asset price prediction Gan et al. (2020). Recent studies have shown that machine learning algorithms, such as Random Forest, KNN, and SVM, can be particularly effective in predicting short-term price movements and identifying subtle trends in financial data Weigand (2019). Other studies compare the performance of machine learning with traditional indicators. According to Bouasabah (2024), the performance of machine learning algorithms compared to traditional technical indicators in real estate, technology, and healthcare sectors reveals the limitations of classical indicators. The study explores the predictive capabilities of ML algorithms, highlighting AdaBoost and SVM. The results demonstrate the superiority of ML algorithms in precision, recall, and F1 score, particularly in the healthcare sector.
An emerging trend in the financial literature is the comparison between approaches based on stochastic processes and machine learning methods. These studies aim to evaluate the advantages and limitations of each approach and determine under what conditions each method is most appropriate. For example, a recent study compared the performance of traditional stochastic models with that of machine learning algorithms in predicting stock prices, highlighting the strengths and weaknesses of each approach in different market contexts Chandrika et al. (2023). This trend of comparing stochastic approaches with machine learning methods has proven to be a promising avenue for enriching our understanding of stock price prediction mechanisms. These studies provide valuable insights for practitioners and researchers in finance, rigorously assessing the performance of each approach in a variety of market contexts. They also stimulate innovation by identifying potential gaps in existing approaches and opening up new avenues of research to improve the accuracy and robustness of stock price prediction models. By combining the advantages of stochastic approaches and machine learning, it is possible to develop more sophisticated hybrid models that fully exploit the richness of data available in financial markets. Thus, this trend toward the comparison and combination of approaches offers considerable potential to advance our ability to anticipate movements in asset prices.
The comparison between stochastic processes and machine learning algorithms in prediction is found in several fields. For example, one study Papacharalampous et al. (2019) compares 11 stochastic methods and 9 machine learning algorithms for forecasting in hydrology. Using 2000 simulated time series and 405 real-time series, the performance of the methods was measured with 18 metrics. The results show that both types of methods can provide similarly effective forecasts. Another study Papacharalampous et al. (2017) compared four stochastic forecasting methods and two machine learning (ML) algorithms using monthly weather data from Greece. The stochastic methods included autoregressive models, exponential smoothing, and the Theta algorithm, while the ML methods comprised neural networks and support vector machines. Sensitivity analysis was conducted for the ML methods, and a comparison between sophisticated and simple ML methods was made in terms of hyperparameter optimization. Another study Chen (2023) examines how stochastic models and machine learning work together to improve the prediction of complex dynamic systems. It highlights the contribution of machine learning in data assimilation to refine ensemble forecasts and its role in developing stochastic closures and parameterizations. It explores how machine learning can predict the trajectories of complex dynamic systems, taking into account additional uncertainty to construct a mixture distribution for the forecast probability density function.
3. Stochastic Processes Used in Financial Prediction
Stochastic processes, such as geometric Brownian motion (GBM), the Vasicek model, and the Cox–Ingersoll–Ross (CIR) model, are essential for modeling financial asset prices and interest rates. These models, based on Brownian motion, are selected for their ability to capture exponential growth, market volatility, and the tendency of interest rates to revert to a historical mean while remaining positive. By integrating these models, our study aims to provide robust and reliable financial forecasts, thus justifying the choice of stochastic processes used.
3.1. Geometric Brownian Motion (GBM)
The GBM model is a stochastic process widely used to model fluctuations in financial asset prices. It is defined by the following stochastic differential equation:
where represents the asset price at time t, is the drift rate (average return) of the asset, is the volatility of the asset, and is the differential of the standard Brownian motion. The GBM model offers simplicity in implementation and provides a theoretical foundation for understanding price movements. However, it assumes prices follow a normal distribution and do not account for changing volatility, which may lead to inaccuracies in volatile market conditions Bouasabah and Khalaf (2023).
The Vasicek Model
The Vasicek model is a stochastic process primarily used to model interest rates. The associated stochastic differential equation for the Vasicek model is:
where represents the interest rate at time t, is the reversion speed, is the mean level of the interest rate, is the volatility of the interest rate, and is the differential of the standard Brownian motion. The Vasicek model captures interest rate convergence and provides a rigorous mathematical foundation for derivative valuation. However, it assumes constant volatility of interest rates and may underestimate risks associated with high volatility periods Svoboda (2004). In this study, the Vasicek model will be utilized to capture the variation of trackers XLF, XLK, and XLV.
3.2. Cox–Ingersoll–Ross (CIR) Model
The Cox–Ingersoll–Ross (CIR) model is a stochastic model commonly used to model short-term interest rate variations. It was developed by John Cox, Jonathan Ingersoll, and Stephen Ross in the 1980s. Unlike other models, the CIR takes into account the constraint that interest rates cannot be negative. It is particularly valued for its ability to capture the mean-reverting behavior of interest rates, making it valuable in estimating the prices of financial products and managing risks associated with interest rate fluctuations. The CIR model extends the Vasicek model and is used to model interest rate dynamics. The associated stochastic differential equation for the CIR model is:
where is the interest rate and , , and are the model parameters. The model exhibits the mean-reversion property, which means that the interest rate moves toward its mean at speed . The CIR model captures stochastic interest rate volatility and reproduces observed interest rates with greater accuracy. However, it may be more complex to calibrate and sensitive to data quality, potentially leading to inaccurate results if not carefully managed Orlando et al. (2019). This model will be used in this study to predict future values of our trackers.
4. Machine Learning Algorithms
In addition to stochastic processes, machine learning algorithms are increasingly utilized in financial prediction tasks. The selection of these algorithms, including Random Forest, k-Nearest Neighbors (KNNs), and Support Vector Machines (SVMs), is based on their demonstrated effectiveness in classifying financial data and identifying relevant patterns. These algorithms offer robust performance and are well suited for handling complex financial datasets, making them suitable choices for the study Bonaccorso (2017).
4.1. Random Forest
Random Forest is an ensemble learning method where multiple decision trees are generated during training. It results in either the mode of the classes (for classification) or the average prediction (for regression) obtained from the individual trees. This technique constructs several decision trees during training and then determines the class mode or the mean prediction based on the collective output of the trees.
Advantages and Disadvantages: Random Forests are robust against overfitting and perform well with large datasets. However, they may not be interpretable and could suffer from high computational costs, especially with large numbers of trees.
4.2. k-Nearest Neighbors (KNNs)
K-Nearest Neighbors (KNNs) is a non-parametric approach utilized for classification and regression assignments. It categorizes data points by determining the majority class among their k-nearest neighbors or predicts the average value of the k-Nearest Neighbors for regression.
Advantages and Disadvantages: KNN is straightforward to apply and does not presume the underlying data distribution. Nevertheless, its efficacy might diminish with high-dimensional data and extensive datasets because of its computational complexity.
4.3. Support Vector Machines (SVMs)
Support Vector Machines (SVMs) are supervised learning models employed for classification and regression analysis. SVM constructs hyperplanes in high-dimensional spaces to delineate data points into distinct classes. It excels in handling both linearly separable and non-linearly separable data by employing kernel tricks to convert the data into higher-dimensional spaces.
Advantages and Disadvantages: SVM proves effective in high-dimensional spaces and is memory-efficient since it utilizes a subset of training points in the decision function. Nonetheless, SVM’s performance can be influenced by the selection of kernel parameters and may not fare well with extensive datasets due to its high computational complexity during training.
These machine learning algorithms offer powerful tools for financial prediction tasks, each with its own strengths and weaknesses. Understanding their characteristics is crucial for selecting the most suitable algorithm for specific financial forecasting applications.
5. Materials and Methods
In this section, we delve into the methodology, dataset, and models utilized to explore the dynamics of financial markets, including both machine learning algorithms and stochastic processes.
5.1. Data and Data Source
In line with the introductory context, this research focuses on three distinct sectors, each represented by the XLF, XLK, and XLV trackers. To initiate this analysis, daily historical data for these trackers is collected from Yahoo Finance, spanning a comprehensive ten-year period from 21 March 2014 to 21 March 2024. We will utilize a Jupyter Notebook to implement machine learning algorithms and computing metrics for stochastic processes. Jupyter Notebook provides a convenient environment for coding, visualization, and analysis, enabling seamless execution of Python code for both tasks. Its interactive nature enhances efficiency and facilitates collaborative work among team members. In this dataset, we examine six key variables that are essential for evaluating the performance of machine learning algorithms. These variables provide valuable insights into the behavior of stock indices and are crucial for predicting their future trends. By analyzing these variables thoroughly, we can better understand the dynamics of the financial market and assess the effectiveness of our models. The initial variables are as follows:
- Open: the opening price on a specific date.
- High: the highest day price at which the tracker was traded.
- Low: the lowest day price at which the tracker was traded.
- Close: the closing price on a given day.
- Volume: the number of shares traded on a given date.
- Adj. Close: the adjusted closing price, accounting for dividend distributions.
5.2. Variables
Using the dataset, three crucial variables are derived to encapsulate significant aspects of market dynamics for each index. Initially, the difference between opening and closing prices for each trading day is computed (OpenClose), providing insights into daily price movements. The second variable signifies the range between the highest and lowest prices within a given trading day (HighLow), serving as a measure of intra-day volatility. Lastly, the third variable quantifies the disparity between the traded volume on the next day and the current day’s volume (DiffVolume). It is noteworthy that this last variable cannot be computed for the final date in the sample, leading to the exclusion of this particular data point from the analysis to maintain accuracy and consistency in calculations. These derived variables are calculated for each index and utilized in conjunction with each algorithm to predict the target variable. The target variable, referred to as Y in this study, corresponds to the label attached to the data and what the model aims to predict based on the independent variables. This variable defines whether the next day’s stock price will close higher or lower, taking either the value 1 or −1. A value of 1 indicates a buy signal for the period concerned, while a value of −1 indicates a sell signal. To achieve this, returns are calculated as a percentage based on the adjusted closing price. Then, a variable is created equal to 1 if the return is positive and −1 if the return is negative. The last line of the database is deleted as it is not possible to calculate the yield at that date, nor the volume difference.
5.3. Exploratory Data Analysis
The analysis of the feature and target variables of the XLF index is illustrated in Figure 1, as an example by dividing the data into two sets (buy and sell) based on the dependent variable. Notably, the HighLow, and DiffVolume variables demonstrate consistent behavior across both sets, while the OpenClose variable exhibits differing patterns in each set. Furthermore, the two sets are nearly evenly distributed (52% for sell decisions and 48% for buy decisions). It is important to highlight that the rationale applied to the XLF tracker is similarly applied to the other trackers XLK and XLV.
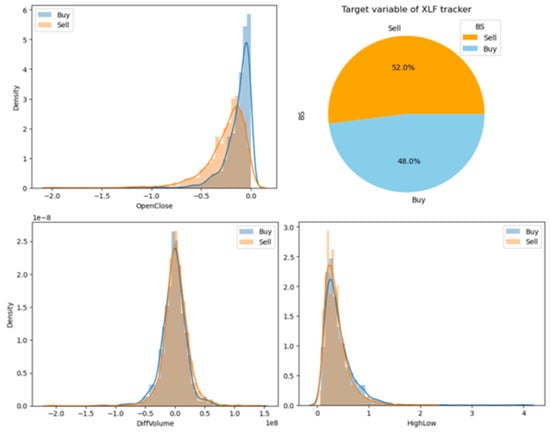
Figure 1.
Features and target variable for XLF tracker.
5.4. Simulated Equations for Stochastic Processes
In the context of this study, predicting indices using stochastic processes relies on utilizing simulated equations that establish a connection between the real value of the index at a given time, denoted as , and the value predicted by the model for the subsequent time, denoted as . By leveraging these relationships, we can calculate the daily return of the index using two successive values predicted by the model. If this return is positive, it indicates a buy signal, with a value of 1 assigned to this event. Conversely, if the return is negative, it signifies a sell signal, with a value of −1 attributed to this occurrence. This approach allows us to transform model predictions into buy or sell signals, thereby facilitating the interpretation of results and their use in the decision-making process in the financial domain. Below, we provide the simulated equations for the three stochastic models.
5.4.1. Geometric Brownian Motion
For the geometric Brownian motion (GBM), discrete-time equations play a pivotal role in capturing the evolution of asset prices over discrete intervals. These equations offer valuable insights into the dynamics of price changes, allowing for the prediction of future prices based on historical data. Unlike continuous-time equations, which model continuous changes, discrete-time equations in GBM highlight changes between successive observations, providing a foundation for understanding market behavior and facilitating risk management strategies. The equation linking two successive observations is given below.
where:
where represents the value of the index at time t, is the estimated value of the drift rate (average return) of the asset, is the estimated volatility of the asset, and is the differential of the standard Brownian motion Le Gall (2016). The values of and are calculated using historical data of the tracker index using the following formulas Ralchenko and Yakovliev (2024):
5.4.2. The Vasicek Model
For the Vasicek model, we will apply the discrete time equation below to simulate the behavior of the index Backus et al. (1998).
The estimated model parameters are:
where:
The third estimate parameter is:
5.4.3. The CIR Model
The simulated equation of the CIR model is Overbeck and Rydén (1997)
where and also as:
where :
The standard deviation, , of the errors is the estimated diffusion parameter:
We will calibrate these models by calculating their parameters using historical data. Then, we will utilize these equations that link two successive observations to predict the value of the next day for each tracker.
5.5. Machine Learning Implementation
Using the linspace function from NumPy, the entire training dataset, which comprises 80% of our dataset, is divided into 10 random batches, each containing 10% of the training data. Each model is then trained on these 10 batches and tested on the test dataset, which contains 20% of the overall dataset. This training–testing methodology ensures that the models undergo rigorous training on a significant portion of the data to effectively capture underlying patterns and relationships. By then evaluating the models on unseen data from the test set, we can assess their performance and generalization capabilities. This approach enables us to develop and validate machine learning models in predicting asset prices within the financial domain. For the implementation of Random Forest, we utilize scikit-learn’s Random Forest Classifier class. This class allows us to adjust parameters such as the number of trees in the forest to fine-tune the model. Once the algorithm is configured, it undergoes a training phase on the training data using the fitting method. Following the training session, the model is primed to make predictions on new data using the prediction method. This systematic approach ensures that the algorithm is well-equipped to interpret and analyze new information effectively.
In the case of Support Vector Machine (SVM), scikit-learn’s SVM classifier class is employed for implementation. This class provides flexibility in selecting different kernel functions and tuning hyperparameters to optimize model performance. After configuring the SVM algorithm, it undergoes training on the training data using the fitting method. Subsequently, the trained model is capable of making predictions on unseen data. This stepwise procedure ensures that the SVM algorithm is adequately trained and prepared for predictive tasks. For the implementation of k-Nearest Neighbors (KNN), scikit-learn’s KNeighborsClassifier class is utilized. This class allows us to specify the number of neighbors (k) and other parameters crucial for the algorithm’s performance. Following configuration, the KNN algorithm is trained on the training data using the fitting method. Once trained, the model is ready to classify new instances based on their proximity to existing data points.
Performance Evaluation Metrics
The evaluation of all models developed in this study relies on three primary metrics: precision, recall, and F1 score. These metrics are computed for each model and subsequently compared to comprehensively assess their predictive capabilities Carvalho et al. (2019).
Precision: Precision gauges the correctness of positive predictions generated by the models. It quantifies the ratio of accurately predicted positive instances (true positives) among all instances predicted as positive (true positives + false positives).
Recall: Recall assesses the model’s capability to correctly identify all relevant positive instances. It computes the proportion of accurately predicted positive instances (true positives) out of the total number of actual positive instances (true positives + false negatives).
F1 Score: The F1 score provides a balanced measure that considers both precision and recall. It is the harmonic mean of precision and recall, offering a comprehensive assessment of the models’ effectiveness in predicting stock price movements.
6. Results and Discussion
6.1. Results
6.1.1. Stochastic Models Metric Values
The values found for the various metrics of stochastic processes used in the study are given in the tables below (Table 1, Table 2 and Table 3).

Table 1.
Metric values for GBM stochastic model applied to XLF tracker.

Table 2.
Metric values for Vasicek stochastic model applied to XLF tracker.

Table 3.
Metric values for CIR stochastic model applied to XLF tracker.
6.1.2. Machine Learning Algorithm Metric Values
The values found for the various metrics of ML algorithms used in the study are given in the tables below (Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9).

Table 4.
Metric values for Random Forest algorithm applied to XLF tracker.

Table 5.
Metric values for SVM algorithm applied to XLF tracker.

Table 6.
Metric values for KNN algorithm applied to XLF tracker.

Table 7.
Metric values for machine learning algorithms and stochastic models for XLF tracker.

Table 8.
Metric values for machine learning algorithms and stochastic models for XLK tracker.

Table 9.
Metric values for machine learning algorithms and stochastic models for XLV tracker.
6.2. Discussion
This study aimed to evaluate how well stochastic processes and machine learning algorithms predict stock index movements across different sectors. The results revealed significant findings regarding the effectiveness of various modeling techniques in financial forecasting. This discussion section explores the implications of these results, emphasizing important insights and considerations for practitioners and researchers in financial analysis. The results shed light on important observations. Firstly, the metrics of the stochastic processes used in prediction exhibit very high values, approaching 100% for the three sectors studied, except for the GBM model, which fails to surpass the 50% threshold (Table 1, Table 2 and Table 3 and Table 7, Table 8 and Table 9). The lower performance of the GBM model compared to the Vasicek and CIR models can be attributed to the fact that these latter models are improvements upon the GBM. Both the Vasicek and CIR models incorporate the mean-reversion property, allowing them to better capture long-term trends in financial data. Unlike the GBM, which does not explicitly incorporate this feature, the Vasicek and CIR models are specifically designed to model interest rates and other financial phenomena that exhibit a tendency to revert to a historical mean. This integration of the mean-reversion property can, therefore, lead to higher performance for the Vasicek and CIR models compared to the GBM in certain financial contexts. Particularly, the metrics of the CIR model stand out with a value of 99% for all three sectors, exceeding the Vasicek model, which is natural considering that the CIR model is an improvement over the Vasicek model. On the other hand, the metrics of the machine learning algorithms hover around 70%, with a slight advantage for the SVM model, as highlighted by Bouasabah (2024) (Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9). It is noteworthy that this study focuses on predicting the next day’s trend of stock indices (rise with +1, fall with −1). For the machine learning algorithms, predicting the target variable is based on three variables (features): OpenClose, HighLow, and DiffVolume. The model is trained on a test dataset, enabling it to predict the next day’s value for different combinations of feature variables. In contrast, prediction based on stochastic processes uses today’s real value to predict tomorrow’s value, which explains the high metrics observed for stochastic processes, as the true value of today’s index is already known. Therefore, the Vasicek and CIR models are excellent if today’s index value is known and one seeks to predict tomorrow’s value. Consequently, these high metric values must be interpreted with caution. It is also important to note that all three stochastic processes provide the predicted value of the index, not just the trend, which sets them apart from machine learning algorithms that only provide the trend. Furthermore, it is worth noting that the parameters of machine learning algorithms are not static and can be dynamically adjusted, unlike the parameters of stochastic models, which are static and calculated for each sample. Another observation we made in this study is that the metrics of stochastic processes reach high values, largely due to the use of the real and current value of the index to predict the future value of the next day. It would be interesting, in a future study, to explore the impact on these metrics if we were to use not the real and current value (today’s real value) of the index, but rather a value predicted by the model (based on the real value of the previous day) to estimate the value of the next day. Similarly, instead of using a real value to estimate the value of the previous day, we could use another predicted value, and so on. By adopting a recursive approach, we could go back in time to determine when it is optimal to stop using the real value of the index without compromising the performance of the stochastic process metrics too much. This is, therefore, a compromise to be established between “the memory of the stochastic model” and thresholds to set for the metrics, an approach that could enrich our understanding of underlying processes and prediction strategies. In summary, confirming the superiority of stochastic processes over machine learning algorithms in absolute terms is difficult to ascertain, but what the study confirms is their performance and superiority only when the value of today is known and one seeks to predict that of tomorrow. Furthermore, considering hyperparameter optimization for machine learning algorithms emerges as a crucial perspective to achieve even higher performance levels Yang and Shami (2020). This strategic approach leverages the inherent flexibility of machine learning, providing a pathway to fine-tune models to suit specific market dynamics. In the end, to take advantage of each approach, one can combine stochastic processes and machine learning algorithms as follows:
(1) Utilize stochastic processes if the number of predicted values does not exceed “the model’s memory”: It is worth noting that, in this study, “the memory of the stochastic process” is defined as the number of future index values that the model can predict between day j and day without using real values from the previous day in the prediction, but only the successive predicted values from a given real value at day j without lowering the metric values beyond a certain preset threshold.
(2) Utilize machine mearning algorithms if the number of values to predict exceeds the memory of the stochastic processes used in the prediction. Finally, the practical application of the study’s findings is to guide traders in selecting the appropriate model for predicting the future value of a tracker. Based on our study, the choice of the prediction model is clear and well justified. By following this method, we can leverage both approaches for better prediction quality. As a perspective, a general and absolute comparison of a test dataset could confirm the superiority of one approach over the other. Additionally, extending the analysis to other sectors could show if there is a sector effect on model performance.
7. Conclusions
In conclusion, our study sheds light on the performance of machine learning algorithms and stochastic processes in predicting the future trends of stock market indices. We found that stochastic processes, particularly the CIR model, exhibited remarkably high metrics, which is thanks to their utilization of the real and current index values for predicting the following day’s value. This highlights the importance of leveraging current market data for accurate predictions. Additionally, while machine learning algorithms demonstrated relatively lower performance, stochastic processes outperformed them when considering the current value of the index. However, it is crucial to interpret these high stochastic process metrics with caution, considering their dependence on the current index value. Furthermore, an intriguing aspect observed in this study is the potential impact on stochastic process metrics if the model’s predictions were recursively used. Exploring how far back in time one can rely on predicted values before the metrics significantly decline warrants further investigation. This recursive approach offers insight into striking a balance between the model’s memory and predefined metric thresholds, contributing to a deeper understanding of stochastic process performance. Moving forward, future studies may benefit from exploring the applicability of different modeling approaches across various sectors and expanding the analysis to include additional context-specific factors. Moreover, examining the trade-offs between model complexity, memory, and prediction accuracy could enhance the development of more robust forecasting frameworks. By delving into these areas, researchers can advance the field’s understanding and application of predictive modeling techniques in financial markets.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Acknowledgments
The author extends sincere gratitude to the anonymous referees for their valuable comments on the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ayyildiz, Nazif, and Omer Iskenderoglu. 2024. How effective is machine learning in stock market predictions? Heliyon 10: e24123. [Google Scholar] [CrossRef] [PubMed]
- Backus, David, Silverio Foresi, and Chris Telmer. 1998. Discretetime Models of Bond Pricing. Technical Report w6736. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Be. 1913. Calcul des probabilités: Par louis bachelier. Tome i. Paris, gauthiers-villars 1912. 4. 516 p. U. Vii. Monatshefte für Mathematik und Physik 24: A4–A8. [Google Scholar] [CrossRef]
- Bernaschi, Massimo, Luca Torosantucci, and Adamo Uboldi. 2007. Empirical evaluation of the market price of risk using the CIR model. Physica A: Statistical Mechanics and its Applications 376: 543–54. [Google Scholar] [CrossRef]
- Bonaccorso, Giuseppe. 2017. Machine Learning Algorithms: A Reference Guide to Popular Algorithms for Data Science and Machine Learning. Birmingham and Mumbai: Packt. [Google Scholar]
- Bouasabah, Mohammed. 2024. Analysis of machine learning’s performance in stock market prediction, compared to traditional technical analysis indicators. International Journal of Data Analysis Techniques and Strategies 16: 32–46. [Google Scholar] [CrossRef]
- Bouasabah, Mohammed, and Oshamah Ibrahim Khalaf. 2023. A technical indicator for a short-term trading decision in the nasdaq market. Advances in Decision Sciences 27: 1–13. [Google Scholar] [CrossRef]
- Carvalho, Diogo V., Eduardo M. Pereira, and Jaime S. Cardoso. 2019. Machine learning interpretability: A survey on methods and metrics. Electronics 8: 832. [Google Scholar] [CrossRef]
- Chandrika, G. Naga, Sai Venkata Rohit Gumudavelli, Ashish Kalleru, Vijitha Kambhampati, and Pragnika Kandaggatlta. 2023. Comparative analysis of machine learning algorithms to forecast indian stock market. ITM Web of Conferences 56: 05009. [Google Scholar] [CrossRef]
- Chen, Nan. 2023. Combining stochastic models with machine learning. In Stochastic Methods for Modeling and Predicting Complex Dynamical Systems: Uncertainty Quantification, State Estimation, and Reduced-Order Models. Berlin/Heidelberg: Springer, pp. 171–77. [Google Scholar]
- Gan, Lirong, Huamao Wang, and Zhaojun Yang. 2020. Machine learning solutions to challenges in finance: An application to the pricing of financial products. Technological Forecasting and Social Change 153: 119928. [Google Scholar] [CrossRef]
- Le Gall, Jean-François. 2016. Brownian motion, martingales, and stochastic calculus. In Graduate Texts in Mathematics. Cham: Springer International Publishing, vol. 274. [Google Scholar] [CrossRef]
- Li, Pei Ze. 2012. Research on stock analysis based on stochastic process. Advanced Materials Research 433–440: 5967–74. [Google Scholar] [CrossRef]
- Mensah, Eric Teye, Alexander Boateng, Nana Kena Frempong, and Daniel Maposa. 2023. Simulating stock prices using geometric Brownian motion model under normal and convoluted distributional assumptions. Scientific African 19: e01556. [Google Scholar] [CrossRef]
- Nadarajan, Sarmela, and Roslan Nur-Firyal. 2024. Comparing vasicek model with ARIMA and GBM in forecasting Bursa Malaysia stock prices. AIP Conference Proceedings 2905: 050004. [Google Scholar] [CrossRef]
- Orlando, Giuseppe, Rosa Maria Mininni, and Michele Bufalo. 2019. Interest rates calibration with a CIR model. The Journal of Risk Finance 20: 370–87. [Google Scholar] [CrossRef]
- Overbeck, Ludger, and Tobias Rydén. 1997. Estimation in the coxingersollross model. Econometric Theory 13: 430–61. [Google Scholar] [CrossRef]
- Papacharalampous, Georgia, Hristos Tyralis, and Demetris Koutsoyiannis. 2017. Forecasting of geophysical processes using stochastic and machine learning algorithms. European Water 59: 161–68. [Google Scholar]
- Papacharalampous, Georgia, Hristos Tyralis, and Demetris Koutsoyiannis. 2019. Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes. Stochastic Environmental Research and Risk Assessment 33: 481–514. [Google Scholar] [CrossRef]
- Ralchenko, Kostiantyn, and Mykyta Yakovliev. 2024. Parameter estimation for fractional mixed fractional Brownian motion based on discrete observations. Modern Stochastics: Theory and Applications 11: 1–29. [Google Scholar] [CrossRef]
- Shinde, Akanksha Sampat, and Kalyanrao Chimaji Takale. 2012. Study of black-scholes model and its applications. Procedia Engineering 38: 270–79. [Google Scholar] [CrossRef]
- Svoboda, Simona. 2004. The vasicek model. In Interest Rate Modelling. London: Palgrave Macmillan, pp. 3–17. [Google Scholar] [CrossRef]
- Weigand, Alois. 2019. Machine learning in empirical asset pricing. Financial Markets and Portfolio Management 33: 93–104. [Google Scholar] [CrossRef]
- Yang, Li, and Abdallah Shami. 2020. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 415: 295–316. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).