Abstract
The risk of lending money collected from savers is that it leaves banks liable to default with depositors if events (and hence repayment demands) become ‘abnormal’. Even though international and national regulation has been introduced to ensure that a certain level of capital is retained by banks, such regulation can be subverted. The current system of international regulation based on the Basel III agreements does not stipulate a standardised approach for inspection frequency or penalty magnitude. This leaves the potential for regulatory arbitrage. The scientific value of an analysis to optimise regulatory efficiency and reduce such arbitrage is therefore considerable. This work therefore assesses the results of the empirical testing of a model based on the Von Neumann–Morgenstern utility function and consequently proposes that this model be used as a basis for standardising capital adequacy limit infraction penalties on an international level to prevent regulatory arbitrage. A survey is undertaken in order to test the responses of participants on the level of penalty which would deter them from regulatory transgression under different theorised levels of profit and probability of discovery. Based on the responses of two distinct subject groups (‘bankers’ and ‘non-bankers’) in different scenarios of hypothetical capital adequacy violation, the Von Neumann–Morgenstern utility function is reviewed against empirical results and revealed to show a semi-strong correlation. Lastly, the analysis reveals the striking similarities of the two groups’ responses, posing regulatory implications for the industry.
1. Introduction
International capital adequacy regulation is fragmented (Claessens 2019). There are two main areas which require standardisation: the inconsistency in the level of penalties and frequency of inspection. The current scale of the problems can be found in the database of the Office of the Comptroller of the Currency (Office of the Comptroller of the Currency 2018), specifically for banks of the United States of America, as well as the violation tracker for British and American banks. There is considerable inconsistency in the level of penalties for a given magnitude of capital adequacy violation. Ulster Bank, for example, was fined EUR 1.96 million on a EUR 313 million shortfall (Ulster Bank Ireland Limited 2010); Manchester Building Society, however, was fined GBP 975,000 on a GBP 2.8 million shortfall—a considerably higher level of penalty (Agnew 2015). Metro Bank was fined GBP 5.37 million on a GBP 100 million shortfall, again a substantially different level of penalty (Bank of England 2022). The fine was imposed by the Prudential Regulation Authority in the UK (PRA). Metro Bank’s early settlement reduced the fine by 30%. Without such a discount, the fine—including costs—would have been GBP 7.68 million. All these banks are now insolvent. In the United States, Integra Bank, the National Bank of Central Florida, and Eastside Commercial Bank were all fined USD 0 (FDIC 2022).
There is also some difference in the frequency of inspection; according to the European Central Bank 15 out of 37 banks were inspected quarterly, 10 out of 37 monthly, 8 out of 37 bi-annually, and 4 out of 37 yearly (European Central Bank 2022). In the United States, an annual on-site inspection of a minimum frequency was officially required for most deposit-taking banks by the Federal Deposit Insurance Corporation Improvement Act of 1991, yet as Iheanyi and Sotonye (2017, p. 14) state, this is not always undertaken. Despite such inconsistencies in current inspection, there has long been a belief that more robust regulations are required in terms of capital adequacy. In 2007, Sheila Bair, the then chair of the United States Federal Deposit Insurance Corporation, claimed (Bair 2007, p. 2) “There are strong reasons for believing that banks left to their own devices would maintain less capital—not more—than would be prudent. The fact is, banks do benefit from implicit and explicit government safety nets”.
There is therefore a high scientific value to any work that can reduce regulatory arbitrage in capital adequacy regulation in the banking sector. In the same domain of research, a model for devising an optimal level for penalties was proposed in Brož et al. (2023); the theoretical model proposed was based on the behavioural characteristics of banks and regulators by examining economic motives and incentives for bank misconduct and was derived from the Shapiro–Stiglitz model in the context of the principal–agent models of Shapiro and Stiglitz (1984). However, the work of Von Neumann and Morgenstern in developing a utility function that describes the most efficient level of penalty to deter a proscribed action provides an alternative opportunity to standardise such penalties on an international level, to prevent regulatory arbitrage. An issue is to test empirically if this function corresponds to the opinions of those who work in the banking industry, and furthermore, as the banking industry has a fluid employment base, whether they correspond to the opinions of those in the wider community who may enter banking as a career at some later stage. This work is organized as follows. The next section (Section 2), explores the theoretical frameworks and empirical studies related to capital adequacy regulation. Then risk perception, decision making and regulatory perspectives in different domains, using a thematic approach. Section 3, after providing a theoretical set up derived from Von Neumann and Morgenstern (1944), defines the demographics of the study and the empirical testing criteria of the model. Section 4 and Section 5 consider the results and discuss regulatory implications. Finally, Section 6 deals with the limitations of the study and provides conclusions.
2. Literature Review
Von Neumann–Morgenstern utility theory has been employed as a useful tool within different areas of study where humans make decisions under uncertainty and the outcomes of decisions are probabilistic in nature. Below, an examination, using thematic categories has been provided.
2.1. Theoretical Frameworks
The collapse of much of the banking system in 2008 further reinforced the view that banks might benefit from implicit and explicit regulatory frameworks (Felton and Reinhart 2011). The utility of models to assess and guide control of banking can be seen in the paper ‘Bank Runs, Deposit Insurance, and Liquidity’ (Diamond and Dybvig 1983), whose authors won a Nobel Prize for their work in this area in 2022. For an exposition of how banks create and are constrained in their ability to provide liquidity to pay for capital shortfalls, see ‘Banks and Liquidity Creation: A Simple Exposition of the Diamond-Dybvig Model’ (Diamond 2007). The seminal paper ‘Crime and Punishment: An Economic Approach’ (Gary Becker 1968, pp. 18–30) outlines the rational basis of some rule-breakers as well as the consequences of varying probabilities of penalties for transgressions. In his theory of “subjective expected utility”, Savage (1954) explores behaviour in a variety of subjective settings of risk. A key issue is the subjective nature of perceived risk and subsequent capital adequacy failures. Real-world uncertainty usually lacks clarity, unlike well-defined objective risk with known consequences and probabilities. For such clear objective risks the basic notion of ‘expected utility’ was constructed, although this has since been superseded by many other models (Pachur and Zilker 2023). Furthermore, risk aversion (characterised as a special preference for riskless outcomes under anticipated value) can be modelled using concave utility. Some generalisations have been made, for example, the certainty effect of Kahneman and Tversky (1979). Given that individuals categorically distinguish between risky and riskless circumstances, all of these generalisations regarding “non-expected utility” share the same particular preference for riskless solutions.
However, due to the subjective nature of risk perception, individuals may under-rate the risk they are facing, and therefore, treat the decision making in terms of capital adequacy inaccurately. Indeed, the instant a predictable outcome is perceived as a risky gamble, the triggering of new emotions can cause people to switch to a different assessment procedure—the one for risky decisions. Different evaluations of risky and risk-free solutions have been proposed in various situations. For instance, a number of publications, including Dyer and Sarini (1982) and Glimcher and Tymula (2023), have indicated that risky decisions ought to be made using a utility function and expected utility, but risk-free decisions should be made using a different function, known as the value function. Riskless evaluations include those that focus on welfare, intertemporal judgements, or intensity of choice. This distinction between usefulness and value has achieved popular recognition even if it is not universally understood. This paper concerns the decision to adhere to, or violate, capital adequacy regulation for potential profit in differing scenarios of probability of discovery, which is clearly a risk-based evaluation, with the only exception being when such violation has occurred truly accidentally.
2.2. Empirical Studies
Despite the above nuances, Von Neumann–Morgenstern utility theory has proved to be a useful tool within different areas: consumer behaviour, marketing risk management, and engineering and system design.
With regard to consumer behaviour, Hauser and Urban’s (1979) study demonstrates Von Neumann–Morgenstern utility theory as being useful for comprehending and forecasting customer behaviour. The conditions under which it proved the most useful are as follows: individual utility parameters are considered to be crucial to the research or managerial question; risk aversion and interaction phenomena are considered to be important in the consumer’s behaviour; there is a sufficient budget allocated to the personal interviews; and consumers are well-educated. It works especially well when there are few decision-makers and many options available. Consumer durables like washers and dryers or automobiles could serve as more helpful examples. It may be relevant to the provision of healthcare, college selection, and career guidance services.
The utility and conjoint axioms, according to Hauser and Urban (1979), appear to be compatible, but further study is required to create a shared set of reliable axioms. In light of this, Hauser and Urban’s application of Von Neumann–Morgenstern utility theory suggests that consumer assessment is possible, that psychological qualities may be incorporated, and that the empirical outcomes are on par with or better than those of two competing approaches. Contemporary sources such as Koçaslan (2019) and Moscati (2021) also concur in this assessment. These positive findings suggest that Von Neumann–Morgenstern utility theory’s appealing aspects of modelling risk, measuring indifference, and identifying practical form have potential for use in consumer research.
With regard to marketing and risk management, Shi and Wang’s (2019) investigation (which took into account all of the different decision-makers’ attitudes toward risk based on individual aspects like personality and status) found that using utility theory in marketing risk management has an unmatched advantage over other decision-making methods. However, some fundamental premises must be included when utility theory is used in such analysis. Although the theoretical model of subjective utility was intended to be a piece of work that should be closely associated with the field, the four fundamental preconditions of subjective expectation utility, (that is, completeness, transitivity, continuity, and independence), make it difficult for practical marketing management to achieve these requirements.
Despite such difficulties, Shi and Wang (2019) note the widespread use of utility theory in marketing and risk management. This is particularly the case where the specifics of positive and negative effects are generally obscure, but where the probabilities of such events are known. The gathering of statistics on past and similar performance is thus of crucial importance to this approach. The ability to monetise benefits or losses is also of great importance in assessing the best management decision to take. It is on this basis, for example, that much of the modern-day insurance industry is based.
Additionally, the utility function’s establishment may be challenging because external environmental circumstances will also alter one’s own attitude toward risk. Indeed, the work of Gary Becker (1968) also emphasises, for example, the role of individual incentive towards rule breaking. Differing levels of ‘risk aversion’ based on individual and group accountability are also explored by Kahneman and Tversky (1979). These, of course, do not negate utility theory’s unmatched advantages, whether they pertain to the risk decision of a straightforward project, a complex project, a project involving large-scale risk decision making or a project involving small-scale risk decision making. In fact, the altering of one’s perception towards risk has also been illustrated within the findings of this paper. Yet, Shi and Wang (2019) agree that utility theory can only be continuously developed and improved upon in the actual decision-making process, which requires continuous application and adjustment in practice. This is particularly so when examining utility theory in light of neurochemistry (Peterson et al. 2021).
The domain of engineering and system design has long acknowledged the significance of decision making (Winch et al. 2023, pp. 18–24). The many approaches to decision making are divided by Tomiyama et al. (2009) into those based on heuristics and those founded upon decision theory. It should be borne in mind that carrying out decision-making tasks in the engineering domain does not automatically qualify one as a decision analysis specialist. On the other hand, being familiar with decision analysis does not automatically make one an engineering expert. Abbas and Cadenbach (2018) suggest an approach whereby a deterministic value function is applied to a design, and the utility function assigned according to that value. Not only does this conceptual and numeric approach illustrate greater flexibility; it also reinforces the concept of ‘utility transversality’ in engineering design. The limitations of utility theory depicted in the recent literature of engineering design (Harackiewicz and Asher 2023; Miranda and Zaffalon 2023; Peterson et al. 2021) are said to be overcome by this value-based approach (Abbas and Cadenbach 2018). However, the widespread applications of Von Neumann–Morgenstern utility theory illustrated above highlight in practical domains its importance in understanding the behaviour of decision-makers.
2.3. Regulatory Perspectives
While Basel III (on which the current system of international regulation is based) does not stipulate a standardised approach to penalty frequency or magnitude, the potential for regulatory arbitrage also leaves room for certain perception of risk. Garoupa’s (2001) “Optimal Magnitude and Probability of Fines” and his reinforcement of Becker’s (1968) analysis in his “The Theory of Optimal Law Enforcement”(Garoupa 1997), and Yokoyama and Takahashi’s (2013) “Mathematical Neurolaw of Crime and Punishment: The q-Exponential Punishment Function” all suggest a rational approach to analysis of risk and reward behaviour in financial matters. Furthermore, Yokoyama and Takahashi’s (2013) work (particularly in section two thereof) describes a method of surveys whereby the impact of risk and reward behaviour can be assessed. Additionally, the methodology of assessing risk judgements by a “willingness to accept” certain hypothetical sums, is asserted in Kahneman and Tversky’s (1992) “Advances in Prospect Theory: Cumulative Representation of Uncertainty”, and it is towards this investigative methodology that this paper is directed.
3. Methodology
The methodology for testing is designed around a standardized penalty model that can reduce the possibility of regulatory arbitrage, based on the most efficient level of deterrence. The ‘efficient penalty’ for a representative bank can be based on a model derived from Von Neumann and Morgenstern (1944) and is shown in Equation (1) below:
where:
: The most efficient level of penalty;
: Amount a bank has reduced its reserve below the mandatory level;
: Percentage return earned on the capital A;
: Probability of a bank discovery when violating the capital adequacy limit;
: The cost of inspection to the bank.
Intuitively, the theoretical model is also based on the work of Gary Becker (1968), who emphasises the role of individual incentive towards rule breaking. In the following work, no account was taken of the costs of inspection (k) as it was thought that this figure would be obscure to the vast majority of individuals if a decision as to whether to direct or simply risk a capital adequacy violation is made.
Figure 1 shows Equation (1) applied in the case of an infraction of USD 100 million and its rate of return of 7%. The solid line illustrates the position with a bank infracting a total of USD 300 million over its capital adequacy limit, resulting in a total illicit profit of 21 million dollars. The same graph would also be true of a group of any size of banks violating their capital adequacy limit and obtaining a total of USD 21 million in illicit profit. The total cost of inspecting banks is tabulated out of a sample of 500 banks in the banking system, assuming an incremental inspection cost of USD 1 million per bank.
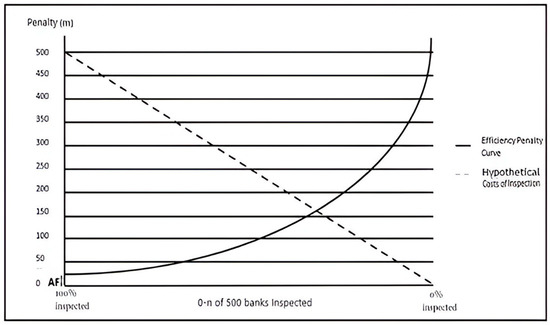
Figure 1.
Efficient penalty curve of banks infracting and hypothetical costs of inspection.
The results of such a model as described above intersect with the total costs of inspecting the banking system given by Equation (2) below. It is assumed that the cost of checking each bank is USD 1 million per bank (Adeleye 2020). It is also assumed that the cumulative costs of inspection rise in a linear manner.
where:
C: Cumulative inspection cost for regulators;
ki: Costs per inspection to regulator;
ni: Number of banks inspected.
The model shown in Equation (1) was therefore adapted further for the purpose of empirical testing, and written as
The term in the numerator may be thought of as a reward from the unlawful action. In the survey the respondents were asked to specify a penalty which would deter them from unlawful behaviour in five different banking and non-banking contexts, while all figures were further standardised. For example, in ‘context 1 (individual risk)’, the reward is equal to USD 10 and in ‘context 2 (assisted risk)’ the gain consists of USD 5 (USD 10 and its profit minus USD 5 shared with the friend). In ‘context 3 (banking risk)’, ‘context 4 (salary-liable banking risk)’, and ‘context 5 (bonus-liable banking risk)’, the AF figures equal USD 10 m. Thus, units of dollars and millions of dollars were equalised for the purposes of the later statistical analysis.
Demographics and Empirical Testing
In order to test the penalty model for () in different scenarios of risk and level of capital inadequacy among English speaking ‘bankers’ (working in the banking industry) and ‘non-bankers’ (working in a variety of different professions) the following survey was undertaken. The survey also investigates at what level other non-financial penalties might deter potential infractors and how the effectiveness of these might vary. An online platform was used where bankers and non-bankers could select to undertake the survey, with the incentive of being entered in a prize draw for free bandwidth. The access to this survey was worldwide, but the language was exclusively English.
The overall structure of the questionnaire (Appendix A) starts with the initial descriptive section, is followed by a scenario-based questionnaire to assess the different levels of risk tolerated by the respondent for certain levels of direct financial penalties (expressed as γ in Equation (1) above), and closes with broad questions that touch on the respondent’s value of certain non-financial penalties.
A further demographic analysis of raw and cleaned data (Appendix B), hereafter referred to as ‘data’, showed that there was no significant demographic skewedness before or after the cleaning.
The data cleaning procedure (Appendix C) removed any individual’s results if they had repeated the same “most efficient” penalty continually throughout all their answers or if they had given “0” as a result for any answer. After this cleaning procedure, the data which remained resulted in the final analysis being based on a survey of raw data of 350 participants (189 ‘bankers’ and 152 ‘non-bankers’, who were English speaking). Full demographic statistics were also assessed in relation to the two subject groups of the empirical analysis in Appendix D. Thus, the main focus of the study was thus the correlation of the results to the Von Neumann–Morgenstern utility function (Von Neumann and Morgenstern 1944), as well as the difference in responses between banking and non-banking respondents.
4. Results and Discussion
In terms of non-financial penalties, ‘bankers’ in the data analysed did not show strong trends in their responses. However, damage to personal reputation and personal liability for a fine were the most common types of responses (see Table 1). ‘Non-bankers’, in contrast, indicated heavier fines as the most important factor, closely followed by damage to personal reputation and the personal liability to a fine. While individuals were allowed to select more than one answer in this section to demonstrate their overall order of preferences, it is important to notice that damage to the reputation may not have the same magnitude or influence for a ‘non-banker’ as for a ‘banker’, considering the amount of time and effort invested in their career, and perhaps a larger potential loss of earnings.

Table 1.
The non-financial factors deterring bankers and non-bankers from unlawful actions in the data (questions E1 to E5).
The plots below further illustrate the risk of being apprehended (γ) on the x-axis and the fines on the y-axis. With two per ‘context’. The following elements are shown:
- (1)
- Each of the possible responses at each risk level is shown by a grey dot.
- (2)
- The mean response for each value of risk (i.e., for each question) is shown by a large dot on the line in the centre of the shaded area.
- (3)
- The 1-sigma standard deviation region around each mean value is shown by a shaded area.
- (4)
- The theoretical model of the ‘efficient penalty’ is shown by the curved upper line.
- (5)
- The best-fit model based on the actual data is shown by the curved lower line.
- (6)
- The indicator for the goodness of the fit, , is shown.
In case of individual risk, ‘bankers’ have a fit to the model at 0.53 (shown in Figure 2a), and the narrowest standard deviation at around the 50 percent probability of detection. Its widest point is at the 12.5 percent detection probability, and its second widest at 100 percent. ‘Non-bankers’, on the other hand (shown in Figure 2b) seem to require a slightly higher level of deterrent fine than ‘bankers’ at 0.57. The standard deviation is wide, with the narrowest level being at the 25 percent chance of detection.
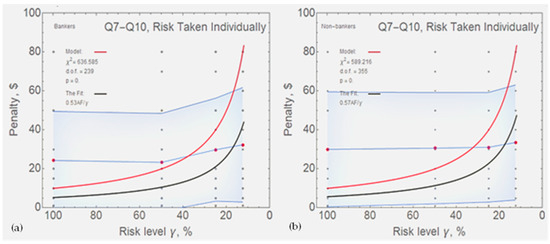
Figure 2.
The model against results for risk taken individually: ‘bankers’ (a) and ‘non-bankers’ (b).
In case of individual assisted risk, the group of ‘bankers’ (shown in Figure 3a) demonstrated the lowest correlation with the model amongst all contexts, at 0.36, with the highest standard deviation at 12.5 percent chance and the lowest one at the 100 percent chance of being caught. The correlation for ‘non-bankers’ (shown in Figure 3b) equalled 0.37, the second narrowest in the ‘non-bankers’ section apart from in ‘context 5’.
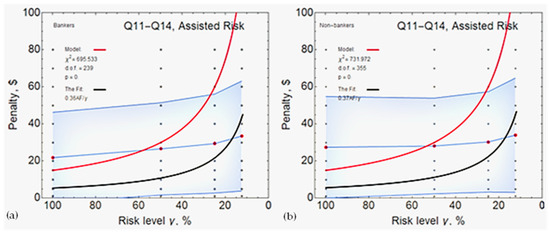
Figure 3.
Model against results for individual assisted risk: ‘bankers’ (a) and ‘non-bankers’ (b).
Placing the scenario clearly in a ‘banking context’ for ‘bankers’ seems to bring the correlation with the model up to 0.57 (shown in Figure 4a). The widest standard deviation is at 12.5 percent, and almost as wide at 100 percent chance of detection. Conversely, despite being generally quite wide, standard deviation’s narrowest point is at the 50 percent chance of being detected. Compared to the previous scenario it becomes clear that the lack of an ‘assistant’ in the infraction means that the amount of fine required for deterrence is markedly larger than that for the ‘assisted risk’ results, and thus, the results appear to have a higher correlation with the model. This context also shows a high correlation (0.64) for ‘non-bankers’ in Figure 4b. This is the highest result out of all subsets investigated. Similar to the first group, the standard deviation is wide but there are two places where it narrows, at 50 and 25 percent probability of detection.
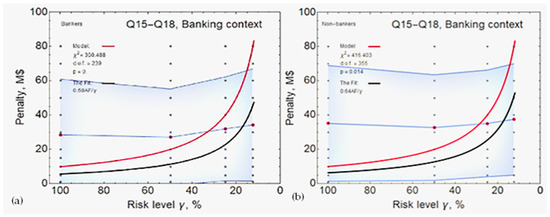
Figure 4.
The model against results for banking context: ‘bankers’ (a) and ‘non-bankers’ (b).
Establishing a salary liability for ‘bankers’ increases the amount of deterrent fine to 0.59, in agreement with the model (as shown in Figure 5a). There is a particularly close agreement between Figure 5a,b and Figure 6a perhaps indicating that ‘bankers’ do not see much difference between their salary and bonus. The standard deviation is wide, with the narrowest point being at the 25 percent chance of detection. For ‘non-bankers’(Figure 5b), the correlation was also high, the second highest of the overall analysis, at 0.61. The exception here is Figure 6b where the standard deviation is narrowest at the 50 percent chance of being caught and is generally narrower than that any other group.
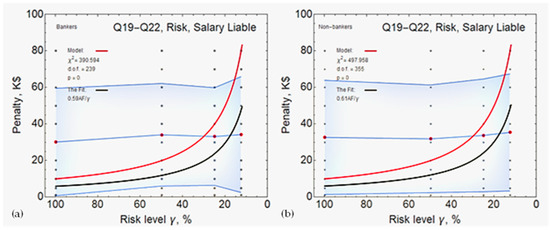
Figure 5.
The model against results for salary liable: ‘bankers’ (a) and ‘non-bankers’ (b).
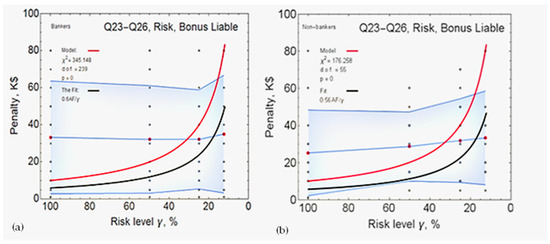
Figure 6.
The model against results for risk bonus liable: ‘bankers’ (a) and ‘non-bankers’ (b).
In ‘context 5’, there is a 0.59 correlation to the model overall. The standard deviation is again wide and is very similar in shape to the results of ‘context 4’. In Figure 6a the standard deviation reaches its narrowest point at the 25 percent chance of detection and Figure 6b is at its narrowest point at 50 percent. The results for ‘non-bankers’ produced a 0.56 correlation to the model. The standard deviation was much narrower than any other subset of results, with its narrowest point at the 50 percent chance of being caught.
5. Discussion
5.1. Best Fit to Model
All results have been produced against the same graph template so that comparison is possible and, apart from Figure 6b for the ‘non-bankers’ which seems an outlier, some overall similarities and differences can be noted. The standard deviation of all answers is quite wide, narrowing somewhere between a 20 and 80 percent chance of being caught. In Figure 2a and Figure 3a, the results (for ‘bankers’) also show a markedly narrower standard deviation than others at a 100 percent chance of being caught. No set of results runs counter to the model and each markedly declines with decreased probability of being caught.
To identify their statistical significance the empirical results were further examined by the function
where is the unknown number we are to determine. A nonlinear model fit procedure was used to obtain values of for each of the contexts. Intrinsically, the algorithm tries many different values of and picks the one which makes Equation (4) closest to the data points (by minimising the sum of the squares of differences between the curve and the data).
The goodness of fit was further evaluated by calculating the statistic for each fitted curve:
Specifically, for every response (i.e., for every grey dot on the plots), the distance to the corresponding mean response is considered (the corresponding red dot on the plot), and is compared to the standard deviation corresponding to the same point (the thickness of the shaded area on the plot). The number obtained in Equation (5) follows a chi-square distribution, with the number of degrees of freedom (D.O.F.) equal to the number of grey data points minus 1. The best-fit parameters , the corresponding values of , the degrees of freedom, and the corresponding -values for the data are presented in Table 2 and Table 3. This shows the closeness of fit of the empirical data to the proposed model and its statistical soundness.

Table 2.
Best-fit parameters (X) from Equation (4) for each of the contexts.

Table 3.
χ2 parameters, numbers of degrees of freedom (D.O.F.), and p-values, from Equation (5), for each of the contexts.
When the averages of each context, regardless of risk, are analysed in Table 2, it can be noted that the highest correlation to the model is ‘non-bankers’ in ‘context 3’ and ‘context 4’. The latter is also where the closest correlation between ‘bankers’ and ‘non-bankers’ was identified. On the contrary, the smallest correlation between ‘bankers’ and ‘non-bankers’ appears in ‘context 3’. There seems generally to be a closer fit to the model for ‘bankers’ in every context apart from ‘context 5’. The small difference between ‘context 4’ and ‘context 5’ might be explained by the fact that ‘non-bankers’ may not have enough experience of being paid a bonus to produce reasoned results; yet, according to Bell and Van Reenen (2010), some bonus elements and this method of payment are not exclusive to the banking industry.
The most interesting results, therefore, occur when comparing the two subject groups. Despite the general idea that ‘bankers’ through experience generally have a better idea than others of what risks may lead to, or the general effect on their health or future earning potential of transgressing the given rules, these two groups do not show strikingly different results. The latter has been determined to be statistically significant given that the degrees of freedom (in Table 3) offered are enough to provide robust data for the purposes of this analysis. Therefore, as in every survey concerning people, the nature of perception of risk proved to be different and non-dependent on the field of occupation.
The chi-square, degrees of freedom, and p-values are shown below.
The plots for all of the scenarios show generally higher deterrent penalties with decreasing risk. The best-fit curve in the plots for the data lies relatively close to the curve produced when results from the model are shown graphically, particularly for the low values of risk. While 100 percent risk shows less correlation with the model, real-life risk levels are typically less than 100 percent; therefore, the fit may be expected to be reasonably close to that shown by the model in this case.
The figure below shows the mean number of responses as a function of the fine specified for the data, accumulated over all contexts of risk and scenario (individual context penalties elevated to millions of dollars). It may be seen that the trends are relatively clear for ‘bankers’ and ‘non-bankers’ in the data, with higher fines corresponding to lower numbers of responses, apart from the very high penalties at the apex of the range appearing to cause a leap in responses.
For presentation purposes, Figure 7 was used to construct Figure 8 by representing the empirical data through Gaussian functions with the same mean and standard deviation. In this way, the curves in Figure 8 are described by
where the mean of the Gaussian and the standard deviation were set to be equal, corresponding to the mean and the standard deviation of the data. The scaling parameter was chosen so that the peak of the Gaussian curve corresponded to the number of respondents in each group.
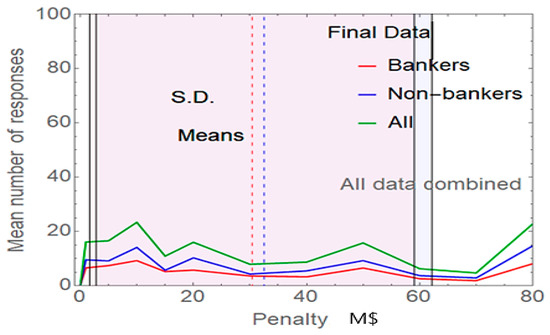
Figure 7.
Cumulative mean numbers of answers as a function of penalty, for the data.
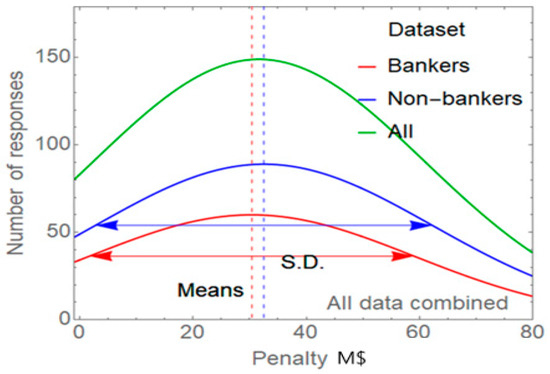
Figure 8.
The cumulative mean numbers of responses as a function of penalty, for the data, represented by the best-matching Gaussian distribution.
Notably, in Figure 8 the curves for ‘bankers’ and ‘non-bankers’ lie close to each other, and thus, illustrate that risk aversion based on penalty is very similar for both subject groups. The red dotted line is the mean average for ‘bankers’ and the blue dotted line that for ‘non-bankers’. The statistical significance of the difference was assessed by running a t-test of independence on the mean values of the deterrent fines indicated for each of the questions in the survey by both subject groups. This demonstrates that in the data there is no statistical evidence that ‘non-bankers’ chose lower values of fine than bankers. This is similar for the raw data. In both cases, there is no statistically significant evidence that ‘bankers’ are deterred by different fines than ‘non-bankers’. Lastly, for all of the numerically answered questions in the raw data and data, Cronbach’s alpha was calculated. The data resulted in a Cronbach’s alpha of 0.966, indicating excellent internal consistency.
5.2. Regulatory Implications
While on the basis illustrated above, the Von Neumann–Morgenstern utility function was proved to be a solid tool for standardisation of capital adequacy violation penalties on an international level to prevent risk taking within the banking industry, given the average correlation at 0.54, responses for all contexts in the data showed a clear dependence of the deterrent penalty on the risk of being caught. The fit was found to be the best for 12.5 and 25 percent risk, perhaps because this degree of risk exists in reality. Only one of the contexts—‘assisted risk’—produced a marked divergence from the model, which could be attributed to the specification of this particular context and consequent potential profits. When the assisted risk context is removed, the average amount of correlation to the model rises to 0.572 for ‘bankers’ and 0.593 for ‘non-bankers’ as an average of all the other contexts.
While the consistency of the data was evaluated by calculating Cronbach’s alpha, which confirmed systematic excellent consistency, showing seriously considered answers by respondents, another key point of the empirical results was concerned with striking similarities between the responses of ‘bankers’ and ‘non-bankers’. The key focus of any penalty system is concerned with the decisions made in a ‘banking context’, whether they include assisted risk or truly individual action. Here, the average correlation of ‘bankers’ and ‘non-bankers’ combined with the model is 0.61 (0.57 and 0.64, respectively). Such similarity between the two groups sufficiently impacts the modern regulatory dialectics—liberalisation and deregulation alternating with re-regulation—as well as the way possible advantages and disadvantages (benefits and costs) of the two approaches for the economy are discussed.
When overregulation is costly and limiting, lenient regulations are mostly underpinned by the assumption that bankers, through experience, generally have a better idea than others of what risks may lead to, or the general effect on their future earning potential of transgressing the given rules. The markets have shown particular volatility during the last twenty years of under-regulation. Examples are legion, from the 1997 Asian crisis, the dotcom ‘bubble’ of 1997 to 2000, the US subprime mortgage crisis, and the European debt crisis. In each case, deregulation was followed by accelerated growth and increased bank lending. Whether through introducing asset-backed securities (ABSs) or mis-selling payment protection insurance (PPI), it is clear that regulations (or gaps in regulation) are frequently abused in the name of competitive advantage.
The empirical results of this paper concluded that risk aversion based on penalty is very similar for ‘bankers’ and ‘non-bankers’, signifying similarities within the overall risk attitude of both groups. The curves of the distribution of the mean numbers of answers as a function of the deterring fine to identify the differences between the responses of ‘bankers’ and ‘non-bankers’ lie close to each other (Figure 8), with only small visual differences. Based on a t-test of independence, it was found that there was no statistically significant evidence for any difference in the combined means for the answers by ‘bankers’ and ‘non-bankers’, amplifying that there is no statistical evidence that ‘bankers’ are deterred by different fines than ‘non-bankers’. Put simply, ‘bankers’ seemed to be no more risk averse than ‘non-bankers’. This may raise significant questions about the wisdom of ‘self-regulation’ in banking. Given the potential for damage as a result of undesirable developments and the incentives to which ‘bankers’ are exposed, self-regulation alone does not prove to be sufficient in financial markets, which was also illustrated by the empirical analysis.
A stable banking system requires properly implemented and well-supervised regulation. Only in this way can excessive risk be limited. Most importantly, and contingent to the industry, regulation ensure that banks are not tempted to make bad investments, acting something like a shock absorber in such cases. In the same way, deposit guarantee schemes ensure that even in the case of failure, all deposits under a certain amount are protected. The same goes for the newly created ring-fence practices. It is, nevertheless, questionable whether too tight a regulatory regime might throw up its own problems. Chief among these is an inflexibility and an inability to keep up to date with changing requirements. Too rigid a rulebook might also prove to be too excessive in its restrictions.
There is a need for well-balanced proportions of legal standards and voluntary, negotiated rules. Such an approach addresses responsibilities without strangling the core ability of the banks to function. Whatever the case, any regulatory system must acknowledge the importance and significance of risk. Not to do so is to make the industry a hostage to fortune.
6. Conclusions and Limitations
Although national and international regulations have been put in place to make sure that banks preserve a specific amount of capital, these regulations are consistently flouted. There is no set method for inspection frequency or penalty amount in the present system of international regulation based on the Basel III accords. The possibility of regulatory arbitrage thus remains. In order to prevent such arbitrage, this paper evaluated the findings of an empirical test of a Von Neumann–Morgenstern utility function-based model and suggests that the latter be utilised as a foundation for standardising capital adequacy limit infringement penalties globally. The model has not only shown to have a semi-strong connection with empirical outcomes based on testing of ‘bankers’ or ‘non-bankers’ under various situations of hypothetical capital adequacy violation, but also shows a significant similarity in the answers of both groups, which has regulatory ramifications for the sector.
The empirical findings concluded that ‘bankers’ and ‘non-bankers’ have relatively comparable risk aversion based on penalty, indicating similarity in both groups’ general risk attitudes. The curves of the distribution of the mean numbers of replies as a function of the separating fine to distinguish the variations in responses from ‘bankers’ and ‘non-bankers’ are almost identical, with only minor visual deviations. Simply put, ‘bankers’ did not seem any less risk-averse than ‘non-bankers’. The results are influenced by the Allais (Allais 1953) and Ellsberg (Ellsberg 1961) paradoxes where decision-makers under uncertainty tend to violate the classic axioms of utility theory because their individual preferences are not consistent with the assumptions of the theory. Practically speaking, while self-regulation alone is not shown to be sufficient in financial markets, the wisdom of “self-regulation” in the banking industry may be seriously questioned in light of these empirical outcomes, especially given the potential for harm as a result of the unfavourable events and incentives to which ‘bankers’ are susceptible. Furthermore, ‘bankers’ do not have subjective probabilities that are any “more defined” than ‘non-bankers’ in uncertain situations. This is particularly the case in the area of capital adequacy, where extra profits, and hence, bonus payments may be achieved by temporarily operating below the required limit. As the results of the study highlight, a standardized capital adequacy limit infringement based on the Von Neumann–Morgenstern utility function could potentially mitigate regulatory arbitrage and benefit the banking sector by enhancing its stability. This is especially important as the recent insolvency of Silicon Valley Bank and Signature Bank in the United States of America shows regrettably that bank collapse is still an ever-present danger.
Author Contributions
Conceptualisation, Methodology, Research, Data Collection, Statistics and Original Draft Preparation, T.D. Theoretical Background, Conceptualization, Validation, Revision, Review and Editing S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of University of Buckingham (protocol code ETHICS 1) 20.12.2018 for studies involving humans.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are available online at links shown in Appendix A and Appendix B below.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Survey Questions
Available online at:
https://docs.google.com/document/d/1WzZDcxB4-I2C3fv0zMiyrqbAsyNklpIB/edit#heading=h.gjdgxs (accessed on 1 July 2023).
Appendix B. Supplementary Tables and Figures
Available online at:
https://docs.google.com/document/d/1L8pHZfgeMRQRfXj68zCz3gWBbLuwtdRB/edit#heading=h.gjdgxs (accessed on 1 July 2023).
Appendix C. Data Cleaning

Table A1.
The effect of each step of data cleaning on the sample size.
Table A1.
The effect of each step of data cleaning on the sample size.
| Cleaning Step | ‘Bankers’ | ‘Non-Bankers’ | All |
|---|---|---|---|
| Raw Data | 159 | 191 | 350 |
| Data Step I | 151 | 181 | 332 |
| Data Step II—Cleaned Data | 60 | 89 | 149 |

Table A2.
Volume of the rejected data at each step of data cleaning.
Table A2.
Volume of the rejected data at each step of data cleaning.
| Cleaning Step | ‘Bankers’ | ‘Non-Bankers’ | All |
|---|---|---|---|
| Rejected Data—Step I | 8 | 10 | 18 |
| Rejected Data—Step II | 91 | 92 | 183 |
Appendix D. Demographics Analysis

Table A3.
Working experience of ‘bankers’ in the data.
Table A3.
Working experience of ‘bankers’ in the data.
| Working Experience (Years) | Number of ‘Bankers’ (Data) |
|---|---|
| <=1 | 4 |
| 1–3 | 18 |
| 3–5 | 8 |
| 5–10 | 5 |
| 10–20 | 9 |
| >20 | 16 |
| Mean | 10.02 |
| Standard deviation | 7.75 |

Table A4.
Age distribution of respondents in the data.
Table A4.
Age distribution of respondents in the data.
| Age Group | ‘Bankers’ | ‘Non-Bankers’ | All |
|---|---|---|---|
| 18–25 | 7 | 5 | 12 |
| 26–35 | 24 | 17 | 41 |
| 36–45 | 15 | 13 | 28 |
| 46–55 | 9 | 13 | 22 |
| 55–66 | 5 | 26 | 31 |
| >67 | 15 | 15 |

Table A5.
Gender distribution in the data.
Table A5.
Gender distribution in the data.
| Gender | ‘Bankers’ | ‘Non-Bankers’ | All |
|---|---|---|---|
| Male | 33 | 54 | 87 |
| Female | 27 | 35 | 62 |

Table A6.
Education statistics for the data.
Table A6.
Education statistics for the data.
| Data | ||||
|---|---|---|---|---|
| All | Status | Frequency | Percent | Cumulative Percent |
| Associate Degree | 13 | 8.7 | 8.7 | |
| Bachelor’s Degree | 48 | 32.2 | 40.9 | |
| Doctorate Degree | 1 | 0.7 | 41.6 | |
| High School Graduate Diploma, or Equivalent | 24 | 16.1 | 57.7 | |
| Master’s Degree | 26 | 17.4 | 75.2 | |
| Professional Degree | 6 | 4 | 79.2 | |
| Some College Credit, No Degree | 23 | 15.4 | 94.6 | |
| Some High School, No Diploma | 1 | 0.7 | 95.3 | |
| Trade/Technical/Vocational Training | 7 | 4.7 | 100 | |
| Total | 149 | 100 | ||
| ‘Banker’ | Associate Degree | 6 | 10 | 10 |
| Bachelor’s Degree | 22 | 36.7 | 46.7 | |
| Doctorate Degree | 0 | 0 | 46.7 | |
| High School Graduate Diploma, or Equivalent | 5 | 8.3 | 55 | |
| Master’s Degree | 14 | 23.3 | 78.3 | |
| Professional Degree | 2 | 3.3 | 81.7 | |
| Some College Credit, No Degree | 8 | 13.3 | 95 | |
| Some High School, No Diploma | 0 | 0 | 95 | |
| Trade/Technical/Vocational Training | 3 | 5 | 100 | |
| Total | 60 | 100 | ||
| ‘Non-Banker’ | Associate Degree | 7 | 7.9 | 7.9 |
| Bachelor’s Degree | 26 | 29.2 | 37.1 | |
| Doctorate Degree | 1 | 1.1 | 38.2 | |
| High School Graduate Diploma, or Equivalent | 19 | 21.3 | 59.6 | |
| Master’s Degree | 12 | 13.5 | 73 | |
| Professional Degree | 4 | 4.5 | 77.5 | |
| Some College Credit, No Degree | 15 | 16.9 | 94.4 | |
| Some High School, No Diploma | 1 | 1.1 | 95.5 | |
| Trade/Technical/Vocational Training | 4 | 4.5 | 100 | |
| Total | 89 | 100 | ||
References
- Abbas, Ali, and Andrea Cadenbach. 2018. On the Use of Utility Theory in Engineering Design. IEEE Systems Journal 12: 1129–38. [Google Scholar] [CrossRef]
- Adeleye, Hakeem O. 2020. Adams and Moore Capital Ltd. pers.com Email to Thomas Draper. August 19. Available online: https://drive.google.com/file/d/1k_Old1P9Yzvk27i8gdq4894gufNpGOrG/view?usp=sharing (accessed on 8 June 2023).
- Agnew, Harriet. 2015. Grant Thornton Fined £975,000 over Building Society Audit. July 8. Available online: https://www.ft.com/content/dad4e22a-2573-11e5-bd83-71cb60e8f08c (accessed on 2 May 2022).
- Allais, Maurice. 1953. Le comportement de l’homme rationnel devant le risque: Critique des postulats et axiomes de l’école Américaine. Econometrica 21: 503–46. [Google Scholar] [CrossRef]
- Bair, Sheila. 2007. Remarks by Sheila Bair (Chairperson, U.S. Federal Deposit Insurance Corporation). Paper presented at Risk Management and Allocation Conference, Online, Paris, France, June 25; Available online: https://archive.fdic.gov/view/fdic/935 (accessed on 4 August 2021).
- Bank of England. 2022. PRA Fines Metro Bank £5,376,000 for Failing in Its Regulatory Reporting Governance and Controls. Available online: https://www.bankofengland.co.uk/news/2021/december/pra-fines-metro-bank-5376000-for-failing-in-its-regulatory-reporting-governance-and-controls (accessed on 1 July 2023).
- Becker, Gary. 1968. Crime and Punishment: An Economic Approach. Journal of Political Economy 76: 169–217. [Google Scholar] [CrossRef]
- Bell, Brian, and John Van Reenen. 2010. Bankers’ Pay and Extreme Wage Inequality in the UK. In Centre for Economic Performance Special Papers (CEPSP21). London: London School of Economics and Political Science. [Google Scholar]
- Brož, Vaclav, Domenico Pace, Bruce Gahir, Thomas Draper, and Stefano Cavagnetto. 2023. Do not mention Russia: A theoretical framework for bank penalties due to economic sanction violations and policy implications. Banks and Bank Systems 18: 161–76. [Google Scholar] [CrossRef]
- Claessens, Stijn. 2019. Fragmentation in Global Financial Markets: Good or Bad for Financial Stability? BIS Working Paper No. 815. Available online: https://ssrn.com/abstract=3463898 (accessed on 1 May 2020).
- Diamond, Douglas W. 2007. Banks and Liquidity Creation: A Simple Exposition of the Diamond-Dybvig Model. Economic Quarterly 93: 189–200. Available online: http://www.richmondfed.org/publications/research/economic_quarterly/2007/spring/diamond (accessed on 2 January 2020).
- Diamond, Douglas W., and Philip H. Dybvig. 1983. Bank Runs, Deposit Insurance and Liquidity. Journal of Political Economy 91: 401–19. [Google Scholar] [CrossRef]
- Dyer, James S., and Rakesh K. Sarini. 1982. Relative Risk Aversion. Management Science 28: 875–86. [Google Scholar] [CrossRef]
- Ellsberg, Daniel. 1961. Risk, Ambiguity and the Savage Axioms. Quarterly Journal of Economics 75: 643–69. [Google Scholar] [CrossRef]
- European Central Bank. 2022. ECB Report on Banks’ ICAAP Practices. Available online: https://www.bankingsupervision.europa.eu/ecb/pub/pdf/ssm.reportbanksicaappractices202007~fc93bf05d9.en.pdf (accessed on 3 May 2023).
- FDIC. 2022. Failed Bank List. Available online: https://www.fdic.gov/resources/resolutions/bank-failures/failed-bank-list/ (accessed on 1 January 2023).
- Felton, Andrew, and Carmen Reinhart. 2011. The First Global Financial Crisis of the 21st Century Part II: June–December 2008. London: Centre for Economic Policy Research. [Google Scholar]
- Garoupa, Nuno. 1997. The Economics of Organized Crime and Optimal Law Enforcement. Economics Working Papers. Barcelona: Department of Economics and Business, Universitat Pompeu Fabra. [Google Scholar]
- Garoupa, Nuno. 2001. Optimal Magnitude and Probability of Fines. European Economic Review 45: 1765–71. [Google Scholar] [CrossRef]
- Glimcher, Paul, and Agnieszka Tymula. 2023. Expected subjective value theory (ESVT): A representation of decision under risk and certainty. Journal of Economic Behavior & Organization 207: 110–28. [Google Scholar]
- Harackiewicz, Judith, and Michael Asher. 2023. The utility value of a broad, comprehensive theory of motivation. Motivation Science 9: 13–14. [Google Scholar] [CrossRef]
- Hauser, John R., and Glen L. Urban. 1979. Assessment of Attribute Importances and Consumer Utility Functions: Von Neumann-Morgenstern Theory Applied to Consumer Behavior. Journal of Consumer Research 5: 251–62. Available online: http://www.jstor.org/stable/2488678 (accessed on 10 March 2020). [CrossRef]
- Iheanyi, Ihenetu H., and Iwo Sotonye. 2017. Assessing the Performance of Nigeria’s Bank through Camel Model. Journal of Accounting and Financial Management 3: 14–22. [Google Scholar]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 263–91. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 1992. Advances in Prospect Theory: Cumulative Representation of Uncertainty. Journal of Risk and Uncertainty 5: 297–323. [Google Scholar]
- Koçaslan, Gelengul. 2019. Rational Economic Decision Making: The Relevance Among the Axioms of The Theory of Expected Utility. Gaziantep University Journal of Social Sciences 18: 535–48. [Google Scholar] [CrossRef][Green Version]
- Miranda, Enrique, and Marco Zaffalon. 2023. Nonlinear desirability theory. International Journal of Approximate Reasoning 154: 176–99. [Google Scholar] [CrossRef]
- Moscati, Ivan. 2021. History of Utility Theory. London: Routledge, pp. 23–36. [Google Scholar]
- Office of the Comptroller of the Currency. 2018. OCC: About the OCC. Available online: https://www.occ.treas.gov/about/what-we-do/mission/index-about.html (accessed on 2 April 2020).
- Pachur, Thorsten, and Veronika Zilker. 2023. Psychological Theories of Decision Making Under Risk. In The Cambridge Handbook of Behavioral Data Science. Cambridge: Cambridge University Press. [Google Scholar]
- Peterson, Joshua C., David D. Bourgin, Mayank Agrawal, Daniel Reichman, and Thomas L. Griffiths. 2021. Using large-scale experiments and machine learning to discover theories of human decision-making. Science 372: 1209–14. [Google Scholar] [CrossRef] [PubMed]
- Savage, Leonard J. 1954. The Foundations of Statistics. New York: Wiley. [Google Scholar]
- Shapiro, Carl, and Joseph E. Stiglitz. 1984. Equilibrium unemployment as a worker discipline device. The American Economic Review 74: 433–44. [Google Scholar]
- Shi, Gonglong, and Qian Wang. 2019. The Application of Utility Theory in the Decision-Making of Marketing Risk Management. In Advances in Economics, Business and Management Research. Amsterdam: Atlantis Press, pp. 302–9. [Google Scholar] [CrossRef]
- Tomiyama, Tetsuo, Peihua Gu, Yan Jin, Diederick Lutters, Charles Kind, and Fumihiko Kimura. 2009. Design methodologies: Industrial and educational applications. CIRP Annals 58: 543–65. [Google Scholar] [CrossRef]
- Ulster Bank Ireland Limited. 2010. Ulster Bank Ireland Limited Report of Directors and Financial Statements 31 December 2010. Available online: https://investors.natwestgroup.com/~/media/Files/R/RBS-IR-V2/annual-reports/ubil-annual-report-may2011.pdf (accessed on 1 May 2020).
- Von Neumann, John, and Oskar Morgenstern. 1944. Theory of Games and Economic Behavior. Princeton: Princeton University Press. [Google Scholar]
- Winch, Graham, Maude Brunet, and Dongping Cao, eds. 2023. Research Handbook on Complex Project Organizing. Cheltenham: Edward Elgar Publishing, pp. 18–24. [Google Scholar]
- Yokoyama, Taku, and Taiki Takahashi. 2013. Mathematical Neurolaw of Crime and Punishment: The q-Exponential Punishment Function. Applied Mathematics 4: 37368. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).