Abstract
This study utilized both single-regime GARCH and double-regime GARCH models to investigate oil price volatility, Spanish macroeconomic factors, and stock prices during major crises such as geopolitical conflicts, the global financial crisis (GFC), and COVID-19, covering the period from Q2-1995 to Q4-2023. Additionally, the impact of crude oil price volatility on these factors was examined. The empirical results confirmed the presence of the leverage effect and identified multiple volatility switches associated with remarkable events like the GFC, the European debt crisis, the COVID-19 pandemic, and the Russian war. ARDL model analysis revealed a statistically significant positive relationship between oil prices and both unemployment and inflation rates in the long term, while other factors showed a negative correlation.
Keywords:
GARCH-type models; MS-GARCH models; macroeconomic factors; oil price fluctuation; ADRL model JEL Classification:
D53; E31; E32; G15; C32
1. Introduction
In the contemporary global economy, oil plays a fundamental role as a primary energy source. Despite the notable rise in alternative and renewable sources such as wind, water, nuclear, and solar energy, oil is predominant in the worldwide energy landscape. According to the International Energy Agency (), oil has remained the most essential form of energy consumption from the mid-20th century to now. Given the significant role oil plays in the global economy, its price level holds considerable importance as a benchmark for all countries. In theory, low global oil prices prove advantageous for oil-importing nations: lower oil prices lead to reduced production costs, increased consumer activity, and accelerated economic growth (; ; ; ). Conversely, high global oil prices benefit oil-exporting countries; elevated oil prices result in increased export income, greater investments in infrastructure, and improved welfare for the populations of these countries (; ; ; ).
The dynamics of oil prices have witnessed substantial transformations over the years. While the pricing mechanism in the oil market used to be oligopolistic for an extended period, since 1986, crude oil prices have been determined by a stock exchange market. In this market, oil prices undergo daily fluctuations and are shaped by a diverse array of geopolitical and natural crises, weather, transportation, and other factors. Minor price fluctuations may not exert a significant impact on the economies of oil-exporting countries, but abrupt shifts in global oil prices have the potential to destabilize national economies. To analyze how alterations in oil prices affect the economy of Spain, it is fundamental to recognize that this country is evolving within distinct economic circumstances.
In today’s interconnected world economy, numerous factors exert an influence on the worldwide prices of energy resources, particularly oil. These include local and global economic crises, the economic growth rates of major countries, revolutionary shifts in oil production technology, and the substantial impact on global prices stemming from decisions made by IEA and OPEC. Furthermore, embargoes, military events, geopolitical events, and other related factors play a significant role in shaping world prices. Given these circumstances, it is impossible to predict global oil prices solely based on statistical data, as the fluctuations and sudden surges in the energy market are mostly influenced by qualitative factors. Hence, in a dynamic environment where indicators frequently and sometimes unexpectedly shift, preparedness for change is crucial, along with understanding the potential effects on national economies. This underscores the significance and relevance of the study. The focus of this study is on the economy of Spain, examining key macroeconomic indicators and the repercussions of global crude oil price fluctuations.
Striving for precision in assessing macroeconomic variable uncertainties, including the crude oil price and stock price for Spain, our approach involves the careful consideration of the Markov Switching Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model, commonly referred to as the MS-GARCH model, and its variant, MS-GARCH. This model is employed to estimate regime-switching conditional volatility, serving as a proxy for macroeconomic variables uncertainty. The choice of the MS-GARCH model is deliberate, driven by a valid concern that macroeconomic time series may exhibit structural breaks. It is well established in the literature that estimates from GARCH-type models can be biased when structural breaks in volatility dynamics are present (; ; ; ).
From 1995 to 2023, Spain experienced a tumultuous economic journey with periods of stability and crises. This included major events such as the GFC in 2007–2008, the Eurozone debt crisis in 2009–2010, the COVID-19 pandemic in 2020–2021, and geopolitical conflicts like the Russian war in 2022–2023. These events had a lasting impact on Spain’s economy, leading to fluctuations in financial markets, disruptions in global trade, and overall economic uncertainty. Remarkably, previous research has not extensively examined the specific temporal dynamics between crude oil prices and the macroeconomy factors during this period. Therefore, the aim of this study is to bridge this gap by investigating the effects of crude oil price shocks on various macroeconomic factors in Spain.
The novelty and contribution of the paper studying the impact of oil price volatility on Spain’s macroeconomic variables using the MS-GARCH model from 1995 to 2023 lie in several key aspects: first, the methodological innovation; introducing the MRS-GARCH model to analyze the relationship between oil price volatility and Spain’s macroeconomic variables represents a methodological innovation. This model allows for a more nuanced understanding of how changes in oil prices affect various economic indicators, considering the dynamic nature of volatility. Second, the temporal scope that covers the period from 1995 to 2023 provides a comprehensive analysis of how oil price volatility has influenced Spain’s economy over more than two decades. This extensive temporal scope allows for the identification of long-term trends, cyclical patterns, and potential structural shifts in the relationship between oil prices and macroeconomic variables. Third, a regional context that focuses specifically on Spain adds value by examining the impact of oil price volatility within a distinct economic and geopolitical context. This approach enables researchers to uncover Spain-specific dynamics that may not be captured in broader, global analyses. Four, there are policy implications; by elucidating the effects of oil price volatility on various macroeconomic variables in Spain, the paper offers valuable insights for policymakers. Understanding these dynamics can inform the development of more effective economic policies aimed at mitigating the adverse effects of oil price fluctuations and promoting stability and resilience in the face of external shocks. Finally, there is a contribution to the academic literature; the paper contributes to the academic literature by advancing our understanding of the complex relationship between oil prices and macroeconomic variables, particularly within the context of Spain. By employing the MRS-GARCH model and providing empirical evidence from a considerable timespan, the study enriches the theoretical framework and empirical basis for future research in this area. Overall, the paper’s novelty and contribution lie in its methodological innovation, extensive temporal scope, focus on the regional context of Spain, implications for policy formulation, and advancement of academic knowledge in the fields of oil price volatility and macroeconomics.
The results uncovered notable and consistent volatility persistence in macroeconomic variables across both regimes. Both single-regime GJR-GARCH and double-regime MS-GJR-GARCH models confirmed the presence of the leverage effect. MS-GARCH-type models, especially, allowed for the identification of multiple volatility switches, notably associated with events like the GFC, the European debt crisis, the COVID-19 pandemic, and the Russian war. Notably intriguing results emerged for the unemployment rate and inflation rate, where a pronounced leverage effect suggested distinct specifications of volatility regimes, as indicated by the double-regime MS-GJR-GARCH model. Consequently, the influence of crude oil price fluctuations on these macroeconomic factor’s uncertainty measures was assessed using the ARDL model. The findings indicate a statistically significant positive relationship between the crude oil price and the unemployment rate, as well as the inflation rate, in the long term, while the remaining factors exhibit a negative correlation.
The rest of the paper is structured as follows: Section 2 delves into a comprehensive literature review of the Spanish economy. Section 3 is dedicated to presenting the MS-GARCH method. Section 4 provides details on the data sources and empirical results. Finally, Section 5 outlines the main conclusions derived from the study.
2. Literature Review
The literature review is divided into two main sections. The first section will concentrate on examining the impact of crude oil price changes on macroeconomic variables, while the second section will focus on exploring the applications of GARCH models.
2.1. The Relationship between Crude Oil Price Changes and Macroeconomic Variables
Previous studies on the relationship between crude oil prices and macroeconomic activity have primarily investigated two distinct facets: the effects of crude oil price shocks and volatility on the macroeconomy. These two approaches vary in their methods of integrating crude oil prices into their models.
The first approach considers crude oil prices at their current levels, whereas the second approach utilizes various volatility measures to grasp the uncertainty surrounding crude oil prices. Considering two consecutive crude oil shocks experienced during the early and late 1980s, numerous studies have investigated the effects of these shocks on macroeconomic activities. This extensive array of studies was pioneered by () and further expanded upon by (), (), (), (), (), (, ), (), (), (), (), (), (), (), and, more recently, by (), (), (), and several authors yet to be named.
Within the extensive literature concerning the relationship between commodity prices and the economy, works such as those by () and () suggest that, for certain economies, this influence of crude oil prices on macroeconomic activities is asymmetric. Specifically, the negative effect of increases in crude oil prices outweighs the positive impact of decreases in crude oil prices.
Unlike the above studies that examine the effects of crude oil price shocks, investigations into the influence of crude oil price volatility on macroeconomies are scarce and trace their origins to the rise in crude oil price volatility starting from the 1980s. () argued that fluctuations in crude oil prices exert a significant influence on the economic activities of the United States, particularly affecting unemployment and GNP, but notably, this impact is more pronounced during periods of price stability rather than high volatility or unpredictability. () analyzed data from the United States spanning from January 1970 to December 1990 to investigate the significance of the relationship between crude oil price volatility and macroeconomic performance.
The author utilizes the simple standard deviation to measure crude oil price volatility, and it suggests that uncertainty channels and sectoral shocks provide a partial explanation for the asymmetry observed between output and crude oil prices. Utilizing the measure volatility calculated from daily crude and WTI oil futures prices traded on the New York Mercantile Exchange, () ascertain that during the period from 1984 to 2005, crude and WTI oil price volatility significantly impacted several crucial economic indicators in the United States, including the unemployment rate, employment rate, fixed investment, and consumption. The results indicate that fluctuations in crude and WTI oil prices have a greater significance compared to uncertainties surrounding future prices. It is noteworthy that all the studies mentioned above, which aim to identify the influence of crude oil price volatility, focus on the United States economy. A recent paper exploring the effects of crude oil price volatility within the context of Spain is authored by ().
() examines the influence of crude oil price volatility on macroeconomic indicators in Spain, employing an autoregressive distributed lag (NARDL) model. The variables considered include crude oil price volatility, GDP growth, capita GDP, inflation, and the budget deficit of Spain, spanning from 1945 and 2018. The impacts of such fluctuations on per capita GDP are enduring, with long-term decreases in crude oil prices having a greater effect on per capita GDP than increases in crude oil prices. Despite these asymmetric effects, the energy policy agenda should tackle issues related not only to tax management but also to market competition and efficient wage mechanisms. The findings suggest that changes in oil prices are less significant than the uncertainty about future prices.
There are fewer references to studies on the relationship between crude oil prices and the macroeconomy for Spain, the focus of our analysis. () examined the influence of crude oil price shocks on industrial production and inflation across several European countries from 1960 to 1999. The authors observed short-term and asymmetric effects on production growth rates for Spain, although such effects were not apparent in the long term. Recently, () conducted a study examining the connection between crude oil price volatility and economic growth across OECD countries over an extended period from 1870 to 2013 using a panel cointegration approach for its analysis. For Spain specifically, the authors found a consistently negative and significant elasticity throughout the entire period. () investigated the connections between crude oil price shocks and stock price returns among European countries that either export or import crude oil. The study employed an A vector autoregression (VAR) model to estimate the significance of stock market responses to fluctuations in crude oil prices during the COVID pandemic period from 2019 to 2021. A Granger causality test is utilized to ascertain both the direction and strength of the relationship between crude oil price shocks and indices within the European stock markets. The authors argued that the results of this study remain consistent regardless of the presence of the COVID-19 pandemic episode, demonstrating a clear interaction between the crude oil price shocks and European stock markets. The findings indicate that during stable periods—both prior to the COVID-19 outbreak crisis and following the introduction of vaccinations—there is no correlation between stock price returns and crude oil prices. However, during periods of high volatility, the causality from stock price returns to crude oil prices increases, affecting both oil-importing and oil-exporting countries equally.
Finally, () investigated the crucial relationship between crude oil price fluctuations and stock price returns, considering oil-importing and oil-exporting countries separately. The authors provide evidence utilizing Granger causality, error variance decomposition, and impulse response analysis through panel vector autoregression. The findings from the panel Granger causality analysis indicated that following the crude oil price crash during the COVID-19 pandemic, the correlation between stock price and crude oil price changes increased. This trend was also corroborated by the findings from both forecast error variance decomposition and impulse response graphs. During the period characterized by the sudden onset of the COVID-19 pandemic, the causality from crude oil to stock price returns increased. While both oil-importing and oil-exporting countries experienced similar effects, crude oil price fluctuations had a greater impact on oil-exporting countries.
2.2. Applications of GARCH Models
The conclusive importance of crude oil prices regarding macroeconomy factors is evident. Serving as a critical upstream product in the supply chain, the abrupt and substantial volatility of crude oil often triggers shocks in productive capacity, leading to economic fluctuations. Moreover, oil-exporting and oil-importing countries experience economic instability due to changes in purchasing power. Furthermore, crude oil, being a unique commodity with political and financial characteristics, is influenced by non-fundamental factors such as the US dollar exchange rate, financial crisis, geopolitics, global health crisis, and speculation. Therefore, modeling and forecasting volatility in the oil market represent vital and intricate challenges within both financial and commodity markets (; ; ; ; ; ; ; ; ; ; ; ).
Forecasts of oil price volatilities commonly rely on time-varying high-frequency data, where samples with high volatility frequently exhibit clustering features. Therefore, the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model, introduced by (), is widely employed for predicting oil market volatility. This model is favored for its effectiveness in capturing the time-varying characteristics of high-frequency data, as demonstrated by studies such as (), (), (), (), (), (), and (). Recent contributions to this field, including those of () and (), further underscore the ongoing relevance and applicability of the GACH model in forecasting oil market volatility.
Nevertheless, the conventional GARCH model inherently possesses symmetry, and when dealing with skewed time series, forecast outcomes using this standard model may be biased (; ). In response to this issue, various nonlinear and asymmetric GARCH models have been introduced for forecasting macroeconomic variables volatility. Examples include the EGARCH model proposed by (), TGARCH suggested by (), and the GJR-GARCH model developed by (). It is important to highlight that the GARCH-type models mentioned primarily concentrate on a single regime of macroeconomic factors, stock prices, and oil price changes. However, experts argue that structural breaks in the variance process of single-regime GARCH-type models frequently result in high volatility persistence. This is because these models typically fit both in-sample and out-of-sample time series data with the same pattern, neglecting potential structural changes (; ; ; ; ).
To address this issue, () and () incorporate the regime-switching process () into the GARCH model to account for potential structural breaks. Specifically, the Markov Switching-based GARCH (MS-GJRGARCH) model allows the regimes in the Markov chain to exhibit different GARCH behaviors, implying distinct volatility structures. This extension of the GARCH model to dynamic forms aims to achieve improved estimation and forecasting performance (; ; ; ; ; ; ; ; ). However, in the context of forecasting macroeconomic factors, oil price volatility, and stock price volatility using GARCH-type models, there are still intriguing challenges to investigate. For example, while Markov Switching models are adept at capturing potential changes in state transitions and non-linearities in macroeconomic factor volatility, it remains uncertain whether the MS-GARCH-type model consistently outperforms single-regime GARCH-type models in forecasting macroeconomic factors (including the oil prices and stock prices) volatility across all samples.
In the meantime, considering that the precision of forecasts by GARCH-type models is frequently influenced by the data frequency and time horizon employed for volatility measurement (; ; ; ), it becomes intriguing to examine how the outcomes vary when calculating macroeconomic variables volatility (including oil prices and stock prices) at distinct data frequencies—specifically, quarterly. Furthermore, within the empirical literature comparing the forecast performance of linear and nonlinear GARCH-type models, there is no unanimous consensus.
3. Methodology
Analyzing the individual returns of the time series data allows for the determination of the continuous compounded returns. These returns are represented as , with the subscript denoting time.
where x is a time series variable.
3.1. The GARCH(1,1) Models
As per () and (), the conventional linear GARCH (1,1) model for macroeconomic factors, encompassing crude oil price and stock price returns, can be expressed as follows:
where the coefficients and must be greater than zero to guarantee a positive conditional variance and represents the persistence of shocks to volatility. The unconditional volatility for GARCH, represented by , can be computed as follows:
Sollowing the () and () studies, we employ the student’s . As suggested by (), (), and (), the student’s is preferred due to its thicker tails, allowing for a higher probability of encountering outliers or extreme values. This characteristic is advantageous when working with real-economic and financial data, which frequently deviates from the idealized bell-shaped curve of the normal distribution.
To account for the asymmetric leverage effect in macroeconomic factors volatility, including the crude oil price and stock price, () introduced the non-linear GJR-GARCH model. The variance equation for this model is specified as follows:
The indicator function, indicated as , is utilized to assign values 1 if and 0 if , and represents the persistence of shocks to volatility. The unconditional volatility for the GJR-GARCH model can be computed as follows:
3.2. MS-GARCH Model
The primary distinction between the multi-regime MS-GARCH-type models and the conventional single-regime GARCH-type models lies in the ability of the parameters in the MS-GARCH model to transition between different regimes based on the Markov process. To elaborate, the regime variable has the potential to switch in accordance with a Markov process, and the probability of transitioning from regime at time to regime at time is denoted as . In the context of this study, it is assumed, as per (), (), and (), that the innovation of MS-GARCH adheres to a student’s depending on the degree of freedom . The conditional variance, the conditional mean following the GARCH process, and the expectation of squared innovations are specified as the equations below:
The conditional expectation is written as follows:
In the MS-GARCH-type models, the symbols represent the two regimes.
where the term denotes the information set at time .
The anticipated duration in each regime (denoted as for ), signifying the average length of staying in a specific regime, can be computed as outlined in previous studies ().
The stable probabilities (also known as the unconditional probabilities), denoted as , of being in a particular regime can be determined using the following formula:
3.3. ARDL Model
After quantifying the uncertainty in macroeconomic factors and the stock prices, we proceed to evaluate the impact of oil price fluctuations on the uncertainty of macroeconomic factors and stock prices through the ARDL model. The specification of the ARDL model is outlined as follows:
where, represents the time series data of uncertainty and denotes the crude oil price return. The term stands for the vector of other parameters, including both the time term and intercept trends.
and
where represents a lag operator. From Equations (11) and (12), the long-term effect in the ARDL model is expressed as follows:
The short-term effect in the ARDL model is computed using the following equation:
where denotes the short-term effect in the ARDL model.
is calculated using the following equation:
SIC (Schwarz Information Criterion) is employed to choose the optimal lags for the ARDL model relationship involving macroeconomic factors, stock price uncertainty, and oil price fluctuation.
3.4. The Evaluation Criteria
In this stage, the optimal model is selected from the chosen models in each variable (conventional linear GARCH and MS-GARCH) based on two methods, namely, information criteria and forecast accuracy measures. The criteria include the Schwarz Information Criterion (SIC) and Akaike Information Criterion (AIC), providing a relative measure of information loss. Additionally, two forecast accuracy measures, the root mean squared error (RMSE) and mean absolute percentage error (MAPE), are employed for evaluation.
where indicates forecasted values and indicates actual values.
4. Data Description
The dataset being examined consists of quarterly data on four major macroeconomic factors for Spain: the economic growth (GDPS), inflation rate (INFS), unemployment rate (UES), and interest rate (IRS). Additionally, two more factors, namely, stock prices (IBEX) and crude oil prices (COP), are included in the dataset. All data were obtained from the Federal Reserve Bank of St. Louis (FRED), except for the stock market (IBEX 35), which was obtained from Yahoo Finance. For commodity indicators, the data reflect a combination of both spot prices and futures prices. The IBEX 35 data reflect a total return (including dividends).
Incorporating a combination of both spot prices and futures prices for commodity indicators can provide a more comprehensive view of market dynamics, capturing both current market conditions and future price expectations. This approach allows for a deeper analysis of commodity markets, including assessments of supply–demand dynamics, speculation, and hedging activities. By considering both spot and futures prices, the analysis can better reflect the complexities and uncertainties inherent in commodity markets, potentially leading to more robust and nuanced results. Regarding the IBEX 35 data reflecting a total return (including dividends), this choice provides a more accurate representation of investors’ actual returns from holding the index, as it accounts for dividends distributed by the component stocks. Total return indices offer a more complete assessment of investment performance compared to price indices, which only reflect changes in stock prices.
The data cover the period from Q2-1995 to Q4-2023, resulting in 112 observations. Analyzing this period of over 28 years provides comprehensive insights into the examined time series’ behavior during periods of stability and various crises and turmoil. These include events such as the Dot-com Bubble Burst in 2000, the Iraq war and oil price shock in 2003, Spain’s accession to the EU in 2004, the GFC in 2007–2008, the European debt crisis in 2011, the shale oil boom and price slump in 2014, the Russia–Saudi Arabia oil price war in 2020, the COVID-19 pandemic in 2020–2021, and the Russian war in 2022–2023.
5. Empirical Results
Utilizing the models outlined in Section 3, estimation is performed for two single-regime GARCH-type models: the linear GARCH model and the non-linear GJR-GARCH model. Concurrently, estimation is also carried out for the two double-regime GARCH-type models: the MS-GARCH model and MS-GJR-GARCH model. The results are presented in Table 1, Table 2 and Table 3, revealing various findings.

Table 1.
Estimation results of GARCH and GJR-GARCH models.

Table 2.
Estimation results of the MS-GARCH model.

Table 3.
Estimation results of the MS-GJR-GARCH model.
Table 1 shows that all estimated parameters were statistically significant, except for the parameter in the linear GARCH model for the stock price and inflation rate returns, and the parameter was not statistically significant for crude oil price returns, interest rate returns, and inflation rate returns. The estimates of the parameter in the non-linear GJR-GARCH model for all macroeconomic factors, crude oil price, and the stock price returns were positive, indicating the presence of an asymmetric effect of past returns on conditional volatility. The economic growth (GDP) exhibited the strongest volatility reaction to past negative returns, followed by the crude oil prices, while the inflation rate showed a significantly weaker leverage effect. Regarding log-likelihood values, the non-linear GJR-GARCH model demonstrated higher values than the GARCH model for all analyzed time series returns. The “covariance stationarity” assumption for both the linear GARCH and non-linear GJR-GARCH models was met for all-time series returns. Additionally, these totals suggested a high volatility persistence, ranging between 0.76 and 0.99 for the non-linear GJR-GARCH model and between the slightly lower values of 0.74 and 0.98 for the linear GARCH model. The crude oil price and interest rate returns, when compared to other factors under consideration, exhibited the lowest estimate for the degree of freedom , suggesting a significantly fat-tailed distribution. The choice of the student’s was thus validated as appropriate, given the small degrees-of-freedom parameters , suggesting a significant departure from normality (; ; ; ; ; ). The computed unconditional volatilities closely aligned with their sample counterparts in Table 1. Specifically, for both the linear GARCH and non-linear GJR-GARCH models, the highest values of unconditional volatilities were observed for the inflation rate returns, while lower values were noted for the economic growth (GDP) returns.
The results of the estimations for the double-regime MS-GARCH and MS-GJR-GARCH models were formulated assuming student’s innovations and double regimes, regime 1 signifying low volatility and regime 2 representing high volatility, as shown in Table 2. The degrees-of-freedom parameters for the student’s t were consistently applied across both regimes, following the approach of (). The estimated values, ranging from 4.3 to 19.5, affirm that the modeled distributions exhibit finite variance (given ) and possess tails that are heavier than those of a normal distribution.
In regime 1, all estimated parameters revealed statistical significance in both models. However, in regime 2, this significance was observed in all parameters except for for the interest rate and stock price returns in the MS-GJR-GARCH specification. The asymmetry parameters varied across individual regimes. Specifically, in both regimes, the crude oil price and inflation rate returns demonstrated a more pronounced impact of negative news in the case of MS-GJR-GARCH. Conversely, during the turbulent regime 1 and regime 2, both the unemployment rate and interest rate returns exhibited a significantly stronger reaction to adverse news in the MS-GARCH model.
The estimated parameters affirmed that the volatility process displayed a heterogeneous nature between the two regimes. The within-regime volatility persistence in the double- regime MS-GARCH-type models is equal to that of the single-regime GARCH-type models. The findings indicated that the within-regime volatility persistence differed across both regimes. In regime 1 (low volatility), there was a notably higher within-regime volatility persistence compared to that of regime 2 (high volatility) for both model specifications. However, for both the crude oil price and inflation rate returns, the immediate impact of a shock on conditional volatility was greater in the high-volatility regime than in regime 1. This suggests that a significant source of volatility clustering in regime 2 could be regime persistence rather than the persistence of a particular shock (; ).
The second factor contributing to the enduring nature of volatility is the persistence of regimes, as indicated by transition probabilities and. These probabilities represent the likelihood of remaining in regime 1 and regime 2, respectively. Particularly, the probabilities associated with staying in the low-volatility regime for all-time series returns in double-regime MS-GARCH-type models ranged from 0.89 to 0.98 and were found to be statistically significant. In contrast, the probabilities of remaining in the high-volatility regime were lower and, in certain instances, even statistically insignificant. Consequently, regime 1 demonstrated a greater persistence compared to regime 2, with the exception being the unemployment rate and interest rate returns in the MS-GJR GARCH model.
Concerning the expected durations and stability probabilities outlined in Equations (11) and (12), respectively, in Section 3, the stable probabilities for being in the high volatility (regime 2) and the expected durations of regime 2 (high volatility) were found to be higher for the crude oil price, economic growth (GDP), unemployment rate, and stock price returns when compared to the corresponding values for the low-volatility regime 1.
For the inflation rate and the interest rate returns, both the MS-GARCH and MS-GJR-GARCH models produced divergent outcomes. According to the MS-GARCH model, the stable probabilities distinctly revealed a significantly higher-volatility regime 2. Also, the expected durations of regime 2 were higher than the values associated with the lower-volatility regime 1. However, the results of the MS-GJR-GARCH estimation, considering the substantial leverage effect, demonstrated an increased stable probability for the low-volatility regime 1. Furthermore, the expected durations of regime 1 were found to be higher compared to the values associated with the high-volatility regime 2. The log-likelihood values provide an initial perspective for evaluating the significance of regime persistence in volatility (). Specifically, for the macroeconomics factors, stock price and crude oil price, the log-likelihoods associated with double-regime MS-GARCH-type models (refer to Table 2 and Table 3) were higher than their single-regime GARCH-type model counterparts (refer to Table 1). The comparison of log-likelihoods indicates that accounting for regimes can enhance the ability to capture volatility persistence.
The smoothed probabilities for the low-volatility regime 2 from the MS-GARCH and MS-GJR-GARCH models are represented in Figure 1. These probabilities offer valuable insights into the behavior of specific time series returns. The results demonstrate unique characteristics among the variables that were analyzed. When examining the inflation rate, interest rate, and unemployment rate returns, both double-regime models consistently yielded the same results. This suggests that the market experienced stable periods with occasional abrupt shifts to high-volatility regimes. Notably, these transitions coincided with well-known periods of turmoil, such as the GFC in 2007–2008 and the emergence of the COVID-19 pandemic in 2020–2021 for the unemployment rate returns. However, for interest rate returns, shifts to the high-volatility regime were observed during the COVID-19 pandemic and the Russian war in 2022. This detailed analysis provides a deeper understanding of market dynamics during remarkable events, highlighting the double-regime MS-GARCH-type models’ ability to capture subtle variations in volatility regimes. Moreover, when analyzing the returns of crude oil prices, economic growth (GDP), and stock prices from 1995 to 2023, both double-regime models consistently produced similar results.
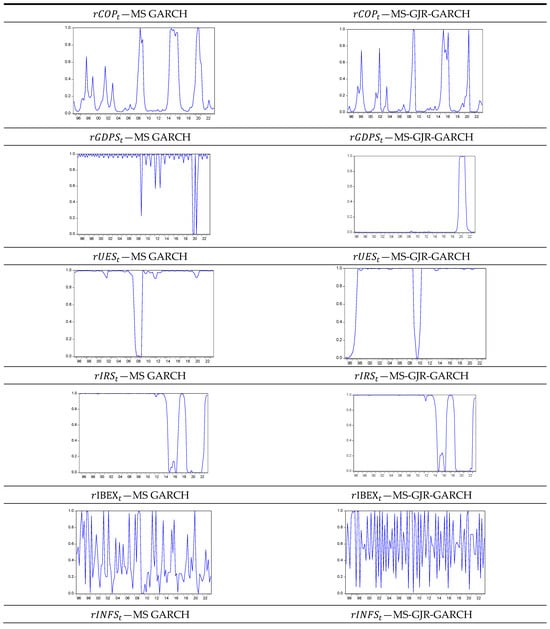

Figure 1.
Smoothed probabilities for the high volatility (regime 2).
These results suggest that the market experienced periods of calm, with occasional sudden shifts to high volatility. These shifts coincided with well-known periods of turmoil, including various crises and global events. The identified turmoil periods, characterized by changes in volatility, align with significant global influences. The analysis considers the impact of events such as the GFC in 2007–2008, speculative bubbles from 2000 to 2004, the European debt crisis in the summer of 2011, the onset of the COVID-19 pandemic in 2020–2021, and the Russian war in 2022, which led to economic sanctions on Russia. Each of these events had a significant impact on international financial markets, causing fluctuations and uncertainties that also affected the crude oil market and the Spanish stock market.
By conducting double-regime MS-GARCH-type models, which distinguish between periods of increased volatility and tranquility, we gain valuable insights into how the market reacts to various GFCs, health global crises, and geopolitical conflicts. This in-depth analysis not only helps us comprehend the market’s behavior but also enables us to identify and assess crucial factors that drive market trends during specific periods. Consequently, this comprehensive understanding of Spain’s financial markets enhances our knowledge of how significant international and domestic events have influenced market conditions over the years.
Another surprising finding concerning interest rate returns is the significant volatility observed during two distinct periods: the Eurozone sovereign debt crisis in 2009–2010 and the economic recovery of Spain spanning from 2014 to 2015. During the Eurozone sovereign debt crisis, Spain, like other Eurozone countries, faced severe economic challenges. The crisis was marked by concerns over the sustainability of sovereign debt, leading to increased market uncertainty and financial instability. The impact on interest rates can be attributed to market reactions, government debt dynamics, and efforts to address fiscal imbalances. In the subsequent crisis from 2014 to 2015, labeled as the economic recovery Spain crisis, it becomes crucial to delve into specific economic events and policy measures undertaken during this period. Identifying the factors contributing to interest rate volatilities during this period could involve examining economic recovery strategies, external influences, or changes in monetary policy that might have influenced market sentiments and interest rate dynamics.
Table 4 shows the dynamics of conditional volatilities in individual markets for the next four quarters, with a particular emphasis on the period coinciding with the COVID-19 pandemic, the Russian war, and the imposition of restrictions on Russia by the United States and European countries. The estimated double-regime GARCH-type models were utilized to calculate the five-step-ahead conditional volatilities. Notably, the forecasted values from both model specifications indicated that the crude oil price, stock prices, and economic growth (GDP) demonstrated the highest conditional volatility, followed by inflation rates, unemployment rate, and interest rates.

Table 4.
Five-step-ahead conditional volatilities of double-regime MS-GARCH models.
Increased volatility in inflation rate forecasts may signal heightened uncertainty about the future purchasing power of consumers (price levels) in Spain. This could result from several factors, including supply chain disruptions, shifts in consumer behavior, or monetary policy adjustments. Higher volatility may indicate potential risks of inflationary pressures or deflationary trends, impacting consumers’ purchasing power and businesses’ pricing strategies.
Elevated volatility in unemployment rate forecasts could indicate greater uncertainty in labor market conditions. This uncertainty may stem from factors such as the changing demand for labor, technological disruptions, or policy interventions. Higher volatility may reflect challenges in predicting future job market trends, making it difficult for policymakers and businesses to plan effectively.
Higher volatility in forecasted interest rates suggests increased uncertainty regarding future monetary policy decisions by the European Central Bank (ECB) or the Bank of Spain. This uncertainty can stem from ambiguous economic signals, fluctuating inflation expectations, or external economic shocks. Elevated interest rate volatility can lead to unpredictable borrowing costs for businesses and consumers, potentially delaying or scaling back capital expenditures due to uncertain financing conditions. For consumers, such volatility can influence saving and spending behaviors, as unpredictable interest rate movements may encourage saving overspending, potentially slowing economic growth. In financial markets, higher volatility in interest rates can destabilize the bond market, leading to higher risk premiums and yield fluctuations, thereby affecting bond prices and returns. Additionally, increased interest rate volatility can impact the exchange rate of the euro against other currencies, as international investors adjust their portfolios based on varying expected returns across different markets. This can lead to heightened exchange rate volatility, further complicating the economic landscape.
This information provides insights into the expected volatility patterns in Spain macroeconomic factors including the oil price and stock markets, underscoring the heightened volatility anticipated during the specified period, as captured by the models.
Table 5 illustrates the optimal model selection for variables displaying the ARCH effect, determined through a comprehensive evaluation of information criteria such as SIC and AIC and forecast accuracy measures. Based on the results of SIC and AIC, the double-regime MS-GARCH-type models emerge as the most suitable choice for all variables under scrutiny. This decision is grounded in the meticulous scrutiny of information criteria and forecast accuracy, with the double-regime MS-GARCH-type models identified as the preferred option for capturing the volatility characteristics of the variables in question. The SIC and AIC values in double-regime MS-GARCH-type models are remarkably lower than those in single-regime GARCH-type models, a trend clearly depicted in Table 5. Across all variables examined, the double-regime MS-GARCH-type models exhibit smaller RMSE and MAPE values compared to their single-regime GARCH-type counterparts. The reduced prediction errors in the chosen double-regime MS-GARCH-type models, as indicated by these evaluation criteria, affirm its efficacy in providing accurate predictions for various variables. This compelling evidence underscores the superior performance of the double-regime MS-GARCH-type models over single-regime GARCH-type models, emphasizing its robustness in capturing the inherent dynamics of the time series returns under investigation.

Table 5.
The optimal model of variables.
Table 6 displays the conclusive ADRL model, encompassing both the short-term and long-term effects of crude oil price fluctuations on the macroeconomic factor’s uncertainty within the optimal model that encompasses single- and double-regimes.

Table 6.
Short-term and long-term effect of the crude oil prices on the macroeconomic factors including stock prices uncertainty.
In the short term, the statistical analysis reveals a notable negative correlation between the crude oil price and stock price, signifying that higher crude oil prices coincide with a downturn in stock prices. This adverse association can be attributed to the heightened operational costs for businesses, potentially leading to diminished profit margins and constraints on consumer spending. Simultaneously, a statistically significant positive correlation is evident between crude oil price fluctuations and inflation rate uncertainty. Increased crude oil price activity contributes to cost-push effects on the inflation rate, resulting in elevated production costs that may be transferred to consumers, thereby intensifying uncertainty regarding the inflation rate.
The findings are consistent with several research studies, including those conducted by (), (), (), (), (), (), (), and (). These studies collectively support the notion of a negative correlation between the crude oil price and stock price, along with a positive correlation between the crude oil price and inflation rate. Moreover, the lack of statistical significance in the correlation between crude oil price fluctuations and other macroeconomic factors under investigation, such as the interest rate, economic growth (GDP), and unemployment rate, is consistent in both regimes. This observation aligns with the findings of previous research studies, such as those conducted by (), (), (), (), and (), which similarly highlighted the absence of a significant relationship between crude oil price fluctuations and these economic metrics in the short-term context. This reinforces the understanding that, within the specified period, the dynamics of the crude oil price may not distinctly impact variables like the interest rate, economic growth (GDP), and unemployment rate. These findings can be interpreted to support two plausible explanations. First, it is conceivable that the European Central Bank (ECB) has implemented adept monetary policies to counteract the adverse impacts of crude oil price shocks. Such policies could involve strategic adjustments to interest rate adjustments or well-timed liquidity injections, aimed at supporting economic growth and mitigating the effects on the unemployment rate. Second, it is possible that Spain has successfully implemented robust energy policies and technologies, thereby reducing their reliance on crude oil as a primary energy source. This strategic move could serve to minimize the economy’s susceptibility to the negative impacts of crude oil price shocks, highlighting the effectiveness of their energy diversification efforts.
Over the long term, every estimated parameter exhibited statistical significance in the correlation between crude oil price fluctuations and the macroeconomic factors uncertainty. Similarly, a significant negative relationship was observed between crude oil price fluctuations and the uncertainties associated with economic growth (GDP), stock prices, and the interest rate in both regimes. The considerable magnitude of these parameters underscores their substantial impact on the economic dynamics in Spain. The negative correlation identified can be ascribed to many factors.
First, an upsurge in the crude oil price has a cascading effect on production across various industries, such as transportation and manufacturing. This surge, in turn, contributes to an increase in price for both services and goods, resulting in a potential reduction in consumer demand and a slowdown in overall economic growth. Additionally, the uncertainty associated with the crude oil price can instill caution in business trading activities, as companies grapple with uncertainty regarding future costs and profitability. This cautious approach by businesses can further impact economic dynamics as companies navigate uncertainties and make strategic decisions amidst fluctuating crude oil price conditions. The second explanation is that the repercussions of soaring crude oil price extend to adversely affect the uncertainty of the stock price. Crude oil plays a pivotal role as an essential input cost for numerous companies, and when prices experience an upward surge, it tends to impede their cash flow and overall profitability. The subsequent decline in earnings, coupled with the inherent uncertainty linked to the crude oil price, can contribute to a reduction in the stock price. This interplay between crude oil price dynamics and broader economic indicators emphasizes the interconnectedness of financial markets and the potential cross-border impact on monetary conditions.
Finally, a surge in the crude oil price tends to contribute to an upswing in the interest rate. The rise in the crude oil price triggers heightened inflationary pressures, prompting the European Central Bank (ECB) in European countries (including Spain) to elevate the interest rate level as a measure to mitigate economic growth. However, this subsequent increase in the interest rate can pose challenges for the respective countries, as it results in a scenario where the cost of borrowing becomes more expensive for both individuals and businesses.
Overall, the negative correlation identified between crude oil price fluctuations and uncertainties related to the stock price, economic growth (GDP), and interest rate indicates that a thriving crude oil price can potentially have adverse effects on Spain’s economy over the long term. These empirical findings are consistent with prior research conducted by researchers such as (), (), (), (), (), (), and (), reinforcing the agreement and further contributing to an expanding body of literature that emphasizes the intricate interplay between the crude oil price and various elements of economic indicators within the context of Spain.
Regarding the realms of the unemployment rate and inflation rate, the empirical findings reveal a robust positive statistical significance at the 5% level concerning the interdependence between crude oil price fluctuations and uncertainty in the unemployment rate. Simultaneously, a notably stronger positive statistical significance is evident at the 1% level for the interdependence between crude oil price fluctuations and uncertainty in the inflation rate.
This finding can be clarified through the consideration of three key factors. First, the significant reliance of Spain on imported crude oil plays a crucial role in its economy. Spain heavily depends on imports of crude oil to meet their energy needs, resulting in any fluctuations in the global crude oil price directly influencing their domestic economies. An increased crude oil price contributes to elevated transportation, consumption, and production costs, thereby exerting inflationary pressures on the economy. The second explanation is that Spain is characterized by a significant presence of energy-intensive industries encompassing the transportation, manufacturing, chemical, and automotive industries. These industries heavily rely on crude oil and petroleum products as essential inputs for their operations. Consequently, any upswing in the crude oil price directly influences the cost dynamics of these industries, potentially leading to job losses and layoffs, thereby contributing to an increase in the unemployment rate. Third, a plausible explanation lies in the fact that Spain stands as one of the world’s premier tourist destinations, with its economy shaped by the tourism industry. An increase in the price of crude oil contributes to heightened transportation costs, encompassing airfares and fuel expenses for tourist vehicles, thereby directly impacting the affordability of travel for both international and domestic tourists. Therefore, a decrease in tourist arrivals carries adverse implications for the hospitality industry, leading to reduced employment opportunities within this industry. The results align with the outcomes of earlier research conducted by (), (), (), (), and ().
6. Conclusions
In this study, the volatilities of macroeconomic factors, the crude oil price, and the stock price in Spain is assessed through the application of two single-regime GARCH-type models, namely, the linear GARCH model and the non-linear GJR-GARCH model, alongside the two double-regime MS-GARCH-type models. Subsequently, their performances are contrasted with those of the single-regime GARCH-type models under Student’s . To conclude, the study delves into estimating the influence of crude oil price fluctuations on macroeconomic factors uncertainty and stock price uncertainty within a regime-switching environment. The study results unequivocally validate that the double-regime MS-GARCH-type models extend the generality of the single-regime GARCH-type models by offering enhanced flexibility in the volatility process. Beyond the specific results associated with each macroeconomic factor, several overarching conclusions can be inferred. The estimated double-regime MS-GARCH-type models effectively identify breakpoints in inflation rate volatilities, notably during the GFC, the European debt crisis, and the COVID-19 pandemic. Meanwhile, interest rate returns exhibited heightened volatilities in two periods, COVID-19 and the Russian war, and unemployment rate returns displayed notable volatility transitions during the GFC and small volatilities during the COVID-19 pandemic period. Analyzing crude oil price returns, economic growth (GDP) returns, and stock price returns in Spain (2000–2023) using double-regime models revealed consistent outcomes. Periods of stability were interrupted by occasional shifts to high volatility, aligning with global upheavals like the 2007–2008 GFC, speculative bubbles, the European debt crisis, the COVID-19 pandemic, the oil price war between OPEC and Russia, and the Russian war, inducing economic sanctions. These events impacted international financial markets, causing fluctuations in both the crude oil and Spanish stock market. Another primary objective of the study is to assess and compare the performance of single-regime GARCH-type models and double-regime MS-GARCH-type models in characterizing and predicting the volatility of the macroeconomic factors, crude oil price, and stock price. Overall, the empirical findings indicate that double-regime MS-GARCH-type models exhibit a significantly superior performance compared to single-regime GARCH-type models when forecasting volatility over quarterly horizons. Additionally, the impact of the crude oil price fluctuations on macroeconomic factors and stock price uncertainties is estimated in a regime-switching environment. Short-term outcomes reveal both negative and positive effects of the crude oil price fluctuations on the stock price and inflation rate, respectively, under both regimes. In the long term, a positive relationship is observed between the crude oil price fluctuations and unemployment rate and inflation rate, while a negative relationship is identified between the crude oil price fluctuations and other the macroeconomic factors such as the economic growth, interest rate, and stock price in both regimes.
The instability of crude oil price fluctuations during financial crises, global health crises, and geopolitical conflicts holds substantial practical implications for policymakers and investors, particularly in oil-import-dependent countries like Spain. The financial crises and geopolitical conflicts, especially in oil-rich regions like the GCC countries, often trigger an increase in oil prices due to concerns about supply disruptions. This surge in oil prices directly impacts industries reliant on oil, such as agriculture, manufacturing, and transportation. Investors may witness increased costs for companies in these sectors, leading to potential decreases in profitability and subsequent decreases in stock prices. Policymakers face the challenge of mitigating these negative effects on the economy. Striking a balance between crude oil price stability and economic growth becomes crucial. In response to higher oil prices, policymakers may implement measures like interest rate adjustments or fuel subsidies to address inflation and support consumers. These policy decisions directly influence stock prices as investors react to their potential implications for businesses in various industries. Macroeconomic factors in Spain are significantly affected by high oil prices due to the country’s heavy reliance on oil imports. Increased oil prices result in a higher cost of living as transportation expenses rise, potentially reducing consumer spending and slowing economic growth. Consequently, macroeconomic indicators such as GDP growth rates and inflation may experience negative effects. The impact of oil price fluctuations on Spain’s stock market depends on specific industries. Sectors heavily dependent on oil may witness decreases in stock prices due to increased costs, while companies in renewable energy and alternative fuels may benefit, leading to stock price increases. These nuanced effects contribute to the broader landscape of Spain’s stock market. The practical implications of crude oil price fluctuations during financial crises and geopolitical conflicts reverberate across various aspects of Spain’s economy. From industries reliant on crude oil to macroeconomic indicators and specific sectors within the stock market, these implications underscore the importance of monitoring and understanding these dynamics for informed decision-making by policymakers and investors.
Even more notable are the empirical results regarding the relationships between crude oil price changes and macroeconomic variables in Spain, offering valuable insights for investors, portfolio managers, and policymakers. However, there are potential limitations in the methodology due to the sample size. Nonetheless, this presents an opportunity for future research to expand the dataset and time periods and to apply additional techniques such as Copula transformation to the selected variables.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agnolucci, Paolo. 2009. Volatility in crude oil futures: A comparison of the predictive ability of GARCH and implied volatility models. Energy Economics 31: 316–21. [Google Scholar] [CrossRef]
- Ahsanullah, Mohammad, B. M. Golam Kibria, and Mohammad Shakil. 2014. Student’s t Distribution. In Normal and Student’s t Distributions and Their Applications. Paris: Atlantis Press, pp. 51–62. [Google Scholar] [CrossRef]
- Aktan, Bora, Renata Korsakienė, and Rasa Smaliukiene. 2010. Time-varying volatility modelling of Baltic stock markets. Journal of Business Economics and Management 11: 511–32. [Google Scholar] [CrossRef]
- Aladwani, Jassim. 2023. Wavelet Coherence and Continuous Wavelet Transform—Implementation and Application to the Relationship between Exchange Rate and Oil Price for Importing and Exporting Countries. International Journal of Energy Economics and Policy 13: 531–41. [Google Scholar] [CrossRef]
- Aloui, Chaker, Besma Hkiri, and Larisa Yarovaya. 2015. On the effects of oil price uncertainty on stock returns in major oil-importing countries: Evidence from quantile regression. Journal of Quantitative Economics 13: 95–115. [Google Scholar]
- Álvarez, Luis J., and Alberto Urtasun. 2013. Variation in the cyclical sensitivity of Spanish inflation. In Economic Bulletin. Madrid: Banco de España, July–August. [Google Scholar]
- Ardia, David, Keven Bluteau, Kris Boudt, Leopoldo Catania, and Denis-Alexandre Trottier. 2019. Markov-switching GARCH models in R: The MSGARCH package. Journal of Statistical Software 91: 1–38. [Google Scholar] [CrossRef]
- Babatunde, S. Omotosho. 2019. Oil Price Shocks, Fuel Subsidies and Macroeconomic (In)stability in Nigeria. CBN Journal of Applied Statistics 10: 2. [Google Scholar] [CrossRef] [PubMed]
- Baillie, Richard, and Tim Bellerslev. 2003. A multivariate generalized ARCH approach to modeling risk. Journal of International Money and Finance 22: 625–49. [Google Scholar]
- Barrios, Salvador, and Diego Rodríguez-Palenzuela. 2015. Understanding the oil price–macroeconomy relationship: The role of asymmetries for US real GDP. Energy Economics 52: 77–93. [Google Scholar]
- Baumeister, Christiane, and Lutz Kilian. 2016. Forty Years of Oil Price Fluctuations: Why the Price of Oil May Still Surprise Us. Journal of Economic Perspectives 30: 139–60. [Google Scholar] [CrossRef]
- Bauwens, Luc, Sébastien Laurent, and Jeroen V. K. Rombouts. 2006. Multivariate GARCH models: A survey. Journal of Applied Econometrics 21: 79–109. [Google Scholar] [CrossRef]
- Becken, Susanne, and James Lennox. 2012. Implications of a long-term increase in oil prices for tourism. Tourism Management 33: 133–42. [Google Scholar] [CrossRef]
- Bergareche, Juan Carpizo. 2019. Regional and Local Energy Taxation: Problems and Possible Solutions. Studies on the Spanish Economy. Madrid: FEDEA, p. 21. [Google Scholar]
- Bialkowski, Jedrzej. 2004. Modelling returns on stock indices for western and central European stock exchanges—A Markov switching approach. South-Eastern Europe Journal of Economics 2: 81–100. Available online: http://www.asecu.gr/Seeje/issue03/bialkowski.pdf (accessed on 12 February 2024).
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Braun, M., Michael Kvasnicka, and M. Schmidt. 2019. Movin’up to the east side: Oil and gas extraction and intraregional migration in Russia. Journal of Development Economics 139: 165–86. [Google Scholar]
- Brown, Stephen P. A., and Mine K. Yücel. 2002. Energy Prices and Aggregate Economic Activity: An Interpretative Survey. Quarterly Review of Economics and Finance 42: 193–208. [Google Scholar] [CrossRef]
- Burbridge, John, and Alan Harrison. 1984. Testing for the effects of oil price rises using vector autoregressions. International Economic Review 25: 459–84. [Google Scholar] [CrossRef]
- Cai, Jun. 1994. A Markov Model of Switching-Regime ARCH. Journal of Business & Economic Statistics 12: 309–16. [Google Scholar]
- Camarero, Mariam, Josep Lluís Carrion-i-Silvestre, and Cecilio Tamarit. 2006. The relationship between oil prices, stock prices, and inflation: Evidence from Spain. International Journal of Finance & Economics 11: 175–88. [Google Scholar]
- Cantavella-Jordá, Manuel. 2020. Fluctuations of Oil Prices and Gross Domestic Product in Spain. International Journal of Energy Economics and Policy 10: 57–63. Available online: https://www.econjournals.com/index.php/ijeep/article/view/8806 (accessed on 23 December 2023).
- Carrion-i-Silvestre, Lluis, and Dukpa Kim. 2000. The dynamic relationship between stock prices and inflation: Evidence from Spain. Journal of Macroeconomics 22: 331–51. [Google Scholar]
- Castro, César, Rebeca Jiménez-Rodríguez, Pilar Poncela, and Eva Senra. 2017. A new look at oil prices passes through into inflation: Evidence from disaggregated European data. Journal of Analytical and Institutional Economics 34: 55–82. [Google Scholar]
- Chen, Shiu-Sheng, and Hung-Chyn Chen. 2007. Oil prices and real exchange rates. Energy Economics 29: 390–404. [Google Scholar] [CrossRef]
- Cheratian, Iman, Mohammad Reza Farzanegan, and Saleh Goltabar. 2019. Oil Price Shocks and Unemployment Rate: New Evidence from the MENA Region. MAGKS Papers on Economics 201931. Marburg: Philipps-Universität Marburg. [Google Scholar]
- Chkili, Walid, and Duc Khuong Nguyen. 2017. Stock returns and oil price changes in France: A multiscale analysis using wavelets. Energy Economics 64: 568–77. [Google Scholar]
- Cologni, Alessandro, and Matteo Manera. 2008. Oil prices, inflation, and interest rates in a structural cointegrated VAR model for the G-7 countries. Energy Economics 30: 856–88. [Google Scholar] [CrossRef]
- Cunado, Juncal, and F. Perez de Gracia. 2005. Oil prices, economic activity, and inflation: Evidence for some Asian countries. Quarterly Review of Economics and Finance 45: 65–83. [Google Scholar] [CrossRef]
- Cunado, Juncal, and Fernando Pérez de Gracia. 2003. Do oil price shocks matter? Evidence for some European countries. Energy Economics 25: 137–54. [Google Scholar] [CrossRef]
- De Blas, Beatriz, and Katheryn Russ. 2015. The macroeconomic effects of oil price shocks in Spain: A SVAR approach. Energy Economics 51: 599–612. [Google Scholar]
- Del Rio, Pablo, and Jiménez Rodríguez-López. 2016. The relationship between oil price shocks and stock market: Evidence from Spain. International Journal of Energy Economics and Policy 6: 477–83. [Google Scholar]
- de Miguel, Carlos, Baltasar Manzano, and Jose M. Martin-Moreno. 2003. Oil price shocks and aggregate fluctuations. The Energy Journal 24: 47–61. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Ewing, Bradley, and Mark A. Thompson. 2007. The impact of oil price shocks on the term structure of stock returns. The Quarterly Review of Economics and Finance 47: 582–95. [Google Scholar]
- Fahrmeir, Ludwig, Thomas Kneib, Stefan Lang, and Brian Marx. 2010. Regression: Models, Methods, and Applications. Berlin/Heidelberg: Springer. [Google Scholar]
- Fan, Ying, Yue-Jun Zhang, Hsien-Tang Tsai, and Yi-Ming Wei. 2008. Estimating ‘Value at Risk’ of crude oil price and its spillover effect using the GED-GARCH approach. Energy Economics 30: 3156–71. [Google Scholar] [CrossRef]
- Ferderer, J. Peter. 1996. Oil price volatility and the macroeconomy. Journal of Macroeconomics 18: 1–26. [Google Scholar] [CrossRef]
- Franses, Philip Hans, and Dick Van Dijk. 1996. Forecasting stock market volatility using (non-linear) Garch models. Journal of Forecasting 15: 229–335. [Google Scholar] [CrossRef]
- Frommel, Michael. 2010. Volatility regimes in Central and Eastern European countries’ exchange rates. Czech Journal of Economics and Finance 60: 2–21. Available online: https://journal.fsv.cuni.cz/storage/1177_1177_str_2 (accessed on 24 December 2023).
- Gelman, Andrew. 2004. Bayesian Data Analysis, 2nd ed. Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- Gisser, Micha, and Thomas H. Goodwin. 1986. Crude oil and the macroeconomy: Tests of some popular notions. Journal of Money, Credit and Banking 18: 95–103. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Gormus, N. Alper, and Ugur Soytas. 2020. Oil price shocks, stock market, and inflation in the Eurozone. Energy & Environment 31: 1353–75. [Google Scholar]
- Gómez-Loscos, Ana, Antonio Montañés, and M. Dolores Gadea. 2011. The Impact of Oil Shocks on The Spanish Economy. Occasional Papers 1914. Madrid: Bank of Spain. [Google Scholar]
- Guo, Hui, and Kevin L. Kliesen. 2005. Oil price volatility and U. S. macroeconomic activity. Review-Federal Reserve Bank of St. Louis 57: 669–83. [Google Scholar] [CrossRef]
- Güntner, Jochen H. F. 2014. How do oil producers respond to oil demand shocks? Energy Economics 44: 1–13. [Google Scholar] [CrossRef]
- Haas, Markus, Stefan Mittnik, and Marc S. Paolella. 2004. A new approach to Markov-switching GARCH models. Journal of Financial Econometrics 2: 493–530. [Google Scholar] [CrossRef]
- Haas, Markus, and Marc S. Paolella. 2012. Mixture and regime-switching GARCH models. In Handbook of Volatility Models and Their Applications. Edited by Luc Bauwens, Christian Hafner and Sebastien Laurent. Hoboken: John Wiley & Sons, pp. 71–102. [Google Scholar] [CrossRef]
- Hamilton, James D. 1983. Oil and the Macroeconomy since World War II. Journal of Political Economy 91: 228–48. [Google Scholar] [CrossRef]
- Hamilton, James D. 1988. Rational expectations econometric analysis of changes in regime: An investigation of the term structure of interest rates. Journal of Economic Dynamics and Control 12: 385–423. [Google Scholar] [CrossRef]
- Hamilton, James D. 1994. Time Series Analysis. Princeton: Princeton University Press. [Google Scholar]
- Hamilton, James D. 2008. Oil and the Macroeconomy. In The New Palgrave Dictionary of Economics: Palgrave Macmillan. Edited by Steven N. Durlauf and Lawrence E. Blume. London: Palgrave Macmillan. [Google Scholar]
- Hooker, Mark A. 1996. What Happened to the Oil Price-Macroeconomy Relationship? Journal of Monetary Economics 38: 195–213. [Google Scholar] [CrossRef]
- Hou, Aijun, and Sandy Suardi. 2012. A nonparametric GARCH model of crude oil price return volatility. Energy Economics 34: 618–26. [Google Scholar] [CrossRef]
- Huang, Bwo-Nung, M. J. Hwang, and Hsiao-Ping Peng. 2005. The asymmetry of the impact of oil price shocks on economic activities: An application of the multivariate threshold model. Energy Economics 27: 455–76. [Google Scholar] [CrossRef]
- Hung, Jui-Cheng, Ming-Chih Lee, and Hung-Chun Liu. 2008. Estimation of Value-at-Risk for Energy Commodities via Fat-Tailed GARCH Models. Energy Economics 30: 1173–91. [Google Scholar] [CrossRef]
- Huntington, Hillard G. 2007. Oil shocks and real U.S. income. The Energy Journal 28: 31–46. [Google Scholar] [CrossRef]
- IEA. 2020. World Energy Outlook 2020. Paris: IEA, Licence: CC BY 4.0. Available online: https://www.iea.org/reports/world-energy-outlook-2020 (accessed on 14 January 2024).
- IMF (International Monetary Fund). 2016. World Economic Outlook: Too Slow for Too Long. Washington, DC: International Monetary Fund. [Google Scholar]
- Jimenez-Rodriguez, Rebeca. 2009. Oil price shocks and real GDP growth: Testing for non-linearity. The Energy Journal 30: 1–23. [Google Scholar] [CrossRef]
- Jimenez-Rodriguez, Rebeca, and Marcelo Sanchez. 2005. Oil price shocks and real GDP growth: Empirical evidence for some OECD countries. Applied Economics 37: 201–28. [Google Scholar] [CrossRef]
- Kang, Sang Hoon, Sang-Mok Kang, and Seong-Min Yoon. 2009. Forecasting volatility of crude oil markets. Energy Economics 31: 119–25. [Google Scholar] [CrossRef]
- Kanjilal, Kakali, and Sajal Ghosh. 2017. Dynamics of crude oil and gold price post 2008 global financial crisis—New evidence from threshold vector error-correction model. Resources Policy 52: 358–65. [Google Scholar] [CrossRef]
- Katsampoxakis, Ioannis, Apostolos Christopoulos, Petros Kalantonis, and Vasileios Nastas. 2022. Crude oil price shocks and European stock markets during the COVID-19 period. Energies 15: 4090. [Google Scholar] [CrossRef]
- Kilian, Lutz. 2009. Not all oil price shocks are alike: Disentangling demand and supply shocks in the crude oil market. American Economic Review 99: 1053–69. [Google Scholar] [CrossRef]
- Kilian, Lutz, and Robert Vigfusson. 2011. Are the Responses of the U.S. Economy Asymmetric in Energy Price Increases and Decreases? Quantitative Economics 2: 419–53. [Google Scholar] [CrossRef]
- Kitous, Alban, Bert Saveyn, Kimon Keramidas, Toon Vandyck, Luis Rey Los Santos, and Krzysztof Wojtowicz. 2016. Impact of Low Oil Prices on Oil Exporting Countries. EUR 27909. Luxembourg: Publications Office of the European Union, JRC101562. [Google Scholar]
- Klaassen, Franc. 2002. Improving GARCH volatility forecasts with regime-switching GARCH. International Journal of Forecasting 27: 363–94. [Google Scholar]
- Koirala, Niraj Prasad, and Xiaohan Ma. 2020. Oil price uncertainty and U.S. employment growth. Energy Economics 91: 104910. [Google Scholar] [CrossRef]
- Lamoureux, Christopher G., and William D. Lastrapes. 1990. Heteroskedasticity in Stock Return Data: Volume versus GARCH Effects. Journal of Finance 45: 221–29. [Google Scholar]
- Lardic, Sandrine, and Valerie Mignon. 2006. The impact of oil prices on GDP in European countries: An empirical investigation based on asymmetrical cointegration. Energy Policy 34: 3910–15. [Google Scholar] [CrossRef]
- Lee, Kiseok, Shawn Ni, and Ronald A. Ratti. 1995. Oil shocks and the macroeconomy: The role of price variability. The Energy Journal 16: 39–56. [Google Scholar] [CrossRef]
- Lescaroux, François, and Valérie Mignon. 2008. On the Influence of Oil Prices on Economic Activity and Other Macroeconomic and Financial Variables. Working Papers from CEPII research center. Paris: CEPII Research Center. [Google Scholar]
- Linne, Thomas. 2002. A Markov switching model of stock returns: An application to the emerging markets in Central and Eastern Europe. In East European Transition and EU Enlargement. Edited by Wojciech W. Charemza and Krystyna Strzała. Heidelberg: Physica, pp. 371–84. [Google Scholar] [CrossRef] [PubMed]
- Litzenberger, Robert H., and Nir Rabinowitz. 1995. Backwardation in oil futures markets: Theory and empirical evidence. The Journal of Finance 50: 1517–45. [Google Scholar] [CrossRef]
- Liu, Ming-Lei, Qiang Ji, and Ying Fan. 2013. How Does Oil Market Uncertainty Interact with Other Markets? An Empirical Analysis of Implied Volatility Index. Energy 55: 860–68. [Google Scholar] [CrossRef]
- Manera, Matteo, Chiara Longo, Anil Markandya, and Elisa Scarpa. 2007. Evaluating the Empirical Performance of Alternative Econometric Models for Oil Price Forecasting. FEEM Fondazione Eni Enrico Mattei Research Paper Series [Working Paper] (4), 1–49. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=958942# (accessed on 4 January 2024).
- Marcucci, Juri. 2005. Forecasting stock market volatility with regime-switching GARCH Models. Studies in Nonlinear Dynamics & Econometrics 9: 1–55. [Google Scholar] [CrossRef]
- Mohammadi, Hassan, and Lixian Su. 2010. International evidence on crude oil price dynamics: Applications of ARIMA-GARCH models. Energy Economics 32: 1001–1008. [Google Scholar]
- Mohd, Atif, Mustafa Raza Rabbani, Hana Bawazir, and Iqbal Thonse Hawaldar. 2022. Oil price changes and stock returns: Fresh evidence from oil exporting and oil importing countries. Cogent Economics & Finance 10: 2018163. [Google Scholar] [CrossRef]
- Moore, Tomoe, and Ping Wang. 2007. Volatility in stock returns for new EU member states: Markov regime switching model. International Review of Financial Analysis 16: 282–92. [Google Scholar] [CrossRef]
- Mork, Knut Anton, and Olstein Olsen. 1994. Macroeconomic responses to oil price increases and decreases in seven OECD countries. Energy Journal 15: 19–35. [Google Scholar] [CrossRef]
- Muşetescu, Radu-Cristian, George-Eduard Grigore, and Simona Nicolae. 2022. The Use of GARCH Autoregressive Models in Estimating and Forecasting the Crude Oil Volatility. European Journal of Interdisciplinary Studies 14: 13–38. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Ordóñez, Javier, Mercedes Monfort, and Juan Carlos Cuestas. 2019. Oil prices, unemployment, and the financial crisis in oil-importing countries: The case of Spain. Energy 181: 625–34. [Google Scholar] [CrossRef]
- Pérez-Quiros, Gabriel, and Allan Timmermann. 2000. Business conditions and asset returns. The Quarterly Journal of Economics 115: 161–201. [Google Scholar]
- Raihan, Tasneem. 2017. Performance of Markov-Switching GARCH Model Forecasting Inflation Uncertainty (MPRA Paper No. 82343). Available online: https://mpra.ub.uni-muenchen.de/82343/1/MPRA_paper_82343.pdf (accessed on 8 February 2021).
- Robays, Ine Van. 2012. Macroeconomic Uncertainty and the Impact of Oil Shocks. Working Paper Series, NO 1479. Available online: https://www.ecb.europa.eu/pub/pdf/scpwps/ecbwp1479.pdf (accessed on 15 February 2024).
- Rodríguez-Zúñiga, J., M. Sánchez, and D. León. 2019. Effects of oil price shocks on Spanish macroeconomic variables. International Journal of Energy Economics and Policy 9: 376–84. [Google Scholar]
- Rotta, Pedro Nielsen, and Pedro L. Valls Pereira. 2016. Analysis of contagion from the dynamic conditional correlation model with Markov Regime switching. Applied Economics 48: 2367–82. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 1999. Oil price shocks and stock market activity. Energy Economics 21: 449–69. [Google Scholar] [CrossRef]
- Sekati, Boitumelo Nnoi Yolanda, Johannes Tshepiso Tsoku, Lebotsa Daniel Metsileng, and Damir Tokic. 2020. Modelling the oil price volatility and macroeconomic variables in South Africa using the symmetric and asymmetric GARCH models. Cogent Economics & Finance 8: 1792153. [Google Scholar]
- Serletis, Apostolos, and John Elder. 2011. Introduction To Oil Price Shocks. Macroeconomic Dynamics 15: 327–36. [Google Scholar] [CrossRef]
- Szczygielski, Jan Jakub, and Chimwemwe Chipeta. 2023. Properties of returns and variance and implications for time series modeling: Evidence from South Africa. Modern Finance 1: 35–55. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Arif Billah Dar, and Niyati Bhanja. 2013. Oil price and exchange rates: A wavelet based analysis for India. Economic Modelling 31: 414–22. [Google Scholar] [CrossRef]
- Topan, Ligia, César Castro, Miguel Jerez, and Andrés Barge-Gil. 2020. Oil price pass-through into inflation in Spain at national and regional level. Journal of the Spanish Economic Association 11: 561–83. [Google Scholar] [CrossRef] [PubMed]
- Tuna, Vedat Ender, Gülfen Tuna, and Nurcan Kostak. 2021. The effect of oil market shocks on the stock markets: Time-varying asymmetric causal relationship for conventional and Islamic stock markets. Energy Reports 7: 2759–74. [Google Scholar] [CrossRef]
- van Eyden, Renee, Mamothoana Difeto, Rangan Gupta, and Mark Wohar. 2019. Oil price volatility and economic growth: Evidence from advanced economies using more than a century’s data. Applied Energy 233–34: 612–21. [Google Scholar] [CrossRef]
- Van Robays, Ine. 2016. Macroeconomic Uncertainty and Oil Price Volatility. Oxford Bulletin of Economics and Statistics 78: 671–93. [Google Scholar] [CrossRef]
- Wacuka Ng’ang’a, Faith, and Meleah Oleche. 2022. Modelling and Forecasting of Crude Oil Price Volatility Comparative Analysis of Volatility Models. Journal of Financial Risk Management 11: 154–87. [Google Scholar] [CrossRef]
- Wang, Jun, Huopo Pan, and Fajiang Liu. 2012. Forecasting Crude Oil Price and Stock Price by Jump Stochastic Time Effective Neural Network Model. Journal of Applied Mathematics 2012: 646475. [Google Scholar] [CrossRef]
- Wang, Yudong, and Chongfeng Wu. 2012. Forecasting energy market volatility using GARCH models: Can multivariate models beat univariate models? Energy Economics 34: 2167–81. [Google Scholar] [CrossRef]
- Westfall, Peter. 2014. Adequacy of normal approximation for the t distribution using formal and informal tests. Statistics in Medicine 33: 659–74. [Google Scholar]
- Zagaglia, Paolo. 2010. Macroeconomic factors and oil futures prices: A data-rich model. Energy Economics 32: 409–17. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar] [CrossRef]
- Zhang, Hai-Ying, Qiang Ji, and Ying Fan. 2015. What drives the formation of global oil trade patterns? Energy Economics 49: 639–48. [Google Scholar] [CrossRef]
- Zhang, Yue-Jun, and Jing Wang. 2015. Exploring the WTI crude oil price bubble process using the Markov regime switching model. Physica A: Statistical Mechanics and its Applications 421: 377–87. [Google Scholar] [CrossRef]
- Zhang, Qin, and Jin Boon Wong. 2023. The influence of oil price uncertainty on stock liquidity. Futures Markets 43: 141–67. [Google Scholar] [CrossRef]
- Zhang, Yue-Jun, and Lu Zhang. 2015. Interpreting the crude oil price movements: Evidence from the Markov regime switching model. Applied Energy 143: 96–109. [Google Scholar] [CrossRef]
- Živkov, Dejan, and Jasmina Đurašković. 2021. How does oil price uncertainty affect output in the Central and Eastern European economies?—The Bayesian-based approaches. Central and Eastern European Economies 31: 39–54. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).