Monetary Policy Spillovers and Inter-Market Dynamics Perspective of Preferred Habitat Model
Abstract
1. Introduction
2. Literature Review
2.1. Theoretical Underpinning of Spillover Effects
2.2. Inter-Market Transmissions Dynamics
3. Data and Methods
3.1. Data and Sample
3.2. Methods and Econometric Techniques
3.3. Markov-Switching Econometric Model
3.4. EGARCH with DCC Specification
4. Findings and Discussion
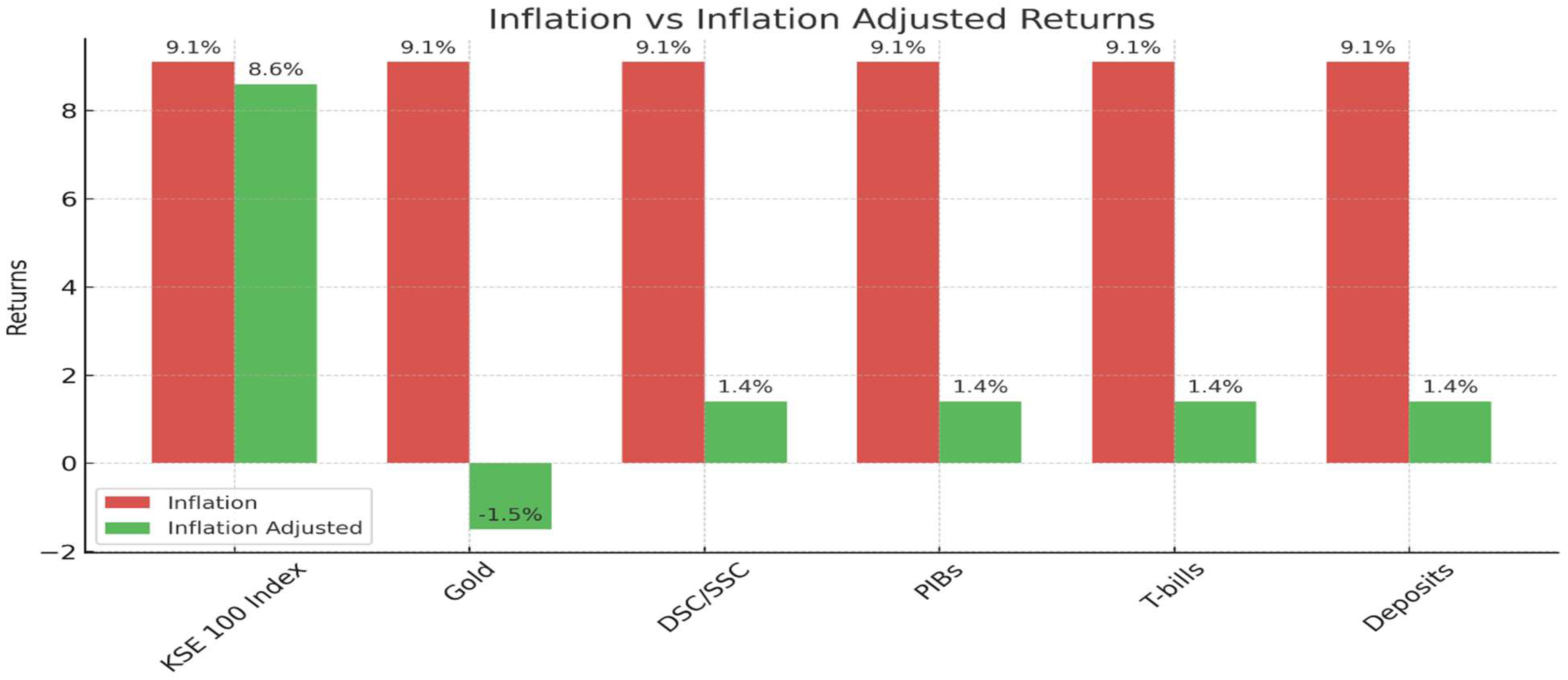
4.1. Descriptive Analysis
4.2. Transmission Effects on Overall Markets
4.3. Transmission Effects on Real Estate Market of Different Regions
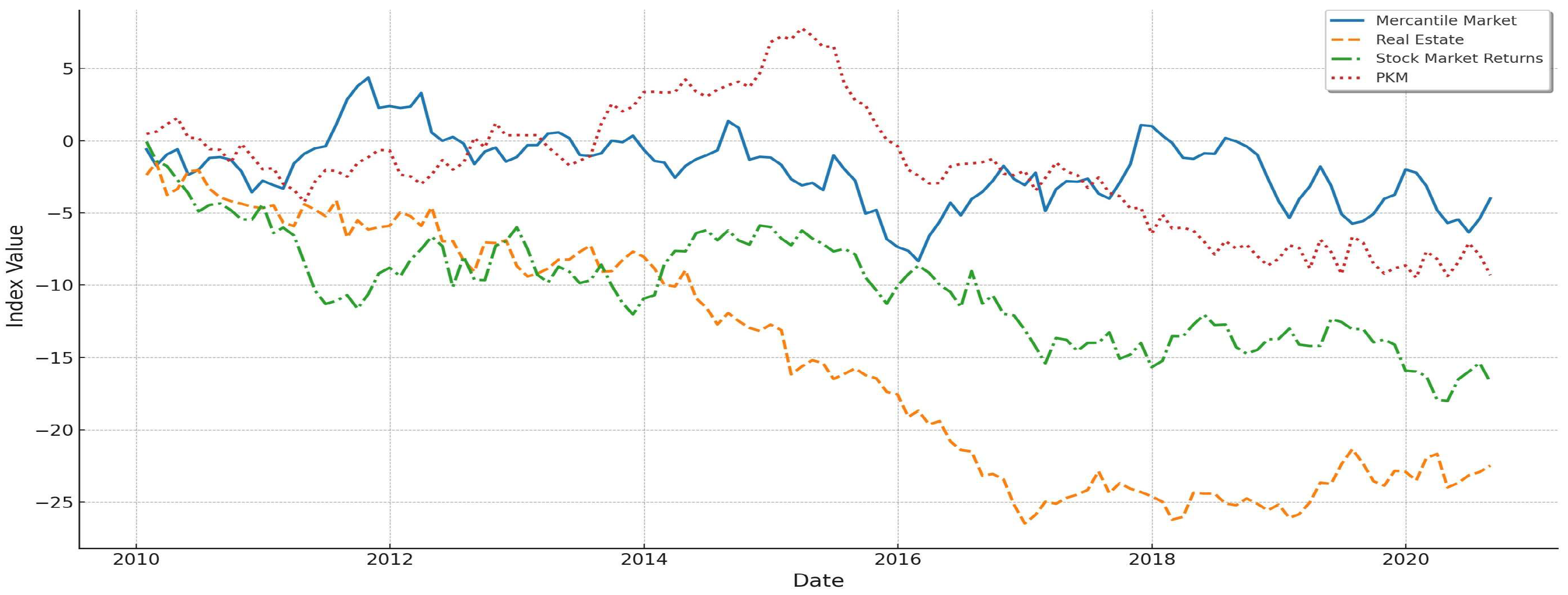
4.4. Transmission Effects on Mercantile Market’s Products
4.5. Transmission Effects on Stock Market’s Sectors
4.6. Inter-Market Transmission Effects
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alemohammad, Nafise, Saeid Rezakhah, and Sasan H. Alizadeh. 2013. Markov Switching Component ARCH Model: Stability and Forecasting. Communications in Statistics-Theory and Methods 45: 4332–48. [Google Scholar] [CrossRef]
- Alikhanov, Abdulla. 2013. To What Extent are Stock Returns Driven by Mean and Volatility Spillover Effects?—Evidence from Eight European Stock Markets. Review of Economic Perspectives 13: 3–29. [Google Scholar] [CrossRef]
- Alotaibi, Abdullah R., and Anil V. Mishra. 2015. Global and regional volatility spillovers to GCC stock markets. Economic Modelling 45: 38–49. [Google Scholar] [CrossRef]
- Ampountolas, Apostolos. 2022. Cryptocurrencies Intraday High-Frequency Volatility Spillover Effects Using Univariate and Multivariate GARCH Models. International Journal of Financial Studies 10: 51. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Zeynel Abidin Ozdemir, and Huseyin Ozdemir. 2021. Dynamic return and volatility spillovers among SandP 500, crude oil, and gold. International Journal of Finance and Economics 26: 153–70. [Google Scholar] [CrossRef]
- Bhar, Ramaprasad, and Biljana Nikolova. 2007. Analysis of mean and volatility spillovers using BRIC countries, regional and world equity index returns. Journal of Economic Integration 22: 369–81. Available online: http://sejong.metapress.com/index/65L58LM88L636016.pdf (accessed on 22 June 2022). [CrossRef]
- Costa, Celso J. 2019. Preferred habitat and the term structure of interest rates in DSGE models. Journal of Applied Economics 22: 581–601. [Google Scholar] [CrossRef]
- Dale, Jonathan J., Stephanie Brodie, Aaron B. Carlisle, Michael Castleton, Elliott L. Hazen, Steven J. Bograd, and Barbara A. Block. 2022. Global habitat loss of a highly migratory predator, the blue marlin (Makaira nigricans). Diversity and Distributions 28: 2020–34. [Google Scholar] [CrossRef]
- Dornbusch, Rudiger. 1976. Expectations and Exchange Rate Dynamics. Journal of Political Economy 84: 1161–76. [Google Scholar] [CrossRef]
- Fleming, J. Marcus. 1962. Domestic Financial Policies under Fixed and under Floating Exchange Rates. Staff Papers, International Monetary Fund 9: 369. [Google Scholar] [CrossRef]
- Frenkel, Jacob A., and Assaf Razin. 1987. The Mundell-Fleming Model: A Quarter Century Later: A Unified Exposition. Staff Papers—International Monetary Fund 34: 567–620. [Google Scholar] [CrossRef]
- Frenkel, Jacob A., and Assaf Razin. 1989. The Mundell-Flemming Model: A Quarter Century Later. National Bureau of Economic Research Working Paper Series. Cambridge, MA: National Bureau of Economic Research. [Google Scholar]
- Goodwin, Thomas H., and Thomas H. Goodwin. 2017. Business-Cycle Analysis with a Markov-Switching Model. Journal of Business & Economic Statistics 11: 331–39. [Google Scholar]
- Hamilton, James D. 1989. A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica 57: 357. [Google Scholar] [CrossRef]
- Hildebrand, George H., and Clark Kerr. 1986. The Future of Industrial Societies: Convergence or Continuing Diversity? Industrial and Labor Relations Review 39: 302–3. [Google Scholar] [CrossRef]
- Huang, Yu-Lieh. 2014. Testing Markov switching models. Applied Economics 46: 2047–51. [Google Scholar] [CrossRef]
- Koulis, Alexandros, and Constantinos Kyriakopoulos. 2023. On Volatility Transmission between Gold and Silver Markets: Evidence from A Long-Term Historical Period. Computation 11: 25. [Google Scholar] [CrossRef]
- Li, Haitao, Chongfeng Wu, and Chunyang Zhou. 2021. Time-Varying Risk Aversion and Dynamic Portfolio Allocation. Operations Research 70: 23–37. [Google Scholar] [CrossRef]
- Liu, Yaqing, and Hongbing Ouyang. 2014. Spillover and Comovement: The Contagion Mechanism of Systemic Risks Between the U.S. and Chinese Stock Markets. Emerging Markets Finance and Trade 50: 109–21. [Google Scholar] [CrossRef]
- Majumder, Sayantan Bandhu, and Ranjanendra Narayan Nag. 2018. Shock and Volatility Spillovers Among Equity Sectors of the National Stock Exchange in India. Global Business Review 19: 227–40. [Google Scholar] [CrossRef]
- Moon, Gyu-Hyen, and Wei-Choun Yu. 2010. Volatility spillovers between the US and China stock markets: Structural break test with symmetric and asymmetric GARCH approaches. Global Economic Review 39: 129–49. [Google Scholar] [CrossRef]
- Mundell, Robert Alexander. 1963. Capital Mobility and Stabilization Policy under Fixed and Flexible Exchange Rates. The Canadian Journal of Economics and Political Science 29: 475–85. [Google Scholar] [CrossRef]
- Musampa, Kongolo, Joel Hinaunye Eita, and Christelle Meniago. 2024. The Effects of Oil Price Volatility on South African Stock Market Returns. Economies 12: 4. [Google Scholar] [CrossRef]
- Nafisi-Moghadam, Maryam, and Shahram Fattahi. 2022. A Hybrid Model of VAR-DCC-GARCH and Wavelet Analysis for Forecasting Volatility. Engineering Proceedings 18: 6. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Olbrys, Joanna. 2013. Price and Volatility Spillovers in the Case of Stock Markets Located in Different Time Zones. Emerging Markets Finance and Trade 49: 145–57. [Google Scholar] [CrossRef]
- Pakistan Bureau of Statistics. 2019. LABOUR FORCE SURVEY. Islamabad. Available online: https://www.pbs.gov.pk/sites/default/files//LabourForce/publications/lfs2018_19/lfs_2018_19_final_report.pdf (accessed on 15 June 2022).
- Pakistan Stock Exchange. 2020. Saving & Investing. Pakistan Stock Exchange. Available online: https://www.psx.com.pk/psx/resources-and-tools/investors/for-new-investors (accessed on 15 June 2022).
- Petrakis, Nikolaos C., Christos Lemonakis, Christos Floros, and Constantin Zopounidis. 2022. Eurozone Stock Market Reaction to Monetary Policy Interventions and Other Covariates. Journal of Risk and Financial Management 15: 56. [Google Scholar] [CrossRef]
- Raza, Naveed, Syed Jawad Hussain Shahzad, Aviral Kumar Tiwari, and Muhammad Shahbaz. 2016. Asymmetric impact of gold, oil prices and their volatilities on stock prices of emerging markets. Resources Policy 49: 290–301. [Google Scholar] [CrossRef]
- Sahabuddin, Mohammad, Md Aminul Islam, Mosab I. Tabash, Md Kausar Alam, Linda Nalini Daniel, and Imad Ibraheem Mostafa. 2023. Dynamic Conditional Correlation and Volatility Spillover between Conventional and Islamic Stock Markets: Evidence from Developed and Emerging Countries. Journal of Risk and Financial Management 16: 111. [Google Scholar] [CrossRef]
- Siddiqui, Saif, and Preeti Roy. 2019. Predicting volatility and dynamic relation between stock market, exchange rate and select commodities. Acta Universitatis Agriculturae et Silviculturae Mendelianae Brunensis 67: 1597–611. [Google Scholar] [CrossRef]
- Sohail Sarfraz. 2020. Foreign investment: PSX saw $284.832 million outflow in FY19: SECP. Business Recorder. December 26. Available online: https://www.brecorder.com/news/40044750/foreign-investment-psx-saw-284832-million-outflow-in-fy19-secp (accessed on 15 June 2022).
- Strohsal, Till. 2017. Bond yields and debt supply: New evidence through the lens of a preferred-habitat model. Quantitative Finance 17: 1509–22. [Google Scholar] [CrossRef]
- The Federation of Pakistan Chambers of Commerce and Industry. 2017. Construction Sector of Pakistan. Islamabad. Available online: https://fpcci.org.pk/ (accessed on 10 May 2022).
- Tiwari, Aviral Kumar, Samia Nasreen, Subhan Ullah, and Muhammad Shahbaz. 2021. Analysing spillover between returns and volatility series of oil across major stock markets. International Journal of Finance and Economics 26: 2458–90. [Google Scholar] [CrossRef]
- Vayanos, Dimitri, and Jean-Luc Vila. 2021. A Preferred-Habitat Model of the Term Structure of Interest Rates. Econometrica 89: 77–112. [Google Scholar] [CrossRef]
- Viceira, Luis M. 2001. Optimal portfolio choice for long-horizon investors with nontradable labor income. Journal of Finance 56: 433–70. [Google Scholar] [CrossRef]
- Vissing-Jorgensen, Annette, and Arvind Krishnamurthy. 2011. The Effects of Quantitative Easing on Interest Rates: Channels and Implications for Policy. Brookings Papers on Economic Activity 43: 215–87. [Google Scholar]
- Wahid, Abdul, and Muhammad Zubair Mumtaz. 2018. The Paradigm Shift in the Pakistan Stock Exchange’s Financial Integration Post-FTA and CPEC. In The Lahore Journal of Economics 23: 21–50. [Google Scholar] [CrossRef]
- Zhu, Bing. 2018. The multi-country transmission of sovereign and banking risk: A spatial vector autoregressive approach. Spatial Economic Analysis 13: 422–41. [Google Scholar] [CrossRef]
| Variable | (β1) | (β2) | p11 | p21 | Duration (I) | Duration (II) |
|---|---|---|---|---|---|---|
| 0.085 ** (12.43) | 0.111 ** (15.39) | 0.979 | 0.045 | 4.849 | 22.492 | |
| −0.011 ** (3.60) | 0.040 ** (3.33) | 0.675 | 0.578 | 71.600 | 72.543 | |
| 0.005 ** (7.14) | 0.023 ** (13.06) | 0.957 | 0.208 | 33.083 | 6.582 | |
| −0.219 ** (3.59) | 0.013 ** (2.68) | 0.854 | 0.145 | 6.853 | 2.923 | |
| 0.048 ** (4.33) | 0.049 ** (4.34) | 0.528 | 0.471 | 2.119 | 3.403 | |
| −0.021 ** (3.80) | −0.003 (1.43) | 0.914 | 0.016 | 1.231 | 1.000 | |
| 0.037 ** (6.30) | 0.087 ** (15.00) | 0.973 | 0.026 | 37.791 | 86.285 |
| Mercantile | Real Estate | Stock Market | ||||
|---|---|---|---|---|---|---|
| I | II | I | II | I | II | |
| −0.001 ** | −0.022 ** | 0.044 ** | 0.056 ** | −0.112 ** | −0.148 ** | |
| (−4.12) | (−5.68) | (8.09) | (6.45) | (−4.12) | (−10.28) | |
| −0.096 ** | −0.097 ** | 0.017 ** | 0.025 ** | −0.129 ** | −0.217 * | |
| (−18.31) | (−8.17) | (6.15) | (5.24) | (−4.12) | (−2.45) | |
| −3.155 ** | −3.472 ** | −5.697 ** | −5.219 ** | −2.715 ** | −4.713 ** | |
| −36.6 | −23.34 | −54.57 | −60.96 | −25.15 | −16.27 | |
| −4.509 ** | −2.959 ** | −4.434 ** | −4.927 ** | −3.459 ** | −2.847 ** | |
| −16.05 | −30.36 | −39.96 | −16.41 | −12.04 | −35.29 | |
| 0.243 | 0.159 * | 0.05 | −0.155 ** | −1.064 ** | ||
| −0.6 | −2.35 | −0.97 | −6.51 | −4.01 | ||
| p11 | −0.773 | −0.915 | 0.051 | 0.925 | 0.946 | 0.919 |
| −0.986 ** | −0.026 ** | −1.080 ** | ||||
| (−3.21) | (−3.82) | (−8.07) | ||||
| 0.356 ** | −0.055 ** | −0.244 ** | ||||
| (−4.03) | (−3.27) | (−5.19) | ||||
| −1.448 ** | −0.115 ** | −2.420 ** | ||||
| (−5.41) | (−5.02) | (−4.59) | ||||
| p21 | −0.744 | −0.968 | 0.776 | 0.107 | 0.223 | 0.156 |
| 0.302 ** | 0.101 ** | 0.980 ** | ||||
| (−3.79) | (−4.47) | (−3.63) | ||||
| −0.403 ** | 0.213 ** | 0.986 ** | ||||
| (−4.03) | (−5.16) | (−3.95) | ||||
| 0.477 ** | 0.298 ** | −1.521 ** | ||||
| (−4.39) | (−3.61) | (−4.27) | ||||
| AIC | −3.111 | −6.86 | −2.821 | |||
| HQIC | −2.9813 | −6.73 | −2.691 | |||
| SBIC | −2.79 | −6.539 | −2.5 | |||
| Log likelihood | 182.575 | 386.91 | 166.767 | |||
| N | 126 | 126 | 126 | 126 | 126 | 126 |
| I | II | III | IV | V | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable | β | SE | Β | SE | Β | SE | β | SE | β | SE |
| 0.004 | 0.008 | 0.013 | 0.005 | 0.01 | 0.008 | −0.005 | 0.003 | 0.009 | 0.006 | |
| 0.307 ** | 0.103 | 0.040 ** | 0.054 | 0.091 ** | 0.123 | 0.292 ** | 0.041 | 0.159 ** | 0.083 | |
| −0.191 | 0.252 | 0.083 ** | 0.028 | 0.015 | 0.028 | 0.028 ** | 0.01 | 0.03 | 0.028 | |
| −0.038 | 0.07 | −0.034 | 0.056 | −0.136 | 0.116 | −0.247 ** | 0.051 | 0.161 ** | 0.072 | |
| −0.377 ** | 0.081 | −0.107 | 0.126 | −0.411 | 0.254 | −0.094 | 0.115 | −0.003 | 0.228 | |
| −4.158 | 2.046 | −2.032 ** | 0.000 | −2.389 | 0.982 | −13.272 ** | 0.116 | −2.484 ** | 0.824 | |
| Γ | 0.760 ** | 0.342 | −0.920 ** | 0.000 | 0.989 | 0.327 | 2.371 ** | 0.232 | 0.266 | 0.216 |
| Σ | −0.081 | 0.188 | 0.546 ** | 0.062 | 0.373 | 0.244 | 0.134 | 0.135 | 0.587 ** | 0.196 |
| λ | 0.593 | 0.189 | 0.666 ** | 0.000 | 0.863 ** | 0.086 | −0.213 ** | 0.072 | 0.819 ** | 0.066 |
| −24.388 ** | 14.50 | −13.968 ** | 0.000 | 0.810 ** | 10.7 | 7.045 ** | 23.43 | 9.188 ** | 9.612 | |
| 37.948 | 30.52 | 42.693 ** | 4.096 | −7.231 | 11 | 19.308 ** | 8.023 | −32.513 ** | 6.973 | |
| 12.769 | 11.043 | 11.222 ** | 0.001 | −1.069 | 10.6 | 21.058 | 25.14 | −8.172 | 7.621 | |
| 24.604 ** | 13.942 | 24.896 ** | 0.015 | 12.746 | 18.56 | −82.574 ** | 33.32 | 1.277 | 15.260 | |
| AIC | −5.328 | −5.938 | −5.682 | −6.232 | −6.118 | |||||
| SC | −4.915 | −5.525 | −5.27 | −5.819 | −5.705 | |||||
| HQC | −5.161 | −5.77 | −5.515 | −6.065 | −5.95 | |||||
| Likelihood | 315.372 | 349.521 | 335.208 | 365.988 | 359.597 | |||||
| I | II | III | IV | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | β | SE | Β | SE | β | SE | β | SE |
| −0.023 | 0.021 | −0.039 | 0.036 | 0.039 | 0.058 | −0.037 | 0.043 | |
| −0.211 ** | 0.340 | −0.177 ** | 0.633 | −0.117 ** | 0.930 | −0.181 ** | 0.581 | |
| −0.569 | 0.164 | −0.827 | 0.425 | −0.898 | 0.413 | −0.525 | 0.229 | |
| 0.058 | 0.270 | −0.112 ** | 0.504 | −0.150 ** | 0.776 | 0.009 ** | 0.442 | |
| −0.194 ** | 0.676 | −1.125 ** | 1.185 | −0.746 ** | 1.389 | −0.599 ** | 0.864 | |
| −7.178 | 1.452 | −10.751 | 1.491 | −3.520 | 2.081 | −0.720 | 0.660 | |
| γ | 1.125 | 0.190 | 0.174 | 0.226 | 0.053 | 0.401 | −0.298 | 0.213 |
| σ | 0.545 | 0.226 | 0.288 | 0.169 | 0.258 | 0.220 | 0.348 | 0.174 |
| λ | 0.235 | 0.165 | −0.734 | 0.174 | −0.155 | 0.530 | 0.386 | 0.243 |
| −15.925 ** | 17.827 | −9.855 ** | 26.777 | −20.420 ** | 17.497 | −39.544 ** | 16.498 | |
| −21.314 | 14.591 | 0.719 | 7.992 | 9.628 | 13.919 | 13.769 | 10.819 | |
| −3.186 | 15.747 | 34.190 | 22.015 | 5.575 | 15.504 | 30.324 | 13.626 | |
| −1.917 ** | 33.375 | −28.570 ** | 45.479 | −46.092 ** | 44.549 | −37.979 ** | 25.291 | |
| AIC | −3.301 | −2.652 | −2.230 | −2.787 | ||||
| SC | −2.985 | −2.336 | −1.915 | −2.471 | ||||
| HQC | −3.173 | −2.524 | −2.102 | −2.659 | ||||
| likelihood | 197.852 | 161.502 | 137.886 | 169.070 | ||||
| I | II | III | IV | V | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable | β | SE | Β | SE | β | SE | Β | SE | β | SE |
| 0.012 | 0.019 | 0.017 | 0.012 | 0.017 | 0.078 | −0.018 | 0.341 | 0.114 | 0.014 | |
| 0.410 ** | 0.121 | 0.045 ** | 0.051 | 0.077 ** | 0.215 | 0.223 ** | 0.281 | −0.132 ** | 0.078 | |
| −0.201 ** | 0.91 | 0.051 | 0.012 | 0.011 | 0.065 | 0.023 ** | 0.121 | 0.112 | 0.121 | |
| −0.149 ** | 0.098 | −0.012 | 0.041 | −0.211 ** | 0.227 | −0.212 ** | 0.034 | 0.114 ** | 0.143 | |
| −0.266 ** | 0.067 | −0.191 ** | 0.141 | −0.511 | 0.321 | −0.141 ** | 0.221 | −0.115 ** | 0.118 | |
| −3.671 | 2.067 | −1.012 | 0.013 | −3.611 | 0.452 | −1.272 | 0.112 | −2.484 | 0.321 | |
| γ | 0.581 | 0.651 | −0.123 | 0.016 | 0.651 | 0.331 | 1.371 | 0.123 | 0.266 | 0.241 |
| σ | −0.051 | 0.211 | 0.144 | 0.071 | 0.415 | 0.231 | 0.431 | 0.145 | 0.587 | 0.213 |
| λ | 0.516 | 0.231 | 0.112 | 0.071 | 0.877 | 0.087 | −0.161 | 0.112 | 0.819 | 0.771 |
| −13.123 ** | 10.671 | −11.612 ** | 0.018 | 0.122 ** | 1.121 | 8.133 ** | 23.321 | 8.188 ** | 6.213 | |
| 25.611 ** | 28.511 | 23.711 | 3.081 | −1.121 | 1.321 | 12.308 ** | 8.112 | −12.545 | 5.973 | |
| 10.881 ** | 12.081 | 10.161 ** | 0.021 | −1.076 ** | 1.321 | −19.221 ** | 25.223 | −7.172 ** | 5.443 | |
| 21.112 ** | 15.881 | 11.331 ** | 0.054 | 1.481 ** | 1.321 | −34.561 ** | 33.112 | −1.231 ** | 13.121 | |
| AIC | −4.118 | −4.112 | −3.121 | −5.121 | −5.118 | |||||
| SC | −3.123 | −4.211 | −4.321 | −4.154 | −4.705 | |||||
| HQC | −4.123 | −5.231 | −4.321 | −5.431 | −4.95 | |||||
| likelihood | 411.271 | 366.121 | 411.208 | 322.254 | 233.112 | |||||
| SM | MM | REM | REM | SM | MM | MM | SM | REM | |
|---|---|---|---|---|---|---|---|---|---|
| −0.312 (0.021) | −0.212 (0.022) | 0.134 (0.010) | −0.113 (0.031) | 0.011 (0.011) | 0.341 (0.005) | −0.001 (0.001) | 0.001 (0.005) | 0.001 (0.005) | |
| −0.113 * (1.970) | 0.739 ** (4.169) | 0.682 ** (3.154) | 0.821 ** (4.681) | 0.464 ** (4.293) | 1.603 (1.901) | −1.381 (1.610) | 1.469 (1.906) | 1.461 (1.929) | |
| 0.123 * (2.144) | −0.431 * (2.183) | −0.377 ** (4.356) | −0.517 ** (5.318) | 0.066 ** (4.754) | 0.029 (2.320) | 1.328 * (2.077) | 0.525 (2.265) | 0.395 (2.296) | |
| −0.067 * (2.021) | −0.009 ** (3.398) | −0.098 (1.377) | −0.229 ** (3.978) | −0.253 ** (2.722) | −1.601 (1.145) | 0.091 * (2.050) | −1.966 (1.125) | −1.833 (1.130) | |
| −0.034 ** (4.020) | −0.054 ** (4.107) | −0.116 ** (4.172) | −0.234 ** (4.075) | 0.082 * (2.065) | 0.045 ** (0.052) | ||||
| 0.024 * (2.011) | 0.023 ** (4.002) | 0.003 (0.002) | 0.010 ** (2.004) | 0.004 (0.118) | 0.002 (0.004) | 0.121 (3.211) | 0.132 (0.653) | 0.001 (0.004) | |
| 0.154 ** (3.039) | 0.578 ** (4.064) | 0.678 ** (4.054) | 3.087 ** (4.015) | 0.139 ** (3.036) | 0.265 (0.060) | 0.044 ** (3.024) | 0.272 ** (3.062) | 0.272 (0.063) | |
| 0.136 ** (4.012) | 0.593 ** (5.028) | 0.602 * (2.019) | 0.881 ** (4.023) | 0.314 ** (4.195) | 0.699 * (0.048) | 0.901 ** (4.231) | 0.693 * (2.051) | 0.691 (0.052) | |
| −0.045 ** (5.012) | −0.091 ** (4.003) | −0.212 ** (4.001) | −0.078 ** (0.004) | 0.145 ** (0.000) | 0.012 ** (0.002) | ||||
| Q(24) Q(24) Sq | 0.341 0.455 | 0.671 0.681 | 0.587 0.597 | 0.781 0.892 | 0.891 0.861 | 0.881 0.897 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wahid, A.; Kowalewski, O. Monetary Policy Spillovers and Inter-Market Dynamics Perspective of Preferred Habitat Model. Economies 2024, 12, 98. https://doi.org/10.3390/economies12050098
Wahid A, Kowalewski O. Monetary Policy Spillovers and Inter-Market Dynamics Perspective of Preferred Habitat Model. Economies. 2024; 12(5):98. https://doi.org/10.3390/economies12050098
Chicago/Turabian StyleWahid, Abdul, and Oskar Kowalewski. 2024. "Monetary Policy Spillovers and Inter-Market Dynamics Perspective of Preferred Habitat Model" Economies 12, no. 5: 98. https://doi.org/10.3390/economies12050098
APA StyleWahid, A., & Kowalewski, O. (2024). Monetary Policy Spillovers and Inter-Market Dynamics Perspective of Preferred Habitat Model. Economies, 12(5), 98. https://doi.org/10.3390/economies12050098







