Tourism and Economic Misery: Theory and Empirical Evidence from Mexico
Abstract
1. Introduction
2. Literature Review
2.1. Tourism, Employment, and Inflation
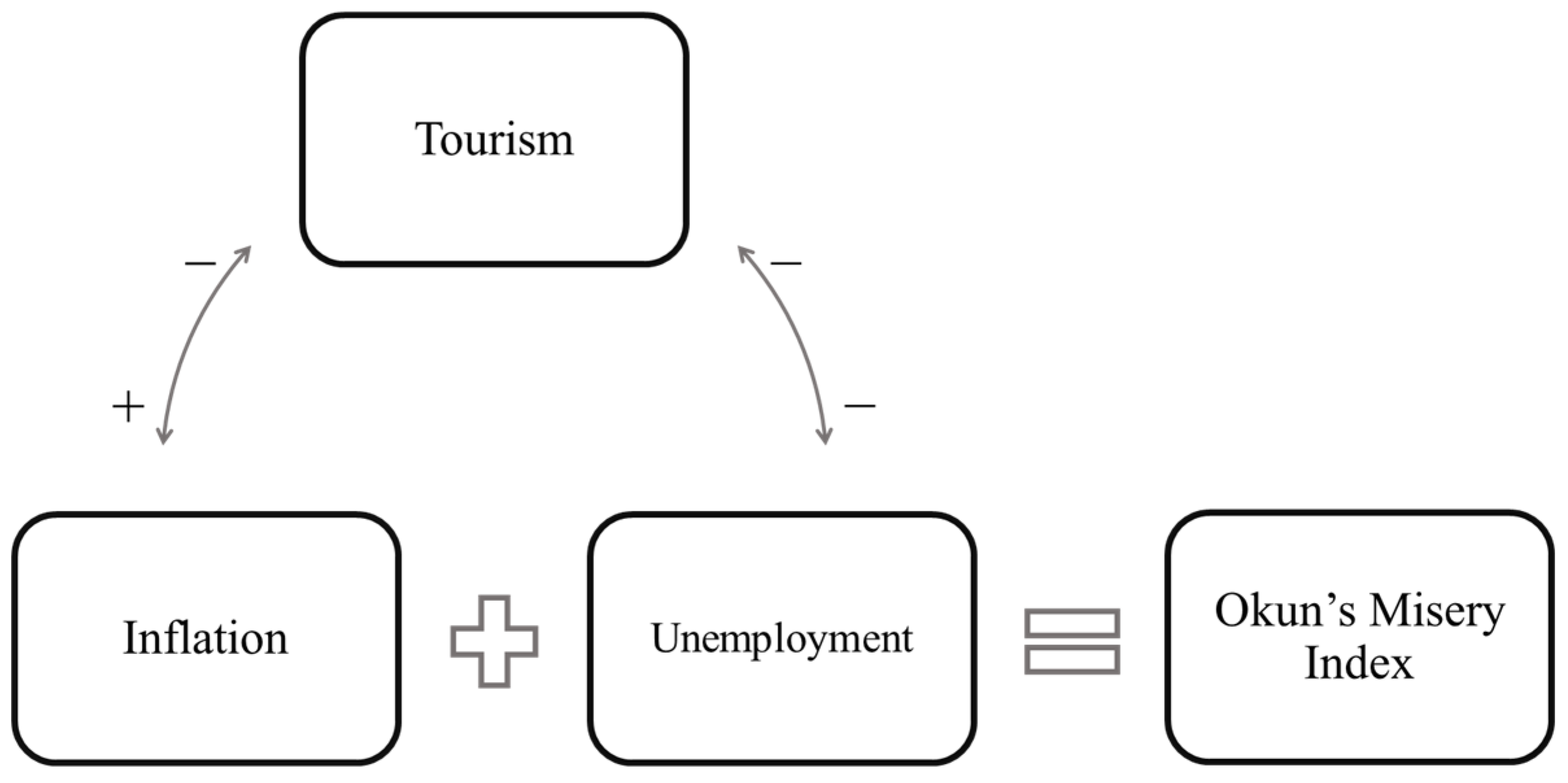
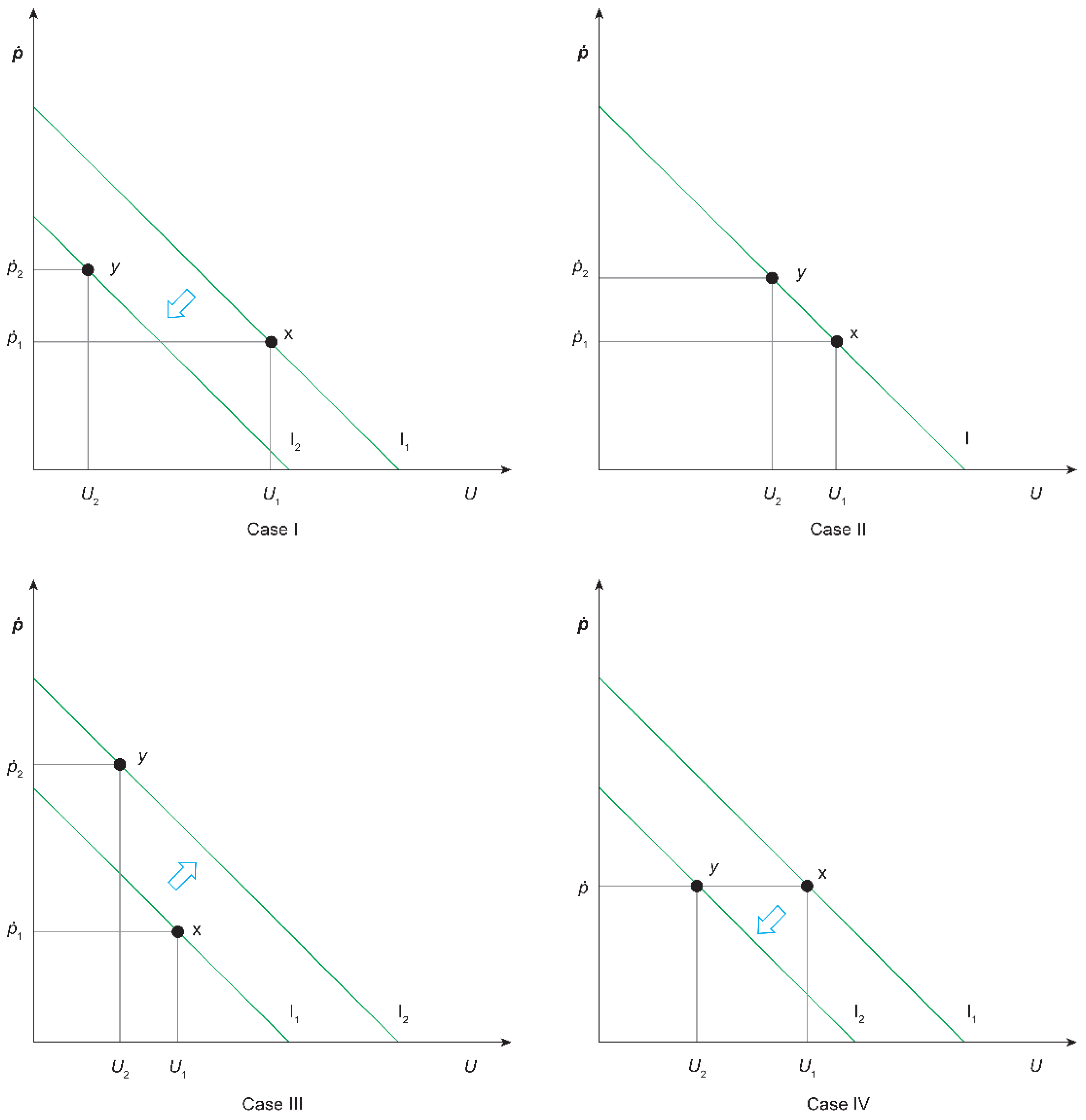
2.2. Misery Index and Tourism: A Theoretical Approach
3. Materials and Methods
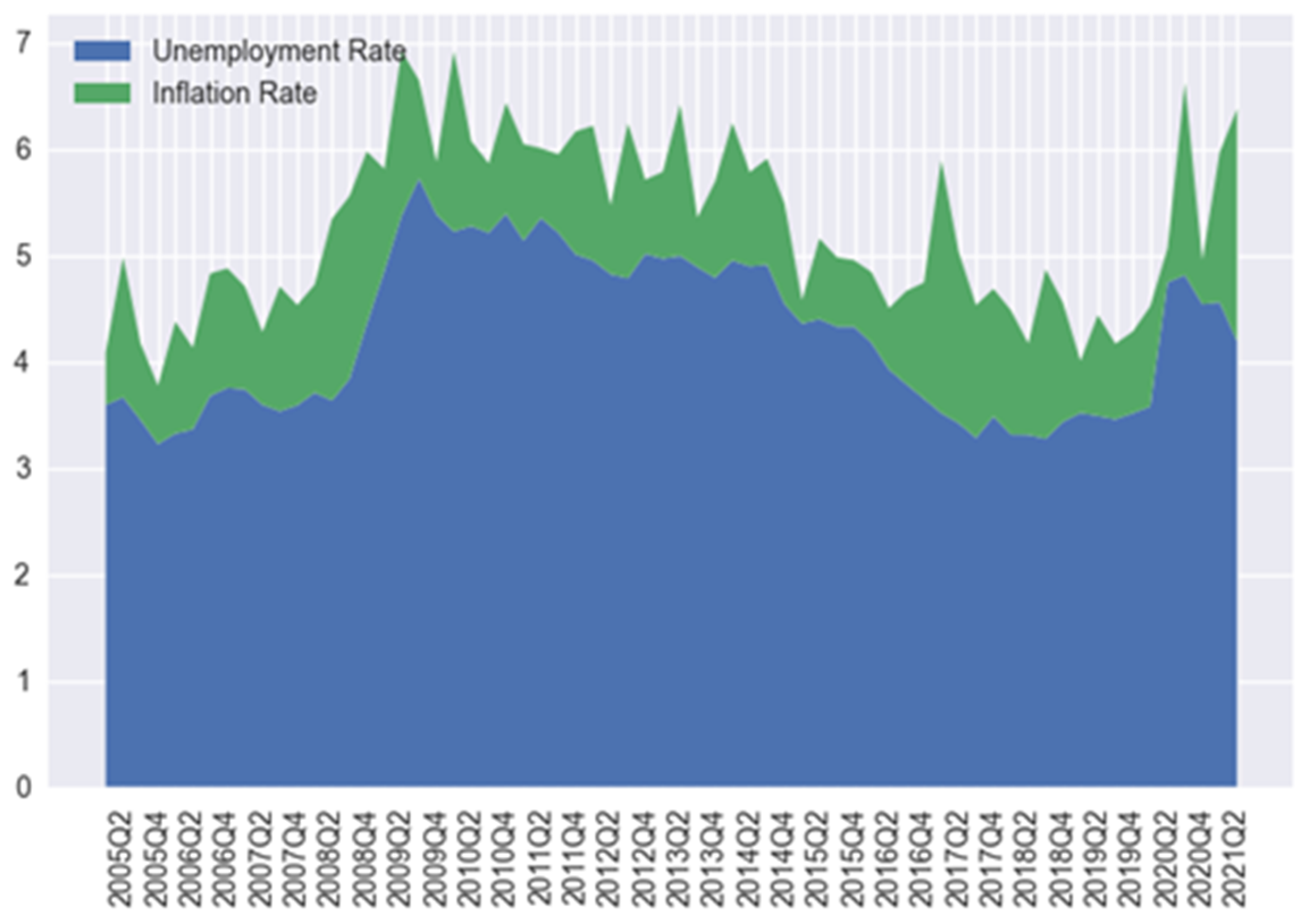
3.1. Data and Sources
3.2. Empirical Design
4. Econometric Results
4.1. Toda–Yamamoto Test
4.2. ARDL and NARDL Results
5. Discussion and Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | ||
|---|---|---|
| 0.486370 [3.71632] | −0.036460 [−0.28766] | |
| 0.190697 [1.40937] | −0.029390 [−0.22428] | |
| 0.301351 [2.38583] | 0.085348 [0.69772] | |
| −0.552577 [−3.76699] | 0.620055 [4.36469] | |
| 0.582592 [3.26334] | 0.170552 [0.98645] | |
| −0.274248 [−1.40300] | 0.016430 [0.08679] | |
| 1.435474 [2.44629] | 1.173544 [2.06506] | |
| −0.187397 [−1.56600] | 0.022278 [0.19223] | |
| 0.008204 [0.04996] | −0.077588 [−0.48791] | |
| R2 | 0.741200 | 0.575877 |
| Adjusted R2 | 0.702136 | 0.511859 |
| † No Serial Correlation at Lag h | † No Serial Correlation at Lags 1 to h | |||||||
|---|---|---|---|---|---|---|---|---|
| Lag | LRE Statistic | Probability | Rao F-Statistic | Probability | LRE statistic | Probability | Rao F-Statistic | Probability |
| 1 | 0.466954 | 0.9766 | 0.115850 | 0.9766 | 0.466954 | 0.9766 | 0.115850 | 0.9766 |
| 2 | 3.727481 | 0.4441 | 0.939881 | 0.4442 | 6.219976 | 0.6226 | 0.778125 | 0.6229 |
| 3 | 2.596007 | 0.6275 | 0.650905 | 0.6276 | 8.509696 | 0.7441 | 0.702972 | 0.7448 |
| 4 | 6.803495 | 0.1466 | 1.742048 | 0.1467 | 18.17077 | 0.3140 | 1.159333 | 0.3164 |
| 5 | 7.132377 | 0.1291 | 1.829269 | 0.1291 | 20.96745 | 0.3991 | 1.062157 | 0.4037 |
| 6 | 4.386771 | 0.3562 | 1.109760 | 0.3562 | 24.03872 | 0.4594 | 1.007796 | 0.4670 |
| 7 | 6.628582 | 0.1569 | 1.695776 | 0.1569 | 30.58035 | 0.3360 | 1.112894 | 0.3478 |
| 8 | 7.640418 | 0.1057 | 1.964563 | 0.1057 | 35.50292 | 0.3066 | 1.133835 | 0.3236 |
| 9 | 2.043158 | 0.7278 | 0.510882 | 0.7278 | 46.24712 | 0.1178 | 1.365721 | 0.1337 |
| 10 | 5.366479 | 0.2517 | 1.364259 | 0.2518 | 50.52674 | 0.1230 | 1.341029 | 0.1454 |
| 11 | 4.710405 | 0.3183 | 1.193558 | 0.3184 | 50.04443 | 0.2459 | 1.165777 | 0.2877 |
| 12 | 0.717403 | 0.9492 | 0.178207 | 0.9492 | 57.59061 | 0.1617 | 1.251829 | 0.2083 |
| Statistic | 1/ ARDL | 2/ NARDL | ||
|---|---|---|---|---|
| Value | Probability | Value | Probability | |
| Maximum LR F-statistic | 1.6565 | 0.4992 | 2.0874 | 0.1162 |
| Maximum Wald F-statistic | 18.2222 | 0.4992 | 25.0494 | 0.1162 |
| Exponential LR F-statistic | 0.5571 | 0.5713 | 0.7200 | 0.2215 |
| Exponential Wald F-statistic | 6.9326 | 0.4185 | 10.0447 | 0.1070 |
| Average LR F-statistic | 1.0969 | 0.3290 | 1.4207 | 0.1019 |
| Average Wald F-statistic | 12.0662 | 0.3290 | 17.0488 | 0.1019 |
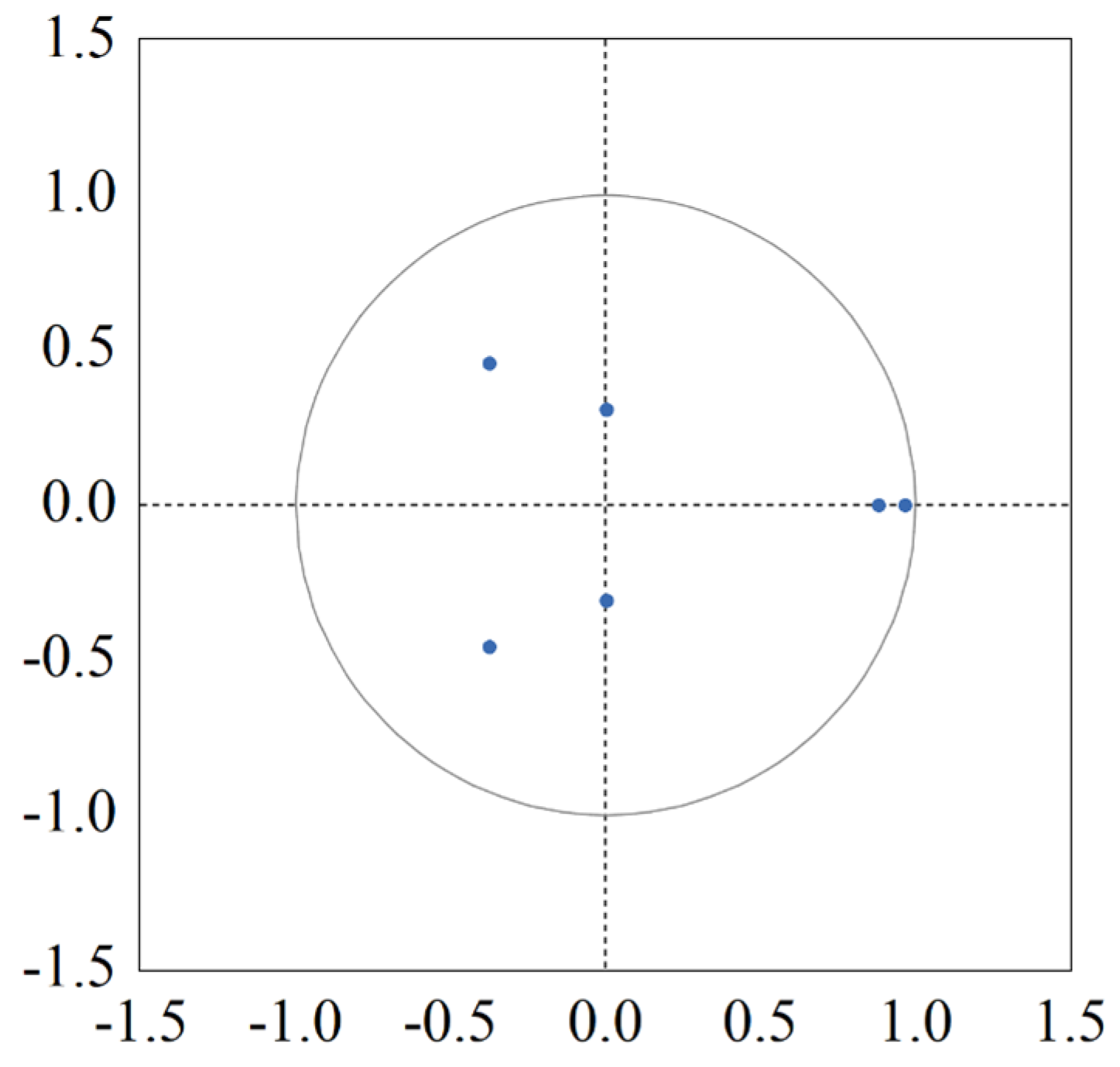
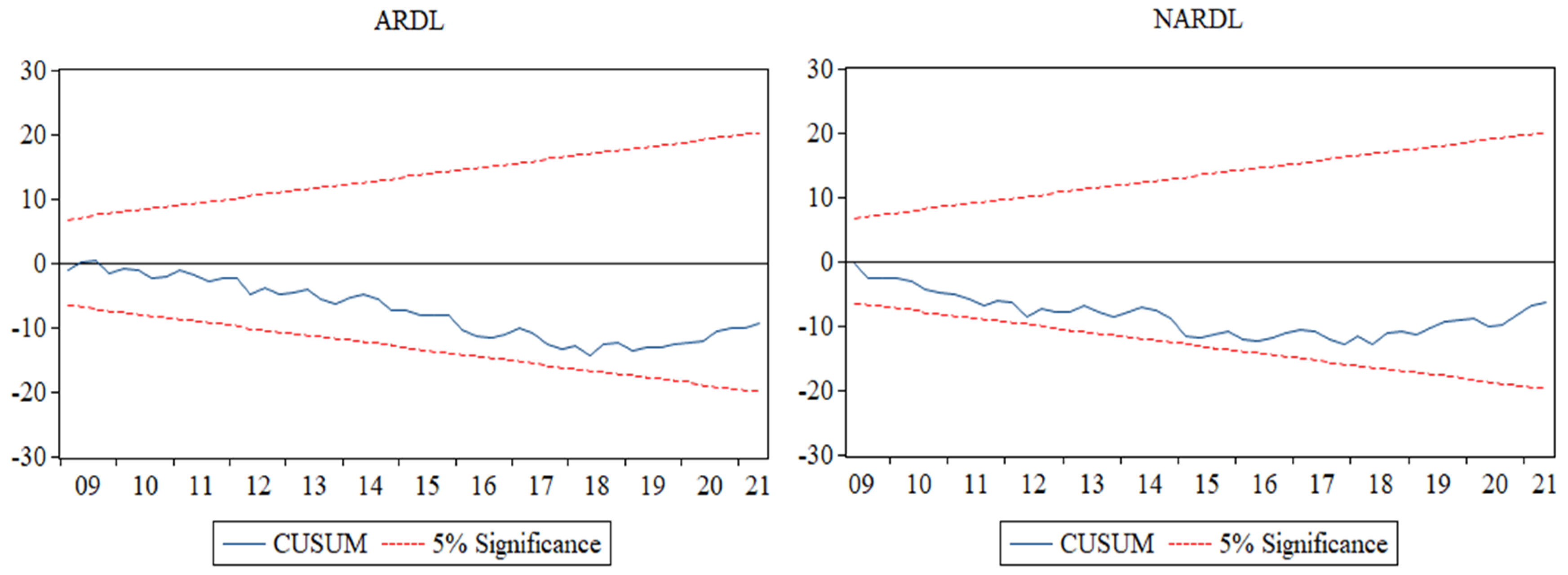

References
- Acerenza, Miguel Ángel. 2006. Efectos Económicos, Socioculturales y Ambientales del Turismo. Mexico: Trillas. [Google Scholar]
- Adrangi, Bahram, and Joseph Macri. 2019. Does the misery index influence a U.S. President’s political re-election prospects? Journal of Risk and Financial Management 12: 22. [Google Scholar] [CrossRef]
- Alegre, Joaquín, Llorenç Pou, and Maria Sard. 2019. High unemployment and tourism participation. Current Issues in Tourism 22: 1138–49. [Google Scholar] [CrossRef]
- Amiri, Arshia, and Bruno Ventelou. 2012. Granger causality between total expenditure on health and GDP in OECD: Evidence from the Toda–Yamamoto approach. Economics Letters 116: 541–44. [Google Scholar] [CrossRef]
- Andrés-Rosales, Roldán, Leobardo de Jesús-Almonte, Luis Quintana-Romero, and José Álvarez-García. 2023. National tourism and its role in the post-COVID economic recovery of the Mexican Regions. El Periplo Sustentable 45: 296–315. [Google Scholar] [CrossRef]
- Asher, Martin A., Robert H. Defina, and Kishor Thanawala. 1993. The misery index: Only part of the story. Challenge 36: 58–62. [Google Scholar] [CrossRef]
- Bhattarai, Kumar, Ghanshyam Upadhyaya, and Surendra Kumar Bohara. 2021. Tourism, employment generation and foreign exchange earnings in Nepal. Journal of Tourism & Hospitality Education 11: 1–21. [Google Scholar] [CrossRef]
- Blanchflower, David G., David N. F. Bell, Alberto Montagnoli, and Mirko Moro. 2014. The happiness trade-off between unemployment and inflation. Journal of Money, Credit and Banking 46: 117–41. [Google Scholar] [CrossRef]
- Brooks, Douglas H., and Pilipinas F. Quising. 2002. Dangers of Deflation. ERD Policy Brief Nº 12. Manila: Asian Development Bank. [Google Scholar]
- Burggraeve, K., G. De Walque, and H. Zimmer. 2015. The relationship between economic growth and employment. Economic Review 1: 31–50. [Google Scholar]
- Cakici, Nusret, and Adam Zaremba. 2023. Misery on Main Street, victory on Wall Street: Economic discomfort and the cross-section of global stock returns. Journal of Banking and Finance 149: 106760. [Google Scholar] [CrossRef]
- Candela, Guido, and Paolo Figini. 2012. The Economics of Tourism Destinations. Heidelberg: Springer. [Google Scholar] [CrossRef]
- Castillo, Fernando. 2022. CNET: Inflación en Turismo Dobla la Inflación General. La Agencia de Viajes México. Available online: https://mexico.ladevi.info/cnet/cnet-inflacion-turismo-dobla-la-inflacion-general-n42859#:~:text=A%20saber%2C%20al%20cierre%20de,Paquetes%20tur%C3%ADsticos%2016.3%25 (accessed on 24 September 2023).
- Clemens, Jason, Milagros Palacios, and Nathaniel Li. 2022. The Misery Index Returns. Fraser Research Bulletin. Available online: https://www.fraserinstitute.org/sites/default/files/misery-index-returns.pdf (accessed on 10 April 2023).
- Cohen, Ivan K., Fabrizio Ferretti, and Bryan McIntosh. 2014. Decomposing the misery index: A dynamic approach. Cogent Economics & Finance 2: 991089. [Google Scholar] [CrossRef]
- Coppin, Addington. 1993. Recent evidence on the determinants of inflation in a tourism-oriented economy: Barbados. Social and Economic Studies 42: 65–80. [Google Scholar]
- Dadgar, Yadollah, and Rouhollah Nazari. 2018. The impact of economic growth and good governance on misery index in Iranian economy. European Journal of Law and Economics 45: 175–93. [Google Scholar] [CrossRef]
- Di Tella, Rafael, Robert J. MacCulloch, and Andrew J. Oswald. 2001. Preferences over inflation and unemployment: Evidence from surveys of happiness. American Economic Review 91: 335–41. [Google Scholar] [CrossRef]
- Dornbusch, Rudiger, Stanley Fischer, and Richard Startz. 2002. Macroeconomía. Madrid: McGraw-Hill. [Google Scholar]
- Fahmi, Muhamad Shameer, Caroline Geetha, and Rosle Mohidin. 2019. Testing for unit roots and structural breaks in Malaysia unanticipated macroeconomic variables. Malaysian Journal of Business and Economics 6: 1–12. [Google Scholar]
- Ferguson, Lucy. 2010. Tourism as a Development Strategy in Central America: Exploring the Impact on Women’s Lives. CAWN Briefing Paper: March 2010. London: Central America Women’s Network. [Google Scholar]
- Forbes Staff. 2022. Alta Inflación e Inseguridad Afectan la Inversión en el Turismo Mexicano. Forbes México. Available online: https://www.forbes.com.mx/alta-inflacion-e-inseguridad-afectan-la-inversion-en-el-turismo-mexicano/ (accessed on 24 April 2023).
- Frent, Cristi. 2016. An overview on the negative impacts of tourism. Journal of Tourism—Studies and Research in Tourism 22: 32–7. [Google Scholar]
- Frisch, Helmut. 1983. Theories of Inflation. New York: Cambridge University Press. [Google Scholar] [CrossRef]
- Glynn, John, Nelson Perera, and Reetu Verma. 2007. Unit root tests and structural breaks: A survey with applications. Revista de Métodos Cuantitativos para la Economía y la Empresa 3: 63–79. [Google Scholar]
- Gould, John P., and Edward P. Lazear. 1994. Teoría Microeconómica. Mexico: Fondo de Cultura Económica. [Google Scholar]
- Grabia, Tomasz. 2011. The Okun misery index in the European Union countries from 2000 to 2009. Comparative Economic Research. Central and Eastern Europe 14: 97–115. [Google Scholar] [CrossRef]
- Gujarati, Damodar N., and Dawn C. Porter. 2009. Econometría. Mexico: McGraw-Hill. [Google Scholar]
- Hodrick, Robert J., and Edward C. Prescott. 1997. Postwar U.S. business cycles: An empirical investigation. Journal of Money, Credit and Banking 29: 1–16. [Google Scholar] [CrossRef]
- Hortalà, Joan, and Damià Rey. 2011. Relevancia del índice de malestar económico. Cuadernos de Economía 34: 162–69. [Google Scholar] [CrossRef]
- INEGI. 2021. Banco de Información Económica. Available online: https://www.inegi.org.mx/sistemas/bie/ (accessed on 11 December 2021).
- Jan, Ahmad Ali, Fong-Woon Lai, Mohammad Asif, Shakeb Akhtar, and Sami Ullah. 2023. Embedding sustainability into bank strategy: Implications for sustainable development goals reporting. International Journal of Sustainable Development & World Ecology 30: 229–43. [Google Scholar] [CrossRef]
- Khan, Mohd Naved, Ahmad Ali Jan, Mohammad Asif, Fong-Woon Lai, Muhammad Kashif Shad, and Saima Shadab. 2023. Do domestic innovations promote trade openness? Empirical evidence from emerging economies. Heliyon 9: e22848. [Google Scholar] [CrossRef]
- Kumar, Jeetesh, Kashif Hussain, and Suresh Kannan. 2015. Positive vs. negative economic impacts of tourism development: A review of economic impact studies. Paper presented at 21st Asia Pacific Tourism Association Annual Conference, Kuala Lumpur, Malaysia, May 14–17; Kuala Lumpur: APTA, pp. 405–13. [Google Scholar]
- Lechman, Ewa. 2009. Okun’s and Barro’s Misery Index as an Alternative Poverty Assessment Tool: Recent Estimations for European Countries. MPRA Paper No. 37493. Available online: http://mpra.ub.uni-muenchen.de/37493/ (accessed on 15 March 2023).
- Loría, Eduardo, and Emmanuel Salas. 2022. La ley de Okun en México, una relación asimétrica, 2005.01–2021.10. Investigación Económica 81: 156–73. [Google Scholar] [CrossRef]
- Loría, Eduardo Gilberto, Fernando Sánchez, and Emmanuel Salas. 2017. Efectos de la llegada de viajeros internacionales en el desempleo y el crecimiento económico en México, 2000.2–2015.2. El Periplo Sustentable 32: 1–24. [Google Scholar]
- Lovell, Michael C., and Pao-Lin Tien. 2000. Economic discomfort and consumer sentiment. Eastern Economic Journal 26: 1–8. [Google Scholar] [CrossRef]
- Masárová, Jana, Eva Koišová, and Valentinas Navickas. 2022. Changes in the Visegrad Group economies in light of the misery index. Intellectual Economics 16: 102–16. [Google Scholar]
- Mihalič, Tanja. 2014. Tourism and economic development issues. In Tourism and Development: Concepts and Issues. Edited by Richard Sharpley and David J. Telfer. Bristol: Channel View Publications, pp. 77–117. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar. 2005. The saving and investment nexus for China: Evidence from cointegration tests. Applied Economics 37: 1979–90. [Google Scholar] [CrossRef]
- Neely, Christopher J. 2010. Okun’s Law: Output and unemployment. Economic Synopses 4: 1–2. [Google Scholar] [CrossRef]
- Nessen, Ron. 2008. The Brookings Institution’s Arthur Okun—Father of the “Misery Index”. Brookings. Available online: https://www.brookings.edu/opinions/the-brookings-institutions-arthur-okun-father-of-the-misery-index/ (accessed on 10 March 2023).
- Nkoro, Emeka, and Aham Kelvin Uko. 2016. Autoregressive Distributed Lag (ARDL) cointegration technique: Application and interpretation. Journal of Statistical and Econometric Methods 5: 63–91. [Google Scholar]
- Olayeni, Olaolu Richard. 2019. NARDL: Implementation Using EViews Add-In. Research Gate Working Paper. Ile-Ife: Obafemi Awolowo University. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Phong, Le Hoang, Dang Thi Bach Van, and Ho Hoang Gia Bao. 2019. A nonlinear autoregressive distributed lag (NARDL) analysis on the determinants of Vietnam’s stock market. In Beyond Traditional Probabilistic Methods in Economics. Edited by Vladik Kreinovich, Nguyen Ngoc Thach, Nguyen Duc Trung and Dang Van Thanh. ECONVN 2019. Studies in Computational Intelligence. Cham: Springer, vol. 809, pp. 363–76. [Google Scholar] [CrossRef]
- Postma, Albert, and Dirk Schmuecker. 2017. Understanding and overcoming negative impacts of tourism in city destinations: Conceptual model and strategic framework. Journal of Tourism Futures 3: 144–56. [Google Scholar] [CrossRef]
- Riascos, Julio C. 2009. El índice de malestar económico o índice de miseria de Okun: Breve análisis de casos, 2001–2008. Tendencias 10: 92–124. [Google Scholar]
- Robinson, Richard N. S., Antje Martins, David Solnet, and Tom Baum. 2019. Sustaining precarity: Critically examining tourism and employment. Journal of Sustainable Tourism 27: 1008–25. [Google Scholar] [CrossRef]
- Rotar, Laura Južnik, Sergej Gričar, and Štefan Bojnec. 2023. The relationship between tourism and employment: Evidence from the Alps-Adriatic country. Economic Research-Ekonomska Istraživanja 36: 2080737. [Google Scholar] [CrossRef]
- Sam, Chung Yan, Robert McNown, and Soo Khoon Goh. 2019. An augmented autoregressive distributed lag bounds test for cointegration. Economic Modelling 80: 130–41. [Google Scholar] [CrossRef]
- Sánchez, Fernando. 2019. Unemployment and Growth in the Tourism Sector in Mexico: Revisiting the Growth-Rate Version of Okun’s Law. Economies 7: 83. [Google Scholar] [CrossRef]
- Sánchez, Fernando. 2022a. The effect of international visitors on poverty alleviation in Mexico: An approach from the misery index. Journal of Applied Economics 25: 839–55. [Google Scholar] [CrossRef]
- Sánchez, Fernando. 2022b. The influence of registered divorces on outbound tourism: Empirical evidence from Mexico. Current Issues in Tourism 25: 2939–954. [Google Scholar] [CrossRef]
- Sancho, Amparo. 1998. Introducción al Turismo. Madrid: Organización Mundial del Turismo. [Google Scholar]
- Santos, Eleonora. 2023. Does inbound tourism create employment? In Rethinking Management and Economics in the New 20′s. Edited by Eleonora Santos, Neuza Ribeiro and Teresa Eugénio. Singapore: Springer, pp. 483–90. [Google Scholar] [CrossRef]
- Shaari, M. S., T. Salha Tunku Ahmad, and R. Razali. 2018. Tourism led-Inflation: A case of Malaysia. MATEC Web of Conferences 150: 06026. [Google Scholar] [CrossRef][Green Version]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In Festschrift in Honor of Peter Schmidt: Econometric Methods and Applications. Edited by Robin C. Sickles and William C. Horrace. New York: Springer, pp. 281–314. [Google Scholar] [CrossRef]
- Sulasmiyati, Sri. 2018. Analyzing inflation influence toward the number of foreign tourists visiting Indonesia and their impact on Indonesia’s economic growth. Media Bina Ilmiah 14: 2181–186. [Google Scholar] [CrossRef]
- Szczepański, Marcin. 2015. Understanding Deflation: Falling Prices and Their Impact on the Economy. EPRS Briefing: June 2015. Brussels: European Parliament Research Service. [Google Scholar]
- Tangarife, Carmen Lucía. 2013. La economía va bien pero el empleo va mal: Factores que han explicado la demanda de trabajo en la industria colombiana durante los años 2002–2009. Perfil de Coyuntura Económica 21: 39–61. [Google Scholar]
- Toda, Hiro Y., and Taku Yamamoto. 1995. Statistical inference in vector autoregressions with possibly integrated processes. Journal of Econometrics 66: 225–50. [Google Scholar] [CrossRef]
- Tribe, John. 2011. The Economics of Recreation, Leisure and Tourism. London: Routledge. [Google Scholar] [CrossRef]
- Tule, K. Moses, Eunice Ngozi Egbuna, Eme Dada, and Godday Uwawunkonye Ebuh. 2017. A dynamic fragmentation of the misery index in Nigeria. Cogent Economics & Finance 5: 1336295. [Google Scholar] [CrossRef]
- Vanhove, N. 1981. Tourism and employment. International Journal of Tourism Management 2: 162–75. [Google Scholar] [CrossRef]
- Varian, Hal R. 1999. Microeconomía Intermedia: Un Enfoque Actual. Barcelona: Antoni Bosch. [Google Scholar]
- Walmsley, Andreas. 2017. Overtourism and underemployment: A modern labour market dilemma. In 13th International Conference on Responsible Tourism in Destinations. Reykjavik: Icelandic Tourism Research Centre. [Google Scholar]
- Wang, Jinli, and Wanqing Lv. 2023. Tourism poverty alleviation hotspots in China: Topic evolution and sustainable development. Sustainable Development 31: 1902–920. [Google Scholar] [CrossRef]
- Weinz, Wolfgang, and Lucie Servoz. 2013. Poverty Reduction through Tourism. Geneva: International Labour Office. [Google Scholar]
- Winkelmann, Liliana, and Rainer Winkelmann. 1998. Why are the unemployed so unhappy? Evidence from panel data. Economica 65: 1–15. [Google Scholar] [CrossRef]
- Wiseman, Clark. 1992. More on misery: How consistent are alternative indices? A comment. The American Economist 36: 85–88. [Google Scholar] [CrossRef]
- Yılancı, Veli, and Mustafa Kırca. 2023. Testing the relationship between employment and tourism: A fresh evidence from the ARDL bounds test with sharp and smooth breaks. Journal of Hospitality and Tourism Insights 7: 394–413. [Google Scholar] [CrossRef]
- Zhao, Jinfang, Dongxu Yang, Xia Zhao, and Minghua Lei. 2023. Tourism industry and employment generation in emerging seven economies: Evidence from novel panel methods. Economic Research-Ekonomska Istraživanja 36: 2206471. [Google Scholar] [CrossRef]




| Series | Innovation Outlier | Additive Outlier | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | C | D | |
| −3.507 | −4.282 | −4.476 | −3.685 | −3.578 | −4.611 | −4.636 | −2.515 | |
| −3.481 | −7.556 *** | −6.806 *** | −7.299 *** | −3.536 | −7.482 *** | −5.248 ** | −6.512 *** | |
| −12.42 *** | −12.32 *** | −12.18 *** | −12.19 *** | −12.89 *** | −12.95 *** | −13.03 *** | −12.45 *** | |
| −28.07 *** | −28.01 *** | −20.98 *** | −10.72 *** | −18.85 *** | −18.53 *** | −12.83 *** | −11.09 *** | |
| Lag | LR | FPE | AIC | SIC | HQ |
|---|---|---|---|---|---|
| 0 | NA | 0.000220 | −2.744238 | −2.673188 | −2.716562 |
| 1 | 77.30244 | 6.21 × 10−5 | −4.011806 | −3.798656 * | −3.928780 |
| 2 | 12.67513 | 5.61 × 10−5 | −4.113028 | −3.757779 | −3.974651 |
| 3 | 13.06379 * | 4.99 × 10−5 * | −4.231250 * | −3.733901 | −4.037522 * |
| 4 | 2.207954 | 5.50 × 10−5 | −4.138379 | −3.498931 | −3.889301 |
| 5 | 7.979417 | 5.35 × 10−5 | −4.170223 | −3.388675 | −3.865794 |
| 6 | 2.130441 | 5.89 × 10−5 | −4.079635 | −3.155988 | −3.719856 |
| 7 | 5.211766 | 6.04 × 10−5 | −4.062908 | −2.997161 | −3.647778 |
| 8 | 7.286233 | 5.87 × 10−5 | −4.102690 | −2.894844 | −3.632209 |
| Null Hypothesis | d.f. | Probability | |
|---|---|---|---|
| does not Granger—cause | 19.87448 | 3 | 0.0002 *** |
| does not Granger—cause | 0.535597 | 3 | 0.9110 |
| Test | ARDL | NARDL | ||
|---|---|---|---|---|
| Value | Probability | Value | Probability | |
| Jarque–Bera Normality Test | 0.8963 | 0.6388 | 0.0112 | 0.9943 |
| Breusch–Godfrey Serial Correlation LM Test (12) | 14.0657 | 0.2965 | 19.4222 | 0.0788 |
| Breusch–Pagan–Godfrey Heteroskedasticity Test | 3.9469 | 0.9497 | 7.1621 | 0.7858 |
| ARCH LM Test (12) | 11.5906 | 0.4791 | 12.3488 | 0.4181 |
| RESET Ramsey Test | 0.1220 | 0.7284 | 1.0141 | 0.3190 |
| F-Statistic | 39.6356 | 0.0000 *** | 26.8249 | 0.0000 *** |
| 0.8879 | - | 0.8575 | - | |
| 0.8655 | - | 0.8256 | - | |
| Variable | ARDL | NARDL | ||
|---|---|---|---|---|
| Coefficient | t-Statistic | Coefficient | t-Statistic | |
| 2.5372 | 5.9071 *** | 0.4741 | 4.0594 *** | |
| −0.2097 | −3.7625 *** | −0.2277 | −3.4680 *** | |
| −0.4751 | −5.4399 *** | - | - | |
| † | - | - | −0.5268 | −4.6388 *** |
| - | - | −0.5442 | −3.9848 *** | |
| −0.3889 | −4.2147 *** | −0.3575 | −3.3278 *** | |
| −0.3172 | −3.3692 *** | −0.2363 | −2.1240 ** | |
| 0.0715 | 0.8072 | 0.1864 | 1.7436 * | |
| −0.2560 | −3.0522 *** | −0.1994 | −2.0504 ** | |
| −0.3212 | −3.3133 *** | - | - | |
| −0.2388 | −2.2550 ** | - | - | |
| 0.2967 | 2.7638 *** | - | - | |
| - | - | −0.3829 | −3.2130 *** | |
| - | - | −0.2850 | −1.8594 * | |
| - | - | 0.4729 | 2.9682 *** | |
| 0.1965 | 7.1478 *** | - | - | |
| - | - | 0.2495 | 5.3856 *** | |
| Model | Actual Sample | Overall
-Bounds Test | Exogenous -Bounds Test | -Bounds Test | ||||
| ARDL | 18.44210 *** | 29.59347 *** | −3.762507 ** | |||||
| NARDL | 9.005597 *** | 11.12199 *** | −3.468082 * | |||||
| Critical values. | ||||||||
| Model | Finite Sample | Overall F-Bounds Test | Exogenous -Bounds Test | -Bounds Test | ||||
| ARDL | 7.32 | 8.435 | 7.22 | 11.85 | −3.13 | −3.5 | ||
| 7.4 | 8.51 | 7.03 | 11.84 | |||||
| NARDL | 5.583 | 6.853 | 4.99 | 8.24 | −2.57 | −3.21 | ||
| 5.697 | 6.987 | 5.03 | 8.10 | |||||
| ARDL | NARDL | |||
|---|---|---|---|---|
| Long-term coefficients | ||||
| Variables | Coefficient | t-Statistic | Coefficient | t-Statistic |
| −2.2645 | −3.4440 *** | - | - | |
| - | - | −2.3129 | −3.2705 *** | |
| - | - | −2.3896 | −3.0275 *** | |
| Constant | 12.0938 | 3.9923 *** | 2.0818 | 15.2320 *** |
| Error correction terms. | ||||
| −0.2097 | −6.3581 *** | - | - | |
| - | - | −0.2277 | −5.3551 *** | |
| Long-Term Asymmetries | |||
|---|---|---|---|
| Test Statistic | Value | df | Probability |
| 0.109720 | 1 | 0.7405 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez López, F. Tourism and Economic Misery: Theory and Empirical Evidence from Mexico. Economies 2024, 12, 88. https://doi.org/10.3390/economies12040088
Sánchez López F. Tourism and Economic Misery: Theory and Empirical Evidence from Mexico. Economies. 2024; 12(4):88. https://doi.org/10.3390/economies12040088
Chicago/Turabian StyleSánchez López, Fernando. 2024. "Tourism and Economic Misery: Theory and Empirical Evidence from Mexico" Economies 12, no. 4: 88. https://doi.org/10.3390/economies12040088
APA StyleSánchez López, F. (2024). Tourism and Economic Misery: Theory and Empirical Evidence from Mexico. Economies, 12(4), 88. https://doi.org/10.3390/economies12040088






