The Asymmetric Effects of Unemployment and Output on Inflation in Greece: A Nonlinear ARDL Approach
Abstract
1. Introduction
2. Literature Review
3. Methodology and Model
4. Data
5. Empirical Analysis
5.1. Unit Root Tests
5.2. BDS Test
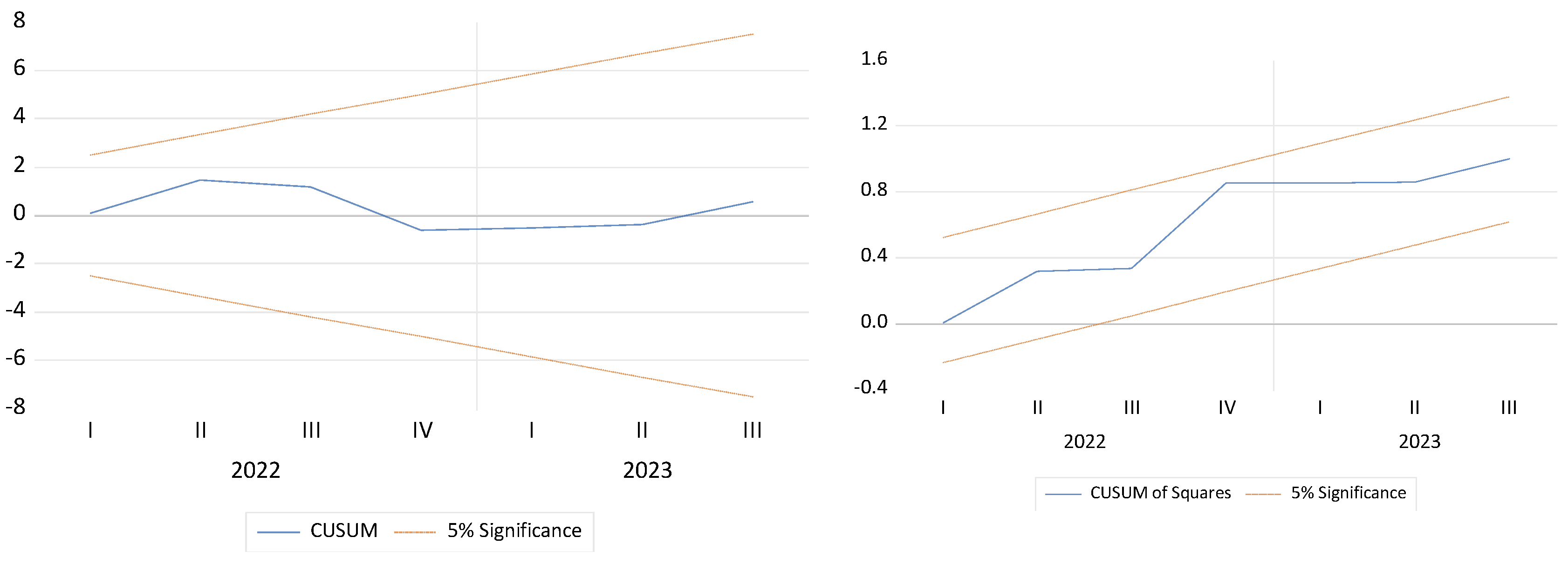
5.3. Robustness Checks
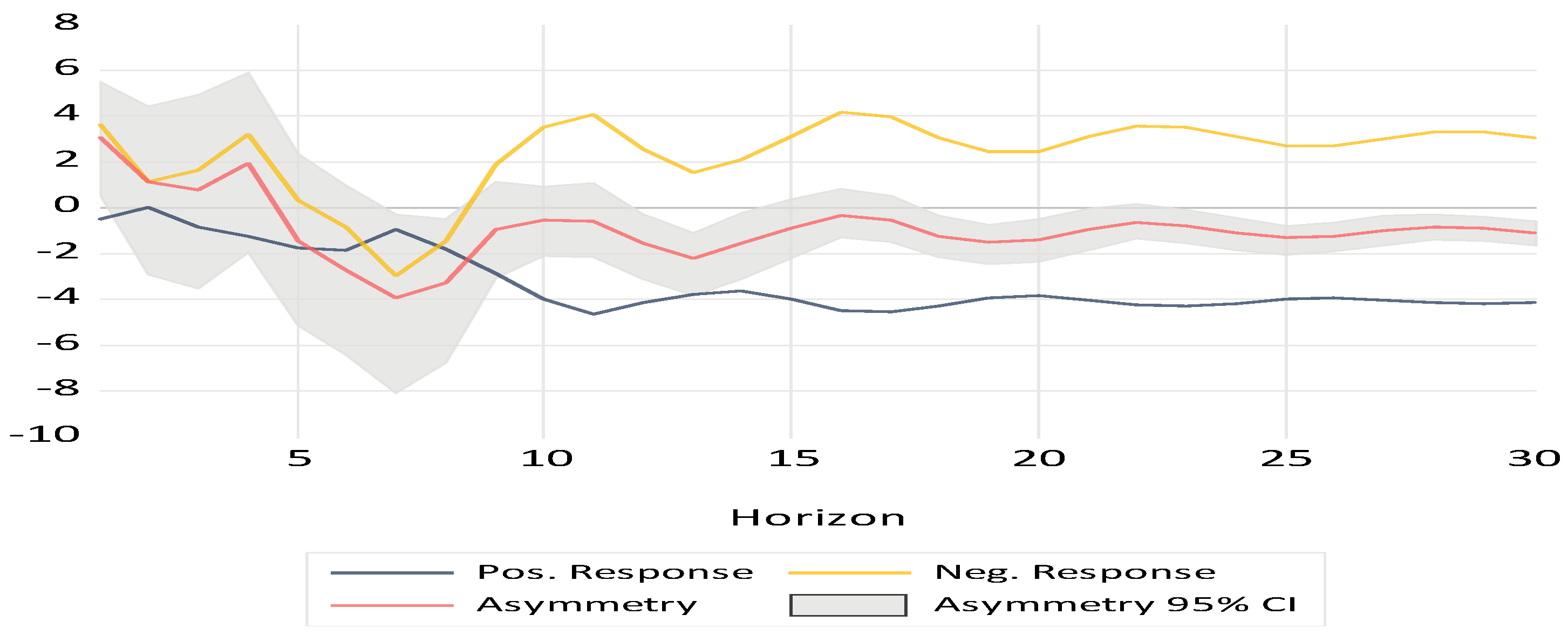
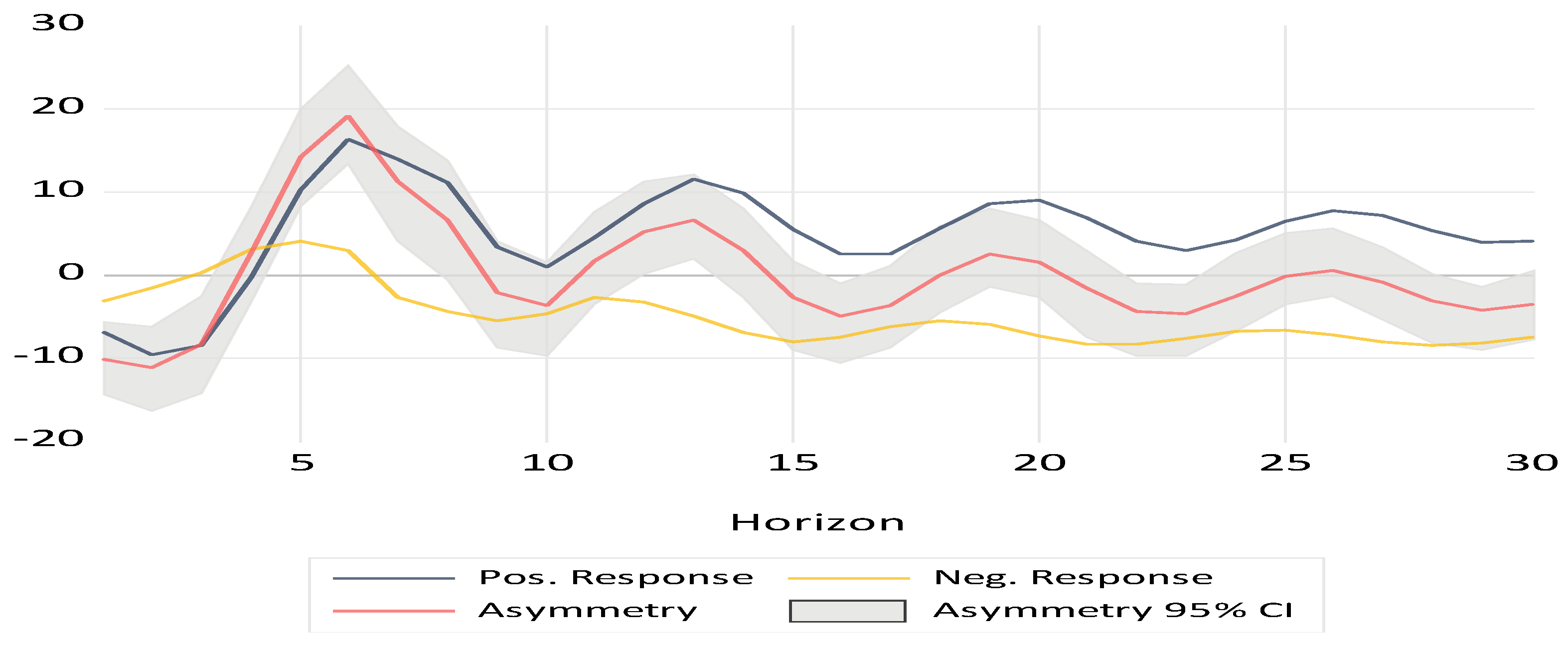
6. Discussion of the Empirical Findings
7. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The NAIRU is the lowest unemployment rate that can be sustained without causing wages growth and inflation to rise. Below this level of unemployment, inflationary pressures tend to increase, and above these inflationary pressures tend to decrease. |
| 2 | Available at: https://www.ecb.europa.eu/press/key/date/2020/html/ecb.sp200211_2~eae18c54ff.en.html (accessed on 1 September 2024). |
References
- Abid, Mehdi, Mohammed Benmeriem, Zouheyr Gheraia, Habib Sekrafi, Hanane Abdelli, and Abdelhadi Meddah. 2023. Asymmetric effects of economy on unemployment in Algeria: Evidence from a nonlinear ARDL approach. Cogent Economics & Finance 11: 2192454. [Google Scholar] [CrossRef]
- Ahn, JaeBin, and Jiwon Lee. 2023. The Role of Import Prices in Flattening the Phillips Curve: Evidence from Korea. Journal of Asian Economics 86: 101605. [Google Scholar] [CrossRef]
- Akaike, Hirotugu. 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19: 716–23. [Google Scholar] [CrossRef]
- Al-Nassar, Nassar S., and Abdulrahman A. Albahouth. 2023. Inflation Spillovers among Advanced and Emerging Economies: Evidence from the G20 Group. Economies 11: 126. [Google Scholar] [CrossRef]
- Ascari, Guido, and Luca Fosso. 2021. The Inflation Rate Disconnect Puzzle: On the International Component of Trend Inflation and the Flattening of the Phillips Curve. Norges Bank Working Papers. Available online: https://ssrn.com/abstract=3999368 (accessed on 10 September 2024).
- Baba, Chikako, Mr Romain A. Duval, Romain Duval, Ting Lan, and Petia Topalova. 2023. The 2020–2022 Inflation Surge Across Europe: A Phillips-Curve-Based Dissection. IMF Working Paper, No. 2023/030. Bretton Woods: International Monetary Fund. [Google Scholar]
- Baghli, Mustapha, Christophe Cahn, and Henri Fraisse. 2007. Is the inflation–output Nexus asymmetric in the Euro area? Economics Letters 94: 1–6. [Google Scholar] [CrossRef]
- Ball, Laurence M., and Sandeep Mazumder. 2011. Inflation Dynamics and the Great Recession. NBER Working Paper No. w17044. Available online: https://ssrn.com/abstract=1841281 (accessed on 10 August 2024).
- Ball, Laurence M., Gita Gopinath, Daniel Leigh, Prachi Mishra, and Antonio Spilimbergo. 2021. US Inflation: Set for Takeoff? Voxeu.org. CEPR Policy Portal 7. Available online: https://cepr.org/voxeu/columns/us-inflation-set-take (accessed on 10 August 2024).
- Benigno, Pierpaolo, and Gauti B. Eggertsson. 2023. It’s Baaack: The Surge in Inflation in the 2020s and the Return of the Non-Linear Phillips Curve. Cambridge, MA: National Bureau of Economic Research, p. w31197. [Google Scholar] [CrossRef]
- Biçer, Burhan, and Almila Burgac Cil. 2023. Symmetric and Asymmetric Dynamics of Output Gap and Inflation Relation for Turkish Economy. Prague Economic Papers 32: 520–49. [Google Scholar] [CrossRef]
- Bildirici, Melike, and Fulya Ozaksoy. 2016. Non-linear analysis of post Keynesian Phillips curve in Canada labor market. Procedia Economics and Finance 38: 368–77. [Google Scholar] [CrossRef]
- Bildirici, Melike, and Fulya Ozaksoy. 2018. Backward bending structure of Phillips curve in Japan, France, Turkey and the U.S.A. Economic Research 31: 537–49. [Google Scholar] [CrossRef]
- Blanchard, Olivier, Eugenio Cerutti, and Lawrence Summers. 2015. Inflation and Activity: Two Explorations and Their Monetary Policy Implications. ECB Forum on Central Banking. Cambridge, MA: National Bureau of Economic Research. [Google Scholar]
- Boehm, Christoph E., and Nitya Pandalai-Nayar. 2022. Convex Supply Curves. American Economic Review 112: 3941–69. [Google Scholar] [CrossRef]
- Broock, William A., José Alexandre Scheinkman, W. Davis Dechert, and Blake LeBaron. 1996. A test for independence based on the correlation dimension. Econometric Reviews 15: 197–235. [Google Scholar] [CrossRef]
- Brown, Robert L., James Durbin, and James M. Evans. 1975. Techniques for testing the constancy of regression relationships over time. Journal of the Royal Statistical Society Series B: Statistical Methodology 37: 149–92. [Google Scholar] [CrossRef]
- Caballero, Ricardo J., and Mohamad Hammour. 1994. The cleansing effect of recession. American Economic Review 84: 1350–68. [Google Scholar]
- Ciccarelli, Matteo, and Benoit Mojon. 2010. Global Inflation. The Review of Economics and Statistics 92: 524–35. [Google Scholar] [CrossRef]
- Clark, Peter, Douglas Laxton, and David Rose. 1996. Asymmetry in the US output-inflation nexus. IMF Staff Papers 43: 216–51. [Google Scholar] [CrossRef]
- Coibion, Olivier, and Yuriy Gorodnichenko. 2015. Is the Phillips Curve Alive and Well after All? Inflation Expectations and the Missing Disinflation. American Economic Journal: Macroeconomics 7: 197–232. [Google Scholar] [CrossRef]
- Cristini, Annalisa, and Piero Ferri. 2021. Nonlinear models of the Phillips curve. Journal of Evolutionary Economics 31: 1129–55. [Google Scholar] [CrossRef]
- Del Negro, Marco, Michele Lenza, Giorgio E. Primiceri, and Andrea Tambalotti. 2020. What’s Up with the Phillips Curve? NBER Working Paper No. 27003. Cambridge, MA: National Bureau of Economic Research. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1979. Distributions of the estimators for autoregressive time series with a unit root. Journal of American Statistical Association 74: 427–31. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Dixon, Huw. 1988. Controversy: The macroeconomics of unemployment in the OECD. The Economic Journal 108: 779–81. [Google Scholar] [CrossRef]
- Donayre, Luiggi, and Irina Panovska. 2016. Nonlinearities in the U.S. wage Phillips Curve. Journal of Macroeconomics 48: 19–43. [Google Scholar] [CrossRef]
- Economides, George, and Apostolis Philippopoulos. 2022. What Is Next? Public Debt and Economic Growth in Greece. CESifo Forum. Munich: Ifo Institute—Leibniz Institute for Economic Research at the University of Munich, vol. 23, pp. 24–29. [Google Scholar]
- Economides, George, Dimitris Papageorgiou, and Apostolis Philippopoulos. 2021. Austerity, Assistance and Institutions: Lessons from the Greek Sovereign Debt Crisis. Open Economies Review 32: 435–78. [Google Scholar] [CrossRef]
- Forbes, Kristin J., Joseph Gagnon, and Christopher G. Collins. 2021. Pandemic Inflation and Nonlinear, Global Phillips Curves. Voxeu.org. CEPR Policy Portal 21. Available online: https://voxeu.org/article/pandemic-inflation-and-nonlinear-global-phillips-curves (accessed on 19 August 2024).
- Friedman, Milton. 1968. The Role of Monetary Policy. American Economic Review 58: 1–17. [Google Scholar]
- Gagnon, Joseph, and Madi Sarsenbayev. 2022. 25 Years of Excess Unemployment in Advanced Economies: Lessons for Monetary Policy. Working Paper Series WP22-17. Washington, DC: Peterson Institute for International Economics. [Google Scholar]
- Granger, Clive W. J., and Yongil Jeon. 2011. The evolution of the Phillips curve: A modern time series viewpoint. Economica 78: 51–66. [Google Scholar] [CrossRef]
- Gross, Marco, and Willi Semmler. 2019. Mind the output gap: The disconnect of growth and inflation during recessions and convex phillips curves in the euro area. Oxford Bulletin of Economics and Statistics 81: 817–48. [Google Scholar] [CrossRef]
- Gürkaynak, Refet S., Andrew Levin, and Eric Swanson. 2010. Targeting anchor long-run inflation expectations? evidence from long-term bond yields in the U.S., U.K., and Sweden. Journal of the European Economic Association 8: 1208–42. [Google Scholar]
- Harding, Martín, Jesper Lindé, and Mathias Trabandt. 2023. Understanding Post-COVID Inflation Dynamics. Journal of Monetary Economics 140: 101–18. [Google Scholar] [CrossRef]
- Haschka, Rouven E. 2024. Examining the New Keynesian Phillips Curve in the U.S.: Why has the relationship between inflation and unemployment weakened? Research in Economics 78: 100987. [Google Scholar] [CrossRef]
- Hindrayanto, Irma, Anna Samarina, and Irina M. Stanga. 2019. Is the Phillips curve still alive? Evidence from the euro area. Economics Letters 174: 149–52. [Google Scholar] [CrossRef]
- Hobijn, Bart, Russell Miles, James Royal, and Jing Zhang. 2023. The Recent Steepening of Phillips Curves. Chicago Fed Letter 475. Available online: https://www.chicagofed.org/publications/chicago-fed-letter/2023/475 (accessed on 11 December 2024). [CrossRef]
- Hodrick, Robert J., and Edward C. Prescott. 1997. Business Cycles: An Empirical Investigation. Journal of Money, Credit and Banking 29: 1–16. [Google Scholar] [CrossRef]
- Huh, Hyeon-seung, and Inwon Jang. 2007. Nonlinear Phillips curve, sacrifice ratio, and the natural rate of unemployment. Economic Modelling 24: 797–813. [Google Scholar] [CrossRef]
- Inoue, Atsushi, Barbara Rossi, and Yiru Wang. 2024. Has the Phillips Curve Flattened? CEPR Discussion Paper, No. 18846. London: Centre for Economic Policy Research. [Google Scholar]
- International Monetary Fund. 2013. The Dog that Didn’t bark: Has Inflation Been Muzzled or Was It Just Sleeping? In World Economic Outlook: Hopes, Realities, Risks. Bretton Woods: International Monetary Fund, pp. 79–96. [Google Scholar]
- Jašová, Martina, Richhild Moessner, and Előd Takáts. 2018. Domestic and global output gaps as inflation drivers: What does the Phillips curve tell? Economic Modelling 87: 238–53. [Google Scholar] [CrossRef]
- Jorgensen, Peter Lihn, and Kevin J. Lansing. 2024. Anchored Inflation Expectations and the Slope of the Phillips Curve. Federal Reserve Bank of San Francisco Working Paper No. 2019–27. San Francisco: Federal Reserve Bank of San Francisco. [Google Scholar]
- Kumar, Anil, and Pia M. Orrenius. 2016. A closer look at the Phillips curve using state-level data. Journal of Macroeconomics 47: 84–102. [Google Scholar] [CrossRef]
- Lahcen, Mohammed Ait, Garth Baughman, Stanislav Rabinovich, and Hugo van Buggenum. 2022. Nonlinear unemployment effects of the inflation tax. European Economic Review 148: 104247. [Google Scholar] [CrossRef]
- Laxton, Douglas, David Rose, and Demosthenes Tambakis. 1999. The U.S. Phillips curve: The case for asymmetry. Journal of Economic Dynamics and Control 23: 1459–85. [Google Scholar] [CrossRef]
- Lepetit, Antoine. 2020. Asymmetric unemployment fluctuations and monetary policy trade-offs. Review of Economic Dynamics 36: 29–45. [Google Scholar] [CrossRef]
- Li, Youshu, and Junjie Guo. 2022. The asymmetric impacts of oil price and shocks on inflation in BRICS: A multiple threshold nonlinear ARDL model. Applied Economics 54: 1377–95. [Google Scholar] [CrossRef]
- Lucas, Robert E. 1973. Some International Evidence on Output-Inflation Trade-offs. American Economic Review 63: 326–34. [Google Scholar]
- MacKinnon, James. 1996. Numerical Distribution Functions for Unit Root and Cointegration Tests. Journal of Applied Econometrics 11: 601–18. [Google Scholar] [CrossRef]
- Macklem, Tiff. 1997. Capacity constraints, price adjustment, and monetary policy. Bank of Canada Review 1997: 39–56. [Google Scholar]
- McLeay, Michael, and Silvana Tenreyro. 2020. Optimal inflation and the identification of the Phillips Curve. The University of Chicago Press Journals 34: 199–255. [Google Scholar] [CrossRef]
- Mihajlović, Vladimir, and Gordana Marjanović. 2020. Asymmetries in effects of domestic inflation drivers in the Baltic States: A Phillips curve-based nonlinear ARDL approach. Baltic Journal of Economics 20: 94–116. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar. 2005. The saving and investment nexus for China: Evidence from cointegration tests. Applied Economics 37: 1979–90. [Google Scholar] [CrossRef]
- Newey, Whitney K., and Kenneth D. West. 1994. Automatic lag selection in covariance matrix estimation. Review of Economic Studies 61: 631–53. [Google Scholar] [CrossRef]
- OECD Statistics. 2024. Available online: https://data.oecd.org/ (accessed on 1 August 2024).
- Orphanides, Athanasios, and John C. Williams. 2005. Inflation scares and forecast-based monetary policy. Review of Economic Dynamics 8: 498–527. [Google Scholar] [CrossRef]
- Önder, A. Özlem. 2009. The stability of the Turkish Phillips curve and alternative regime shifting models. Applied Economics 41: 2597–604. [Google Scholar] [CrossRef]
- Passamani, Giuliana, Alessandro Sardone, and Roberto Tamborini. 2022. Inflation puzzles, the Phillips Curve and output expectations: New perspectives from the Euro Zone. Empirica 49: 123–53. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Pham, Binh Thai, and Hector Sala. 2022. Cross-country connectedness in inflation and unemployment: Measurement and macroeconomic consequences. Empirical Economics 62: 1123–46. [Google Scholar] [CrossRef] [PubMed]
- Phelps, Edmund S. 1967. Phillips Curves, Expectations of Inflation and Optimal Unemployment Over Time. Economica 34: 254–81. [Google Scholar] [CrossRef]
- Phillips, Alban W. 1958. The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861–957. Economica 25: 283–99. [Google Scholar]
- Phillips, Peter C., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Pissarides, Christopher A. 2000. Equilibrium Unemployment Theory. Cambridge, MA: MIT Press. [Google Scholar]
- Pissarides, Christopher A. 2013. Unemployment in the great recession. Economica 80: 385–403. [Google Scholar] [CrossRef]
- Ratner, David, and Jae Sim. 2022. Who Killed the Phillips Curve? A Murder Mystery; Board of Governors of the Federal Reserve System Working Paper, No. 2022–28; Washington, DC: Board of Governors of the Federal Reserve System.
- Rudd, Jeremy, and Karl Whelan. 2007. Modeling Inflation Dynamics: A Critical Review of Recent Research. Journal of Money, Credit and Banking 39: 155–70. [Google Scholar] [CrossRef]
- Samuelson, Paul A., and Robert M. Solow. 1960. Analytical Aspects of Anti-Inflation Policy. American Economic Review 50: 177–94. [Google Scholar]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In The Festschrift in Honor of Peter Schmidt: Econometric Methods and Applications. Edited by Robin C. Sickles and William C. Horrace. New York: Springer, pp. 281–314. [Google Scholar]
- Tang, Bo, and Carlos Bethencourt. 2017. Asymmetric unemployment-output tradeoff in the Eurozone. Journal of Policy Modeling 39: 461–81. [Google Scholar] [CrossRef]
- Xu, Qifa, Xufeng Niu, Cuixia Jiang, and Xue Huang. 2015. The Phillips Curve in the US: A nonlinear quantile regression approach. Economic Modelling 49: 186–97. [Google Scholar] [CrossRef]
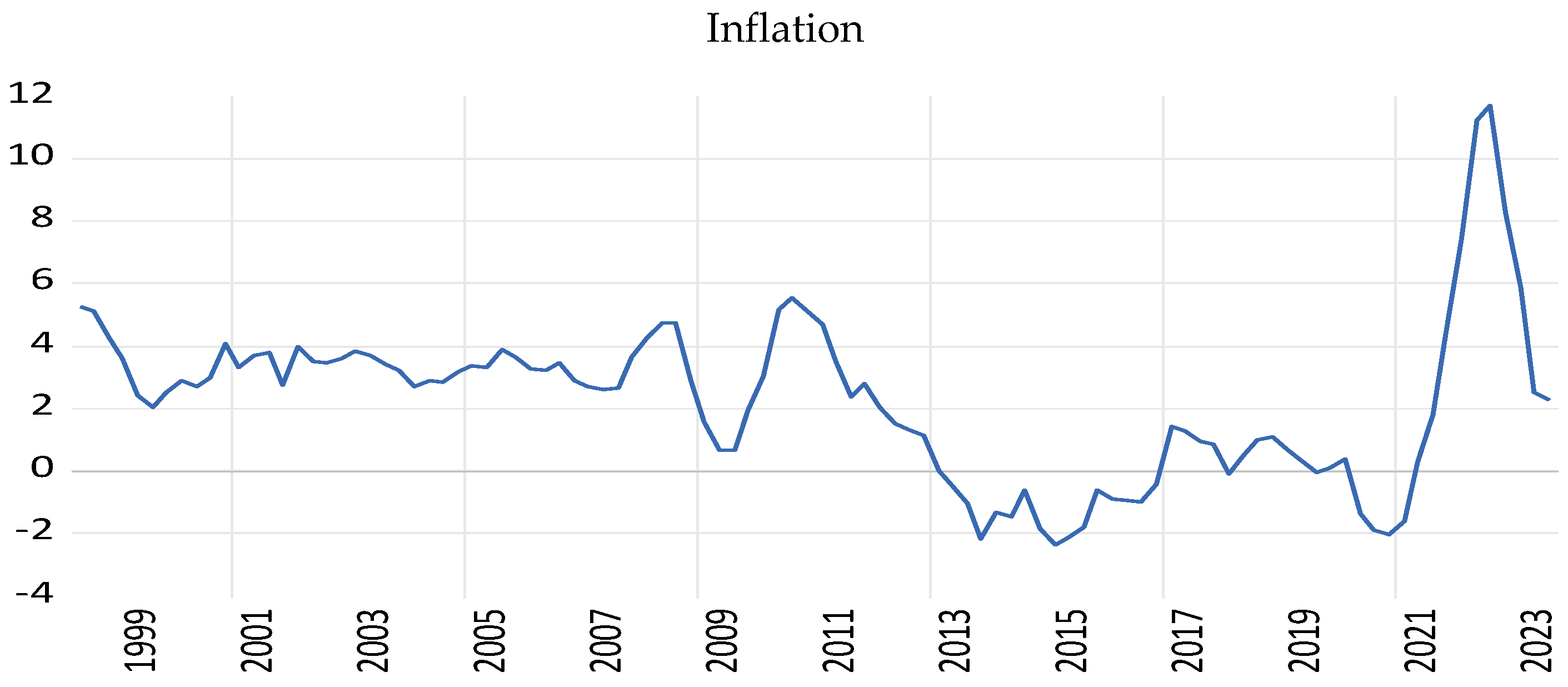
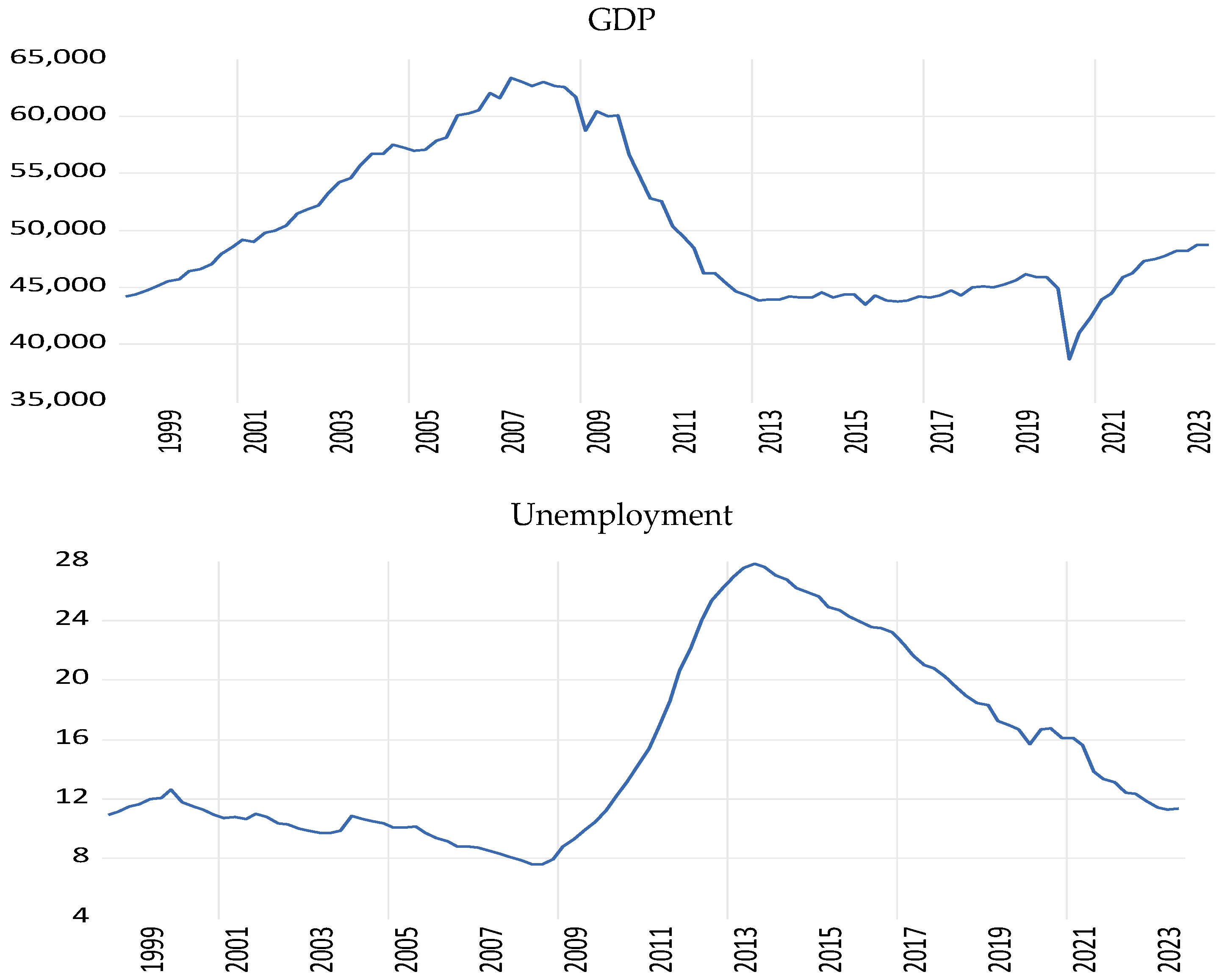
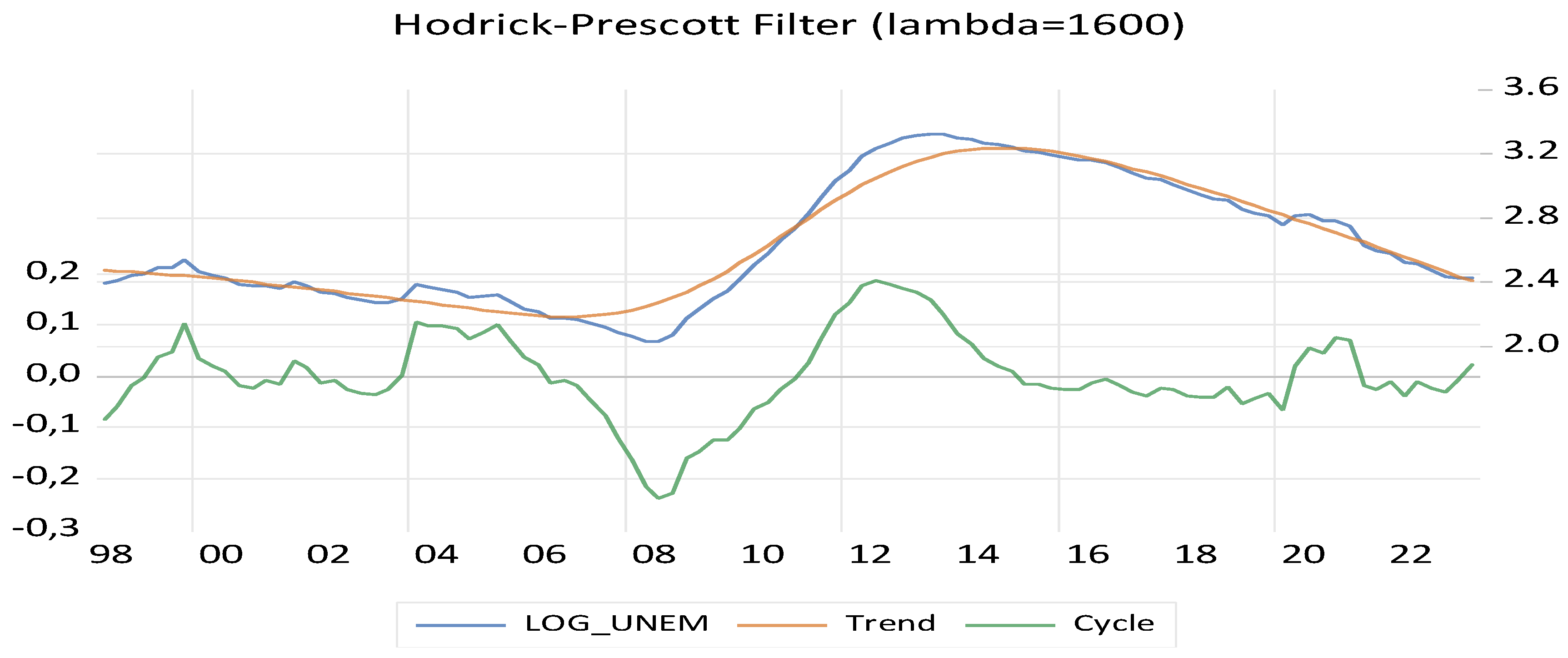
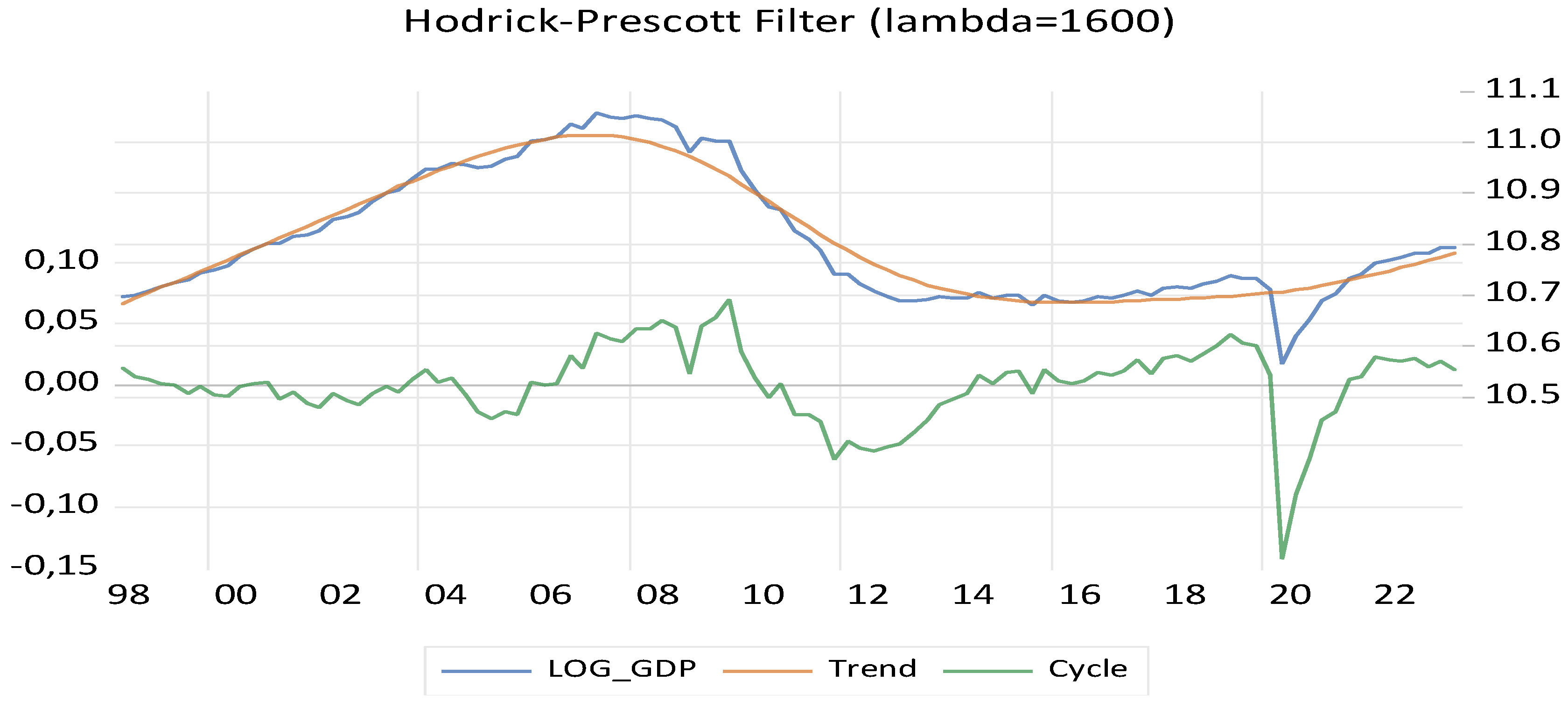
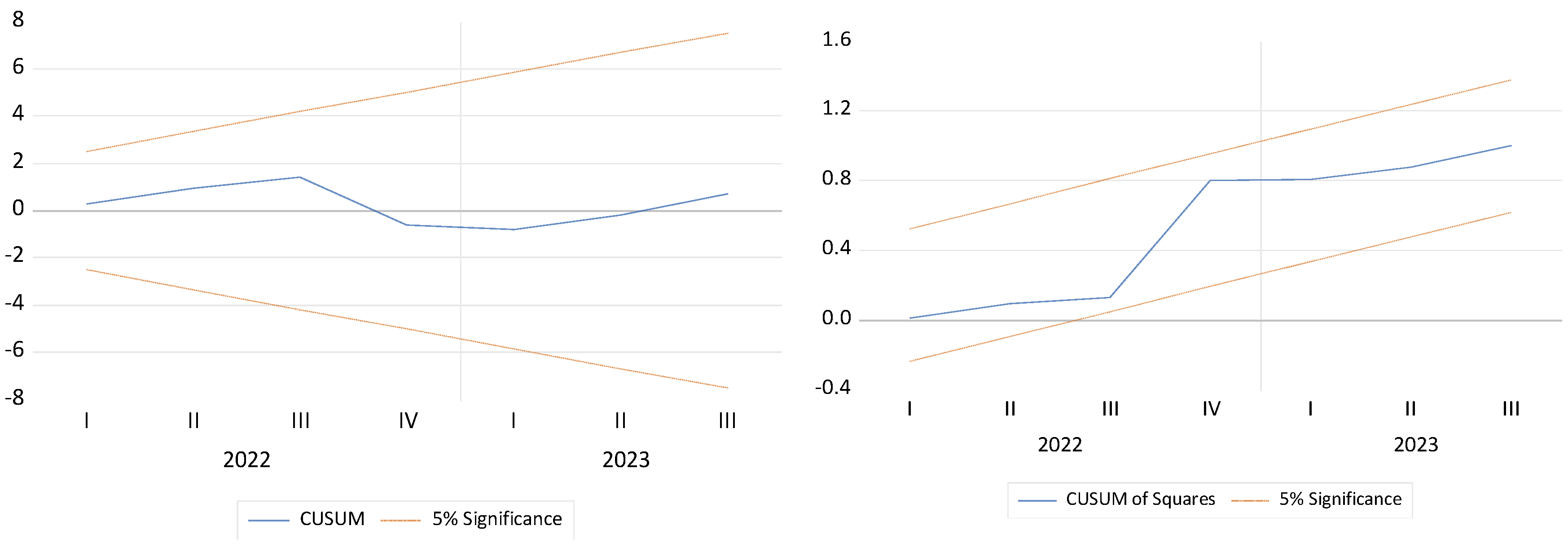
| Variables | Mean | Median | Max | Min | Std. Dev | Skewness | Kurtosis | Jarque–Bera |
|---|---|---|---|---|---|---|---|---|
| Inflation | 2.234 | 2.667 | 11.675 | −2.379 | 2.587 | 0.676 | 4.743 | 20.712 (0.00) |
| Unemployment gap | 0.001 | −0.127 | 3.622 | −2.520 | 1.328 | 0.617 | 3.919 | 0.069 (0.006) |
| Output gap | 0.000 | 122.47 | 3693.5 | −5979.4 | 1539.8 | −0.557 | 4.719 | 17.852 (0.000) |
| ADF | Phillips–Perron | |||
|---|---|---|---|---|
| Variables | Intercept | Intercept and Trend | Intercept | Intercept and Trend |
| Inflation | −1.75 | −1.47 | −2.94 ** | −2.95 |
| Unemployment gap | −3.99 *** | −3.97 ** | −2.61 ** | −2.60 |
| Output gap | −3.55 *** | −3.53 ** | −3.57 *** | −3.53 ** |
| ΔInflation | −3.08 ** | −3.33 ** | −5.19 *** | −5.17 *** |
| ΔUnemployment gap | −3.35 ** | −3.93 ** | −7.33 *** | −7.29 *** |
| ΔOutput gap | −10.88 *** | −10.83 *** | −11.30 *** | −11.24 *** |
| Explanatory Variable | F Statistic | Critical Values | Cointegration | |||||
|---|---|---|---|---|---|---|---|---|
| 1% | 5% | 10% | ||||||
| I(0) | I(1) | I(0) | I(1) | I(0) | I(1) | |||
| Unemployment gap | 12.488 | 4.13 | 5.00 | 3.10 | 3.87 | 2.63 | 3.35 | Yes |
| Output gap | 9.397 | Yes | ||||||
| BDS Statistics | Embedding Dimension = m | ||||
|---|---|---|---|---|---|
| Variables | M2 | M3 | M4 | M5 | M6 |
| Inflation | 0.150 *** (0.000) | 0.246 *** (0.000) | 0.299 *** (0.000) | 0.326 *** (0.000) | 0.340 *** (0.000) |
| Unemployment gap | 0.160 *** (0.000) | 0.264 *** (0.000) | 0.327 *** (0.000) | 0.361 *** (0.000) | 0.378 *** (0.000) |
| Output gap | 0.124 *** (0.000) | 0.209 *** (0.000) | 0.259 *** (0.000) | 0.283 *** (0.000) | 0.290 *** (0.000) |
| Dependent Variable Inflation | |||
|---|---|---|---|
| NARDL Model (6, 7) | |||
| Long-Run Nonlinear Effect | Dummy Variables | ||
| Unem_gap+ | −4.103 *** (−4.991) | Dum (crisis) | −0.055 * (−1.798) |
| Unem_gap− | −3.048 *** (−3.822) | Dum (covid) | −0.226 *** (−2.920) |
| Constant | 1.358 *** (5.998) | Dum (energy) | 0.724 *** (6.561) |
| Short-run nonlinear effect | Diagnostic Tests | ||
| DInf(−1) | 0.375 *** (4.243) | R2 | 0.75 |
| DInf(−2) | 0.050 (0.532) | J-B | 1.684 (0.430) |
| DInf(−3) | −0.146 (−1.604) | B-G LM test | 2.516 (0.095) |
| DInf(−4) | −0.242 ** (−2.372) | Arch test | 0.523 (0.471) |
| DInf(−5) | 0.270 ** (2.614) | Symmetry Test | |
| DUnem_gap+ | −0.514 (−0.623) | WLR | 22.067 *** [0.000] |
| DUnem_gap− | −3.596 *** (−3.207) | WSR | 0.036 [0.849] |
| DUnem_gap+(−1) | 2.003 ** (2.335) | Wjoint (LR and SR) | 11.603 *** [0.000] |
| DUnem_gap−(−1) | 3.628 *** (3.425) | ||
| DUnem_gap+(−2) | 0.464 (0.558) | ||
| DUnem_gap−(−2) | −0.581 (−0.582) | ||
| DUnem_gap+(−3) | 1.019 (1.272) | ||
| DUnem_gap−(−3) | −1.491 (−1.438) | ||
| DUnem_gap+(−4) | 0.647 (0.797) | ||
| DUnem_gap−(−4) | 2.919 *** (2.746) | ||
| DUnem_gap+(−5) | 1.075 (1.294) | ||
| DUnem_gap−(−5) | 2.651 ** (2.474) | ||
| DUnem_gap+(−6) | 1.406 * (1.743) | ||
| DUnem_gap−(−6) | 1.935 * (1.714) | ||
| Ect(−1) | −0.361 *** (−7.222) | ||
| Dependent Variable Inflation | |||
|---|---|---|---|
| NARDL Model (5, 8) | |||
| Long-Run Nonlinear Effect | Dummy Variables | ||
| Output_gap+ | 5.453 ** (2.229) | Dum (crisis) | −0.153 *** (−4.402) |
| Output_gap− | 7.878 *** (3.215) | Dum (covid) | −0.081 (−0.641) |
| Constant | 0.884 *** (7.194) | Dum (energy) | 0.643 *** (4.413) |
| Short-Run Nonlinear Effect | Diagnostic Tests | ||
| DInf(−1) | 0.191 ** (2.261) | R2 | 0.73 |
| DInf(−2) | −0.108 (−1.098) | J-B | 2.187 (0.335) |
| DInf(−3) | −0.220 ** (−2.308) | B-G LM test | 0.662 (0.519) |
| DInf(−4) | −0.402 *** (−3.695) | Arch test | 0.015 (0.899) |
| DOutput_gap+ | 7.011 *** (3.036) | Symmetry Test | |
| DOutput_gap− | 3.182 *** (2.770) | WLR | 20.637 *** [0.000] |
| DOutput_gap+(−1) | −5.531 ** (−2.264) | WSR | 12.440 *** [0.849] |
| DOutput_gap−(−1) | −3.801 *** (−2.900) | Wjoint (LR and SR) | 11.085 *** [0.000] |
| DOutput_gap+(−2) | −4.251 * (−1.777) | ||
| DOutput_gap−(−2) | −3.239 ** (−2.282) | ||
| DOutput_gap+(−3) | 1.380 (0.595) | ||
| DOutput_gap−(−3) | −4.673 *** (−3.590) | ||
| DOutput_gap+(−4) | 3.729 (1.587) | ||
| DOutput_gap−(−4) | −3.455 ** (−2.570) | ||
| DOutput_gap+(−5) | 5.669 ** (2.312) | ||
| DOutput_gap−(−5) | −0.404 *** (−2.853) | ||
| DOutput_gap+(−6) | 3.582 (1.448) | ||
| DOutput_gap−(−6) | 0.306 (0.237) | ||
| DOutput_gap+(−7) | 6.786 *** (3.237) | ||
| DOutput_gap−(−7) | −2.272 * (−1.843) | ||
| Ect(−1) | −0.338 *** (−6.268) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pegkas, P. The Asymmetric Effects of Unemployment and Output on Inflation in Greece: A Nonlinear ARDL Approach. Economies 2024, 12, 346. https://doi.org/10.3390/economies12120346
Pegkas P. The Asymmetric Effects of Unemployment and Output on Inflation in Greece: A Nonlinear ARDL Approach. Economies. 2024; 12(12):346. https://doi.org/10.3390/economies12120346
Chicago/Turabian StylePegkas, Panagiotis. 2024. "The Asymmetric Effects of Unemployment and Output on Inflation in Greece: A Nonlinear ARDL Approach" Economies 12, no. 12: 346. https://doi.org/10.3390/economies12120346
APA StylePegkas, P. (2024). The Asymmetric Effects of Unemployment and Output on Inflation in Greece: A Nonlinear ARDL Approach. Economies, 12(12), 346. https://doi.org/10.3390/economies12120346





