Using Short Time Series of Monofractal Synthetic Fluctuations to Estimate the Foreign Exchange Rate: The Case of the US Dollar and the Chilean Peso (USD–CLP)

Abstract

Short time series are fundamental in the foreign exchange market due to their ability to provide real-time information, allowing traders to react quickly to market movements, thus optimizing profits and mitigating risks. Economic transactions show a strong connection to foreign currencies, making exchange rate prediction challenging. In this study, the exchange rate estimation between the US dollar (USD) and the Chilean peso (CLP) for a short period, from 2 August 2021 to 31 August 2022, is modeled using the nonlinear Schrödinger equation (NLSE) and calculated with the fourth-order Runge–Kutta method, respectively. Additionally, the daily fluctuations of the current exchange rate are characterized using the Hurst exponent, H, and later used to generate short synthetic fluctuations to predict the USD–CLP exchange rate. The results show that the USD–CLP exchange rate can be estimated with an error of less than $5\%$, while when using short synthetic fluctuations, the exchange rate shows an error of less than $10\%$.

1. Introduction

When we talk about global economic crises, it is essential to think of the great depression of the 1930s and the 2008 world crisis as the most important and worth studying (Bernstein 1989). Likewise, Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) is undoubtedly at the level of those mentioned above; this is because the effects caused by the COVID-19 pandemic on economies worldwide have been devastating, managing to stagnate the production of goods and services on a regular basis (Araújo 2020).

A scenario where it is possible to clearly appreciate the effects of COVID-19 corresponds to economic transactions. Economics subsidies, import/export of goods/services, and income/capital flows are carried out through the exchange of values. These economic activities show a connection between the currencies of the countries involved in terms of the exchange rate or purchasing power. In this sense, the exchange and exchange of money from one country to another is facilitated by the structure of the foreign exchange market. The foreign exchange market facilitates the interaction between buyers/sellers, financial institutions, companies, and foreign exchange brokers, among others, depending on the needs demanded and offered by other countries or the diversification of investments.

One of the main works on financial markets and their interrelationships corresponds to (Fama 1970). The author points out that the efficiency of the markets can be measured at three different levels: (i) weak efficiency, which only incorporates historical information; (ii) semi-strong efficiency, incorporating historical and public information; and (iii) strong efficiency, which incorporates historical, public, and private information. This hypothesis has been tested by several researchers in different works (Guptha and Rao 2019; Jensen 1972; Jones and Netter 2008). Guptha and Rao (2019) studied the efficiency of the five main emerging economies of the 2000s (BRIC) in conjunction with the emerging markets of the European Union. For their part, Dicle and Levendis (2010) proved that the distribution of returns on one day differs from those on other days for 51 stock markets in 33 countries.

Different methods and models have been used to study cross-correlations and long-term dynamics (Aslam et al. 2023; Chaudhari and Crane 2020; Quintino et al. 2021; Wang et al. 2023), determine trends, and predict the rate exchange between foreign currencies or their relationship with cryptocurrency (Tripathi and Sharma 2022). Among prediction methods, we can name the Monte Carlo method (MMC) (Hersugondo et al. 2022; Rodríguez Nava and Venegas Martínez 2010; Soleymani and Itkin 2019), forecast models (FMs) (Afuecheta et al. 2022), artificial neural networks (ANNs) (Chen and Leung 2004; Galeshchuk 2016; Leung et al. 2000; Xu et al. 2021; Zapata Garrido and Díaz Mojica 2008), support vector machine model (SVM) (Kamruzzaman et al. 2003), Markov chains (MCs) (Lee and Chen 2006), the Navier–Stokes equations (NSEs) (Kartono et al. 2020), Runge–Kutta methods (RKMs), and the Black–Scholes model by nonlinear Shrödinger equation (NLSE) (Kartono et al. 2021). Zapata Garrido and Díaz Mojica (2008) analyzed different types of neural networks in order to determine the one with the best performance for the exchange rate between the US dollar and the Colombian peso (USD–COP). Within the models with favorable results, Kamruzzaman et al. (2003) applied SVM to test different kernel types for the prediction of the Australian currency, showing that the polynomial kernel and radial basis give the best results. On the other hand, numerical methods present a different alternative to predict the rate of exchange between foreign currencies (Kamruzzaman et al. 2003; Kartono et al. 2020, 2021; Lee and Chen 2006). In this sense, Gencay (1999) achieved promising results for rate exchange performance by working only with regression methods. Instead, Kartono et al. (2020) explained the analogy between different economic variables, the classic Navier–Stokes equations, and their application to the exchange rate between the US dollar and the Indonesian rupiah (USD–IDR). Finally, in (Kartono et al. 2021), the authors worked with RKM as a predictor of the USD–IDR exchange rate, using the nonlinear Shrödinger equation as a basis and the Black–Scholes model as a dynamic analog to the exchange rate.

Another important aspect in the study of the rate of change is the length of the records. López and Contreras (2013) pointed out that some main currencies are relatively new or their exchange to other currencies has been subject to new policies in the near past. In this sense, the dynamics of historical records (long time series) can change over time, and an analysis of short pieces is required to obtain an idea of the process. Likewise, short-time series are important in forecasting, anomaly detection, and trend analysis (Braei and Sebastian 2020; Deng and Jirutitijaroen 2010; Gajbhiye et al. 2016). Short-time series can reveal patterns and trends that can inform decision-making, to identify short-term trends in stock prices or other market data (Wu et al. 2018). Related to the length of short time series, we can made the distinction between short-term and very short-term depends on the context and the specific characteristics of the data. For example, in time-series analysis, very short-term variations typically refer to changes that occur over relatively brief time intervals, such as seconds or hours (market volatility). Now, by understanding the monofractal nature of a very short time series, better forecasting models can be develop. These model can be used for very short-term predictions were rapid and accurate forecasting is essential (Look AHEAD Research Group and Wing 2010).

In general, methods used to analyze the rate exchange between foreign currencies work directly on the value of the currency, ignoring the fluctuations between consecutive days. Fluctuations in the exchange rate respond to unforeseeable changes; these fluctuations reflect variations in macroeconomic indicators with respect to the previous day. These fluctuations are due to a set of successive and constant changes due to various economic, political, and social reasons or to the action of supply and demand in most markets, which leads to a permanent evolution, both upward and downward, and demonstrates a certain degree of instability in currencies. Often, the existence of fluctuations in currencies entails losses and profits for the participants in the map of the economy due to changes in the value or price of goods, services, merchandise, or financial values.

Trend and long-range correlation study to characterize quantitatively the fluctuations is wide. The Hurst exponent by the rescaled range analysis $(R/S)$ (Mandelbrot and Wallis 1969), the detrended fluctuation analysis (DFA) (Ferreira 2018; Ferreira et al. 2018; López and Veleva 2022; López et al. 2021; Peng et al. 1994), and the multifractal detrended fluctuation analysis (MF-DFA) (Jiang et al. 2018; Kantelhardt et al. 2002; Wang and Shao 2021) make up a long list of high-performance methods. Rossi (2013) analyzed different exchange rate prediction models, concluding that the error correction model (ECM) is the most successful and that data transformation such as filtering, trend removal, and seasonal adjustments can alter the prediction. Ferreira (2018, 2020); Kanapickienė et al. (2023) studied the long-term dependence on the Eastern European stock market and the Swiss stock market, respectively. Ferreira (2018) used a dynamic financial analysis of sliding windows to analyze dependencies in eighteen different stock markets, observing that in markets with little and medium development, there was a long-range trend, while (Ferreira 2020) applied a fluctuation analysis without trend (DFA) in the Swiss market, one of the main ones in Europe, where he verified that the actions analyzed in the Swiss stock market had some degree of dependence on time.

Based on the background presented, we set out to answer the following research questions:

• Is it possible to use RK4 to estimate the exchange rate between the US dollar and the Chilean peso (USD–CLP) with only a few percentage points of error using a short time series?
• Is it possible to characterize daily fluctuations in the exchange rate (USD–CLP) as monofractal fluctuations?
• Is it possible to use short monofractal fluctuations to estimate the exchange rate (USD–CLP) with only a few percentage points of error?

The above research questions allow us to achieve the following contributions:

• Different studies have been conducted to estimate the exchange rate between foreign currencies: USD–EUR, USD–IDR, and USD–AUD, to name a few. However, this is the first attempt to study short time series for the exchange rate between the US dollar and the Chilean peso (USD–CLP), one of the main economies in Latin America.
• Methods that analyze the exchange rate between foreign currencies are typically focused on estimating future values based on historical records, with little attention paid to existing fluctuations. In this regard, we demonstrate that it is possible to characterize fluctuations in short records using the Hurst exponent (H) and detrended fluctuation analysis (DFA).
• We show that it is possible to use a synthetic time series of fluctuations (with the H parameter defined), the nonlinear Schrödinger equation, and the fourth-order Runge–Kutta method to estimate the exchange rate between the US dollar and the Chilean peso (USD–CLP) with only a few percentage points of error.

The aim of this research, as a first approximation, focuses on the use of monofractal synthetic fluctuations to estimate the foreign exchange rate. Specifically, we want to show how monofractal synthetic fluctuations, for a given Hurst exponent value, can be used to estimate the actual value of the foreign exchange rate with minimal percent error. Likewise, knowing the Hurst exponent of past fluctuations could be used to generate synthetic fluctuations and estimate future values by starting with an initial exchange rate value and adding the fluctuation. Understanding synthetic fluctuations is of great importance as it can significantly enhance our ability to create better models, make more accurate predictions, and facilitate improved decision making in a wide range of domains. With this study, we aim to open new opportunities for the complex field of fractal theory combined with financial analysis. This perspective can offer new tools for analyzing and predicting movements in the forex market, always bearing in mind the unpredictability of financial markets.

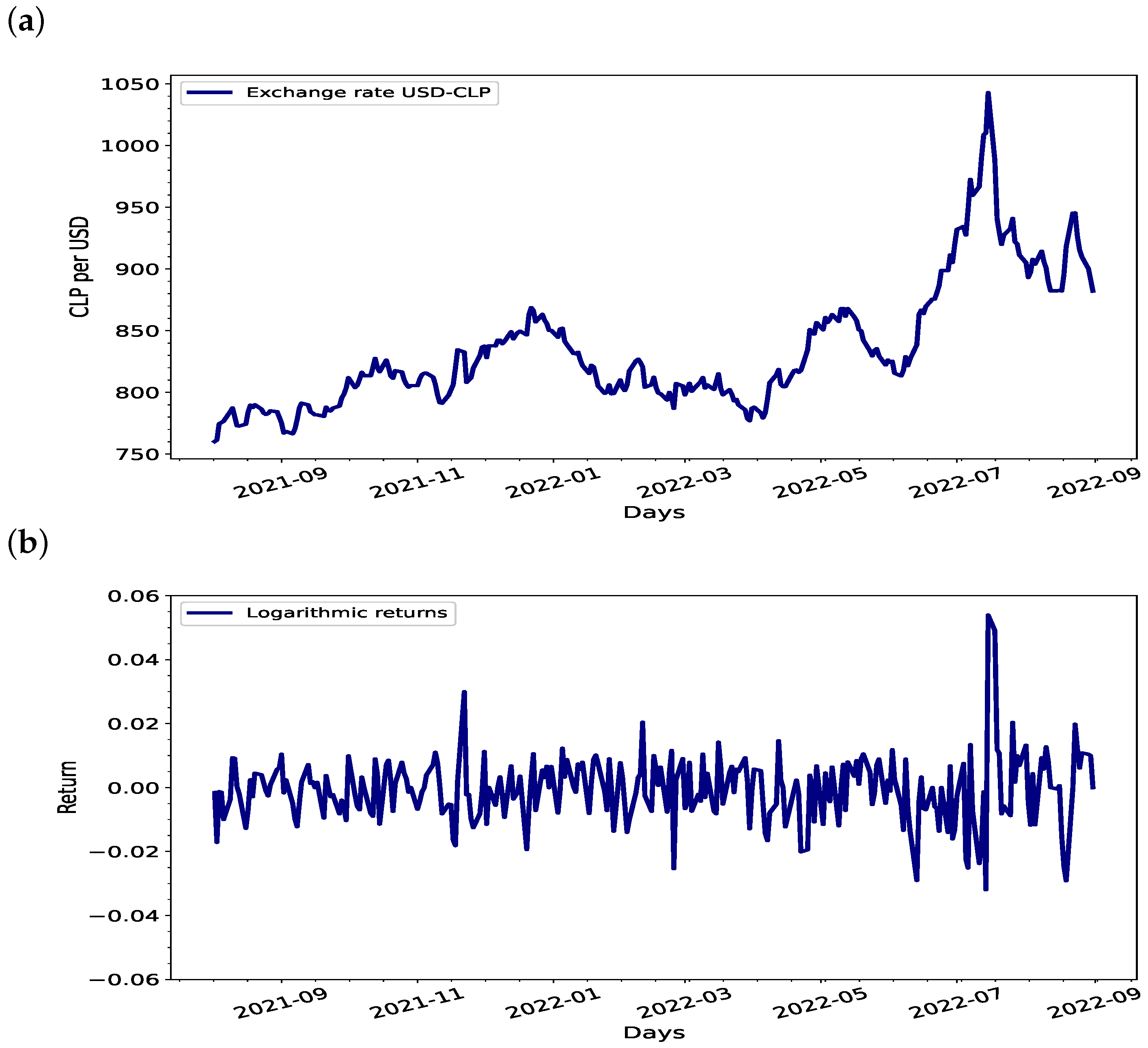
2. The Exchange Rate between the US Dollar and the Chilean Peso (USD–CLP)

The rate exchange movement, gross domestic product, the interest rate, the inflation rate, the return rate, and the change from one season to another are used to estimate the exchange rate currency. However, the econometrics data are short, and measuring and estimating them represent a big challenge. Therefore, the selection of a suitable method to assess changes in long-range correlations, moreover in short exchange rate currency series, is very important due to some important currencies being relatively new, their exchange to other currencies having been subject to new policies in the near past, and that the dynamics of historic records (long time series) may change with time.

Chile between the Social Outbreak and COVID-19

After the social outbreak, the Chilean peso began a period of strong depreciation, which was accentuated by the effects on the economy caused by the confinement measures due to the arrival of COVID-19. A year after such events, the exchange rate was positioned at levels prior to the social outbreak, reinforced by the Association of Pension Funds (AFP) after the start of payment of pension fund withdrawals. However, after strong demonstrations and violence since then, the dollar has been subject to strong fluctuations that have led it to reach historical values and increased uncertainty regarding the price of this currency. Along the same lines, another important factor that contributes to the increase in the uncertainty of the exchange rate of USD–CLP is the COVID-19 vaccine effects, through million-dollar contracts contract to guarantee the dose number (Atria et al. 2020; Taborda et al. 2022). After such events, the nominal exchange rate has been highly volatile. While the sharp drop in copper prices in January 2020 weighed on the peso during February, the currency continued its downward spiral in March, as the spread of the coronavirus and the drop in oil prices caused capital outflows from the emerging markets. At the beginning of 2020, the Chilean peso traded at a historical low, where the exchange rate was CLP 749 per USD. On March 13, the CLP was quoted at a maximum of CLP 839 per USD, a depreciation of 5.4% compared to the same day of the previous month (Banco Central de Chile 2022). The exchange rate levels seem not to be consistent with fundamental variables of the local economy. The reason for this lies in the risk incorporated in the Chilean peso as a result of political and social uncertainty, which moderates the prospects of further declines in the dollar. However, Chilean local money is seen favorably in Latin America. In actuality, with the open border and the new government beginning, Chile could be in a good place to start an economic recovery. The Credit and Investment Bank (BCI) study indicates that the price of the dollar reflects a more favorable external scenario and health conditions that are improving throughout the year (Banco de Crédito e Inversiones 2022).

3. Materials and Methods

3.1. Nonlinear Schrödiger Equation (NLSE)

The NLSE (see Equation (1)) is similar to the classical Shrödinger equation that has probabilistic solutions of the time evolution of a particle (Cazenave 1989). The NSLE, widely used in fiber optics, allows one to obtain soliton solutions in nonlinear mediums. (Vázquez et al. 2014) showed the solution to the NSLE for the case of simulated temporal pulses in an optical fiber. Likewise, Yan (2003) showed several families of wave solutions. Another perspective was provided in (Kartono et al. 2021). The authors showed that the NLSE (Equation (1)) is better suited to economic forecasting, due to the high nonlinearity of financial markets.

$${\displaystyle \frac{\partial \psi {\left(q\right)}^2}{\partial q^2}}-(k^2-{\displaystyle \frac{2\omega }{\sigma }})\psi \left(q\right)-{\displaystyle \frac{2\beta }{\sigma }}\psi {\left(q\right)}^3=0$$

(1)

Nonlinear Schrödiger and Black–Scholes Equations

Vukovic (2015) showed that there is a connection between the Black–Scholes model and the Schrödinger equation. The authors pointed out that the Black–Sholes model can be derived from the Schrödinger equation, in the sense that the fusion of both creates a powerful model for finance where it can predict the exchange rate, just as the Schrödinger equation does in a free particle in quantum mechanics. Kartono et al. (2021) exposed an analogy between the nonlinear Schrödiger equation and the Black–Scholes model. In their work, the authors equated the variables responsible for the movement of the exchange rate between both models; gross domestic product (GDP), interest rate, inflation rate, and rate of return. The relationship between both models is summarized in

Table 1. The parameters analogy between the nonlinear Shrödinger equation and the Black–Scholes.

Economic Indicators	NLSE Parameters
The exchange rate movement	Wave function ($\psi$)
The exchange rate at time	Position variable (q)
Gross domestic product	Wave number (k)
The interest rate	Landau coefficient ($\beta$)
The inflation rate	Dissipation ($\sigma$)
The return rate	Angular frequency ($\omega$)

. An important detail is that this model does not consider external potentialities, that is, external influences such as wars, catastrophes, or other causes. Vera Moreno (2014) analyzed the effect of the external potential on the NLSE and concluded that the simple integration of this term can make the equation unsolvable, so it is convenient to exclude the external potentials and leave only the economic variables defined.

3.2. Runge–Kutta Numerical Method

Runge–Kutta is an iterative numerical method for solving differential equations with initial conditions (Tan and Chen 2012). In general, differential equations solved by numerical methods do not have a simple analytical solution or simply do not have one. For the differential Equation (1), the algorithm considers a function $\psi (t,q(t\left)\right)$ that satisfies (2) and (3):

$$\dot{\psi }={\displaystyle \frac{\partial \psi }{\partial t}}=F(t,q,\psi )$$

(2)

$${\displaystyle \frac{\partial {\psi }^2}{\partial t^2}}=G(t,q,\psi )$$

(3)

where

$$G(t,q,\psi ))=(k^2-{\displaystyle \frac{2\omega }{\sigma }})\psi \left(q\right)-{\displaystyle \frac{2\beta }{\sigma }}\psi {\left(q\right)}^3$$

(4)

and whose solution can be obtained by discretizing the temporary variable t in constant time intervals h.

Considering fourth-order Runge–Kutta and Equations (2)–(4), the following algorithm is obtained:

$$\begin{array}{cc}\hfill k_{1q}& =h\ast F(t,q,\psi )\hfill \\ \hfill k_{1\psi }& =h\ast G(t,q,\psi )\hfill \\ \hfill k_{2q}& =h\ast F(t+h/2,q+k_{1q}/2,\psi +k_{1\psi }/2)\hfill \\ \hfill k_{2\psi }& =h\ast G(t+h/2,q+k_{1q}/2,\psi +k_{1\psi }/2)\hfill \\ \hfill k_{3q}& =h\ast F(t+h/2,q+k_{2q}/2,\psi +k_{2\psi }/2)\hfill \\ \hfill k_{3\psi }& =h\ast G(t+h/2,q+k_{2q}/2,\psi +k_{2\psi }/2)\hfill \\ \hfill k_{4q}& =h\ast F(t+h,q+k_{3q},\psi +k_{3\psi })\hfill \\ \hfill k_{4\psi }& =h\ast G(t+h,q+k_{3q},\psi +k_{3\psi })\hfill \\ \hfill q& =q+1/6\ast (k_{1q}+2\ast k_{2q}+2\ast k_{3q}+k_{4q})\hfill \\ \hfill \psi (t+h)& =\psi \left(t\right)+1/6\ast (k_{1\psi }+2\ast k_{2\psi }+2\ast k_{3\psi }+k_{4\psi })\hfill \end{array}$$

3.3. Monofractal Fluctuations

A monofractal time series displays self-similarity across all timescales, where the scaling characteristics of the series are defined by a single fractal dimension that captures how the patterns and structures within the series change as the scale changes Kantelhardt (2008); Lopes and Betrouni (2009); López and Contreras (2013). Monofractal time series are commonly observed in numerous natural systems. Monofractal time series appear in diverse systems like weather patterns, river flows, and physiological processes in the human body Curto-Risso et al. (2010); Huang et al. (2010); López et al. (2021); Shi et al. (2009). Additionally, monofractal time series are frequently employed in various fields of study, such as economics, finance, and physics, to model, analyze, and compare the fractal properties of more intricate time series Pastén et al. (2011); Saadaoui (2023); Shi et al. (2014); Xu et al. (2012).

Monofractal fluctuations in exchange rates are very important as they are related to the variability in currency prices that exhibits fractal properties, which means that price movements at different timescales can be described by self-similar patterns. Usually, the variability in currency prices is characterized by a single Hurst exponent (monofractality) López and Contreras (2013). In this sense, the Hurst exponent is a crucial indicator in fractal analysis. The H distinguished three different cases: (i) $H<0.5$ for anticorrelation cases/antipersistent processes (mean-reverting), (ii) the absence of long-range correlations (white noise) with $H=0.5$, and (iii) persistent processes/long-range correlations with $H>0.5$ (trending).

3.4. Detrended Fluctuation Analysis (DFA)

An important technique to detect long-range correlation in noisy and nonstationary time series, studying at the same time their scaling properties, is the detrended fluctuation analysis (DFA) (Hu et al. 2001; Peng et al. 1994). The DFA method considers five steps, as follows:

• For a time serie $y\left(j\right)$ of finite length N, where only a tiny proportion of $y\left(j\right)$ are equal to zero, the new time series $Z\left(l\right)$, where $l=1$, …, N, is computed as follows:

  $$Z\left(l\right)=\sum _{j=0}^l\left[y\left(j\right)-<y>\right].$$

  (5)
• The new series $Z\left(j\right)$ is divided into $N_s$ segments of size s. Repeating the procedure from the beginning to the end, $2N_r$ segments are obtained.
• For all segments $\mu$ and all sizes s, the variance from the local trend of order n, $P_{\mu }^n$, is computed as follows:

  $$F^2(\mu ,s)={\displaystyle \frac{1}{s}}\sum _{j=1}^s{\left\{Z\left[(\mu -1)s+j\right]-P_{\mu }^n\left(j\right)\right\}}^2.$$

  (6)
• For all segments of a given size s, the average over 2-order fluctuations are computed as follows:

  $$F_2\left(s\right)={\left\{{\displaystyle \frac{1}{2N_s}}\sum _{\mu =1}^{2N_s}\left[F^2(\mu ,s)\right]\right\}}^{1/2},$$

  (7)
• For a range of sizes, $s_{\min }<s<s_{\max }$,

  $$F_2\left(s\right)\sim s^H.$$

  (8)
  The H index, called Hurst exponent, is the output of the DFA algorithm.

3.5. Data Source

As mentioned above, companies and governments buying or selling goods and services are subject to a foreign exchange purchase or sale operation, some with speculative, hedging, or arbitration fines. This set of transactions transforms the foreign currency market into the basis for international capital transactions. We have focused on the local Exchange Market (Chilean Market), due to its great importance in the different sectors (importers and substitutes, exporters, banks, investors institutional, and others). The exchange rate time series contains 281 data entries from 2 August 2021 to 31 August 2022. The data, shown in the left panel of Figure 1a, are obtained from the Banco Central de Chile (https://si3.bcentral.cl/, accessed on 20 January 2024) and Ministerio de hacienda (www.hacienda.cl, accessed on 25 January 2024).

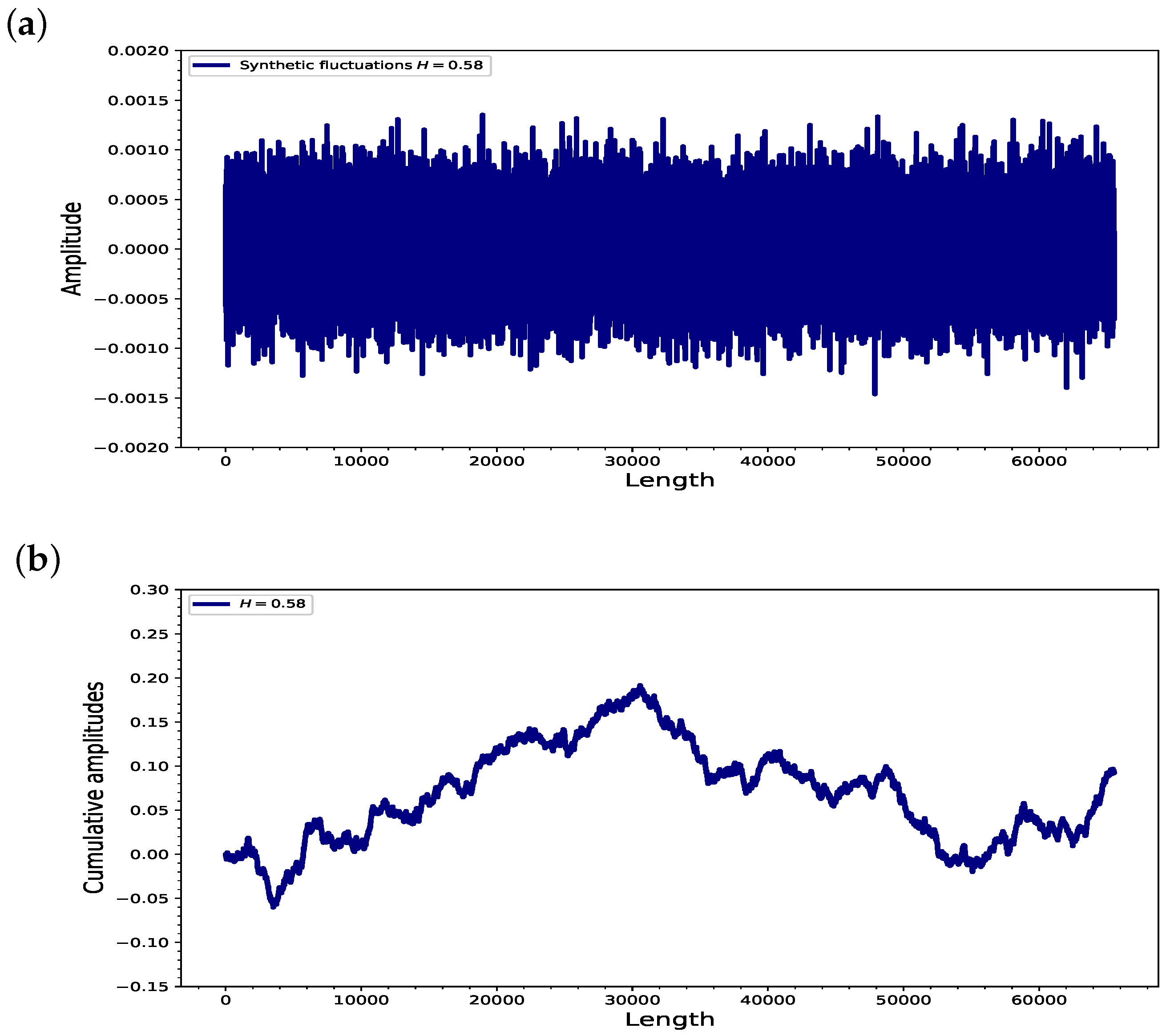
3.6. Computer-Generated Exchange Rate Fluctuation Currency

Very long series of $2^{20}$ in length were generated according to the algorithms of (Abry and Sellan 1996; Bardet 2002), and from there, 10 independent realizations of $2^8$ length data were taken for the synthetic model to be analyzed. The fluctuations generated will be used to estimate the synthetic result of the CLP–USD exchange rate for RK4 and later compared with the real case.

4. Results and Discussion

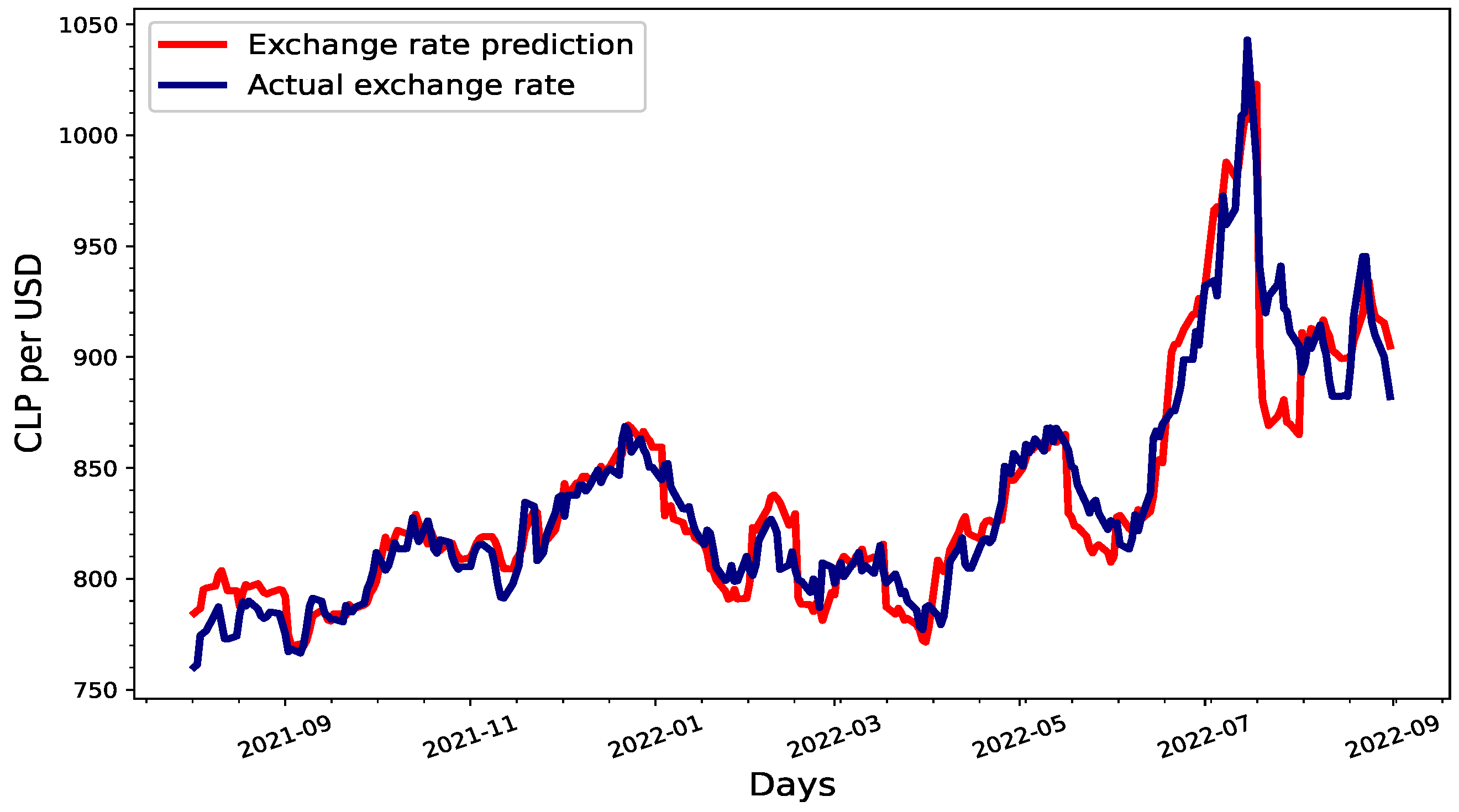
4.1. Estimating USD–CLP by the Fourth-Order Runge–Kutta Method

The USD–CLP exchange rate was estimated using the fourth-order Runge–Kutta method. For USD–CLP estimate calculation, the economics variables (see

Table 2. The economics variables of the Black–Sholes model are used as data input for the nonlinear Shrödinger equation parameters. Data for variables affecting the USD–CLP exchange rate from August 2021 to August 2022 period.

Period	$\mathit{\omega }$ (%)	$\mathit{\sigma }$ (%)	$\mathit{\beta }$ (%)	GDP (k) (Billion CLP)
August 2021	0.0283	0.4	0.75	49,073
September 2021	0.0303	1.2	1.50	49,676
October 2021	0.0023	1.3	1.50	49,676
November 2021	0.0388	0.5	2.75	49,676
December 2021	0.0162	0.8	2.75	54,865
January 2022	−0.0472	1.2	4.00	54,865
February 2022	−0.0060	0.3	5.50	54,865
March 2022	−0.0225	1.9	5.50	50,278
April 2022	0.0822	1.4	7.00	50,278
May 2022	−0.0354	1.2	7.00	50,278
June 2022	0.1134	0.9	8.25	51,704
July 2022	−0.0093	1.4	9.00	51,704
August 2022	−0.0322	1.2	9.75	51,704

), actual data of the USD–CLP exchange rate (see Figure 1a), and the exchange rate daily fluctuations (see Figure 1b) for the last week are required. Only the Monday to Friday exchange rate is taken into account because there is no activity on Saturday, Sunday, and holidays due to the market and banking being closed. The prediction calculation is made each 2 weeks, carried out using the same procedure, and the new beginning input is taken from the exchange rate and the current economic variables, while the fluctuations are taken from the previous week. This prediction procedure can be conducted for the desired time.

Following the previous procedure, the exchange rate for the August 2021–2022 period was estimated and the results are shown in Figure 2. The results show a good accuracy between the estimated and actual data. The quantification of the accuracy was made through the mean percent error for each month in accordance with (9) and summarized in

Table 3. Absolute percentage error in the USD–CLP exchange rate prediction from August 2021 to August 2022.

Period	RK4 (%)	H = 0.58 (%)
August 2021	1.01	1.93
September 2021	0.68	0.31
October 2021	0.76	0.52
November 2021	1.06	0.75
December 2021	0.83	0.67
January 2022	2.50	1.42
February 2022	1.76	1.68
March 2022	1.88	0.92
April 2022	1.89	1.47
May 2022	2.23	1.51
June 2022	2.49	1.60
July 2022	5.24	3.98
August 2022	1.43	1.10

. The best estimation was $0.68\%$ in September 2021 and the worst was $5.24\%$ in July 2022.

$${ϵ}_{\%}={\displaystyle \frac{\left|{\text{USD–CLP}}_{actual}-{\text{USD–CLP}}_{estimated}\right|}{{\text{USD–CLP}}_{actual}}}\ast 100\%.$$

(9)

An important observation to consider corresponds to what is shown in Figure 2. It shows that the profile corresponding to the accumulated daily real fluctuations is identical to the value of the real exchange rate (Figure 2). This suggests that economic variables such as gross domestic product (GDP), interest rate, inflation rate, and rate of return are responsible for adjusting the value of the exchange rate; however, they are not responsible for the variability. Moreover, characterizing the daily fluctuations opens a new window to make estimates of the future.

4.2. Characterization of Exchange Rate Fluctuations USD–CLP

As noted above, the fluctuations in the exchange rate are very important because they are linked to variations in macroeconomic indicators, which generate instability in currencies. Estimating the exchange rate between foreign currencies represents a huge challenge, and knowing its dynamics would allow better decisions to be made in the different local economies, minimizing losses and maximizing profits.

In this subsection, we characterized the exchange rate daily fluctuation USD–CLP (see Figure 1b) through the Hurst exponent by detrended fluctuation analysis (DFA). The analysis has been carried out not in the daily exchange rate $r_i$ but on the logarithmic differences of the rate in consecutive days $R_i=\ln \left(r_{i+1}\right)-\ln \left(r_i\right)$. The result by applying DFA are shown in Figure 3, which shows that there is a scale range s where $F_2\left(s\right)\sim s^H$ and H can be extracted by a linear fit. For the exchange rate daily fluctuations USD–CLP, the Hurst exponent is close to white noise $H=0.58$.

With the characterization of exchange rate fluctuations based on the Hurst exponent, in the next subsection, we will generate synthetic fluctuations with the same properties as real fluctuations and use them to estimate the USD–CLP exchange rate.

4.3. Exchange Rate USD–CLP by Synthetic Fluctuation

As we mentioned earlier, the exchange rate fluctuation is very important and necessary to estimate the USD–CLP; however, there is an unknown when we want to make future estimations. To solve this problem, synthetic fluctuations series were taken to estimate the USD–CLP by RK4 following Section 3.6. Figure 4a shows a long synthetic fluctuations series with parameter $H=0.58$, while Figure 4b shows the cumulative fluctuations.

Remember that to estimate the exchange rate of USD–CLP by synthetic fluctuation and RK4, we have taken 10 aleatory and independent realizations of $2^8$ length data from a very long series of $2^{20}$ in length and characterized by the Hurst exponent $H=0.58$. The economic variables used to make the estimation are the same as the real case (see Table 2).

Figure 5 shows the results of each aleatory and independent realization of $2^8$ length data. Focusing independently on each realization, we can see that the results are not good. However, when we take the exchange rate mean value for all independent realizations, the result is very good. The result for the mean value of the exchange rate using synthetic fluctuations are shown in Figure 5b and summarized in Table 3. The results are consistent with the actual exchange rate behavior and have very good accuracy. The best estimation was $0.31\%$ in September 2021 and the worst was $3.98\%$ in July 2022. According to (Kristoufek 2012; Morales et al. 2012; Peters 1994), a Hurst exponent greater than 0.5 may indicate a market stability; in our study, $H=0.58$ (weak stability).

To summarize, taking into account absolute percentage error in the exchange rate USD–CLP value, the estimation delivers good accuracy results, both for estimates based on RK4 from real and synthetic fluctuation. The smaller the error value obtained, the closer the exchange rate is estimated to be to the actual data, and the NLSE can be used as a good estimator of the model for foreign currency exchange rates.

4.4. Policy Recommendations and Limitations

The Central Bank of Chile should make gradual interest rate adjustments to avoid worsening long-term trends, while managing both inflation and currency stability. At the same time, businesses should adopt long-term hedging strategies to protect themselves from the persistent trends in the USD–CLP exchange rate, as short-term speculation may not be effective Claro and Soto (2013).

Additionally, reducing reliance on dollar-sensitive sectors through economic diversification can help minimize the peso’s exposure to prolonged unfavorable trends against the dollar.

With daily exchange rate fluctuations characterized by a Hurst exponent (H = 0.58), the exchange rate shows persistent but moderately volatile trends, making short-term predictions less reliable.

However, using short time series may not capture all external shocks or changes in global markets, which limits the accuracy of long-term forecasts. Lastly, relying on specific economic models may not account for sudden geopolitical or economic disruptions.

5. Conclusions

Estimating the foreign exchange rate, particularly between the US dollar (USD) and the Chilean peso (CLP), is highly complex. The fourth-order Runge–Kutta (RK4) algorithm, combined with the nonlinear Schrödinger equation and the Black–Scholes model, allows for precise estimations using Chilean economic variables such as GDP, interest rate, inflation, and return rate, achieving an error of less than $6\%$. The detrended fluctuation analysis (DFA) method, used to characterize daily exchange rate fluctuations, resulting in a Hurst exponent of $H=0.58$, indicating moderate volatility. The results obtained highlight the important potential of using monofractal synthetic short time series for predicting the USD–CLP exchange rate, improving forecasting accuracy and decision making in economic models. Likewise, characterizing the daily exchange rate fluctuations by the Hurst exponent and generating synthetic fluctuations with the same characteristic could allow us to make future estimates. For this, it is recommended to generate a long time series of fluctuations and take some short sections.

The policy implications of our results suggest that the Central Bank of Chile should implement gradual interest rate adjustments to manage inflation and stabilize the currency. Additionally, businesses are encouraged to adopt long-term hedging strategies to mitigate the effects of persistent trends, as short-term speculation is less effective. Overall, combining advanced modeling techniques with sound economic policy enhances the management and prediction of currency fluctuations.

These conclusions suggest that combining advanced modeling techniques with thoughtful economic policy can improve both the management and prediction of currency fluctuations. In addition, the fourth-order Runge–Kutta (RK4) algorithm, combined with the nonlinear Schrödinger equation and the Black–Scholes model and monofractal fluctuations, can offer better accuracy in predicting market behavior and aid decision making across various sectors, benefiting financial institutions and policymakers.