Croatian Regional Export Value-Added Chains

Abstract

This paper examines Croatian Regional Value Chains (RVCs). We use the value chain approach to study supply chains, examining data specifically for Croatia and its proximate trading partners in the European Union, as well as some other European countries. The value added in Croatian exports is statistically related to the value added in the exports of Croatian trading partners. We argue that Croatian RVCs are organized around regional production centers, with proximity to production capacity, raw materials, and customers as driving factors, and thus most of the value added originates in these RVCs. This paper emphasizes the advantages of representing trade through value added over traditional gross trade statistics and highlights the robustness of RVCs in Croatia to global shocks and transportation reliability issues. We conclude that despite its small absolute size, the Croatian economy is dynamically well-integrated into the EU RVCs, which is crucial for increasing business efficiency and competitiveness, notwithstanding the constraints of relatively low returns to scale. Overall, this study contributes to a better understanding of RVCs in Croatia and their potential benefits for Croatia in the global production organization.

1. Introduction

This study focuses on regional value chains (RVCs) and their impact on the economic development of European countries, especially Croatia. RVCs are a set of activities that firms undertake to produce goods and services within a given region for the regional market, while international value chains (IVCs) refer to a set of activities that firms undertake to produce goods and services for markets outside the region (UNCTAD 2013, p. 2). The choice between RVCs and IVCs can be influenced by several factors, such as transportation costs, access to inputs, and consumer preferences.

To examine supply networks and compare the value added of countries’ imports and exports, we use the value chain method. RVCs are built around regional production centers, using accessibility to customers, raw materials, and production capacity as organizing principles. This article highlights the advantages of value chain trade over traditional gross trade data and emphasizes the resilience of RVCs to global shocks and transportation reliability issues. The benefits of regional economic integration through RVCs must be weighed against the costs of lost economies of scale. Local specialization and division of labor are critical to the resilience of regional economic development in Europe. This study examines the impact of RVCs on European countries, using the UNCTAD–Eora database to obtain values for the basic RVC indicator. The UNCTAD–Eora Conference on Trade and Development Economic Input–Output and Environment tables on the global value chain (GVC) provide a detailed breakdown of production processes and linkages between industries within and across countries. The UNCTAD Eora Global Value Chain Database is a collaboration between UNCTAD and the College of Sydney’s Eora research team. The database covers all 195-member countries and provides data on trade in goods, value added (VA), and employment in global value chains. Policy makers can use this information to promote economic growth and development. Although international value chains have emerged as a new model for global production organization, recent global uncertainties have revived concerns that full specialization at the global level is not possible. The COVID-19 pandemic, the war in Ukraine, the disruption of global distribution chains, and natural disasters have highlighted the shortcomings of relying solely on globalized specialization. Economic theory and history demonstrate the benefits of specialization, division of labor, and economic gains through trade. However, globalization has not historically favored the resilience of economies to shocks, reliability of shipments, and overall robustness. If the VA of Croatia’s trading partners increases, this could lead to an increase in demand for Croatian exports and potentially increase Croatian value added. The concept of the value chain is fundamental to understanding how companies create value, from product conception to consumption.

The objective of our analysis is to examine Croatian RVCs and Croatian integration within these RVCs. Our analysis is based first on a pairwise Dumitrescu–Hurlin panel non-causality test (based on a Granger non-causality test) to falsify “non-causalities” and second on a panel EGLS fixed effects test with first differencing to identify coefficients. When we use differenced variables, we are actually performing a dynamic analysis: We ask how much the dependent variable changes when the independent variable changes.

The panel EGLS test for VA in imports from selected countries and VA in exports from Croatia is based on the economic principles of specialization and division of labor in the context of economic integration. The model accounts for the impact of VA of imports from selected countries in the RVC on VA of exports from Croatia, while controlling for heterogeneity and bias due to omitted variables. The model can contribute to a better understanding of the factors driving economic growth and development in Croatia, as well as the benefits of economic integration with other countries.

One of the research questions we ask is “Does the recipient country of value added (VA) influence the VA re-exported by Croatia?” This research question aims to investigate the extent to which value added imported by Croatia from different countries is subsequently re-exported to other countries, and how this pattern varies between recipient countries’ VA. Thus, the null hypothesis is “There is no statistically significant relationship between the recipient countries’ VA and the value added re-exported by Croatia’s VA”. The null hypothesis assumes that the coefficients and t-statistics are not statistically significant.

2. Literature Review

This literature review examines the impact of RVCs (RVCs) on export engines in general and for Croatia in particular. International specialization is a key factor in increasing the efficiency and competitiveness of firms. The Organization for Economic Cooperation and Development (OECD 2013a, 2013b, 2013c, 2013d) reports that intermediate goods account for more than 50% of global imports of manufactured goods and more than two-thirds of global imports of services. Michael E. Porter, in his seminal book “Competitive advantage: creating and sustaining superior performance” (Porter 1985), introduced the value chain as a systematic approach to assessing a company’s competitive advantage.

The value chain is critical to understanding how companies create value from conception to consumption. Globalization has led to the emergence of regional and international value chains that have a significant impact on a country’s export performance. This literature review examines the impact of regional and international value chains on Croatia’s export factors. RVCs contribute to economic growth and development by creating jobs, generating income, and increasing exports. The EU is a major player in the field of regional value chains and has taken several policy initiatives to promote them. However, some of the issues that exist in GVCs are now surfacing in RVCs. Overall, RVCs play a critical role in promoting economic growth and job creation. (Cernat and Mustilli 2018; European Commission 2020; Eurostat 2021; Gereffi and Fernandez-Stark 2016; Gereffi et al. 2005). Gereffi et al. (2005) discuss the governance of global value chains and how different actors within a value chain can affect its competitiveness. They argue that RVCs can be particularly effective in promoting development in specific regions and increasing the competitiveness of firms in those regions. OECD (2013b) highlights the importance of RVCs in promoting economic growth and reducing poverty. Porter (1998) discusses the role of clusters, a form of RVC, in promoting competitiveness within regions. UNCTAD (2019, 2020) and the United Nations (2021) emphasize the potential of RVCs in promoting economic development and resilience to external shocks, particularly in emerging economies. Finally, the World Bank (2021) highlights the importance of policies that promote inclusiveness and sustainability within global value chains.

Regional integration leads to more regionally oriented economic cycles, with proximity to production capacity, raw materials, and customers being key factors in the emergence of RVCs (Koopman et al. 2010, 2014). However, traditional trade data that measure a country’s value added are becoming increasingly unreliable due to repetitive product accounting. To address this problem, De Backer and Yamano (2007) propose the use of input–output tables instead of arbitrary categorization methods in international trade statistics. Aslam et al. (2017) explain the theory and matrix algebra used to calculate trade statistics in value added using the Eora Multi-Region Input–Output Database, while Hirata et al. (2013) argue that regional business cycles have replaced global business cycles in the current phase of globalization. They conclude that regional output is favored by factors such as economic growth and development, transaction, transportation, tax, and other costs, and economies of scale. However, in the context of uninsured production risk, industrial specialization can lead to welfare losses that outweigh gains (Kalemli-Ozcan et al. 2003).

Hummels et al. (2001) estimate that vertical integration accounts for 21% of exports and 30% of the growth of these exports in the OECD countries studied. Even small reductions in tariffs and transportation costs can lead to significant vertical specialization, strong trade growth, and enormous trade benefits. Numerous studies have examined various aspects of RVCs and regional economic integration. Lee et al. (2021) measured the impact of regional integration on the development of RVCs in the automotive industry in ASEAN countries. Usman et al. (2018) provided a conceptual framework and literature review on the relationship between trade, real exchange rates, and unemployment. These studies highlight the importance of RVCs in enhancing competitiveness, improving productivity, and creating employment opportunities. Mance et al. (2021) further contributed to this literature by attempting to correlate the value added of individual countries in imports from their regional trading partners with the value added included in their exports.

Regarding studies about Croatia, the European Commission’s “Croatia: Trade Profile” provides an overview of Croatia’s international trade in goods and services. According to the report, Croatia’s economy is heavily reliant on the services sector, which accounts for over 70% of the country’s GDP. The country’s top export categories include machinery, transport equipment, and chemical products. Croatia’s main trading partners are other European Union countries, with Germany being the largest export market and Italy being the largest import partner. Despite the impact of the COVID-19 pandemic on global trade, Croatia’s exports and imports have remained relatively stable. However, Croatia’s exports are heavily concentrated in a few product categories and markets, which may pose a risk to the country’s economic stability. Croatia is a small open economy that has undergone significant economic and social transformation since the 1990s. The country has traditionally relied on trade with the EU as an engine of economic growth, with exports to the EU accounting for over 60% of the country’s total exports (European Commission 2020). In recent years, Croatia has sought to diversify its export markets by increasing its participation in RVCs.

Participation in RVCs can offer significant benefits to Croatian exporting firms, such as access to larger markets and the use of local knowledge and know-how. RVCs also provide opportunities for technological improvements and skills development through learning from peers in the region. While Croatia has traditionally relied on the EU for economic growth through trade, participation in RVCs provides an opportunity to diversify export markets (European Commission 2020).

3. Data and Methods

Panel data analysis is a widely used statistical technique in economics, finance, and social sciences. Panel data consist of observations of multiple individuals or entities over time, which makes them useful for analyzing the effects of both time-invariant and time-varying variables on the outcomes of interest. We collected data on 27 EU countries plus Albania, Bosnia and Herzegovina, Macedonia, Montenegro, Norway, Switzerland, and the United Kingdom. Our dataset spans 20 years, from 2000 to 2019. The table’s data are structured such that the cell at row i and column j at time t represents the value added of country i present in the exports of country j in year t. The cell at row i and column j is the value added of country j in year t. This cell represents the intermediate use of country i’s exports by country j. The Eora is an input–output table that shows the flow of value added from a country in a row to a country in a column. For more information on the data, please see OECD (2013b, 2013c, 2013d).

Table 1. Example of a UNCTAD–Eora Global Value Chain (GVC) basic input–output table.

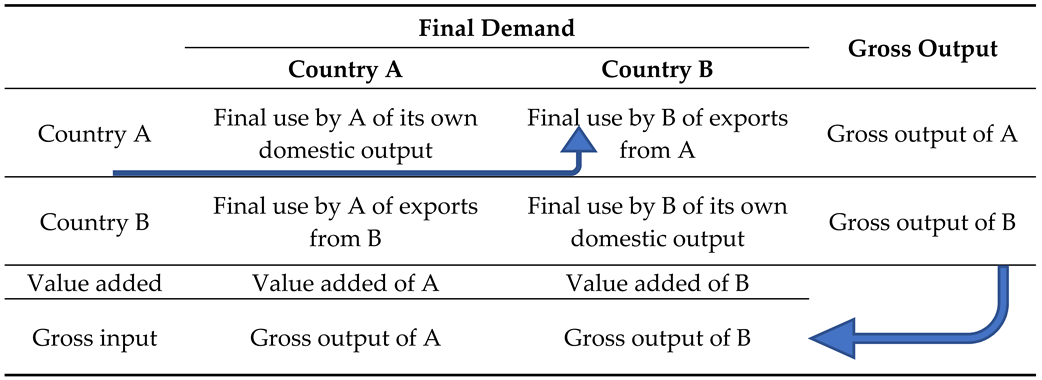
Source: Own depiction based on UNCTAD (2013).

shows the data aggregation methodology used by the UNCTAD–Eora Global Value Chain (GVC) database.

The GVC country matrix reflects for each exporting country the value added by all other countries in the world. The rows represent the country that created VA and the columns represent the country that exported it.

To analyze the Eora panel data, which contain non-stationary variables, we use dynamic panel techniques following Baltagi (2008) and Wooldridge (2011). We first differenced all data to achieve stationarity in level and trend. Since the first differences represent changes from the previous year, they measure changes in value, leading to a dynamic analysis. We want to know whether and to what extent changes in one country’s economic capacity, as measured by changes in value added, “cause” changes in another country’s productive capacity.

To test Granger causality, we use Granger’s (1969) noncausality test and its fixed-effects derivation: the pairwise Dumitrescu–Hurlin test. The null hypothesis for the Granger causality test states that lagged values of i do not explain the variation of j. This method accounts for differences in fixed effects in the form of different constants and other idiosyncratic effects across countries.

To avoid the overly restrictive assumption of Granger causality for all cross-sections simultaneously, we choose to assume it for only a portion of the cross-sectional structure. To this end, we use the approach of Dumitrescu and Hurlin (2012), which is based on the panel unit root tests of Im et al. (2003) in heterogeneous panels. The pairwise Dumitrescu–Hurlin panel non-causality test (PDH), which accounts for the possibility of cross-sectional dependence and common factors in panel data, is used to examine the direction of causality between two variables in a panel data set. This test allows the investigation of non-causality in both directions and identifies cases where the causal relationship runs from the dependent to the independent variable as well as from the independent to the dependent variable. If the Dumitrescu and Hurlin test yields a statistically significant result, we conclude that countries are dynamically integrated.

To achieve stationarity, we perform the “non-causality test” by testing the nominal values of the cross-sections with various tests, including t-stat tests, W-stat tests, and chi-square tests. We then use first-differenced variables in the panel data analysis to eliminate the effects of time-invariant factors and control for omitted variable bias, address endogeneity problems in the data by eliminating time-invariant individual heterogeneity, and reduce the influence of cross-sectional dependence. To determine whether there are fixed effects due to cross-sectional effects, we use the Hausman test to compare the results of the random effects equation with the fixed effects results. If the null hypothesis is rejected, a fixed effects model is computed using Panel-Estimated Generalized Least Squares (EGLS) Fixed Effects (FE) First Differences (FD), with Cross-sectional Seemingly Unrelated Regression (SUR) and Panel-Corrected Standard Errors (PCSE). This method is robust and versatile and accounts for correlation between same-unit residuals over time and cross-sectional units over time, resulting in more accurate parameter estimates and less risk of biased results due to misspecification of the variance–covariance matrix. PCSE is a powerful and versatile method for analyzing panel data that provides comprehensive information about the relationship between the variables of interest; researchers can benefit from its application in their studies. For a detailed description of methods for analyzing panel data, see Baltagi (2008, 2021) or Wooldridge (2011).

For the concept of stationarity, the concept of co-integration and a common co-integrating variable is of utmost importance. Co-integration is a statistical concept that describes a long-term equilibrium between variables. It occurs when variables, while not individually stationary, exhibit a stable relationship when combined. Co-integrated variables move together in the long run despite short-term fluctuations. To this end, a co-integrating variable must be found to ensure that all deviations from equilibrium are corrected over time.

Panel FMOLS is an estimation method for cointegrating relationships in panel data. It extends the FM-OLS estimator for a time series. It addresses the problems of endogeneity and serial correlation in panel data by regressing levels of variables on lagged differences and predetermined variables. FMOLS includes common factors and fixed effects to account for cross-sectional dependence and heterogeneity. It provides consistent and efficient estimates of cointegration coefficients that capture long-run equilibrium. It uses instrumental variables and a two-step procedure. FMOLS is suitable for stationary or non-stationary variables and allows dynamic analysis of the co-integrating relationship.

4. Results

We began our panel analysis by performing a series of standard unit root tests, including the Levin, Lin and Chu t-test; the Breitung t-statistic; the Im, Pesaran and Shin W-statistic; the Augmented Dickey Fuller–Fisher Chi-square test; and the Phillips–Perron–Fisher Chi-square test. The results of these tests indicated that the variables were non-stationary, requiring either testing for co-integration or differentiation for stationarity.

After differentiation, the individual time series achieved stationarity. The summary results of the Augmented Dickey Fuller (ADF) Unit Root test are shown in

Table 2. Augmented Dickey Fuller (ADF) Unit Root test.

		Croatia	Austria	BiH	Germany	Italy	Slovenia
	At Level
With Constant	t-Statistic	0.3475	0.4611	0.4952	0.5538	0.4143	0.5840
	Prob.	0.4049	0.0634	0.8257	0.2055	0.4692	0.4572
With Constant and Trend	t-Statistic	0.7528	0.7491	0.6131	0.5355	0.7238	0.5777
	Prob.	0.2665	0.9395	0.0094	0.3674	0.2551	0.2306
Without Constant and Trend	t-Statistic	0.6478	0.7781	0.7465	0.8270	0.7394	0.8503
	Prob.	0.9358	0.9224	0.9867	0.9631	0.9458	0.9736
	At First Difference
With Constant	t-Statistic	0.0010	0.0005	0.0005	0.0002	0.0007	0.0003
	Prob.	0.0000	0.0000	0.0007	0.0000	0.0000	0.0000
With Constant and Trend	t-Statistic	0.0028	0.0014	0.0196	0.0009	0.0020	0.0014
	Prob.	0.0002	0.0099	0.0042	0.0002	0.0003	0.0089
Without Constant and Trend	t-Statistic	0.0001	0.0000	0.0000	0.0000	0.0000	0.0000
	Prob.	0.0000	0.2175	0.0000	0.0000	0.0000	0.0000

Data source: UNCTAD–Eora database. Calculation: E-views 9.0. Sample: 2000 2019. Included observations: 3780. Null Hypothesis: the variable has a unit root.

.

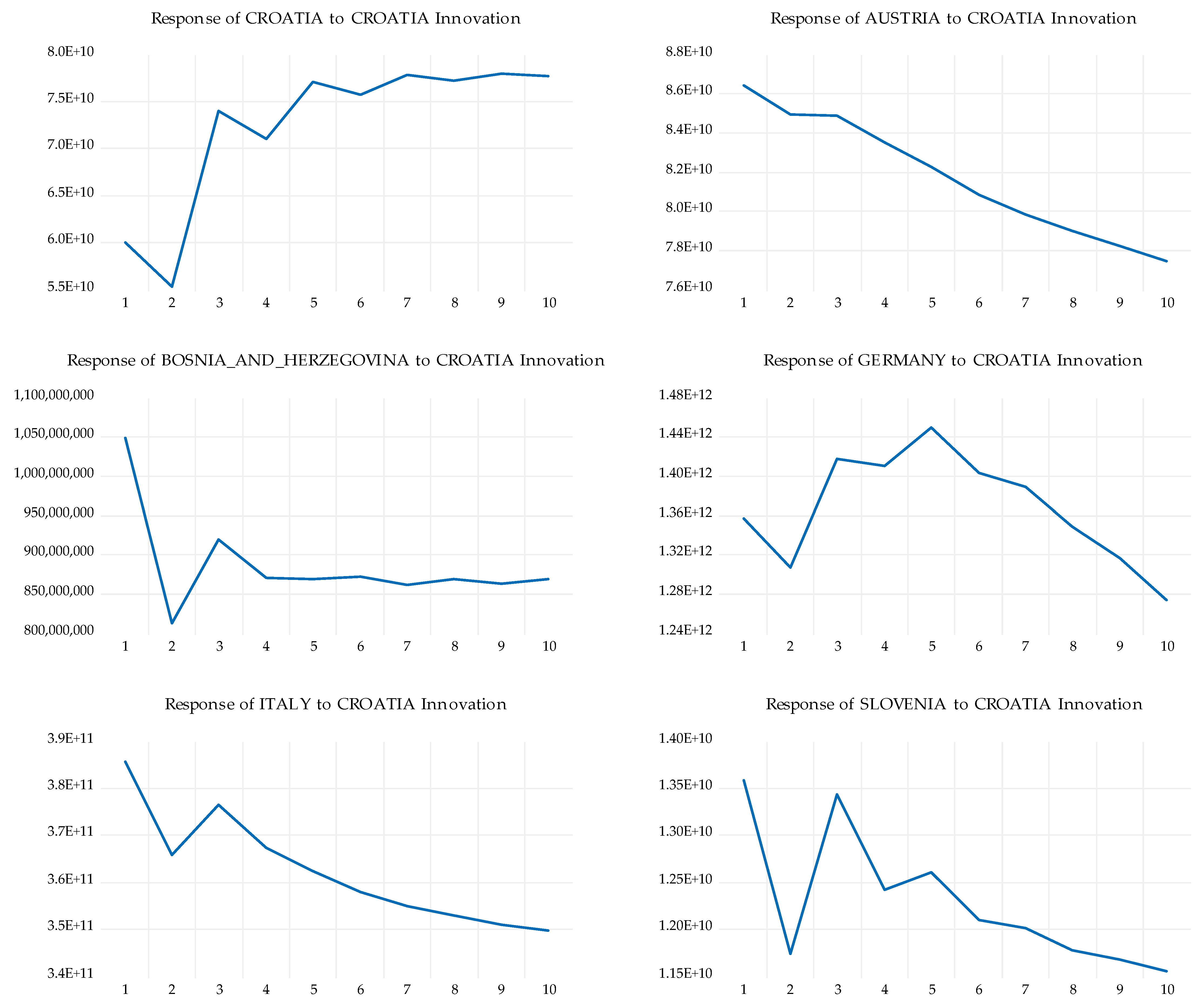
In the presence of co-integrating statistical associations for a smaller sample of countries consisting of the five largest trading partners, we used the Vector Error Correction Model (VECM), with subsequent impulse response functions to study the effects of shocks. The impulse response function records a one standard deviation shock to one endogenous variable and its effects on all endogenous variables in a VECM, while holding all other variables and shocks constant. The impulse response functions for 1 standard deviation are in Appendix A and the Cholesky Impulse response function diagrams for 1 standard deviation of impulse (d.f. corrected) are in Appendix B.

For the purpose of testing for co-integration, we performed the Kao Residual Co-integration based on the Augmented Dickey Fuller stationarity test on a limited selection of Croatia’s neighboring countries and largest trading partners including Austria, Bosnia and Herzegovina, Germany, Italy, and Slovenia (

Table 3. Kao Residual Cointegration Test based on the Augmented Dickey Fuller (ADF) test.

	t-Statistic	Prob.
ADF	4.826007	0.0000
Residual variance	3.54 × 1021
HAC variance	3.71 × 1021

Data source: UNCTAD–Eora database. Calculation: E-views 9.0. Sample: 2000 2019. Included observations: 3780. Null Hypothesis: No co-integration. Trend assumption: No deterministic trend. Automatic lag length selection based on SIC with a max lag of 4 Newey–West automatic bandwidth selection and Bartlett kernel.

).

The null hypothesis of no co-integration was successfully falsified with p < 0.0001 and a t-statistic of 4.826, which demonstrates significant evidence of countries’ integration for the common AR coefficients.

Table 4. Pedroni Residual Cointegration Test.

Test	Statistic	Prob.	Weighted Statistic	Prob.
Panel v-Statistic	−3.953738	1.0000	−4.207404	1.0000
Panel rho-Statistic	2.146333	0.9841	9.466748	1.0000
Panel PP-Statistic	−16.10268	0.0000	−6.685998	0.0000
Panel ADF-Statistic	−6.850227	0.0000	−6.132245	0.0000

Data source: UNCTAD–Eora database. Calculation: E-views 9.0. Sample: 2000 2019. Included observations: 3780. Cross-sections included: 188 (1 dropped). Null Hypothesis: No co-integration.

shows the results of the Pedroni Residual Cointegration Test, which examines the presence of co-integration between a set of variables.

The panel v-statistic measures the presence of co-integration assuming common autoregressive (AR) coefficients within each dimension. The panel rho statistic tests for common AR coefficients within each dimension. The panel PP statistic is used to test for co-integration assuming common coefficients within each dimension. The panel ADF statistic is another test for co-integration assuming common AR coefficients for each dimension. In all cases, the null hypothesis of no co-integration is rejected. Thus, based on these results, there is evidence of co-integration between the analyzed series.

The test results of the Panel Fully Modified Least Squares (FMOLS) of Croatia as a dependent variable and its five most important trading partners is given in

Table 5. Panel FMOLS of Croatia as a dependent variable and its five most important trading partners.

Variable	Coefficient	Std. Error	t-Statistic	Prob.
Austria	0.002964	7.88 × 105	37.59653	0.0000
Bosnia and Herzegovina	0.164040	0.005108	32.11730	0.0000
Germany	0.000489	1.01 × 105	48.42860	0.0000
Italy	0.002084	1.90 × 105	109.4095	0.0000
Slovenia	0.024038	0.000637	37.73323	0.0000
R-squared	0.987002	Mean dependent var		5.22 × 1010
Adjusted R-squared	0.985454	S.D. dependent var		5.24 × 1011
S.E. of regression	6.32 × 1010	Sum squared resid		1.28 × 1025
Long-run variance	2.67 × 1019

Data source: UNCTAD–Eora database. Calculation: E-views 9.0. Sample: 2000 2019. Periods included: 19. Cross-sections included: 189. Total panel (balanced) observations: 3591.

.

The test results’ R-squared value of 0.98, indicates that the independent variables in the model (the VA of imports present in the VA of exports) explain about 98% of the variation in the dependent variable, the VA of Croatian imports present in the VA of the Croatian exports.

Table 6. Co-integrating equations for Croatia’s five most important trading partners.

Cointegrating Equation	CointEq1	Std. Error	t-Statistic
Croatia	1.000000
Austria	0.023376	0.01336	1.75004
Bosnia and Herzegovina	1.069346	1.07956	0.99054
Germany	−0.036086	0.00151	−23.8624
Italy	−0.000588	0.00320	−0.18378
Slovenia	0.145186	0.10083	1.43991
C	2.43 × 1011

Data source: UNCTAD–Eora database. Calculation: E-views 9.0. Sample: 2003 2019. Total panel (balanced) observations: 3213 after adjustments.

represents the co-integrating equations for Croatia’s five most important trading partners.

We proceed with the Pairwise Dumitrescu–Hurlin (PDH) Panel Non-Causality Test with differenced values. This is a statistical test used in the analysis of panel data and is specifically designed to falsify the null hypothesis of non-causality between two variables in a panel data set while controlling for possible cross-sectional dependence. Differentiation of the data, with the subsequent loss of information, is necessary when the panel data have unit root processes. For each pair of variables, the test checks whether one variable (e.g., D(Croatia)) “causes” the other variable (e.g., D(Albania)) in a homogeneous way—and in a Clive Granger sense of the meaning of the word “causation”. The null hypothesis in each case is that the variable does not cause the other variable in a homogeneous way. The column “W-Stat.” contains the test statistic, which is a measure of the strength of the evidence against the null hypothesis. The “Zbar-Stat.” column contains the standardized test statistic used to calculate the probability (or p-value) of the test and the “Prob.” column contains the probability of the null hypothesis being true. The results are presented in

Table 7. Pairwise Dumitrescu–Hurlin Panel Non-Causality Test.

Null Hypothesis:	W-Stat.	Zbar-Stat.	Prob.
D(Croatia) does not homogeneously cause D(Albania)	4.73941	10.9416	0.0000 ***
D(Albania) does not homogeneously cause D(Croatia)	4.07469	7.83264	5 × 10−15 ***
D(Croatia) does not homogeneously cause D(Austria)	1.98366	−1.94726	0.0515 *
D(Austria) does not homogeneously cause D(Croatia)	2.09091	−1.44562	0.1483
D(Croatia) does not homogeneously cause D(Belgium)	3.17131	3.60749	0.0003 ***
D(Belgium) does not homogeneously cause D(Croatia)	2.65826	1.20789	0.2271
D(Croatia) does not homogeneously cause D(B and H)	2.09611	−1.42130	0.1552
D(B and H) does not homogeneously cause D(Croatia)	3.32079	4.30659	2 × 10−5 ***
D(Croatia) does not homogeneously cause D(Bulgaria)	2.24385	−0.73033	0.4652
D(Bulgaria) does not homogeneously cause D(Croatia)	2.05558	−1.61089	0.1072
D(Cyprus) does not homogeneously cause D(Croatia)	2.91546	2.41083	0.0159 **
D(Croatia) does not homogeneously cause D(Cyprus)	2.32479	−0.35178	0.7250
D(Czech Republic) does not homogeneously cause D(Croatia)	2.25382	−0.68368	0.4942
D(Croatia) does not homogeneously cause D(Czech Republic)	1.48171	−4.29491	2 × 10−5 ***
D(Denmark) does not homogeneously cause D(Croatia)	2.83225	2.02167	0.0432 **
D(Croatia) does not homogeneously cause D(Denmark)	4.57231	10.1601	0.0000 ***
D(Estonia) does not homogeneously cause D(Croatia)	2.81573	1.94440	0.0518 *
D(Croatia) does not homogeneously cause D(Estonia)	4.65166	10.5312	0.0000 ***
D(Finland) does not homogeneously cause D(Croatia)	2.34980	−0.23480	0.8144
D(Croatia) does not homogeneously cause D(Finland)	3.21952	3.83298	0.0001 ***
D(France) does not homogeneously cause D(Croatia)	2.28543	−0.53584	0.5921
D(Croatia) does not homogeneously cause D(France)	2.57316	0.80988	0.4180
D(Germany) does not homogeneously cause D(Croatia)	1.58634	−3.80556	0.0001 ***
D(Croatia) does not homogeneously cause D(Germany)	1.66480	−3.43858	0.0006 ***
D(Greece) does not homogeneously cause D(Croatia)	3.24479	3.95114	8 × 10−5 ***
D(Croatia) does not homogeneously cause D(Greece)	3.66795	5.93030	3 × 10−9 ***
D(Hungary) does not homogeneously cause D(Croatia)	2.43310	0.15483	0.8770
D(Croatia) does not homogeneously cause D(Hungary)	4.47090	9.68576	0.0000 ***
D(Ireland) does not homogeneously cause D(Croatia)	3.37137	4.54315	6 × 10−6 ***
D(Croatia) does not homogeneously cause D(Ireland)	3.45546	4.93648	8 × 10−7 ***
D(Italy) does not homogeneously cause D(Croatia)	5.21176	13.1508	0.0000 ***
D(Croatia) does not homogeneously cause D(Italy)	5.86089	16.1868	0.0000 ***
D(Latvia) does not homogeneously cause D(Croatia)	3.21646	3.81862	0.0001 ***
D(Croatia) does not homogeneously cause D(Latvia)	7.88969	25.6757	0.0000 ***
D(Lithuania) does not homogeneously cause D(Croatia)	1.07467	−6.19868	0.2693 ***
D(Croatia) does not homogeneously cause D(Lithuania)	1.07467	−6.19868	6 × 10−10 ***
D(Luxembourg) does not homogeneously cause D(Croatia)	4.27635	8.77584	0.0000 ***
D(Croatia) does not homogeneously cause D(Luxembourg)	3.18565	3.67454	0.0002 ***
D(Malta) does not homogeneously cause D(Croatia)	2.77577	1.75751	0.0788 *
D(Croatia) does not homogeneously cause D(Malta)	3.87207	6.88496	6 × 10−12 ***
D(Montenegro) does not homogeneously cause D(Croatia)	3.02660	2.93064	0.0034 ***
D(Croatia) does not homogeneously cause D(Montenegro)	4.63360	10.4467	0.0000 ***
D(Netherlands) does not homogeneously cause D(Croatia)	1.98600	−1.93632	0.0528 *
D(Croatia) does not homogeneously cause D(Netherlands)	2.82592	1.99205	0.0464 **
D(Norway) does not homogeneously cause D(Croatia)	2.45703	0.26672	0.7897
D(Croatia) does not homogeneously cause D(Norway)	4.19727	8.40597	0.0000 ***
D(Poland) does not homogeneously cause D(Croatia)	2.39348	−0.03049	0.9757
D(Croatia) does not homogeneously cause D(Poland)	14.5790	56.962	0.0000 ***
D(Portugal) does not homogeneously cause D(Croatia)	3.14093	3.46539	0.0005 ***
D(Croatia) does not homogeneously cause D(Portugal)	2.68997	1.35621	0.175
D(Romania) does not homogeneously cause D(Croatia)	2.97246	2.67742	0.0074 ***
D(Croatia) does not homogeneously cause D(Romania)	5.98296	16.7578	0.0000 ***
D(Serbia) does not homogeneously cause D(Croatia)	3.45135	4.91723	9 × 10−7 ***
D(Croatia) does not homogeneously cause D(Serbia)	7.43262	23.5379	0.0000 ***
D(Slovakia) does not homogeneously cause D(Croatia)	8.61229	29.0553	0.0000 ***
D(Croatia) does not homogeneously cause D(Slovakia)	17.7106	71.6087	0.0000 ***
D(Slovenia) does not homogeneously cause D(Croatia)	2.29569	−0.48785	0.6257
D(Croatia) does not homogeneously cause D(Slovenia)	2.42684	0.12551	0.9001
D(Spain) does not homogeneously cause D(Croatia)	2.61885	1.0236	0.306
D(Croatia) does not homogeneously cause D(Spain)	4.14085	8.14208	4 × 10−16 ***
D(Sweden) does not homogeneously cause D(Croatia)	2.25898	−0.65955	0.5095
D(Croatia) does not homogeneously cause D(Sweden)	3.47464	5.02615	5 × 10-7 ***
D(Switzerland) does not homogeneously cause D(Croatia)	4.74707	10.9774	0.0000 ***
D(Croatia) does not homogeneously cause D(Switzerland)	4.00554	7.50923	6 × 10−14 ***
D(Macedonia) does not homogeneously cause D(Croatia)	3.92450	7.13019	1 × 10−12 ***
D(Croatia) does not homogeneously cause D(Macedonia)	4.27454	8.76738	0.0000 ***
D(Uk) does not homogeneously cause D(Croatia)	2.90427	2.35851	0.0183 *
D(Croatia) does not homogeneously cause D(Uk)	3.11013	3.32135	0.0009 ***
D(Norway) does not homogeneously cause D(Croatia)	2.45703	0.26672	0.7897
D(Croatia) does not homogeneously cause D(Norway)	4.19727	8.40597	0.0000 ***

Data source: UNCTAD–Eora database. Calculation: E-views 9.0. Sample: 2000 2019. Lags: 2. Results significant at 10% = *. Results significant at 5% = **. Results significant at 1% = ***. D(COUNTRY) means first difference.

.

The results of the Pairwise Dumitrescu–Hurlin Panel Causality Test demonstrate that Croatia has a strong integration in the RVC (RVC) comprising the EU countries, Albania, Bosnia and Herzegovina, Norway, Switzerland, and the UK, when considering the value added (VA) of all countries. The majority of selected countries show a significant statistical association between changes in their VA and those of Croatia, indicating a strong causality between them. The null hypothesis of non-causation was successfully refuted in most cases. However, France, one of Croatia’s major trading partners, shows an exception to this trend, as it is not economically integrated with Croatia in terms of intermediate value chains. Some of the countries are integrated in the Croatian VA just in one direction. For example, the increase in the VA of Croatia increases the value of the Czech VA present in Croatian exports in a statistically significant manner but the inverse relationship is not statistically significant (Table 7). The Granger causality test is used to predict future values of a time series of D(VA) in one country based on prior values of D(VA) in the time series of another country. However, this test is designed to deal with pairs of variables and may produce misleading results when the true relationship involves three or more variables. Therefore, we will continue to assess the VA of Croatia’s immediate neighbors and trading partners. In conclusion, Croatia plays a significant role in the RVC of these 25 European nations, and further analysis is necessary to fully understand the economic relationships among these countries. By focusing on Croatia and its additional value within the RVC, we can gain a more comprehensive understanding of the complex economic dynamics at play.

Table 8. Panel EGLS of Croatia as a dependent variable and its most important trading partners.

Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(Germany)	0.000656	0.000118	5.571276	0.0000
D(Italy)	0.001761	0.000202	8.695464	0.0000
D(Slovenia)	0.046667	0.006444	7.242123	0.0000
D(Bosnia and Herzegovina)	0.176261	0.030783	5.725872	0.0000
D(Austria)	0.001589	0.000478	3.324360	0.0009
C	1.47 × 109	90491160	16.22353	0.0000
Weighted statistics
R-squared	0.715470	Mean dependent var		2.66 × 1010
Adjusted R-squared	0.699393	S.D. dependent var		8.98 × 1010
S.E. of regression	5.07 × 1010	Sum squared resid		8.72 × 1024
F-statistic	44.50263	Durbin–Watson stat		2.363742
Prob(F-statistic)	0.000000
Unweighted statistics
R-squared	0.225991	Mean dependent var		2.71 × 109
Sum squared resid	1.01 × 1025	Durbin–Watson stat		2.967953

Method: Panel EGLS, Cross-section SUR (PCSE). Sample (adjusted): 2001–2019. Periods included: 19. Cross-sections included: 189. Total panel (balanced) observations: 3591. D() means 1st difference.

shows the statistical results of a regression analysis of panel data using the panel EGLS estimator with the cross-section SUR and PCSE correction method. The dependent variable is the value added of Croatia, and the independent variables are the VAs of the five main trading partners, namely Germany, Italy, Slovenia, Bosnia and Herzegovina and Austria—measured in USD.

The results show that changes in the exported VA of these trading partners have a statistically significant positive effect on Croatia’s VA present in the Croatian exports. Specifically, Croatian exports’ VA increases by 0.0656%, 0.1761%, 0.0016%, and 0.0467% for every 1% increase in value added in Germany, Italy, Austria, and Slovenia, respectively. Bosnia and Herzegovina have the largest effect: a 1% increase in value added there leads to a 0.1763% increase in Croatian value added. The intercept term (C) is also statistically significant at a very high level, suggesting that there are other factors not included in the model that affect Croatia’s value added. The Weighted Statistics R-squared value of 0.715 indicates that the model explains a significant amount of the variance in the dependent variable, and the adjusted R-squared value of 0.699 indicates that the model is a good fit.

In a panel data EGLS (Error Component Generalized Least Squares) model, “Weighted Statistics” refers to the use of weighted regression techniques that account for heteroskedasticity and correlation of errors between individuals and time periods, since it assumes that the variance of error terms is not constant across individuals and time periods. To address this issue, Panel EGLS applies a weighted regression technique that gives higher weights to observations with smaller errors and lower weights to observations with larger errors. On the other hand, unweighted statistics assume that the variance of errors is the same across all cross-sectional units and time periods and do not account for the possibility of correlation between errors within the same unit or over time. This can lead to biased and inefficient estimates, especially if there is significant heteroskedasticity or correlation in the data.

The F-statistic of 44.5 and the associated p-value of p < 0.0001 indicate that the overall model is statistically significant. The unweighted statistics shows the same results, but for unweighted observations. The Durbin–Watson statistic is used to test for autocorrelation in the errors. A value of 2.96 indicates that there is no significant autocorrelation in the residuals. The sample includes observations from 2001 to 2019 after adjustment, with 189 cross-sections and a total of 3591 balanced panel observations. We can explain 70% of the Croatian change in the VA through changes in the RVC with the first five Croatian trading partners (Table 8).

The Croatian RVC, composed of 27 EU member states and another 7 European countries, explains 86% of the change in Croatian VA (

Table 9. Panel EGLS of the reexported D(VA) by Croatia as a dependent variable (recipient of VA).

Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	1.50 × 109	87925883	17.11053	0.0000
D(Albania)	0.021174	0.006139	3.448873	0.0006
D(Austria)	0.001608	0.000512	3.138342	0.0017
D(Bulgaria)	−0.000735	0.000196	−3.755261	0.0002
D(Cyprus)	0.000340	7.34 × 10−5	4.632465	0.0000
D(Czech Republic)	0.000711	9.57 × 10−5	7.429050	0.0000
D(Denmark)	0.000195	3.47 × 10−5	5.623734	0.0000
D(Estonia)	0.001339	0.000372	3.598627	0.0003
D(Finland)	7.61 × 10−5	2.73 × 10−5	2.787739	0.0053
D(France)	7.79 × 10−5	2.26 × 10−5	3.453824	0.0006
D(Germany)	0.000382	0.000112	3.411127	0.0007
D(Greece)	0.000624	0.000234	2.663730	0.0078
D(Hungary)	0.001893	0.000251	7.556514	0.0000
D(Italy)	0.001621	0.000196	8.263685	0.0000
D(Lithuania)	0.003464	0.000895	3.870772	0.0001
D(Luxembourg)	0.009074	0.001606	5.649169	0.0000
D(Macedonia)	0.135922	0.016075	8.455215	0.0000
D(Montenegro)	0.040124	0.013362	3.002829	0.0027
D(Netherlands)	0.000165	2.84 × 10−5	5.811924	0.0000
D(Norway)	0.000184	5.00 × 10−5	3.688172	0.0002
D(Poland)	0.000136	7.63 × 10−5	1.784833	0.0744
D(Slovakia)	0.001346	0.000207	6.505240	0.0000
D(Slovenia)	0.025625	0.006534	3.921874	0.0001
D(Spain)	0.000167	5.78 × 10−5	2.895061	0.0038
D(Sweden)	0.000151	3.21 × 10−5	4.715953	0.0000
D(Switzerland)	0.000266	2.71 × 10−5	9.807755	0.0000
R-squared	0.863941	Mean dependent var		3.64 × 1010
Adjusted R-squared	0.855359	S.D. dependent var		1.34 × 1011
S.E. of regression	5.21 × 1010	Sum squared resid		9.17 × 1024
F-statistic	100.6721	Durbin–Watson stat		2.035146
Prob(F-statistic)	0.000000

Method: Panel EGLS, Cross-section SUR (PCSE). Sample (adjusted): 2001–2019. Periods included: 19. Cross-sections included: 189. Total panel (balanced) observations: 3591. D() means 1st difference.

).

The results in Table 9 clearly show that most relationships are statistically significant at the level p < 0.01 or even below, except for Poland, which is significant at the p < 0.1 level. We do not have an immediate and clear answer to this result, as Poland is a growing trading partner of Croatia. A noticeable outlier is Bulgaria with a negative sign of the coefficient, which means that trade relations with this country are actually decreasing in terms of additional export VA and the two countries are becoming less and less integrated economically. How is this possible? Bulgaria is plagued by huge emigration. Emigration can lead to a loss of skills, labor, and entrepreneurial talent, which can negatively impact the competitiveness of local firms and industries. This can result in a reduction in the quality and quantity of goods and services produced in Bulgaria. Only countries with statistically significant values were considered. Regarding the impact of changes in the value of foreign value added included in Croatian re-exports, the results of the EGLS fixed effects panel estimation show a strong integration of the Croatian economy into the European value chain (R² = 0.86). The coefficient of determination of 0.86 indicates that the changes in exports of selected countries’ VA explain 86% of the variation in Croatian re-exports from VA. This is a higher value than the two-thirds usually reported in the media.

5. Discussion

RVCs refer to production and trade activities that take place within a specific geographic region, while global value chains refer to production and trade activities that span multiple countries and regions. For Croatia, the economic intuition behind the importance of RVCs lies in the potential for greater regional integration and specialization, which can lead to greater productivity gains.

One of the main benefits of RVCs is that they can facilitate closer economic ties and better coordination between neighboring countries, which can lead to increased trade, investment, and economic growth. By focusing on RVCs, Croatia can strengthen its economic ties with other countries in the region, such as Slovenia, Hungary, Italy, Austria, and Slovakia, all of which are EU members, as well as Bosnia and Herzegovina, Serbia, Montenegro, Macedonia, and Albania, which are not members of the common market but could still mutually benefit from complementarities.

RVCs contribute to greater specialization by allowing companies to focus on producing goods and services that best match their particular strengths and resources. This can lead to greater efficiency and productivity gains as companies become more competitive in their respective markets. RVCs save on transportation and distribution costs because production is local rather than global. The benefits of such a production organization were exacerbated by the disruption of international transportation and distribution chains during the COVID-19 pandemic. However, RVCs also have their limitations, especially for smaller countries such as Croatia. First, RVCs can be even more vulnerable to shocks and disruptions because they tend to be more concentrated in a particular geographic area. The most famous such disruption was caused by the 1995 Kobe earthquake for memory chip production, as many of the leading manufacturers were located in the affected region. The earthquake damaged factories, disrupted supply chains, and caused power outages that exacerbated the decline in production. The impact on the global technology industry was significant, as shortages of memory French fries led to price increases and supply chain disruptions that affected the entire sector. In addition, RVCs may not provide the same access to global markets and technologies as global value chains. Overall, RVCs offer a lower degree of division of labor and specialization. Nevertheless, most of today’s production processes and technologies achieve full economies of scale and scope at the regional rather than international level. Therefore, RVCs may represent the sweet spot of production for most production processes.

In terms of policy implications, policymakers should consider how to support the development of RVCs without forgetting global value chains. This could include measures to improve infrastructure and transport links with neighboring countries, as well as measures to encourage more innovation and investment in key sectors. The importance of regional or global value chains may depend on a number of factors, including the size and level of development of the economy, the nature of trade relations with neighboring countries, and the degree of specialization and competitiveness of industries.

Overall, RVCs are important for promoting economic development, reducing poverty, and increasing competitiveness, particularly in the context of the EU and emerging economies. They also underscore the need for measures to promote inclusion and sustainability within value chains to ensure that their benefits are more widely shared.

6. Conclusions

As regions grow economically and achieve economies of scale, production and trade increasingly revolve around RVCs organized around regional production centers. This study extends previous research by examining supply chains using the value chain concept, including the entire EU and other countries in the region. It examines the impact of RVCs on export engines and the importance of local specialization for regional economic resilience. In analyzing Croatian RVCs and their integration, the study uses a panel Granger non-causality test and panel estimation (EGLS FE SUR PCSE) after examining the data for stationarity. The results show significant relationships between changes in RVCs in most of the countries analyzed and changes in Croatian RVCs, indicating successful rejection of the null hypotheses. These results illustrate that RVCs are a crucial factor for economic integration and growth in Europe. Croatia is well integrated into the European RVCs, as shown by the statistically significant relationships between changes in the value added of European countries (mainly EU members) and changes in Croatian value added in exports. Although the degree of integration may be modest in terms of level changes, the mutual changes in value added between Croatia and its neighbors demonstrate statistical integration. Participation in RVCs provides opportunities for market expansion, technological improvement, and skill development, which requires policies to promote RVC development in sectors where Croatia has a comparative advantage. In terms of limitations, the chosen estimation methods considered small sample bias, subjectivity of lag selection, and stationarity through differentiation. Non-cointegration could not be definitively disproved. The panel estimator EGLS FE SUR PCSE accounted for endogeneity, heterogeneity, cross-sectional dependence, and unobserved effects. Future research should examine individual industry sectors within the VA RVCs in Croatia for modernization and integration efforts.