You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Economies
Download PDF
  • Feature Paper
  • Article
  • Open Access

24 February 2023

Economic Policy Uncertainty, Energy and Sustainable Cryptocurrencies: Investigating Dynamic Connectedness during the COVID-19 Pandemic

,
,
,
and
1
Business School, Liaoning University, Shenyang 110036, China
2
VALORIZA—Research Center for Endogenous Resource Valorization, 7300-555 Portalegre, Portugal
3
Department of Economic Sciences and Organizations, Polytechnic Institute of Portalegre, 7300-555 Portalegre, Portugal
4
Center for Advanced Studies in Management and Economics, Palácio do Vimioso, Largo Marquês de Marialva, 8, 7000-809 Évora, Portugal
Economies2023, 11(3), 76;https://doi.org/10.3390/economies11030076
This article belongs to the Special Issue International Financial Markets and Monetary Policy 2.0
Version Notes
Order Reprints

Abstract

The purpose of the research is to explore the dynamic multiscale linkage between economic policy uncertainty, equity market volatility, energy and sustainable cryptocurrencies during the COVID-19 period. We use a multiscale TVP-VAR model considering level (EPUs and IDEMV) and returns series (cryptocurrencies) from 1 December 2019 to 30 September 2022. The data are then decomposed into six wavelet components, based on the wavelet MODWT method. The TVP-VAR connectedness approach is used to uncover the dynamic connectedness among EPUs, energy and sustainable cryptocurrency returns. Our findings reveal that CNEPU (USEPU) is the strongest (weakest) NET volatility transmitter. IDEMV is the most consistent volatility NET transmitter among all uncertainty indices across the original returns and wavelet scales (D1~D6). Energy cryptocurrencies, i.e., GRID, POW and SNC, are more likely to receive volatility spillovers than sustainable cryptocurrencies during a turbulent period (COVID-19). XLM (XNO) is least (most) affected by volatility spillover in system-wide connectedness, and XLM (ADA and MIOTA) showed a consistent (heterogeneous) non-recipient behavior across the six wavelet (D1~D6) scales and original return series. This study uncovers the dynamic connectedness across multiscale, which will support investors considering different investment horizons (D1~D6).

1. Introduction

Uncertainty has been considered one of the major concerns among investors and policymakers. Regarding investors and academics, uncertainty started with the analysis of standard deviation as a risk measure and evolved to the analysis of variables such as the Chicago Board Options Exchange Volatility Index (VIX) (), the economic policy uncertainty index (EPU) (), cryptocurrency policy uncertainty index (UCRY policy) () or index of cryptocurrency environmental attention (ICEA) (). Importantly, financial crises are key predictors of volatility and uncertainty in financial markets (; ). Due to global interconnectedness, financial crises cause spillovers for the different economies and transmit to international financial markets country-wide (). These events shake the trust of individual and institutional investors in financial institutions () and are considered major reasons to avoid or delay investments during these periods, considering potential losses and high uncertainty levels. Due to this, it is crucial to study the impact of uncertainty or volatility on the cryptocurrency market, focusing on energy and sustainable cryptocurrencies during the period of COVID-19.
Starting with Bitcoin, the first cryptocurrency introduced in 2009, there are already more than 19,850 cryptocurrencies, with more than 70 having a market value higher than $1 billion (). Traditional cryptocurrency mining uses a tremendous amount of energy, which has drawn a lot of criticism (). Initially, studies on cryptocurrencies regarded all of them equally, but with time, some crypto assets have come to be seen as intrinsically different, especially in terms of sustainability. For instance, () investigate the time-frequency co-movement between bitcoin, sustainable cryptocurrencies and sustainable financial markets and find that conventional cryptocurrencies, i.e., Bitcoin, have an adverse effect on sustainability. Contrarily, sustainable cryptocurrencies show a favorable impact on sustainability and sustainable financial assets. Likewise, () analyze clean and dirty cryptocurrencies, claiming that the clean energy crypto markets do not often exhibit herding behavior while the dirty energy crypto markets exhibit asymmetric and severe herding tendencies in negative markets. () explore the linkage of clean energy with green and dirty cryptocurrencies, finding that clean energy has weak connectedness with dirty and green cryptocurrencies, suggesting weak hedging or safe-haven properties of clean energy, regarding sustainable cryptocurrencies. Green cryptocurrencies are weakly connected with Bitcoin and Ethereum, while financial and macro-economic factors influence the tail dependence of carbon, dirty and green cryptocurrency markets (). Policy and price uncertainty might influence the returns of sustainable and conventional (dirty) cryptocurrencies (). However, how economic policy uncertainty and COVID-19 affect equity market volatility and the capacity to predict the returns of energy and sustainable cryptocurrencies is still a key question for sustainable policymakers and investors.
Interests in the cryptocurrency market have evolved during the last few years and crypto traders (amateur and informed investors) are now more concerned about the environmental and social effects of the conventional cryptocurrency market (; ). For instance, Elon Musk, the CEO of Tesla Corporation expressed that traditional cryptocurrency (Bitcoin) consumes large amounts of electricity and fossil fuel and produces a carbon footprint that makes the global environment dirty and unclean, and this could affect investors’ trust. Meanwhile, crypto investors are revising their priorities, with an increased preference for sustainable, green or clean cryptocurrencies (; ; ; ). Generally, three well-known cryptocurrencies support energy trades in the renewable energy sector: Powerledger (POWR), GridPlus (GRID+) and SunContract (SNC) (). Additionally, SolarCoin (SLR), Bitcoin Green (BITG), Cardano (ADA), Steller (XLM) and Ripple (XRP) are recognized as committed to sustainability (; ). In this research, we study the dynamic multiscale connectedness between economic policy uncertainty, energy and sustainable cryptocurrencies. Additionally, we explore the linkage between the Daily Infectious Disease Equity Market Volatility Tracker (IDEMV) and cryptocurrencies.
Previous research has investigated the connectedness between EPU and conventional cryptocurrencies from several methodological and empirical perspectives. A first strand of research analyzes the connectedness and the impact of EPU in traditional cryptocurrencies using different time series and empirical approaches (; ; ; ; ; ; ; ). A second strand of literature is focused on the impact of EPU or risk measures on the time-varying relationship between cryptocurrency and financial markets, through the use of GARCH family models (, ; ; ; ; ). A third strand of research examines the connectedness between economic/financial risk measures and cryptocurrencies across time-and frequency domains (; ; ; ; ; ; ). This area of research studies the impact of risk measures such as EPU, index of cryptocurrency environmental attention (ICEA), UCRY policy, UCRY price and cryptocurrency implied volatility index (VCRIX), and conventional cryptocurrencies. A final strand of research investigates the linkage (impact) between EPU and the cryptocurrency market (; ; ; ).
To the best of our knowledge, no research has investigated the impact of EPU and IDEMV on energy and sustainable cryptocurrencies during the fragile economic and crisis period associated with COVID-19. The rest of the paper is designed as follows. Section 2 reviews related studies. Section 3 explains the data and TVP-VAR method. Section 4 presents the empirical findings and relates them to previous research. Finally, the last section concludes and presents the implications.

3. Methodology

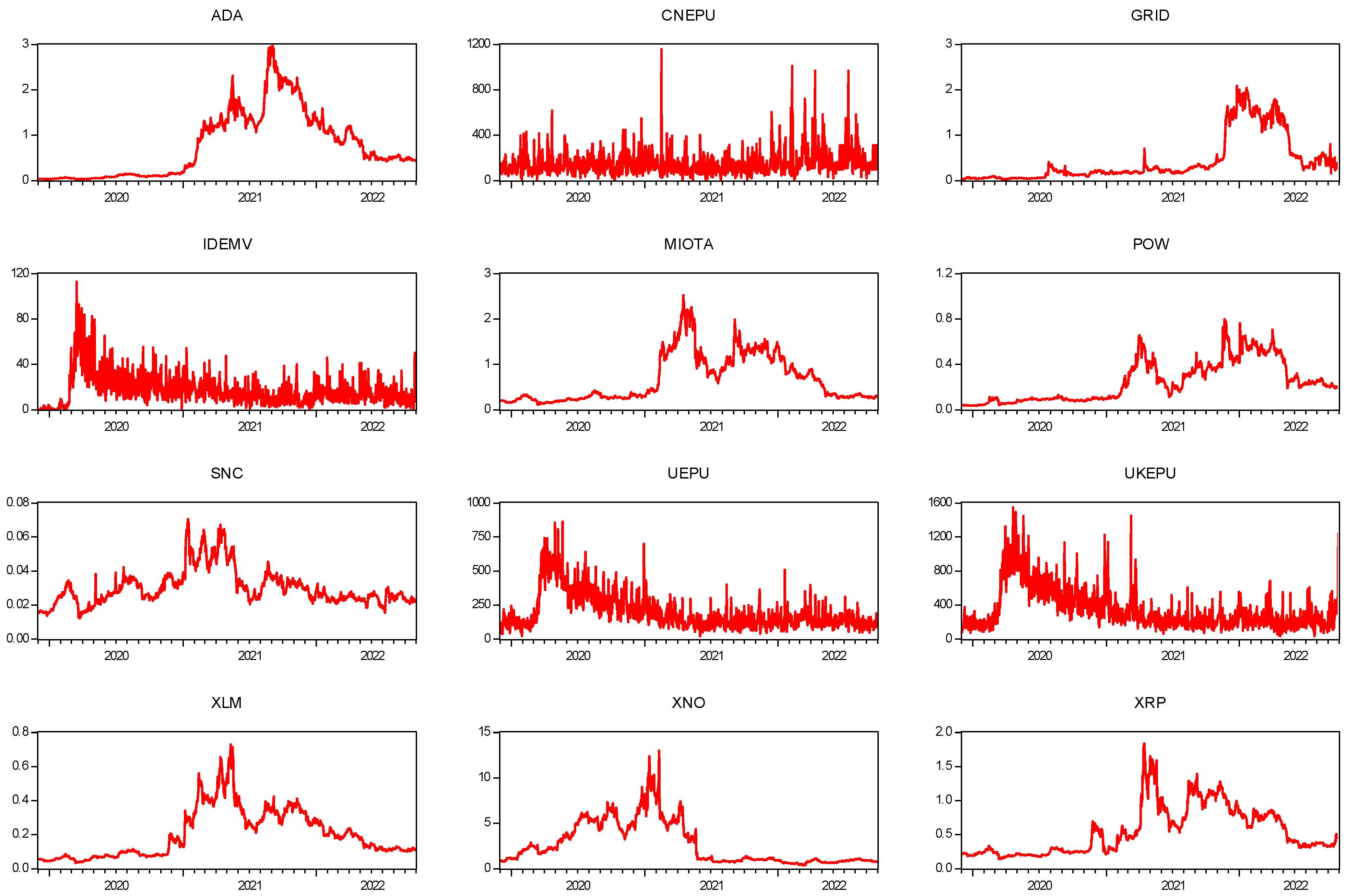
3.1. Data

This study considers the daily data of three EPU indices (USA, China and the UK) as well as a Daily Infectious Disease Equity Market Volatility Tracker (IDEMV), sourced from https://www.policyuncertainty.com. Additionally, three energy cryptocurrencies (Powerledger—POWR, GridPlus—GRID, and SunContract—SNC) and five sustainable cryptocurrencies (SolarCoin—SLR, Bitcoin Green—BITG, Cardano—ADA, Steller—XLM and Ripple—XRP) were considered, due to their sustainable mechanisms and mining processes. The daily closing prices for cryptocurrencies were sourced from coinmarketcap.com. The closing prices of energy and sustainable cryptocurrencies were transformed into returns with the daily return as R i , t = l n P i , t − P i , t − 1 . The dataset starts on 1 December 2019 and ends on 30th September 2022, covering the period of turmoil related to the COVID-19 pandemic, and the returns of energy and sustainable cryptocurrencies are found in Figure 1.
Figure 1. Returns of energy and sustainable cryptocurrencies.

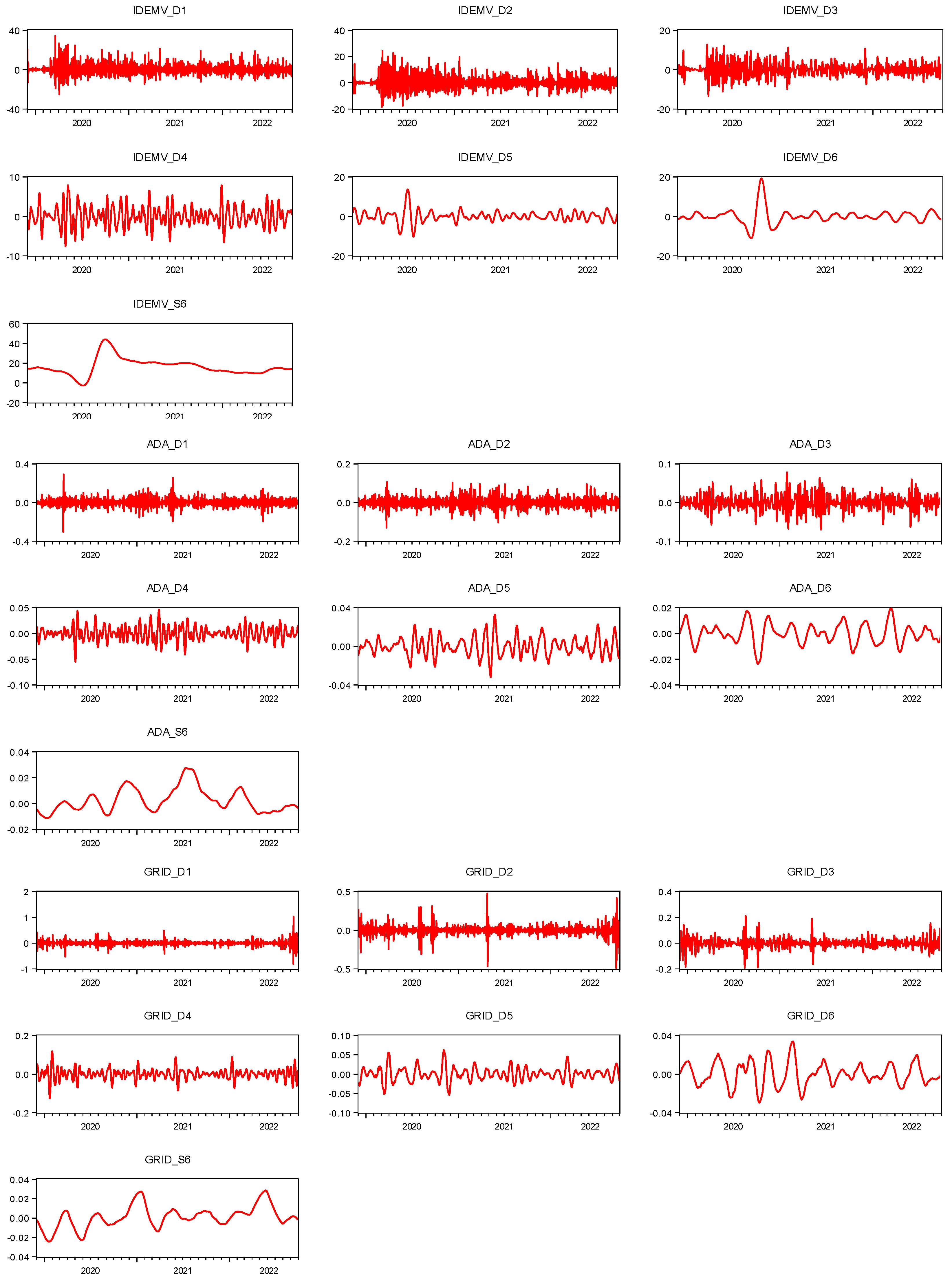
3.2. Maximum Overlap Discrete Wavelet Transform Method

We used the () maximum overlap discrete wavelet transform (MODWT) in order to decompose the original EPU and cryptocurrency return series into six wavelet components (i.e., D1, D2… D6), focusing on the multiscale analysis and considering the importance of investment horizons (short-term, medium-term and long-term). This wavelet technique can distinguish between the main types of variability and examine each wavelet component at a resolution according to its scale (). The MODWT, a non-orthogonal transform, outperforms the discrete wavelet transform (DWT) in several ways, including non-specific sample length, constant conversion process, incremental resolution at larger scales, and a more asymptotically efficient wavelet variance estimate (). In numerous existing research studies, the MODWT has been used to divide the original return series into various wavelet components as part of the wavelet-based analytic framework (; ).
Equations (1)–(4) can be used to get the wavelet coefficients V j , t and scaling coefficients S j , t of the return series ( R i , t ) at the jth level:
V ~ i , j = ∑ I = 0 L j − 1 x ~ j , l   R t − j   m o d   T   t = 0 , 1 , … , T − 1
S ~ i , j = ∑ I = 0 L j − 1 y ~ j , l   R t − j   m o d   T   t = 0 , 1 , … , T − 1
Considering the wavelet filter length represented by L, and x ~ j , l = x j , l 2 j 2 and y ~ j , l = y j , l 2 j 2 as the wavelet filter and the scale filter, respectively. We have the following properties ():
∑ l = 0 L j − 1 x ~ l = 0 , ∑ l = 0 L j − 1 y ~ l = 0 ; ∑ l = 0 L j − 1 x ~ 2 l = ∑ l = 0 L j − 1 y ~ 2 l = 1 2 l ; ∑ − ∞ + ∞ y ~ l y ~ l + 2 n = ∑ − ∞ + ∞ x ~ l x ~ l + 2 n
Following () and (), we employed the MODWT wavelet filter for decomposition, due to its linear phase and symmetric properties. The MODWT can be expressed as follows:
R t = A j t + ∑ j − 1 J B j ( t )
where A j t = ∑ I = − ∞ + ∞ x l A J − 1 ( t + 2 j − 1 × l ) represents the smoothed form of the return series R ( t ) at the scale J. Furthermore, B j t = ∑ I = − ∞ + ∞ y l A J − 1 ( t + 2 j − 1 × l ) expresses the detailed wavelet components that can capture the local dynamics of R(t) over the sample period at each scale j, where J = ( 1 , 2 , … , J ) . The wavelet decomposition of the level series for EPUs is found in Figure 2. In addition, the level and return series of IDEMV and cryptocurrencies are decomposed into D1~D6 as presented in Figure A2.
Figure 2. Wavelet decomposition graphs.

3.3. TVP-VAR Approach

The TVP-VAR approach is the combination of Time-Varying Parameters (TVP) and Vector Autoregressive (VAR). Considering the entire dataset, the static approach considers the use of a vector autoregressive model, whereas the dynamics are estimated using a rolling-window VAR method. Initially proposed by (), the TVP-VAR has been applied by () and developed by (, ) and (), being used in this study to assess the dynamic connectedness among economic policy uncertainty indices, energy and sustainable cryptocurrencies. Generally, it is a widely adopted approach to track and assess spillovers in a specified network () because it offers researchers and practitioners both a static and a dynamic approach to time series network analysis. This model estimates potential changes in the degree to which EPUs and cryptocurrencies are interconnected in order to demonstrate whether the linear structure is derived from the likelihood of shocks or from the extension of the change mechanism response (). The model also offers odd characteristics to spot probable structural breaks and offers compelling explanations to understand the relationship between EPU indices and cryptocurrencies.
Previous research highlighted several additional benefits of using this approach, which are key motivations behind using the TVP-VAR model (; ; ). First, it enables the variance to change via a Kalman Filter estimation with forgetting components. Second, it eliminates the need to arbitrarily select the rolling-window size. Third, it does not cause a loss of observations during the estimation process. Finally, it can be applied to low-frequency datasets.
The model equation can be written as follows:
C t = β 0 , t + β 1 , t Y t − 1 + … + β p , t Y t − p + u t + X t ″ Θ t + u t
with C t indicating the vector of the dependent variable with dimension n × 1 and β 0 , t … p , t as n × n dynamic coefficients varying over time, which are rewritten as the Θ t matrix (; ) and with u t representing structural shocks and n × 1 has zero mean with a heteroskedastic distribution.
It is also possible to represent
D t ′ = [ 1 , C t − 1 ′ , … , C t − p ′ ]
with D t ′ as an n × k matrix that incorporates both the intercept and the lags of time-varying variables and
Ω t = M t − 1 H t ( M t − 1 )
with the term Ω t indicating the time-varying variance-covariance matrix. Therefore, the variance-covariance matrix of cryptocurrencies and green financial assets returns series can be written as in Equation (7), where M t − 1 and H t represent the simultaneous relationship between time series and stochastic connectedness, respectively.
The transition in dynamic parameters over time is assumed to be as follows:
Θ t = Θ t − 1 + v t , v t ≈ N ( 0 , S )
α t = α t − 1 + ξ t , ξ t ≈ N ( 0 , Q )
Here, the time-varying parameters are estimated through Equations (8) and (9) by following the random walk process ().
Finally, we can get
ln   h i t − 1 = l n   h i , t − 1 + σ t μ i , t , μ i , t ≈ N ( 0,1 )
to estimate the stochastic connectedness using the random walk process. Overall, the error term is determined to be independent of the transition equation. Therefore, the variables’ coefficients vary independently to maintain efficient and simplified estimates (; ; ).

4. Results and Discussion

4.1. Summary Statistics

Figure A1 indicates the evolution of economic policy uncertainty and cryptocurrency prices during the COVID-19 pandemic period. The IDEMV, UKEPU and USEPU indices followed a dynamic pattern over time, and a sharp hike can be noticed near the COVID-19 outbreak, from the start of 2020 to the end of 2021. However, policy uncertainty became slightly more stable after 2021 except for the CHEPU whose fluctuations were homogenous and followed more dispersion in 2022. The prices of energy and sustainable cryptocurrencies followed a spike at the start of 2021, and cryptocurrency prices were always high during COVID-19. However, GRID and POW prices increased in 2022. These findings suggest that at times of high policy uncertainty and equity market volatility, investors prefer the cryptocurrency market as an attractive investment avenue, increasing the demand for cryptocurrencies and their prices. These findings are consistent with (), who documented the relationship between financial markets and uncertainty during the coronavirus period.
Table 1 reports the output of descriptive statistics, which includehte mean, standard deviation, skewness, kurtosis, and the Jarque–Bera and Augmented Dickey–Fuller test. In Panel A (original return series), UKEPU (CNEPU and USEPU) remains the most (least) volatile EPU index. Mean returns of all cryptocurrencies are positive with ADA and POW (XLM, XRP, GRID) showing the highest (lowest) positive returns. Among all cryptocurrencies, GRID (XLM) is the most (least) volatile. Additionally, returns of cryptocurrencies have negative skewness coefficients (with the exception of the XLM returns) and kurtosis values above three, indicating negative skewness and leptokurtic characteristics. By using the Jarque–Bera (JB) statistic, we rejected the normal hypothesis of the return (cryptocurrency) and level (EPU) distributions at the 1% level of significance, confirming that the original return series have non-normal distributions. Applying the Augmented Dickey– Fuller test, we conclude that all return (cryptocurrency) and level (EPU) series are stationary.
Table 1. Descriptive statistics.
Further descriptive statistics of wavelet components are also presented in Table 1. The results of wavelet components are homogenous to the original returns. In particular, the crypto returns and EPU indices have mean values of zero over all time horizons, indicating that positive and negative shocks balance one another over longer investment horizons (; ). The lower the scales, the greater the unconditional volatility as measured by the standard deviation (high-frequency components). Wavelet components of cryptocurrency returns exhibit larger swings at several scales. Additionally, we see that the wavelet scales for crypto returns and EPU indices are all skewed and leptokurtic. The non-normality of the wavelet components was also confirmed by the JB statistic results. Interestingly, the returns of cryptocurrencies and EPU indices are closer to normality and follow somewhat non-normal distribution at higher wavelet scales, which is consistent with earlier research (; ). Additionally, we use the ADF unit root test to check if each wavelet component is stationary. The returns and level series of cryptocurrencies and EPU level series are stationary considering a 1% level of significance, respectively.
Table 2 reports the unconditional correlation between EPUs, IDEVM, energy and sustainable cryptocurrencies. The results of Panel A show that the correlation coefficients of CNEPU and IDEVM with MIOTA, GRID and POW are negative. Contrarily, the coefficient signs of UKEPU and USEPU with energy and sustainable cryptocurrencies are predominantly positive for the original return series, meaning that we could find safe-haven properties of energy and sustainable cryptocurrencies for UKEPU and USEPU. The unconditional correlation coefficients of EPUs and IDEVM are mostly negative with both types of cryptocurrencies at D1 (2 to 4 days), D2 (4 to 8 days) and D3 (8 to 16 days) scales, indicating lower safe-haven avenues across very short and short wavelet scales. For the D4 (16 to 32 days) scale, XLM shows positive correlation coefficients with EPUs and IDEVM, suggesting that an increase in EPUs leads to an increase in XLM returns. However, conditional correlation coefficients of SNC are negative and other cryptocurrencies show heterogeneous signs. These findings suggest mixed safe-haven properties of energy and sustainable cryptocurrencies during the COVID-19 period for EPUs and IDEVM. Noticeably, in a medium-term investment horizon, the correlation coefficients show positive signs between EPUs/energy and EPUs/sustainable cryptocurrencies. However, IDEVM shows predominantly negative signs with both classes of cryptocurrency. These findings reveal that energy and sustainable cryptocurrencies could be seen as having a safe-haven behavior for policy uncertainty.
Table 2. Correlation Matrix.

4.2. Evidence from TVP-VAR Approach

Table 3 reports the output of the TVP-VAR dynamic connectedness approach. We investigate the connectedness between EPU level series and cryptocurrency returns (energy and sustainable cryptocurrencies) from 1st December 2019 to 30th September 2022. Generally, the output of TVP-VAR across multiple scales shows heterogeneous connectedness. Notably, the total connectedness index followed an increasing trajectory from a low-frequency scale to a high-frequency scale. Table 3 shows the total connectedness indices or system-wide connectedness for Panel A (40.41%), Panel B (42.13%), Panel C (47.66%), Panel D (54.78%), Panel E (63.86%), Panel F (63.91%) and Panel G (65.12%). These findings suggest that the connection became stronger with the frequency of scale. They also show that the connectedness is stronger in the medium-term than in the very short and short term. These findings are consistent with previous research ().
Table 3. Return Connectedness.
The results of Panel A (original returns) reveal that EPU failed to act as a spillover transmitter. However, COVID-19-induced equity market volatility remains the strongest volatility transmitter as the NET spillover coefficient is 26.76%. Interestingly, energy cryptocurrencies (GRID, POW and SNC) are major volatility recipients among cryptocurrencies with NET connectedness values of −8.18%, −10.59% and −7.25%, respectively. However, only one sustainable cryptocurrency (XNO) is a recipient of volatility transmission, with a NET connectedness coefficient of 6.74%. Results of Panel B (2 to 4 days scale) demonstrate that CNEPU, UKEPU and IDEMV are NET volatility transmitters regarding uncertainty measures, with NET connectedness values of 14.08%, 6.73%, and 13.80%, respectively. Among energy and sustainable cryptocurrencies, XNO (−18.45%) and XRP (−1.00%) are NET volatility recipients, as well as GRID and SNC, with NET connectedness coefficients of 10.41% and 14.94%, respectively. For wavelet scales of 4–8 days (Panel C), all considered uncertainties are NET volatility transmitters, with UKEPU being the leading transmitter, followed by CNEPU, with NET connectedness values of 13.18 and 8.05%, respectively. Among energy cryptocurrencies (sustainable), POW and SNC (ADA and XNO) are higher (lower) NET volatility receivers, with NET connectedness coefficients of −17.04% and −16.27% (−2.26% and −18.99%). Considering the results of Panel D (8 to 16 days), only CNEPU and USEPU are NET volatility transmitters, with NET connectedness values of 16.49% and 4.73%, respectively. Among cryptocurrencies, only XRP is the highest NET recipient, showing a NET connectedness of −23.75%, while two other energy cryptocurrencies have negative values: GRID (−5.96%) and POW (−1.60%). Notably, Panel D is the only wavelet scale where more than three cryptocurrencies are volatility recipients. Focusing on the output of Panel E (16 to 32 days), all uncertainty indices are volatility transmitters, CNEPU being the leading volatility transmitter with a value of 31.11% of NET connectedness, followed by UKEPU (18.59%), and with IDEMV as the weakest volatility transmitter (5.75%).
Among cryptocurrencies, all energy cryptocurrencies (GRID, POW and SNC) are volatility recipients, with values of −35.15%, −11.22% and −7.64%, with sustainable cryptocurrencies (ADA, MIOTA, XNO) also as volatility recipients, with NET connectedness values of −4.39%, −14.86% and −6.10%. The results of Panel F (scales from 32 to 64) confirm that EPUs (CNEPU, UKEPU and USEPU) and IDEMV indices are major transmitters, while all energy cryptocurrencies (GRID, POW and SNC) are NET volatility receivers and MIOTA, XNO and XRP returns are also volatility recipients with sustainable cryptocurrencies (−4.10%, −19.43% and −2.51%).
Finally, the results of Panel G (64 to 128 days) show that all EPUs (CNEPU, USKEPU, USEPU), as well as IDEMV, are NET volatility transmitters. More specifically, the NET connectedness values are 1.68%, 27.42% and 28.58%, for CNEPU, USKEPU and USEPU, with IDEMV showing the least volatility spillover effect, with a NET connectedness value of 0.95%. Among sustainable cryptocurrencies, MIOTA, XNO and XRP are volatility recipients (NET connectedness values of −1.73%, −30.47% and −3.09%), with two energy cryptocurrencies (GRID and POW) also as significant volatility receivers, with NET connectedness values of −18.20% and −23.05%, respectively (see Figure 3).
Figure 3. Dynamic return connectedness.
Generally, we find that EPUs and COVID-19 induced equity market volatility are consistent with the results of (), who concluded that the cryptocurrency market is a NET volatility receiver from EPU, with a peak in 2015, and dropping down gradually. The role of UKEPU and CNEPU in volatility transmission is supported by previous research (; ) which found that Chinese restrictions influence the cryptocurrency market and that the UK is a net source of volatility contribution. These findings are particularly corroborated by earlier research, which found that the spillover from EPU to Bitcoin is marginal and Bitcoin is a safe-haven or diversifier during the time of EPU shocks (). Moreover, more cryptocurrencies are linked to EPU in bearish market and less in bullish market conditions ().
On the other hand, only XLM shows consistent non-recipient behavior of volatility from EPU and IDEMV across all wavelet components and original return series, also consistent with previous research, which documented negative connectedness between cryptocurrencies, EPU and IDEMV, while traditional cryptocurrencies are effective hedges for high EPU. Additionally, () documented that EPU and VIX failed to influence traditional cryptocurrency returns and uncertainties. Nor did () find a causal relationship between EPU and traditional cryptocurrency returns during the COVID-19 pandemic. Therefore, the cryptocurrency market generally has low hedging and safe-haven properties. Our study confirmed that only XLM can be considered a safe-haven sustainable cryptocurrency during the turbulent period of COVID-19. Finally, our findings show that few sustainable cryptocurrencies (MIOTA and ADA) were not volatility recipients from EPUs and IDEMV, although showing scale-dependent safe-haven properties. These findings are consistent with (), who found that Bitcoin-uncertainty co-movement indices are time and frequency dependent.

5. Conclusions and Implications

Using the TVP-VAR technique from 1 December 2019 to 30 September 2022, our paper provides evidence of the connectedness between national economic policy uncertainty, energy, and sustainable cryptocurrencies during the turbulent period of the COVID-19 pandemic. Furthermore, we looked into how the COVID-19 equities market volatility, energy, and sustainable cryptocurrencies are interconnected. In general, focusing on the volatility transmission perspective, our findings reveal that CNEPU (USEPU) is the strongest (weakest) NET volatility transmitter, followed by UKEPU, among the EPUs. Additionally, IDEMV is the most volatile NET transmitter among all uncertainty indices across the original returns and wavelet scales (D1~D6). Considering volatility recipients, energy cryptocurrencies (GRID, POW and SNC) are more likely to receive volatility spillovers than sustainable cryptocurrencies during the period under analysis. Notably, XLM (XNO) is the least (most) affected by volatility spillover in system-wide connectedness, and XLM showed a consistent behavior as non-recipient, across the six wavelet (D1~D6) scales. Moreover, the additional least effected sustainable cryptocurrencies are ADA and MIOTA as summarized in Table 4.
Table 4. Summary of NET Volatility Transmitters and Recipients based on TVP-VAR.
These findings have several relevant implications. Firstly, cryptocurrency traders and sustainable investors should exercise caution when diversifying their portfolios between traditional assets, which are impacted by equity-economic news and political uncertainties, with the returns of cryptocurrencies showing consistent fluctuation throughout the period. Secondly, in the case of participants, institutional investors can choose energy and sustainable cryptos in the cryptocurrency market that offer greater diversification and reduce higher risks following periods of economic instability. Along with considering the potential advantages of diversifying their portfolios while focusing on the multiscale findings, portfolio managers can also acquire a variety of investment options to prevent significant losses. Our analysis identifies a variety of cryptocurrencies with various levels of risk absorption and diversification and their corresponding ramifications. Thirdly, because we discovered pass-through mechanisms between the economy and digital markets, cryptocurrencies are also regarded as a component of traditional investment channels. The results suggest that those who plan to invest in or trade on the cryptocurrency market should keep a watch on the volatility of the equity market as well as regular news coverage of issues such as economic growth, political shifts, and catastrophes. In a similar line, stabilizing the financial system and monetary policies should also include stabilizing the cryptocurrency markets. The role of government is crucial in protecting the environment from fund inflows through effective supervision (). Finally, policymakers must promote energy and sustainable investments for portfolio diversification since the cryptocurrency market has faced various concerns. Regulators and investors should consider this investment opportunity when constructing a risk-free portfolio, according to implications drawn from the fact that high EPUs and the COVID-19 equity market volatility index also transmitted volatility spillovers. Sustainable and crypto investors can also look at a number of energy-related and sustainable cryptocurrencies with the lowest risk and highest return, which exhibit less volatility throughout the COVID-19 period.
There are a few limitations to our study. Firstly, we considered the COVID-19 period to study the multiscale relationship. These findings inherit the pandemic flavor. Secondly, we employed the multiscale TVP-VAR approach to examine the dynamic connectedness, indicating TVP-VAR-specific output. Finally, our study focused on energy/sustainable cryptocurrencies and daily EPU measures. Future research needs to uncover the connectedness with other country-level EPU indices on a monthly or investigate the impact of financial and economic uncertainties on the sectoral level (). Another extension to the current study is employing dynamic connectedness models, i.e., LASSO-VAR.

Author Contributions

Conceptualization, I.U.H., P.F., D.D.Q. and N.H.; Methodology, I.U.H., P.F., D.D.Q., N.H. and S.S.; Formal analysis, I.U.H., P.F., D.D.Q. and N.H.; Data curation, I.U.H., P.F., D.D.Q. and N.H.; Writing—original draft, I.U.H., P.F., D.D.Q. and N.H.; Writing—review & editing, I.U.H., P.F., D.D.Q. and N.H. All authors have read and agreed to the published version of the manuscript.

Funding

P.F. is pleased to acknowledge financial support from Fundação para a Ciência e a Tecnologia (grant UIDB/05064/2020).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Economies 11 00076 g0a1
Figure A1. Evolution of EPU and cryptocurrencies.
Economies 11 00076 g0a2aEconomies 11 00076 g0a2bEconomies 11 00076 g0a2c
Figure A2. Wavelet decomposition graphs for all assets.

References

  1. Adekoya, Oluwasegun, and Johnson Oliyide. 2021. How COVID-19 drives connectedness among commodity and financial markets: Evidence from TVP-VAR and causality-in-quantiles techniques. Resources Policy 70: 101898. [Google Scholar] [CrossRef] [PubMed]
  2. Ah Mand, Abdollah. 2021. Cryptocurrency Returns and Cryptocurrency Uncertainty: A Time-Frequency Analysis. Available online: https://ssrn.com/abstract=3950087 (accessed on 25 October 2022).
  3. Al-Thaqeb, Saud, and Barrak Algharabali. 2019. Economic policy uncertainty: A literature review. The Journal of Economic Asymmetries 20: e00133. [Google Scholar] [CrossRef]
  4. Al-Yahyaee, Khamis, Mobeen Rehman, Walid Mensi, and Idries Al-Jarrah. 2019. Can uncertainty indices predict Bitcoin prices? A revisited analysis using partial and multivariate wavelet approaches. The North American Journal of Economics and Finance 49: 47–56. [Google Scholar] [CrossRef]
  5. Antonakakis, Nikolaos, Ioannis Chatziantoniou, and David Gabauer. 2020. Refined Measures of Dynamic Connectedness based on Time-Varying Parameter Vector Autoregressions. Journal of Risk and Financial Management 13: 84. [Google Scholar] [CrossRef]
  6. Baker, Scott, Nicholas Bloom, and Steven Davis. 2016. Measuring economic policy uncertainty. The Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
  7. Bouri, Elie, and Rangan Gupta. 2021. Predicting Bitcoin returns: Comparing the roles of newspaper-and internet search-based measures of uncertainty. Finance Research Letters 38: 101398. [Google Scholar] [CrossRef]
  8. Bouri, Elie, Oguzhan Cepni, David Gabauer, and Rangan Gupta. 2021. Return connectedness across asset classes around the COVID-19 outbreak. International Review of Financial Analysis 73: 101646. [Google Scholar] [CrossRef]
  9. Chen, Tiejun, Chi Lau, Sadaf Cheema, and Chun Koo. 2021. Economic policy uncertainty in China and bitcoin returns: Evidence from the COVID-19 period. Frontiers in Public Health 9: 651051. [Google Scholar] [CrossRef]
  10. Cheng, Hui-Pei, and Kuang-Chueh Yen. 2020. The relationship between the economic policy uncertainty and the cryptocurrency market. Finance Research Letters 35: 101308. [Google Scholar] [CrossRef]
  11. Cui, Jinxin, Mark Goh, and Huiwen Zou. 2021. Information spillovers and dynamic dependence between China’s energy and regional CET markets with portfolio implications: New evidence from multi-scale analysis. Journal of Cleaner Production 289: 125625. [Google Scholar] [CrossRef]
  12. Demir, Ender, Giray Gozgor, Chi Lau, and Samuel A. Vigne. 2018. Does economic policy uncertainty predict the Bitcoin returns? An empirical investigation. Finance Research Letters 26: 145–49. [Google Scholar] [CrossRef]
  13. Diebold, Francis, and Kamil Yilmaz. 2009. Measuring financial asset return and volatility spillovers, with application to global equity markets. The Economic Journal 119: 158–71. [Google Scholar] [CrossRef]
  14. Diebold, Francis, and Kamil Yilmaz. 2012. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
  15. Diebold, Francis, and Kamil Yilmaz. 2014. On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef]
  16. Fang, Libing, Honghai Yu, and Lei Li. 2017. The effect of economic policy uncertainty on the long-term correlation between US stock and bond markets. Economic Modelling 66: 139–45. [Google Scholar] [CrossRef]
  17. Fang, Libing, Elie Bouri, Rangan Gupta, and David Roubaud. 2019. Does global economic uncertainty matter for the volatility and hedging effectiveness of Bitcoin? International Review of Financial Analysis 61: 29–36. [Google Scholar] [CrossRef]
  18. Foglia, Matteo, and Peng-Fei Dai. 2021. “Ubiquitous uncertainties”: Spillovers across economic policy uncertainty and cryptocurrency uncertainty indices. Journal of Asian Business and Economic Studies 29: 35–49. [Google Scholar] [CrossRef]
  19. Gallersdörfer, Ulrich, Lena Klaaßen, and Christian Stoll. 2020. Energy consumption of cryptocurrencies beyond bitcoin. Joule 4: 1843–46. [Google Scholar] [CrossRef]
  20. Gulzar, Saqib, Ghulam Mujtaba Kayani, Hui Xiaofen, Usman Ayub, and Amir Rafique. 2019. Financial cointegration and spillover effect of global financial crisis: A study of emerging Asian financial markets. Economic Research-Ekonomska Istraživanja 32: 187–218. [Google Scholar] [CrossRef]
  21. Haq, Inzamam Ul, and Elie Bouri. 2022. Sustainable versus Conventional Cryptocurrencies in the Face of Cryptocurrency Uncertainty Indices: An Analysis across Time and Scales. Journal of Risk and Financial Management 15: 442. [Google Scholar] [CrossRef]
  22. Haq, Inzamam Ul, Apichit Maneengam, Supat Chupradit, and Chunhui Huo. 2022a. Are green bonds and sustainable cryptocurrencies truly sustainable? Evidence from a wavelet coherence analysis. Economic Research-Ekonomska Istraživanja 36: 807–26. [Google Scholar] [CrossRef]
  23. Haq, Inzamam Ul, Paulo Ferreira, Apichit Maneengam, and Worakamol Wisetsri. 2022b. Rare Earth Market, Electric Vehicles and Future Mobility Index: A Time-Frequency Analysis with Portfolio Implications. Risks 10: 137. [Google Scholar] [CrossRef]
  24. Huynh, Nhan, Anh Dao, and Dat Nguyen. 2021a. Openness, economic uncertainty, government responses, and international financial market performance during the coronavirus pandemic. Journal of Behavioral and Experimental Finance 31: 100536. [Google Scholar] [CrossRef] [PubMed]
  25. Huynh, Nhan, Dat Nguyen, and Anh Dao. 2021b. Sectoral performance and the government interventions during COVID-19 pandemic: Australian evidence. Journal of Risk and Financial Management 14: 178. [Google Scholar] [CrossRef]
  26. Jiang, Yonghong, Lanxin Wu, G. Tian, and He Nie. 2021. Do cryptocurrencies hedge against EPU and the equity market volatility during COVID-19?—New evidence from quantile coherency analysis. Journal of International Financial Markets, Institutions and Money 72: 101324. [Google Scholar] [CrossRef]
  27. Kamal, Javed, and Mohammad Hassan. 2022. Asymmetric connectedness between cryptocurrency environment attention index and green assets. The Journal of Economic Asymmetries 25: e00240. [Google Scholar] [CrossRef]
  28. Karaömer, Yunus. 2022. The time-varying correlation between cryptocurrency policy uncertainty and cryptocurrency returns. Studies in Economics and Finance 39: 297–310. [Google Scholar] [CrossRef]
  29. Karim, Sitara, and Muhammad Naeem. 2021. Clean Energy, Australian Electricity Markets, and Information Transmission. Energy Research Letters 3: 29973. [Google Scholar] [CrossRef]
  30. Karim, Sitara, and Muhammad Naeem. 2022. Do global factors drive the interconnectedness among green, Islamic and conventional financial markets? International Journal of Managerial Finance 18: 639–60. [Google Scholar] [CrossRef]
  31. Karim, Sitara, Muhammad Naeem, Nawazish Mirza, and Jessica Paule-Vianez. 2022. Quantifying the hedge and safe-haven properties of bond markets for cryptocurrency indices. The Journal of Risk Finance 23: 191–205. [Google Scholar] [CrossRef]
  32. Khalfaoui, Rabeh, Mohamed Boutahar, and Heni Boubaker. 2015. Analyzing volatility spillovers and hedging between oil and stock markets: Evidence from wavelet analysis. Energy Economics 49: 540–49. [Google Scholar] [CrossRef]
  33. Koumba, Ur, Calvin Mudzingiri, and Jules Mba. 2020. Does uncertainty predict cryptocurrency returns? A copula-based approach. Macroeconomics and Finance in Emerging Market Economies 13: 67–88. [Google Scholar] [CrossRef]
  34. Li, Zheng-Zheng, Chi-Wei Su, and Meng Zhu. 2022. How Does Uncertainty Affect Volatility Correlation between Financial Assets? Evidence from Bitcoin, Stock and Gold. Emerging Markets Finance and Trade 58: 2682–94. [Google Scholar] [CrossRef]
  35. Lucey, Brian, Samuel Vigne, Larisa Yarovaya, and Yizhi Wang. 2022. The cryptocurrency uncertainty index. Finance Research Letters 45: 102147. [Google Scholar] [CrossRef]
  36. Maghyereh, Aktham, Basel Awartani, and Hussein Abdoh. 2019. The co-movement between oil and clean energy stocks: A wavelet-based analysis of horizon associations. Energy 169: 895–913. [Google Scholar] [CrossRef]
  37. Mokni, Khaled, Ahdi Ajmi, Elie Bouri, and Xuan Vo. 2020. Economic policy uncertainty and the Bitcoin-US stock nexus. Journal of Multinational Financial Management 57: 100656. [Google Scholar] [CrossRef]
  38. Mokni, Khaled, Manel Youssef, and Ahdi Ajmi. 2022. COVID-19 pandemic and economic policy uncertainty: The first test on the hedging and safe haven properties of cryptocurrencies. Research in International Business and Finance 60: 101573. [Google Scholar] [CrossRef]
  39. Papadamou, Stephanos, Nikolaos Kyriazis, and Panayiotis Tzeremes. 2021. Non-linear causal linkages of EPU and gold with major cryptocurrencies during bull and bear markets. The North American Journal of Economics and Finance 56: 101343. [Google Scholar] [CrossRef]
  40. Percival, Donald, and Andrew Walden. 2000. Wavelet Methods for Time Series Analysis. Cambridge: Cambridge University Press. [Google Scholar]
  41. Pham, Linh, Sitara Karim, Muhammad Naeem, and Cheng Long. 2022. A tale of two tails among carbon prices, green and non-green cryptocurrencies. International Review of Financial Analysis 82: 102139. [Google Scholar] [CrossRef]
  42. Primiceri, Giorgio. 2005. Time varying structural vector autoregressions and monetary policy. The Review of Economic Studies 72: 821–52. [Google Scholar] [CrossRef]
  43. Ren, Boru, and Brian Lucey. 2022a. A clean, green haven?—Examining the relationship between clean energy, clean and dirty cryptocurrencies. Energy Economics 109: 105951. [Google Scholar] [CrossRef]
  44. Ren, Boru, and Brian Lucey. 2022b. Do clean and dirty cryptocurrency markets herd differently? Finance Research Letters 47: 102795. [Google Scholar] [CrossRef]
  45. Rubbaniy, Ghulame, Ali Khalid, and Aristeidis Samitas. 2021. Are cryptos safe-haven assets during covid-19? Evidence from wavelet coherence analysis. Emerging Markets Finance and Trade 57: 1741–56. [Google Scholar] [CrossRef]
  46. Shaikh, Imlak. 2020. Policy uncertainty and Bitcoin returns. Borsa Istanbul Review 20: 257–68. [Google Scholar] [CrossRef]
  47. Tran, Quang Thien, Nhan Huynh, and Nhu An Huynh. 2022. Trading-off between being contaminated or stimulated: Are emerging countries doing good jobs in hosting foreign resources? Journal of Cleaner Production 379: 134649. [Google Scholar] [CrossRef]
  48. Wang, Gang-Jin, Chi Xie, Danyan Wen, and Longfen Zhao. 2019. When Bitcoin meets economic policy uncertainty (EPU): Measuring risk spillover effect from EPU to Bitcoin. Finance Research Letters 31. [Google Scholar] [CrossRef]
  49. Wang, Pengfei, Xiao Li, Dehua Shen, and Wei Zhang. 2020. How does economic policy uncertainty affect the bitcoin market? Research in International Business and Finance 53: 101234. [Google Scholar] [CrossRef]
  50. Wang, Yizhi, Brian Lucey, Samuel Vigne, and Larisa Yarovaya. 2022. An index of cryptocurrency environmental attention (ICEA). China Finance Review International 12: 378–414. [Google Scholar] [CrossRef]
  51. Wu, Wansah, Aviral Tiwari, Giray Gozgor, and Huang Leping. 2021. Does economic policy uncertainty affect cryptocurrency markets? Evidence from Twitter-based uncertainty measures. Research in International Business and Finance 58: 101478. [Google Scholar] [CrossRef]
  52. Xiong, Xiong, Yuxiang Bian, and Dehua Shen. 2018. The time-varying correlation between policy uncertainty and stock returns: Evidence from China. Physica A: Statistical Mechanics and Its Applications 499: 413–19. [Google Scholar] [CrossRef]
  53. Yen, Kuang-Chieh, and Hui-Pei Cheng. 2021. Economic policy uncertainty and cryptocurrency volatility. Finance Research Letters 38: 101428. [Google Scholar] [CrossRef]
  54. Yousaf, Imran, Yasir Riaz, and John Goodell. 2022. Energy cryptocurrencies: Assessing connectedness with other asset classes. Finance Research Letters, 103389. [Google Scholar] [CrossRef]
  55. Zhao, Wen, and Yu-Dong Wang. 2022. On the time-varying correlations between oil-, gold-, and stock markets: The heterogeneous roles of policy uncertainty in the US and China. Petroleum Science 19: 1420–32. [Google Scholar] [CrossRef]
  56. Zhu, Huiming, Yiwen Chen, Yinghua Ren, Zhanming Xing, and Liya Hau. 2022. Time-frequency causality and dependence structure between crude oil, EPU and Chinese industry stock: Evidence from multiscale quantile perspectives. The North American Journal of Economics and Finance 61: 101698. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Correction: Seip and Zhang (2022). A High-Resolution Lead-Lag Analysis of US GDP, Employment, and Unemployment 1977–2021: Okun’s Law and the Puzzle of Jobless Recovery. Economies 10: 260
Previous
The Mediating Effect of the Internal Control System on the Relationship between the Accounting Information System and Employee Performance in Jordan Islamic Banks
Next