Testing Taylor’s Law in Urban Population Dynamics Worldwide with Simultaneous Equation Models
Abstract
:1. Introduction
Literature and Logical Framework
2. Methodology
2.1. Empirical Data
2.2. Econometric Model
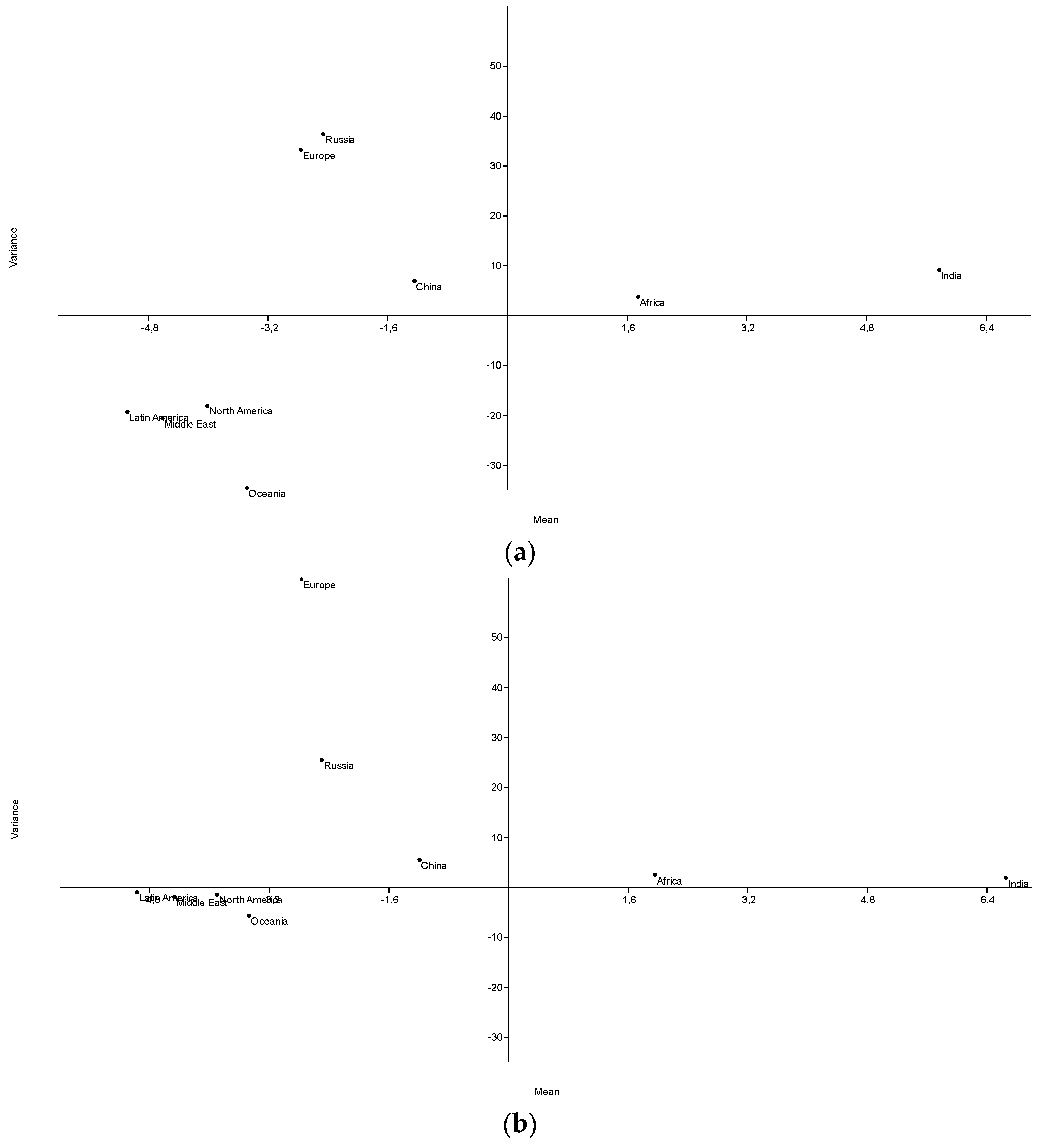
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akaike, Hirotugu. 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19: 716–23. [Google Scholar] [CrossRef]
- Benassi, Federico, and Alessia Naccarato. 2019. Modelling the spatial variation of human population density using Taylor’s power law, Italy, 1971–2011. Regional Studies 53: 206–16. [Google Scholar] [CrossRef]
- Bohk, Christina, Roland Rau, and Joel E. Cohen. 2015. Taylor’s power law in human mortality. Demographic Research 33: 589–610. [Google Scholar] [CrossRef]
- Breusch, Trevor S., and Adrian R. Pagan. 1979. A simple test for heteroskedasticity and random coefficient variation. Econometrica 47: 1287–94. [Google Scholar] [CrossRef]
- Carlucci, Margherita, Carlotta Ferrara, Kostas Rontos, Ilaria Zambon, and Luca Salvati. 2020. The long breadth of cities: Revisiting worldwide urbanization patterns, 1950–2030. Applied Economics 52: 4162–74. [Google Scholar] [CrossRef]
- Carlucci, Margherita, Efstathios Grigoriadis, Kostas Rontos, and Luca Salvati. 2017. Revisiting a hegemonic concept: Long-term ‘Mediterranean urbanization’ in between city re-polarization and metropolitan decline. Applied Spatial Analysis and Policy 10: 347–362. [Google Scholar] [CrossRef]
- Carlucci, Margherita, Francesco Maria Chelli, and Luca Salvati. 2018. Toward a new cycle: Short-term population dynamics, gentrification, and re-urbanization of Milan (Italy). Sustainability 10: 3014. [Google Scholar] [CrossRef]
- Casella, George, and Roger L. Berger. 2002. Statistical Inference, 2nd ed. Pacific Groove: Duxbury Advanced Series. [Google Scholar]
- Chelleri, Lorenzo, Thorsten Schuetze, and Luca Salvati. 2015. Integrating resilience with urban sustainability in neglected neighborhoods: Challenges and opportunities of transitioning to decentralized water management in Mexico City. Habitat International 48: 122–30. [Google Scholar] [CrossRef]
- Ciommi, Mariateresa, Francesco Maria Chelli, and Luca Salvati. 2019. Integrating parametric and non-parametric multivariate analysis of urban growth and commuting patterns in a European metropolitan area. Quality & Quantity 53: 957–79. [Google Scholar]
- Ciommi, Mariateresa, Francesco Maria Chelli, Margherita Carlucci, and Luca Salvati. 2018. Urban growth and demographic dynamics in southern Europe: Toward a new statistical approach to regional science. Sustainability 10: 2765. [Google Scholar] [CrossRef]
- Cohen, Joel E. 2013. Taylor’s power law of fluctuation scaling and the growth-rate theorem. Theoretical Population Biology 88: 94–100. [Google Scholar] [CrossRef] [PubMed]
- Cohen, Joel E. 2014. Stochastic population dynamics in a Markovian environment implies Taylor’s power law of fluctuation scaling. Theoretical Population Biology 93: 30–37. [Google Scholar] [CrossRef] [PubMed]
- Cohen, Joel E., and Meng Xu. 2015. Random sampling of skewed distributions implies Taylor’s power law of fluctuation scaling. Proceedings of the National Academy of Sciences USA 112: 7749–54. [Google Scholar] [CrossRef]
- Cohen, Joel E., Meng Xu, and Helge Brunborg. 2013a. Taylor’s law applies to spatial variation in a human population. Genus 69: 25–60. [Google Scholar]
- Cohen, Joel E., Meng Xu, and William S. F. Schuster. 2013b. Stochastic multiplicative population growth predicts and interprets Taylor’s power law of fluctuation scaling. Proceedings of the Royal Society 280: 20122955. [Google Scholar] [CrossRef] [PubMed]
- Cohen, Joel E., Robert Poulin, and Clément Lagrue. 2017. Linking parasite populations in hosts to parasite populations space through Taylor’s law and negative binomial distribution. Proceedings of the National Academy of Sciences USA 114: E47–E56. [Google Scholar] [CrossRef]
- Dey, Sutirth, and Amitabh Joshi. 2006. Stability via asynchrony in Drosophila metapopulations with low migration rates. Science 312: 434–36. [Google Scholar] [CrossRef]
- Di Feliciantonio, Cesare, and Luca Salvati. 2015. ‘Southern’ Alternatives of Urban Diffusion: Investigating Settlement Characteristics and Socio-Economic Patterns in Three Mediterranean Regions. Tijdschrift voor Economische en Sociale Geografie 106: 453–70. [Google Scholar] [CrossRef]
- Egidi, Gianluca, Luca Salvati, and Sabato Vinci. 2020. The long way to tipperary: City size and worldwide urban population trends. 1950–2030. Sustainable Cities and Society 60: 102148. [Google Scholar] [CrossRef]
- Eisler, Zoltan, Imre Bartos, and Janos Kertész. 2008. Fluctuation scaling in complex systems: Taylor’s law and beyond. Advances in Physics 57: 89–142. [Google Scholar] [CrossRef]
- Fox, Sean. 2012. Urbanization as a global historical process: Theory and evidence from sub-Saharan Africa. Population and development review 38: 285–310. [Google Scholar] [CrossRef]
- Fronczak, Agata, and Piotr Fronczak. 2010. Origins of Taylor’s power law for fluctuation scaling in complex systems. arXiv arXiv:0909.1896. [Google Scholar] [CrossRef] [PubMed]
- Gavalas, Vassilis, Kostas Rontos, and Luca Salvati. 2014. Who becomes an unwed mother in Greece? Sociodemographic and geographical aspects of an emerging phenomenon. Population, Space and Place 20: 250–63. [Google Scholar] [CrossRef]
- Giometto, Andrea, Marco Formentin, Andrea Rinaldo, Joel E. Cohen, and Amos Maritan. 2015. Sample and population exponents of generalized Taylor’s law. Proceedings of the National Academy of Sciences USA 112: 7755–60. [Google Scholar] [CrossRef]
- Hanski, Ilkka. 1999. Metapopulation Ecology. New York: Oxford University Press. [Google Scholar]
- Kendal, Wayne S. 2004. Taylor’s ecological power law as a consequence of scale invariant exponential dispersion models. Ecological Complexity 1: 193–209. [Google Scholar] [CrossRef]
- Kendal, Wayne S., and Bent Jørgensen. 2011. Taylor’s power law and fluctuation scaling explained by a central-limit-like convergence. Physical Review E 83: 066115. [Google Scholar] [CrossRef]
- Kilpatrick, Marm A., and Anthony Ives. 2003. Species interactions can explain Taylor’s power law for ecological time series. Nature 422: 65–68. [Google Scholar] [CrossRef]
- Kroll, Franziska, and Nadja Kabisch. 2012. The Relation of Diverging Urban Growth Processes and Demographic Change along an Urban–Rural Gradient. Population Space and Place 18: 260–76. [Google Scholar] [CrossRef]
- Lagrue, Clément, Robert Poulin, and Joel E. Cohen. 2015. Parasitism alters 3 power laws of scaling in a metazoan community: Taylor’s law, density-mass allometry, and variance-mass allometry. Proceedings of the National Academy of Sciences USA 112: 1791–96. [Google Scholar] [CrossRef]
- Lamonica, Giuseppe Ricciardo, Maria Cristina Recchioni, Francesco Maria Chelli, and Luca Salvati. 2020. The efficiency of the cross-entropy method when estimating the technical coefficients of input–output tables. Spatial Economic Analysis 15: 62–91. [Google Scholar] [CrossRef]
- Marquet, Pablo A., Renato A. Quiñones, Sebastian Abades, Fabio Labra, Marcelo Tognelli, Matias Arim, and Marcelo Rivadeneira. 2005. Scaling and power-laws in ecological systems. Journal of Experimental Biology 208: 1749–69. [Google Scholar] [CrossRef] [PubMed]
- Naccarato, Alessia, and Federico Benassi. 2018. On the relationship between mean and variance of world’s human population density: A study using Taylor’s power law. Letters in Spatial and Resource Sciences 11: 307–14. [Google Scholar] [CrossRef]
- Naccarato, Alessia, and Federico Benassi. 2022. World population densities: Convergence, stability, or divergence? Mathematical Population Studies 29: 17–30. [Google Scholar] [CrossRef]
- Newman, Mark E. 2005. Power laws, Pareto distributions and Zipf’s law. Contemporary Physics 46: 323–51. [Google Scholar] [CrossRef]
- Ramsayer, Johan, Simon Fellous, Joel E. Cohen, and Michael E. Hochberg. 2012. Taylor’s Law holds in experimental bacterial populations but competition does not influence the slope. Biology Letters 8: 316–19. [Google Scholar] [CrossRef]
- Rogers, Andrei. 1975. Introduction to Multiregional Mathematical Demography. New York: Wiley. [Google Scholar]
- Rozenfeld, Hernán D., Diego Rybski, José S. Andrade, Michael Batty, H. Euegne Stanley, and Hernán A. Makse. 2008. Laws of population growth. Proceedings of the National Academy of Sciences USA 105: 18702–7. [Google Scholar] [CrossRef]
- Saitoh, Takashi, and Joel E. Cohen. 2018. Environmental variability and density dependence in the temporal Taylor’s law. Ecological Modelling 387: 134–43. [Google Scholar] [CrossRef]
- Salvati, Luca, and Marco Zitti. 2009. Substitutability and weighting of ecological and economic indicators: Exploring the importance of various components of a synthetic index. Ecological Economics 68: 1093–99. [Google Scholar] [CrossRef]
- Salvati, Luca, and Pere Serra. 2016. Estimating rapidity of change in complex urban systems: A multidimensional, local-scale approach. Geographical Analysis 48: 132–56. [Google Scholar] [CrossRef]
- Salvati, Luca, and Vittorio Gargiulo Morelli. 2014. Unveiling Urban Sprawl in the Mediterranean Region: Towards a Latent Urban Transformation? International Journal of Urban and Regional Research 38: 1935–53. [Google Scholar] [CrossRef]
- Salvati, Luca, Marco Zitti, and Adele Sateriano. 2013. Changes in city vertical profile as an indicator of sprawl: Evidence from a Mediterranean urban region. Habitat International 38: 119–25. [Google Scholar] [CrossRef]
- Salvati, Luca, Mariateresa Ciommi, Pere Serra, and Francesco Maria Chelli. 2019. Exploring the spatial structure of housing prices under economic expansion and stagnation: The role of socio-demographic factors in metropolitan Rome, Italy. Land Use Policy 81: 143–52. [Google Scholar] [CrossRef]
- Taylor, L. Robert. 1961. Aggregation, variance and the mean. Nature 189: 732–35. [Google Scholar] [CrossRef]
- Taylor, L. Robert, Robin A. J. Taylor, Ian P. Woiwod, and John N. Perry. 1983. Behavioural dynamics. Nature 303: 801–4. [Google Scholar] [CrossRef]
- Taylor, L. Robin, Ian P. Woiwod, and John N. Perry. 1978. The density dependence of spatial behavior and the rarity of randomness. Journal of Animal Ecology 47: 383–406. [Google Scholar] [CrossRef]
- Xu, Meng, and Joel E. Cohen. 2021. Spatial and temporal autocorrelations affect Taylor’s law for US county populations: Descriptive and predictive models. PLoS ONE 16: e0245062. [Google Scholar] [CrossRef]
- Xu, Meng, Helge Brunborg, and Joel E. Cohen. 2017. Evaluating multiregional population projections with Taylor’s law of mean-variance scaling and its generalization. Journal of Population Research 34: 79–99. [Google Scholar] [CrossRef]
- Zambon, Ilaria, Andrea Colantoni, Margherita Carlucci, Nathan Morrow, Adele Sateriano, and Luca Salvati. 2017. Land quality, sustainable development and environmental degradation in agricultural districts: A computational approach based on entropy indexes. Environmental Impact Assessment Review 64: 37–46. [Google Scholar] [CrossRef]
- Zambon, Ilaria, Anna Benedetti, Carlotta Ferrara, and Luca Salvati. 2018. Soil matters? A multivariate analysis of socioeconomic constraints to urban expansion in Mediterranean Europe. Ecological Economics 146: 173–83. [Google Scholar] [CrossRef]
- Zellner, Arnold. 1962. An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias. Journal of the American Statistical Association 57: 348–68. [Google Scholar] [CrossRef]
| Geographical Area | Parameter | Estimated Coefficient | Standard Error | p-Value |
|---|---|---|---|---|
| Africa | 1.305 | 0.025 | <0.001 | |
| β | 1.707 | 0.010 | <0.001 | |
| Adjusted R-square | 0.998 | |||
| AIC | −293.0 | |||
| Other Asia and Oceania | 2.683 | 0.079 | <0.001 | |
| β | 1.397 | 0.028 | <0.001 | |
| Adjusted R-square | 0.975 | |||
| AIC | −200.6 | |||
| China | 1.951 | 0.058 | <0.001 | |
| β | 1.495 | 0.023 | <0.001 | |
| Adjusted R-square | 0.983 | |||
| AIC | −188.7 | |||
| Europe | 2.023 | 0.158 | <0.001 | |
| β | 1.389 | 0.055 | <0.001 | |
| Adjusted R-square | 0.908 | |||
| AIC | −300.7 | |||
| India | 1.167 | 0.012 | <0.001 | |
| β | 1.832 | 0.004 | <0.001 | |
| Adjusted R-square | 0.999 | |||
| AIC | −422.5 | |||
| Latin America | 1.775 | 0.031 | <0.001 | |
| β | 1.615 | 0.011 | <0.001 | |
| Adjusted R-square | 0.997 | |||
| AIC | −305.1 | |||
| Middle East | 0.990 | 0.045 | <0.001 | |
| β | 1.805 | 0.017 | <0.001 | |
| Adjusted R-square | 0.994 | |||
| AIC | −209.9 | |||
| North America | 3.235 | 0.039 | <0.001 | |
| β | 1.098 | 0.013 | <0.001 | |
| Adjusted R-square | 0.990 | |||
| AIC | −373.0 | |||
| Russia | 1.837 | 0.123 | <0.001 | |
| β | 1.462 | 0.044 | <0.001 | |
| Adjusted R-square | 0.944 | |||
| AIC | −217.4 |
| Geographical Area | Parameter | Estimated Coefficient | Standard Error | p-Value |
|---|---|---|---|---|
| Africa | 2.552 | 0.137 | <0.001 | |
| β | 0.698 | 0.110 | <0.001 | |
| 0.200 | 0.022 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| AIC | −346.7 | |||
| Other Asia and Oceania | −5.483 | 0.209 | <0.001 | |
| β | 7.251 | 0.150 | <0.001 | |
| −1.041 | 0.027 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| AIC | −411.9 | |||
| China | 5.618 | 0.360 | <0.001 | |
| β | −1.377 | 0.281 | <0.001 | |
| 0.554 | 0.054 | <0.001 | ||
| Adjusted R-square | 0.994 | |||
| AIC | −251.4 | |||
| Europe | 58.078 | 2.146 | <0.001 | |
| β | −37.775 | 1.485 | <0.001 | |
| 6.838 | 0.257 | <0.001 | ||
| Adjusted R-square | 0.975 | |||
| AIC | −386.8 | |||
| India | 1.950 | 0.106 | <0.001 | |
| β | 1.246 | 0.079 | <0.001 | |
| 0.108 | 0.015 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| AIC | −461.9 | |||
| Latin America | −0.806 | 0.179 | <0.001 | |
| β | 3.514 | 0.132 | <0.001 | |
| −0.346 | 0.024 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| AIC | −399.5 | |||
| Middle East | −1.618 | 0.163 | <0.001 | |
| β | 3.936 | 0.133 | <0.001 | |
| −0.427 | 0.026 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| AIC | −315.5 | |||
| North America | −0.987 | 0.680 | 0.152 | |
| β | 4.005 | 0.468 | <0.001 | |
| −0.499 | 0.080 | <0.001 | ||
| Adjusted R-square | 0.994 | |||
| AIC | −402.5 | |||
| Russia | 21.689 | 2.104 | <0.001 | |
| β | −13.131 | 1.545 | <0.001 | |
| 2.674 | 0.283 | <0.001 | ||
| Adjusted R-square | 0.976 | |||
| AIC | −273.6 |
| Geographical Area | Heteroscedasticity | Autocorrelation of Order 1 | Autocorrelation of Order 2 | Autocorrelation of Order 3 |
|---|---|---|---|---|
| Africa | p-value = P(χ2(4) > 13.2) = 0.01 | p-value = P(F(1,62) > 697.1) = 1.98 × 10−35 | p-value = P(F(2,61) > 444.6) = 4.27 × 10−37 | p-value = P(F(3,60) > 312.1) = 1.50 × 10−36 |
| Other Asia and Oceania | p-value = P(χ2(4) > 31.7) = 2.16 × 10−6 | p-value = P(F(1,62) > 1010.2) = 4.38 × 10−40 | p-value = P(F(2,61) > 708.6) = 5.97 × 10−43 | p-value = P(F(3,60) > 481.2) = 6.58 × 10−42 |
| China | p-value = P(χ2(4) > 34.2) = 6.69 × 10−7 | p-value = P(F(1,62) > 191.6) = 1.25 × 10−20 | p-value = P(F(2,61) > 96.7) = 1.22 × 10−19 | p-value = P(F(3,60) > 64.1) = 1.06 × 10−18 |
| Europe | p-value = P(χ2(4) > 13.4) = 0.009 | p-value = P(F(1,62) > 744.2) = 3.05 × 10−36 | p-value = P(F(2,61) > 416.7) = 2.69 × 10−36 | p-value = P(F(3,60) > 291.0) = 1.07 × 10−35 |
| India | p-value = P(χ2(4) > 13.7) = 0.008 | p-value = P(F(1,62) > 539.7) = 2.68 × 10−32 | p-value = P(F(2,61) > 289.9) = 7.06 × 10−32 | p-value = P(F(3,60) > 207.7) = 1.23 × 10−31 |
| Latin America | p-value = P(χ2(4) > 13.5) = 0.009 | p-value = P(F(1,62) > 545.0) = 2.05 × 10−32 | p-value = P(F(2,61) > 309.1) = 1.20 × 10−32 | p-value = P(F(3,60) > 215.1) = 4.63 × 10−32 |
| Middle East | p-value = P(χ2(4) > 20.4) = 0.0004 | p-value = P(F(1,62) > 1939.9) = 1.70 × 10−48 | p-value = P(F(2,61) > 3780.0) = 1.12 × 10−64 | p-value = P(F(3,60) > 2482.6) = 7.47 × 10−63 |
| North America | p-value = P(χ2(4) > 28.1) = 1.21 × 10−5 | p-value = P(F(1,62) > 1392.7) = 3.40 × 10−44 | p-value = P(F(2,61) > 2436.5) = 6.46 × 10−59 | p-value = P(F(3,60) > 1649.8) = 1.40 × 10−57 |
| Russia | p-value = P(χ2(4) > 24.2) = 7.29 × 10−5 | p-value = P(F(1,62) > 1032.6) = 2.31 × 10−40 | p-value = P(F(2,61) > 544.1) = 1.29 × 10−39 | p-value = P(F(3, 60) > 369.6) = 1.25 × 10−38 |
| Geographical Area | Parameter | Estimated Coefficient | Standard Error | p-Value |
|---|---|---|---|---|
| Africa | 2.498 | 0.099 | <0.001 | |
| β | 0.745 | 0.079 | <0.001 | |
| 0.190 | 0.016 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| Other Asia and Oceania | −5.625 | 0.165 | <0.001 | |
| β | 7.354 | 0.118 | <0.001 | |
| −1.060 | 0.021 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| China | 5.475 | 0.255 | <0.001 | |
| β | −1.248 | 0.198 | <0.001 | |
| 0.526 | 0.526 | <0.001 | ||
| Adjusted R-square | 0.997 | |||
| Europe | 61.716 | 2.505 | <0.001 | |
| β | −40.281 | 1.747 | <0.001 | |
| 7.270 | 0.305 | <0.001 | ||
| Adjusted R-square | 0.975 | |||
| India | 1.876 | 0.071 | <0.001 | |
| β | 1.303 | 0.053 | <0.001 | |
| 0.098 | 0.010 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| Latin America | −0.945 | 0.135 | <0.001 | |
| β | 3.615 | 0.099 | <0.001 | |
| −0.364 | 0.018 | <0.001 | ||
| Adjusted R-square | 0.999 | |||
| Middle East | −1.798 | 0.134 | <0.001 | |
| β | 4.085 | 0.108 | <0.001 | |
| −0.457 | 0.022 | <0.001 | ||
| Adjusted R-square | 0.998 | |||
| North America | −1.366 | 0.511 | <0.001 | |
| β | 4.278 | 0.351 | <0.001 | |
| −0.548 | 0.060 | <0.001 | ||
| Adjusted R-square | 0.993 | |||
| Russia | 25.472 | 1.395 | <0.001 | |
| β | −15.903 | 1.021 | <0.001 | |
| 3.182 | 0.187 | <0.001 | ||
| Adjusted R-square | 0.975 |
| Africa | Other Asia and Oceania | China | Europe | India | Latina America | Middle East | North America | Russia | |
|---|---|---|---|---|---|---|---|---|---|
| Africa | 0.00028 | (0.027) | (0.555) | (0.748) | (0.843) | (−0.606) | (−0.043) | (0.854) | (0.686) |
| Other Asia and Oceania | 4.63 × 10−6 | 0.00011 | (0.071) | (0.280) | (−0.274) | (0.410) | (0.842) | (0.308) | (0.349) |
| China | 0.00032 | 2.56 × 10−5 | 0.0012 | (0.861) | (0.466) | (−0.625) | (−0.047) | (0.416) | (0.747) |
| Europe | 0.00016 | 3.60 × 10−5 | 0.00038 | 0.00016 | (0.682) | (−0.479) | (0.292) | (0.765) | (0.942) |
| India | 9.96 × 10−5 | −1.98 × 10−5 | 0.00011 | 6.02 × 10−5 | 4.95 × 10−5 | (−0.512) | (−0.031) | (0.778) | (0.673) |
| Latin America | −0.00011 | 4.74 × 10−5 | −0.00025 | −6.78 × 10−5 | −4.06 × 10−5 | 0.00013 | (0.627) | (−0.298) | (−0.235) |
| Middle East | 1.54 × 10−5 | 0.00018 | −3.53 × 10−5 | 7.86 × 10−5 | −4.63 × 10−5 | 0.00015 | 0.00046 | (0.400) | (0.478) |
| North America | 0.00016 | 3.51 × 10−5 | 0.00016 | 0.00011 | 6.07 × 10−5 | −3.73 × 10−5 | 9.52 × 10−5 | 0.00012 | (0.778) |
| Russia | 0.00034 | 0.00011 | 0.00078 | 0.00035 | 0.00014 | −7.91 × 10−5 | 0.00031 | 0.00026 | 0.00089 |
| Geographical Area | |
|---|---|
| Africa | 1.26 |
| Other Asia and Oceania | 4.22 |
| China | 0.17 |
| Europe | −19.14 |
| India | 1.58 |
| Latin America | 2.56 |
| Middle East | 2.87 |
| North America | 2.64 |
| Russia | −6.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benassi, F.; Naccarato, A.; Salvati, L. Testing Taylor’s Law in Urban Population Dynamics Worldwide with Simultaneous Equation Models. Economies 2023, 11, 56. https://doi.org/10.3390/economies11020056
Benassi F, Naccarato A, Salvati L. Testing Taylor’s Law in Urban Population Dynamics Worldwide with Simultaneous Equation Models. Economies. 2023; 11(2):56. https://doi.org/10.3390/economies11020056
Chicago/Turabian StyleBenassi, Federico, Alessia Naccarato, and Luca Salvati. 2023. "Testing Taylor’s Law in Urban Population Dynamics Worldwide with Simultaneous Equation Models" Economies 11, no. 2: 56. https://doi.org/10.3390/economies11020056
APA StyleBenassi, F., Naccarato, A., & Salvati, L. (2023). Testing Taylor’s Law in Urban Population Dynamics Worldwide with Simultaneous Equation Models. Economies, 11(2), 56. https://doi.org/10.3390/economies11020056








