Accounting for Heterogeneity in Performance Evaluation of Norwegian Dairy and Crop-Producing Farms
Abstract
1. Introduction
2. Review of Stochastic Frontier (SF) Analysis
3. Empirical Model
4. Data
5. Results and Discussion
6. Conclusions and Policy Implications
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agrell, Per, Mehasi Farsi, and Martin Koller. 2014. Unobserved Heterogeneous Effects in the Cost Efficiency Analysis of Electricity Distribution Systems. In The Interrelationship between Financial and Energy Markets. Berlin/Heidelberg: Springer, pp. 281–302. [Google Scholar]
- Aigner, Dennis, CA Knox Lovell, and Peter Schmidt. 1977. Formulation and estimation of stochastic frontier production function models. Journal of Econometrics 6: 21–37. [Google Scholar] [CrossRef]
- Alem, Habtamu. 2018. Effects of model specification, short-run, and long-run inefficiency: An empirical analysis of stochastic frontier models. Zemedelska Economika 64: 508–16. [Google Scholar] [CrossRef]
- Alem, Habtamu. 2020. Economic performance among Norwegian crop farms accounting for farm management and socio-economic factors. International Journal of Business Performance Management 21: 417–36. [Google Scholar] [CrossRef]
- Alem, Habtamu. 2021a. A metafrontier analysis on the performance of grain-producing regions in Norway. Economies 9: 10. [Google Scholar] [CrossRef]
- Alem, Habtamu. 2021b. The Role of Technical Efficiency Achieving Sustainable Development: A Dynamic Analysis of Norwegian Dairy Farms. Sustainability 13: 1841. [Google Scholar] [CrossRef]
- Alem, Habtamu, Gudbrand Lien, and Brian Hardaker. 2018. Economic performance and efficiency determinants of crop-producing farms in Norway. International Journal of Productivity and Performance Management 67: 9. [Google Scholar] [CrossRef]
- Alem, Habtamu, Gudbrand Lien, Brian Hardaker, and Atle Guttormsen. 2019. Regional differences in technical efficiency and technological gap of Norwegian dairy farms: A stochastic meta-frontier model. Applied Economics 51: 409–21. [Google Scholar] [CrossRef]
- Alvarez, Antonio, Julio Corral, and Loren Tauer. 2012. Modeling unobserved heterogeneity in New York dairy farms: One-stage versus two-stage models. Agricultural and Resource Economics Review 41: 275. [Google Scholar] [CrossRef]
- Battese, George E., and Tim J. Coelli. 1992. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. Journal of Productivity Analysis 3: 153–69. [Google Scholar] [CrossRef]
- Battese, George Edward, and Tim J. Coelli. 1995. A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empirical Economics 20: 325–32. [Google Scholar] [CrossRef]
- Cornwell, Christopher, Peter Schmidt, and Robin C. Sickles. 1990. Production frontiers with cross-sectional and time-series variation in efficiency levels. Journal of Econometrics 46: 185–200. [Google Scholar] [CrossRef]
- Greene, William. 2005a. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. Journal of Econometrics 126: 269–303. [Google Scholar] [CrossRef]
- Greene, William. 2005b. Fixed and Random Effects in Stochastic Frontier Models. Journal of Productivity Analysis 23: 7–32. [Google Scholar] [CrossRef]
- Jondrow, James, CA Knox Lovell, Ivan S. Materov, and Peter Schmidt. 1982. On the estimation of technical inefficiency in stochastic frontier production function model. Journal of Econometrics 19: 233–38. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C. 1990. Production frontiers, panel data, and time-varying technical inefficiency. Journal of Econometrics 46: 201–11. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., and Gudbrand Lien. 2009. Productivity and profitability decomposition: A parametric distance function approach. Food Economics—Acta Agriculturae Scandinavica, Section C 6: 143–55. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., Gudbrand Lien, and J. Brian Hardaker. 2014. Technical efficiency in competing panel data models: A study of Norwegian grain farming. Journal of Productivity Analysis 41: 321–37. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., Gudbrand Lien, Ola Flaten, and Ragnar Tveterås. 2008. Impacts of Norwegian milk quotas on output growth: A modified distance function approach. Journal of Agricultural Economics 59: 350–69. [Google Scholar] [CrossRef]
- Kumbhakar, Subal C., Hongren Wang, and Alen P. Horncastle. 2015. A Practitioner’s Guide to Stochastic Frontier Analysis Using Stata. Cambridge: Cambridge University Press. [Google Scholar]
- Latruffe, Laura, Ambre Diazabakana, Christian Bockstaller, Yann Desjeux, John Finn, Edel Kelly, Mary Ryan, and Sandra Uthes. 2016. Measurement of sustainability in agriculture: A review of indicators. Studies in Agricultural Economics 118: 123–30. [Google Scholar] [CrossRef]
- Lien, Gudbrand, Subal C. Kumbhakar, and Alem Habtamu. 2018. Endogeneity, heterogeneity, and determinants of inefficiency in Norwegian crop-producing farms. International Journal of Production Economics 201: 53–61. [Google Scholar] [CrossRef]
- Meeusen, Wim, and Julien van den Broeck. 1977. Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error. International Economic Review 18: 435–44. [Google Scholar] [CrossRef]
- Pitt, Mark M., and Lung-Fei Lee. 1981. The measurement and sources of technical inefficiency in the Indonesian weaving industry. Journal of Development Economics 9: 43–64. [Google Scholar] [CrossRef]
- Schmidt, Peter, and Robin C. Sickles. 1984. Production frontiers and panel data. Journal of Business & Economic Statistics 2: 367–74. [Google Scholar]
- Sipiläinen, Timo, Subal C. Kumbhakar, and Gudbrand Lien. 2013. Performance of dairy farms in Finland and Norway for 1991–2008. European Review of Agricultural Economics 41: 63–86. [Google Scholar] [CrossRef]
- SSB. 2021. Agriculture, Forestry, Hunting, and Fishing. Available online: https://www.ssb.no/en/jord-skog-jakt-og-fiskeri/jordbruk (accessed on 24 October 2022).
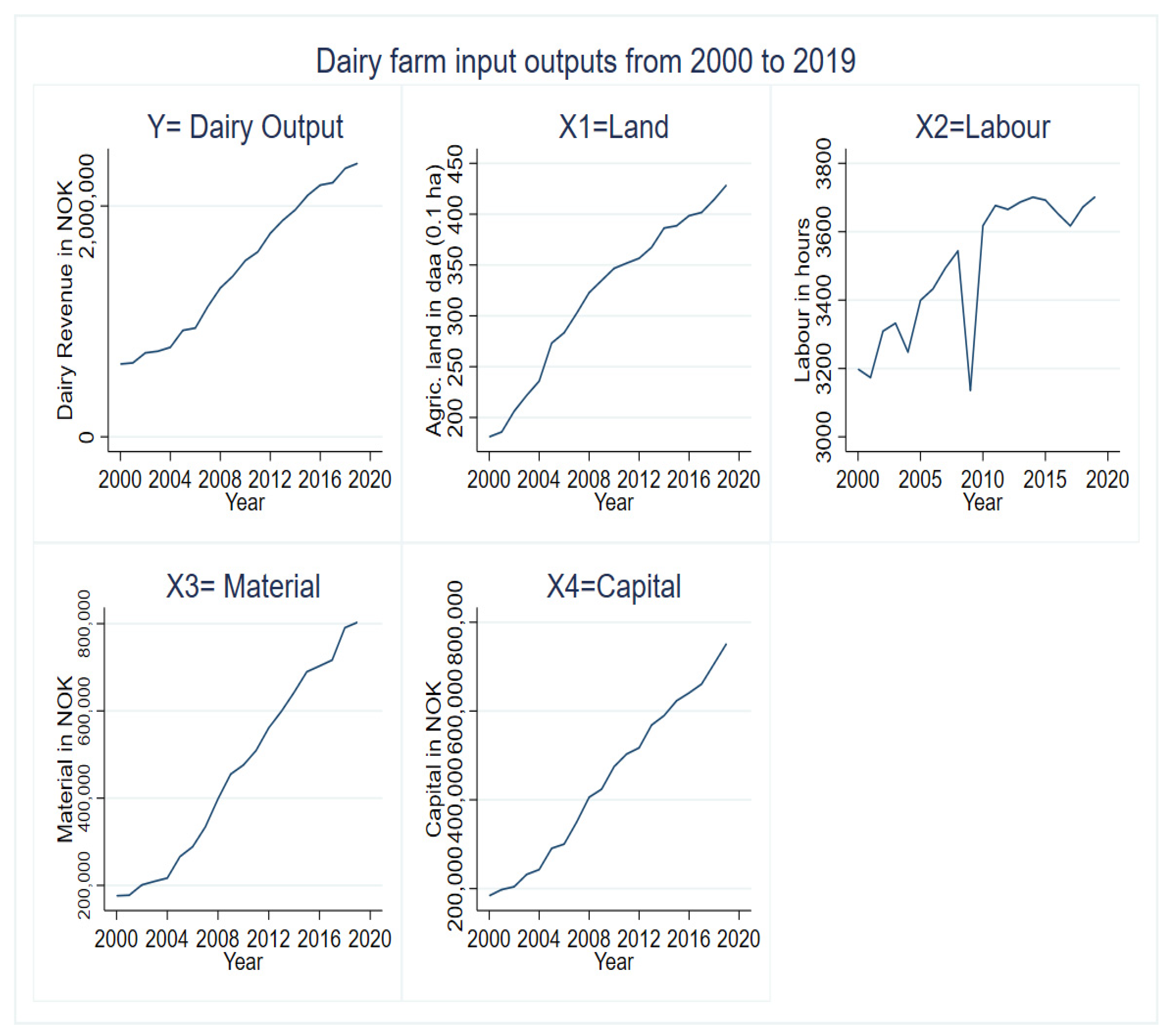
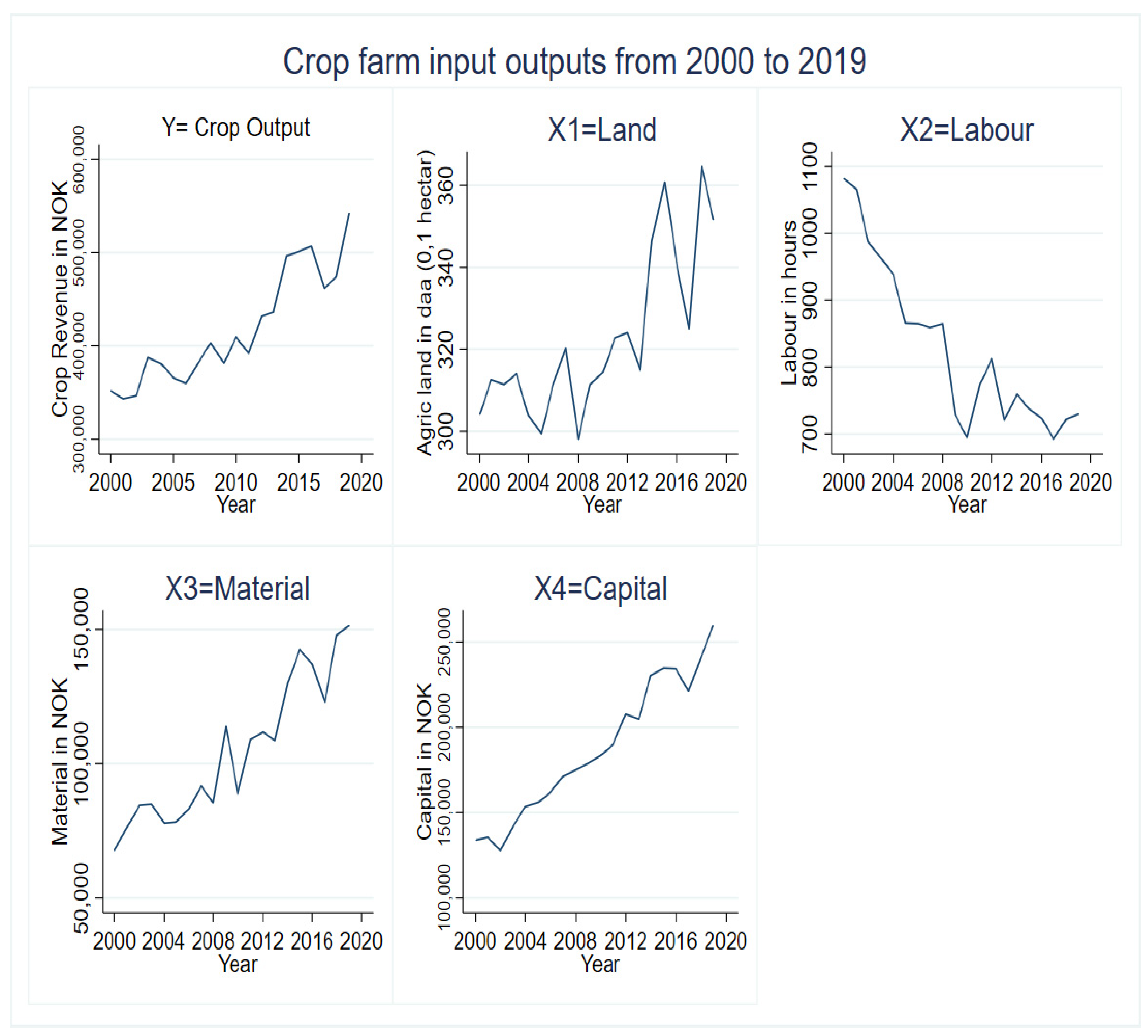

| Region | N | Output NOK * | Land (hectare) | Labor (h) | Materials NOK | Capital Inputs NOK |
|---|---|---|---|---|---|---|
| Dairy | ||||||
| Mean | 5884 | 1,564,994 | 34 | 3534 | 499,085 | 477,652 |
| Stand. Dev | (955,094) | (18) | (1032) | (359,437) | (300,762) | |
| Crop | ||||||
| Mean | 1880 | 489,228 | 35 | 929 | 117,249 | 196,021 |
| Stand. Dev | (353,439) | (22) | (676) | (88,190) | (141,701) |
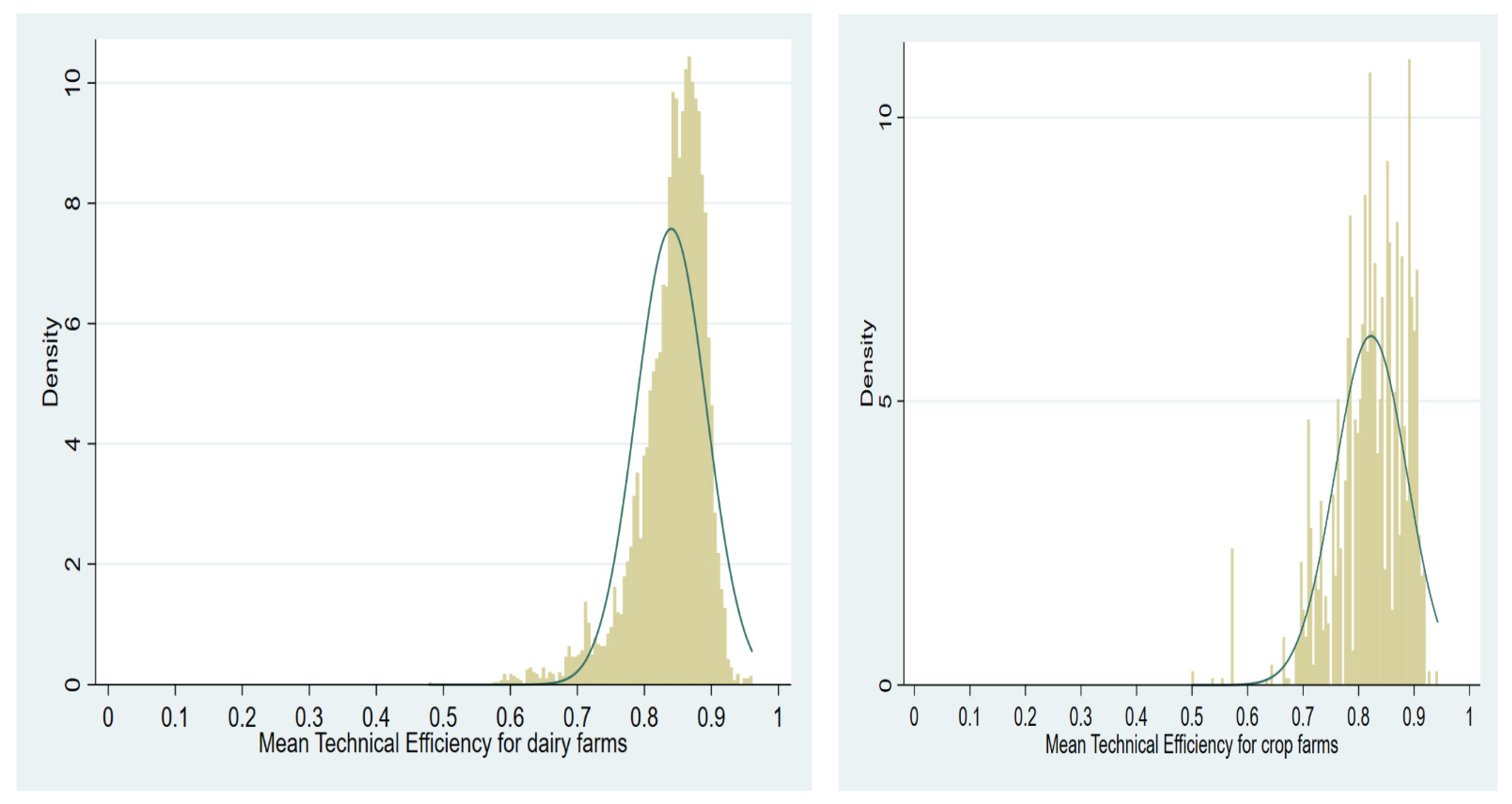
| Percentile | Technical Efficiency Dairy Farms | Technical Efficiency Crop Farms |
|---|---|---|
| 1% | 0.65 | 0.57 |
| 5% | 0.73 | 0.71 |
| 10% | 0.77 | 0.73 |
| 25% | 0.82 | 0.78 |
| Mean | 0.85 | 0.82 |
| 75% | 0.87 | 0.86 |
| 90% | 0.89 | 0.88 |
| 95% | 0.90 | 0.90 |
| 99% | 0.92 | 0.91 |
| Standard Deviation | 0.05 | 0.06 |
| Observation | 5884 | 1880 |
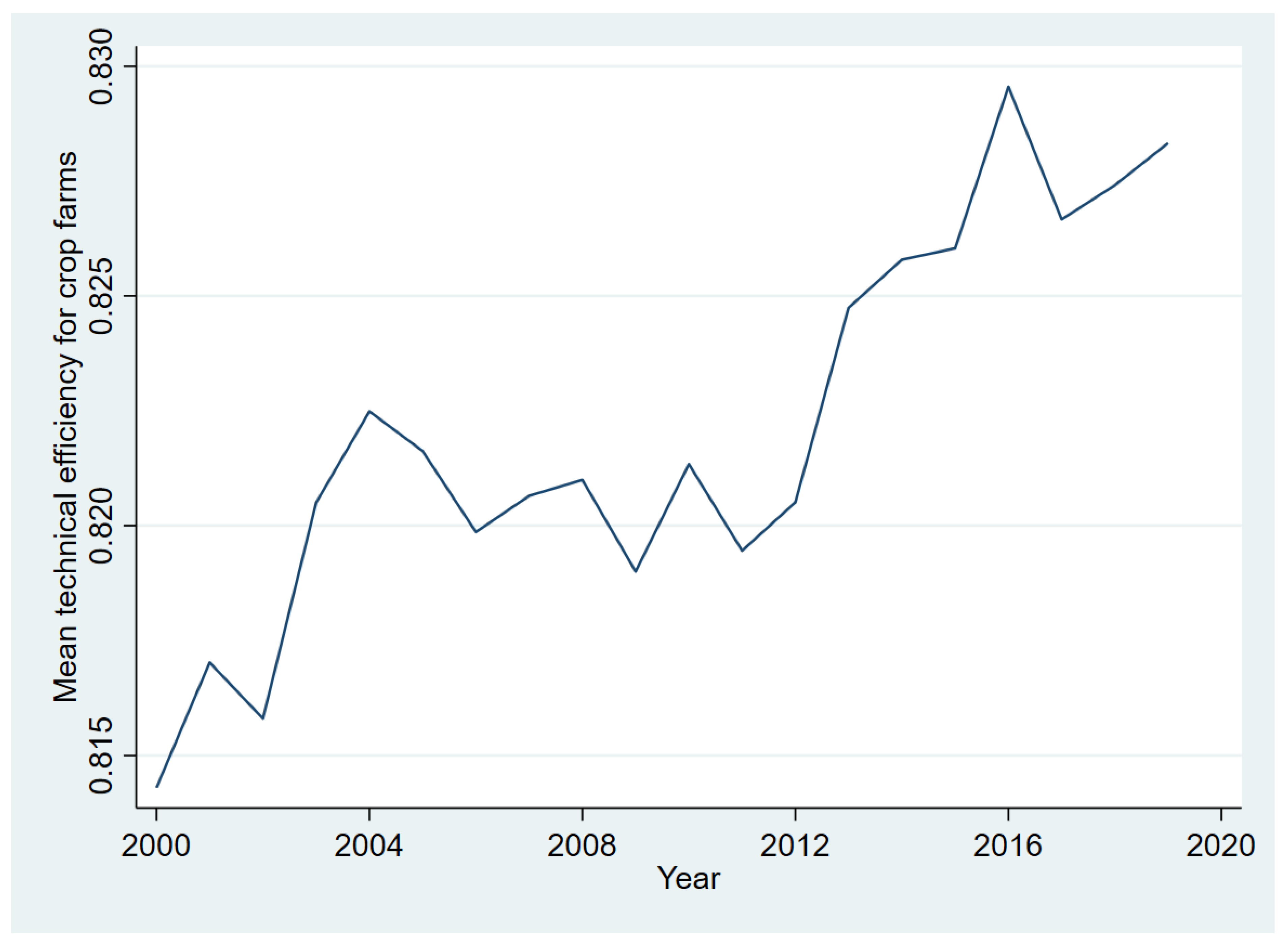
| Dairy Farms | Crop Farms | |||||
|---|---|---|---|---|---|---|
| Year | Mean | Std. Dev. | Freq. | Mean | Std. Dev. | Freq. |
| 2000 | 0.807 | 0.079 | 114 | 0.814 | 0.074 | 90 |
| 2001 | 0.808 | 0.077 | 108 | 0.817 | 0.069 | 92 |
| 2002 | 0.812 | 0.074 | 124 | 0.816 | 0.068 | 89 |
| 2003 | 0.816 | 0.072 | 126 | 0.820 | 0.068 | 87 |
| 2004 | 0.820 | 0.072 | 127 | 0.822 | 0.064 | 90 |
| 2005 | 0.834 | 0.064 | 439 | 0.822 | 0.067 | 89 |
| 2006 | 0.837 | 0.062 | 401 | 0.820 | 0.067 | 89 |
| 2007 | 0.840 | 0.058 | 398 | 0.821 | 0.062 | 94 |
| 2008 | 0.842 | 0.059 | 378 | 0.821 | 0.064 | 90 |
| 2009 | 0.843 | 0.059 | 351 | 0.819 | 0.068 | 97 |
| 2010 | 0.844 | 0.058 | 333 | 0.821 | 0.066 | 95 |
| 2011 | 0.849 | 0.055 | 344 | 0.819 | 0.066 | 98 |
| 2012 | 0.847 | 0.053 | 347 | 0.821 | 0.069 | 97 |
| 2013 | 0.849 | 0.054 | 342 | 0.825 | 0.064 | 92 |
| 2014 | 0.854 | 0.050 | 347 | 0.826 | 0.061 | 96 |
| 2015 | 0.852 | 0.050 | 335 | 0.826 | 0.062 | 94 |
| 2016 | 0.852 | 0.048 | 332 | 0.830 | 0.059 | 97 |
| 2017 | 0.853 | 0.048 | 315 | 0.827 | 0.058 | 99 |
| 2018 | 0.854 | 0.050 | 314 | 0.827 | 0.063 | 101 |
| 2019 | 0.855 | 0.049 | 309 | 0.828 | 0.063 | 104 |
| Total | 0.849 | 0.059 | 5884 | 0.822 | 0.064 | 1880 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alem, H. Accounting for Heterogeneity in Performance Evaluation of Norwegian Dairy and Crop-Producing Farms. Economies 2023, 11, 9. https://doi.org/10.3390/economies11010009
Alem H. Accounting for Heterogeneity in Performance Evaluation of Norwegian Dairy and Crop-Producing Farms. Economies. 2023; 11(1):9. https://doi.org/10.3390/economies11010009
Chicago/Turabian StyleAlem, Habtamu. 2023. "Accounting for Heterogeneity in Performance Evaluation of Norwegian Dairy and Crop-Producing Farms" Economies 11, no. 1: 9. https://doi.org/10.3390/economies11010009
APA StyleAlem, H. (2023). Accounting for Heterogeneity in Performance Evaluation of Norwegian Dairy and Crop-Producing Farms. Economies, 11(1), 9. https://doi.org/10.3390/economies11010009







