Mathematical Modeling of Physical Capital Diffusion Using a Spatial Solow Model: Application to Smuggling in Venezuela

Abstract

This study proposes a mathematical modeling approach for the physical capital diffusion through the borders of countries. Physical capital is considered a crucial variable for the economic growth of a nation. Here, we use an extension of the economic Solow model to describe how smuggling affects the economic growth of countries. In particular, we focus on the situation in Venezuela from 2012 to 2015. In this regard, we rely on a nonconcave production function instead of the classical Cobb–Douglas production function. Moreover, we investigate the effect of different physical capital fluxes on economic growth. The physical capital diffusion through the borders of a country is modeled based on a parabolic partial differential equation describing the dynamics of physical capital and boundary conditions of the Neumann type. Smuggling is present at numerous borders between countries and may include fuel, machinery, and food. This smuggling through the borders places challenges on a particular country’s economy. The smuggling problem usually is related to a non-official exchange rate different from the official rate or subsidies. We study the effect of smuggling on the physical capital of a country using an extended Solow model. Numerical simulations are obtained using an explicit finite difference scheme describing how the physical capital diffusion through the border of a country affects its economic growth. The study of physical capital is a paramount aspect of the economic growth of several countries. The results show that when boundary conditions of Neumann type are different from zero, the dynamics of the physical capital differ from the classical economic behavior observed in the classical spatial Solow model without physical capital flux through the borders of countries. In particular, the numerical results show that the physical capital of a country decreases faster as the flux increases on the boundaries. Thus, we can conclude that avoiding smuggling through the frontiers is a crucial factor affecting economic growth.

1. Introduction

The Solow model presented in 1956 is the starting point for most analyses of economic growth. This dynamical model is still used in today’s macroeconomic theory despite its relative simplicity. Solow’s purpose was to develop a model describing the dynamics of the growth process and long-term evolution of the economy (Allsopp 2012; Solow 1956). In particular, the Solow model describes the dynamics of the gross domestic product based on variables such as labor, capital and technology. Thus, the classical Solow model can estimate the evolution of the physical capital over time through a differential equation. Moreover, the Solow model has been used in other areas such as religion, e-commerce, internal brain drain, and evaluation of the social benefit of water-saving agriculture (Chu and Chen 2009; Gundlach and Paldam 2012; Huang et al. 2011; Piras 2013). The Solow model or its extended versions have been used for different situations in economics (Aguana et al. 2022; Fernández-Anaya et al. 2019; Grassetti et al. 2020; Lin and Wang 2021; Matsumoto and Szidarovszky 2020; McIsaac 2021; Neto et al. 2019). For instance, in (Matsumoto and Szidarovszky 2020), the authors extended the Solow model with physical and human capitals incorporating time delays. These delays were related to the gestation time in physical capital and maturation time in human capital. Moreover, spatial versions of Solow’s Swan model of economic growth have been developed (Camacho and Zou 2004; Camacho et al. 2008; Capasso et al. 2010; Xepapadeas and Yannacopoulos 2016; Zhang 2020; Zhong and Huang 2018). In (Zhong and Huang 2018), the authors investigated a generalized Solow model with continuous space and bounded time. They introduced, concave and nonconcave production functions into the generalized Solow model in close regions, and they obtained the steady states of the model under some conditions. In addition, the authors developed a numerical scheme for a system of partial differential equations. Recent studies have reported that the spatial factor is a critical component in the economy, and this factor should be considered (Boucekkine et al. 2009; Fabbri 2016; Krugman 1991; La Torre et al. 2015; Mossay 2003; Zhang 2020).

Several economic growth models (discrete and continuous) for countries or regions consider physical and human capital. Thus, developing economic models focusing on spatial and time factors is essential. These models can be constructed using partial differential equations to deal with space and time. In this study, we use an extension of the economic Solow model to investigate spatial factors in the economy. In particular, we study the Venezuela situation regarding how smuggling affects the economic growth of the country. Although we particularize the study to the Venezuela situation, the proposed model can be extended to other countries with similar conditions. Venezuela faced an extraordinary amount of smuggling in the period 2012–2015 due to many economic aspects such as subsidized petroleum products, large inflation, huge monetary depreciation, private capital flight, and government-regulated priced products (Barredo-Zuriarrain 2022; Cerra 2016; Lander 2016; Purcell 2017; Reinhart and Santos 2016; Riano-Garzón et al. 2020; Rock 2016; Schwartz 2021). Thus, studying the impact of smuggling on the economy of Venezuela is highly relevant as a case study.

The size and rate of economic growth are of considerable interest to governments and the public. The growth of the economy is related to numerous factors (Jolo et al. 2022; Krugman 1991; Mohamed et al. 2022; Ziberi et al. 2022). One crucial factor for each country is the commercial relations with its neighbors. The smuggling phenomenon is a universal concern that has become a significant problem in numerous countries. Smuggling is inappropriate because it negatively impacts the economy, weakens economic strategies, and sometimes shows itself as a silent battle against the economy (Biabani 2009). Porous borders and weak government capacity are critical problems faced by several countries (Andreas 2013). Furthermore, a large and growing underground economy may have severe economic implications on the country’s economic growth. For instance, smuggling can erode the tax base and cause important measurement errors in official economic statistics (Fougere 2000). Owing to its hidden nature, the underground economy is challenging to measure. Moreover, from a much broader historical perspective, illicit cross-border flows of various sorts have been a defining feature of the U.S. commercial relations with its neighbors from the very beginning, suggesting that there is much more continuity with the past than conventional accounts recognize. Porous borders and weak government capacity have long defined the region. Thus, attempts to secure borders and tighten controls have often had the perverse and unintended consequence of creating a more formidable smuggling challenge. Simultaneously, efforts to regulate illicit border crossings have expanded the reach of central government authority and stimulated the development of border enforcement infrastructure and capacity.

Recently, subsidies for petroleum products have increased. Various countries have not fully passed through the sharp increase in international petroleum product prices that occurred in 2007 and early 2008, thereby increasing subsidies. After declining along with oil prices during the second half of 2008, subsidies have again started to rise, renewing concerns about the fiscal costs. These concerns have been reinforced as many countries need to formulate an exit strategy from the crisis-related accumulation of public debt (2012–2015) (Coady et al. 2010). A subsidy, by definition, is any measure maintaining the prices consumers pay for goods or products below market levels for consumers or for producers above market. Subsidy implies a benefit given by the government to individuals or businesses, whether in the form of cash, tax reduction, or reduction in the cost of goods and services. The purpose of the subsidy is to help individuals and businesses purchase/acquire essential goods and services that they could not afford under normal circumstances. Moreover, subsidies take different forms, and some directly affect prices. These include grants, tax reductions, and exemptions or price controls (Onyeizugbe and Onwuka 2012). Fuel subsidy is applied in oil-producing countries, such as Venezuela, Iran, Saudi Arabia, Egypt, Burma, Malaysia, Kuwait, China, Taiwan, South Korea, Trinidad and Tobago, and Brunei (Majekodunmi 2013). In general, two main government subsidies exist: fuel subsidy, where consumers pay a fraction of the price consumers are supposed to pay, and price controls regarding several essential products, including food. In an economic sense, a subsidy exists when consumers of a given commodity are assisted by the government to pay less than its prevailing market price (Majekodunmi 2013).

Based on the previous aspects, Venezuela faced from 2012 to 2015 an extraordinary smuggling of subsidized petroleum products and other regulated priced products through the borders. This economic behavior is usual in a country having lower prices than their border countries. The countries with higher prices are often substantial beneficiaries of cross-border smuggling. When relevant, governments should also highlight that subsidies promote smuggling, shortages, and black markets (del Granado et al. 2012). In particular, the supply and demand for smuggled goods depend on interregional price disparities under a trade ban (Peyton 2008). The smuggling through the borders of Venezuela increased during the period of study, 2012–2015. People from Venezuela, Colombia, and Brazil often participated in the informal circulation of legal and illegal goods across the border. This economic behavior was also presented in other places or regions. Due to the discrepancy between the local understanding of legality and national laws, several potentially newsworthy illegal exchanges were not addressed in the media (Jusionyte 2013). Several roads between Colombia and Venezuela exist. However, the main one connects the Venezuelan city of San Antonio with Cúcuta, the capital of the Colombian province Norte de Santander, the Simón Bolívar international bridge can be crossed by foot, car, or bicycle. Moreover, no documents are required, and few inspections through the bridge exist. On the Colombian side, small-scale vendors of gasoline, known as pimpineros, peddle the fuel along the highway, without safety precautions, from small plastic containers. A gallon (3.8 L) of gasoline costs the equivalent of 4.92 dollars in Colombia, compared to just eight cents in Venezuela, because of the heavy subsidies making gasoline in this country among the cheapest in the world (Inter Press Service 2012). The price differential allows 1000 percent profits from smuggling gasoline. Moreover, the smuggling problem was not only focused on gasoline but also on food and medicines, which were highly subsidized in Venezuela.

Fuel smuggling to Colombia costs Venezuela USD 1.4 billion per year, with 30,000 barrels smuggled daily, according to a report from bilateral meetings between the Colombian and Venezuelan governments in August 2013 (Venezuelanalysis.com 2013). In addition, fuel smuggling to other countries such as Brazil, the islands of Curazao, Aruba, and Trinidad and Tobago occurred. Recently, international studies point to the existence of a correlation between globalization and trans-border economic crimes (Garuba 2010). Moreover, some authors have argued that the human use of the single international political economy has retreated to the logic of thinking globally and acting locally (Garuba 2010).

Venezuela, officially the Bolivarian Republic of Venezuela, is organized as a federal republic. Venezuela is an emerging/developing nation (International Monetary Fund). Much of the Venezuelan economy is dominated by and dependent upon the petroleum industry, which accounts for approximately 95% of export earnings, approximately 40% of the country’s federal budget revenues, and approximately 12% of GDP (The World Fact Book). The former country’s currency, the Venezuelan Bolivar Fuerte (VEF), lost a significant amount of its value against the U.S. dollar on the official and black market in the last 30 years (Zimmerman and Chu 2013). Moreover, in the period of study, the smuggling problem in Venezuela was huge due mainly to a non-official exchange rate that was more than ten times the official rate. Venezuela is one of the largest oil-producing countries worldwide. Thus, for several years, Venezuela’s economic policies, growth, and other related activities have been primarily influenced by the petroleum industry.

This paper sheds some new light on the effects of smuggling on the economic growth of Venezuela or other countries facing similar conditions. In particular, we address the following questions: (1) Which mathematical model allows studying the effect of smuggling? (2) How does smuggling impact the economic growth of a country and particularly for Venezuela in the time period of 2012–2015? (3) How do the boundary conditions (related to government policies) affect the physical capital stock? We first try to address those questions by studying the suitability of an extension of the Solow model to deal with smuggling. Then, we evaluate the effects of the smuggling of goods across the borders of Venezuela, and an extension of the Solow model is implemented to evaluate how the smuggling impacts the economic growth of Venezuela. The extended Solow model is based on a parabolic partial differential equation describing the dynamics of physical capital, and the boundary conditions are of Neumann type to model the physical capital diffusion through the borders of the country. In addition, we need to design and implement a numerical scheme that allows us to numerically solve the extended Solow model under different Neumann boundary conditions representing various smuggling types. Note that many other options have been proposed to deal with this economic issue. Nevertheless, smuggling is still an open economic debate (Farmer and Foley 2009). The numerical solutions will provide the quantitative and qualitative effects of smuggling on the physical capital. Finally, a contribution of this study is to bring awareness regarding the impact of smuggling on the economic growth of a country. The results can help the government, policymakers, economic authorities, and population implement measures.

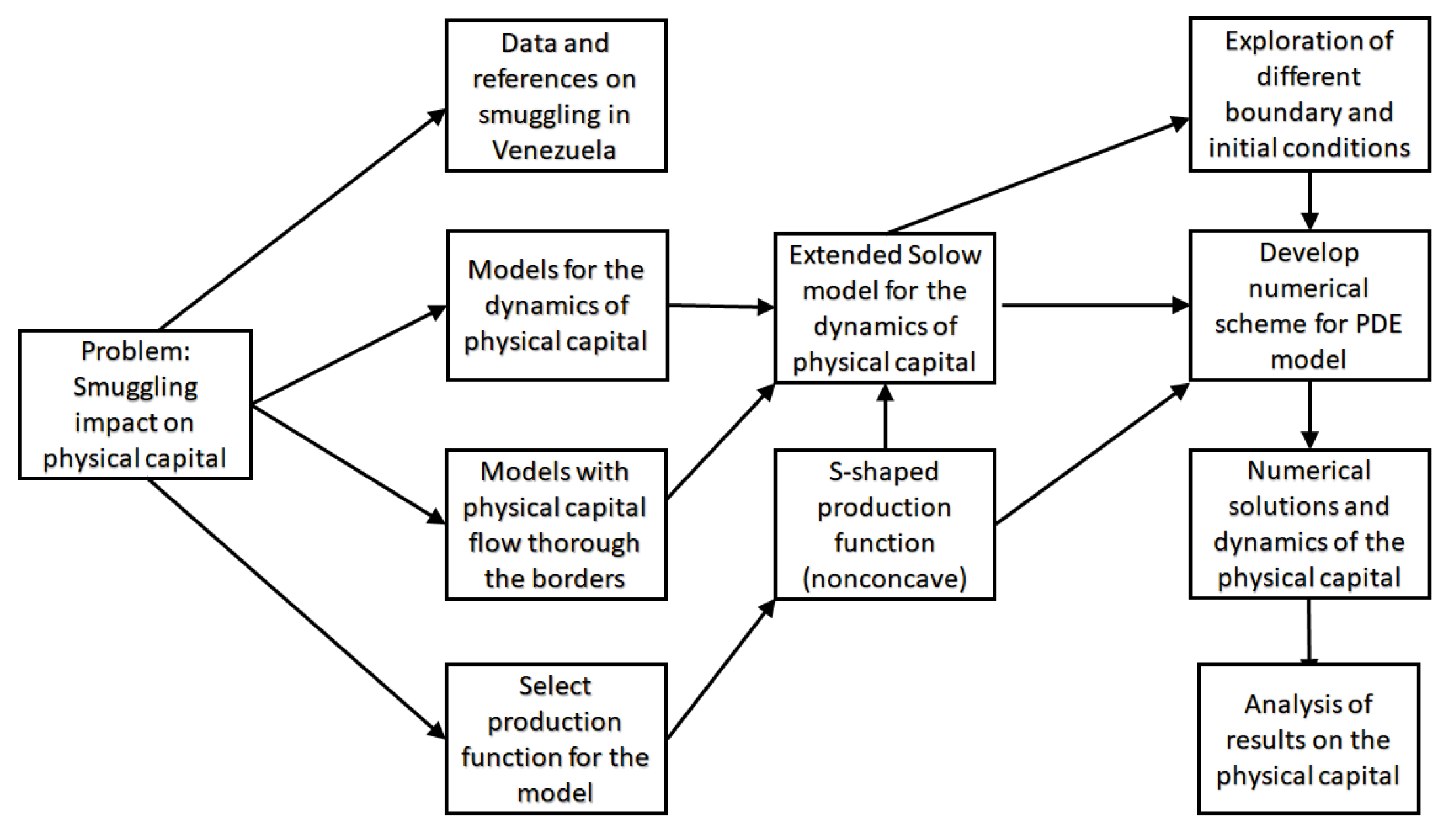
Here we present the proposed modeling approach to deal with all the above-mentioned aspects. In a broad sense, we identified the type of smuggling problem that Venezuela had from 2012 to 2015 and explored several economic models to study the impact on the economy of the country. In addition, references to the smuggling problem were found. A literature review of different production functions and potential extensions of the Solow model were considered to deal with the specific situation of Venezuela. We explored various alternatives to solve the mathematical model numerically. Finally, we analyze the results and provide a thorough discussion of the results and economic consequences. A diagram with the conceptual model of this research is presented in Figure 1. The research methodology is shown in a general view.

2. Spatial Solow Model for Physical Capital with Nononcave Production Function

The Solow model describes the dynamics of the gross domestic product based on the variables labor, capital, and technology. Thus, the classical Solow model can estimate the time evolution of the physical capital through a differential equation. In regard to physical capital, there is no complete agreement about what this term refers to and how to measure it (Nehru and Dhareshwar 1993). Some authors have introduced the concept of social capital (Robison et al. 2002). However, in general, for economists, physical capital refers to a factor of production (or input into the process of production), such as machinery, buildings, or computers (Samuelson and Nordhaus 1995). In economic theory, physical capital is one of the three primary factors of production, also known as the inputs production function. Another capital considered in the economy is human capital, resulting from investment in the human agent and financial capital. Human capital is the stock of competencies, knowledge, social, and personality attributes, including creativity, embodied in the ability to perform labor so as to produce economic value (Judson 2002; Samuelson and Nordhaus 1995).

The Solow model or its extensions have been used extensively in economics (Aguana et al. 2022; Fernández-Anaya et al. 2019; Grassetti et al. 2020; Lin and Wang 2021; Matsumoto and Szidarovszky 2020; McIsaac 2021; Neto et al. 2019). For instance, in (Matsumoto and Szidarovszky 2020), the authors extended the Solow model with physical and human capital by incorporating time delays. These delays are related to the gestation time in physical capital and maturation time in human capital. In addition, spatial versions of the Solow’s Swan model of economic growth have been developed and applied to different economic situations (Camacho and Zou 2004; Camacho et al. 2008; Capasso et al. 2010; Ding et al. 2021; Xepapadeas and Yannacopoulos 2016; Zhang 2020; Zhang et al. 2022; Zhong and Huang 2018). In (Ding et al. 2021), the authors introduced human capital into the Solow model to compare the importance of physical capital and human capital on economic growth. In (Zhong and Huang 2018), a generalized Solow model with continuous space and bounded time was developed. Moreover, concave and nonconcave production functions were introduced into the generalized Solow model in close regions. The spatial Solow model and its extensions are relevant since the spatial factor is a critical component in the economy (Boucekkine et al. 2009, 2013; Fabbri 2016; Hu and Lai 2021; Krugman 1991; La Torre et al. 2015; Mossay 2003; Zhang 2020).

The mathematical expression for the total production or output in terms of the input variables labor $L\left(t\right)$, physical capital $K\left(t\right)$, and technology $A\left(t\right)$ is given as follows:

$$Y\left(t\right)=A\left(t\right)F\left(K\right(t),L(t\left)\right),$$

(1)

where F denotes the production function. Moreover, the stock of capital depreciates over time at a constant rate $\delta$, and only a fraction of the output $\left(cY\right(t)$ with $0<c<1)$ is consumed; $sY\left(t\right)$ is the savings (s = 1 − c). Thus, the Solow model describes the change of the physical capital as follows:

$$\frac{dK\left(t\right)}{dt}=sY\left(t\right)-\delta K\left(t\right).$$

(2)

In addition, using the production function, one obtains

$$\frac{dK\left(t\right)}{dt}=sA\left(t\right)F(K\left(t\right),L\left(t\right))-\delta K\left(t\right).$$

(3)

Now, if we introduce the change of variable $k\left(t\right)=\frac{K\left(t\right)}{L\left(t\right)}$ to compute the per capita physical capital, one obtains

$$f\left(k\right(t)=F(K\left(t\right)/L\left(t\right),1).$$

(4)

Thus, one obtains

$$\frac{dk\left(t\right)}{dt}=sA\left(t\right)f\left(k\left(t\right)\right)-(\delta +n\left(t\right))k\left(t\right),$$

(5)

where $n\left(t\right)$ denotes the labor growth rate. Notice that the labour-augmenting technology or technology progress, $A\left(t\right)$, positively affects the variation of physical capital and negatively affects depreciation and labor growth rate.

Several variations can be included in the basic Solow model (5). For instance, if we consider a net flow of physical capital to a given location or space interval, we need to extend the Solow model to account for the flow of physical capital (Aniţa et al. 2013, 2017; Camacho and Zou 2004; Camacho et al. 2008; Capasso et al. 2010, 2012). Thus, $k(x,t)$ denotes the physical capital stock held by a representative household located at x at the time t, in a bounded domain $\mathsf{\Omega }\in {\mathbf{R}}^n$. Moreover, here, we consider that the production function $f\left(k\right(t\left)\right)$ is the same regardless of the location x. In addition, the initial physical capital distribution, $k(x,0)$, is assumed to be known, and $C^0$. Thus, one obtains the following model for the dynamics of the physical capital:

$$\begin{array}{cc}\hfill & \frac{\partial k(x,t)}{\partial t}-\Delta k(x,t)=sA(x,t)f\left(k\left(t\right)\right)-\delta k(x,t),\mathsf{\Omega }\times [0,T]\hfill \\ \hfill & \nabla k(x,t)=h\left(k\right(x,t\left)\right),\partial \mathsf{\Omega }\times [0,T]\hfill \\ \hfill & k(x,0)=k_0\left(x\right),x\in \mathsf{\Omega }.\hfill \end{array}$$

(6)

This model has been called a spatial Solow model (Camacho and Zou 2004; Capasso et al. 2010). Note that we introduced Neumann-type boundary conditions to deal with the illegal flow of physical capital through the borders of a country. Moreover, the boundary conditions are related in $\partial \mathsf{\Omega }$ with the initial physical capital distribution to have a well-posedness model. In addition, the model (6) is still open because the production function $f\left(k\right(t\left)\right)$, the technological progress function $A(x,t)$, and the initial physical capital distribution $k_0\left(x\right)$ are unknown.

Several economic growth models are based on production functions. These functions play a crucial role in the economy. In particular, different types of functions have been used. The function specifies the maximum output for all possible combinations of input factors; therefore, it determines the way the economic model evolves in time (Allsopp 2012; Capasso et al. 2010; Solow 1956). The Cobb–Douglas production function represents the first time an aggregate or economy-wide production-function had been developed, estimated, and then presented to the profession for analysis; it marked a landmark change in how economists approached macroeconomics (Felipe and Adams 2005). Furthermore, the function was not developed based on any knowledge of engineering, technology, or management of the production process. Nowadays, the Cobb–Douglas production function is the most frequently used to represent the technological relationship between the amounts of two or more inputs, particularly physical capital and labor, and the amount of output that those inputs can produce. The Cobb–Douglas production function is non-negative, increasing, and concave; this function satisfies the well-known Inada conditions (Barelli and de Abreu Pessoa 2003; Felipe and Adams 2005). However, other production functions may be used in conjunction with economic models such as the Solow model. For instance, Leontief production or nonconcave functions are accepted in the applied literature. Here, we rely on a particular production function introduced in (Capasso et al. 2010). This function is called an S-shaped production function (nonconcave), allowing the Solow model to have richer dynamics, including the existence of a poverty trap. As it has been mentioned in (Capasso et al. 2010), the complexity of the Solow model using the nonconcave function suggests conducting the analysis using numerical techniques. Thus, for our numerical simulations, we consider the following nonconcave production function:

$$f\left(k\right)=\frac{\alpha k^p}{1+\beta k^q},$$

(7)

where the parameters $\alpha$, $\beta$, p, and q are usually determined by adjusting the production function by least squares to economic data. In regard to the technological progress function $A(x,t)$, many mathematical expressions have been used. However, a constant value has been assumed in several works. For instance, in (Camacho et al. 2008), the authors used a function such that the economy has a technological center that may coincide with the geographical center. In particular, in (Capasso et al. 2010), the authors assumed that technological progress could be modeled by a diffusion process coupled with physical capital diffusion. Thus, these authors assumed that $A(x,t)$ must be determined. In our numerical simulations, we assume for the function $A(x,t)$ different mathematical expressions, including constant in space and time and varying linearly or exponentially with time, as suggested in the literature.

There is substantial evidence regarding smuggling activities in many countries; however, there are no reliable statistics available, which can be quite misleading (Biabani 2009). Numerical simulations are performed in the following section to study different economic scenarios. The parameter values are challenging to estimate for each country; thereby, general numerical values are assumed without loss of generality. In regard to the initial physical capital distribution $k_0\left(x\right)$, we use in the numerical simulations four different types. The first one is a constant but is only consistent when the function $h(x,t)$ involved in the Neumann-type boundary conditions is equal to zero. The other three types are consistent with $h(k,x)\ne 0$. The first one has a Gaussian form with higher values of physical capital in the middle of the physical space. The last two functions are given by parts, where one is composed of linear forms, and the last one is more complex because the function $h(k,x)$ depends explicitly on the physical capital available at the border. More details regarding these mathematical expressions are given in the following section.

3. Numerical Simulations

We perform several numerical simulations of the spatial Solow model for different scenarios to study the effect of physical capital diffusion through the borders of countries. The proposed model relies on a parabolic partial differential equation, and the boundary conditions are of Neumann type. The numerical results are obtained using an explicit finite difference scheme and small-time steps to fulfill the Courant Friedrich Lewy condition for the numerical stability of the solution. However, implicit methods without stability problems to solve the spatial Solow model numerically can be found in (Camacho and Zou 2004; Camacho et al. 2008; Capasso et al. 2010). In (Zhong and Huang 2018), the authors developed a numerical scheme for the system of partial differential equations related to the generalized Solow model. In this work, we developed a numerical scheme for the particular mathematical model and varied it depending on the boundary conditions related to government policies on the border of a country and other factors. For the mathematical details of the developed numerical scheme, the readers can proceed to Appendix A at the end of the manuscript.

We study four important spatial Solow economic model factors: the depreciation rate, technological progress, initial conditions, and boundary conditions. For all these factors, we use different numerical values or types of functions to observe the effect of each one on the physical capital dynamics. In addition, we simulate several unit times to observe transient and steady states. Note that in this first study, we do not rely on real-world data because our first main goal here is to develop the methodology and analyze the effect of physical capital diffusion through the borders of countries. Moreover, real-world numerical values are challenging to estimate. Particularly, some variables are not observable, such as the level of technology. Thereby, estimated values need to be used (Arnold et al. 2011). In contrast, estimation for the production function also would be necessary, and a vast amount of economic panel data would be required, which is out of the scope of this study. Thus, in the simulations of the model, we do not use spatial dynamic panel data because in Venezuela, during the period of study, the data were incomplete, unreliable, or both due to many factors, including huge changes in the exchange rates, hyperinflation, and lots of smuggling (Daniels 2018; Palma and Stiglitz 2016; Pittaluga et al. 2021; Inter Press Service 2012; Venezuelanalysis.com 2013).

Here, we show the behavior of physical capital under different scenarios regarding the boundary conditions related to the borders of countries. For each scenario, numerical simulations were performed to understand the effect of each boundary condition on the dynamics of the physical capital. The numerical results considered the S-shaped nonconcave production function (7) with $\alpha =0.0005$, $\beta =0.0005$, $p=4$, and $q=4$. Finally, note that a spatial dimension of $L=100$ was used for all the numerical simulations without loss of generality, and a numerical value for the saving rate $s=1$ was considered to simplify the analysis of the dynamics. In particular, the saving rate s in the long term had no effect on the growth rate of the economy (Capasso et al. 2010).

3.1. No Physical Capital Flux through the Borders

In this first case, we consider the classical spatial Solow model without flux on the borders of countries. In addition, we considered that the initial condition for the physical capital was given by a uniform distributed function $k(x,0)=100$, and no technological progress was considered, i.e., $A(x,t)=1$. The boundary conditions in explicit form for the physical capital model (6) are given as follows:

$$\frac{\partial k(0,t)}{\partial x}=0\mathrm{and}\frac{\partial k(L,t)}{\partial x}=0.$$

(8)

In these first numerical simulations, we evaluated how the depreciation rate $\delta$ affected the physical capital dynamics. Figure 2 shows that the physical capital decreases to zero for depreciation rates of $\delta =0.05$ and $\delta =0.5$. However, for the latter case, the decrease rate is higher due to the depreciation. Note that one way to avoid the physical capital decrease is to increase the technological progress $A(x,t)$ of the country.

3.2. No Physical Capital Flux through the Borders with Technological Progress

In this second case, we again considered the classical spatial Solow model without flux on the borders of countries. However, in this case, we considered that the technological progress increased every year (time). In regard to the initial condition, we set a uniform distributed function $k(x,0)=100$. For the technological progress, we consider two scenarios; the first one with a linear increase $A(x,t)=t$ and the second one with an exponential increase in the technological progress $A(x,t)=e^{0.01t}$. These scenarios allowed the evaluation of how the technological progress $A(x,t)$ affected the physical capital dynamics. Figure 3 shows that, in both scenarios, the physical capital decreases initially, and then after some time, the physical capital starts to increase due to technological progress. Notice that in the previous cases, where no technological progress was included, the physical capital dropped to zero after some time. Thus, the technological progress $A(x,t)$ of the country can help improve the country’s growth, as this variable is related to physical capital (Allsopp 2012; Aniţa et al. 2013; Capasso et al. 2010; Solow 1956; Yuan and Guowei 2007). Furthermore, spatial diffusion mechanisms of technological progress allow for the development of other regions, and it depends on the spatial distance (Capasso et al. 2010; Yuan and Guowei 2007). Technological progress may be obtained by investment in human resources, specialization, and industrial structures.

3.3. Physical Capital Flux through the Borders

In this case study, we evaluated the effect of the physical capital flux through the borders using the spatial Solow model. In particular, we considered that technological progress was constant to focus on the effect of capital flux through the borders. We focused on three types of boundary conditions to simulate the flow of physical capital, and they were consistent with $h\left(k\right(x,t\left)\right)\ne 0$. The first one presented a Gaussian form with higher values of physical capital in the middle of the physical space to simulate a country where the regions near the borders were usually more exposed to the consequences of smuggling. For the first case, we consider the following boundary conditions:

$$\frac{\partial k(0,t)}{\partial x}=D_0\mathrm{and}\frac{\partial k(L,t)}{\partial x}=-D_0,$$

(9)

where the parameter $D_0=10e^{-\left({50}^2\right)/1000}$ measures the amount or intensity of physical capital flow through the borders of the country. In regard to the initial condition, we set a Gaussian distributed function $k(x,0)=100e^{-{(x-50)}^2/d}$, where d is a parameter measuring the differences between the central and the border regions, where a large value of the parameter d implies small differences for the region’s physical capital. Thus, initial physical capital decreases as we depart from the center. Note that the initial condition must be different from a constant uniform distribution, as in the previous cases, to have consistency with the physical capital flux through the borders. In other words, the flux induces a nonuniform distribution of the physical capital. We considered also two scenarios with different depreciation rates $\delta =0.5$ and $\delta =0.01$. Figure 4 shows that when the depreciation rate is large, the physical capital decreases faster and steadily to zero. However, for the smallest value of the depreciation rate, the physical capital is almost time-invariant despite its flux through the borders. However, due to the physical capital flux, now a smaller depreciation rate is required to avoid a capital decrease. Thus, the flux of physical capital through the borders of a country can undermine the country’s growth regardless of the depreciation rate.

In the second scenario with physical capital flux, we considered that the initial condition is given by the following function given by parts, as follows:

$$k(x,0)=\left\{\begin{array}{cc}mx& \mathrm{if} 0\le x\le 10\hfill \\ C_{max}& \mathrm{if} 10\le x\le 90\hfill \\ -m(x-90)+C_{max}& \mathrm{if} 90\le x\le 100.\hfill \end{array}\right.$$

where we assume $C_{max}=1000$ and $m=100$. Note that this physical capital’s initial condition varies with respect to space in the regions near the borders. Moreover, in the central regions, it is assumed to be constant to simulate a real scenario as close as possible. In addition, this initial condition is consistent with the boundary conditions, allowing the flux of physical capital through the borders. For this case, we consider the following boundary conditions:

$$\frac{\partial k(0,t)}{\partial x}=m\mathrm{and}\frac{\partial k(L,t)}{\partial x}=-m,$$

(10)

where the parameter m measures the amount or intensity of physical capital flow through the borders of the country. To study the effect of this type of initial condition, we also include the effect of the depreciation rate with two numerical values $\delta =0.05$ and $\delta =0.005$. Figure 5 shows that the physical capital decreases steadily to zero for the largest depreciation rate. In contrast, for the smallest value of the depreciation rate, the physical capital increases despite its flux through the borders. Notice that the physical capital is larger in the central regions than in the border regions due to the flux on the borders.

In our last scenario, we introduced a more complex boundary condition to avoid possible negative values for the physical capital in the long term and to analyze the effects of physical capital flux, depreciation, and the initial condition on the economy (physical capital). In this scenario, we consider that the initial condition is the following function given by parts:

$$k(x,0)=\left\{\begin{array}{cc}{e}^{Dx}& \mathrm{if} 0\le x\le 10\hfill \\ e^{10D}& \mathrm{if} 10\le x\le 90\hfill \\ e^{D(100-x)}& \mathrm{if} 90\le x\le 100.\hfill \end{array}\right.$$

where we set the parameter $D=1$. This initial condition is consistent with the boundary conditions that allow the flux of physical capital through the borders. For this case, we consider the following boundary conditions:

$$\frac{\partial k(0,t)}{\partial x}=Dk(0,t)\mathrm{and}\frac{\partial k(L,t)}{\partial x}=-Dk(0,t),$$

(11)

where the parameter D measures the fraction of physical capital that flows through the borders of a country.

In order to study the effect of the depreciation rate, we considered two numerical values $\delta =0.5$ and $\delta =0.05$. Figure 6 shows that for the largest depreciation rate, the physical capital decreases faster than for the smallest depreciation rate (as expected). Notice again that the physical capital is larger in the central regions than in the border regions due to the flux on the borders. In this way, as has been mentioned previously, the flux of physical capital through the borders is an economical issue affecting the economic growth of the countries.

4. Discussion and Conclusions

In this study, we proposed specific boundary conditions of Neumann type for the spatial Solow model to explain and understand the effect of physical capital diffusion through the borders of countries, and in particular, the case of Venezuela. Physical capital has been considered a crucial variable for the economic growth of a country. In the last decade, fuel, medicine, machinery, and food smuggling through the borders of the country have been problematic for the Venezuelan economy. Moreover, over the studied period 2012–2015, the smuggling problem in Venezuela was huge due mainly to a non-official exchange rate that was more than ten times the official rate.

Here, we have used an extension of the economic Solow model to describe how the smuggling of fuel, machinery, goods, and others elements affects the economic growth of countries. The extended Solow model was based on a parabolic partial differential equation describing the dynamics of physical capital, and the boundary conditions were of Neumann type to model the physical capital diffusion through the borders of the country. In this study, we relied on a nonconcave production function instead of the classical Cobb–Douglas production function. We investigated the effect of different physical capital fluxes on economic growth. These fluxes had variability due to the illegal nature of the smuggling and, therefore, lack of reliable data. Thus, we studied different forms of physical capital fluxes, which are related to the type of smuggling, and then it was worth studying. The numerical results were obtained using an explicit finite difference scheme highlighting how the diffusion of physical capital to the border countries is a paramount issue for the economic growth of countries. The results showed that the dynamics of the physical capital when boundary conditions of Neumann type were different from zero differed from the classical economic behavior observed in the classical spatial Solow model without physical capital flux through the borders of countries.

We can summarize the results using four factors: the depreciation rate, technological progress, initial conditions, and boundary conditions. We found that when no outflow of physical capital exists, the country would require less effort regarding the variables depreciation rate and technological progress to achieve an increase in capital. In contrast, when the flux of capital was considered thorough the borders of the country, increasing the physical capital was demanding because a lower depreciation rate and an increasing function for the technological progress may be necessary for the economic growth of the country.

Finally, we found that the initial condition for the distribution of the physical capital in conjunction with the boundary condition had some effect on the dynamics of the physical capital in the long term. This fact differs from the scenario when there is no flux since, in the long term, the physical flux was distributed uniformly. Thus, the flux of physical capital through the borders of the country can undermine the country’s growth. Furthermore, numerical simulations showed that the physical capital was larger in the central regions than in the border regions due to the flux on the borders. In this way, we can conclude that the flux of physical capital through the borders is an economic issue that may affect Venezuela’s economy and its growth. These results can be extended to other countries under similar economic and geographical circumstances.

In this study, we investigated the economic effects of smuggling on the economic growth of Venezuela, which can be applied to other countries facing similar conditions. From 2012 to 2015, Venezuela faced a large amount of smuggling of fuel, machinery and goods. There were many economic and political factors that contributed to this such as subsidized petroleum products, large inflation, huge monetary depreciation, private capital flight and government-regulated priced products (Barredo-Zuriarrain 2022; Cerra 2016; Lander 2016; Purcell 2017; Reinhart and Santos 2016; Riano-Garzón et al. 2020; Rock 2016; Schwartz 2021). We studied the suitability of an extended Solow model to deal with the smuggling economic impact. In particular, we evaluated the effects of the smuggling of goods across the borders of Venezuela. We described how different types of smuggling might impact the economic growth of Venezuela during the short time period of 2012–2015. We also developed a numerical scheme that allowed us to solve the extended Solow model numerically under different Neumann boundary conditions. We studied four important factors of the spatial Solow model such as the depreciation rate, technological progress, initial conditions, and boundary conditions. Finally, one of the contributions of this type of study is to bring awareness regarding the impact of smuggling on the economic growth of a country. The results can help the government, economic authorities, and general population implement measures or policies.

As in many mathematical models and studies, there are some limitations in this study. The ideal situation is to include economic panel data related to physical capital, smuggling, and production function. However, real data (panel data) related to the particular case of Venezuela during the period of 2012–2015 contain uncertainty due to various factors. For instance, collecting data related to smuggling through the border is a complex task due to its illegal nature and the corruption involved in the process. Nevertheless, there is evidence of smuggling through the borders of Venezuela. In particular, we provided some references in addition to the information provided in newspapers or the people’s knowledge (Barredo-Zuriarrain 2022; Cerra 2016; Lander 2016; Purcell 2017; Reinhart and Santos 2016; Riano-Garzón et al. 2020; Rock 2016; Schwartz 2021). Another limitation or uncertainty of our research is that the income from smuggling was neglected, and therefore, the smuggling works in some way as a depreciation leading to gradual depletion of capital stock. This is an important point since we assumed that the income from smuggling was insignificant from 2012 to 2015 because Venezuela suffered from unprecedented net transfers of financial resources abroad instead of reinvestment. This private capital flight was partially due to a huge monetary depreciation that made reinvestment not a good economical option at that time. However, we think it is worth studying in future works a case where the income from smuggling is reinvested.

Regarding our results, the outflows of physical capital due to smuggling cause its stock in peripheral regions of a country to decrease faster than in other areas (with other conditions remaining the same). This is a natural consequence of the Solow model, and it affects per capita capital and income. This result can be expected and is logical due to the basic principles of economics involved in the construction of the Solow model. Despite the logical economic results of this work, it brings awareness about the impact of smuggling on the economic growth of a country and the effect of different boundary conditions. Furthermore, the results presented here are useful to the government, economic authorities, and the population in general.

Regarding previous results related to the Solow model considering time and space, some of them have focused on the steady-state solution and properties. In this work, we focused on short dynamics due to the short time period of study and since the economic conditions of Venezuela have been very volatile during the last decade. Thus, steady-state solutions might be impractical from a strictly economic perspective. However, our results relatively align with previous studies related to the physical capital flow using the Solow model or variations (Camacho and Zou 2004; Camacho et al. 2008; Capasso et al. 2010; Xepapadeas and Yannacopoulos 2016; Zhong and Huang 2018).

Finally, we would like to mention that further research on this economic issue should improve the understanding of the economic problem that many countries face. Moreover, our results can help government economic institutions, policymakers, and the population in proposing policies to tackle the flux of physical capital through the borders of the country, such as the smuggling of fuel, machinery, and food. The model also gives likely future outcomes as well as the implications of alternative economic policies. A natural continuation of this research is the extension of the Ramsey model and the introduction of different production functions.