Production Function Based on Input–Output and Growth Rate Indicators as a Tool for Assessment of Innovation Climate in Russian Regions
Abstract
1. Introduction
2. Literature Review
2.1. Economics of Innovation: Connection with the Environment
2.2. Assessment of Innovative Conditions Prevailing in Meso-Territories
2.3. Formulation of the Research Hypothesis (the Case of Russia)
- -
- Analysis of the values of the calculated coefficients of the model will make it possible to establish which factors of production have the most significant impact on returns to scale.
- -
- The values of the calculated coefficients of the model indirectly indicate the type of economic growth inherent in the economic entity. The extensive type indicates low innovative activity, which hinders the development of open innovations. The intensive type indicates a predisposition to innovative transformations.
- -
- By the value of the model constant, one can judge how much the resulting indicator depends on factors not taken into account in the structure of the regression equation, including neutral scientific and technological progress.
- -
- In some cases, the component composition of the Cobb–Douglas function model can be expanded by adding predictors, which is advisable when identifying the impact on the resulting indicator of any unaccounted-for factor in its classical version, for example, open innovations.
3. Methods
3.1. Basic Research Methods: Rationale for Choice
3.2. Relative Statistical Numbers (Adjusted Rate, Indices)
- -
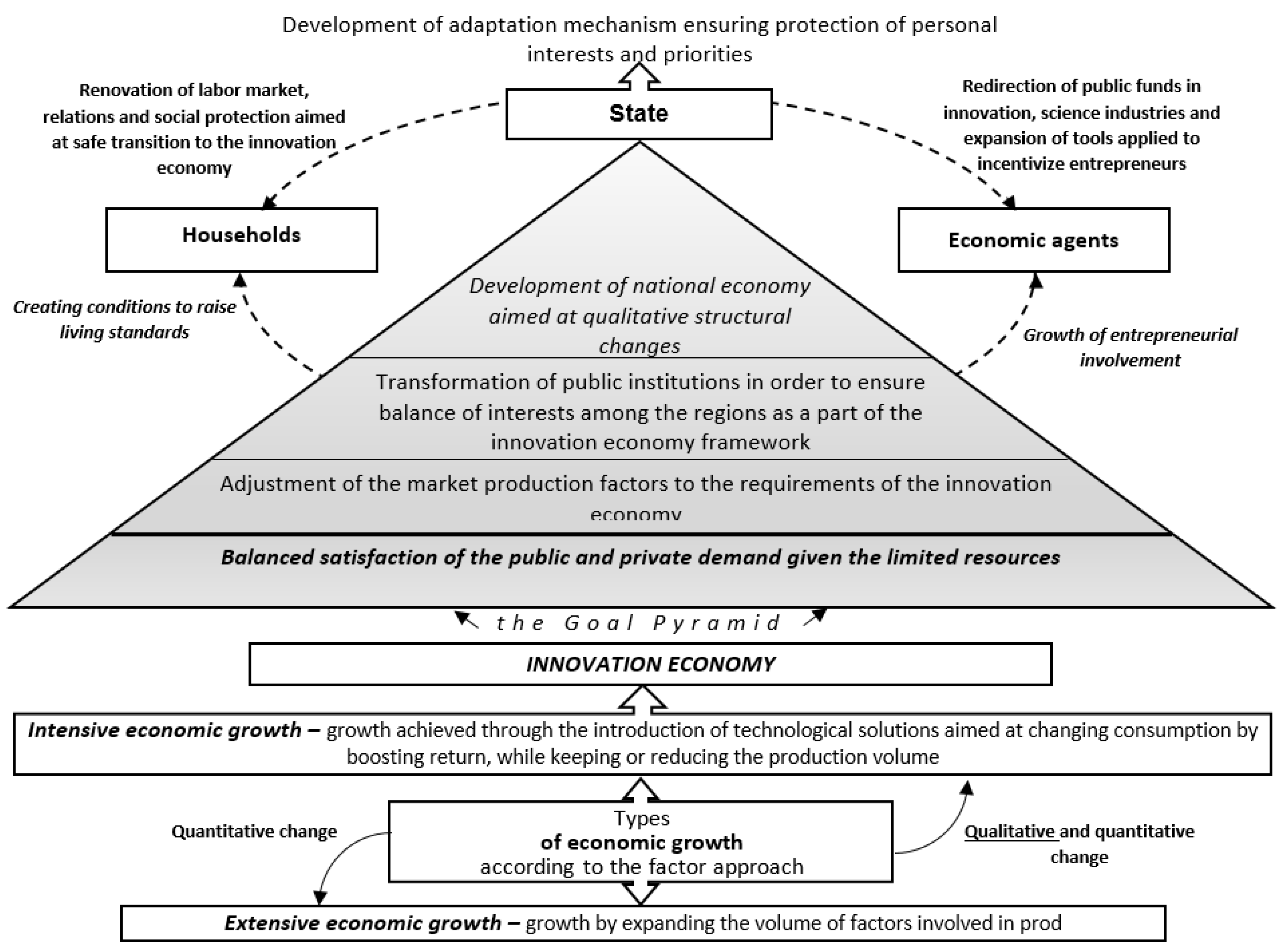
- The first set defines the resource potential of the region with an emphasis on such production factors as capital (physical and real), labor, technologies, information (as an element of product promotion). Without economic resources, it is impossible to create an economic good, which is necessary to meet the needs of individuals. This means that the availability of resources is an important condition for innovative transformations. Emphasis is placed on such resources as “capital” and “labor”, as they are included in the production function. However, it is important to have a certain amount of these resources and their quality in the context of innovative transformations. Therefore, it is essential to assess the degree of depreciation of fixed assets and the volume of investments in fixed capital that contribute to its renewal. It is advisable to consider the provision of the territory with researchers to identify the effectiveness of their activities. It is also appropriate to characterize the availability of “technology” and “information”. The availability of “information” was assessed indirectly through workers’ access to personal computers, since it is personal computers that speed up the process of searching and exchanging information.
- -
- The second set describes the indirect involvement of state institutions in the innovation changes through budget expenditures on the economy and labor market (detailed data on the innovation initiatives implemented at the request of regional authorities are lacking). At the same time, there are no data on the expenditure of funds for direct innovation in Russian regions. However, to a certain extent, spending on the territory’s economy can contribute to innovative reforms. For example, the unemployed retraining should follow the renewal of fixed assets. Another indicator reflects how actively the authorities of the subject of the federation are fighting unemployment, including creating jobs. In the conditions of replacing a person with mechanisms, the released labor force must be employed, or the state will not guarantee the observance of such a right of citizens as the right to work. It should be noted that the above coefficients only indirectly characterize the authorities’ involvement in innovative reforms. And they were applied due to the lack of more informative indicators in official statistics.
- -
- The third set assesses the demand of economic entities and households for innovations. To calculate the indicators of the third block, the indicators presented by the Federal State Statistics Service were used, calculated by this body based on its methodology. In the article, these indicators formed the basis for calculating relative statistical values, making it possible to determine the subjects of the federation in which the need for innovative transformations is most pronounced.
3.3. Interquartile Range
3.4. Production Function
4. Results
4.1. Results of Calculating the Adjusted Rate Indicators (I1–I11)
4.2. Specification of the Results of Calculating the Production Function Based on the Input–Output and Growth Rate Indicators
5. Discussion
5.1. Justification of the Hypothesis on the Possibility of Using the Production Function as a Tool for Assessment of the Innovation Climate in Regions
- -
- In total, 21 regions were included in the Q1 quartile, but only for 18 (excluding Tomsk Region, Perm Region, Chuvash Republic), do the obtained regression equations make economic sense. According to the analysis of these 18 models, nine regions showed an increasing return on production, the rest demonstrated a decreasing trend. In addition, for all the regions characterized by decreasing returns, the constant value exceeds one. If additional calculations were carried out, with the arbitrary values fitted in the constructed models, we would see that a 1% increase in “capital” or “labor” results in the final indicator growing by a percentage equal to the sum of the elasticity coefficients for “capital” and “labor”. Changing the constant by the same rate gives a similar result.
- -
- The Q4 quartile includes 19 regions, while for 5 of them (Kemerovo Region, Orenburg Region, Rep. Dagestan, Rep. North Ossetia, Karachay–Cherkess Rep.) the revealed functional dependencies cannot be adequately interpreted. The analysis of the remaining 14 models shows that in eight regions an increasing return on production is present, while six other regions demonstrate the opposite result. Only in four regression equations is the constant higher than one. In ten models, the value of the elasticity coefficient for “labor” is higher than that for “capital”.
- -
- 2009–2018—the first frame is impossible to expand due to the lack of data.
- -
- 2000–2018—the second frame cannot be reduced because the quality of the regression equations will decrease. However, it is still apparent that the Q1 quartile includes more regions with a constant (describing the influence of other factors, including scientific and technological progress) exceeding one, than the Q4 quartile.
5.2. Discussion of the Prospects for Applying the Production Function Based on Input–Output and Growth Rate Indicators in Meso-Territories
6. Conclusions
- -
- “Brain drain”—leads to the impossibility of exchanging intellectual potential.
- -
- Low interest of the end consumer in an innovative product, the cost of which at the first stages of sales can be significantly higher, since it is necessary to recoup the costs. With a high proportion of poor among the population, an expensive product will not be in demand.
- -
- Investment unattractiveness of the Russian economy for innovative open companies.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdikeev, Niyaz Mustyakimovich, Elena Borisovna Tyutyukina, Yurii Sergeevich Bogachev, and Evgeniya L’vovna Moreva. 2018. Assessment of the Effciency of Financial and Economic Mechanisms of State Stimulation of Innovative Activity in Russia. Finance: Theory and Practice 22: 40–55. [Google Scholar] [CrossRef]
- Afrin, Samina, Tarik Raihan, Ahmed Ishmum Uddin, and Md. Aftab Uddin. 2022. Predicting Innovative Work Behaviour in an Interactive Mechanism. Behavioral Sciences 12: 29. [Google Scholar] [CrossRef]
- Akdil, Kartal Yagiz, Alp Ustundag, and Emre Cevikcan. 2018. Maturity and Readiness Model for Industry 4.0 Strategy. In Industry 4.0: Managing the Digital Transformation. Cham: Springer, pp. 61–94. [Google Scholar] [CrossRef]
- Alvarez-Meaza, Izaskun, Naiara Pikatza-Gorrotxategi, and Rosa Maria Rio-Belver. 2020. Knowledge Sharing and Transfer in an Open Innovation Context: Mapping Scientific Evolution. Journal of Open Innovation: Technology, Market, and Complexity 6: 186. [Google Scholar] [CrossRef]
- Amrina, Uly, Akhmad Hidayatno, and T. Yuri M. Zagloel. 2021. A Model-Based Strategy for Developing Sustainable Cosmetics Small and Medium Industries with System Dynamics. Journal of Open Innovation: Technology, Market, and Complexity 7: 225. [Google Scholar] [CrossRef]
- Averina, Lidiya Mihaylovna, and Dmitry Vladimirovich Sirotin. 2020. Assessment of Spatial Effects from Innovation Activities in the Industrialized Russian Regions. Economy of Region 16: 268–82. [Google Scholar] [CrossRef]
- Bagrinovsky, Kirill Andreevich. 2011. Estimating the Future of Innovation Activities. Economics and Mathematical Methods 47: 102–8. [Google Scholar]
- Baierle, Ismael Cristofer, Julio Cezar Mairesse Siluk, Vinicius Jaques Gerhardt, Cláudia de Freitas Michelin, Álvaro Luiz Neuenfeldt Junior, and Elpidio Oscar Benitez Nara. 2021. Worldwide Innovation and Technology Environments: Research and Future Trends Involving Open Innovation. Journal of Open Innovation: Technology, Market, and Complexity 7: 229. [Google Scholar] [CrossRef]
- Bayev, Igor A., and Irina A. Solovyova. 2014. Empirical Analysis of the Relationship of Investment and Innovative Activity of Regions of Russia. Economy of Region 1: 147–55. [Google Scholar] [CrossRef]
- Beier, Grischa, Silke Niehoff, Tilla Ziems, and Bing Xue. 2017. Sustainability Aspects of a Digitalized Industry—A Comparative Study from China and Germany. International Journal of Precision Engineering and Manufacturing-Green Technology 4: 227–34. [Google Scholar] [CrossRef]
- Buravlev, Alexandr Ivanovich. 2012. Three-Factor the Production Model of the Cobb–Douglas. Ekonomika i Upravlenie: Problemy, Resheniya 3: 13–19. [Google Scholar]
- Chovancova, Bozena, Michaela Dorocakova, and Viera Malacka. 2018. Changes in the Industrial Structure of GDP and Stock Indices Also with Regard to Industry 4.0. Business and Economic Horizons 14: 402–14. [Google Scholar] [CrossRef]
- Christa, Usup Riassy, I Made Wardana, Christantius Dwiatmadja, and Vivy Kristinae. 2020. The Role of Value Innovation Capabilities in the Influence of Market Orientation and Social Capital to Improving the Performance of Central Kalimantan Bank in Indonesia. Journal of Open Innovation: Technology, Market, and Complexity 6: 140. [Google Scholar] [CrossRef]
- Chukhray, Nataliya, Oleksandra Mrykhina, and Ivan Izonin. 2022. Holistic Approach to R&D Products’ Evaluation for Commercialization under Open Innovations. Journal of Open Innovation: Technology, Market, and Complexity 8: 9. [Google Scholar] [CrossRef]
- Cruz-Ruiz, Elena, Elena Ruiz-Romero de la Cruz, Gorka Zamarreño-Aramendia, and F. J. Cristòfol. 2022. Strategic Management of the Malaga Brand through Open Innovation: Tourists and Residents’ Perception. Journal of Open Innovation: Technology, Market, and Complexity 8: 28. [Google Scholar] [CrossRef]
- de las Heras-Rosas, Carlos, and Juan Herrera. 2021. Research Trends in Open Innovation and the Role of the University. Journal of Open Innovation: Technology, Market, and Complexity 7: 29. [Google Scholar] [CrossRef]
- Dementiev, Viktor E. 2019. Productivity Paradox in Regional Dimension. Economy of Region 15: 43–56. [Google Scholar] [CrossRef]
- Dementyev, V. Ye. 2013. Structural Factors of Technological Development. Economics and Mathematical Methods 49: 33–46. [Google Scholar]
- Didenko, Nikolay, Djamilia Skripnuk, Kseniia Kikkas, Olga Kalinina, and Eryk Kosinski. 2021. The Impact of Digital Transformation on the Micrologistic System, and the Open Innovation in Logistics. Journal of Open Innovation: Technology, Market, and Complexity 7: 115. [Google Scholar] [CrossRef]
- Doroshenko, Yury A., Irina O. Malykhina, and Irina v. Somina. 2020. Regional Innovative Development in the Context of Current Trends of Neo-Industrialisation. Economy of Region 16: 1318–47. [Google Scholar] [CrossRef]
- Erol, Selim, Andreas Schumacher, and Wilfried Sihn. 2016. Strategic Guidance towards Industry 4.0—A Three-Stage Process Model. Paper presented at International Conference on Competitive Manufacturing 2016 (COMA’16), Stellenbosch, South Africa, January 27–29; Available online: https://www.researchgate.net/publication/286937652 (accessed on 30 June 2022).
- Farmania, Aini, Riska Dwinda Elsyah, and Michael Aaron Tuori. 2021. Transformation of CRM Activities into E-CRM: The Generating e-Loyalty and Open Innovation. Journal of Open Innovation: Technology, Market, and Complexity 7: 109. [Google Scholar] [CrossRef]
- Franco-Riquelme, José Nicanor, and Luis Rubalcaba. 2021. Innovation and SDGs through Social Media Analysis: Messages from FinTech Firms. Journal of Open Innovation: Technology, Market, and Complexity 7: 165. [Google Scholar] [CrossRef]
- Golova, Irina Markovna. 2007. Innovative Climate of the Region. Problems and Prospects. Ekaterinburg: Institut ekonomiki UrO RAN Publ. [Google Scholar]
- Golova, Irina Markovna, and Alla Filippovna Sukhovey. 2019. Differentiation of Innovative Development Strategies Considering Specific Characteristics of the Russian Regions. Economy of Region 15: 1294–308. [Google Scholar] [CrossRef]
- Hernández-Dionis, Paula, David Pérez-Jorge, Oliver Curbelo-González, and Olga María Alegre de la Rosa. 2022. The Coordinator of Information and Communication Technologies: Its Implication for Open Innovation. Journal of Open Innovation: Technology, Market, and Complexity 8: 42. [Google Scholar] [CrossRef]
- Hizam-Hanafiah, Mohd, and Mansoor Ahmed Soomro. 2021. The Situation of Technology Companies in Industry 4.0 and the Open Innovation. Journal of Open Innovation: Technology, Market, and Complexity 7: 34. [Google Scholar] [CrossRef]
- Huang, Xiaojing, Lei Ma, Rao Li, and Zheng Liu. 2020. Determinants of Innovation Ecosystem in Underdeveloped Areas—Take Nanning High-Tech Zone in Western China as an Example. Journal of Open Innovation: Technology, Market, and Complexity 6: 135. [Google Scholar] [CrossRef]
- Ibarra, Dorleta, Jaione Ganzarain, and Juan Ignacio Igartua. 2018. Business Model Innovation through Industry 4.0: A Review. Procedia Manufacturing 22: 4–10. [Google Scholar] [CrossRef]
- Jamai, Kaoutar, Ali Abidar, Hans de Steur, and Xavier Gellynck. 2022. Assessing Firm Readiness to Adopt Cluster-Based Innovative Projects: A Segmentation Analysis. Sustainability 14: 947. [Google Scholar] [CrossRef]
- Ji, Ilyong, and Jinkyung Goo. 2021. Pre-Entrepreneurs’ Perception of the Technology Regime and Their Entrepreneurial Intentions in Korean Service Sectors. Journal of Open Innovation: Technology, Market, and Complexity 7: 179. [Google Scholar] [CrossRef]
- Jonek-Kowalska, Izabela. 2021. Research Institutes in Poland as an Element of the National Innovation System—Complexity, Financing and Effectiveness. Journal of Open Innovation: Technology, Market, and Complexity 7: 162. [Google Scholar] [CrossRef]
- Kantor, Olga G., and Semen I. Spivak. 2019. The Modelling of the Extended Cobb-Douglas Production Function under Uncertainty of Initial Data. Vestnik UGATU (Scientific Journal of Ufa State Aviation Technical University) 23: 104. Available online: http://journal.ugatu.ac.ru (accessed on 23 June 2022).
- Khachatryan, Nerses. 2020. Computer Modelling of Options of Spatial Development of Scientific and Technological Sphere in the Russian Federation. Economics and the Mathematical Methods 56: 45. [Google Scholar] [CrossRef]
- Khadim, Zunaira, Irem Batool, Ahsan Akbar, Petra Poulova, and Minahs Akbar. 2021. Mapping the Moderating Role of Logistics Performance of Logistics Infrastructure on Economic Growth in Developing Countries. Economies 9: 177. [Google Scholar] [CrossRef]
- Kharlamova, Tatiana Lvovna, Andrei Viktorovich Kharlamov, and Yuliia Anatolevna Antohina. 2020. Influence of Information Technologies on the Innovative Development of the Economic System. Papar presented at International Conference on Economic and Social Trends for Sustainability of Modern Society, Krasnoyarsk, Russia, May 20–22; pp. 391–401. [Google Scholar] [CrossRef]
- Kharlamov, Andrei Viktorovich, and Tatiana Lvovna Kharlamova. 2019. Sustainable Development of the Russian Economy in the Context of Global Instability. Papar presented at 33rd International Business Information Management Association Conference, IBIMA 2019, Education Excellence and Innovation Man, Granada, Spain, April 10–11; pp. 822–30. [Google Scholar]
- Kim, Dawon, Rosa Kim, Tongwon Lee, and Seungho Choi. 2021. Related Diversification Using Core Competencies in South Korean Dairy Industry. Journal of Open Innovation: Technology, Market, and Complexity 7: 243. [Google Scholar] [CrossRef]
- Kirilyuk, I. L. 2013. Models of Production Functions for the Russian Economy. Computer Research and Modeling 5: 293–312. [Google Scholar] [CrossRef]
- Kolomak, Evgeniya A. 2011. Efficiency of Infrastructure Capital in Russia. Journal of the New Economic Association 10: 74–93. [Google Scholar]
- Leitão, João, Dina Pereira, and Sónia de Brito. 2020. Inbound and Outbound Practices of Open Innovation and Eco-Innovation: Contrasting Bioeconomy and Non-Bioeconomy Firms. Journal of Open Innovation: Technology, Market, and Complexity 6: 145. [Google Scholar] [CrossRef]
- Liu, Zheng. 2021. The Impact of Government Policy on Macro Dynamic Innovation of the Creative Industries: Studies of the UK’s and China’s Animation Sectors. Journal of Open Innovation: Technology, Market, and Complexity 7: 168. [Google Scholar] [CrossRef]
- Liu, Zheng, Yongjiang Shi, and Bo Yang. 2022. Open Innovation in Times of Crisis: An Overview of the Healthcare Sector in Response to the COVID-19 Pandemic. Journal of Open Innovation: Technology, Market, and Complexity 8: 21. [Google Scholar] [CrossRef]
- Majid Gilani, Sayed Abdul, and Alessio Faccia. 2021. Broadband Connectivity, Government Policies, and Open Innovation: The Crucial IT Infrastructure Contribution in Scotland. Journal of Open Innovation: Technology, Market, and Complexity 8: 1. [Google Scholar] [CrossRef]
- Mamonov, Mikhail E., and Anna A. Pestova. 2015. The Technical Efficiency of National Economies: Do the Institutions, Infrastructure and Resources Rents Matter? Journal of the New Economic Association 27: 44–78. [Google Scholar]
- Maresova, Petra, Ivan Soukal, Libuse Svobodova, Martina Hedvicakova, Ehsan Javanmardi, Ali Selamat, and Ondrej Krejcar. 2018. Consequences of Industry 4.0 in Business and Economics. Economies 6: 46. [Google Scholar] [CrossRef]
- McPhillips, Marita. 2020. Trouble in Paradise? Barriers to Open Innovation in Regional Clusters in the Era of the 4th Industrial Revolution. Journal of Open Innovation: Technology, Market, and Complexity 6: 84. [Google Scholar] [CrossRef]
- Müller, Julian Marius, Daniel Kiel, and Kai-Ingo Voigt. 2018a. What Drives the Implementation of Industry 4.0? The Role of Opportunities and Challenges in the Context of Sustainability. Sustainability 10: 247. [Google Scholar] [CrossRef]
- Müller, Julian Marius, Oana Buliga, and Kai-Ingo Voigt. 2018b. Fortune Favors the Prepared: How SMEs Approach Business Model Innovations in Industry 4.0. Technological Forecasting and Social Change 132: 2–17. [Google Scholar] [CrossRef]
- Nesterenko, N. Y., and D. G. Tcukanov. 2012. Innovation Policy Russia: Regional Aspect. St Petersburg University Journal of Economic Studies 2: 79–90. [Google Scholar]
- Nikonova, A. 2018. Evolution of Innovation Mode within Economic Dynamics. Economics and Mathematical Methods 54: 3–28. [Google Scholar] [CrossRef]
- Osorno-Hinojosa, Roberto, Mikko Koria, and Delia del Carmen Ramírez-Vázquez. 2022. Open Innovation with Value Co-Creation from University–Industry Collaboration. Journal of Open Innovation: Technology, Market, and Complexity 8: 32. [Google Scholar] [CrossRef]
- Oudgou, Mohamed. 2021. Financial and Non-Financial Obstacles to Innovation: Empirical Evidence at the Firm Level in the MENA Region. Journal of Open Innovation: Technology, Market, and Complexity 7: 28. [Google Scholar] [CrossRef]
- Pakhomova, E. A., D. A. Pisareva, and K. S. Kharcheva. 2018. Building the Model for Predicting the Region’s Staffing Needs through the Cobb–Douglas Production Function. National Interests: Priorities and Security 14: 253–68. [Google Scholar] [CrossRef]
- Pakhomova, Nadezhda V., and Sergei A. Smirnov. 2011. Innovation Economy: Structural Priorities and Indicators. St Petersburg University Journal of Economic Studies 4: 3–21. [Google Scholar]
- Pakhomova, Nadezhda V., and Dmitry S. Tkachenko. 2014. Innovations Supporting Institutions in Russia: The Logic of Development and the Current Status. St Petersburg University Journal of Economic Studies 2: 87–105. [Google Scholar]
- Park, HyunJee, and Sang Ok Choi. 2019. Digital Innovation Adoption and Its Economic Impact Focused on Path Analysis at National Level. Journal of Open Innovation: Technology, Market, and Complexity 5: 56. [Google Scholar] [CrossRef]
- Pereira, Leandro, António Fernandes, Mariana Sempiterno, Álvaro Dias, Renato Lopes da Costa, and Nélson António. 2021. Knowledge Management Maturity Contributes to Project-Based Companies in an Open Innovation Era. Journal of Open Innovation: Technology, Market, and Complexity 7: 126. [Google Scholar] [CrossRef]
- Peterková, Jindra, Katarzyna Czerná, and Jarmila Zimmermannová. 2022. Innovation Ecosystem in Selected Regions of the Czech Republic and Poland. Scientific Papers of the University of Pardubice, Series D: Faculty of Economics and Administration 30: 1550. [Google Scholar] [CrossRef]
- Povolná, Lucie, and Jena Švarcová. 2017. The Macroeconomic Context of Investments in the Field of Machine Tools in the Czech Republic. Journal of Competitiveness 9: 110–22. [Google Scholar] [CrossRef]
- Prazdnichnykh, Aleksei N. 2013. Building an Innovation Nation for Future Prosperity. Russian Management Journal 11: 107–50. [Google Scholar]
- Prokop, Viktor, Petr Hajek, and Jan Stejskal. 2021. Configuration Paths to Efficient National Innovation Ecosystems. Technological Forecasting and Social Change 168: 120787. [Google Scholar] [CrossRef]
- Quezada-Téllez, Luis A., Guillermo Fernández-Anaya, Dominique Brun-Battistini, Benjamín Nuñez-Zavala, and Jorge E. Macías-Díaz. 2021. An Economic Model for OECD Economies with Truncated M-Derivatives: Exact Solutions and Simulations. Mathematics 9: 1780. [Google Scholar] [CrossRef]
- Ramírez-Montoya, María Soledad, Isolda Margarita Castillo-Martínez, Jorge Sanabria-Z, and Jhonattan Miranda. 2022. Complex Thinking in the Framework of Education 4.0 and Open Innovation—A Systematic Literature Review. Journal of Open Innovation: Technology, Market, and Complexity 8: 4. [Google Scholar] [CrossRef]
- Raya, Alia Bihrajihant, Riesma Andiani, Abi Pratiwa Siregar, Imade Yoga Prasada, Fairuz Indana, Theresia Gracia Yunindi Simbolon, Agustina Tri Kinasih, and Agus Dwi Nugroho. 2021. Challenges, Open Innovation, and Engagement Theory at Craft SMEs: Evidence from Indonesian Batik. Journal of Open Innovation: Technology, Market, and Complexity 7: 121. [Google Scholar] [CrossRef]
- Rodionov, Dmitry, Olga Nadezhina, and Sergei Yalimov. 2020. Evaluating the Impact of Small and Medium Business on the Innovative Activity of Regions in Russia. In European Conference on Innovation and Entrepreneurship. In Academic Conferences Interna. Reading: Academic Conferences and Publishing International Limited, pp. 562–67. [Google Scholar]
- Roša (Rosha), Angelina, and Natalja Lace. 2021. Assessment of the Impact of Coaching on a Company’s Performance: A Review of Methods. Journal of Open Innovation: Technology, Market, and Complexity 7: 233. [Google Scholar] [CrossRef]
- Rotjanakorn, Atichat, Pornrat Sadangharn, and Khahan Na-Nan. 2020. Development of Dynamic Capabilities for Automotive Industry Performance under Disruptive Innovation. Journal of Open Innovation: Technology, Market, and Complexity 6: 97. [Google Scholar] [CrossRef]
- Rudskaya, Irina Andreevna, and Dmitry Grigorievich Rodionov. 2018. Comprehensive Evaluation of Russian Regional Innovation System Performance Using a Two-Stage Econometric Model Evaluación Integral Del Rendimiento Del Sistema Regional de Innovación de Rusia Mediante Un Modelo Econométrico de Dos Etapas. Revista Espacios 39: 40. [Google Scholar]
- Rudskaya, Irina, Darya Kryzhko, Angi Shvediani, and Magdalena Missler-Behr. 2022. Regional Open Innovation Systems in a Transition Economy: A Two-Stage DEA Model to Estimate Effectiveness. Journal of Open Innovation: Technology, Market, and Complexity 8: 41. [Google Scholar] [CrossRef]
- Rudskaya, Irina, and Dmitry Rodionov. 2017. Econometric Modeling as a Tool for Evaluating the Performance of Regional Innovation Systems (with Regions of the Russian Federation as the Example). Academy of Strategic Management Journal 16. Available online: https://www.abacademies.org/articles/Econometric-modeling-as-a-tool-for-evaluating-the-performance-of-regional-innovation-1939-6104-SI-16-2-131.pdf (accessed on 28 June 2022).
- Sabando-Vera, David, Marcela Yonfa-Medranda, Néstor Montalván-Burbano, Jose Albors-Garrigos, and Katherine Parrales-Guerrero. 2022. Worldwide Research on Open Innovation in SMEs. Journal of Open Innovation: Technology, Market, and Complexity 8: 20. [Google Scholar] [CrossRef]
- Samoilova, Liudmila, Alexander Litvinenko, and Olga Nadezhina. 2021. Assessment of the Availability of Regional Economic Resources to Analyze Their Adaptability to an Innovative Economy. Paper presented at 16th European Conference on Innovation and Entrepreneurship (ECIE 2021), Lisbon, Portugal, September 21–22; Portugal: ISCTE Business School, Instituto Universitário de Lisboa, pp. 846–55. [Google Scholar]
- Seidl da Fonseca, Ricardo. 2017. The Future of Employment: Evaluating Impact of STI Foresight Exercises. Foresight and STI Governance 11: 9–22. [Google Scholar] [CrossRef]
- Seidl da Fonseca, Ricardo. 2018. The Practice and Future of Financing Science, Technology, and Innovation. Foresight and STI Governance 12: 6–22. [Google Scholar] [CrossRef]
- Skordoulis, Michalis, Stamatios Ntanos, Grigorios L. Kyriakopoulos, Garyfallos Arabatzis, Spyros Galatsidas, and Miltiadis Chalikias. 2020. Environmental Innovation, Open Innovation Dynamics and Competitive Advantage of Medium and Large-Sized Firms. Journal of Open Innovation: Technology, Market, and Complexity 6: 195. [Google Scholar] [CrossRef]
- Sönmez, Betül, and Aytolan Yıldırım. 2019. The Mediating Role of Autonomy in the Effect of Pro-Innovation Climate and Supervisor Supportiveness on Innovative Behavior of Nurses. European Journal of Innovation Management 22: 41–58. [Google Scholar] [CrossRef]
- Sukhovey, Alla F., and Irina M. Golova. 2016. Substantionation of the Transformation of the Priorities of Innovation and Technological Development of Russian Regions in the Global Crisis. Economy of Region 12: 911–23. [Google Scholar] [CrossRef]
- Sukhovey, Alla F., and Irina M. Golova. 2020. Differentiation of Innovative Development Strategies of Regions for Improving the Effectiveness of Socio-Economic Policy in the Russian Federation. Economy of Region 16: 1302–17. [Google Scholar] [CrossRef]
- Suvorov, Nikolay Vladimirovich, Rustem Rinatovich Akhunov, Roman Vladimirovich Gubarev, Evgeniy Ivanovich Dzyuba, and Fanil’ Saitovich Fayzullin. 2020. Applying the Cobb-Douglas Production Function for Analysing the Region’s Industry. Economy of Region, 187–200. [Google Scholar] [CrossRef]
- Suwandaru, Agung, Thamer Alghamdi, and Nurwanto Nurwanto. 2021. Empirical Analysis on Public Expenditure for Education and Economic Growth: Evidence from Indonesia. Economies 9: 146. [Google Scholar] [CrossRef]
- Tjahjadi, Bambang, Noorlailie Soewarno, Johnny Jermias, Hariyati Hariyati, Atika Fairuzi, and Dewi Nabilah Anwar. 2022. Does Engaging in Global Market Orientation Strategy Affect HEIs’ Performance? The Mediating Roles of Intellectual Capital Readiness and Open Innovation. Journal of Open Innovation: Technology, Market, and Complexity 8: 29. [Google Scholar] [CrossRef]
- Turoń, Katarzyna. 2022a. From the Classic Business Model to Open Innovation and Data Sharing—The Concept of an Open Car-Sharing Business Model. Journal of Open Innovation: Technology, Market, and Complexity 8: 36. [Google Scholar] [CrossRef]
- Turoń, Katarzyna. 2022b. Open Innovation Business Model as an Opportunity to Enhance the Development of Sustainable Shared Mobility Industry. Journal of Open Innovation: Technology, Market, and Complexity 8: 37. [Google Scholar] [CrossRef]
- Tutak, Magdalena, and Jarosław Brodny. 2022. Business Digital Maturity in Europe and Its Implication for Open Innovation. Journal of Open Innovation: Technology, Market, and Complexity 8: 27. [Google Scholar] [CrossRef]
- Usman, Muhammad, Gulnaz Hameed, Abdul Saboor, Lal K. Almas, and Muhammad Hanif. 2021. R&D Innovation Adoption, Climatic Sensitivity, and Absorptive Ability Contribution for Agriculture TFP Growth in Pakistan. Agriculture 11: 1206. [Google Scholar] [CrossRef]
- Valdez-Juárez, Luis Enrique, and Mauricio Castillo-Vergara. 2020. Technological Capabilities, Open Innovation, and Eco-Innovation: Dynamic Capabilities to Increase Corporate Performance of SMEs. Journal of Open Innovation: Technology, Market, and Complexity 7: 8. [Google Scholar] [CrossRef]
- Vaseyskaya, Natal’ia O., and Vladimir V. Glukhov. 2019. Activities of University in Cluster Structure Based on Cobb–Douglas. St. Petersburg State Polytechnical University Journal. Economics 12: 153–61. [Google Scholar]
- Walter, Cicero Eduardo, Daniel Ferreira Polónia, Manuel Au-Yong-Oliveira, Cláudia Miranda Veloso, Rafael Ângelo Santos Leite, and Iracema Aragão. 2021. Drivers of Innovation Capacity and Consequences for Open Innovation. Journal of Open Innovation: Technology, Market, and Complexity 7: 140. [Google Scholar] [CrossRef]
- Yuana, Rivira, Eko Agus Prasetio, Rizal Syarief, Yandra Arkeman, and Arif Imam Suroso. 2021. System Dynamic and Simulation of Business Model Innovation in Digital Companies: An Open Innovation Approach. Journal of Open Innovation: Technology, Market, and Complexity 7: 219. [Google Scholar] [CrossRef]
- Yun, JinHyo Joseph, DongKyu Won, and Kyungbae Park. 2016. Dynamics from Open Innovation to Evolutionary Change. Journal of Open Innovation: Technology, Market, and Complexity 2: 7. [Google Scholar] [CrossRef]
- Zemtsov, Stepan P., and Yuriy A. Smelov. 2018. Factors of Regional Development in Russia: Geography, Human Capital and Regional Policies. Journal of the New Economic Association 40: 84–108. [Google Scholar] [CrossRef]
- Ziakis, Christos, Maro Vlachopoulou, and Konstantinos Petridis. 2022. Start-Up Ecosystem (StUpEco): A Conceptual Framework and Empirical Research. Journal of Open Innovation: Technology, Market, and Complexity 8: 35. [Google Scholar] [CrossRef]

| Indicator Name | Calculation Formula | Standard Value |
|---|---|---|
| 1. Availability of economic resources | ||
| Capital | ||
| 1.1.1. Degree of depreciation of fixed assets: ratio of the region to the Russian Federation (I1) | I1 = (Degree of depreciation of fixed assets in the region)/(Degree of depreciation of fixed assets in Russia) | Specified value < 1. Assesses the physical capital, its readiness to be used and the need for renovation. |
| 1.1.2. Investments in fixed assets: ratio of the region to the Russian Federation (I2) | I2 = (Investments in fixed assets in the region (per worker))/(Investments in fixed assets in Russia (per worker)) | Specified value ≥ 1. Defines the investment activity—indirect stimulation of the innovation processes. |
| Labor | ||
| 1.2.1. Number of workers involved in scientific research and development to total employment: ratio of the region to the Russian Federation (I3) | I3 = (Number of workers involved in scientific research and development to total employment in the region)/(Number of workers involved in scientific research and development to total employment in Russia) | Specified value ≥ 1. Reflects the availability of scientific staff responsible for the important innovative and technological changes in the economy. |
| 1.2.2. Patent applications filed for inventions per 1000 workers engaged in scientific research and development: ration of the region to the Russian Federation (I4) | I4 = (Patent applications filed for inventions per 1000 workers engaged in scientific research and development in the region)/(Patent applications filed for inventions per 1000 workers involved in scientific research and development in Russia) | Specified value ≥ 1. Indirectly characterizes the labor productivity of workers employed in the research and development sector. |
| Technologies | ||
| 1.3.1. Issued patent applications for inventions per 1000 workers engaged in scientific research and development: ratio of the region to the Russian Federation (I5) | I5 = (Issued patent applications for inventions per 1000 workers engaged in scientific research and development in the region)/(Issued patent applications for inventions per 1000 workers involved in scientific research and development in Russia) | Specified value ≥ 1. Specifies effectiveness of the research and development sector. |
| Information | ||
| 1.4.1. Number of personal computers per 100 employees: ratio of the region to the Russian Federation (I6) | I6 = (Number of personal computers per 100 employees in the region)/(Number of personal computers per 100 employees in Russia) | Specified value ≥ 1. Indirectly specifies the level of availability of information and telecommunications technologies. |
| 2. Involvement of government and authorities in support of the innovation initiatives (indirect impact) | ||
| Support of the regional economy through budget expenditures | ||
| 2.1. Expenditures on the economy (per capita): ratio of the region to the Russian Federation (I7) | I7 = (Expenditures on the economy in the region (per capita))/(Expenditures on the economy in Russia (per capita)) | Specified value ≥ 1. Reflects the volume of money allocated from the budget funds in the regional economy (in terms of meeting the population needs)—indirectly stimulating employment, entrepreneurial activity, innovation processes. |
| Labor supply | ||
| 2.2. Unemployment load represented by the citizens registered with the employment services (per one vacant position): ratio of the region to the Russian Federation (I8) | I8 = (Unemployment load represented by the citizens registered with the employment services (per one vacant position) in the region)/(Unemployment load represented by the citizens registered with the employment services (per one vacant position) in Russia) | Specified value < 1. Indirectly describes the region’s employment policy, which is an important indicator to track in terms of automation when people are vastly replaced by technologies. |
| 3. General need for innovation | ||
| Need of enterprises for the cutting-edge technologies | ||
| 3.1. Level of innovation activity in enterprises: ratio of the region to the Russian Federation (I9) | I9 = (Level of innovation activity in enterprises in the region)/(Level of innovation activity in enterprises in Russia) | Specified value ≥ 1. Reflects the degree of the enterprises’ involvement in innovations in the region. |
| 3.2. Advanced production technologies (per worker): ratio of the region the Russian Federation (I10) | I10 = (Advanced production technologies used in the region (per worker))/(Advanced production technologies used in Russia (per worker)) | Specified value ≥ 1. Defines the level of prevalence of advanced production technologies in the enterprise’s activities. |
| End-user’s interest in innovation | ||
| 3.3. Volume of innovative goods and services (per capita): ratio of the region to the Russian Federation (I11) | I11 = (Volume of innovative goods and services in the region (per capita))/(Volume of innovative goods and services in Russia (per capita)) | Specified value ≥ 1. Indicates the interest of end-users in innovation. |
| 2009 (Overall Rank According to the Set of Indicators) | 2018 (Overall Rank According to the Set of Indicators) | Average for the Period from 2009 to 2018 (Overall Rank According to the Set of Indicators) |
|---|---|---|
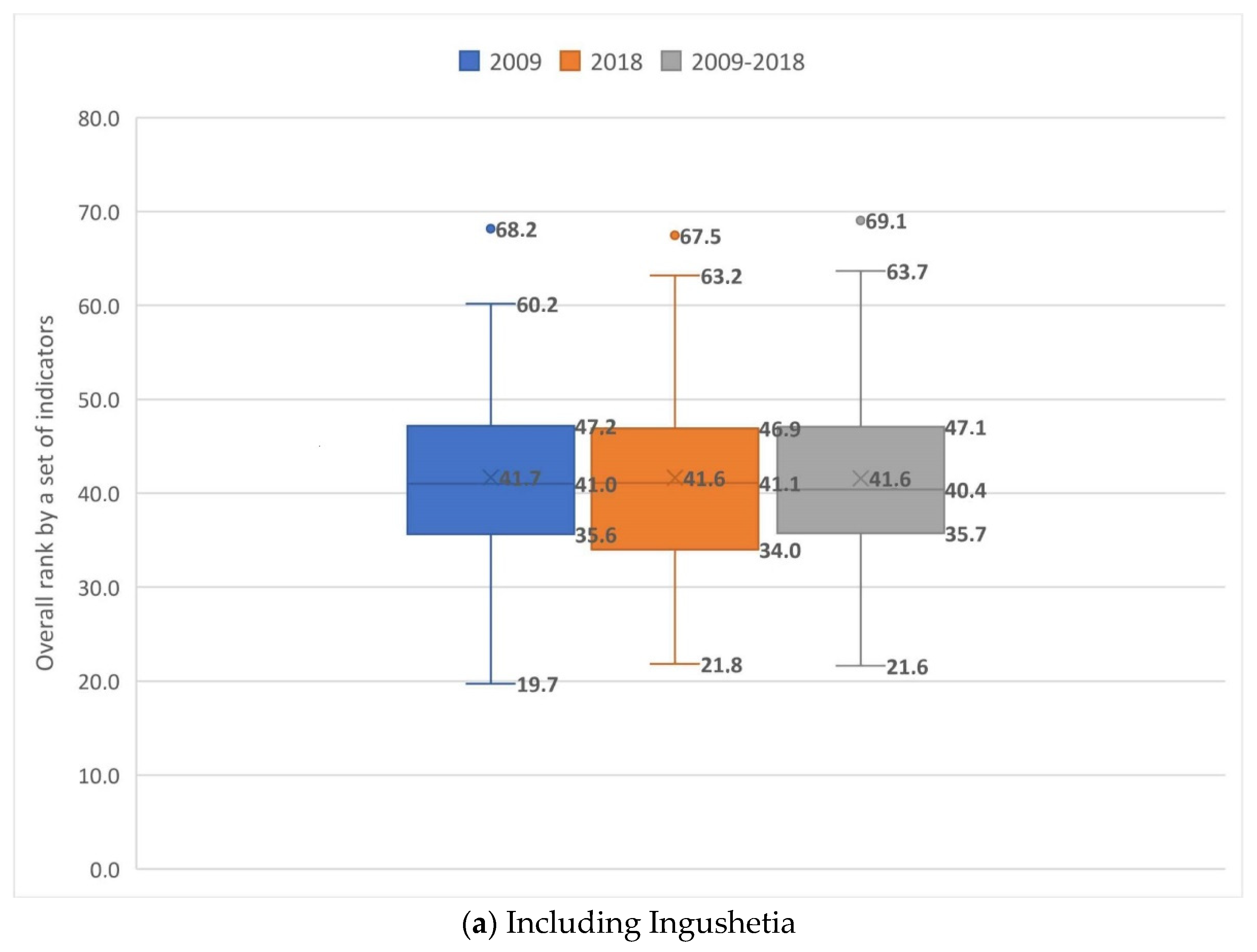
| Quartile—Q1 Moscow; Tomsk Region; St. Petersburg; Lipetsk Region; Khabarovsk Territory; Rep. Tatarstan; Magadan Region; Krasnoyarsk Region; Primorsky Region; Nizhny Novgorod Region; Yamalo–Nenets Autonomous District; Vologda Region; Kaluga Region; Belgorod Region; Perm Region; Moscow Region; Rep. Bashkortostan; Novgorod Region; Tambov region; Yaroslavl Region; Kostroma Region. | Quartile—Q1 Rep. Tatarstan; Belgorod Region; Lipetsk Region; Moscow Region; Yamalo–Nenets Autonomous District; Moscow; Khabarovsk Region; Kaluga Region; Tyumen Region; St. Petersburg; Tambov Region; Krasnoyarsk Region; Tula Region; Kursk Region; Voronezh Region; Rep. Bashkortostan; Rep. Mordovia; Chuvash Republic; Tver Region; Leningrad Region; Vologda Region. | Quartile—Q1 Moscow; Rep. Tatarstan; Khabarovsk Region; St. Petersburg; Lipetsk Region; Magadan Region; Kaluga Region; Tomsk Region; Yamalo–Nenets Autonomous District; Belgorod Region; Krasnoyarsk Region; Nizhny Novgorod Region; Vologda Region; Rep. Mordovia; Voronezh Region; Tula Region; Moscow Region; Chuvash Republic; Rep. Bashkortostan; Perm Region; Tyumen Region. |
| Quartile—Q4 Orenburg Region; Rep. Karelia; Smolensk Region; Altai Region; Stavropol Region; Trans-Baikal Region; Rep. Komi; Kemerovo Region; Bryansk Region; Rep. Adygea; Rep. Khakassia; Rep. Mari El; Rep. Altai; Kabardino-Balkarian Rep; Rep. Tyva; Karachay–Cherkess Republic; Rep. North Ossetia; Chechen Republic; Rep. Kalmykia. | Quartile—Q4 Astrakhan Region; Orenburg Region; Rep. Karelia; Ivanovo Region; Altai Region; Stavropol Region; Rep. Buryatia; Rep. Kalmykia; Nenets Autonomous District; Trans-Baikal Territory; Rep. Altai; Rep. North Ossetia; Rep. Khakassia; Kabardino-Balkar Republic; Jewish Autonomous Region; Rep. Dagestan; Karachay–Cherkess Republic; Rep. Tyva; Chechen Rep. | Quartile—Q4 Kemerovo Region; Zabaykalsky Region; Rep. Altai; Orenburg Region; Altai Region; Smolensk Region; Stavropol Region; Rep. Karelia; Kurgan Region; Nenets Autonomous District; Kabardino-Balkar Republic; Rep. Dagestan; Rep. Khakassia; Rep. Adygea; Rep. Kalmykia; Rep. North Ossetia; Rep. Tyva; Karachay–Cherkess Republic; Chechen Republic. |
| Outlier: Rep. Ingushetia | Outlier: Rep. Ingushetia | Outlier: Rep. Ingushetia |
| Production Function Based on the Input–Output Indicators | Production Function Based on the Growth Rate Indicators |
|---|---|
| Determination coefficient (R-square) | |
| - Bottom value—0.956 (Kalmykia); - Peak value—0.998 (Kaluga Region, Pskov Region, Krasnodar Region, Stavropol Region, Ulyanovsk Region, Rep. Tyva); - High accuracy in the fitting of the regression equation. | - Bottom value—0.035 (Nenets Autonomous District); - Peak value—0.765 (Novosibirsk Region); - for 24 R-square models < 0.5, which implies the insufficient nature of dual regression due to the other factors affecting the final indicator; - for 49 models 0.5 < R-square < 0.7, indicating the satisfactory accuracy of the equation fitting; - for 10 built models (Bryansk region, Kaluga Region, Tula Region, Pskov Region, Krasnodar Region, Rep. Tatarstan, Chuvash Republic, Chelyabinsk Region, Novosibirsk Region, Tomsk Region) R-square > 0.7—the fitting accuracy of the regression equation is high. |
| F-test | |
| - Bottom value—173 (Kalmykia); - Peak value—4476 (Kaluga Region); - The F-test value for all constructed models is several orders greater than the tabular value (F-test = 3.63, a = 0.05)—hypothesis on the random nature of the estimated parameters is rejected, their statistical significance is recognized. | - Bottom value—0.274 (Nenets Autonomous District); - Peak value—25.978 (Novosibirsk Region); - The F-test value for 73 constructed models is higher than the tabular value (F-test = 3.63, a = 0.05)—hypothesis on the random nature of the estimated parameters is rejected, their statistical significance is recognized; - The F-test value for 10 constructed models is lower than the tabular value (Nenets Autonomous District, Vologda Region, Murmansk Region, Rep. Adygea, Rep. Ingushetia, Khanty-Mansi Autonomous Region, Kamchatka Region, Amur Region, Magadan Region, Sakhalin Region)—hypothesis on the random nature of the estimated parameters is not rejected and their statistical significance is doubted. |
| The Durbin-Watson test (the DW test) | |
| - Lack of autocorrelation: The Durbin-Watson test at a 5% significance level belongs to the interval—[1.53; 2.47]. The Durbin–Watson test corresponds to the tabular value in the models constructed for 19 regions; - Lack of autocorrelation: The Durbin–Watson test at a 1% significance level belongs to the interval—[1.26; 2.74]. The Durbin–Watson test corresponds to the tabular value in the models constructed for 39 regions; - For models without an intercept is not considered representative. | - Lack of autocorrelation: The Durbin–Watson test at a 5% significance level belongs to the interval—[1.53; 2.47]. The Durbin–Watson test corresponds to the tabular value in the models constructed for 57 regions; - Lack of autocorrelation: The Durbin–Watson test at a 1% significance level belongs to the interval—[1.26; 2.74]. The Durbin–Watson test corresponds to the tabular value in the models constructed for 74 regions; - For the Durbin–Watson test, at a 5% significance level, the following uncertainty zones are distinguished (1.08; 1.53) and (2.47; 2.92), while at a 1% significance level—(0.83; 1.26) and (2.74; 3.17). For 82 regions (5% significance level) and 83 regions (1% significance level) of the constructed models, this parameter either corresponds to a tabular value or belongs to an uncertainty zone. Consequently, at a 5% significance level, the positive autocorrelation of residuals in the model constructed for Tyumen Region is confirmed, but at a 1% significance level, it is impossible to make an unambiguous judgment on the presence of positive or negative autocorrelation. |
| The Student’s t-test | |
| - Models developed for 41 regions reflect the systematic influence of both, “capital” and “labor” on the final indicator at a 5% significance level; - Models developed for 5 regions reflect the systematic influence of “capital” only on the final indicator at a 5% significance level (Smolensk Region, Rep. Karelia, Astrakhan Region, Chechen Republic, Magadan Region); - Models developed for 32 regions reflect the systematic influence of “labor” only on the final indicator at a 5% significance level; - Models developed for 5 regions reflect no systematic influence on the final indicator at a 5% significance level, either on “capital”, or “labor” (Lipetsk Region, Vologda Region, Rep. Kalmykia, Tyumen Region, Khanty-Mansiysk Autonomous Region); - Models developed for 39 regions reflect the systematic impact of the (A) constant on the final indicator at a 5% significance level; - Models developed for 18 regions reflect the systematic impact of three factor group, including “capital”, “labor”, and “omitted”, on the final indicator at a 5% significance level. | - Models developed for 2 regions (Kalmykia and Altai Region) reflect the systematic impact of two predictors, including “discrete growth rate of capital” and “discrete growth rate of labor”, on the final indicator at a 5% significance level. As the results show, the model developed for Kalmykia cannot be adequately interpreted due to the negative coefficient at a discrete rate of increase in the value of fixed assets. The model built for Altai Republic, in its turn, fails to meet the quality parameters due to the low R-square value; - Models developed for 60 regions (more than a half managed to fit all quality parameters) reflect the systematic impact of one predictor at a 5% significance level—“discrete growth rate of labor”, while one region (Chechen Republic) is represented by “discrete growth rate of labor”; - Models developed for 2 regions (Kamchatka Region, Magadan Region) reflect the systematic influence of a free term (γ) on a final indicator at a 5% significance level, though they should not be considered due to the lack of reliability; - Models developed for 2 regions (Tula Region, Krasnoyarsk Region) reflect the systematic influence of a “discrete growth rate of capital”, a “discrete growth rate of labor” and a free term on the final indicator at a 5% significance level. Nonetheless, these models cannot be adequately interpreted due to the negative coefficient at a discrete growth rate of fixed assets. |
| Production Function Based on the Input–Output Indicators | Production Function Based on the Growth Rate Indicators | |||
|---|---|---|---|---|
| Regions where α > β | Regions where α < β | Regions where α > β | Regions where α < β | |
| 19 regions (Bryansk Region; Voronezh Region; Orel Region; Smolensk Region; Tambov Region; Rep. Karelia; Pskov Region; Rep. Kalmykia; Astrakhan Region; Rep. Ingushetia; Chechen Republic; Rep. Mordovia; Udmurt Republic; Nizhny Novgorod Region; Saratov Region; Rep. Khakassia; Novosibirsk Region; Rep. Sakha; Magadan region) | 64 regions | 8 regions (Moscow Region; Orel Region; Tambov Region; Yaroslavl Region; Vologda Region; Rep. Dagestan; Chechen Republic; Yamalo–Nenets Autonomous District) | 75 regions | |
| Regions where A > 1 | Regions where A ≈ 1 (*) | Regions where 0 < A < 1 | Regions where γ > 0 | Regions where γ < 0 |
| 41 regions | Sverdlovsk Region—A = 1.002; Altai Republic—A = 0.957 | 40 regions | 72 regions | 11 regions (Voronezh Region, Kaluga Region; Lipetsk Rep; Moscow; Tambov Region; Moscow; Volgograd Region; Dagestan; Chechen Republic; Chelyabinsk Region; Omsk Region) |
| Regions where α + β ≥ 1 | Regions where α + β < 1 | |||
| 39 regions (Belgorod Region; Bryansk Region; Vladimir Region; Voronezh Region; Kaluga Region; Kursk Region; Orel Region; Smolensk Region; Tambov Region; Tula Region; Rep. Karelia.; Arkhangelsk Region; Kaliningrad Region; Novgorod Region; Pskov Region; Rep. Adygea; Rep. Kalmykia; Astrakhan Region; Rostov Region; Chechen Republic; Rep. Mari El; Rep. Mordovia; Udmurt Republic; Kirov Region; Penza Region; Saratov Region; Kurgan Region; Sverdlovsk Region; Yamalo–Nenets Autonomous District; Rep. Tyva; Rep. Khakassia; Krasnoyarsk Region; Irkutsk Region; Novosibirsk Region; Kamchatka Region; Khabarovsk Region; Magadan Region; Sakhalin Region; Chukotka Autonomous District) | 44 regions | |||
| Regions where all the parameters of the model quality meet the specified indicator (**) and the calculated coefficients are justified | ||||
| Ivanovo Region: Y = 1.591*K0.317*L0.62; Kursk Region: Y = 0.342*K0.399*L0.69; Oryol Region: Y = 0.216*K0.795*L0.294; Nenets Autonomous District: Y = 3.03*K0.294*L0.698; Kaliningrad Region: Y = 0.722*K0.4*L0.631; Novgorod Region: Y = 0.765*K0.437*L0.584; Stavropol Region: Y = 0.744*K0.49*L0.509; Rep. Mari El: Y = 0.168*K0.455*L0.683; Kirov Region.: Y = 0.381*K0.464*L0.588; Saratov Region: Y = 0.455*K0.576*L0.455; Kurgan Region.: Y = 0.764*K0.363*L0.641; Rep. Altai: Y = 0.957*K0.338*L0.652; Rep. Tyva: Y = 0.91*K0.206*L0.803; Khabarovsk Region: Y = 0.51*K0.482*L0.55 | Vladimir Region: y = 0.163*k + 0.501*l + 0.052; Yaroslavl Region: y = 0.609*k + 0.316*l + 0.028; Arkhangelsk Region: y = 0.177*k + 0.842*l + 0.002; Saint Petersburg: y = 0.365*k + 0.578*l + 0.004; Krasnodar Region: y = 0.018*k + 0.678*l + 0.035; Rostov Region: y = 0.181*k + 0.557*l + 0.038; Karachay–Cherkess Republic: y = 0.17*k + 0.668*l + 0.003; Rep. Mordovia: y = 0.122*k + 0.523*l + 0.04; Rep. Tatarstan: y = 0.047*k + 0.812*l + 0.01; Chuvash Republic: y = 0.271*k + 0.681*l + 0.003; Perm Region: y = 0.046*k + 0.739*l + 0.023; Nizhny Novgorod Region: y = 0.104*k + 0.679*l + 0.026; Ulyanovsk Region: y = 0.31*k + 0.542*l + 0.015; Yamalo–Nenets Autonomous District: y = 0.257*k + 0.123*l + 0.113; Altai Region: y = 0.046*k + 0.78*l + 0.016; Tomsk Region: y = 0.022*k + 0.806*l + 0.017; Rep. Buryatia: y = 0.161*k + 0.677*l + 0.006 | |||
| Regions with the unjustified calculated coefficients | ||||
| Negative sign goes with the capital elasticity coefficient is observed in the models of the following regions: Yaroslavl Region; Volgograd Region; Rep. Dagestan; Karachay–Cherkess Republic; North Ossetia; Chuvash Republic; Perm Region; Orenburg Region; Rep. Buryatia; Kemerovo Region; Omsk Region; Tomsk Region. | Negative sign goes with the coefficient of “discrete growth rate of capital” in the models developed for 33 regions; Negative sign goes with the coefficient of “discrete growth rate of labor” in the models developed for 2 regions, including Ingushetia, Chechen Republic.; Negative sign goes with the free term describing other factors, including neutral technical progress, in the models developed for 11 regions | |||
| Year | GRP Volume in Value Terms (Million Rubles) per Worker | Return on Each Ruble Spent on Labor | Nominal Salary, Calculated in US Dollars | |||
|---|---|---|---|---|---|---|
| Belgorod Region | Sakhalin Region | Belgorod Region | Sakhalin Region | Belgorod Region | Sakhalin Region | |
| 2000 | 0.4493 | 1.3739 | 2.6944 | 3.7942 | 61.02 | 130.80 |
| 2001 | 0.4554 | 1.5877 | 2.5399 | 4.2954 | 85.88 | 170.70 |
| 2002 | 0.4761 | 1.6852 | 2.2273 | 3.8121 | 111.43 | 221.99 |
| 2003 | 0.5152 | 1.9421 | 2.1033 | 3.7742 | 145.60 | 304.04 |
| 2004 | 0.5431 | 2.2565 | 2.0899 | 3.8534 | 183.42 | 406.49 |
| 2005 | 0.5799 | 2.4259 | 2.0011 | 3.6404 | 239.40 | 538.62 |
| 2006 | 0.6428 | 2.6624 | 1.9719 | 3.6222 | 306.84 | 693.49 |
| 2007 | 0.7193 | 3.2806 | 1.9220 | 3.9603 | 409.68 | 912.68 |
| 2008 | 0.7962 | 3.1160 | 1.8943 | 3.3054 | 543.38 | 1209.19 |
| 2009 | 0.8108 | 3.5144 | 2.0677 | 3.8874 | 441.75 | 1025.00 |
| 2010 | 0.8228 | 3.7423 | 1.9852 | 4.1395 | 524.97 | 1180.76 |
| 2011 | 0.9014 | 3.9032 | 1.9970 | 4.0435 | 601.16 | 1319.19 |
| 2012 | 0.9261 | 3.8135 | 1.9385 | 3.7393 | 643.56 | 1422.39 |
| 2013 | 0.9614 | 3.8708 | 1.9425 | 3.6531 | 697.68 | 1538.68 |
| 2014 | 1.0006 | 3.9181 | 2.0197 | 3.5283 | 618.88 | 1421.81 |
| 2015 | 1.0450 | 4.0718 | 2.2631 | 3.6741 | 416.83 | 1003.95 |
| 2016 | 1.0765 | 4.1191 | 2.3129 | 3.7168 | 409.97 | 983.04 |
| 2017 | 1.1147 | 3.9035 | 2.2923 | 3.4578 | 498.64 | 1175.10 |
| 2018 | 1.1506 | 4.2176 | 2.2157 | 3.3657 | 508.09 | 1236.23 |
| Regions | Production Function Model Based on Input–Output Indicators | Quality Parameters of Production Function Model | The Student’s t-Test | |||
|---|---|---|---|---|---|---|
| R2 | F-Test | K | L | A | ||
| Q1 | ||||||
| Moscow | Y = 24.947*K0.406*L0.39 | 0.992 | 458 | 0.015 | 0.008 | 0.002 |
| Rep. of Tatarstan | Y = 0.139*K0.66*L0.467 | 0.989 | 304 | 0.021 | 0.057 | 0.057 |
| Khabarovsk Territory | Y = 0.563*K0.82*L0.172 | 0.972 | 120 | 0.237 | 0.811 | 0.536 |
| St. Petersburg | Y = 5.757*K0.532*L0.342 | 0.984 | 210 | 0.078 | 0.283 | 0.044 |
| Lipetsk Region | Y = 0.147*K1.297*L−0.248 | 0.988 | 278 | 0.000 | 0.315 | 0.018 |
| Magadan Region | Y = 0.01*K0.752*L0.608 | 0.952 | 70 | 0.144 | 0.202 | 0.019 |
| Kaluga Region | Y = 0.412*K0.072*L1.024 | 0.993 | 469 | 0.695 | 0.002 | 0.094 |
| Tomsk Region | Y = 1.242*K0.333*L0.657 | 0.995 | 686 | 0.133 | 0.011 | 0.663 |
| Yamalo–Nenets Autonomous Area | Y = 0.001*K1.099*L0.317 | 0.995 | 674 | 0.005 | 0.409 | 0.000 |
| Belgorod Region | Y = 0.656*K−0.163*L1.279 | 0.989 | 320 | 0.499 | 0.003 | 0.506 |
| Krasnoyarsk Territory | Y = 0.363*K0.45*L0.636 | 0.958 | 80 | 0.339 | 0.307 | 0.591 |
| Nizhny Novgorod Region | Y = 0.269*K0.54*L0.541 | 0.995 | 671 | 0.021 | 0.030 | 0.015 |
| Vologda Region | Y = 0.005*K0.152*L1.3 | 0.970 | 112 | 0.740 | 0.085 | 0.041 |
| Rep. of Mordovia | Y = 0.132*K0.442*L0.706 | 0.997 | 1290 | 0.001 | 0.000 | 0.002 |
| Voronezh Region | Y = 0.048*K0.129*L1.135 | 0.981 | 180 | 0.629 | 0.004 | 0.010 |
| Tula Region | Y = 0.036*K1.208*L−0.016 | 0.995 | 747 | 0.001 | 0.950 | 0.000 |
| Moscow Region | Y = 0.033*K0.898*L0.294 | 0.991 | 403 | 0.006 | 0.181 | 0.010 |
| Chuvash Rep. | Y = 0.674*K0.315*L0.708 | 0.990 | 363 | 0.267 | 0.013 | 0.717 |
| Rep. of Bashkortastan | Y = 0.383*K−0.355*L1.501 | 0.985 | 229 | 0.078 | 0.000 | 0.214 |
| Perm Territory | Y = 0.759*K0.184*L0.866 | 0.963 | 91 | 0.746 | 0.180 | 0.817 |
| Tyumen Region | Y = 0.211*K0.656*L0.423 | 0.978 | 158 | 0.047 | 0.263 | 0.190 |
| Q4 | ||||||
| Kemerovo Region | Y = 5.225*K0.097*L0.803 | 0.829 | 17 | 0.845 | 0.216 | 0.467 |
| Trans-Baikal Territory | Y = 1.355*K0.295*L0.66 | 0.974 | 132 | 0.487 | 0.061 | 0.883 |
| Rep. of Altai | Y = 1.513*K0.444*L0.489 | 0.988 | 285 | 0.055 | 0.173 | 0.737 |
| Orenburg Region | Y = 0.476*K−0.11*L1.241 | 0.983 | 208 | 0.744 | 0.024 | 0.506 |
| Altai Territory | Y = 0.0002*K1.386*L0.216 | 0.986 | 241 | 0.026 | 0.417 | 0.048 |
| Smolensk Region | Y = 0.111*K0.103*L1.103 | 0.986 | 247 | 0.733 | 0.010 | 0.014 |
| Stavropol Territory | Y = 0.376*K0.252*L0.821 | 0.983 | 208 | 0.458 | 0.042 | 0.228 |
| Rep. of Karelia | Y = 0.004*K0.378*L1.078 | 0.990 | 362 | 0.072 | 0.002 | 0.000 |
| Kurgan Region | Y = 0.332*K0.664*L0.369 | 0.995 | 678 | 0.045 | 0.165 | 0.276 |
| Nenets Autonomous Area | Y = 41.143*K0.608*L0.051 | 0.958 | 80 | 0.004 | 0.862 | 0.025 |
| Kabardian–Balkar Rep. | Y = 1.017*K0.789*L0.167 | 0.990 | 334 | 0.077 | 0.579 | 0.991 |
| Rep. of Daghestan | Y = 9.519*K0.159*L0.685 | 0.973 | 128 | 0.557 | 0.029 | 0.031 |
| Rep. of Khakassia | Y = 0.009*K0.806*L0.556 | 0.992 | 444 | 0.014 | 0.048 | 0.000 |
| Rep. of Adygeya | Y = 0.254*K0.463*L0.658 | 0.988 | 300 | 0.164 | 0.044 | 0.146 |
| Rep. of Kalmykia | Y = 0.005*K0.399*L1.098 | 0.991 | 384 | 0.013 | 0.000 | 0.000 |
| Rep. of North Ossetia | Y = 198.817*K−0.599*L1.199 | 0.959 | 82 | 0.128 | 0.002 | 0.019 |
| Rep. of Tyva | Y = 4.666*K0.546*L0.293 | 0.983 | 204 | 0.087 | 0.505 | 0.323 |
| Karachaev-Circassian Rep. | Y = 24.887*K−0.113*L0.851 | 0.981 | 180 | 0.595 | 0.001 | 0.006 |
| Chechen Rep. | Y = 0.076*K1.107*L0.012 | 0.988 | 280 | 0.001 | 0.938 | 0.015 |
| Rep. of Ingushetia | Y = 7.744*K0.263*L0.528 | 0.864 | 22 | 0.305 | 0.025 | 0.220 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samoilova, L.; Rodionov, D. Production Function Based on Input–Output and Growth Rate Indicators as a Tool for Assessment of Innovation Climate in Russian Regions. Economies 2022, 10, 297. https://doi.org/10.3390/economies10120297
Samoilova L, Rodionov D. Production Function Based on Input–Output and Growth Rate Indicators as a Tool for Assessment of Innovation Climate in Russian Regions. Economies. 2022; 10(12):297. https://doi.org/10.3390/economies10120297
Chicago/Turabian StyleSamoilova, Liudmila, and Dmitry Rodionov. 2022. "Production Function Based on Input–Output and Growth Rate Indicators as a Tool for Assessment of Innovation Climate in Russian Regions" Economies 10, no. 12: 297. https://doi.org/10.3390/economies10120297
APA StyleSamoilova, L., & Rodionov, D. (2022). Production Function Based on Input–Output and Growth Rate Indicators as a Tool for Assessment of Innovation Climate in Russian Regions. Economies, 10(12), 297. https://doi.org/10.3390/economies10120297






