A High-Resolution Lead-Lag Analysis of US GDP, Employment, and Unemployment 1977–2021: Okun’s Law and the Puzzle of Jobless Recovery
Abstract
:1. Introduction
A Literature and Hypotheses
2. Data
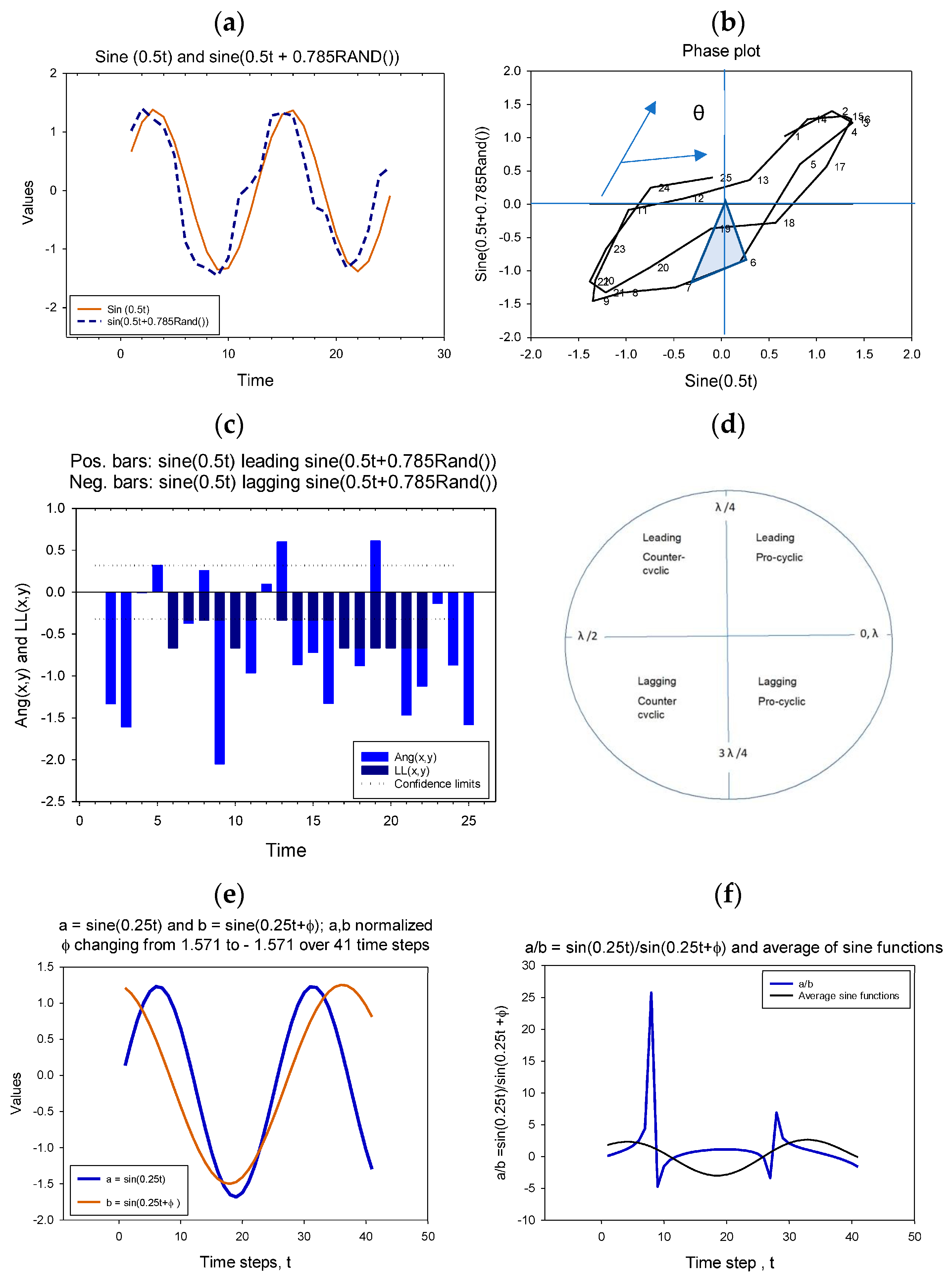
3. Methodology
4. Results
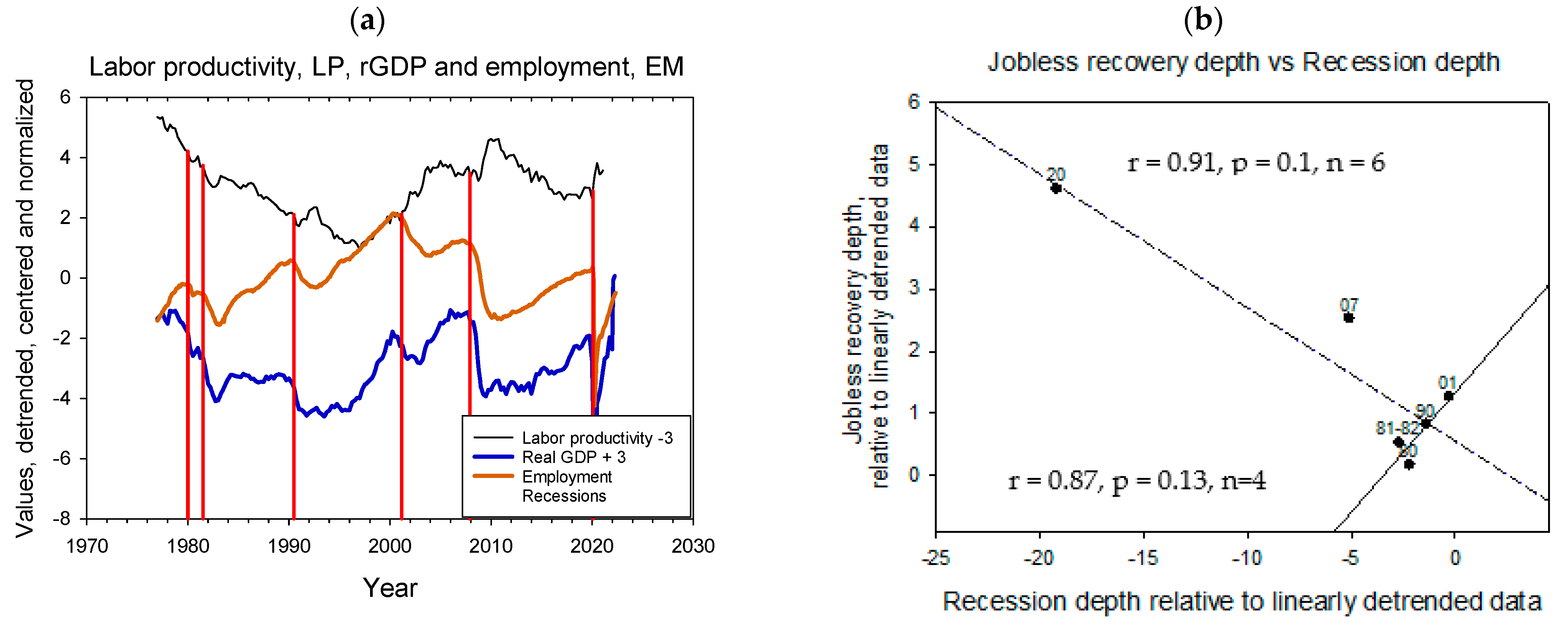
4.1. Data Preparation
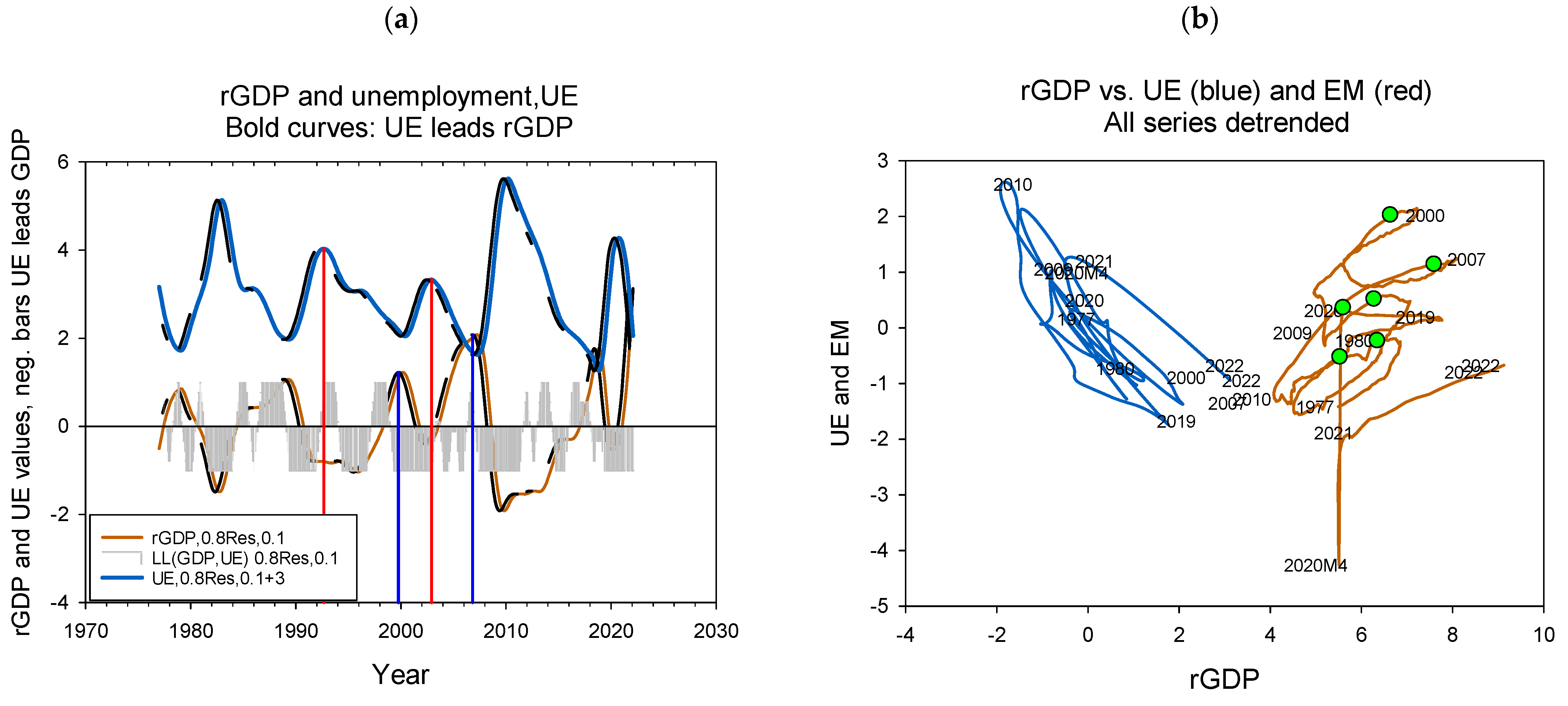
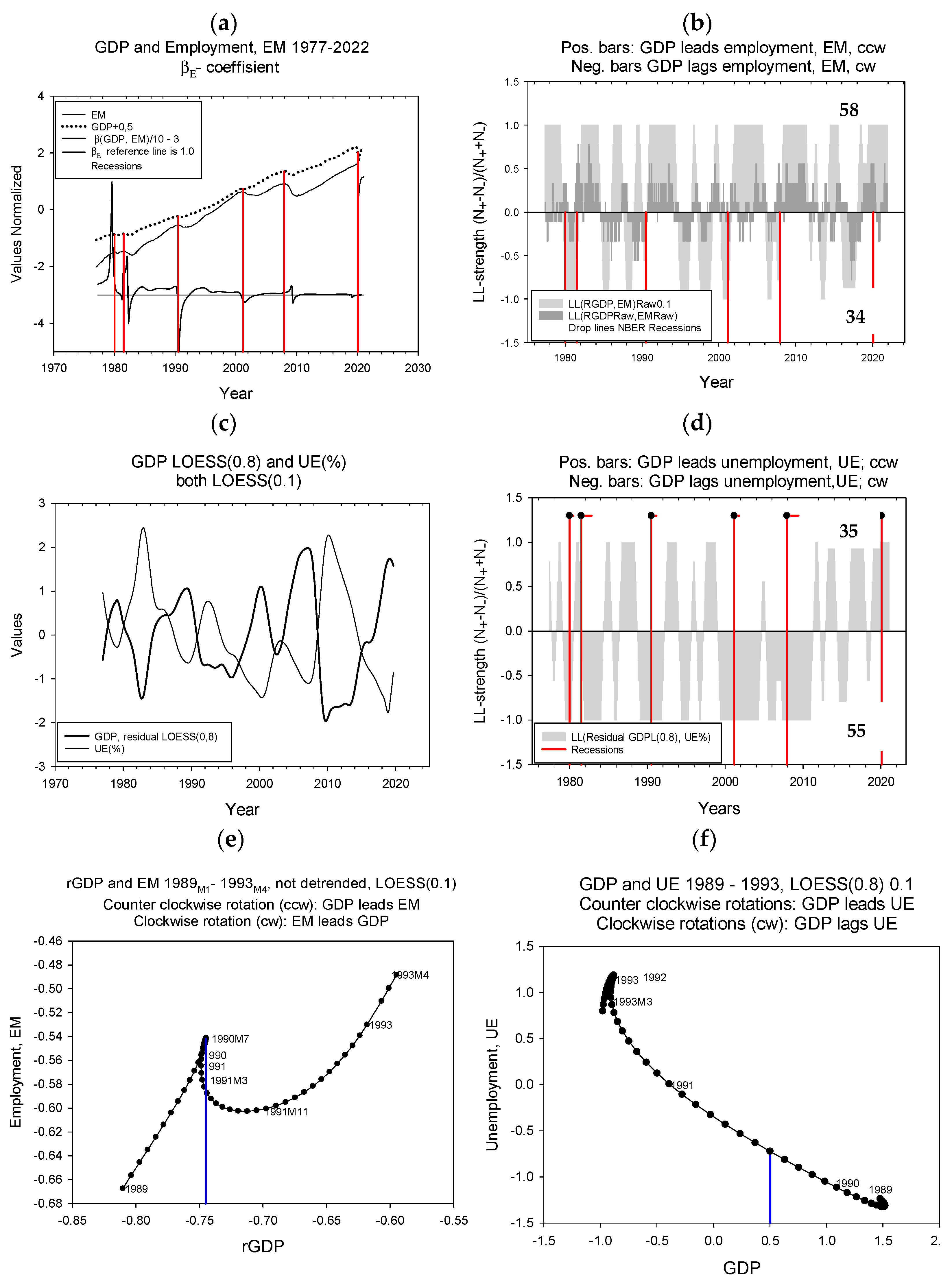
4.2. LL Relations
4.3. The βE Coefficient
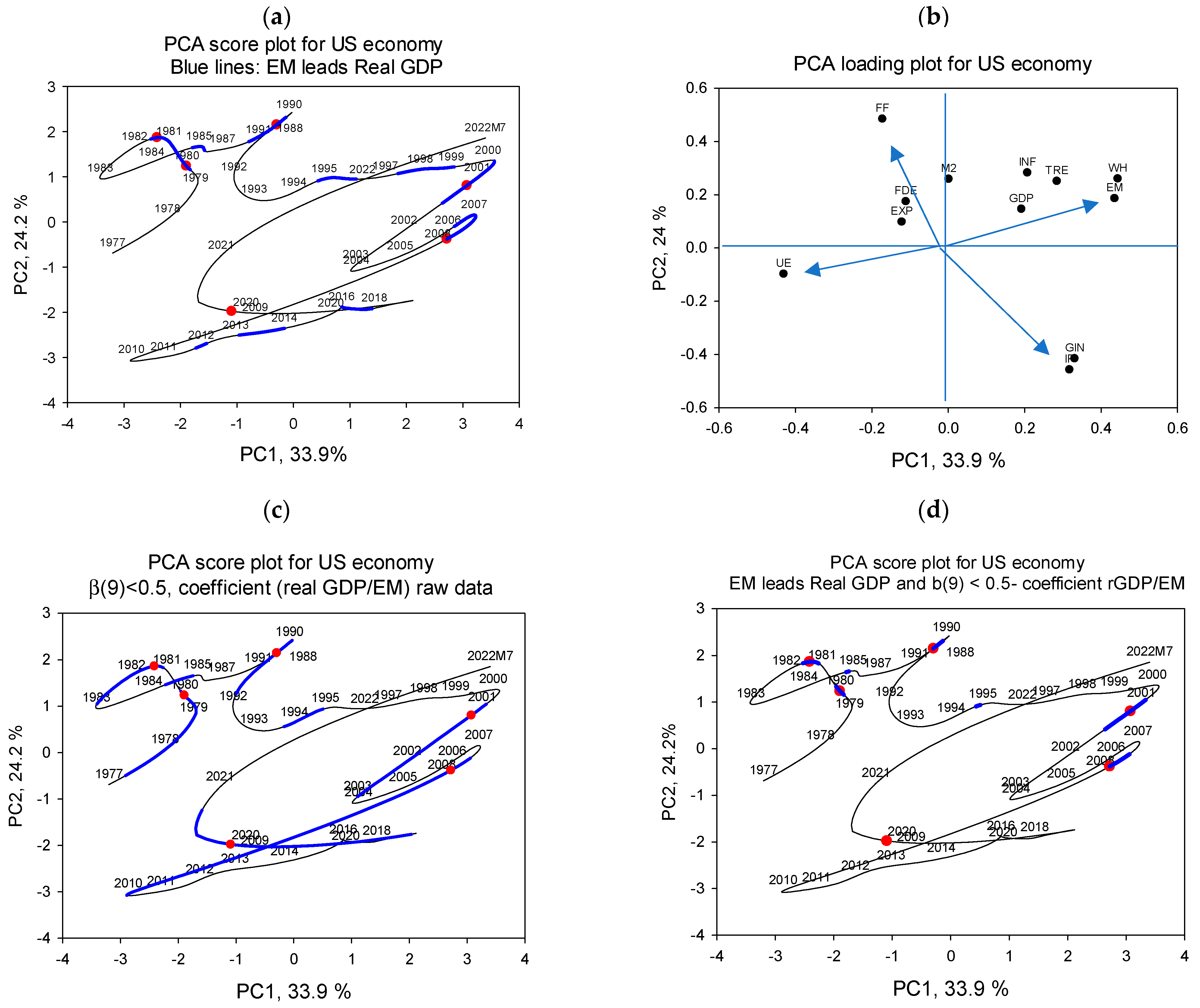
4.4. US Economy Results
4.5. Labor Productivity
5. Discussion
5.1. Lead-Lag Relations
5.2. The βE-Coefficient
5.3. LL-Relations and the βE-Coefficient
5.4. US Economy
5.5. Policy Implications
5.6. Further Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Comparing rGDP to EM and UE
References
- Abel, Andrew, Ben Bernanke, and Robert McNabb. 1998. Macroeconomics. Harlow: Addison-Wesley. [Google Scholar]
- Ahn, Hie Joo, and James D. Hamilton. 2022. Measuring labor-force participation and the incidence and duration of unemployment. Review of Economic Dynamics 44: 1–32. [Google Scholar] [CrossRef]
- Ball, Laurence. 2015. Monetary Policy for a High-Pressure Economy. Policy Futures. Washington: Center on Budget and Policy Priorities, p. 13. [Google Scholar]
- Burns, Arthur F., and Wesley C. Mitchell. 1946. Measuring Business Cycles. New York: National Bureau of Economic Research. [Google Scholar]
- Camacho, Maximo, and Gabriel Perez-Quiros. 2010. Introducing the Euro-Sting: Short-Term Indi-cator of Euro Area Growth. Journal of Applied Econometrics 25: 663–94. [Google Scholar] [CrossRef] [Green Version]
- Capsada-Munsech, Queralt, and Oscar Valiente. 2020. Sub-National Variation of Skill For-mation Regimes: A Comparative Analysis of Skill Mismatch Across 18 European Regions. European Education 52: 166–79. [Google Scholar] [CrossRef]
- Cazes, Sandrine, Sher Verick, and Fares Al Hussami. 2013. Why did unemployment respond so differently to the global financial crisis across countries? Insights from Okun’s Law. IZA Journal of Labor Policy 2: 1–18. [Google Scholar] [CrossRef] [Green Version]
- Donayre, Luiggi, and Irina Panovska. 2021. Recession-specific recoveries: L’s, U’s and everything in between. Economics Letters 209: 110145. [Google Scholar] [CrossRef]
- Elhorst, J. Paul, and Silvia Emili. 2022. A spatial econometric multivariate model of Okun’s law. Regional Science and Urban Economics 93: 103756. [Google Scholar] [CrossRef]
- Galí, Jordi, Frank Smets, and Rafael Wouters. 2012. Slow recoveries: A structural interpretation. Journal of Money, Credit and Banking 44: 9–30. [Google Scholar] [CrossRef] [Green Version]
- Gimbel, Martha E., and Tara M. Sinclair. 2020. Mismatch in Online Job Search. Paper presented at the LERA 2020 Meetings, Virtual, June 13–16; Sa Diego: Labor and Employment Relations Assocciation (LERA). [Google Scholar]
- Hamilton, James D. 2018. Why You Should Never Use the Hodrick-Prescott Filter. Review of Economics and Statistics 100: 831–43. [Google Scholar] [CrossRef]
- Hobbs, Jill E. 2020. Food supply chains during the COVID-19 pandemic. Canadian Journal of Agricultural Economics-Revue Canadienne D Agroeconomie 68: 171–76. [Google Scholar] [CrossRef] [Green Version]
- Krüger, J. Jens. 2021. A Wavelet Evaluation of Some Leading Business Cycle Indicators for the German Economy. Journal of Business Cycle Research 17: 203–319. [Google Scholar] [CrossRef]
- Lazear, Edward P., and James R. Spletzer. 2012. The United States Labor Market: Status quo or a New Normal? The Changing Policy Landscape. Jacson Hole: The Federal Reserve Bank of Kansas City. [Google Scholar]
- Maza, Adolfo. 2022. Regional Differences in Okun’s Law and Explanatory Factors: Some Insights from Europe. Interna-tional Regional Science Review 45: 016001762210823. [Google Scholar] [CrossRef]
- McNown, Robert, and Knut Lehre Seip. 2011. Periods and structural breaks in US economic history 1959–2007: A data driven identification. J. Policy Modelling 33: 169–82. [Google Scholar] [CrossRef]
- Mukoyama, Toshihiko, and Ayşegül Sahin. 2009. Why did the average duration of unemployment become so much longer? Journal of Monetary Economics 56: 200–9. [Google Scholar] [CrossRef] [Green Version]
- Obst, Thomas. 2020. Dynamic version of Okun’s law in the EU15 countries—The role of delays in the unemployment-output nexus. Scottish Journal of Political Economy 69: 225–41. [Google Scholar] [CrossRef]
- Seip, Knut L., and Hui Wang. 2022. The North Atlantic Oscillations: Lead–Lag Relations for the NAO, the AMO, and the AMOC—A High-Resolution Lead–Lag Analysis. Climate 10: 63. [Google Scholar] [CrossRef]
- Seip, Knut L., Øyvind Grøn, and Hui Wang. 2018. Carbon dioxide precedes temperature change during short-term pauses in multi-millennial palaeoclimate records. Palaeogeography Palaeoclimatology Palaeoecology 506: 101–11. [Google Scholar] [CrossRef]
- Seip, Knut L., Yunus Yilmaz, and Michael Schroder. 2019. Comparing Sentiment- and Behavioral-Based Leading Indexes for Industrial Production: When Does Each Fail? Economies 7: 104. [Google Scholar] [CrossRef] [Green Version]
- Seip, Knut L., and Øyvind Grøn. 2019. Atmospheric and Ocean Dynamics May Explain Cycles in Oceanic Oscillations. Climate 7: 77. [Google Scholar] [CrossRef] [Green Version]
- Seip, Knut Lehre, and Renzo Orsi. 2022. Effects of tax changes on GDP and underground economy: Italy 1982 to 2006. submitted. [Google Scholar]
- Søgner, Leopold. 2001. Okun’s law. Does the Austrian unemployment-GDP relationship exhibit structural breaks? Empirical Economics 26: 553–64. [Google Scholar] [CrossRef] [Green Version]
- Sugihara, George, Robert May, Hao Ye, Chih-hao Hsieh, Ethan Deyle, Michael Fogarty, and Stephan Munch. 2012. Detecting Causality in Complex Ecosystems. Science 338: 496–500. [Google Scholar] [CrossRef]
- Taylor, John B., and John C. Williams. 2010. Simple and Robust Rules for Monetary Policy. Working Papers. San Francisco: Federal Reserve Bank of San Francisco. [Google Scholar]
- Vaubel, Roland. 2008. The political economy of labor market regulation by the European Union. Review of International Organizations 3: 435–65. [Google Scholar] [CrossRef]
- Yellen, Janet L. 1991. Comments and discussion. Brookings Papers on Economic Activity 2: 127–33. [Google Scholar]
- Ziegenbein, Alexander. 2021. Macroeconomic shocks and Okun’s Law. Economic Letters 202: 1–4. [Google Scholar] [CrossRef]
| Beginning | End | Duration | GDP Decline (Peak to Trough) | EM Leads GDP before Recession (1) | bE (GDP,EM) Coefficient Peaks | bLP (LP,t) before Rec. (2) | Jobless Depth (3) | Jobless Duration (4) |
|---|---|---|---|---|---|---|---|---|
| Months | Relative Values | 0–12 Months | <0.5 | 0–12 Months | Relative Values | Months | ||
| Jan 1980 | July 1980 | 6 | −2.2 | 3.00 | −0.30 | −0.041 | −0.18 | 14 |
| July 1981 | Nov 1982 | 16 | −2.7 | 12.00 | 0.18 | −0.022 | −0.53 | 18 |
| July 1990 | March 1991 | 8 | −1.4 | 5.00 | −0.16 | 0.000 | −0.83 | 12 |
| March 2001 | Nov 2001 | 8 | −0.3 | 11.00 | −0.64 | −0.010 | −1.27 | 68 (5) |
| Dec 2007 | June 2009 | 18 | −5.1 | 9.00 | 0.48 | 0.019 | −2.54 | 144 (5) |
| Feb 2020 | April 2020 | 2 | −19.2 | 1.00 | −0.1 | −0.015 | −4.62 | 12 |
| Average | 9.67 ± 5.40 | −5.15 ± 1.79 | 6.83 ± 3.87 | −0.25 ± 0.31 | −0.012 ± 0.020 | −1.66 ± 0.91 | 44.67 ± 58.83 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seip, K.L.; Zhang, D. A High-Resolution Lead-Lag Analysis of US GDP, Employment, and Unemployment 1977–2021: Okun’s Law and the Puzzle of Jobless Recovery. Economies 2022, 10, 260. https://doi.org/10.3390/economies10100260
Seip KL, Zhang D. A High-Resolution Lead-Lag Analysis of US GDP, Employment, and Unemployment 1977–2021: Okun’s Law and the Puzzle of Jobless Recovery. Economies. 2022; 10(10):260. https://doi.org/10.3390/economies10100260
Chicago/Turabian StyleSeip, Knut Lehre, and Dan Zhang. 2022. "A High-Resolution Lead-Lag Analysis of US GDP, Employment, and Unemployment 1977–2021: Okun’s Law and the Puzzle of Jobless Recovery" Economies 10, no. 10: 260. https://doi.org/10.3390/economies10100260
APA StyleSeip, K. L., & Zhang, D. (2022). A High-Resolution Lead-Lag Analysis of US GDP, Employment, and Unemployment 1977–2021: Okun’s Law and the Puzzle of Jobless Recovery. Economies, 10(10), 260. https://doi.org/10.3390/economies10100260








