Abstract
A low-cost 1 kHz–400 kHz operating frequency fully-active electrode bioimpedance measurement module, based on Howland current source, is presented in this paper. It includes a buffered positive feedback Howland current source, implemented with operational amplifiers, as well as an AD8421 instrumentation amplifier, for the differential voltage measurements. Each active electrode module can be connected to others, assembling a wearable active electrode module array. From this array, 2 electrodes can be selected to be driven from a THS413 fully differential amplifier, activating a mirrored Howland current source. This work performs a complete circuit analysis, verified with MATLAB and SPICE simulations of the current source’s transconductance and output impedance over the frequency range between 1 kHz and 1 MHz. Resistors’ tolerances, possible mismatches, and the operational amplifiers’ non-idealities are considered in both the analysis and simulations. A comparison study between four selected operational amplifiers (ADA4622, OPA2210, AD8034, and AD8672) is additionally performed. The module is also hardware-implemented and tested in the lab for all four operational amplifiers and the transconductance is measured for load resistors of 150 Ω, 660 Ω, and 1200 Ω. Measurements showed that, using the AD8034 operational amplifier, the current source’s transconductance remains constant for frequencies up to 400 KHz for a 150 Ω load and 250 kHz for a 1200 Ω load, while lower performance is achieved with the other 3 operational amplifiers. Finally, transient simulations and measurements are performed at the AD8421 output for bipolar measurements on the 3 aforementioned load resistor values.
1. Introduction
Bioimpedance measurements are widely used in many applications to provide quantitative or qualitative information about the human vital signs [1,2,3,4,5,6]. Such bio-markers include heart rate (HR), respiration rate (RR), blood pressure (BP), pulse transit time (PPT), and blood glucose levels. These can be acquired either by simple bioimpedance measurement patterns, such as bipolar or tetrapolar measurement, or more complex measurement techniques, such as Electrical Impedance Tomography (EIT) or Electrical Impedance Spectroscopy (EIS) [7,8]. The latter are also very useful for monitoring time or frequency dependent conditions, such as real-time ventilation, brain hemorrhage, or malignant tumors. Furthermore, bioimpedance measurement techniques are safe, radiation-free, and low-cost [7]. In most cases, they are also non-invasive, making the measurement process much simpler [7].
The essential hardware needed to take bioimpedance measurements usually includes an analog front-end and, in many cases, a digital control for the waveform generation and data acquisition [9]. The analog front-end is typically composed of a current source, the electrodes attached on the subject under test (SUT), a filter, and an instrumentation amplifier [10]. This common configuration often varies between implemented systems. For instance, there are readout circuit architectures that employ multiple gain and filter stages for the voltage acquisition in order to increase Common-Mode Rejection Ratio () and decrease the signal noise [11,12,13].
The current sources, often called voltage controlled current sources, (VCCS) can be categorized as voltage-mode and current-mode ones [14]. The voltage-mode approach is characterized by the current generation through the voltage in one or more of the active circuit’s nodes. Such topologies include the well-known Howland current pump (HCP) [14,15,16,17,18,19], the Tietze topology [20], the load-in-the-loop topology [21], and differential-difference topologies [22,23,24]. Current-mode approach makes use of operational transconductance amplifiers (OTAs) [7,11,25,26] or current conveyors (CCII) [15,27,28] for the current excitation. In all cases, the load driven by the output current can be either grounded or floating.
The implementation of HCPs is usually simple and can be done with commercially available active components (operational amplifiers-Opamps), while the implementation of differential-difference and current-mode VCCS topologies necessitates transistor-level fabrication. Thus, although the latter topologies may offer better performance in terms of the main VCCS evaluation characteristics (large and stable transconductance, large output impedance, large bandwidth, and low Total Harmonic Distortion-), the availability of discrete active components, makes the HCPs preferable for the implementation of prototype bioimpedance measurement circuits [14].
The basic HCP topology was introduced in 1963 [22]. However, many improvements have been proposed and applied since then. Most of them present topologies based on the Enhanced HCP [29], with ground or floating loads and single-ended or mirrored topologies [15,18,30,31] (see Figure 1). Further improvements, such as buffered positive feedback [32], as in Figure 1, lead-lag compensation [33,34,35], HCP followed by load-in-the-loop topology stage [34], and bridge topologies [36].
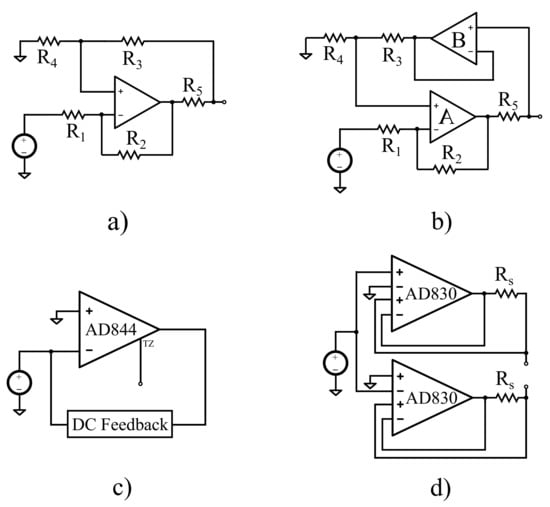
Figure 1.
Discrete component current source configurations. (a) The Enhanced HCP (single-ended). (b) The modified buffered HCP used in this work (single-ended). (c) Current Conveyor based on the AD844 (Bragos CCII). (d) Current Source based on the AD830 differential difference-amplifier (Analog Devices, mirrored).
The HCP’s bandwidth often suffers from degradation at even medium frequencies due to the components’ and cables’ parasitic effects. Specifically, despite the fact that most of the proposed topologies offer wide-band current excitation, in practice, their performance is critically limited by the parasitic capacitances of the electrodes’ lead wires. Some techniques have been applied to eliminate their effect. These include the usage of triaxial or shielded cables with buffers [37,38], the usage of negative impedance circuits (usually implemented with generalized impedance converters-GICs) [38,39,40], or the usage of active electrodes, where either the VCCS, the 1st stage of the voltage readout, or both, are implemented very close to the electrode [11,38,41,42,43]. The first solution is expensive, especially for multi-channel systems, and does not compensate for the buffers’ input capacitances [38]. The second one cancels the VCCS’ output capacitances; however, it might lead to instability due to overcompensation [38]. The active electrode has the advantage of avoiding the cables’ and multiplexers’ (in multi-channel systems) stray capacitances. The use of active electrodes apart from the VCCS’ actual bandwidth, also improves the performance of the voltage readout part, since possible channel impedance imbalances before the 1st readout stage are critically decreased [42]. However, this technique is expensive, since it requires numerous power-consuming active components placed in a small area near each electrode [38].
The mentioned active electrode’s drawbacks still make their design process somewhat challenging, despite their potential advantages. Actually, only partially-active electrode configurations have been implemented for multi-channel bioimpedance measurement systems (such as EIT) that exclusively use commercially available active components [42,43]. The partially-active electrode systems implement only the voltage readout stage near each electrode, while the VCCS is implemented on the system’s core. This leads to the development of stray capacitances on the VCCS output, due to the cables and the multiplexer switches, drastically reducing the actual advantages of the active electrodes. Fully-active electrodes, which include both the VCCS and the 1st voltage readout stage, have actually been designed and implemented only at integrated chip level [11,41,44]. However, they require transistor level application-specific integrated circuit (ASIC) fabrication, making them costly and their applicability still limited. For the passive, partially-active, and fully-active electrode measurement configuration schematics, see Figure 2.
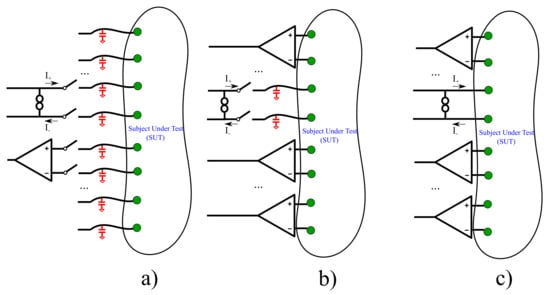
Figure 2.
Simplified schematics of three bioimpedance measurement configurations. (a) Passive electrode configuration. (b) Partially-active electrode configuration. (c) Fully-active electrode configuration (this work). The cables’/switches’ parasitic capacitances are indicated with red color.
In this paper, we attempt to design and implement a low-cost, wearable fully-active electrode bioimpedance measurement module with commercially available components. Each module includes an improved HCP for the generation of the current excitation, a passive electrode connector, an instrumentation amplifier for signal readout and all appropriate signal and power connections between the module and the whole system. At each time, a fully-differential Opamp (which is not included on the modules) generates a differential voltage signal which is provided as an input to the VCCS of two selected modules. In this way, the two selected HCPs act as mirrored ones, while differential voltages from two selected channels are measured from the instrumentation amplifier. We note that voltage measurements can either be bipolar or tetrapolar [45,46]. The mirrored HCP is numerically analyzed, while both HCPs and the voltage readout were simulated in LT SPICE. Furthermore, the proposed system’s modules were implemented in printed circuit boards (PCBs). Measurements over 4 different Opamps’ HCPs configurations showed stable transconductance (less than reduction) up to 400 kHz for a 150 load and up to 250 kHz for a 1200 load. Moreover, transient measurements at the instrumentation amplifier’s output showed low impedance measurement error (0.11–2.36%) at low frequencies, while special account has to be taken for the instrumentation amplifiers’ gain degradation over frequency.
Since it acts as an active electrode, this module is wearable, eliminating stray capacitance effects that significantly degrade the VCCS output impedance. It also reduces channel impedance imbalance that causes common signals at the instrumentation amplifier part. Furthermore, it can be applied for EIT/EIS, allowing current pattern selection and/or multifrequency current injections for frequency-difference EIT.
The rest of this paper is organized as follows. Section 2 presents the proposed active-electrode bioimpedance measurement module and its function, along with the whole system circuitry. In Section 3, an extensive numerical analysis is performed to estimate the transconductance and the output impedance (magnitudes) of the mirrored HCPs, taking into account some Opamps’ non-idealities, their behavior over frequency between 1 kHz and 1 MHz, and resistors’ mismatches. In Section 4, an extensive LT SPICE simulation is performed to estimate the HCP’s and the voltage readout performance. Furthemore, in Section 5, the measurement results and comparisons over 4 Opamp topologies are presented. Finally, Section 6 concludes this work.
2. The Proposed Module
This work proposes a fully active electrode module, as well as a proper configuration and connectivity for bioimpedance measurement techniques, such as EIT and EIS. Briefly, each individual active electrode module consists of a Howland current pump (HCP) voltage-to-current converter source (VCCS) circuit, which is directly connected to the electrode, as shown in Figure 3, and an instrumentation amplifier stage.
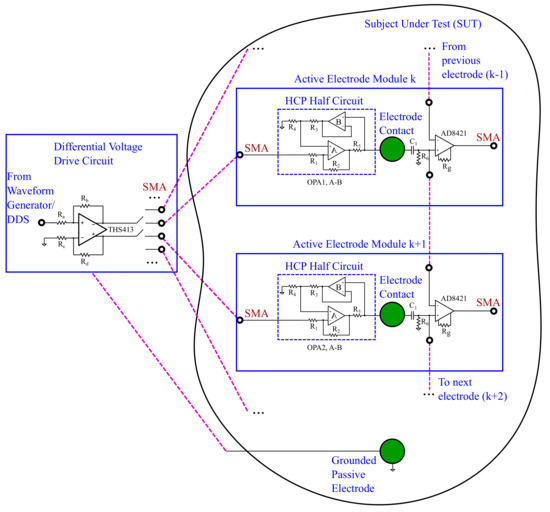
Figure 3.
Brief schematic of the proposed active electrode bioimpedance module and its connectivity.
The implemented VCCS topology is based on the improved HCP [15,18]. The improved HCP topology is further modified by adding a buffer (B) on the positive feedback path [29,32,47]. Ideally, a very large output impedance can be achieved by balancing the resistors – (Figure 3). However, the actual output impedance is decreased due to the resistors’ values imprecision, the Opamps’ non-idealities, and the parasitic impedances presented between the HCP’s output node and the electrode contact. It has been shown in Reference [32] that adding (B) decreases the output impedance’s dependence on the resistors’ tolerances, as well as the bias current, on the positive feedback path. In addition, it increases the output impedance and the total HCP’s slew rate. Furthemore, in the active electrode module, the electrode contact is very close to the HCP’s output node, which minimizes the parasitic capacitances caused by the cables in passive configurations [11,42,43].
Each electrode is also connected with an AD8421 instrumentation amplifier through a DC-cutoff 1st-order high pass filter (). The AD8421 has a sufficiently high input impedance (up to 30 G pF for the differential signal) and , which drops from 120 dB at 1 kHz to 85 dB at 100 kHz, for a selected gain of V/V and no-source imbalance [37,48]. With a 1 k source imbalance between the two input channels, the corresponding drops from 85 dB to 47 dB at the corresponding frequencies for this gain. However, since the instrumentation amplifier is embedded on the active electrode module, these imbalances are minimized, preventing the AD8421 from dropping. Furthermore, the 1st order DC-cutoff filter’s bias current return resistor value can be selected at a range of about 10 times the VCCS’ output impedance at low frequencies (>5 M), in order to prevent degradation. Hence, it will not actually affect the VCCS’ bandwidth. Despite the fact that this actually introduces a maximum output impedance limit on the electrode node, it can be proved beneficial for multi-channel measurements at frequencies more than 10 kHz, compared to the passive-electrode configuration. This is because, in the latter case, a multiplexer is placed between the electrode and the instrumentation amplifier, introducing a parasitic capacitance to ground. Its effect, in addition to the cable’s parasitics is much more significant beyond this frequency. The capacitor’s value must be accordingly adapted, so the filter’s cutoff frequency is kept far from the application’s frequency range. The instrumentation amplifier’s output can be connected to a voltage measurement analog front-end for further processing before the data acquisition [13].
The utilization of an Opamp buffer, instead of the AD8421 instrumentation amplifier, could also be considered as the 1st stage for active electrode signal readout. However, a recent study [41] has demonstrated that this approach leads to noticeable higher noise levels compared to an active stage providing amplification, such as an instrumentation amplifier topology, especially when potentials are measured from neighboring electrodes.
Each active electrode module is connected to the previous and the next one via a short (3 cm) FPC cable. This allows the corresponding AD8421 to take differential potential measurements from both the electrode on the module it is embedded on and the electrode on the previous active-electrode module (see Figure 3). Furthermore, a THS413 fully-differential voltage amplifier is used to drive two 180-degrees phase shifted sinusoidal input voltage signals to two selected active electrode modules. This activates the corresponding HCPs to function in mirrored topology mode, which theoretically doubles the VCCS’ output impedance [18,49]. The THS413 is built on an individual PCB board (not on the active electrode modules), which is connected to the active electrode modules via equal-length SMA cables. This prevents undesirable phase mismatches between the differential voltage inputs on the HCPs. Each time, the THS413 can drive a pair of active electrodes, which can be selected through low parasitic capacitance and resistance switches (Figure 3). This configuration allows the proposed module’s applicability to simple bioimpedance measurements, such as bipolar (current injection and voltage measurement on the same electrode pair) and tetrapolar measurement (current injection and voltage measurement on different electrode pairs), as well as more complex techniques, such as those used in EIT, where an array of multiple electrodes is needed.
3. Circuit Analysis
In this section, we perform a numerical circuit analysis of the mirrored HCP (the topology of which is shown in Figure 3), using the MATLAB software, to derive its transconductance and output impedance. The resistors’ tolerances, which cause undesirable mismatches between the HCP half-circuits, as well as each Opamp’s input impedance magnitude , output impedance magnitude , and open-loop gain, are taken into consideration as a function of the sinusoidal input signal’s frequency f.
To this end, we replace each Opamp with its equivalent circuit in the mirrored-HCP topology, deriving the schematics shown in Figure 4. Specifically, Figure 4a shows the mirrored-HCP equivalent to estimate the transconductance, while Figure 4b shows the configuration to estimate the output impedance. We note that, despite the circuit’s symmetry, we perform the analysis in the whole circuitry instead of the half-HCP, in order to analyze the effect of resistors’ mismatches.
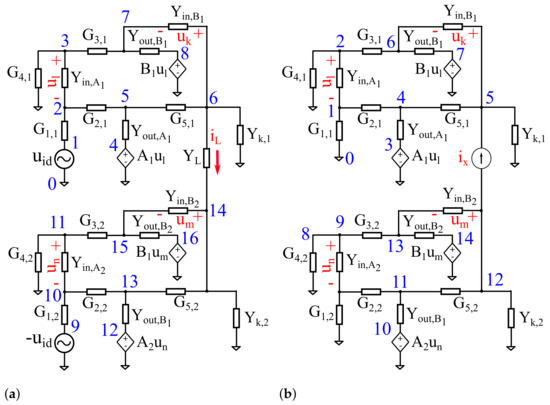
Figure 4.
The mirrored HCP equivalent circuit for (a) the transconductance calculation, (b) the calculation. indicates the parallel combination of and , for .
For the circuit analysis, we set and as the upper half-HCP’s Opamps’ A and B open-loop gains, respectively (see Figure 3), and and as the down half-HCP’s corresponding ones. Furthermore we consider and as the corresponding input and output conductivities of the Opamps, for and , as set above. In addition, we assume that
for , which is the input conductivity magnitude of the 1st-order high pass filter. For the rest of the resistors, we assume , for and . In addition, we set as the load’s conductivity magnitude.
The typical HCP analysis imposes that the resistor (i.e., conductivity) values on each half-circuit should match, such as and . However, since the load is floating, the DC voltage values at nodes 6 and 14 (Figure 4a) might get very high, often near the Opamps’ power supply. This actually could lead the Opamps to saturate and as a consequence, the output current to clip. To avoid this effect in mirrored topologies, Common-Mode feedback configurations have been proposed [7,26]. Nonetheless, this requires additive active components, which is impractical in the case of a fully-active electrode discrete-element configuration. A possible solution, is to add a large-value resistor in parallel to on each half-circuit to set the necessary DC voltage reference for each Opamp A. Despite the fact that this violates the desired balance between the resistors, numerical analysis and simulations show that this affects only the low-frequency output impedance of the HCP. As frequency increases, this violation’s effect disappears, without any consequence to the HCP’s bandwidth. Furthermore, as already mentioned, the buffer B eliminates the effect of the resistors’ imbalances at both the output impedance and the transconductance. However, the usage of resistors of a tolerance of or lower is strongly recommended, in order to avoid mismatches between the upper and the down half-HCP, something that could lead to distortion of the output current. Apart from avoiding saturation, fixing the output nodes’ DC voltage near ground, maximizes the output voltage swing. This allows larger current amplitudes, always in the safety limits, that lead to increased voltage . We note that a high voltage is crucial for EIT applications. Finally, by adding a Common Mode Feedback in a future work, the presence of will not be necessary further.
Taking into consideration the above, the resistors’ and capacitor’s values were selected as shown in Table 1. All the resistor’s tolerances were selected at , while the capacitors’ tolerance is selected at . To estimate the transconductance, numerical computations were performed for 3 different load values: 150 , 660 , and 1200 , that fall within the range of biomedical application interest impedances [7,11].

Table 1.
Selected nominal values for the resistors and capacitors of the mirrored-HCP. .
According to the equivalent, shown in Figure 4a, the following equations are derived from modified nodal analysis in matrix form
where
is the nodes’ potentials vector as numbered in Figure 4a, and
is the vector which denotes the input signals.
The HCP’s transconductance is derived from the following expression
From modified nodal analysis at the equivalent circuit, shown in Figure 4b, the following equation system is derived:
where
is the nodes’ potentials vector as numbered in Figure 4b, and
is the vector which denotes the input signals.
The HCP’s output impedance is derived from the following expression:
Four high-performance Opamps were considered for the numerical analysis: ADA4622, AD8034, AD8672 (Analog Devices), and OPA2210 (Texas Instruments). These Opamps are characterized by very high open-loop gain (at low frequencies), very high input impedance, and low output impedance. They also have very low input bias current and high bandwidth and slew rates of V/s, 80 V/s, V/s, and 4 V/s, respectively, according to the corresponding manufacturers. All these characteristics are very desirable when selecting an Opamp for HCP topologies [18].
For the numerical analysis we assume , , and . However, for the resistors and capacitors, we consider the mismatches, such as , for and . The analysis is performed over the frequency domain, at the range of 1kHz-1MHz, with 10 steps per decade. A number of runs were performed to numerically solve (2) and (9). At each run, the components’ values were randomized, using the mean values shown in Table 1 and according to the following MATLAB command
(accordingly for the capacitors). Furthermore, numerical approximations of the Opamps’ open-loop gains, input and output impedances were derived for each frequency according to the values given from the corresponding manufacturers (shown in Figure 5). We note that, in this numerical analysis, only the magnitude of each metric is considered.
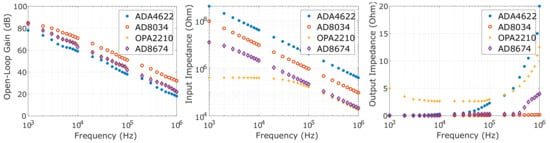
Figure 5.
Numerical approximations of the open loop gain (left), differential input impedance (center), and output impedance (right) of the ADA4622, AD8034, OPA2210, and AD8672 Opamps (based on Analog Devices and Texas Instruments).
The estimated transconductances of the mirrored-HCP per each Opamp, frequency, and load are demonstrated in Figure 6, Figure 7, Figure 8 and Figure 9. In addition, the estimated output impedances for each Opamp and frequency are presented in Figure 10. As observed, the best expected performance is achieved with the AD8034 Opamp, where the expected transconductance is reduced by of its maximum value (S) at 400 kHz, 360 kHz, and 320 kHz approximately (for the 150 , 660 , and 1200 load values, respectively). Furthermore, for the AD8034 configuration, the maximum output impedance varies between 2.3 M and 5.16 M ( resistor tolerance) at kHz and is expected to drop to approximately 1.35 M at 100 kHz and 250 k at 1 MHz. We note that this particular Opamp is characterized by the highest open-loop gain and a relatively high input impedance over the frequency domain (Figure 5). The HCP’s transconductance when using the other 3 Opamps fairly drops behind the region of 100 KHz. Furthermore, despite the fact that the maximum output impedance ranges between the same values as in the AD8034 case, it begins to drop from much lower frequencies. Moreover, the load increase from 150 to 1200 leads to a slight reduction of the transconductances values above 100 kHz for all Opamps cases.
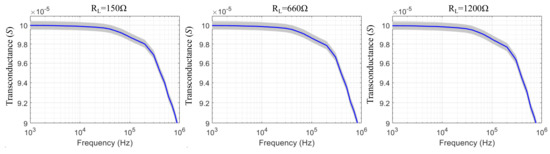
Figure 6.
Calculated transconductance values of the mirrored-HCP for the ADA4622 Opamp and three resistive load values. The blue line indicates the transconductance when all passive components have their nominal values, while the grey region indicates the effect of their tolerances ( for the resistors, for the capacitors).
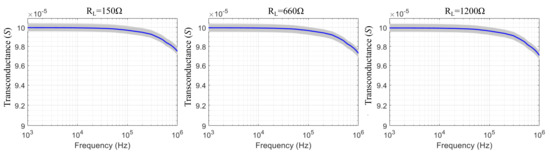
Figure 7.
Calculated transconductance values of the mirrored-HCP for the AD8034 Opamp and three resistive load values. The blue line indicates the transconductance when all passive components have their nominal values, while the grey region indicates the effect of their tolerances ( for the resistors, for the capacitors).
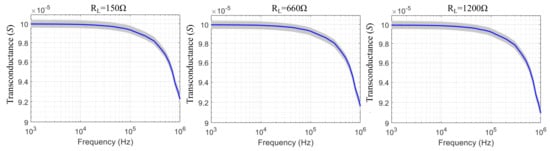
Figure 8.
Calculated transconductance values of the mirrored-HCP for the OPA2210 Opamp and three resistive load values. The blue line indicates the transconductance when all passive components have their nominal values, while the grey region indicates the effect of their tolerances ( for the resistors, for the capacitors).
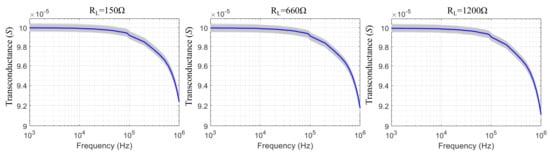
Figure 9.
Calculated transconductance values of the mirrored-HCP for the AD8672 Opamp and three resistive load values. The blue line indicates the transconductance when all passive components have their nominal values, while the grey region indicates the effect of their tolerances ( for the resistors, for the capacitors).
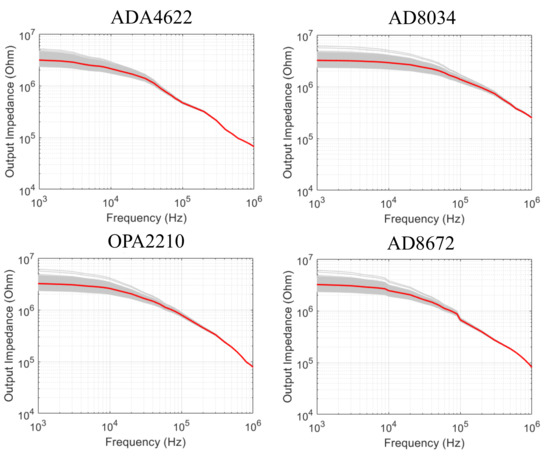
Figure 10.
Calculated output impedance values of the mirrored-HCP for the ADA4622, AD8034, OPA2210, and AD8672 Opamps. The read line indicates the transconductance when all passive components have their nominal values, while the grey region indicates the effect of their tolerances ( for the resistors, for the capacitors).
4. SPICE Simulations
In addition to the previous numerical HCP circuit’s analysis, a number of LT SPICE simulations have been performed on the whole bioimpedance module circuitry. The simulations examine the HCP’s transconductance for each of the four Opamps and for 150 , 660 , and 1200 , respectively, as in the numerical analysis. The output impedance’s magnitude and phase is also simulated for each Opamp configuration. Each AC simulation was performed for a number of cases for resistors’ tolerance of (Monte-Carlo AC simulation), in the range between 1 kHz and 1 MHz (100 points per decade). We note that, in both the transconductance and output impedance simulations, apart from the mirrored HCP, the 1st-order high-pass filter and the AD8421 instrumentation amplifier were considered.
The transconductance SPICE simulation results for all the test cases are shown in Figure 11, Figure 12, Figure 13 and Figure 14. A comparison between the different test cases demonstrates that the AD8034 Opamp-configuration shows an almost constant transconductance ( A/V) magnitude over a wide frequency range, up to 1 MHz. In addition, the transconductance phase shows a slight decrease, from 180 to 176.5 at 1 MHz, for a 150 load, and to 175 at 1 MHz for a 1200 load (for nominal passive components’ values). The other 3 Opamp configurations simulations show a less constant transconductance, as well as slightly more transconductance sensitivity to the load resistance. Despite the fact that the SPICE simulation results seem more optimistic than these obtained from the numerical analysis in the previous section (in terms of the magnitude response), they seem to agree at the point that AD8034 performs better in a wider frequency range.
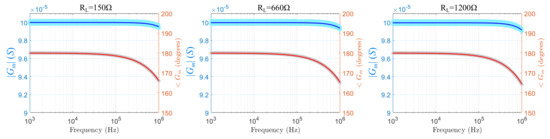
Figure 11.
Simulated transconductance magnitude and phase values of the mirrored-HCP for the ADA4622 Opamp and three resistive load values at LT SPICE. The light-colored regions indicate the effect of the passive components’ tolerances ( for the resistors, for the capacitors).
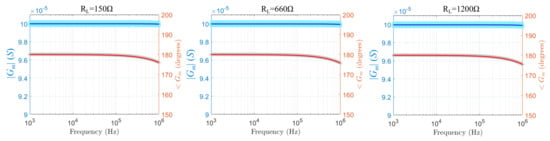
Figure 12.
Simulated transconductance magnitude and phase values of the mirrored-HCP for the AD8034 Opamp and three resistive load values at LT SPICE. The light-colored regions indicate the effect of the passive components’ tolerances ( for the resistors, for the capacitors).
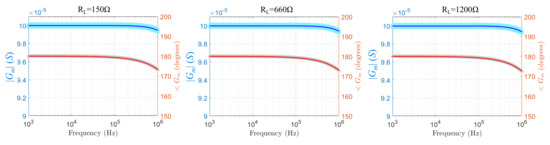
Figure 13.
Simulated transconductance magnitude and phase values of the mirrored-HCP for the OPA2210 Opamp and three resistive load values at LT SPICE. The light-colored regions indicate the effect of the passive components’ tolerances ( for the resistors, for the capacitors).
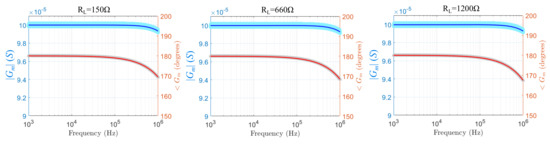
Figure 14.
Simulated transconductance magnitude and phase values of the mirrored-HCP for the AD8672 Opamp and three resistive load values at LT SPICE. The light-colored regions indicate the effect of the passive components’ tolerances ( for the resistors, for the capacitors).
The output impedance SPICE simulation results in Figure 15 show that, with all the 4 Opamp configurations, the mirrored HCP’s output impedance at 1 KHz achieves a magnitude value of 3 M and a phase near zero degrees. However, the AD8034 case achieves the widest frequency range; at 100 kHz, it is more than 1 M, and, at 1 MHz, it drops to 100 k. In addition, the phase also drops slower to than in the other Opamps configurations. The other 3 Opamps configurations show larger drop rates after 10 kHz, with the OPA2210 showing somewhat better performance than the ADA4622 and AD8672. These results overall are in agreement with the numerical analysis performed and indicate that the mirrored-HCP with AD8034 is expected to properly function over a wide frequency range without significant current loss due the the output impedance, at loads within the biompedances’ measurement range.
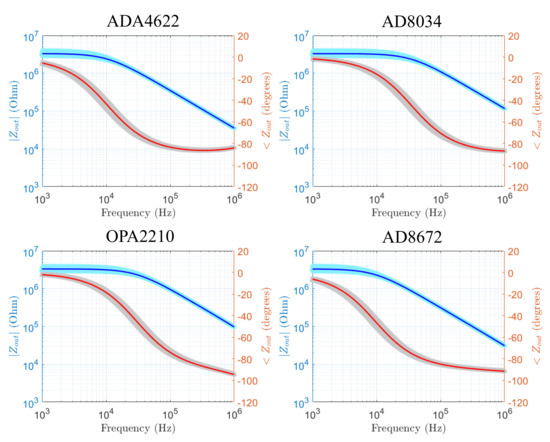
Figure 15.
Simulated output impedance magnitude and phase values of the mirrored-HCP for the ADA4622, AD8034, OPA2210, and AD8672 Opamps. The light-colored regions indicate the effect of the passive components’ tolerances ( for the resistors, for the capacitors).
The MATLAB and SPICE simulation results for the output impedance are quantitatively compared with prior works on HCPs, as well as CCII topologies, in Table 2. As mentioned, the selection of the Opamp (for HCP topologies), the stray capacitances, and the resistors’ tolerance have significant role in the output impedance value while frequency increases. Hence, apart from the topology used, the Opamp selection and the resistors’ tolerance are also mentioned. As observed, the proposed module overall achieves larger output impedance values compared to the cited works, especially at larger frequencies. We note that, except the AD818 case in Reference [32], in the other cases, the effect of stray capacitances has either not been considered or not mentioned as to whether it had been considered. At the same time, the stray capacitances in our module are eliminated due to the active electrode design.

Table 2.
Comparison of implemented discrete-component VCCS output impedances. Ranges denote possible differences between simulated and measured values, and/or variations, due to the resistors’ tolerances.
Apart from the AC simulations for the HCP’s transconductance and output impedance, a number of transient simulations at the AD8421 instrumentation amplifier’s output have been carried out, specifically for the AD8034 Opamp configuration. The simulations were carried out assuming bipolar measurement, for loads of 150 , 660 , and 1200 , and for sinusoidal input frequencies at 10 kHz and 100 kHz. A number of 100 runs per case (Monte-Carlo simulation) was considered to simulate the passive elements’ tolerance effects, while the AD8421’s differential gain was fixed to by placing 2.2 k (see Figure 3). The input voltage signal was set as a sinusoidal signal of a (180 shifted at , as shown in Figure 4a, which is considered as the output of the THS413 fully-differential amplifier. With a HCP transconductance of S, a current amplitude of mA is expected to be produced, resulting at a measured differential voltage amplitude of (bipolar measurement).
The transient simulation results are presented in Figure 16 for input frequency of 10 kHz and in Figure 17 for input frequency of 100 kHz. The resulting voltage amplitudes are close enough to the expected ones, while the effect of the passive components’ low tolerance is not significant. Furthemore, a phase shift is detected (Figure 16c and Figure 17c), which is expected due to the 1st-order high-pass filters before the AD8421, as well as the HCP itself. Although phase shifts from HCP are undesirable, they usually get particular values for each signal frequency. Thus, since the input signal frequency in bioimpedance measurement applications is known, this phase shift can be predicted and subtracted from the measured signal. In addition, in applications where multiple measurement frames are needed, such as difference-EIT, phase shifts are partially compensated due to the subtraction of the—same frequency—measured signals.
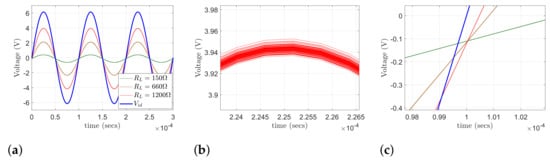
Figure 16.
Transient SPICE analysis on the AD8421 instrumentation amplifier’s output for a 12.3, 100 kHz sinusoidal . (a) The output voltage for loads of 150 , 660 , and 1200 , in relation to the input. (b) The effect of passive components’ tolerance to the output’s amplitude for . (c) Phase delay between voltage input and the output.
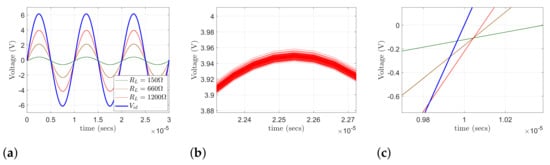
Figure 17.
Transient SPICE analysis on the AD8421 instrumentation amplifier’s output for a 12.3, 100 kHz sinusoidal . (a) The output voltage for loads of 150 , 660 , and 1200 , in relation to the input. (b) The effect of passive components’ tolerance to the output’s amplitude for . (c) Phase delay between voltage input and the output.
5. Implementation and Measurement Results
The fully-active electrode bioimpedance measurement module described, analyzed, and simulated was implemented in a cm × 2.74 cm PCB (Figure 18a). Each active electrode PCB has a 1 cm diameter hole in its center to adapt an AgCl passive electrode at its back side and can be placed on the Subject Under Test (SUT) to receive bioimpedance measurements. Apart from the mirrored HCP half-circuit (Figure 18a left side), the 1st-order high-pass filter and the AD8421 instrumentation amplifier (Figure 18a right side), each active electrode PCB includes 6 essential connectors. These connectors are used to receive the input voltage signal from the THS413 fully-differential Opamp, to send the instrumentation amplifiers’ output signal to the next front-end stage, and to communicate with the previous and the next active-electrode PCB and to maintain power supply. A THS413 fully-differential Opamp PCB breakout is also implemented to produce the and sinusoidal signals, sending them to two active electrodes via equal length SMA cables.

Figure 18.
(a) A fully-active electrode bioimpedance module PCB. An AgCl electrode is placed in the large hole in the center. (b) The bipolar measurement setup (fully differential amplifier connected with two adjacent active electrode modules and nstrumentation).
To get the measurements in this particular work, the sinusoidal waveform in the THS413’s input was produced using an Agilent 33220A waveform generator, while the voltages were measured using a Keysight EDUX1002A oscilloscope (see Figure 18b). Measurements to estimate the real HCP’s transconductance were carried out for all 4 Opamps (ADA4622, AD8034, OPA2210, and AD8672) and load resistor values of 150 , 660 , and 1200 . The transconductance was estimated by measuring the peak-to-peak voltage of each HCP’s half-circuit output node, and by using (8), for frequencies starting from 1 kHz and ending at the point where the output signal’s distortion becomes significant.
To reduce possible mismatching effects, as well as to test whether the HCP output nodes have the same voltage amplitude and 180 phase shift, the load was considered as follows. Two resistors with a value of were placed in series between the HCP’s output nodes, while a ground reference was placed at the resistors’ common node. In bioimpedance applications, a grounded passive electrode can be placed near the current injecting electrodes to cancel parasitic effects between the SUT and the ground (Figure 3). A global Common-Mode feedback circuit could also be considered to eliminate possible mismatching effects; however, this is not included in this particular work. We note that the voltage power supply was set to ±15 V for when using the ADA4610, OPA2210, and AD8672 Opamps, and to ±12 V when using the AD8034 Opamp.
A voltage signal was produced from the waveform generator. The THS413 was used to amplify the input signal, producing two output signals of , shifted by 180, to drive the mirrored-HCP. Since the HCP’s desired transconductance is S, its output nodes must get sinusoidal amplitudes of , , and , with the ground reference between the resistors. Furthermore, an exact phase shift must occur between the two output nodes. The upper-half HCP output node’s voltages for all 3 loads are shown explicitly for the AD8034 implementation, and for 10 kHz, 100 kHz, and 300 kHz input signal frequencies in Figure 19, Figure 20 and Figure 21. It is shown that the voltages measured with the oscilloscope come to agreement with the expected ones that are mentioned above. For lower load resistor values, there is negligible amplitude decrease for frequencies up to 300 kHz. For a 660 load, we observe no degradation at 100 kHz and a degradation at 300 kHz ( from ). Finally, for a 1200 load, the degradation is more intense (from at 10 kHz, to at 100 kHz and at 300 kHz. In summary, we observe a amplitude degradation from 10 kHz to 300 kHz, in this case.
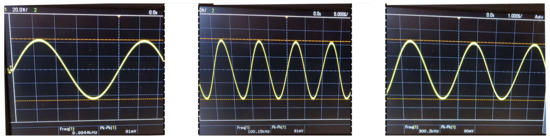
Figure 19.
HCP output node voltages for the AD8034 configuration and 150 resistive load, when inducing a 10 kHz signal (left), a 100kHz signal (center), and a 300 kHz signal (right).
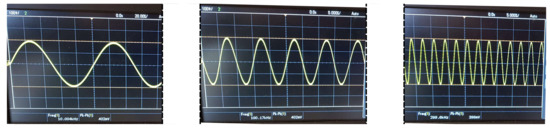
Figure 20.
HCP output node voltages for the AD8034 configuration and 660 resistive load, when inducing a 10 kHz signal (left), a 100 kHz signal (center), and a 300 kHz signal (right).
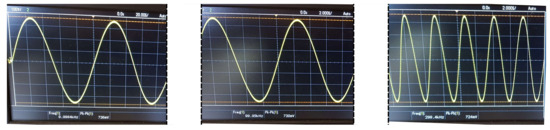
Figure 21.
HCP output node voltages for the AD8034 configuration and 1200 resistive load, when inducing a 10 kHz signal (left), a 100 kHz signal (center), and a 300 kHz signal (right).
The HCP’s output voltages were measured in a similar way for frequency ranges between 1kHz and the frequency in which the signal is significantly distorted, for all 4 Opamps configurations and the 3 load values. The resulting transconductances, for each case, are shown in Figure 22, Figure 23, Figure 24 and Figure 25, along with the expected ones from the numerical analysis and the SPICE simulations, when passive components have their nominal values. As shown, the ADA4622 and AD8034 configurations achieve wider frequency ranges with almost constant transconductance, while the OPA2210 and AD8672 configurations present significant signal distortion for frequencies beyond 180 kHz (Figure 24 and Figure 25). Figure 26 qualitatively shows the sinusoidal signal distortion of the OPA2210 configuration, compared to that of the ADA4622 and the AD8034 configurations at 300 kHz.
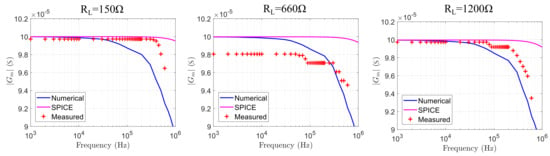
Figure 22.
HCP, ADA4622 configuration transconductance results from the numerical analysis, the SPICE simulation (nominal passive component values) and the lab measurements, for 150 , 660 , and 1200 .
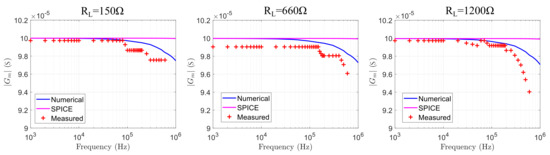
Figure 23.
HCP, AD8034 configuration transconductance results from the numerical analysis, the SPICE simulation (nominal passive component values) and the lab measurements, for 150 , 660 , and 1200 .
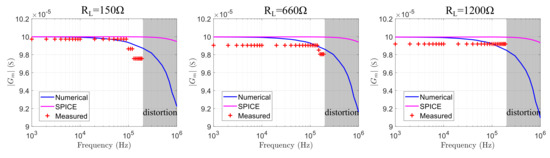
Figure 24.
HCP, OPA2210 configuration transconductance results from the numerical analysis, the SPICE simulation (nominal passive component values) and the lab measurements, for 150 , 660 , and 1200 .
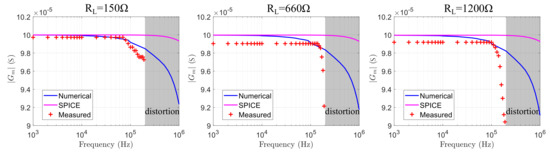
Figure 25.
HCP, AD8672 configuration transconductance results from the numerical analysis, the SPICE simulation (nominal passive component values) and the lab measurements, for 150 , 660 , and 1200 .
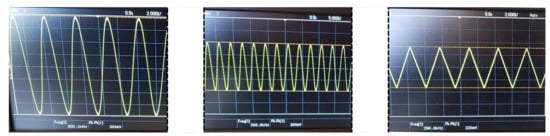
Figure 26.
HCP output node voltages for 300 kHz input signal for the ADA4622 configuration (left), the AD8034 configuration (center), and the OPA2210 (right). The resistive load is 660 . Note the significant distortion for the OPA2210 configuration.
In the ADA4622 case, the transconductance does not degrade within until 500 kHz, 300 kHz, and 250 kHz for 150 , 660 , and 1200 loads, respectively. At the same time, in the AD8034 case, the transconductance degrades more than at 500 kHz (with some small variations), at 400 kHz and 300 kHz for the corresponding load values. Some instrumentation offset errors are also detectable in both cases for 660 load ( and , respectively). The measurements results show that both configurations are suitable for the mirrored-HCP, with the AD8034 achieving a minor advantage. As mentioned in Section 3, the AD8034 is characterized by the highest Open-loop gain and slew rate, compared to the other 3 Opamps. Furthermore, the measurement results are overall closer to the numerical analysis results than the SPICE simulation results.
In addition to the HCP’s transconductance measurement, the voltage output of the AD8421 instrumentation amplifier was tested by performing bipolar measurements for all 3 referred loads. The measurements were performed for a input sinusoidal signal (resulting from a signal acted at the THS413 input), at 10 kHz, 100 kHz, and 300 kHz. For the HCP, the AD8034 Opamp was considered. The corresponding output waveforms are shown in Figure 27, Figure 28 and Figure 29. As mentioned in the previous section, the expected output is . Based on this equation and the measurement results, we perform a comparison in Table 3.
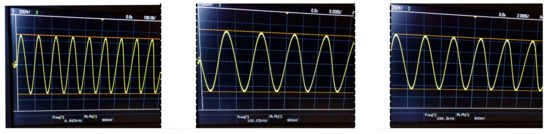
Figure 27.
AD8421 instrumentation amplifier output for a 150 resistive load and sinusoidal at 10 kHz (left), 100 kHz (center), and 300 kHz (right). The AD8034 Opamp configuration has been used in the HCP.
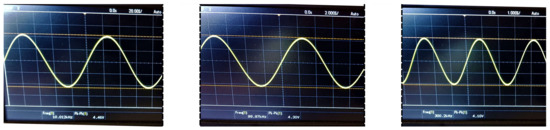
Figure 28.
AD8421 instrumentation amplifier output for a 660 resistive load and sinusoidal at 10 kHz (left), 100 kHz (center), and 300 kHz (right). The AD8034 Opamp configuration has been used in the HCP.
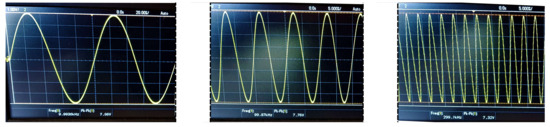
Figure 29.
AD8421 instrumentation amplifier output for a 1200 resistive load and sinusoidal at 10 kHz (left), 100 kHz (center), and 300 kHz (right). The AD8034 Opamp configuration has been used in the HCP.

Table 3.
Comparison between expected and measured voltage amplitudes at the AD8421 output (bipolar measurement).
As observed, the output signal’s amplitude for certain load values is decreased, while frequency increases. For instance, at 10 kHz we get an impedance measurement error of 0.11–2.36%, while this error becomes significant at 300 kHz (8.17–11.2%). This error, which is larger than the expected one from the transconductance reduction estimated, primarily comes from the instrumentation amplifier’s gain degradation when frequency increases. This effect can be significantly reduced with proper calibration, since the measurement frequency is a-priori known in bioimpedance measurement applications. However, a second source of error comes from the instrumentation amplifier’s non-linearity error, while additional error is introduced by the common-signal effect and the oscilloscope measurement itself. Such errors’ effects are minimized in applications, such as difference-EIT, where two or more measurement sequences between each electrode pair are acquired. Then, their difference is used as raw data to get a qualitative estimation of the conductivity distribution of the SUT. Finally, it is noted that the bipolar measurements themselves introduce errors related to polarization effects due to the common current injection and voltage measuring path [46,50]. However, the fully-active electrode bioimpedance measurement modules can be easily applied to tetrapolar measurements.
6. Conclusions
A bioimpedance measurement module, based on a fully-active electrode configuration, was presented in this paper. It consists of a HCP, an electrode connector, a 1st-order high-pass filter, and an AD8421 instrumentation amplifier. Multiple bioimpedance measurement modules can be connected, consisting an electrode array for bipolar, tetrapolar, or more complex measuring techiniques, such as EIT and EIS. Two active electrode modules can be selected to inject an AC current, with the corresponding HCPs acting as a mirrored-HCP. Numerical analysis, SPICE simulations, and lab measurements on the implemented setup have shown that the mirrored HCP presents constant transconductance up to 400 kHz when using the AD8034 Opamp. Furthermore, transient bipolar measurements have taken place. As a future work, a global common-mode feedback can be connected to all the modules to further compensate possible mismatches. Furthemore, noise analysis and measurements can further confirm the bioimpedance modules’ proper operation [51]. Finally, an active-electrode array consisting of these modules can be used in numerous applications employing bioimpedance measurements.
Author Contributions
Investigation, C.D., V.A. and I.G.; Writing—original draft, C.D. and V.A.; Writing—review and editing, C.D., V.A., I.G., N.V., N.U. and P.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is co-financed by Greece and the European Union (European Social Fund- ESF) through the Operational Program ”Human +Resources Development, Education and Lifelong Learning” in the context of the project ”Strengthening Human Resources Research Potential via Doctorate Research” (MIS-5000432), implemented by the State Scholarships Foundation (IKY).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gabriel, S.; Gabriel, C.; Corthout, E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 68, 2231. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: III. parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, B.; Jafari, R. Cuffless blood pressure monitoring from an array of wrist bio-impedance sensors using subject-specific regression models: Proof of concept. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 1723–1735. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Hall, D.A.; Jafari, R. Bio-impedance simulation platform using 3D time-varying impedance grid for arterial pulse wave modeling. In Proceedings of the 2019 IEEE Biomedical Circuits and Systems Conference (BioCAS), Nara, Japan, 17–19 October 2019. [Google Scholar]
- Ibrahim, B.; Hall, D.A.; Jafari, R. Pulse Wave Modeling Using Bio-Impedance Simulation Platform Based on a 3D Time-Varying Circuit Model. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 143–158. [Google Scholar] [CrossRef]
- Wu, Y.; Hanzaee, F.F.; Jiang, D.; Bayford, R.H.; Demosthenous, A. Electrical Impedance Tomography for Biomedical Applications: Circuits and Systems Review. IEEE Open J. Circuits Syst. 2021, 2, 380–397. [Google Scholar] [CrossRef]
- Padilha Leitzke, J.; Zangl, H. A review on electrical impedance tomography spectroscopy. Sensors 2020, 20, 5160. [Google Scholar] [CrossRef]
- Takhti, M.; Odame, K. Structured design methodology to achieve a high SNR electrical impedance tomography. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 364–375. [Google Scholar] [CrossRef]
- XMurphy, E.K.; Takhti, M.; Skinner, J.; Halter, R.J.; Odame, K. Signal-to-noise ratio analysis of a phase-sensitive voltmeter for electrical impedance tomography. IEEE Trans. Biomed. Circuits Syst. 2016, 11, 360–369. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Jiang, D.; Bardill, A.; De Gelidi, S.; Bayford, R.; Demosthenous, A. A high frame rate wearable EIT system using active electrode ASICs for lung respiration and heart rate monitoring. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3810–3820. [Google Scholar] [CrossRef]
- Rao, A.; Teng, Y.C.; Schaef, C.; Murphy, E.K.; Arshad, S.; Halter, R.J.; Odame, K. An analog front end ASIC for cardiac electrical impedance tomography. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 729–738. [Google Scholar] [CrossRef]
- Takhti, M.; Odame, K. A power adaptive, 1.22-pW/Hz, 10-MHz read-out front-end for bio-impedance measurement. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 725–734. [Google Scholar] [CrossRef]
- Bouchaala, D.; Kanoun, O.; Derbel, N. High accurate and wideband current excitation for bioimpedance health monitoring systems. Measurement 2016, 79, 339–348. [Google Scholar] [CrossRef]
- Bertemes-Filho, P.; Brown, B.H.; Wilson, A.J. A comparison of modified Howland circuits as current generators with current mirror type circuits. Physiol. Meas. 2018, 21, 1. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Rahal, M.; Demosthenous, A.; Bayford, R.H. Comparison of a new integrated current source with the modified Howland circuit for EIT applications. Physiol. Meas. 2009, 30, 10999. [Google Scholar] [CrossRef]
- Bertemes-Filho, P.; Vincence, V.C.; Santos, M.M.; Zanatta, I.X. Low power current sources for bioimpedance measurements: A comparison between Howland and OTA-based CMOS circuits. J. Electr. Bioimpedance 2012, 3, 66–73. [Google Scholar] [CrossRef] [Green Version]
- Bertemes-Filho, P.; Felipe, A.; Vincence, V.C. High Accurate Howland Current Source: Output Constraints Analysis. Circuits Syst. 2013, 4, 451. [Google Scholar] [CrossRef] [Green Version]
- Batista, D.S.; Silva, G.B.; Granziera, F.; Tosin, M.C.; Gazzoni, D.L.; Melo, L.F. Howland Current Source Applied to Magnetic Field Generation in a Tri-Axial Helmholtz Coil. IEEE Access 2019, 7, 125649–125661. [Google Scholar] [CrossRef]
- Bouchaala, D.; Shi, Q.; Chen, X.; Kanoun, O.; Derbel, N. Comparative study of voltage controlled current sources for biompedance measurements. In Proceedings of the IEEE 2012 9th International Multi-Conference on Systems, Signals and Devices, Chemnitz, Germany, 20–23 March 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Seoane, F.; Bragós, R.; Lindecrantz, K. Current source for multifrequency broadband electrical bioimpedance spectroscopy systems. A novel approach. In Proceedings of the IEEE 2006 9th International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), New York, NY, USA, 30 August–3 September 2006; pp. 5121–5125. [Google Scholar] [CrossRef]
- Zhang, F.; Teng, Z.; Zhong, H.; Yang, Y.; Li, J.; Sang, J. Wideband mirrored current source design based on differential difference amplifier for electrical bioimpedance spectroscopy. Biomed. Phys. Eng. Express 2018, 4, 025032. [Google Scholar] [CrossRef]
- Constantinou, L.; Triantis, I.F.; Bayford, R.; Demosthenous, A. High-power CMOS current driver with accurate transconductance for electrical impedance tomography. IEEE Trans. Biomed. Circuits Syst. 2014, 8, 575–583. [Google Scholar] [CrossRef]
- Constantinou, L.; Bayford, R.; Demosthenous, A. A wideband low-distortion CMOS current driver for tissue impedance analysis. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 154–158. [Google Scholar] [CrossRef]
- Hong, H.; Rahal, M.; Demosthenous, A.; Bayford, R.H. Floating voltage-controlled current sources for electrical impedance tomography. In Proceedings of the 18th European Conference on Circuit Theory and Design, Seville, Spain, 27–30 August 2007; pp. 208–211. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, D.; Langlois, P.; Bayford, R.; Demosthenous, A. A CMOS current driver with built-in common-mode signal reduction capability for EIT. In Proceedings of the 43rd IEEE European Solid State Circuits Conference (ESSCIRC), Leuven, Belgium, 11–14 September 2017; pp. 227–230. [Google Scholar] [CrossRef]
- Bragos, R.; Rosell, J.; Riu, P. A wide-band AC-coupled current source for electrical impedance tomography. Physiol. Meas. 1994, 15, 91. [Google Scholar] [CrossRef]
- Rao, A.J.; Murphy, E.K.; Shahghasemi, M.; Odame, K.M. Current-conveyor-based wide-band current driver for electrical impedance tomography. Physiol. Meas. 2019, 40, 034005. [Google Scholar] [CrossRef] [Green Version]
- Texas, I. An-1515 a comprehensive study of the Howland current pump. In Application Report SNOA474A; Texas Instruments: Dallas, TX, USA, 2008. [Google Scholar]
- Filho, P.B. Tissue Characterization Using Impedance Spectroscopy Probe. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2002. [Google Scholar]
- Nouri, H.; Ayed, E.B.; Bouchaala, D.; Derbel, H.B.J.; Kanoun, O. Comparative Study of Howland Current Source Configurations for Accurate Biomedical Devices. In Proceedings of the IEEE 2019 5th International Conference on Nanotechnology for Instrumentation and Measurement (NanofIM), Sfax, Tunisia, 30–31 October 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Mahnam, A.; Yazdanian, H.; Samani, M.M. Comprehensive study of Howland circuit with non-ideal components to design high performance current pumps. Measurement 2016, 82, 94–104. [Google Scholar] [CrossRef]
- Tucker, A.S.; Fox, R.M.; Sadleir, R.J. Biocompatible, high precision, wideband, improved Howland current source with lead-lag compensation. IEEE Trans. Biomed. Circuits Syst. 2012, 7, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Morcelles, K.F.; Sirtoli, V.G.; Bertemes-Filho, P.; Vincence, V.C. Howland current source for high impedance load applications. Rev. Sci. Instruments 2017, 88, 114705. [Google Scholar] [CrossRef]
- Liu, J.; Qiao, X.; Wang, M.; Zhang, W.; Li, G.; Lin, L. The differential Howland current source with high signal to noise ratio for bioimpedance measurement system. Rev. Sci. Instruments 2014, 85, 055111. [Google Scholar] [CrossRef]
- Sirtoli, V.G.; Morcelles, K.F.; Vincence, V.C. Design of current sources for load common mode optimization. J. Electr. Bioimpedance 2018, 9, 59–71. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Li, W.; You, F.; Huo, X.; Xu, C.; Ji, Z.; Dong, X. High-precision electrical impedance tomography data acquisition system for brain imaging. IEEE Sens. J. 2018, 18, 5974–5984. [Google Scholar] [CrossRef]
- Simini, F.; Bertemes-Filho, P. Bioimpedance in Biomedical Applications and Research; Springer: New York, NY, USA, 2018. [Google Scholar]
- Wi, H.; Sohal, H.; McEwan, A.L.; Woo, E.J.; Oh, T.I. Multi-frequency electrical impedance tomography system with automatic self-calibration for long-term monitoring. IEEE Trans. Biomed. Circuits Syst. 2013, 8, 119–128. [Google Scholar]
- Zarafshani, A.; Bach, T.; Chatwin, C.; Xiang, L.; Zheng, B. Current source enhancements in Electrical Impedance Spectroscopy (EIS) to cancel unwanted capacitive effects. Biomed. Appl. Mol. Struct. Funct. Imaging 2017, 10137, 101371X. [Google Scholar]
- Wu, Y.; Jiang, D.; Bardill, A.; Bayford, R.; Demosthenous, A. A 122 fps, 1 MHz bandwidth multi-frequency wearable EIT belt featuring novel active electrode architecture for neonatal thorax vital sign monitoring. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 927–937. [Google Scholar] [CrossRef] [Green Version]
- Gaggero, P.O.; Adler, A.; Brunner, J.; Seitz, P. Electrical impedance tomography system based on active electrodes. Physiol. Meas. 2012, 33, 831. [Google Scholar] [CrossRef] [Green Version]
- Mellenthin, M.M.; Mueller, J.L.; De Camargo, E.D.L.B.; De Moura, F.S.; Santos, T.B.R.; Lima, R.G.; Alsaker, M. The ACE1 electrical impedance tomography system for thoracic imaging. IEEE Trans. Instrum. Meas. 2018, 68, 3137–3150. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Mitra, S.; Matsumoto, A.; Patki, S.; Van Hoof, C.; Makinwa, K.A.; Yazicioglu, R.F. A wearable 8-channel active-electrode EEG/ETI acquisition system for body area networks. IEEE J. Solid-State Circuits 2014, 49, 2005–2016. [Google Scholar] [CrossRef] [Green Version]
- Alimisis, V.; Dimas, C.; Pappas, G.; Sotiriadis, P.P. Analog Realization of Fractional-Order Skin-Electrode Model for Tetrapolar Bio-Impedance Measurements. Technologies 2020, 8, 61. [Google Scholar] [CrossRef]
- Hanbin, M.; Su, Y.; Nathan, A. Cell constant studies of bipolar and tetrapolar electrode systems for impedance measurements. Sens. Actuators B Chem. 2015, 221, 1264–1270. [Google Scholar]
- Dimas, C.; Tsampas, P.; Ouzounoglou, N.; Sotiriadis, P.P. Development of a modular 64-electrodes electrical impedance tomography system. In Proceedings of the 2017 6th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 4–6 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Kassanos, P.; Seichepine, F.; Yang, G.Z. A Comparison of Front-End Amplifiers for Tetrapolar Bioimpedance Measurements. IEEE Trans. Instrum. Meas. 2020, 70, 1–14. [Google Scholar] [CrossRef]
- Dimas, C.; Uzunoglu, N.; Sotiriadis, P.P. A parametric EIT system spice simulation with phantom equivalent circuits. Technologies 2020, 8, 13. [Google Scholar] [CrossRef] [Green Version]
- Kassanos, P.; Ip, H.M.; Yang, G.Z. A tetrapolar bio-impedance sensing system for gastrointestinal tract monitoring. In Proceedings of the 2015 IEEE 12th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Cambridge, MA, USA, 9–12 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Sun, J. Noise analysis of a driven chain with improved Howland current source for electrical impedance tomography. Meas. Sci. Technol. 2021, 32, 095903. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).