1. Introduction
Supervised learning [
1,
2] is an approach in Machine Learning (ML) for classification [
3] or regression tasks [
4], where a set of labeled data is used to train a prediction model. However, in practice, obtaining sufficient labeled data for training a model can be difficult. There may be a strict privacy-control policy that restricts one from obtaining labeled data or human error that can cause false or missing labels in the dataset. Additionally, there may not be enough of a budget to obtain all information labeled by human annotators, especially when expert knowledge is needed for the annotations. For example, during the COVID-19 pandemic, online shopping drastically increased, and shop owners needed to update their products. Manually finding the category of each product is time-consuming, therefore, it is important to develop a framework that can automatically categorize new data on the basis of a small amount of labeled data. In this scenario, an approach called Semisupervised Learning (SSL) can be useful to solve the problem of weakly labeled data. SSL algorithms are applied in such cases where a very limited amount of label data along with a large number of unlabeled data are used as input. SSL algorithms learn a better prediction rule than supervised ML would learn if trained only on a small amount of label data. Considering this approach in mind, we designed a semisupervised framework to detect the labels or categories of unlabeled data. The concept behind our approach is that similar data points lie very close to each other in vector space. In this regard, our objective was to learn a similarity measure to detect the distance of data points in vector space and then detect the labels of unlabeled data through label propagation.
Distance metric learning (DML) is a popular concept in modern ML research to learn a similarity measure between two entities. DML aims at automatically constructing task-specific distance metrics from data in an ML manner. It is often difficult to design metrics that are well-suited to the particular data and task of interest. In this work, we designed a novel DML model to detect the distance between every two images in an image dataset with fashion products called the Fashion dataset [
5], and then we propagated the label information from a small subset of labeled data to the entire set of unlabeled data. It was assumed that similar objects have a distance very close to zero and they share the same label information.
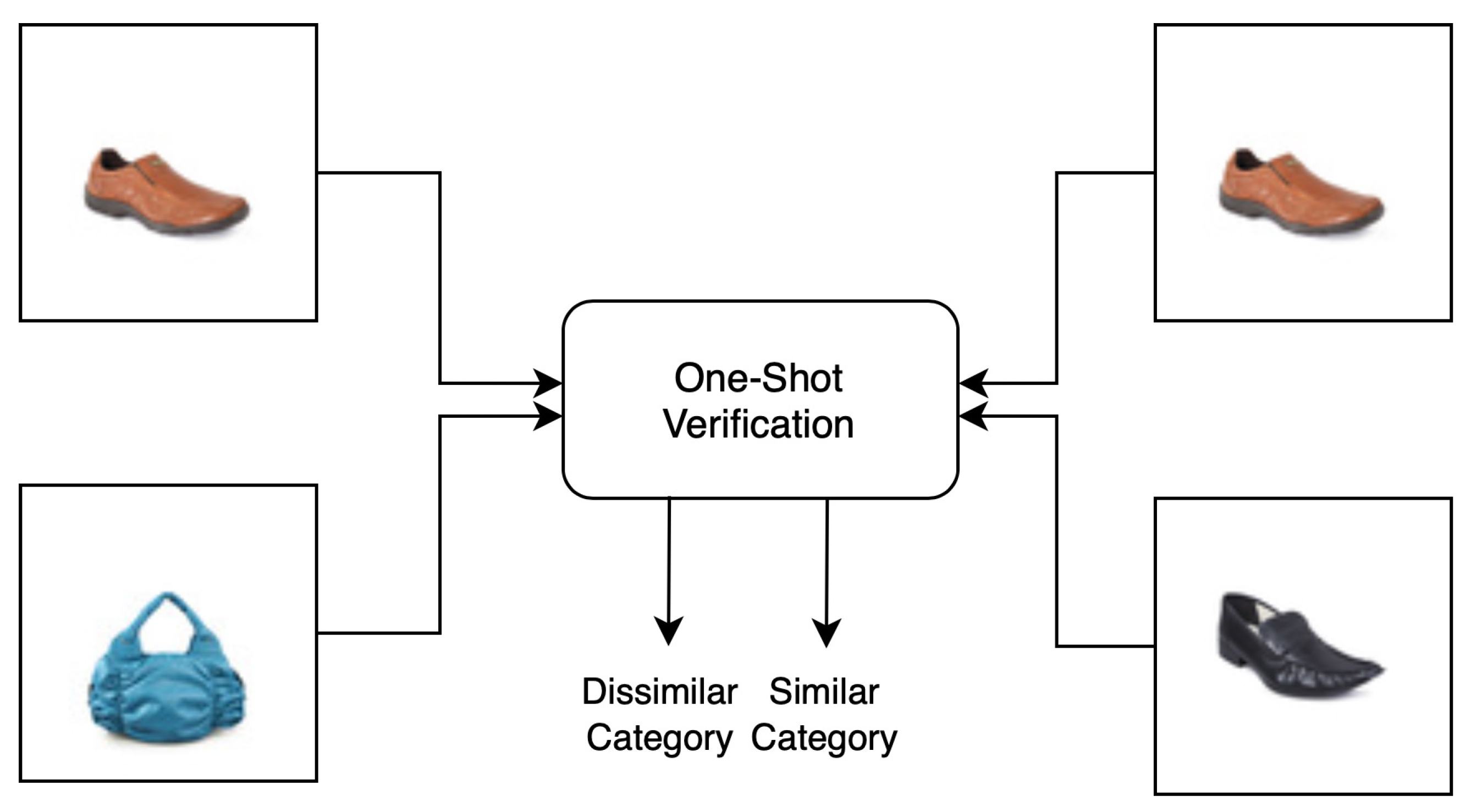
Figure 1 shows a visual representation of when similar objects share the same label information.
The second component, label propagation, is a popular problem in SSL, where a small subset of data points has label information, and the challenge is to propagate labels to the unlabeled points from the labeled points through an algorithm. We adopted a method introduced in [
6] that exploits graph harmonics and sparse coding of graph signals in the dual space of the graph. Here, we consider the labels of images as the graph signal on their nodes, and the metric learned by DML consists of the edge between nodes (i.e., images). In the end, our pipeline predicts the image labels of the entire dataset on the basis of a small subset of images with given labels.
In this work, we designed a novel approach combining DML and label propagation for SSL. Our contributions are summarized as follows:
Designing a novel DML model to learn good similarity measures between every two images in an image dataset and create a graph with their distances.
Recovering labels for all images from the graph using a label-propagation algorithm.
The rest of the paper is structured as follows:
Section 2 describes related work,
Section 3 describes preliminary works that we performed as part of our experiments,
Section 4 and
Section 5 present our proposed methodology and implementation, and
Section 6 discusses the numerical experiments.
2. Related Work
SSL [
7] is an algorithm family that falls between supervised [
1,
2] and unsupervised learning, making use of labeled and unlabeled data to perform learning tasks. For SSL, a smaller set of labeled data in combination with a large set of unlabeled data are typically used for the construction of a better learning technique. In recent years, due to the lack of labeled data, SSL gained more popularity than supervised learning. Our model gained inspiration from recent works on distance metric learning and label-propagation algorithms. We provide a brief overview of the related work in both of these areas.
Label propagation is a way in which SSL detects the labels of unlabeled observations. Inductive learning [
8] regards learning general rules for making predictions, while transductive learning learns prediction rules from training data for specific testing data. SSL is transductive, as labels are gradually predicted, and the model has to be retrained whenever the testing set changes. In our case, labels were propagating, and if a new instance (i.e., graph node) was added, the model had to be run again, so it was transductive. Puy et al. [
9] first proposed the random sampling of band-limited signals on graphs. Later, Kim et al. [
10] proposed adaptive signal recovery on graphs via harmonic analysis for experimental design in neuroimaging. Bronstein et al. [
11] prepared an exhaustive literature review paper, “geometric deep learning: going beyond Euclidean data”, on this topic. Malkov et al. [
12] first introduced the nearest-neighbor search using small world problem. Saito et al. [
13] proposed a semisupervised domain adaption technique via minimax entropy. Later, Zhai et al. [
14] proposed a self-supervised SSL where they bridged the gap between self-supervised and SSL.
Work on one-shot and few-shot learning has gained popularity in DML. One-shot learning is a learning task where there might be only one training example for a label or category, and few-shot learning can be applied where there are only a few training examples available for each label. One-shot learning is a way of learning similarity measures, and it was first introduced by Bromley et al. [
15] for signature verification using a Siamese time-delay neural network. Then, Fei-Fei et al. [
16] proposed a one-shot-based approach for object categories. The authors assumed that currently learned classes can help to make predictions on new ones when just one or few labels are available. Lake et al. [
17] presented a hierarchical Bayesian model that reached human-level error on few-shot learning alphabet-recognition tasks. Koch et al. [
18] presented a deep-learning model based on computing the pairwise distance between samples using Siamese networks, and Vinyals et al. [
19] presented end-to-end trainable k-nearest neighbors using cosine distance. Schroff et al. [
20] proposed an anchor-based triple network for unified embedding called FaceNet, which is useful for face recognition and clustering. The FaceNet model is trained on the triplet loss function. Kertész et al. [
21] proposed multidirectional image-projection transformation with fixed vector lengths (MDIPFL) for one-shot learning, which performed significantly better.
Many recent works on SSL were based on generative models with deep neural networks. Few of such examples are graph neural networks (GNN) [
22], variational autoencoders [
23,
24], and generative adversarial networks [
25,
26,
27]. A GNN is a deep-learning approach to deal with graph-structured data, and it was first proposed by Gori et al. [
22]. Kim et al. [
6] proposed a select-recovery-based model to recover multivariate signals in an online manner using graph-signal processing. Kipf and Welling [
28] proposed deep-learning-based GNN models on semisupervised classification problems. Chang et al. [
29] develop graph interaction networks that learn pairwise particle interactions and apply them to discrete particle-physical dynamics. Duvenaud et al. [
30] and Kearnes et al. [
31] studied molecular fingerprints using variants of the GNN architecture, and Gilmer et al. [
32] further developed the model by combining it with set representations. Vinyals et al. [
19] showed state-of-the-art results on molecular prediction. Appalaraju et al. [
33] proposed a Siamese-network-based deep CNN model using curriculum learning and transfer learning for image-similarity measurements.
Our method is based on the combination of DML and a label-propagation algorithm. We used a one-shot-learning [
18,
19] approach to learn DML and construct graphs on the basis of distance learned from DML. Unlike traditional one-shot learning networks, we propose a novel DML network that we combined with a label-propagation algorithm to achieve the best results.
3. Preliminary Work
We focused on the Fashion dataset [
5], which was downloaded from an online fashion e-commerce store called Myntra. Although we focused on this dataset, this approach can be applied to other image datasets or modalities. The fashion data consisted of a set of images of fashion products with their label information. Each of these images was processed to grayscale and resized to
pixels. It was then processed to extract features.
The one-shot-learning approach is a very popular technique to learn domain-specific features from input images when the number of input images per class is limited. This technique is very useful, even for DML, when the similarity measure is to be calculated between input images. In this work, we used this approach as our baseline model to calculate a good similarity measure between images. Koch et al. [
18] focused on a twin Siamese network to perform DML, and then reused that network’s features for one-shot learning without any retraining.
A twin Siamese network performs well for one-shot learning tasks, but training this network is a time-consuming process. While training this network, it takes two inputs at a time and calculates a similarity score from their distances. Therefore, the number of comparisons was more ( for N number of images and k is 2) to calculate the distance of all images in our dataset. This twin Siamese network is sensitive with respect to context and fails to capture fine-grain differences between two images. The above-mentioned problems motivated us to focus on DML, creating a novel network that quickly converges and captures fine-grained differences of labels.
4. Proposed Methodology
In this section, we discuss the design approach we propose. SSL is an approach where a learning algorithm requires a small amount of training data and a large amount of unlabeled data. Our goal in this research is to learn a prediction rule to detect the labels of unlabeled datasets with the help of a small amount of labeled data points. We divided our algorithm into two steps: distance metric learning and label propagation.
4.1. Distance Metric Learning
DML focuses on automatically constructing domain-specific distance metrics from supervised data. In this step, our framework learns a good similarity measure between two images. There are a few popular standard distance metrics, e.g., Euclidean distance and cosine similarity, where we need prior knowledge of the domain. The aim of DML is to construct a task-specific distance metric from a particular dataset.
Twin Siamese networks are one of the ways of learning distance between two images. The concept of a twin Siamese network is that there are two parallel networks that share the same weights. These two parallel networks are basically identical and learn the encoding of input images. We used the twin Siamese network as our baseline model.
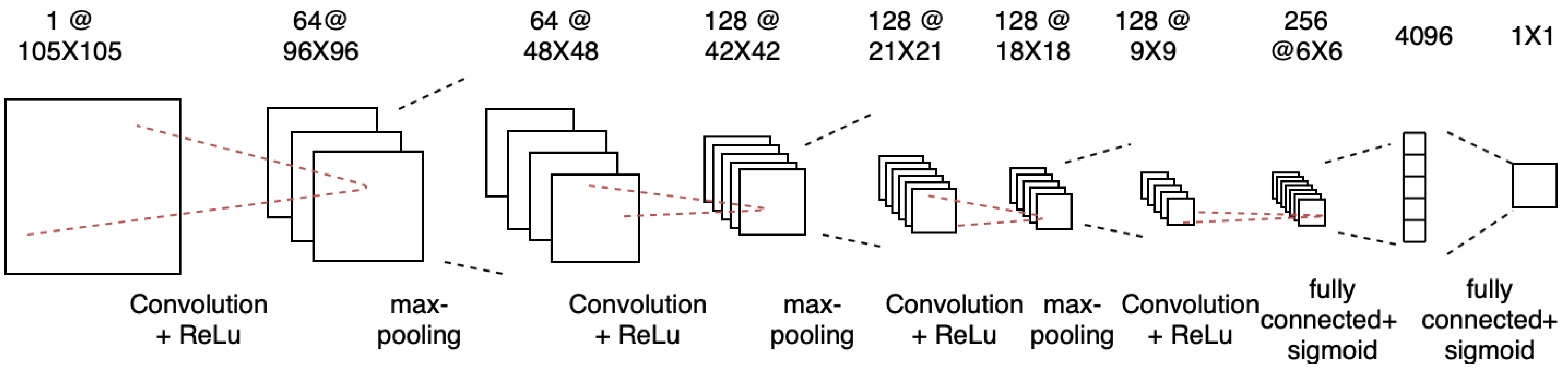
Our baseline model is a convolutional neural network (CNN) version of the twin Siamese network, which takes two input images and learns the encoding of two input images through this twin network. In the end, it learns the distance of two feature vectors and produces a distance score between 0 and 1 through a sigmoid layer. The detailed architecture of this network is as follows: the model consists of a sequence of convolutional layers, each of which uses a single channel with filters of varying size. The network applies a rectified linear unit (ReLU) activation function to the output feature maps, followed by max-pooling with a filter size and stride of 2.
Twin Siamese networks perform well compared to all other DML mentioned in
Section 2. However, Twin Siamese network performance is very slow. The convergence time of this network is extremely large, taking almost 2000 epochs to converge. Detailed hardware specifications are provided in
Section 5.3. If we have an N number of images in the dataset, the number of comparisons that happen in this network is
, which is very large to obtain the distance of every pair of images in our dataset. Therefore, we propose the concept of a triple Siamese network to optimize these points.
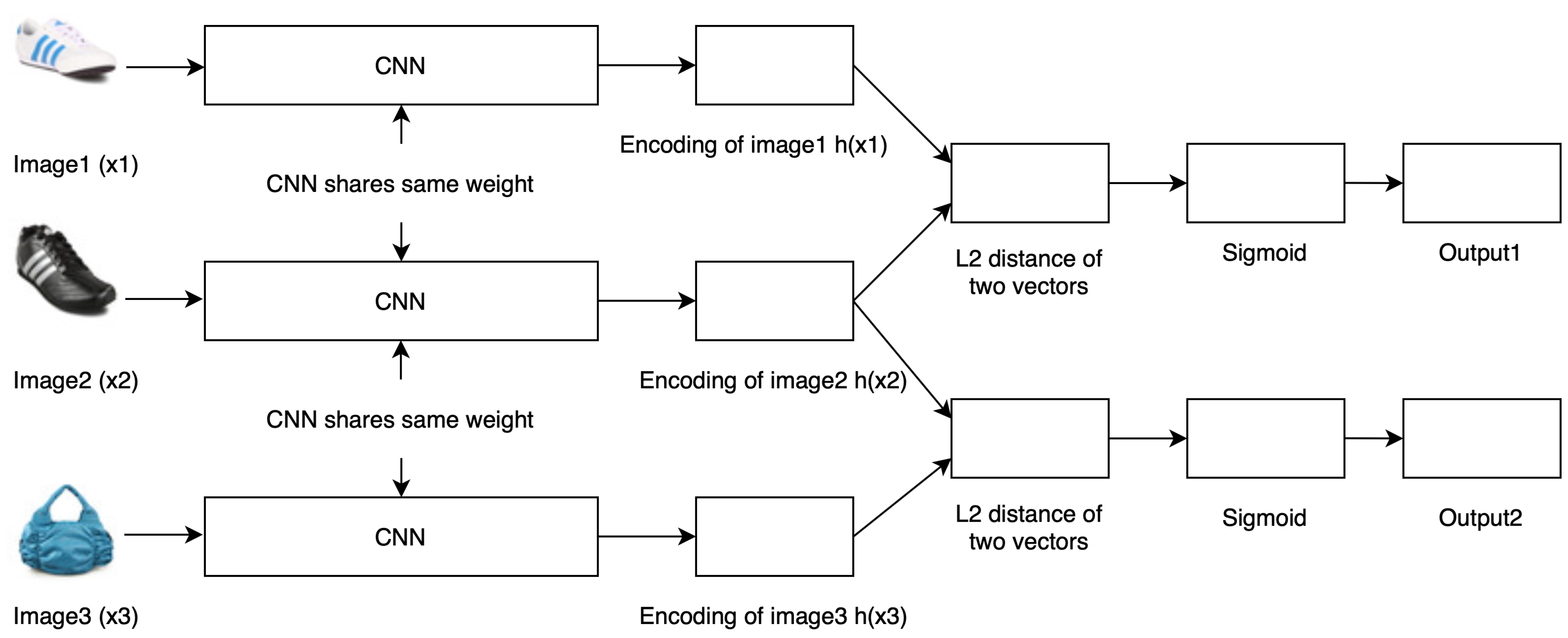
4.1.1. Triple Siamese Network
In this network, we used three parallel networks that shared the same weights. The architecture of each network is the same CNN network as the one that we used in the twin Siamese network. Through this network, we learned the similarity function as
, where
, here
and
are input images to the network, and
and
are the encoding of
and
by the CNN.
Figure 2 shows the system architecture of the triple Siamese network.
This network takes three images as input in such a way that and are taken from the same class, and and are taken from different classes. The goal is to maximize the distance between and , and minimize the distance between and . This network learns two distances from these two pairs at a time.
4.1.2. Graph Representation
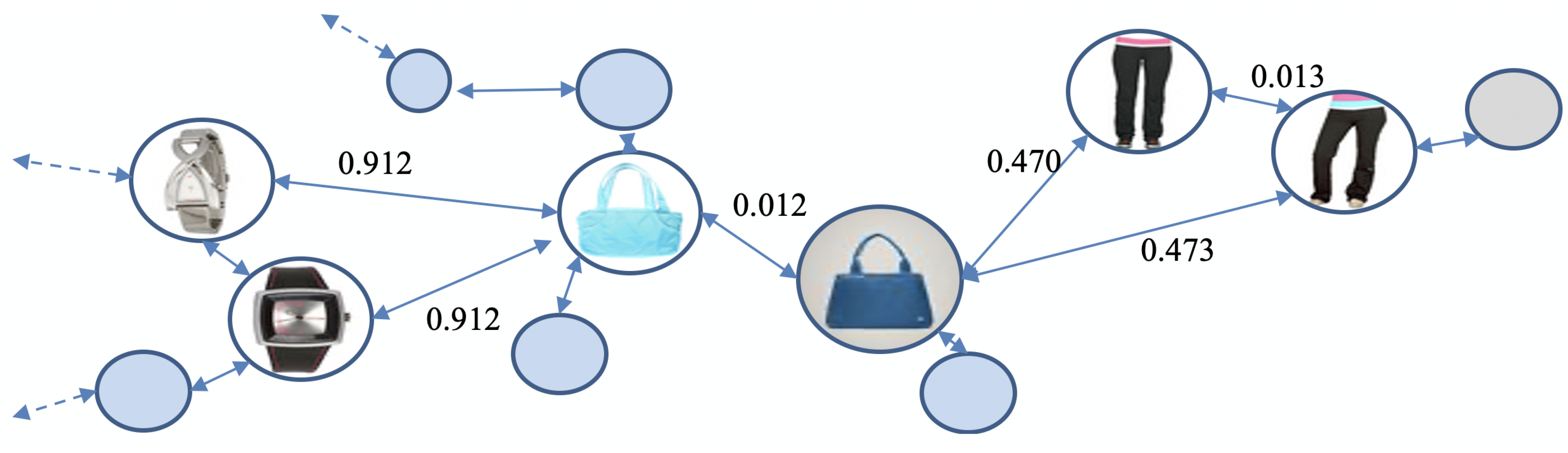
After the triple Siamese Network provided the distance of each pair of images in the Fashion dataset, we graphically represented our data. We have graph
, where
V is a set of images, and
E is the set of distances of each pair of images. Hence,
V = {
,
…
},
E = {
, where
= dist(
,
)}, and
N = total number of images.
Figure 3 displays a graphical representation of the Fashion dataset [
5].
4.2. Label Propagation
Label propagation determines the labels of unlabeled data from a very small amount of labeled data. In this project, we considered the graph as graph signal and ran the RA (Kim et al. [
6]) on the graph. We recovered the graph signal using the harmonic analysis of the graph. We applied two useful concepts, spectral graph theory [
34] and harmonic analysis of the graph [
6,
10], for our RA.
4.2.1. Spectral Graph Theory
Spectral graph theory [
34] is the study of the properties of a graph in relationship to the eigenvalues and eigenvectors of matrices associated with the graph, such as its distance matrix or Laplacian matrix. Graph
is represented by a set of vertices
V of size
N and a set of edges
E that connect the vertices. Another matrix, graph Laplacian
, where a degree matrix
, is a diagonal matrix with the
ith diagonal element being the sum of edge weights connected to the
ith vertex and
being a distance matrix where it is the most common way to represent a graph G, where each element
denotes the distance between the
ith and
jth vertices.
4.2.2. Graph Harmonic Analysis
Graph harmonic analysis [
6,
10] utilizes the Fourier/wavelet transform of the original signal and filters in the frequency domain. The reason behind using harmonic analysis is making use of sparsity in terms of representation obtained in the Fourier/wavelet space of the graphs. By constructing different shapes of band-pass filters in the frequency space and transforming them back into the original space, we can construct a mother wavelet
on the nodes of a graph coming from its representation in the frequency space. For this implementation, using spectral graph theory, we used orthonormal bases to design kernel function
in the space spanned by the bases. Graph Laplacian
L provided eigenvalues and corresponding eigenvector for
N number of vertices. This eigenvector is used to define the graph Fourier transform of a function
defined on a vertex
n. If signal
lies in the spectrum of the first
k eigenvectors, then
is
k-band-limited. Graph Fourier transform of a function
is defined on vertices
n as:
and
where
is a set of eigenvectors that provide orthonormal bases, and
is a conjugate of
. Graph Fourier coefficient
is obtained by forward transform, and the original function
can be reconstructed by the inverse transform.
4.2.3. Problem Setup
We formulated the problem setup as graph signal , where measurement p at each node is the one-shot encoding of the node labels, and N is a number of images or nodes. We had an available partial observation at m vertices, where . Therefore, partial signal , and the goal is to complete the full graph and recover signal f from partially observed y.
4.2.4. Recover Algorithm
As part of the RA [
6,
9,
10], we solved the optimization problem for the estimation
g of original signal
f:
where
,
,
is random uniform distribution probability. Sample
m nodes from
N (random uniform sampling strategy) and the locations where we observed the signal can be denoted as
. On the basis of
m observations, a projection matrix [
6]
was built:
This framework solves Equation (
3) entirely in a dual space by projecting the problem to a low-dimensional space where we search for a solution of size
[
10]. We took the graph Fourier transform of the function as
g, and
are the first
k coefficients. Reformulating Equation (
3) using
[
10], where
as:
From Equation (
4), we recovered low-rank estimation
, that reconstructed our original signal
f.
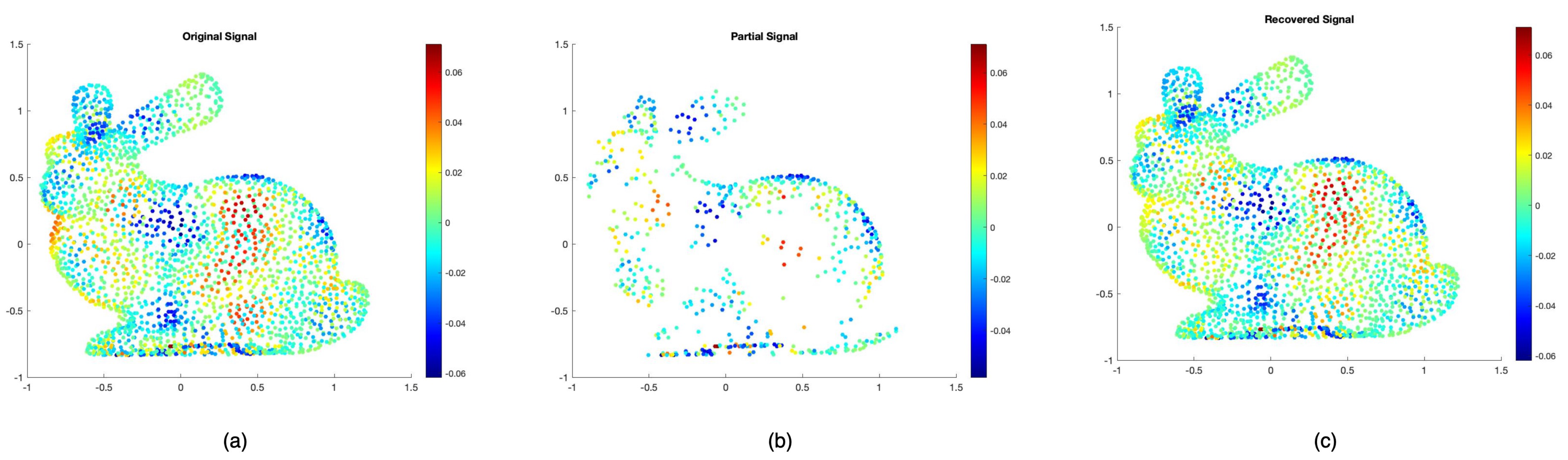
Figure 4 shows a toy example of this RA. Here, given a GSP bunny [
35] mesh with N = 2503 vertices, we defined a random signal
that was band-limited in the spectrum of
with Gaussian noise of
,
was the sampling distribution, and sample size
m = 600 vertices, which was 20% of the total vertices without replacement. Our estimation
g using
k = 500 bases is shown in
Figure 4. The error between true
f and
g was extremely small despite using such little data [
10].
5. Implementation
CNN-based Siamese networks were first introduced by Koch et al. [
18] for one-shot image recognition. Our triple Siamese network architecture was inspired by twin Siamese networks, but with three instead of two parallel networks. These three parallel networks are individually CNN networks. Each CNN network consists of a sequence of convolutional layers, each of which uses a single channel with filters of varying size and a fixed stride of 1. The network applies a ReLU activation function to output feature maps by max-pooling with a filter size and stride of 2. Each layer
l takes the following form:
where
W is the shared weight matrix,
is the shared bias vector, and ∗ is the valid convolutional operation corresponding to each convolutional filter and the input feature maps.
This layer is followed by a fully connected layer, and at the top, we have another layer to compute the distance between feature vectors generated by three networks; each distance is passed through a sigmoid output to obtain the distance between two pairs of inputs.
Figure 5 shows an example of a CNN architecture used in the triple Siamese network, where three of these CNNs are used. Each CNN consists of a sequence of convolutional layers with a single channel and filters of varying size, with a fixed stride of 1. This architecture consists of a number of convolution layers as a multiple of 16. The ReLU activation function is used on the output feature maps, followed by max- pooling with a filter size and stride of 2. The 4096 unit fully connected layer was followed by another layer where we calculated the
distance of each pair.
5.1. Learning
We initialized all network weights in the convolutional layers from normal distribution with zero mean and a standard deviation of
. Biases were initialized from normal distribution with mean
and standard deviation
. In the fully connected layers, biases were initialized in the same way as the convolutional layers were, but weights were drawn from a much wider normal distribution with zero mean and standard deviation
according to Koch et al. [
18]. In the network, training is performed by feeding the network with three samples (
) at a time when
and
are of the same class, and
is of a different class. The goal is to maximize the distance between
and
, and minimize the distance between
and
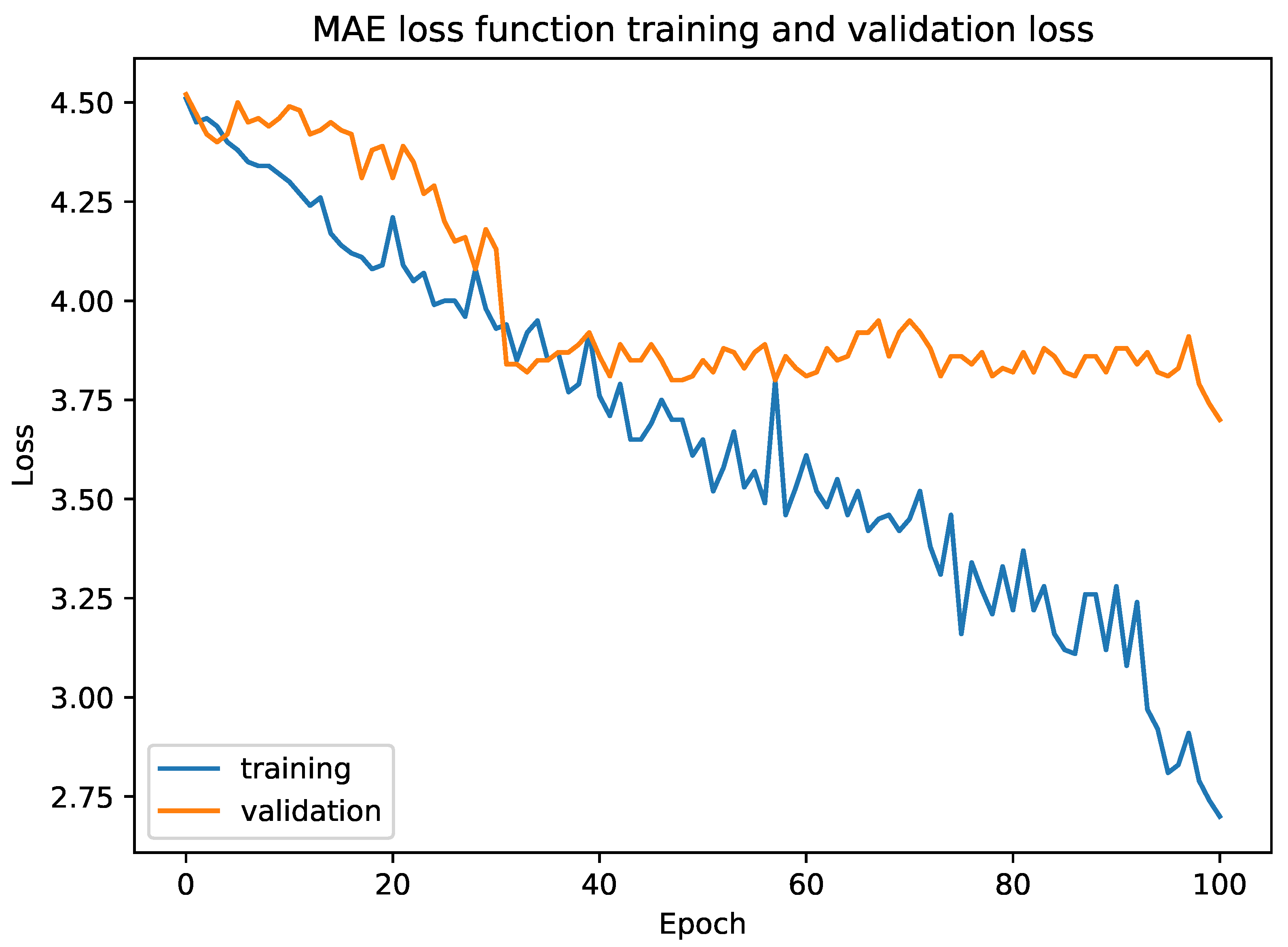
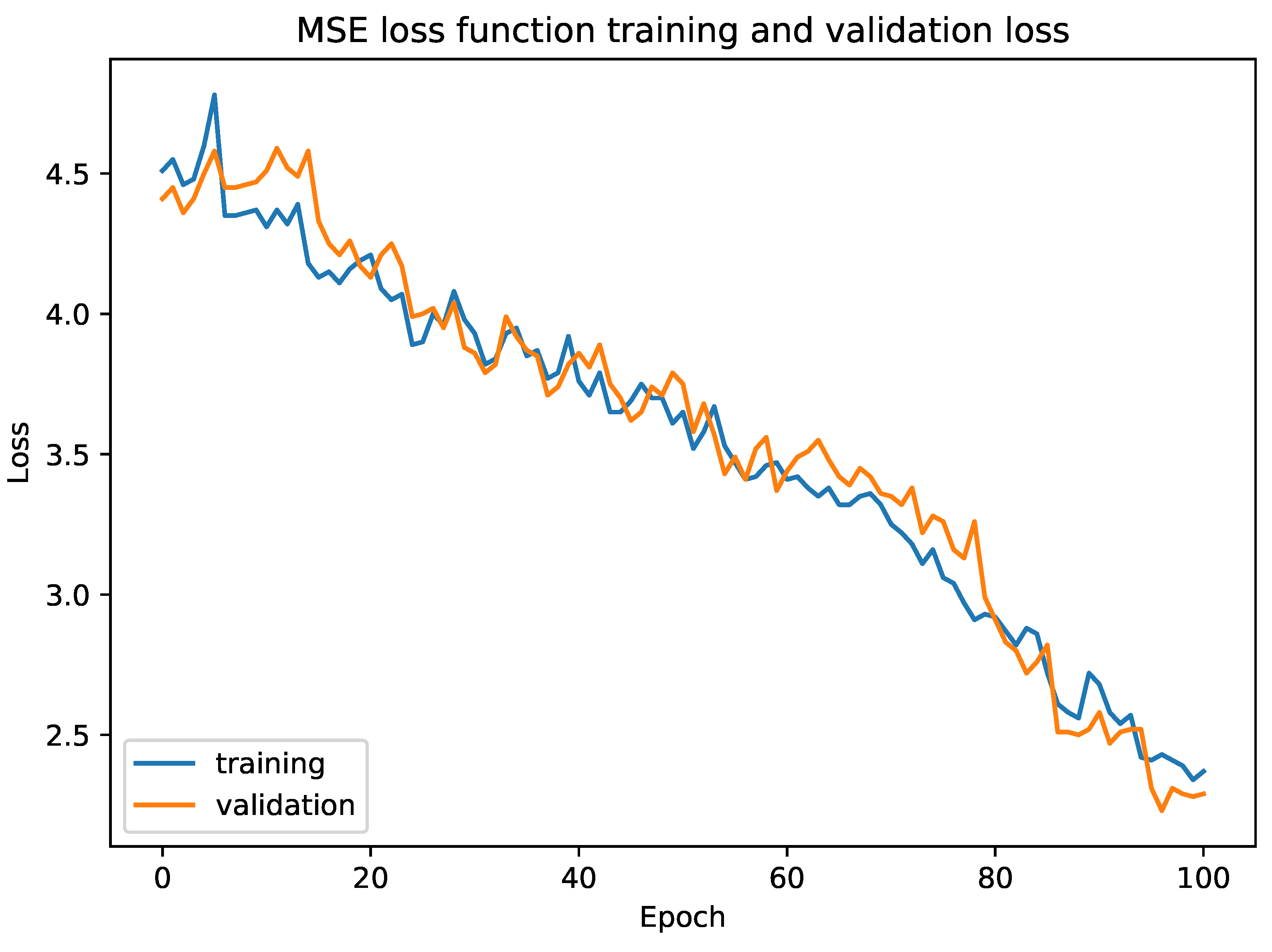
. At the top, there is a comparison layer to compare both similarities, followed by a sigmoid layer to normalize the output in the range of 0 and 1. We used mean square error (MSE) as the loss function. We tested our model with triplet loss function and mean absolute error (MAE). The empirical results showed that our model converged much faster in the case of the Fashion dataset with MSE whereas MAE overfitted our model.
Figure 6 shows the training and validation loss for MAE. The back-propagation algorithm ran to simultaneously update the weights for all three networks. Therefore, the loss function is:
where
is the sigmoid output of the first distance, and
is the sigmoid output of the second distance in
Figure 2. Here,
is the
-norm of the first two inputs (from the same category), and
is the
-norm of the second two inputs (from a different category).
Here,
, as they are formed as a probability. Therefore, Equation (
8) can be rewritten as:
where
is a constant.
Figure 7 shows that the triple Siamese network converged after 150 epochs while training on the Fashion dataset [
5]. To obtain optimal results, the triplet could be chosen through three strategies [
21]: (i) random mining, (ii) semihard mining, and (iii) hard mining. Our goal was to minimize the distance between positive pairs and maximize the distance between negative pairs. As random mining is the most efficient strategy [
21], we used this mining technique for learning.
5.2. Validation
For every pair of input images, this model generated a similarity score between 0 and 1. N-way one-shot methods [
18] were applied to measure the performance of this network. We considered
N as 2 to perform one-shot learning, and repeated this
k times to calculate percentage of prediction
p as:
where
n is the number of correct predictions out of
k trials. For validation, we used 50 trials. Therefore,
k was 50.
Figure 8 shows the training and validation loss for MSE.
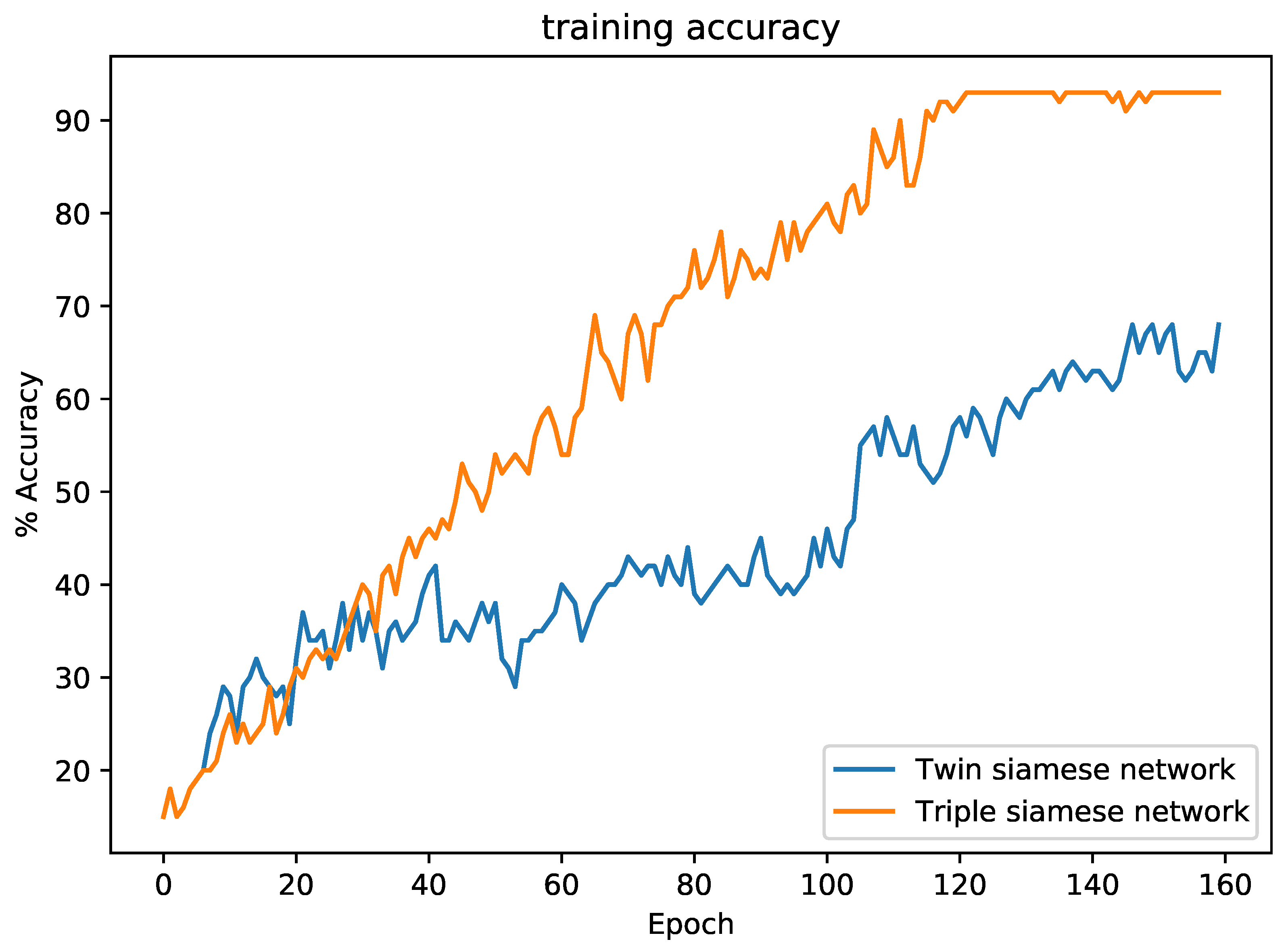
5.3. Twin Siamese vs. Triple Siamese Network
The triple Siamese network converges very quickly compared to the twin Siamese network. For example, the triple Siamese network converged in 7.5 min when training on the Fashion dataset, while the twin Siamese network required 1.6 h. Training-system characteristics: CPU 2.3 GHz, 8-Core Intel Core i9, memory 16 GB, 2667 MHz DDR4, GPU AMD Radeon Pro 5500M 4 GB. To detect the distance between each pair of images in our dataset, fewer comparisons were required in the triple Siamese network, and we obtained two distance scores at a time. The triple Siamese network has two parallel layers to calculate the distance metrics, which gives two distance measures at a time. This approach helps to reduce training time in the triple Siamese network. The objective of using three layers of a CNN network is to feed the network with three input images in such a way that two images are from the same class, and the third is from a different class; then, we produce two pairs (two from the same class and the other two from a different class) out of these three input images to calculate two pairs of distance. This model helps to minimize the distance between the two images in the first pair, and maximize the distance between the images in the second pair. Through this model, we captured fine-grained differences between classes that resided very closely in vector space.
6. Experiments and Results
In this section, we demonstrate the results of our algorithm using the Fashion dataset [
5]. We downloaded the image dataset from the Myntra Fashion website, out of which we used 1000 images for training, 1000 images for validation, and 4000 images for testing.
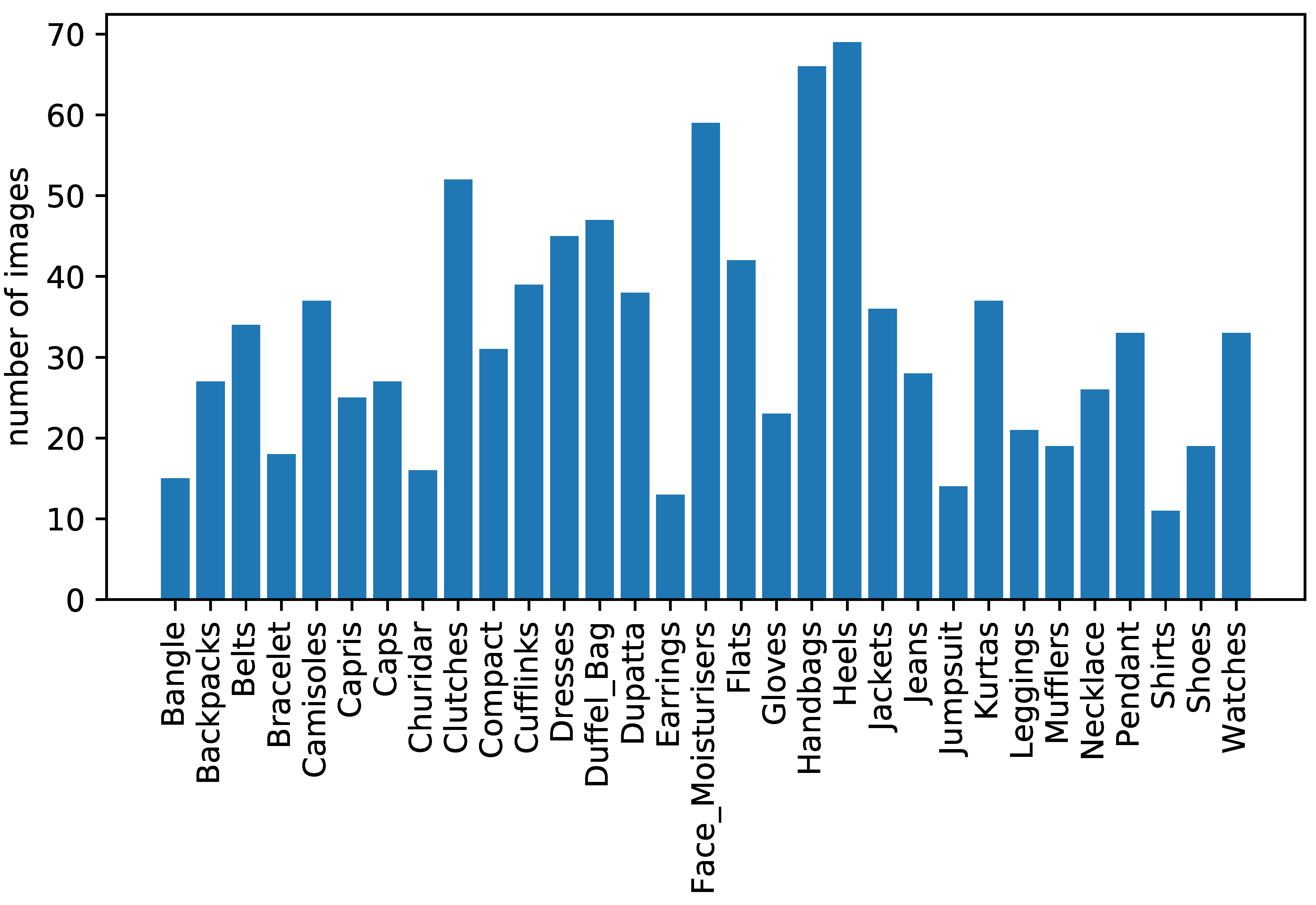
Figure 9 shows the class distribution of the validation dataset.
The images had 31 different labels or categories, e.g., handbags, shirts, and shoes. For our experiment, we first created a graph using our triple Siamese network with the images, where images were defined as vertices or nodes, and edges denoted the similarity score between two images. Measurements at each vertex were defined by one-shot encoding of the label vector representing object labels where nonzero elements indicated whether the corresponding objects existed in the image. As our dataset consisted of 31 labels, each measurement was vectors. Therefore, we obtained a matrix for our entire image dataset, which served as the ground truth of our algorithm. We assumed that our sample m was to be chosen using uniform random sampling and . Therefore, m was our partially observed dataset. The k value of our experiment was empirically selected to be 500, which gave optimal accuracy.
We ran our SSL algorithm on this dataset first to create a graph using our proposed triple Siamese network; then, we applied our label-propagation algorithm to recover the signal at each vertex. We compared our algorithm with the baseline twin Siamese network model and k-NN along with a state-of-the-art graph convolutional network.
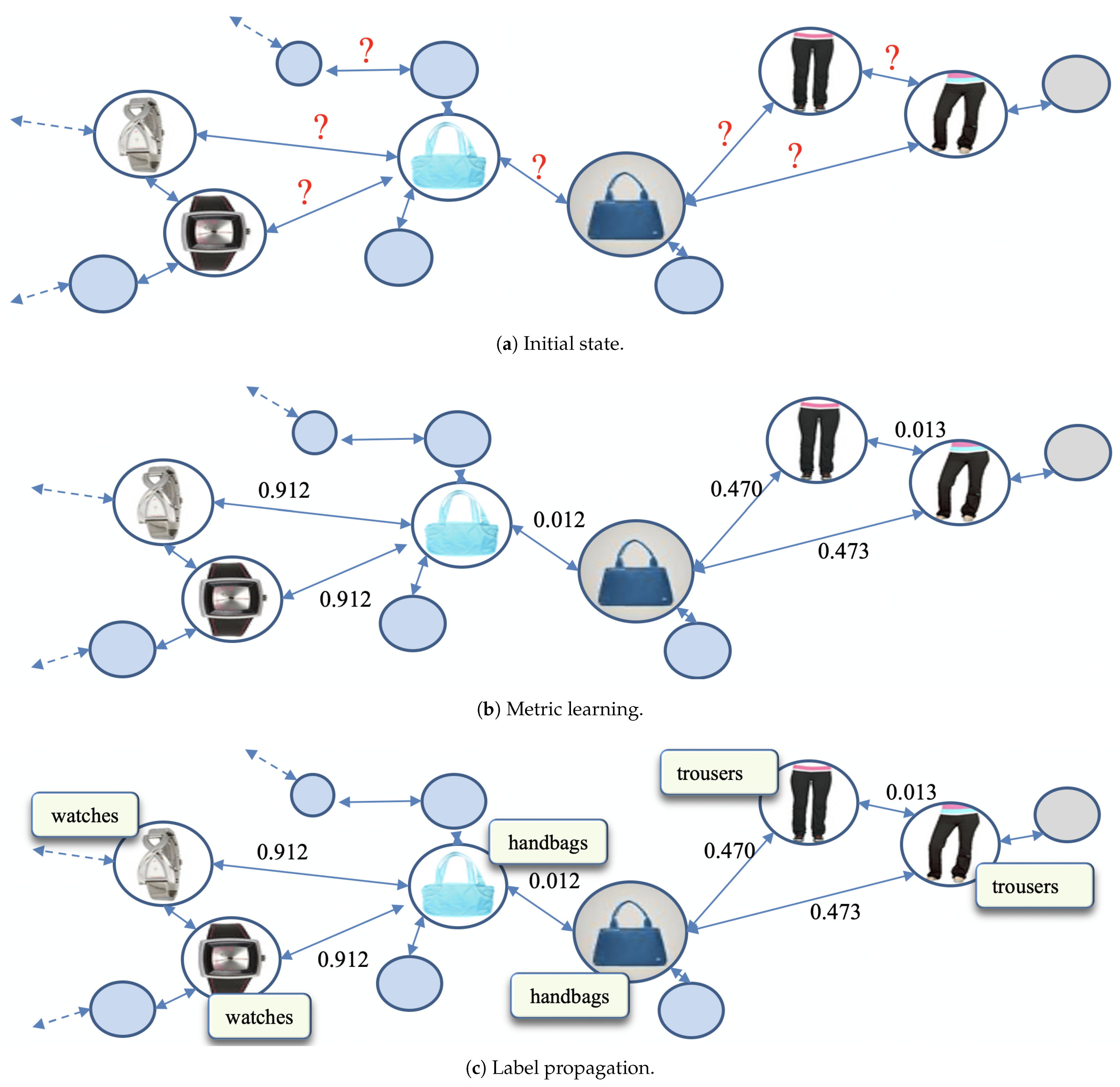
Figure 10 demonstrates the step-by-step operations of our algorithm.
Figure 10a indicates the initial state of our dataset with graphical representation.
Figure 10b indicates the state after DML, and
Figure 10c indicates the final state after label propagation.
Results
After recovering the labels of all images in the Fashion dataset [
5], we channeled our output to a sigmoid layer to convert the recovered labels as binary. Since we chose our sample by random uniform sampling, we performed each experiment 50 times to obtain the average accuracy and average precision. We also computed the variance of accuracy and precision of each model for different partial observations. We compared the performance of our algorithm with that of random guess. Random guess [
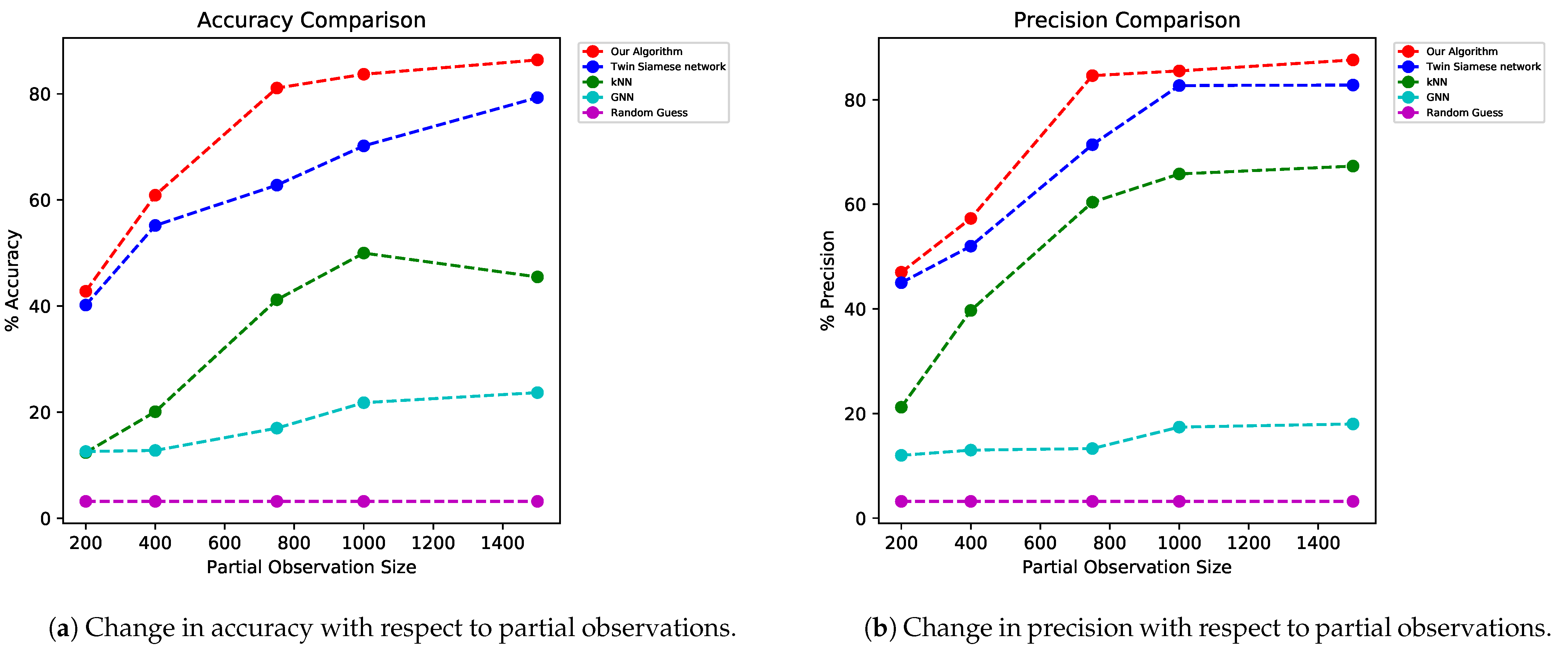
36] is the method of choosing elements at random where they all have an equal chance of being chosen. Our algorithm outperformed other baseline (random guess) and state-of-the-art algorithms, such as twin Siamese, k-nearest neighbors (k-NN), and GNN. We show the performance of our triple Siamese network with RA in
Figure 11a,b.
In
Figure 11, we observed the performance of our algorithm with different samples or partial-observation sizes. We sampled 5%, 10%, 18.75%, 25%, and 37.5% data points as our partial observations, and recovered the signal using this. With a very small number of samples (10% of sample size), our method performed significantly well compared to other methods.
We compared the performance of our model with different partial-observation sizes, and even with 400 partial-observation sizes out of 4000 data points, our model performed significantly better than other models did.
Table 1 and
Table 2 show the accuracy and precision comparison of our model with respect to other models for different partial-observation sizes, and the variance of the performance metrics with respect to partial observations.
7. Conclusions
In this work, we introduce a novel approach for SSL in the Fashion dataset, where we had a limited amount of labeled data to train our model. As the backbone of our algorithm, we assumed that similar data points resided close to each other in vector space, and different data points reside far away from each other in vector space. We then discussed a novel algorithm for DML approaches to retrieve similarity measures from image-feature vectors. Our DML model quickly converged and was able to capture fine-grain differences between class labels. We also discussed the concept of spectral graph theory and the application of harmonic analysis on the graph signal to recover the signal from our partially observed graph data. Our algorithm performed significantly better than GCN and the twin Siamese network did, even for the very small amount of labeled data in the Fashion dataset.
We plan to extend our work towards designing a generalized triple Siamese network in combination with transfer learning [
38], and evaluating its performance on other standard image datasets in the same or different domains, such as the Fashion-MNIST dataset [
39] and ImageNet [
40].
In the future, this work can be extended using different DML architectures such as FaceNet [
20]. This architecture is mainly used for classifying facial image datasets. The loss function used in this model was triplet loss function, which can be further extended in our framework.
Furthermore, this work can be extended towards other modalities using multimodal fusion architectures [
41], and can be compared with our framework for measuring performance. Moreover, we aim to extend this work using active learning [
42] and to evaluate the performance of the framework.