An Intelligent Model for the Prediction of Bond Strength of FRP Bars in Concrete: A Soft Computing Approach
Abstract
:1. Introduction
2. Genetic Programming
Multi-Gene Genetic Programming
3. Data Acquisition
4. Model Development
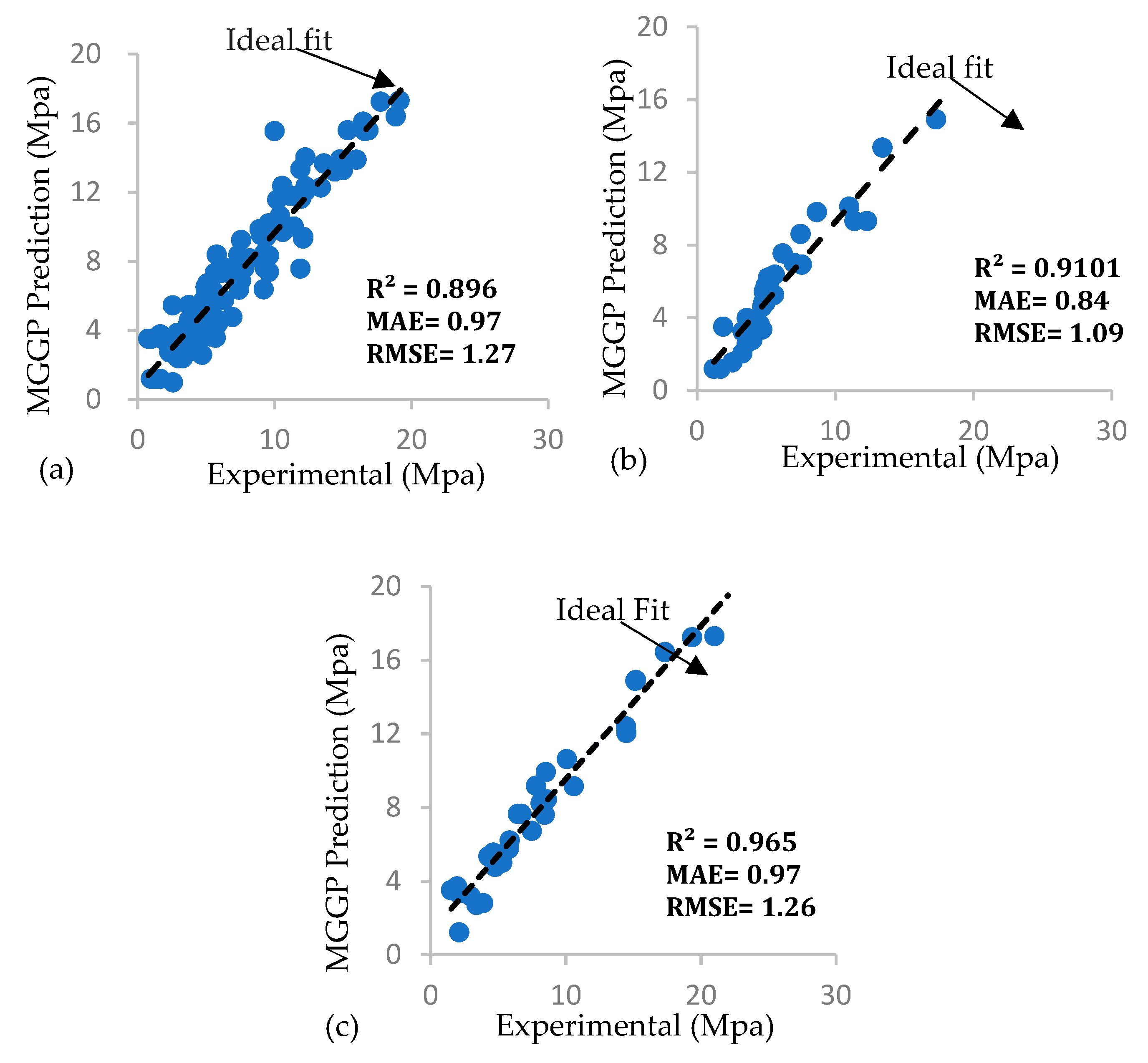
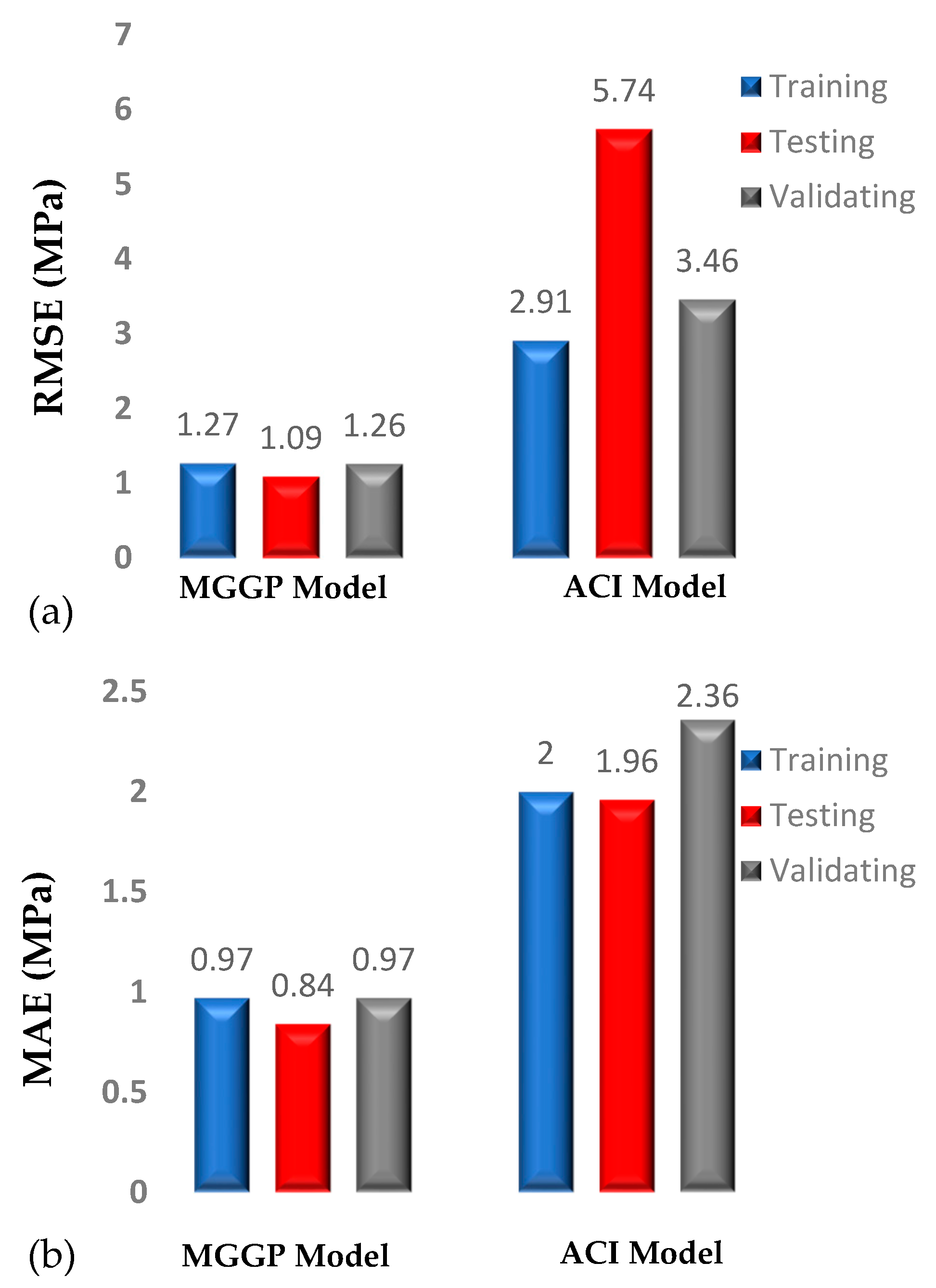
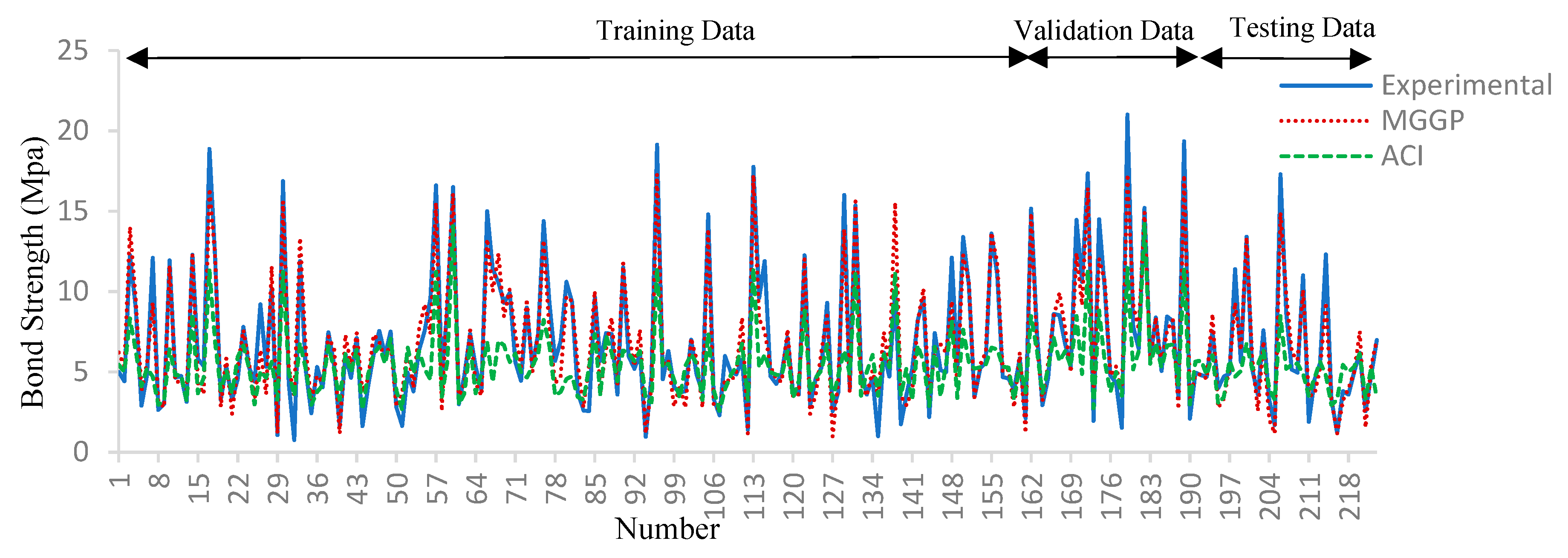
5. Results and Discussions
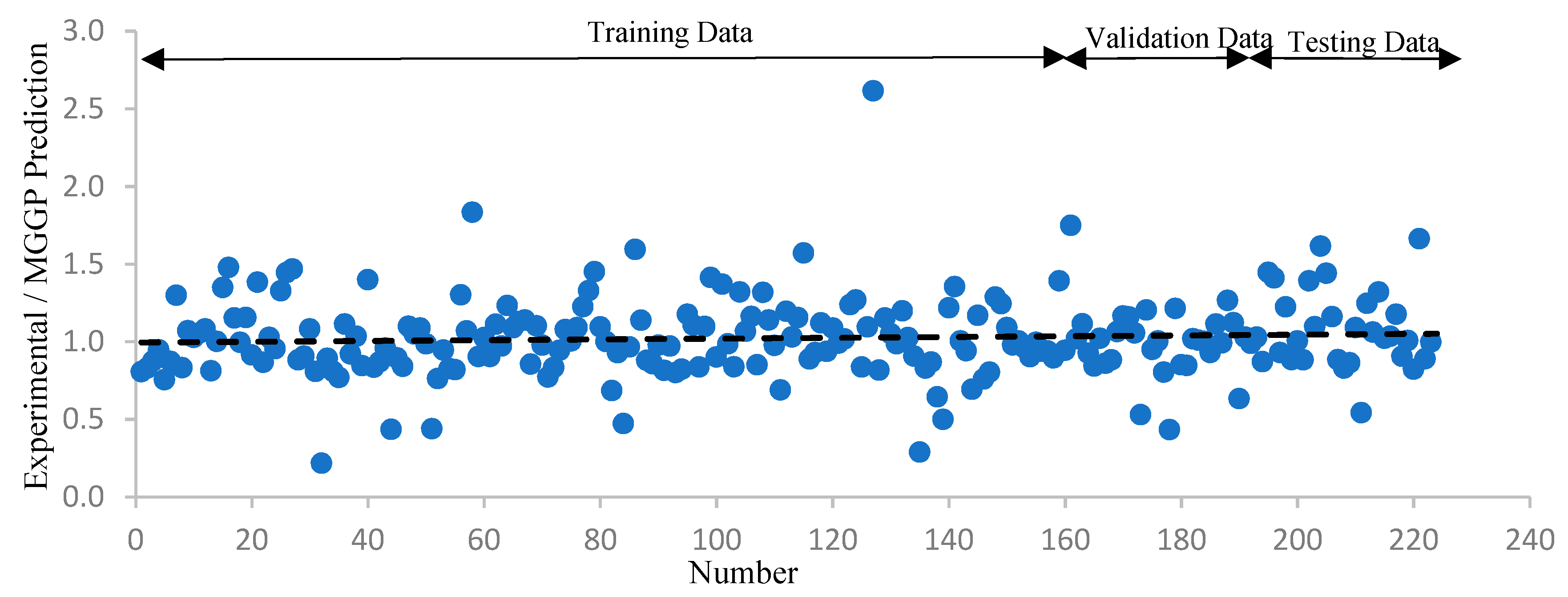
5.1. The MGGP-Based Formulation for Bond Strength
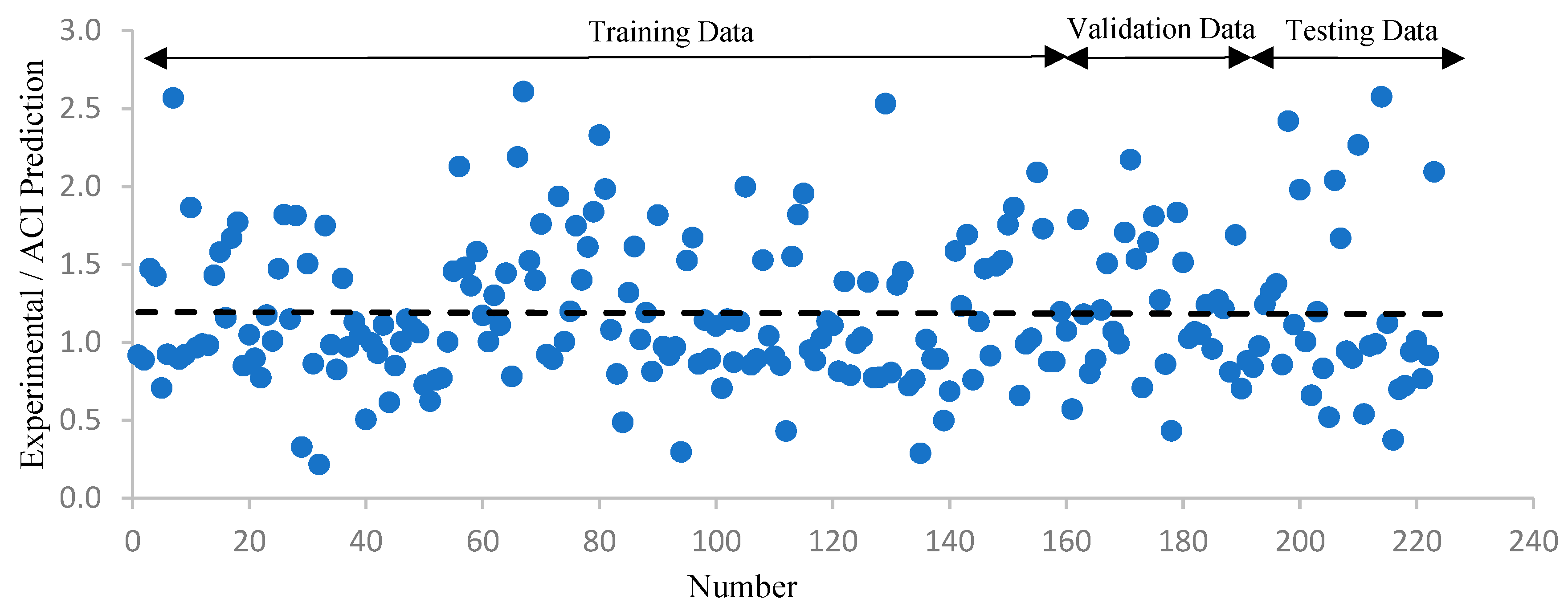
5.2. Comparative Study
6. Conclusion and Future Directions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Test No. | Pos | Surf | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 18.44 | 39.06 | 6 | 24.79 | 5.26 |
| 2 | 2 | 1 | 9.53 | 29.81 | 2 | 10.67 | 11.5 |
| 3 | 2 | 1 | 28.58 | 47.33 | 4 | 23.11 | 3.8 |
| 4 | 2 | 3 | 19.1 | 43.03 | 1.68 | 36.65 | 3.28 |
| 5 | 2 | 2 | 10 | 29.05 | 4 | 10 | 11.89 |
| 6 | 2 | 1 | 12.7 | 39.94 | 9.3 | 20 | 7.36 |
| 7 | 2 | 3 | 19.1 | 39.94 | 2.09 | 36.65 | 3.28 |
| 8 | 2 | 1 | 19.05 | 28.94 | 3.7 | 5 | 15.35 |
| 9 | 2 | 1 | 15.75 | 44.36 | 3 | 24.19 | 4.29 |
| 10 | 2 | 3 | 15.9 | 39.94 | 2.52 | 44.03 | 2.95 |
| 11 | 1 | 1 | 9.53 | 49 | 4 | 16 | 8.2 |
| 12 | 2 | 1 | 15.75 | 44.36 | 2 | 24.19 | 4.1 |
| 13 | 2 | 3 | 12.7 | 43.03 | 2.52 | 62.99 | 4.71 |
| 14 | 2 | 2 | 15.88 | 28.94 | 4.4 | 7.5 | 12.26 |
| 15 | 1 | 1 | 9.53 | 49 | 6 | 21.33 | 7 |
| 16 | 2 | 1 | 15.75 | 44.36 | 2 | 24.19 | 3.74 |
| 17 | 2 | 3 | 15.9 | 49 | 2.01 | 31.45 | 4.04 |
| 18 | 2 | 1 | 12.7 | 49.98 | 5.41 | 30 | 4.6 |
| 19 | 2 | 2 | 10 | 29.38 | 4 | 40 | 5.1 |
| 20 | 2 | 2 | 19.3 | 38.69 | 2 | 13.16 | 6.11 |
| 21 | 2 | 2 | 19.66 | 43.56 | 2 | 19.38 | 5.02 |
| 22 | 2 | 2 | 19.66 | 43.56 | 3 | 25.84 | 4.92 |
| 23 | 2 | 3 | 19.1 | 39.94 | 2.09 | 36.65 | 3.3 |
| 24 | 2 | 1 | 12.7 | 51.98 | 9.34 | 20 | 7.5 |
| 25 | 2 | 2 | 9.68 | 34.93 | 4 | 15.75 | 9.58 |
| 26 | 2 | 1 | 10.6 | 35.05 | 1.89 | 75.47 | 2.2 |
| 27 | 2 | 2 | 9.68 | 29.81 | 2 | 10.5 | 11.07 |
| 28 | 2 | 2 | 19.3 | 38.69 | 2 | 13.16 | 6.74 |
| 29 | 1 | 2 | 18.44 | 47.61 | 6 | 24.79 | 4.96 |
| 30 | 1 | 3 | 10 | 49.14 | 2.5 | 15 | 9.3 |
| 31 | 1 | 1 | 15.88 | 44.36 | 2 | 47 | 2.12 |
| 32 | 2 | 2 | 18.44 | 47.61 | 6 | 24.79 | 5.58 |
| 33 | 2 | 2 | 19.66 | 43.56 | 3 | 19.38 | 4.81 |
| 34 | 2 | 3 | 9.5 | 39.94 | 3.37 | 84.21 | 5.16 |
| 35 | 2 | 1 | 9.53 | 49 | 6 | 21.33 | 6.2 |
| 36 | 2 | 1 | 12.7 | 31.02 | 2.36 | 97.24 | 1.65 |
| 37 | 2 | 2 | 12.7 | 28.94 | 5.5 | 5 | 17.76 |
| 38 | 2 | 2 | 6.35 | 46.51 | 3.12 | 78 | 1.52 |
| 39 | 2 | 1 | 12.7 | 51.98 | 5.41 | 20 | 7.5 |
| 40 | 2 | 1 | 12.7 | 37.95 | 9.34 | 10 | 12.29 |
| 41 | 1 | 1 | 19.05 | 47.75 | 6 | 24 | 4.8 |
| 42 | 2 | 1 | 12.7 | 36.97 | 9.3 | 10 | 14.45 |
| 43 | 2 | 2 | 10 | 25.1 | 4 | 10 | 16 |
| 44 | 2 | 2 | 10 | 30.14 | 4 | 20 | 9 |
| 45 | 2 | 2 | 10 | 26.63 | 4 | 20 | 11.4 |
| 46 | 2 | 1 | 15.75 | 44.36 | 3 | 20.16 | 5 |
| 47 | 2 | 1 | 10.6 | 40.2 | 1.89 | 61.32 | 3 |
| 48 | 2 | 2 | 10 | 31.81 | 4 | 20 | 12.3 |
| 49 | 2 | 2 | 19.66 | 43.56 | 2 | 25.84 | 4.61 |
| 50 | 2 | 1 | 12.7 | 30.91 | 3.4 | 10 | 10.56 |
| 51 | 2 | 3 | 9.5 | 40.96 | 3.37 | 52.63 | 5.8 |
| 52 | 2 | 2 | 10 | 31.25 | 3.8 | 20 | 12.09 |
| 53 | 2 | 1 | 15.75 | 44.36 | 3 | 24.19 | 4.74 |
| 54 | 2 | 1 | 15.75 | 44.36 | 3 | 24.19 | 4.64 |
| 55 | 2 | 1 | 10.6 | 40.2 | 1.89 | 61.32 | 2.6 |
| 56 | 2 | 2 | 12.7 | 28.94 | 5.5 | 7.5 | 15.15 |
| 57 | 2 | 2 | 19.66 | 43.56 | 3 | 19.38 | 6.3 |
| 58 | 2 | 2 | 27.41 | 44.62 | 6 | 27.8 | 3.43 |
| 59 | 1 | 2 | 27.41 | 44.62 | 6 | 27.8 | 3.57 |
| 60 | 2 | 1 | 10.6 | 35.05 | 1.89 | 70.75 | 3.3 |
| 61 | 2 | 1 | 15.75 | 44.36 | 2 | 75.81 | 1.7 |
| 62 | 1 | 1 | 19.05 | 43.56 | 3 | 15 | 7.58 |
| 63 | 2 | 3 | 9.5 | 43.03 | 3.37 | 68.42 | 5.69 |
| 64 | 2 | 1 | 15.75 | 44.36 | 2 | 20.16 | 4.84 |
| 65 | 2 | 1 | 15.75 | 44.36 | 3 | 20.16 | 5.14 |
| 66 | 2 | 1 | 15.75 | 44.36 | 2 | 24.19 | 4.26 |
| 67 | 2 | 1 | 15.9 | 31.02 | 1.89 | 97.17 | 2.31 |
| 68 | 2 | 3 | 19.1 | 39.94 | 2.09 | 36.65 | 2.8 |
| 69 | 1 | 1 | 9.53 | 35.05 | 4 | 16 | 8.9 |
| 70 | 2 | 2 | 19.66 | 43.56 | 3 | 19.38 | 5.79 |
| 71 | 2 | 1 | 10.6 | 38.32 | 1.89 | 76.42 | 4 |
| 72 | 2 | 2 | 9.68 | 48.86 | 4 | 15.75 | 9.3 |
| 73 | 2 | 1 | 12.7 | 31.02 | 2.36 | 78.74 | 1.96 |
| 74 | 2 | 2 | 6.35 | 46.51 | 3.12 | 78 | 1.01 |
| 75 | 2 | 3 | 9.5 | 40.96 | 3.37 | 52.63 | 5.3 |
| 76 | 2 | 2 | 18.44 | 39.06 | 4 | 22.04 | 5.62 |
| 77 | 2 | 1 | 15.9 | 31.02 | 1.89 | 54.72 | 2.64 |
| 78 | 2 | 2 | 15.88 | 28.94 | 4.4 | 5 | 18.87 |
| 79 | 2 | 1 | 9.53 | 49 | 4 | 16 | 9.3 |
| 80 | 2 | 2 | 19.66 | 43.56 | 3 | 19.38 | 6.02 |
| 81 | 2 | 1 | 12.7 | 55.06 | 9.34 | 20 | 7.41 |
| 82 | 2 | 1 | 15.75 | 44.36 | 3 | 20.16 | 4.98 |
| 83 | 2 | 2 | 10 | 26.63 | 4 | 10 | 13.61 |
| 84 | 2 | 3 | 19.05 | 23.43 | 3.7 | 7.5 | 14.8 |
| 85 | 2 | 1 | 15.75 | 44.36 | 2 | 20.16 | 5.06 |
| 86 | 2 | 1 | 12.7 | 28.94 | 5.5 | 5 | 19.14 |
| 87 | 2 | 1 | 15.75 | 44.36 | 2 | 20.16 | 4.72 |
| 88 | 2 | 3 | 9.5 | 39.94 | 4.21 | 52.63 | 6.91 |
| 89 | 2 | 3 | 9.5 | 43.03 | 3.37 | 84.21 | 3.74 |
| 90 | 2 | 3 | 9.5 | 39.94 | 4.21 | 68.42 | 5.69 |
| 91 | 2 | 1 | 15.9 | 31.02 | 1.89 | 42.45 | 3.14 |
| 92 | 2 | 1 | 12.7 | 39.94 | 9.3 | 10 | 12.25 |
| 93 | 2 | 2 | 19.66 | 43.56 | 2 | 25.84 | 4.53 |
| 94 | 2 | 1 | 15.75 | 44.36 | 2 | 75.81 | 1.65 |
| 95 | 2 | 2 | 19.66 | 43.56 | 3 | 25.84 | 4.64 |
| 96 | 2 | 2 | 19.05 | 28.94 | 3.7 | 5 | 10 |
| 97 | 2 | 2 | 6.35 | 46.51 | 3.12 | 78 | 0.76 |
| 98 | 2 | 3 | 15.9 | 39.94 | 2.52 | 31.45 | 4.04 |
| 99 | 2 | 2 | 6.35 | 46.51 | 3.12 | 78 | 1.9 |
| 100 | 2 | 1 | 10.6 | 35.05 | 1.89 | 66.04 | 2.1 |
| 101 | 2 | 2 | 19.66 | 43.56 | 2 | 25.84 | 5.37 |
| 102 | 1 | 2 | 9.68 | 48.86 | 4 | 15.75 | 8.15 |
| 103 | 2 | 2 | 16 | 31.25 | 2.38 | 20 | 9.59 |
| 104 | 2 | 1 | 15.88 | 28.94 | 4.4 | 5 | 17.35 |
| 105 | 2 | 1 | 12.7 | 39.94 | 9.34 | 10 | 14.49 |
| 106 | 2 | 2 | 10 | 36.84 | 3.8 | 10 | 13.39 |
| 107 | 2 | 1 | 15.75 | 44.36 | 3 | 24.19 | 4.45 |
| 108 | 1 | 3 | 8 | 49.14 | 3.13 | 15 | 5.77 |
| 109 | 2 | 1 | 12.7 | 28.94 | 5.5 | 5 | 21 |
| 110 | 2 | 2 | 19.66 | 43.56 | 2 | 25.84 | 5.33 |
| 111 | 2 | 1 | 28.58 | 27.56 | 2 | 3.56 | 15.19 |
| 112 | 2 | 1 | 19.05 | 39.19 | 6 | 24 | 5.1 |
| 113 | 2 | 3 | 12.7 | 39.94 | 3.15 | 62.99 | 4.71 |
| 114 | 2 | 2 | 6.35 | 46.51 | 3.12 | 78 | 1.75 |
| 115 | 1 | 3 | 10 | 49.14 | 2.5 | 15 | 7.8 |
| 116 | 2 | 1 | 15.75 | 44.36 | 2 | 20.16 | 4.55 |
| 117 | 2 | 2 | 10 | 28.84 | 4 | 10 | 13.41 |
| 118 | 2 | 1 | 19.05 | 28.94 | 3.7 | 5 | 16.87 |
| 119 | 2 | 2 | 10 | 32.38 | 3.8 | 15 | 10.09 |
| 120 | 2 | 1 | 12.7 | 28.94 | 5.5 | 7.5 | 17.29 |
| 121 | 2 | 2 | 10 | 27.25 | 4 | 40 | 6.99 |
| 122 | 2 | 1 | 9.53 | 35.05 | 6 | 21.33 | 7.8 |
| 123 | 2 | 1 | 12.7 | 39.94 | 9.34 | 5 | 16.49 |
| 124 | 2 | 1 | 15.75 | 44.36 | 3 | 16.13 | 5.97 |
| 125 | 2 | 2 | 10 | 39.31 | 3.8 | 20 | 9.6 |
| 126 | 2 | 1 | 12.7 | 30.91 | 3.4 | 16 | 8.67 |
| 127 | 2 | 1 | 15.75 | 44.36 | 2 | 24.19 | 4.71 |
| 128 | 2 | 2 | 19.66 | 43.56 | 2 | 19.38 | 4.86 |
| 129 | 2 | 2 | 9.68 | 34.93 | 6 | 21 | 7.55 |
| 130 | 1 | 3 | 10 | 49.14 | 2.5 | 15 | 8.45 |
| 131 | 2 | 2 | 10 | 32.38 | 3.8 | 15 | 10.4 |
| 132 | 2 | 2 | 12.7 | 30.91 | 3.4 | 10 | 12.27 |
| 133 | 2 | 1 | 8 | 31.02 | 5 | 20 | 11.01 |
| 134 | 2 | 2 | 19.3 | 38.69 | 2 | 13.16 | 7.15 |
| 135 | 2 | 1 | 15.75 | 43.56 | 2 | 20.16 | 4.83 |
| 136 | 2 | 1 | 9.53 | 35.05 | 4 | 16 | 9.9 |
| 137 | 2 | 1 | 19.05 | 39.19 | 4 | 21.33 | 5.4 |
| 138 | 2 | 2 | 19.66 | 43.56 | 3 | 19.38 | 4.96 |
| 139 | 2 | 2 | 10 | 29.48 | 4 | 10 | 15 |
| 140 | 2 | 2 | 12.7 | 28.94 | 5.5 | 5 | 19.35 |
| 141 | 1 | 3 | 11 | 49.14 | 2.27 | 15 | 7.47 |
| 142 | 1 | 1 | 15.88 | 44.36 | 3 | 12.5 | 8.61 |
| 143 | 2 | 3 | 9.5 | 39.94 | 4.21 | 52.63 | 5.3 |
| 144 | 2 | 3 | 12.7 | 39.94 | 3.15 | 39.37 | 6 |
| 145 | 2 | 3 | 19.1 | 39.94 | 2.09 | 41.88 | 3.3 |
| 146 | 2 | 1 | 10.6 | 40.2 | 1.89 | 61.32 | 3.7 |
| 147 | 2 | 3 | 9.5 | 39.94 | 4.21 | 52.63 | 4.78 |
| 148 | 2 | 2 | 13.46 | 38.69 | 2 | 10.38 | 9.69 |
| 149 | 2 | 3 | 9.5 | 40.96 | 3.37 | 52.63 | 4.78 |
| 150 | 2 | 1 | 15.9 | 31.02 | 1.89 | 54.72 | 2.44 |
| 151 | 2 | 1 | 10.6 | 35.05 | 1.89 | 66.04 | 4.4 |
| 152 | 2 | 2 | 27.41 | 39.69 | 6 | 27.8 | 3.79 |
| 153 | 2 | 1 | 15.75 | 44.36 | 3 | 20.16 | 5.59 |
| 154 | 1 | 1 | 28.58 | 47.33 | 6 | 26.67 | 3.6 |
| 155 | 2 | 1 | 9.53 | 49 | 2 | 10.67 | 12.1 |
| 156 | 2 | 1 | 10.6 | 40.2 | 1.89 | 61.32 | 3.9 |
| 157 | 2 | 2 | 19.66 | 43.56 | 2 | 32.3 | 3.41 |
| 158 | 2 | 2 | 19.66 | 43.56 | 2 | 19.38 | 4.68 |
| 159 | 2 | 1 | 15.75 | 44.36 | 3 | 16.13 | 6.15 |
| 160 | 2 | 1 | 15.75 | 44.36 | 3 | 24.19 | 4.31 |
| 161 | 2 | 2 | 19.3 | 38.69 | 2 | 13.16 | 6.31 |
| 162 | 2 | 2 | 10 | 31.25 | 4 | 20 | 9.39 |
| 163 | 2 | 1 | 15.75 | 44.36 | 3 | 16.13 | 6.11 |
| 164 | 2 | 1 | 19.05 | 47.75 | 4 | 21.33 | 5.2 |
| 165 | 2 | 1 | 28.58 | 39.69 | 6 | 26.67 | 3.6 |
| 166 | 2 | 1 | 19.05 | 28.94 | 3.7 | 7.5 | 14.39 |
| 167 | 1 | 2 | 9.68 | 34.93 | 4 | 15.75 | 8.53 |
| 168 | 1 | 2 | 27.41 | 39.69 | 6 | 27.8 | 3.84 |
| 169 | 2 | 2 | 19.3 | 38.69 | 2 | 13.16 | 6.46 |
| 170 | 2 | 3 | 15.9 | 43.03 | 2.01 | 44.03 | 2.95 |
| 171 | 2 | 1 | 19.05 | 47.75 | 6 | 24 | 4.9 |
| 172 | 1 | 1 | 19.05 | 39.19 | 6 | 24 | 5.2 |
| 173 | 2 | 1 | 12.7 | 31.02 | 2.36 | 36.22 | 3.73 |
| 174 | 2 | 1 | 12.7 | 51.84 | 9.3 | 30 | 4.61 |
| 175 | 2 | 2 | 10 | 41.47 | 3.8 | 15 | 9 |
| 176 | 2 | 1 | 12.7 | 37.95 | 9.3 | 20 | 7.5 |
| 177 | 2 | 3 | 9.5 | 39.94 | 4.21 | 84.21 | 3.74 |
| 178 | 2 | 2 | 19.66 | 43.56 | 3 | 25.84 | 5 |
| 179 | 2 | 1 | 8 | 31.02 | 5 | 15 | 10.2 |
| 180 | 2 | 1 | 15.75 | 44.36 | 2 | 75.81 | 1.07 |
| 181 | 2 | 3 | 19.1 | 39.94 | 2.09 | 26.18 | 3.6 |
| 182 | 2 | 3 | 9.5 | 40.96 | 3.37 | 115.79 | 4.76 |
| 183 | 1 | 3 | 8 | 49.14 | 3.13 | 15 | 8.38 |
| 184 | 1 | 1 | 15.88 | 44.36 | 3 | 15 | 7.11 |
| 185 | 2 | 2 | 10 | 31.25 | 3.8 | 20 | 11.39 |
| 186 | 2 | 1 | 15.75 | 44.36 | 2 | 75.81 | 1.41 |
| 187 | 1 | 3 | 13 | 49.14 | 1.92 | 15 | 4.96 |
| 188 | 2 | 2 | 10 | 33.18 | 4 | 20 | 10.6 |
| 189 | 2 | 2 | 16 | 41.47 | 2.38 | 15 | 11.89 |
| 190 | 2 | 1 | 15.75 | 44.36 | 3 | 24.19 | 4.43 |
| 191 | 2 | 1 | 15.75 | 43.56 | 2 | 20.16 | 5.28 |
| 192 | 2 | 2 | 19.05 | 28.94 | 3.7 | 5 | 16.6 |
| 193 | 2 | 1 | 15.75 | 44.36 | 3 | 16.13 | 5.65 |
| 194 | 2 | 1 | 12.7 | 55.06 | 5.41 | 20 | 7.41 |
| 195 | 2 | 2 | 19.66 | 43.56 | 2 | 19.38 | 5.3 |
| 196 | 2 | 2 | 10 | 28.94 | 4 | 20 | 10.61 |
| 197 | 1 | 1 | 28.58 | 39.69 | 6 | 26.67 | 3.6 |
| 198 | 2 | 3 | 19.1 | 39.94 | 2.09 | 57.59 | 2.56 |
| 199 | 2 | 3 | 9.5 | 39.94 | 4.21 | 84.21 | 5.16 |
| 200 | 2 | 1 | 12.7 | 31.02 | 2.36 | 97.24 | 1.63 |
| 201 | 1 | 3 | 10 | 49.14 | 2.5 | 15 | 7.37 |
| 202 | 2 | 1 | 15.75 | 44.36 | 2 | 20.16 | 5.23 |
| 203 | 2 | 1 | 12.7 | 49.98 | 9.34 | 30 | 4.6 |
| 204 | 2 | 2 | 9.68 | 48.86 | 6 | 21 | 6.19 |
| 205 | 2 | 2 | 19.66 | 43.56 | 2 | 19.38 | 5.37 |
| 206 | 2 | 3 | 19.1 | 40.96 | 1.68 | 26.18 | 3.6 |
| 207 | 2 | 1 | 15.75 | 44.36 | 2 | 75.81 | 0.97 |
| 208 | 2 | 1 | 15.75 | 43.56 | 2 | 20.16 | 4.66 |
| 209 | 1 | 2 | 27.41 | 39.69 | 4 | 24.1 | 3.94 |
| 210 | 2 | 2 | 16 | 39.31 | 2.38 | 20 | 9.2 |
| 211 | 1 | 3 | 12 | 49.14 | 2.08 | 15 | 7.54 |
| 212 | 2 | 3 | 19.1 | 39.94 | 3.66 | 36.65 | 2.9 |
| 213 | 2 | 1 | 15.75 | 44.36 | 2 | 75.81 | 1.22 |
| 214 | 1 | 2 | 18.44 | 39.06 | 6 | 24.79 | 5.35 |
| 215 | 2 | 2 | 19.66 | 43.56 | 3 | 25.84 | 4.75 |
| 216 | 2 | 1 | 15.75 | 44.36 | 3 | 16.13 | 7.35 |
| 217 | 1 | 1 | 28.58 | 44.76 | 2 | 19.56 | 3.8 |
| 218 | 2 | 3 | 9.5 | 39.94 | 4.21 | 68.42 | 5.13 |
| 219 | 2 | 1 | 15.75 | 44.36 | 2 | 20.16 | 2.57 |
| 220 | 2 | 1 | 10.6 | 35.05 | 1.89 | 66.04 | 3 |
| 221 | 1 | 2 | 9.68 | 29.81 | 2 | 10.5 | 11.94 |
| 222 | 2 | 1 | 15.75 | 44.36 | 3 | 20.16 | 5.85 |
| 223 | 2 | 3 | 19.1 | 40.96 | 1.68 | 57.59 | 2.56 |
References
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Behavior and modeling of bond of FRP rebar to concrete. J. Compos. Constr. 1987, 1, 40–45. [Google Scholar] [CrossRef]
- Edwards, A.D.; Yannopoulos, P.J. Local bond stress to slip relationship for hot rolled deformed bars and mild steel plain bars. ACI J. 1979, 7, 405–419. [Google Scholar]
- Galati, N.; Nanni, A.; Dharani, L.R.; Focacci, F.; Aiello, M.A. Thermal effects on bond between FRP rebars and concrete. Compos. Manuf. A 2006, 37, 1223–1230. [Google Scholar] [CrossRef]
- Hao, Q.D.; Wang, B.; Ou, J.P. Fiber reinforced polymer rebar’s application to civil engineering. Concrete 2006, 9, 38–40. [Google Scholar]
- Benmokrane, B.; Tighiouart, B. Bond strength and load concrete. ACI Mater. J. 1996, 93, 254–259. [Google Scholar]
- Makitani, E.; Irisawa, I.; Nishiura, N. Investigation of bond in concrete member with fiber reinforced plastic bars. Fiber-Reinf.-Plast. Reinf. Concr. Struct.-Int. Symp. 1993, 138, 315–331. [Google Scholar]
- Mazaheripour, H.; Barros, J.A.; Sena-Cruz, J.M.; Pepe, M.; Martinelli, E. Experimental study on bond performance of GFRP bars in self-compacting steel fiber reinforced concrete. Compos. Struct. 2013, 95, 202–212. [Google Scholar] [CrossRef]
- Okelo, R.; Yuan, R.L. Bond strength of fiber reinforced polymer rebars in normal strength concrete. J. Compos. Constr. 2005, 9, 203–213. [Google Scholar] [CrossRef]
- Yan, F.; Lin, Z.; Zhang, D.; Gao, Z.; Li, M. Experimental study on bond durability of glass fiber reinforced polymer bars in concrete exposed to harsh environmental agents: Freeze-thaw cycles and alkaline-saline solution. Compos. Part B Eng. 2017, 116, 206–421. [Google Scholar] [CrossRef]
- Yan, F.; Lin, Z.B. Bond durability assessment and long-term degradation prediction for GFRP bars to fiber-einforced concrete under saline solutions. Compos. Struct. 2017, 161, 393–406. [Google Scholar] [CrossRef]
- Ametrano, D. Bond Characteristics of Glass Fiber Reinforced Polymer Bars Embedded in High Performance and Ultra-High-Performance Concrete. Master’s Thesis, Ryerson University, Toronto, ON, Canada, 2011; pp. 1–132. [Google Scholar]
- Dahou, Z.; Sbartai, Z.M.; Castel, A.; Ghomari, F. Artificial neural network model for steel-concrete bond prediction. Eng. Struct. 2009, 31, 1724–1733. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Rahai, A.; Sebt, M.H.; Akbarpour, H. Prediction of bond strength of spliced steel bars in concrete using artificial neural network and fuzzy logic. Constr. Build. Mater. 2012, 36, 411–418. [Google Scholar] [CrossRef]
- Nehdi, M.; EI Chabib, H.; EI Naggar, M.H. Predicting performance of self-compacting concrete mixtures using artificial neural networks. ACI Mater. J. 2001, 98, 394–401. [Google Scholar]
- Parsaie, A.; Azamathulla, H.M.; Haghiabi, A.H. Prediction of discharge coefficient of cylindrical weir–gate using GMDH-PSO. ISH J. Hydraul. Eng. 2018, 24, 116–123. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Haghiabi, A.H.; Parsaie, A. Prediction of side weir discharge coefficient by support vector machine technique. Water Sci. Technol. Water Supply 2016, 16, 1002–1016. [Google Scholar] [CrossRef]
- D’Angelo, G.; Laracca, M.; Rampone, S. Automated eddy current non-destructive testing through low definition Lissajous figures. In Proceedings of the 2016 IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 22–23 June 2016; pp. 280–285. [Google Scholar]
- D’Angelo, G.; Laracca, M.; Rampone, S.; Betta, G. Fast eddy current testing defect classification using lissajous figures. IEEE Trans. Instrum. Meas. 2018, 67, 821–830. [Google Scholar] [CrossRef]
- Coelho, M.R.F.; Sena-Cruz, J.M.; Neves, L.A.C.; Pereira, M.; Cortez, P.; Miranda, T. Using data mining algorithms to predict the bond strength of NSM FRP systems in concrete. Constr. Build. Mater. 2016, 126, 484–495. [Google Scholar] [CrossRef]
- Köroğlu, M.A. Artificial neural network for predicting the flexural bond strength of FRP bars in concrete. Sci. Eng. Compos. Mater. 2018, 26, 12–29. [Google Scholar] [CrossRef]
- Bashir, R.; Ashour, A. Neural network modelling for bars. J. Compos. B 2012, 43, 3198–3207. [Google Scholar] [CrossRef]
- Banzhaf, W.; Nordin, P.; Keller, R.; Francone, F. Genetic Programming—An Introduction; Morgan Kaufmann: San Francisco, CA, USA, 1998. [Google Scholar]
- Koza, J.R. Genetic Programming-on the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Alavi, A.H.; Gandomi, A.H. A robust data mining approach for formulation of geotechnical engineering systems. Eng. Comput. 2011, 28, 242–274. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H.; Modaresnezhad, M.; Mousavi, M. New ground-motion prediction equations using multi expression programing. J. Earthq. Eng. 2011, 15, 511–536. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Expression programming techniques for formulation of structural engineering systems. In Metaheuristic Applications in Structures and Infrastructures; Newnes: Burlington, MA, USA, 2013; pp. 439–455. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H.; Sahab, M.G. New formulation for compressive strength of CFRP confined concrete cylinders using linear genetic programming. Mater. Struct. 2010, 43, 963–983. [Google Scholar] [CrossRef]
- Mohammadi Bayazidi, A.; Wang, G.G.; Bolandi, H.; Alavi, A.H.; Gandomi, A.H. Multigene genetic programming for estimation of elastic modulus of concrete. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef]
- Sarveghadi, M.; Gandomi, A.H.; Bolandi, H.; Alavi, A.H. Development of prediction models for shear strength of SFRCB using a machine learning approach. Neural Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Kara, I.F. Prediction of shear strength of FRP-reinforced concrete beams without stirrups based on genetic programming. Adv. Eng. Softw. 2011, 42, 295–304. [Google Scholar] [CrossRef]
- Searson, D.P. GPTIPS: Genetic Programming and Symbolic Regression for MATLAB; Newcastle University Library: Newcastle upon Tyne, UK, 2009. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H. A new multi-gene genetic programming approach to nonlinear system modeling—Part I: Materials and structural engineering problems. Neural Comput. Appl. 2012, 21, 171–187. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. A new multi-gene genetic programming approach to non-linear system modeling—Part II: Geotechnical and earthquake engineering problems. Neural Comput. Appl. 2012, 21, 189–201. [Google Scholar] [CrossRef]
- Muduli, P.K.; Das, S.K. CPT-based seismic liquefaction potential evaluation using multi-gene genetic programming approach. Indian Geotech. J. 2014, 44, 86–93. [Google Scholar] [CrossRef]
- Rezaei, M.; Eftekhari, M.; Mahin, S.; Ranjbar, M. A CO2-oil minimum miscibility pressure model based on multi-gene genetic programming. Energy Explor. Exploit. 2013, 31, 607–622. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Aminian, P.; Gandomi, A.H.; Alavi, A.H.; Bolandi, H. A new predictive model for compressive strength of HPC using gene expression programming. Adv. Eng. Softw. 2012, 45, 105–114. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Rahai, A.; Sebt, M.H. Artificial neural network and genetic programming for predicting the bond strength of GFRP bars in concrete. Mater. Struct. 2015, 48, 1581–1602. [Google Scholar] [CrossRef]
- Searson, D.P.; Leahy, D.E.; Willis, M.J. GPTIPS: An open source genetic programming toolbox for multigene symbolic regression. In Proceedings of the International Multi-Conference of Engineers and Computer Scientists (IMECS ’10), Hong Kong, China, 17–19 March 2010; pp. 77–80. [Google Scholar]
- Aly, R.; Benmokrane, B. Bond splitting strength of lap splicing of GFRP bars in concrete. In Proceedings of the 33rd Annual General Conference of the Canadian Society for Civil Engineering, Toronto, ON, Canada, 2–4 June 2010. [Google Scholar]
- Aly, R.; Benmokrane, B.; Ebead, U. Tensile lap splicing of fibre-reinforced polymer reinforcing bars in concrete. ACI Struct. J. 2006, 103, 857–864. [Google Scholar]
- Cosenza, E.; Manfredi, G.; Pecce, M.; Realfonzo, R. Bond between glass fiber reinforced plastic reinforcing bars and concrete-experimental analysis. ACI SP Int. Symp. FRP Reinf. Concr. 1999, 188, 347–358. [Google Scholar]
- DeFreese, J.M.; Wollmann, R.C.L. Glass Fiber Reinforced Polymer Bars as Top Mat Reinforcement for Bridge Decks; Contract Report for Virginia Transportation Research Council: Charlottesville, VA, USA, 2002. [Google Scholar]
- Ehsani, M.R.; Saadatmanesh, H.; Tao, S. Bond of GFRP rebars to ordinary-strength concrete. ACI IntSympon Non-Met. Contin. Reinf. 1993, 138, 333–346. [Google Scholar]
- Ehsani, M.R.; Saadatmanesh, H.; Tao, S. Design recommendations for bond of GFRP rebars to concrete. J. Struct. Eng. 1996, 122, 247–254. [Google Scholar] [CrossRef]
- Kanakubo, T.; Yonemaru, K.; Fukuyama, H.; Fujisawa, M.; Sonobe, Y. Bond performance of concrete members reinforced with FRP bars. Fiber-Reinf.-Plast. Reinf. Concr. Struct.-Int. Symp. 1993, 138, 767–788. [Google Scholar]
- Maji, A.; Orozco, A.L. Prediction of bond failure and deflection of carbon fiber reinforced plastic reinforced concrete beams. Exp. Mech. 2005, 45, 35–41. [Google Scholar] [CrossRef]
- Okelo, R. Realistic bond strength of FRP rebars in NSC from beam specimens. J. Aerosp. Eng. 2007, 20, 133–140. [Google Scholar] [CrossRef]
- Pecce, M.; Manfredi, G.; Realfonzo, R.; Cosenza, E. Experimental and analytical evaluation of bond properties of GFRP bars. J. Mater. Civ. Eng. 2001, 13, 282–290. [Google Scholar] [CrossRef]
- Shield, C.K.; French, C.W.; Retika, A. Thermal and mechanical fatigue effects on GFRP rebar-concrete bond. In Proceedings of the Third International Symposium on Non-Metallic Reinforcement for Concrete Structures, Sapporo, Japan, 14–16 October 1997; pp. 381–388. [Google Scholar]
- Shield, C.K.; French, C.W.; Hanus, J.P. Bond of glass fiber reinforced plastic reinforcing bar for consideration in bridge decks. ACI SP Int. Symp. FRP Reinf. Concr. 1999, 188, 393–406. [Google Scholar]
- Thamrin, R.; Kaku, T. Bond behaviour of CFRP bars in simply supported reinforced concrete beam with hanging region. J. Compos. Constr. 2007, 11, 129–137. [Google Scholar] [CrossRef]
- Tughiouart, B.; Benmokrane, B.; Geo, D. Investigation of bond in concrete member with fiber reinforced polymer (FRP) bars. Constr. Build. Mater. 1998, 12, 453–462. [Google Scholar] [CrossRef]
- Tughiouart, B.; Benmokrane, B.; Mukhopadhyaya, P. Bond strength of glass FRP rebar splices in beams under static loading. Constr. Build. Mater. 1999, 13, 383–392. [Google Scholar] [CrossRef]
- Won, J.P.; Park, G.G.; Kim, H.H.; Lee, S.W.; Jang, C.I. Effect of fibers on the bonds between FRP reinforcing bars and high-strength concrete. Compos. Part B Eng. 2008, 39, 747–755. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H.; Sahab, M.G.; Arjmandi, P. Formulation of elastic modulus of concrete using linear genetic programming. J. Mech. Sci. Technol. 2010, 24, 1273–1278. [Google Scholar] [CrossRef]
- American Concrete Institute. ACI Committee 440.1R-06 (2006) Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars; American Concrete Institute: Farmington Hills, MI, USA, 2006. [Google Scholar]
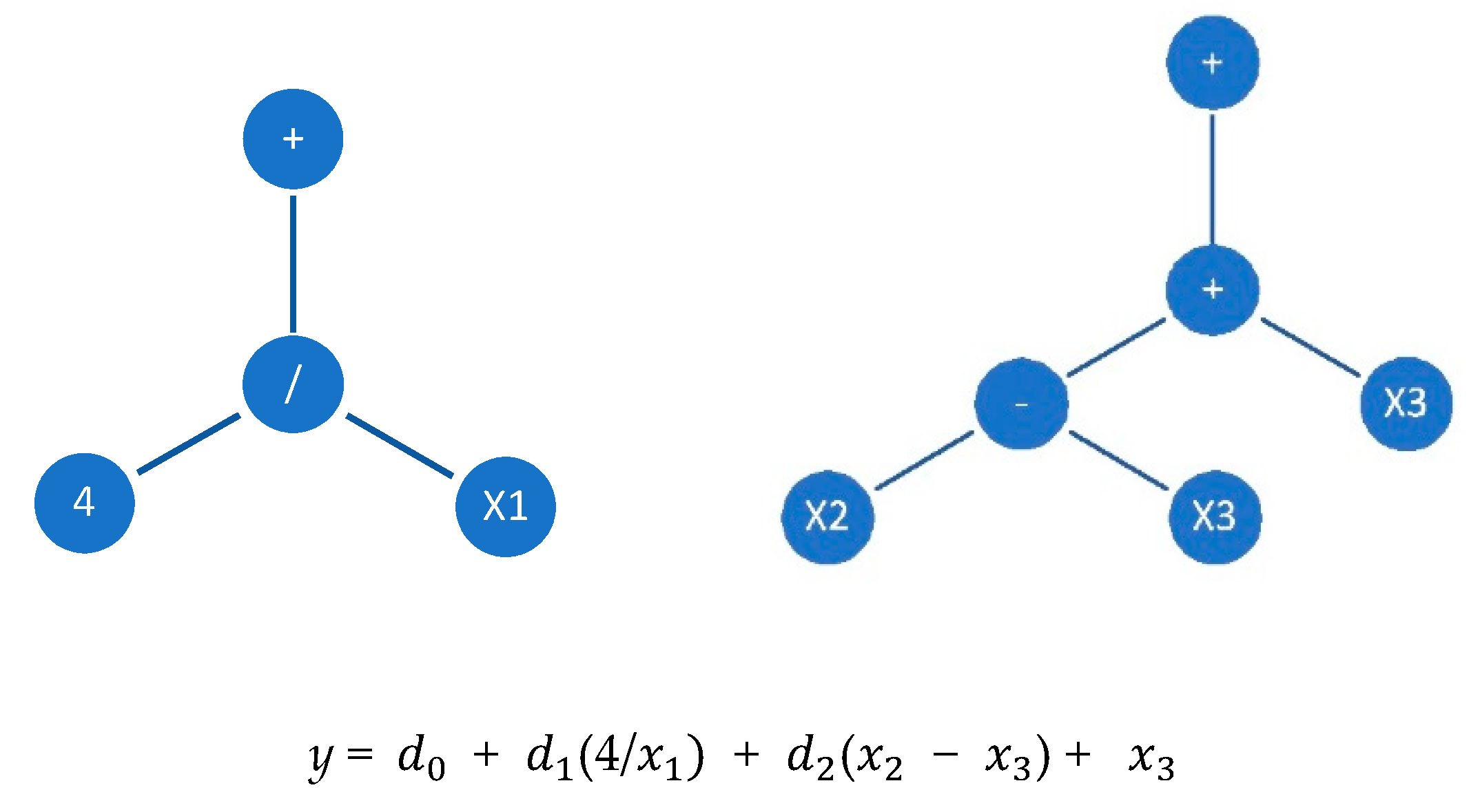



| Variables | Min | Max | Mean | Median | STD |
|---|---|---|---|---|---|
| Surf | 1 | 3 | 1.16 | 1 | 0.44 |
| Pos | 1 | 2 | 1.25 | 1 | 0.43 |
| 6.35 | 21 | 10.54 | 8.5 | 2.88 | |
| / | 1.68 | 9.34 | 3.58 | 3 | 1.82 |
| 3.56 | 115.79 | 30.14 | 20.16 | 23.01 | |
| 23.43 | 55.06 | 40.04 | 40.2 | 6.72 | |
| 0.76 | 21 | 6.79 | 5.3 | 4.15 |
| Parameter | Setting |
|---|---|
| Function set | +, −, /, √, ln, square, cubic power |
| Population size | 1000 |
| Number of generations | 500 |
| Max number of genes | 8 |
| Max tree depth | 6 |
| Tournament size | 12 |
| Elitism | 0.01% of population |
| Crossover events | 0.85 |
| Mutation events | 0.1 |
| Probability of pareto to tournament | 0.2 |
| Term | Value |
|---|---|
| Bias | 4.67 |
| Gene 1 | |
| Gene 2 | −0.00108 |
| Gene 3 | 0.0665 − 0.133 / − 0.0665 + 0.249 |
| Gene 4 | −4.16ln(2surf + / + ( × /) |
| Gene 5 | 0.174/ |
| Gene 6 | 2.26ln(/) |
| Gene 7 | −0.189 |
| Gene 8 | 34.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolandi, H.; Banzhaf, W.; Lajnef, N.; Barri, K.; Alavi, A.H. An Intelligent Model for the Prediction of Bond Strength of FRP Bars in Concrete: A Soft Computing Approach. Technologies 2019, 7, 42. https://doi.org/10.3390/technologies7020042
Bolandi H, Banzhaf W, Lajnef N, Barri K, Alavi AH. An Intelligent Model for the Prediction of Bond Strength of FRP Bars in Concrete: A Soft Computing Approach. Technologies. 2019; 7(2):42. https://doi.org/10.3390/technologies7020042
Chicago/Turabian StyleBolandi, Hamed, Wolfgang Banzhaf, Nizar Lajnef, Kaveh Barri, and Amir H. Alavi. 2019. "An Intelligent Model for the Prediction of Bond Strength of FRP Bars in Concrete: A Soft Computing Approach" Technologies 7, no. 2: 42. https://doi.org/10.3390/technologies7020042
APA StyleBolandi, H., Banzhaf, W., Lajnef, N., Barri, K., & Alavi, A. H. (2019). An Intelligent Model for the Prediction of Bond Strength of FRP Bars in Concrete: A Soft Computing Approach. Technologies, 7(2), 42. https://doi.org/10.3390/technologies7020042





