Embodied Energy Optimization of Prestressed Concrete Slab Bridge Decks
Abstract
1. Introduction
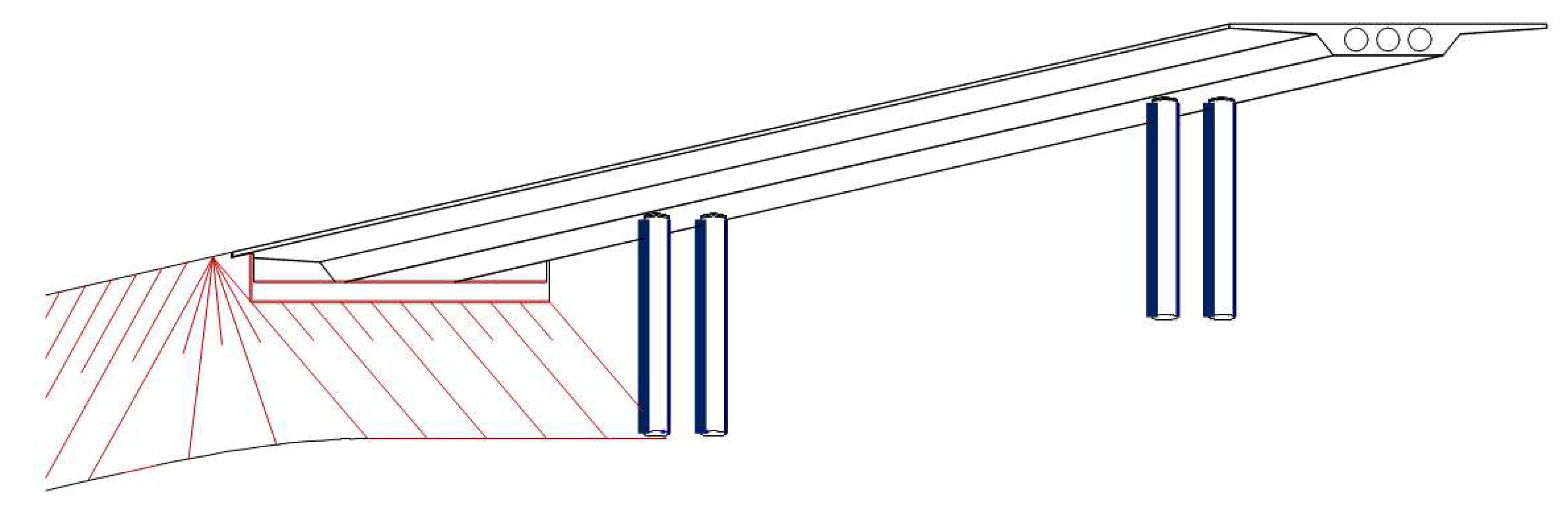
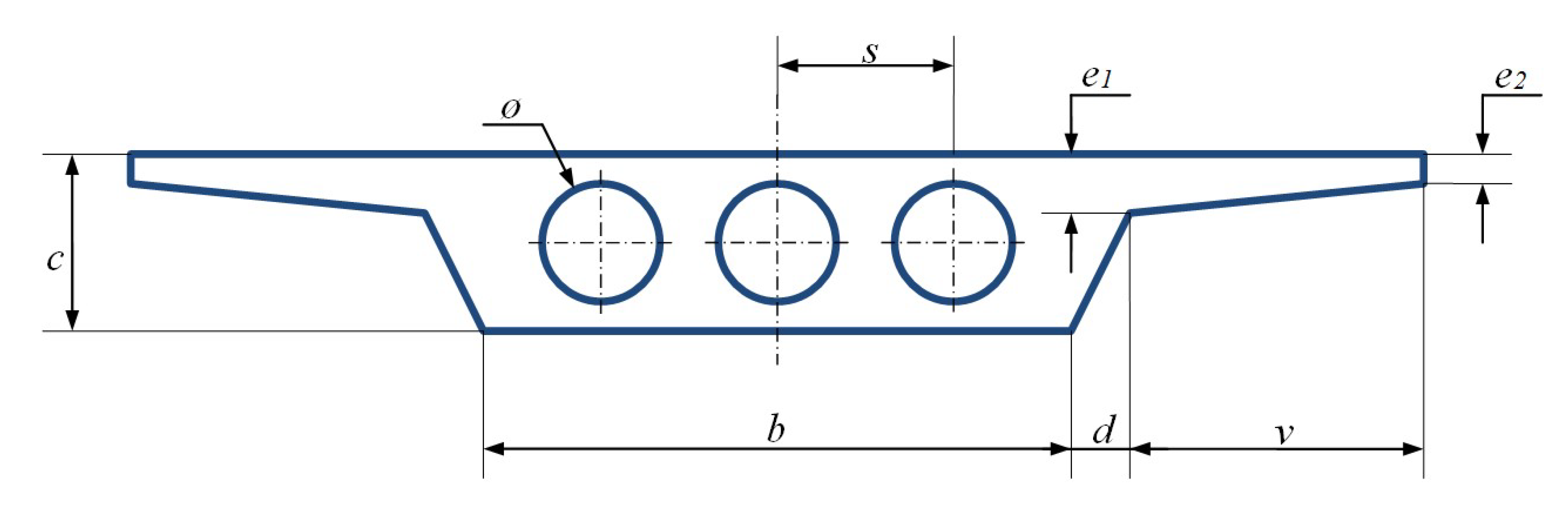
2. The Optimum Design Problem
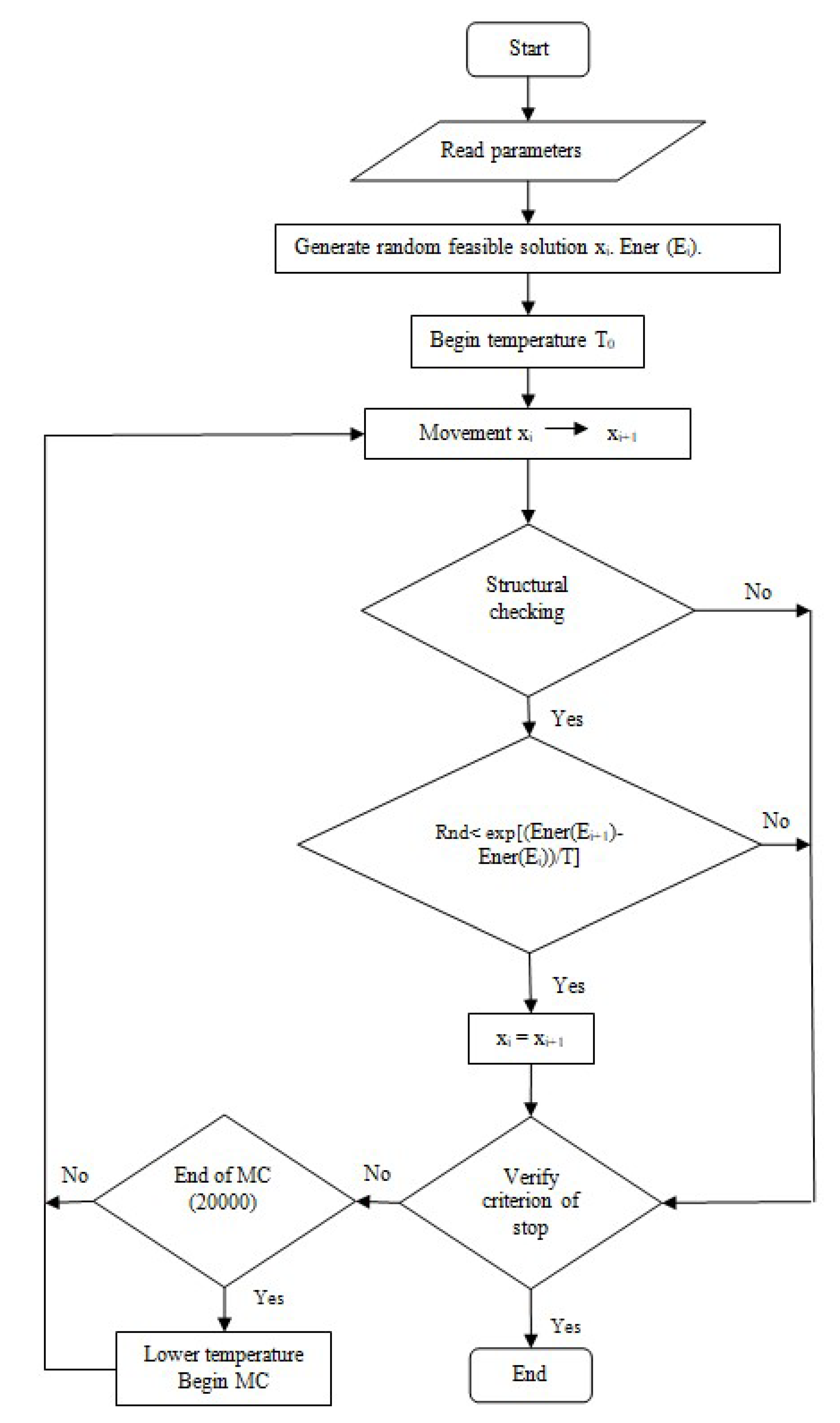
3. Experimental
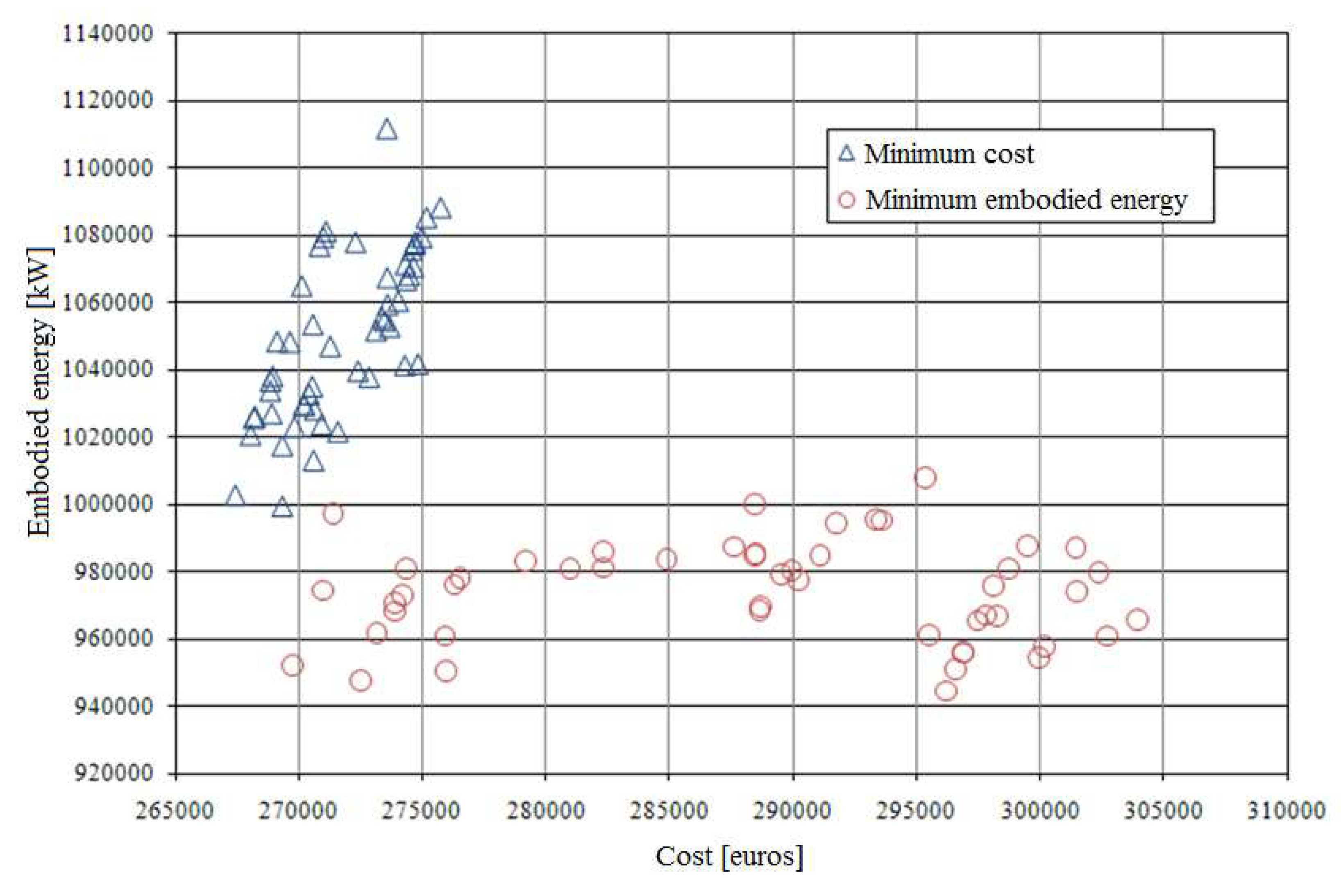
4. Results and Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Waas, T.; Hugé, J.; Block, T.; Wright, T.; Benitez-Capistros, F.; Verbruggen, A. Sustainability Assessment and Indicators: Tools in a Decision-Making Strategy for Sustainable Development. Sustainability 2014, 6, 5512–5534. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.; Yepes, V. A review of multi-criteria decision-making methods applied to the sustainable bridge design. Sustainability 2016, 8, 1295. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Vilutiene, T.; Adeli, H. Sustainable decision making in civil engineering, construction and building technology. Sustainability 2018, 10, 14. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T. Cost and CO2 emission optimization of precast-prestressed concrete U-beam road bridges by a hybrid glowworm swarm algorithm. Autom. Constr. 2015, 49, 123–134. [Google Scholar] [CrossRef]
- Camp, C.V.; Assadollahi, A. CO2 and cost optimization of reinforced concrete footings using a hybrid big bang-big crunch algorithm. Struct. Multidiscip. Optim. 2013, 48, 411–426. [Google Scholar] [CrossRef]
- Martí, J.V.; García-Segura, T.; Yepes, V. Structural design of precast-prestressed concrete U-beam road bridges based on embodied energy. J. Clean. Prod. 2016, 120, 231–240. [Google Scholar] [CrossRef]
- Wang, E.; Shen, Z. A hybrid Data Quality Indicator and statistical method for improving uncertainty analysis in LCA of complex system—Application to the whole-building embodied energy analysis. J. Clean. Prod. 2013, 43, 166–173. [Google Scholar] [CrossRef]
- Miller, D.; Doh, J.-H.; Mulvey, M. Concrete slab comparison and embodied energy optimisation for alternate design and construction techniques. Constr. Build. Mater. 2015, 80, 329–338. [Google Scholar] [CrossRef]
- Foraboschi, P.; Mercanzin, M.; Trabucco, D. Sustainable Structural Design of Tall Buildings Based on Embodied Energy. Energy Build. 2014, 68, 254–269. [Google Scholar] [CrossRef]
- Yeo, D.; Gabbai, R.D. Sustainable Design of Reinforced Concrete Structures through Embodied Energy Optimization. Energy Build. 2011, 43, 2028–2033. [Google Scholar] [CrossRef]
- Yu, R.; Zhang, D.; Haichun, Y. Embodied Energy and Cost Optimization of RC Beam under Blast Load. Math. Probl. Eng. 2017, 2017, 1907972. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; Martí, J.V.; Yepes, V. Carbon embodied optimization for buttressed earth-retaining walls: Implications for low-carbon conceptual designs. J. Clean. Prod. 2017, 164, 812–884. [Google Scholar] [CrossRef]
- Yepes, V.; González-Vidosa, F.; Alcalá, J.; Villalba, P. CO2-Optimization design of reinforced concrete retaining walls based on a VNS-Threshold acceptance strategy. ASCE J. Comput. Civil Eng. 2012, 26, 378–386. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Martí, J.V.; Alcalá, J. Optimization of concrete I-beams using a new hybrid glowworm swarm algorithm. Lat. Am. J. Solids Struct. 2014, 11, 1190–1205. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T.; González-Vidosa, F. Heuristics in optimal detailed design of precast road bridges. Arch. Civ. Mech. Eng. 2017, 17, 738–749. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V. Multiobjective optimization of post-tensioned concrete box-girder road bridges considering cost, CO2 emissions, and safety. Eng. Struct. 2016, 125, 325–336. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Frangopol, D.M. Multi-objective design of post-tensioned concrete road bridges using artificial neural networks. Struct. Multidiscip. Optim. 2017, 56, 139–150. [Google Scholar] [CrossRef]
- Du, G.; Karoumi, R. Life cycle assessment of a railway bridge: Comparison of two superstructure designs. Struct. Infrastruct. Eng. 2012, 9, 1149–1160. [Google Scholar] [CrossRef]
- Du, G.; Safi, M.; Pettersson, L.; Karoumi, R. Life cycle assessment as a decision support tool for bridge procurement: Environmental impact comparison among five bridge designs. Int. J. Life Cycle Assess. 2014, 19, 1948–1964. [Google Scholar] [CrossRef]
- Hammervold, J.; Reenaas, M.; Brattebø, H. Environmental life cycle assessment of bridges. J. Bridge Eng. 2013, 18, 153–161. [Google Scholar] [CrossRef]
- Pang, B.; Yang, P.; Wang, Y.; Kendall, A.; Xie, H.; Zhang, Y. Life cycle environmental impact assessment of a bridge with different strengthening schemes. Int. J. Life Cycle Assess. 2015, 20, 1300–1311. [Google Scholar] [CrossRef]
- Zastrow, P.; Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Life cycle assessment of cost-optimized buttress earth-retaining walls: A parametric study. J. Clean. Prod. 2017, 140, 1037–1048. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Martí, J.V.; García-Segura, T.; Yepes, V. Life-cycle assessment: A comparison between two optimal post-tensioned concrete box-girder road bridges. Sustainability 2017, 9, 1864. [Google Scholar] [CrossRef]
- Hernández, S.; Fontan, A. Practical Applications of Design Optimization; WIT Press: Southampton, UK, 2002. [Google Scholar]
- Azad, A.K.; Qureshi, M.A. Optimum post-tensioning for three-span continuous slab-type bridge decks. Eng. Optim. 1999, 31, 679–693. [Google Scholar] [CrossRef]
- Utrilla, M.A.; Samartín, A. Optimized design of the prestress in continuous bridge decks. Comput. Struct. 1997, 64, 719–728. [Google Scholar] [CrossRef]
- Lounis, Z.; Cohn, M.Z. Multiobjective Optimization of Prestressed Concrete Structures. J. Struct. Eng. 1993, 119, 794–808. [Google Scholar] [CrossRef]
- Cohn, M.Z.; Dinovitzer, A.S. Application of structural optimization. ASCE J. Struct. Eng. 1994, 120, 617–649. [Google Scholar] [CrossRef]
- Carbonell, A.; González-Vidosa, F.; Yepes, V. Design of reinforced concrete road vault underpasses by heuristic optimization. Adv. Eng. Softw. 2011, 42, 151–159. [Google Scholar] [CrossRef]
- Luz, A.; Yepes, V.; González-Vidosa, F.; Martí, J.V. Design of open reinforced concrete abutments road bridges with hybrid stochastic hill climbing algorithms. Inf. Constr. 2015, 67, e114. [Google Scholar]
- Martí, J.V.; Yepes, V.; Gonzalez-Vidosa, F. Memetic algorithm approach to designing of precast-prestressed concrete road bridges with steel fiber-reinforcement. ASCE J. Struct. Eng. 2015, 141, 04014114. [Google Scholar] [CrossRef]
- Yepes, V.; García-Segura, T.; Moreno-Jiménez, J.M. A cognitive approach for the multi-objective optimization of RC structural problems. Arch. Civ. Mech. Eng. 2015, 15, 1024–1036. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. An optimization-LCA of a prestressed concrete precast bridge. Sustainability 2018, 10, 685. [Google Scholar] [CrossRef]
- Catalonia Institute of Construction Technology. BEDEC PR/PCT ITEC Material Database 2016. Available online: https://www.itec.cat/nouBedec.c/bedec.aspx (accessed on 15 January 2017).
- Fomento, M. EHE: Code of Structural Concrete; Fomento: Madrid, Spain, 2008. (In Spanish) [Google Scholar]
- Fomento, M. IAP-98: Code on the Actions for the Design of Road Bridges; Fomento: Madrid, Spain, 1998. (In Spanish) [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Medina, J.R. Estimation of incident and reflected waves using simulated annealing. ASCE J. Waterw. Port Coast. Ocean Eng. 2001, 127, 213–221. [Google Scholar] [CrossRef]
- Yepes, V.; Díaz, J.; González-Vidosa, F.; Alcalá, J. Statistical characterization of prestressed concrete road bridge decks. Rev. Constr. 2009, 8, 95–109. [Google Scholar]
| Unit | Description | Embodied Energy (kW·h) | Cost (€) |
|---|---|---|---|
| m3 | scaffolding | 4.11 | 10.12 |
| m2 | slab formwork | 32.13 | 41.93 |
| m2 | lightening | 82.38 | 110.14 |
| kg | steel B-500-S | 9.72 | 0.59 |
| kg | steel Y-1860-S7 | 20.55 | 5.89 |
| m3 | slab concrete HP 35 | 419.40 | 110.14 |
| m3 | slab concrete HP 40 | 447.13 | 119.32 |
| m3 | slab concrete HP 45 | 471.87 | 131.25 |
| m3 | slab concrete HP 50 | 546.10 | 146.77 |
| Parameter | Value |
|---|---|
| Number of spans | 3 |
| Lengths | 20.0–36.0–20.0 m |
| Pavement thickness | 0.1 m |
| Guard rail weights | 2 × 5 kN/m |
| Vertical thermal gradient | 10 °C |
| Differential settlement between supports | 0.5 cm |
| EHE ambient exposure | IIb |
| Minimum Cost | Minimum Embodied Energy | |||
|---|---|---|---|---|
| Cost (Euros) | Embodied Energy (kW·h) | Cost (Euros) | Embodied Energy (kW·h) | |
| Mean value | 271,759.70 | 1,049,609.81 | 288,357.54 | 974,196.41 |
| Standard deviation | 2354.26 | 24,717.23 | 10,463.24 | 14,770.64 |
| Minimum value | 267,443.44 | 1,002,850.06 | 296,191.13 | 944,517.94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alcalá, J.; González-Vidosa, F.; Yepes, V.; Martí, J.V. Embodied Energy Optimization of Prestressed Concrete Slab Bridge Decks. Technologies 2018, 6, 43. https://doi.org/10.3390/technologies6020043
Alcalá J, González-Vidosa F, Yepes V, Martí JV. Embodied Energy Optimization of Prestressed Concrete Slab Bridge Decks. Technologies. 2018; 6(2):43. https://doi.org/10.3390/technologies6020043
Chicago/Turabian StyleAlcalá, Julián, Fernando González-Vidosa, Víctor Yepes, and José V. Martí. 2018. "Embodied Energy Optimization of Prestressed Concrete Slab Bridge Decks" Technologies 6, no. 2: 43. https://doi.org/10.3390/technologies6020043
APA StyleAlcalá, J., González-Vidosa, F., Yepes, V., & Martí, J. V. (2018). Embodied Energy Optimization of Prestressed Concrete Slab Bridge Decks. Technologies, 6(2), 43. https://doi.org/10.3390/technologies6020043








