Dance Pose Identification from Motion Capture Data: A Comparison of Classifiers ^†

Abstract

In this paper, we scrutinize the effectiveness of classification techniques in recognizing dance types based on motion-captured human skeleton data. In particular, the goal is to identify poses which are characteristic for each dance performed, based on information on body joints, acquired by a Kinect sensor. The datasets used include sequences from six folk dances and their variations. Multiple pose identification schemes are applied using temporal constraints, spatial information, and feature space distributions for the creation of an adequate training dataset. The obtained results are evaluated and discussed.

1. Introduction

Intangible cultural heritage (ICH) is a major element of peoples’ identities and its preservation should be pursued along with the safeguarding of tangible cultural heritage. In this context, traditional folk dances are directly connected to local culture and identity [1]. Recent technological advancements, including ubiquitous mobile devices and applications [2], pervasive video capturing sensors and software, increased camera and display resolutions, cloud storage solutions, and motion capture technologies have completely changed the landscape and unleashed tremendous possibilities in capturing, documenting and storing ICH content, which can now be generated at a greater volume and quality than ever before. However, in order to exploit the full potential of the massive, high-quality multimodal (text, image, video, 3D, mocap) ICH data that are becoming increasingly available, we need to appropriately adapt state-of-the-art technologies, and also build new ones, in the fields of artificial intelligence (AI), computer vision, and image processing. Such progress is essential for the ICH—in our case, dance—content’s efficient and effective organization and management, fast indexing, browsing, and retrieval, but also semantic analysis, such as automatic recognition [3,4] and classification [5,6].

Furthermore, the advent of motion sensing devices and depth cameras has brought about new possibilities in applications related to motion analysis and monitoring, including human tracking, action recognition, and pose estimation. The main advantage of a depth camera is the fact that it produces dense and reliable depth measurements, albeit over a limited range and offers balance in usability and cost. The Kinect sensor has been frequently used in such applications and will be employed in this work to capture sets of dance moves and gestures in 3D space and in real time, resulting in a recorded sequence of points in 3D space for each joint at certain moments in time.

This paper focuses on the evaluation of classification algorithms on Kinect-captured skeleton data from folkloric dance sequences for dance pose identification. We explore the applicability of raw skeleton data from a single low-cost sensor for determining dance genres through well-known classifiers. This paper extends the work presented in [7], in that multiple pose identification schemes are applied using temporal constraints, spatial information, and feature space distributions.

The remainder of this paper is structured as follows: Section 2 briefly reviews the state of the art in the field; Section 3 describes the methodology employed for motion capturing, data preprocessing and feature extraction, while Section 4 presents the classifiers whose applicability for dance pose identification are explored; the related experimental evaluation is given in Section 5; and, finally, Section 6 concludes the paper with a summary of findings.

2. Related Work

Starting with a brief review of approaches proposed for the more general problem of human pose estimation in computer vision, one could note that many techniques are based on the detection of body parts, for example, through pictorial structures [8]. The advent of deep learning [9] has brought forward two main groups of methods: holistic and part-based ones, which differ in the way the input images are processed. The holistic processing methods do not create a separate model for every part. DeepPose [10] is a holistic model that handles pose determination as a joint regression problem without formulating a graphical model. A drawback of holistic-based methods is that they are often inaccurate in the high-precision region due to the difficulty in learning direct regression of complicated posture vectors based on images.

Part-based processing methods focus on detecting the human body parts individually, followed by a graphic model to incorporate the spatial information. In [11], the authors, instead of training the network using the whole image, use the local part patches and background patches to train a convolutional neural network (CNN), in order to learn conditional probabilities of the part presence and spatial relationships. In [12], a multiresolution CNN is designed to carry out body-part-specific heat-map likelihood regression, which is in the sequel succeeded by an implicit graphic model for assuring joint consistency.

As regards the more specific field of dance pose and move analysis, there is a relatively limited number of works. In [13] a gesture classification system is described for skeletal wireframe motion for certain gestures, among several dozen, in real-time and with high accuracy. In [14], a simple non-parametric Moving Pose framework is proposed, for low-latency human action and activity recognition. A method to recognize individual persons from their walking gait using 3D skeletal data from a MS Kinect device using the $k$-means algorithm is described in [15], while a key posture identification method is proposed in [16].

In [17], a methodology is proposed for dance learning and evaluation using multi-sensor and 3D gaming technology. In [18], a 3D game environment for dance learning is presented, which is based on the fusion of multiple depth sensors data in order to capture the body movements of the user/learner. In [19], improved robustness of skeletal tracking is achieved by using sensor data fusion to combine skeletal tracking data from multiple sensors. The fused skeletal data is split into different body parts, which are then transformed to allow view invariant pose recognition using a Hidden State Conditional Random Field (HCRF). The proposed framework is tested on traditional “Tsamiko” folk dance sequences. The attained recognition rates range from 38.4% up to 93.9% depending on the particularities of the dancer and the experimental setup. In [20], a skeletal representation of the dancer is again obtained by using data from multiple depth sensors. Using this information, the dance sequence is partitioned, first, into periods and, subsequently, into patterns.

In [21], human action recognition is treated as a special case of the general problem of classifying multidimensional time-evolving data in dynamic scenes. To solve detection correlations between channels, a generalized form of a stabilized higher-order linear dynamical system and the multidimensional signal is represented as a third-order tensor. The work of [22] focuses on the application of segmentation and classification algorithms to Kinect-captured depth images and videos of folkloric dances in order to identify key movements and gestures and compare them against database instances. However, that work considers individual joints for the analysis, rather than the entire body pose, attaining recognition rates up to 42% in the general case.

The contribution of the paper at hand is twofold. Firstly, it extends the work of [7] by exploiting the information of multiple joints simultaneously and investigates whether temporal dependencies can be modeled using consecutive frame subtraction. Secondly, unlike [7], multiple pose identification schemes are applied using temporal constraints, spatial information, and feature space distributions.

3. Data Capturing and Dance Representation

A three-step approach is adopted for the evaluation of dance pattern over traditional folk dances: (i) motion capturing, (ii) data preprocessing and feature extraction, followed by (iii) comparative evaluation among well-known classification techniques. Motion capturing is performed using markerless, low-cost sensors. The motion sensors provide as an output the position and the rotation of specific body joints at a constant frame rate. The available information is processed to form low-level features which will be used as inputs to the dance recognition mechanism. The problem at hand, i.e., dance recognition, constitutes a traditional multi-class classification problem. Given a frame, or sequence of frames, during the performance of a dancer, our goal is to correctly identify which dance is performed.

3.1. Capturing Dance Poses

Microsoft Kinect 2 is currently one of the most advanced motion sensing input devices that is available to the public. It is a physical device with depth sensing technology, a built-in color camera, infrared (IR) emitter, and microphone array, which projects and captures an infrared pattern to estimate depth information. Based on the depth map data, the human skeleton joints are located and tracked via the Microsoft Kinect 2 for Windows SDK [23]. Figure 1 shows a snapshot of our experiment conducted.

More specifically, the Microsoft Kinect 2 sensor can achieve real-time 3D skeleton tracking while, at the same time, it is relatively cheap and easy to set up and use. The tracked skeleton consists of twenty five joints with each one to include the 3D position coordinates, its rotation and a tracking state property: “Tracked”, “Inferred”, and “UnTracked” [24]. Moreover, the sensor can work in dark and bright environments and the capture frame rate is 30 fps. On the other hand, there are some limitations that should be considered: it is designed to track the front side of the user and, as a result, the front and back sides of the user cannot be distinguished, and that the movement area is limited (approximately 0.7–6 m). In this work, the entirety of the captured joints have been used in the feature extraction process (see [2] for a graphical presentation of the exact joints).

3.2. Identifying Key Poses

There are multiple sources of variation when investigating dance patterns. At first, there are temporal variations that affect the movement speed, the main cause is mainly the music tempo. Another source of variance is the dancer himself. The body build varies from person to person. As such, joints positions span different space despite the same choreography. Furthermore, dancer mentality often adds a personalized touch to the performance. In dances with pre-defined steps, this leads to minor changes in positioning, e.g., different hand movements, legs bend more than expected, and denser body rotations.

When building analytical predictive models for dance analysis, all possible sources of variation must be included in the training dataset, so that the model can provide reliable predictions for new instances; the training data should have a greater variation in feature attributes than the data to be analyzed. Crucial factors influencing the predictive performance of classification models, involve outliers, low-quality features, as well as differences in the size of the classes. In our case three sampling approaches for the creation of an adequate training dataset are employed: temporally-constrained, cluster-based, and uniform feature space selection.

Temporally-constrained selection divides a dance sequence into consecutive clusters by taking into account factors related to both the dance itself and the motion capture device parameters. In each of the initially-created clusters, a density-based approach, i.e., OPTICS algorithm output analysis, identifies possible outliers and representative samples. Since similar instances are likely to be clustered together, the few random samples from each cluster are expected to provide adequate information, over the entire dataset. In this context, density-based approaches have often been employed for more effective data selection [25].

The classic Kennard Stone algorithm is a uniform mapping algorithm; it yields a flat distribution of the data. It is a sequential method that uniformly covers the experimental region. The procedure consists of selecting, as the next sample (candidate object), the one that is most distant from those already selected (calibration objects). For initialization, one can select either the two observations that are most distant from each other, or, preferably, the one closest to the mean.

From all the candidate points, the one is selected that is furthest from those already selected and from its closest neighbors, and added to the set of calibration points. To do this, we measure the distance from each candidate point ${\mathit{x}}_0$ to each point $\mathit{x}$ which has already been selected and determine which is smallest, i.e., $\underset{i}{\min }d\left(\mathit{x},{\mathit{x}}_0\right)$. From these we select the one for which the distance is the maximum:

$$d_{selected}=\underset{i_0}{\max }\left(\underset{i}{\min }d\left(\mathit{x},{\mathit{x}}_0\right)\right).$$

(1)

4. Classifiers for Dance Pose Identification

We have scrutinized the effectiveness of a series of well-known classifiers in dance recognition from skeleton data. In this section, the investigated classification techniques are briefly described.

4.1. k Nearest Neighbors

The $k$-nearest neighbors ($k$-NN) algorithm is a non-parametric method used for classification [26]. A majority vote of its neighbors classifies an object, with the object being assigned to the class most common among its $k$ nearest neighbors; it is, therefore, a type of instance-based learning, where the function is only approximated locally and all computation is deferred until classification.

4.2. Naïve Bayes

Naive Bayes (NB) classifiers are a family of simple probabilistic classifiers based on applying Bayes’ theorem with strong independence assumptions between the features [27]. Abstractly, naive Bayes is a conditional probability model: given a problem instance to be classified, represented by a vector $\mathit{x}=\left\{{\mathit{x}}_1,\dots ,{\mathit{x}}_{\mathit{n}}\right\}$ representing some $\mathit{n}$ features (independent variables), it assigns to this instance probabilities $\mathit{p}\left({\mathit{C}}_k|{\mathit{x}}_1,\dots ,{\mathit{x}}_{\mathit{n}}\right)$ for each of $\mathit{K}$ possible outcomes or classes ${\mathit{C}}_{\mathit{k}}$.

4.3. Discriminant Analysis

Discriminant analysis is a statistical analysis method useful in determining whether a set of variables is effective in predicting category membership. Discriminant analysis (Discr) classifiers assume that different classes generate data based on different Gaussian distributions [28] so that $p\left(\mathit{x}|y={\mathit{C}}_k\right)~N\left({\mathbf{\mu }}_k,𝓢\right),k=1,\dots ,\mathit{K}$. In order to train such a classifier, we need to estimate the parameters of a Gaussian distribution for each class. Then, to predict the classes of new data, the trained classifier finds the class with the smallest misclassification cost: $\widehat{y}=arg\underset{k}{\max }\left\{{\left(\mathit{x}-\frac{{\mathbf{\mu }}_k}{2}\right)}^T{\beta }_k+\log {\pi }_k\right\}$, where ${\beta }_k={𝓢}^{-1}{\mathbf{\mu }}_k$.

4.4. Classification Trees

Decision tree learning uses a decision tree as a predictive model which maps observations about an item to conclusions about the item’s target value. In classification tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels [27]. Each internal (non-leaf) node is labeled with an input feature. The arcs coming from a node labeled with a feature are labeled with each of the possible values of the feature. Each leaf of the tree is labeled with a class or a probability distribution over the classes.

4.5. Ensemble Methods

Ensembles of classifiers is, actually, a combination of classifiers approach [29]; such methods use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone. In the case of classification trees, we have further used the random forests algorithm (denoted as TreeBagger).

4.6. Support Vector Machines

Support vector machines (SVMs) are supervised learning models with associated learning algorithms [30]. An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear margin that is as wide as possible. New examples are then mapped into that same space and predicted to belong to a category based on which side of the margin they fall on.

5. Experimental Results

In order to capture and record the performers’ body motions, we used a motion capture system using one Kinect 2 depth sensor and the i-Treasures Game Design module (ITGD), developed in the context of the i-Treasures project [31]. The ITGD module enables the user to record and annotate motion capture data received from a Kinect sensor.

The recording process took place at the School of Physical Education and Sport Science of the Aristotle University of Thessaloniki. Six Greek traditional dances with a different degree of complexity were recorded. Each dance was performed by three experienced dancers twice: the first time in a straight line, and the second in a semi-circular curving line. Dancers’ movements were limited in a predefined rectangular area.

Experimental results are based on a set of 648 observations. A dancer is selected to provide the training paradigms, the remaining two provide the test sets. Few representative data samples are selected (see Section 5.3) to form the training set, using three different sampling approaches. Then, we have a total of eight test sets, using a 20% holdout approach in each. The problem at hand is a standard multiclass classification problem. We have six classes (as the number of dances).

The investigation emphasizes on the dance recognition per recorded frame. The performance impact of the following factors is investigated:

• Classifier input type: related to the input features’ values. The possible alternatives for the creation of input features are four: (i) leg joints per frame (1Fr Legs), (ii) leg joints and frame difference (FrDiff Legs), (iii) all joints per frame (1Fr All) and, (iv) all joints and frame difference (FrDiff All).
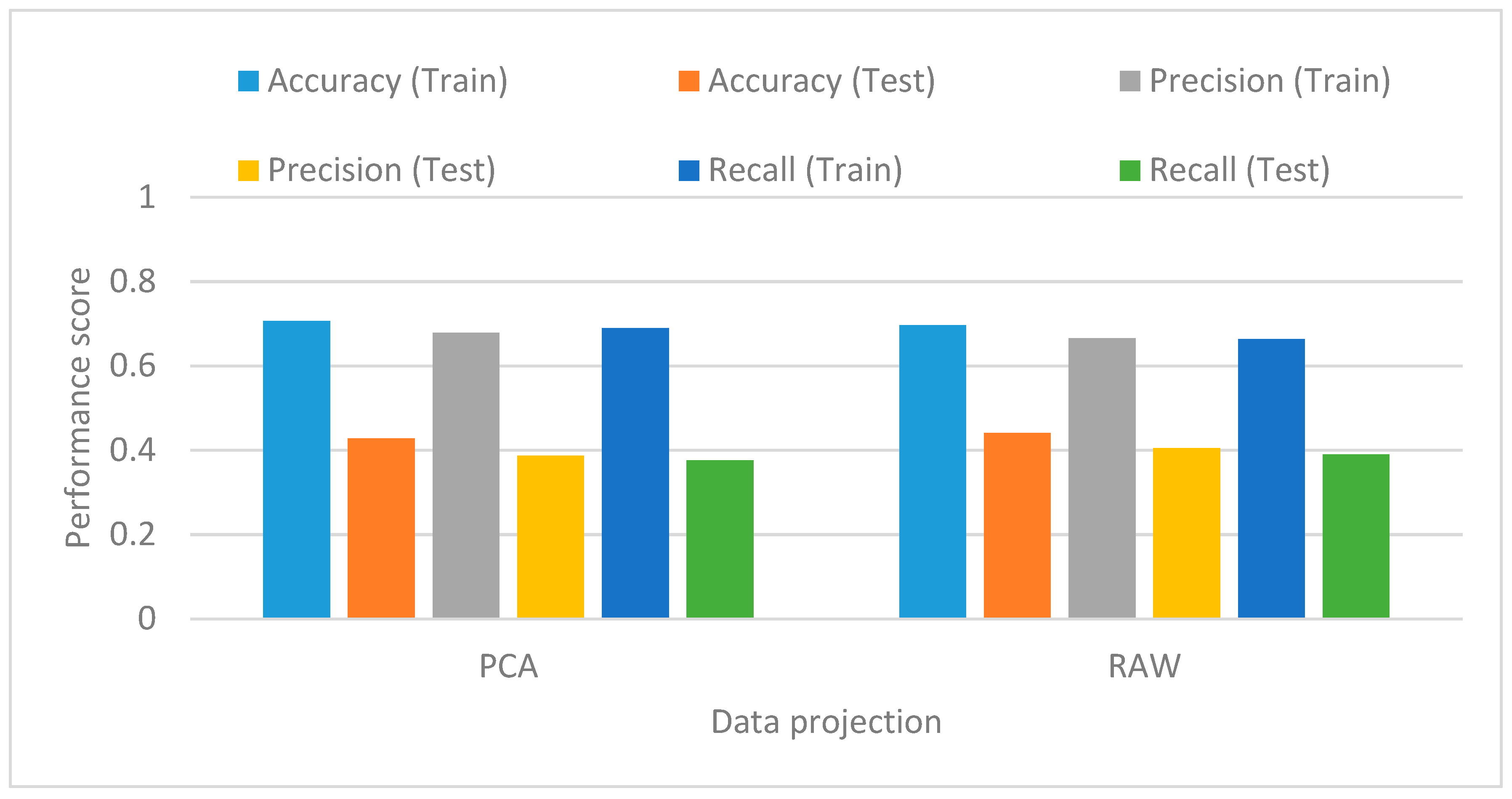
• Projection techniques: related to the dimensionality of inputs. There are two alternatives: PCA or raw data.
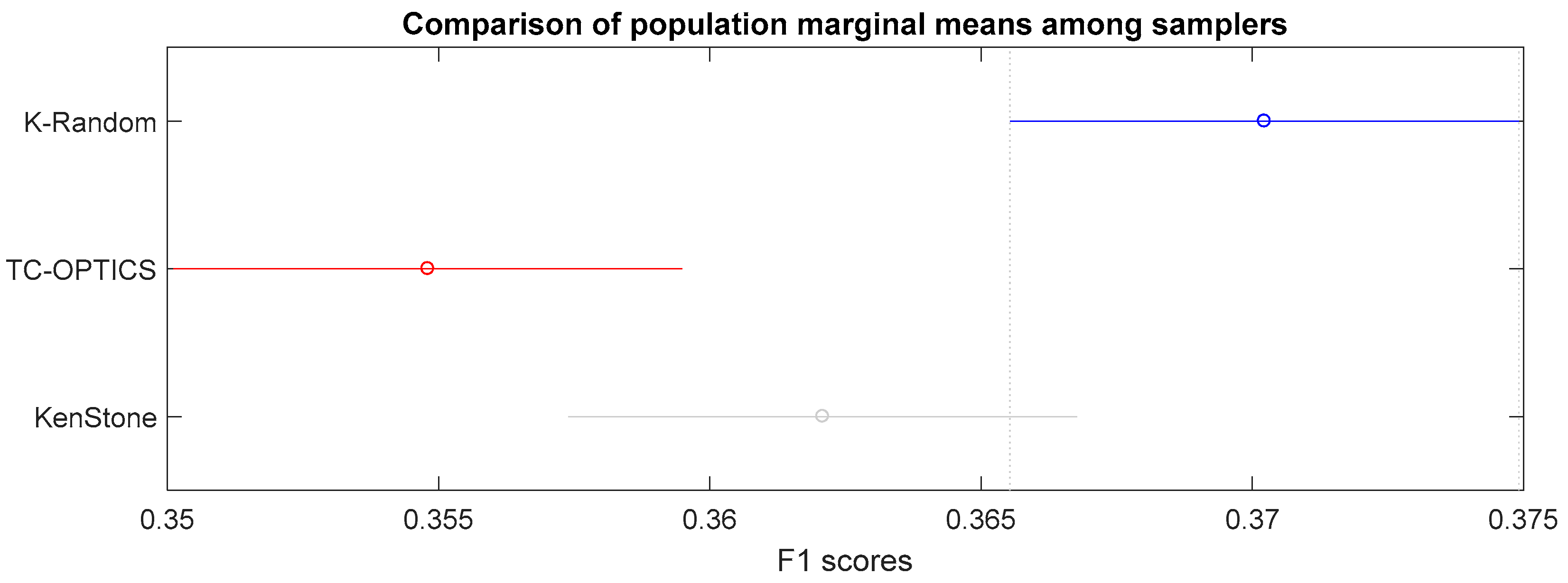
• Sampling approaches: related to training sets creation. There are three approaches: (i) random sampling over kmeans clusters (K-random), (ii) time constrained OPTICS (TC-OPTICS), and (iii) Kennard Stone (KenStone).
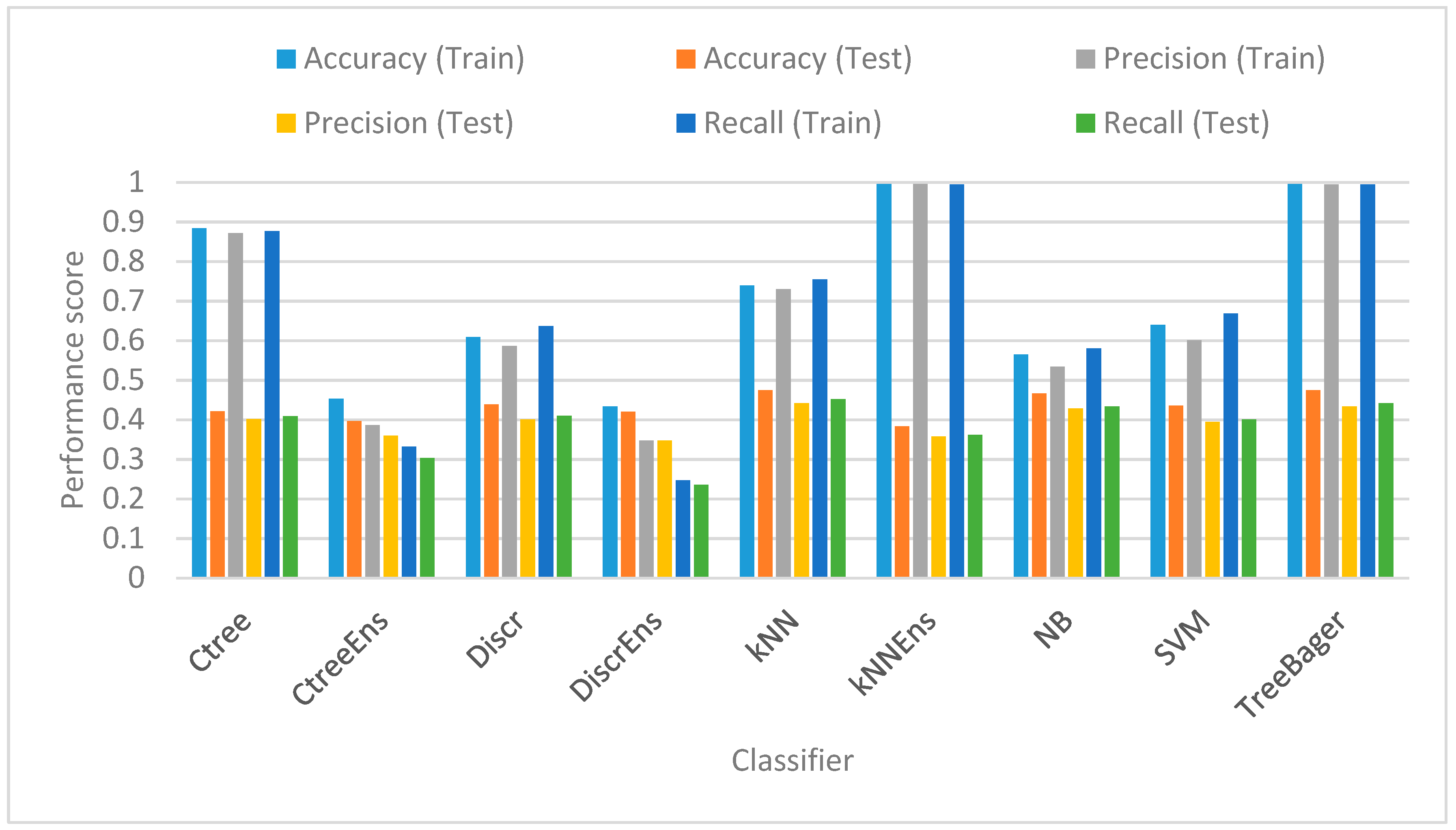
• Classifier: i.e., the classification technique used, i.e., k-nearest neighbors (k-NN), naïve Bayes (NB), classification trees (CT), linear kernel support vector machines (SVMs), a random forest approach (TreeBagger), as well as Ensemble (Ens) versions.

In order to identify the impact of each parameter on the final classification scores, ANOVA analysis has been performed (Section 5.5).

5.1. Dataset Description

The dances dataset consists of six different dances. Their execution was either in a straight line or circle (

Table 1. Number of representative frames per dance when using TC-OPTICS sampler. This example treats straight and circular trajectories as different cases.

	KalCirc	KalStr8	MakCirc	MakStr8	Syrt2Circ	Syrt2Str8	Syrt3Circ	Syrt3Str8	Syrt11Str8	TrehCirc	TrehStr8
Single Frame Legs Only
D1	18	10	11	7	21	19	44	24	19	34	10
D2	19	11	19	10	17	19	31	21	22	22	10
D3	18	14	11	15	9	10	30	16	25	16	11
Frame Difference Legs Only
D1	17	8	14	8	19	18	39	21	18	28	10
D2	16	11	18	11	15	17	32	21	18	17	8
D3	16	14	10	10	11	9	32	16	18	12	10
Frame Difference All Joints
D1	18	8	14	8	18	18	44	20	18	27	8
D2	18	10	16	8	15	21	30	21	22	17	8
D3	17	13	9	11	9	9	34	16	21	12	9

). A set of consecutive image frames describes every dance. Every frame, ${\mathit{I}}_{\mathit{i}}$,$\mathit{i}=1,\dots ,\mathit{n}$, has a corresponding extensible mark-up language (XML) file with positions, rotations, and confidence scores for 25 joints on the body, in addition to timestamps. In the following a brief description of the dances is provided.

Enteka (eleven): A dance, performed by both women and men, which is popular mainly in the large urban centers of Western Macedonia (Grevena, Kozani, Florina, Kastoria, etc.). The dance is performed freely as a street carnival dance, but also around the carnival fires. The dancers’ hands during the dance move freely or are placed at the waist.

Kalamatianos: It is a popular Greek folkdance throughout Greece, Cyprus and internationally, often performed at many social gatherings worldwide. It is a circle dance performed in a counterclockwise rotation with the dancers holding hands. It is a twelve steps dance and the musical beat is 7/8.

Makedonikos: A circle dance, performed by both women and men, with a 7/8 musical beat. The basic pattern of dance is performed in twelve movements/steps. Therefore, it resembles the Kalamatianos dance to a great degree with the difference that it is a more joyous dance. It is popular in the region of Western and Central Macedonia.

Syrtos (two-beat): The Syrtos (two-beat) dance is organized in a quick (two-beat) rhythm. It is a circle dance, performed by both women and men mostly in the region of Pogoni of Epirus. In the past, the dance was performed separately by men and women, in one, two, or more lines.

Syrtos (three-beat): Syrtos is one of the most popular dances throughout Greece and Cyprus. The Syrtos (three-beat) dance is organized in a slow (three-beat) rhythm. It is a line dance and a circle dance, performed by dancers (both women and men) in a curving line holding hands, facing right. It is widespread through Epirus, Western Macedonia, Thessaly, Central Greece, and Peloponnese.

Trehatos (Running): A circle dance, performed by both women and men, which is danced in the village Neochorouda of Thessaloniki. The kinetic theme of the dance is composed of three different dance patterns. The first one resembles the Syrtos (three-beat) pattern, the second takes place once and connects the first and the second pattern, and the third one is characterized by intense motor activity.

An illustration of Syrtos dance is shown in Figure 2. At first the positions and rotation values for each frame, $I_i$, $i=1,\dots ,n$ of a dance, with $n$ consecutive frames, are extracted. Thus, the dance is described by a matrix, ${\mathit{D}}_i,$ of size $b\times m\times n$, where $b$ is the number of body joints (i.e., 25), $m$ is the number of feature vectors (i.e., three coordinates and four rotations, plus two more binary indicators, explaining if values are measured or estimated), and $n$ is the duration of the dance.

5.2. Feature Extraction

For feature extraction, a simple process is followed: For any dance ${\mathit{D}}_i,$ we have 24 × 9 × $n$ values, or, in a 2D form, a 216 × $n$ matrix. A technical limitation did not allow the successful capturing of the right thumb position in a few dances; it was, therefore, excluded from the pattern analysis. Thus, each captured frame describes the entire body pose via 216 values.

One should note that joints’ positions are correlated to each other due to physical restrictions of the body skeleton. As such, the application of a dimensionality reduction approach should be considered. Ideally, a small set of feature values containing most of the available information support a smooth performance for a variety of classifiers [32]. In this case PCA is used, maintaining 99.1% of the initial feature space variance as in [7]. The PCA outcome resulted in a projection space less than nine times that of the original.

However, dance is not a static act; a comparison of the difference among frames could provide significant insights. Therefore, the time dimension should also be considered. We utilized the information of successive frames of $𝓉$ time intervals, $I_i$ and $I_{i+𝓉}$, by subtracting them. In the end, each dance, ${\mathit{D}}_i,$ was of size $b\times \left(2m\right)\times n-1$. Prior to the dimensionality reduction via PCA step, data were normalized using minmax normalization. In the former case, i.e., single frame analysis, PCA resulted in 21 dimensions. For the latter case, i.e., two successive frames, we had 41 dimensions in the reduced space.

5.3. Variation, Space, and Noise Handling

Table 1 illustrates the number of representative frames for each of the investigated dances, using TC-OPTICS sampler. Results indicate that the applied summarization technique is robust to noise, which in our case affects the dance duration. Even for extreme cases, the number of representative frames remains similar for all dancers. The Syrtos 3 line dance is an extreme case. The first dancer performance duration was twice as long to other dancers. Yet, the representative frames are around 20 for all dancers.

Table 2. Number of training samples, depending on the dancer and the sampling algorithm.

Row Labels	Frame_Diff_Legs	FrameDiff_All_Joints	Single_Frame_Legs	Single_Frame_All
KenStone
D1	180	180	189	189
D2	171	171	180	180
D3	146	146	155	155
K-Random
D1	186	186	196	196
D2	176	177	186	187
D3	151	152	160	161
TC-OPTICS
D1	56	56	58	60
D2	56	56	57	60
D3	52	52	51	54

indicates the training sets’ size (i.e., the number of observations) depending on the sampling approach.

5.4. Algorithms Setup

All algorithms were implemented in MATLAB. In our case the $\mathrm{k}$nn parameterization process considers the number of k nearest points, which was set to $k=5$, a similar adaptation as in [22]. The value provides a good tradeoff. If k = 3 or less we are unable to distinguish among different dances that share the same steps. On the other hand, k = 7 or greater results in matching with similar steps of other dances. The ensemble methods used 16 ensemble members. The rest of the parameters were used at the default values.

5.5. Classification Scores

The proposed methodology involved data selection, dimensionality reduction, and samplers-classifiers combinatory approaches. As such, all the above fields were investigated in terms of their impact at the dance identification problem. Their performance was quantified by using traditional performance measures as accuracy, precision, recall, and F1 scores. A further insight is provided via analysis of variance. Figure 3, Figure 4, Figure 5 and Figure 6 illustrate the impact for each of the investigated factors, namely, projection technique (Figure 3), sampling approach (Figure 4), classifier (Figure 5) and input type (Figure 6).

Figure 3 provides comparison results between raw input data and input data using principal component analysis (PCA). The performance scores are average values over all combinations of utilized classifiers, sampling approaches, and input type selection. There are two aspects worth mentioning. At first, the performance scores are close for the two approaches. In both cases, a significant decline is observed over the test set.

Figure 4 describes the samplers’ impact on the dance identification task. Centroid-based random clustering, i.e., K-random sampling, provides better results. Overall, similar results are observed. The K-random sampling is also faster compared to the alternatives.

Figure 5 demonstrates classifiers’ volatility in performance between training and test sets. Regardless of the adopted approach, a significant drop in all performance scores is observed. All classifiers’ average scores are below 0.5.

Figure 6 provides a further insight on the question whether the joint selection or frame difference can boost the classifiers performance. The information of all body joints, based on the current frame, appears to provide (slightly) better results.

5.6. Statistical Analysis

To obtain further insights into the results and the relative performance of the different algorithms we conducted an analysis of variance (ANOVA) on the F1 score results for the test samples. The F1 score is the harmonic mean of precision and recall. Thus, it contains a significant amount of information regarding the overall performance. ANOVA also enables the statistical assessment of the effects that the main design factors of this analysis have (i.e., the sampling schemes, feature extraction, and the classifiers).

Table 3. List of available dances and their variations as well as their duration, depending on the dancer.

Dance	Variation	Short Name	Duration (Frames)
			D1	D2	D3
Enteka	Straight	Syrt_11_Str8	749	807	858
Kalamatianos	Circular	Kal_Circ	655	593	561
	Straight	Kal_Str8	304	378	455
Makedonitikos	Circular	Mak_Circ	424	582	409
	Straight	Mak_Str8	283	367	418
Syrtos 2	Circular	Syrt_2_Circ	608	543	352
	Straight	Syrt_2_Str8	623	639	334
Syrtos 3	Circular	Syrt_3_Circ	608	964	947
	Straight	Syrt_3_Str8	1366	678	511
Trehatos	Circular	Treh_Circ	991	723	443
	Straight	Treh_Str8	315	295	355

shows the results of the ANOVA analysis. In this Table, the Source column corresponds to the source of variation in data (i.e., the performance impact factors described earlier in this section and their combined impact). Sum and Mean Sq. correspond to mean measurements between the $\mathrm{m}$ groups and the grand mean; practically it quantifies the variability among the groups of interest. The degrees of freedom (d.f.) are defined as $\mathrm{d}.\mathrm{f}.=m-1$. The F column refers to the F statistic, i.e., the “average” variability between the groups divided by the “average” variability within the groups. Finally, we calculate the p-value, by comparing the F-statistic to an F-distribution with $m-1$ numerator degrees of freedom and n − m denominator degrees of freedom, for the total set of $\mathrm{n}$ observations.

As shown in

Table 4. ANOVA outcomes.

Source	Sum Sq.	d.f.	Mean Sq.	F	p-Value
Projection	0.0232	1	0.0232	13.3600	0.0003
Sampling	0.0261	2	0.0130	7.5000	0.0006
Classifier	2.2686	8	0.2836	163.3000	0.0000
InputType	0.2790	3	0.0930	53.5600	0.0000
Projection × Sampling	0.0064	2	0.0032	1.8400	0.1590
Projection × Classifier	0.0118	8	0.0015	0.8500	0.5621
Projection × InputType	0.0226	3	0.0075	4.3400	0.0049
Sampling × Classifier	0.0818	16	0.0051	2.9400	0.0001
Sampling × InputType	0.0147	6	0.0025	1.4100	0.2073
Classifier × InputType	0.2830	24	0.0118	6.7900	0.0000
Error	0.9967	574	0.0017
Total	4.0138	647

, all main factors (i.e., projection, sampling, classifier, and input type) are strongly significant for explaining variations in F1 score, since the corresponding p-value is approximately zero.

In addition to the above basic ANOVA results, we use the Tukey honest significant difference (HSD) post-hoc test to identify sampling schemes and classifiers that provide the best results, while considering the statistical significance of the differences between the results.

Figure 7 illustrates that classification scores are better when using information of all body joints, without employing frame differences, i.e., subtracting joint values over specified time intervals. Mean scores for each approach are shown as ‘o’. The average scores from subgroups in the experiment are also provided. Since there is no overlap between the F1 values for the 1FrAll input type compared to the others, 1FrAll scores are clearly statistically better than the others.

Figure 8 indicates that PCA should not be used since the overall scores are statistically worse than using raw feature values.

Figure 9 indicates that, statistically, Kennard Stone sampling is no worse than centroid-based random sampling, since there are partly overlapping areas on the F1 scale. Generally, K-random sampling approach provides the best results.

Figure 10 illustrates that the best classifiers for the problem at hand are $k$-nearest neighbors and random forests (denoted as TreeBagger), with the the kNN approach attaining a slightly greater performance.

Regarding the combined approach of all four factors (i.e., feature type, projection space, sampling, and classifier) the single-frame, PCA projected, $\mathrm{k}$ means-random sampler, $\mathrm{k}$NN classifier provides the best possible results (0.52) with a marginal mean significantly different from 167 different groups. The obtained results denote the superiority of the aforementioned best performing framework over the approach proposed in [19], which is the only one currently in the literature that has been evaluated on the same dataset of the specific folk dances. It is clear, however, that the current experimental setup has not attained a fully satisfactory performance in the problem at hand, which could be justified by the limited capability of a single Kinect sensor to capture the complex spatiotemporal variations residing within folk dance movements, as well as the low amount of data available for training of the utilized classifiers.

6. Conclusions

We have presented a comparative study of classifiers and data sampling schemes for dance pose identification based on motion capture data acquired from Kinect sensors. Skeleton data served as inputs to classifiers. Feature extraction process involved subtraction between successive frames and principal component analysis for dimensionality reduction. Multiple pose identification schemes were applied using temporal constraints, spatial information and feature space distributions for the creation of an adequate training data set. Experimental results show that frame differencing and PCA lead to lower recognition rates and that $k$ nearest neighbors and random forests are the best-performing classifiers among the ones explored. Future work directions include experimenting with data from multiple Kinect sensors, as well as multimodal skeleton and RGB data, which may contribute to greater precision rates.