A Low-Complexity Model-Free Approach for Real-Time Cardiac Anomaly Detection Based on Singular Spectrum Analysis and Nonparametric Control Charts
Abstract
1. Introduction
2. Singular Spectrum Analysis
2.1. Fundamentals of Singular Spectrum Analysis
2.1.1. Basic SSA Algorithm
- Embedding:A trajectory matrix is constructed by mapping into a sequence of lagged column vectors of size M, yieldingNotice the Hankel-structure of , i.e., has equal elements on the anti-diagonalsOne can think of as multivariate data with M characteristics and K observations and accordingly of as vectors in the M-dimensional space .
- Singular Value Decomposition ofTaking the SVD of decomposes the trajectory matrix into its orthogonal bases and yields a collection of M eigenvalues and eigenvectors. Let and denote, respectively, the eigenvalues and eigenvectors of and the rank of be denoted as . The SVD of can then be rewritten as the sum of d elementary matriceswith matrices being of rank 1 and .Note that are the eigenvectors of and the eigentriples of the SVD in Equation (2).Also note that due to the symmetry of left and right singular vectors, the SVD of trajectory matrices obtained with window length M and are equivalent. Accordingly, one can impose the limitation on the window length since there is no additional benefit in using a larger window (see, e.g., [53] at 47, [42] at 69).
- Eigentriple GroupingIn order to separate the signals of interest from noise and artifacts, the third stage of basic SSA aims to find particular disjoint subsets of the set of indices such that the respective systems of eigenvectors span the subspaces associated with the different signal components.Consider the task of separating a signal of interest from unwanted noise. One then looks for a certain subset of indices that span an l-dimensional subspace in , denoted as . Analogously, the remaining eigentriples with span the noise subspace .The trajectory matrix component corresponding to the subset I of eigentriples associated with the signal of interest is thenand the component corresponding to the subset associated with the remainder of the observed signal issuch thatIn the case of separability (see, e.g., [53] at 17), the contribution of to the entire observed signal is represented by the respective share of eigenvalues .
- Diagonal AveragingFor perfectly separable components, all matrices in the expansion of Equation (5) are Hankel matrices. For real world problems, however, such perfect separability is rarely achievable and results in matrices with unequal entries on the antidiagonals. The last step of the basic SSA algorithm therefore performs a Hankelization of said matrices, i.e., a diagonal averaging is performed on all the of Equation (5) yielding matrices that have equal elements on the antidiagonalsOne can then e.g., easily reconstruct the approximation of the signal of interest through the eigentriples with indices I through the one-to-one correspondence between and the respective time series which provides an approximation of the entire time series or some components of it, depending on the particular choice of indices I.
2.2. SSA Based Change Detection: Prior Art
- Apply SSA on the interval (after centering ) to get
- (a)
- Construct the trajectory/base matrixwhere .
- (b)
- Singular Value Decomposition of
- (c)
- Selection of with
- Construct test matrix on the interval (after centering )
- Compute the detection statisticwhere and is the matrix of eigenvectors spanning , i.e., is the sum of squared Euclidean distances between the columns of and . MZ normalizes the sum of distances to the number of elements in , i.e.,and further normalizes the test statistic assuch that it does not depend on the unknown variance of the noise (see [40] at 28) with being an estimator of , e.g., with such that the hypothesis of no change can be accepted.
- Monitoring of using CUSUM-type Control Charts
3. The Proposed Method (l-SSA-CPD)
3.1. Motivation and Informal Description of the Improvements
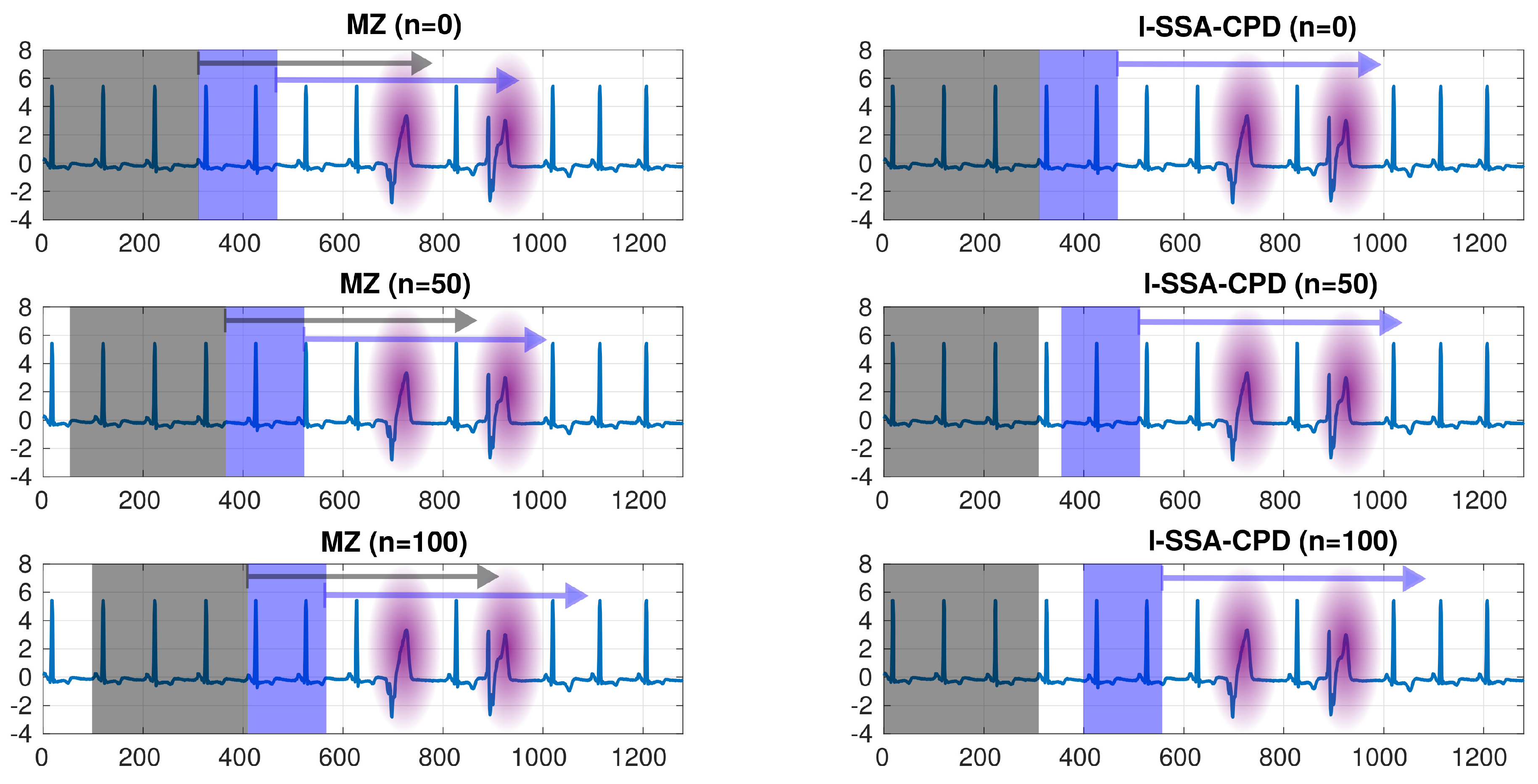
- Low Computational ComplexitySmall variations over time are intrinsic to cardiac signals and may, besides noise and motion artifacts, e.g., be due to Heart Rate Variability. Contrary to anomalies caused by abnormal cardiac excitation phenomena, these changes in the time between consecutive R-peaks are subtle and often not readily discernible. Most importantly, they do not induce changes as severe as to change the signal’s main characteristics which are captured through the decomposition and grouping stages of SSA. This is illustrated in Figure 2 which shows a raw (unfiltered) ECG signal with two distinctly shaped PVCs (highlighted in purple) in the third quarter of the excerpt.For the task at hand, performing the SVD of a newly generated trajectory matrix each time a new data point becomes available is not strictly necessary. We are able to drastically reduce the computational burden by generating only one initial trajectory matrix and relying on the obtained reference subspace throughout the monitoring. This is shown in Figure 2 with the section of the signal highlighted through gray and blue backgrounds representing the intervals used to generate and , respectively. Note how in MZ (left part of Figure 2) both and are being slid over the observations while in our algorithm (right part of Figure 2) only is a sliding window since .Clearly, relying on a fixed reference subspace throughout the entire monitoring process goes along with an inherent limitation of the potential application scenarios l-SSA-CPD would be suited for as it implies the fixed nominal subspace to be a valid representation of the anomaly free signal over long periods of time. While such an assumption may at first appear extreme and untenable, this is not the case when monitoring subjects at rest over relatively short periods of time (e.g., in the order of 2–10 min) as would be the case in a typical prescreening scenario for ambulatory care settings. Said implied assumption however becomes untenable in other relevant scenarios such as continuous long-term monitoring as well as the monitoring of patients not at rest; for in those cases the general cardiovascular responses to homeostatic disturbances triggered by various physical and mental stressors would suffice to move new observations out of the designated nominal subspace.There exist, however, various rather straightforward mitigation strategies to this problem. For instance, we may view the method presented here as a special case of a more general l-SSA-CPD that allows for the regular recalculation of the reference subspace according to an update frequency which depends on the particular scenario. Possibilities to lower the computational burden on the mobile device are equally manifold and include, among others, establishing a wireless data connection to a server or PC and outsourcing demanding tasks such as SVD or substituting SVD with a computationally less expensive alternative such as SVD updating algorithms. Eventually, such considerations inevitably boil down to a scenario specific trade-off between required performance and available resources.
- SimplicityBy sliding only a single instead of two windows over the time series the entire procedure is simplified and benefits from a reduction in tuning parameters.In fact, while the total number Q of columns in is of course relevant, p and q are not since, due to an overlap of and can only occur in the first samples for . While our algorithm allows for such an initial overlap of and , the following discussion is purposely limited to , which is in line with recommendations by Moskvina and Zhigljavsky who point out that and accordingly is a very reasonable choice if minimizing the detection delay is of importance, since entails a smoother behavior of the test statistic and thus a loss of agility (see, e.g., [40] at 30).The question as to whether or not and should overlap and if so by how much is therefore removed. Furthermore, since can generally be recommended (see Section 4), we can omit both tuning parameters p and q.
- Augmentation of Test Statistic by considering the angle between andSome authors [55,56,57] successfully proposed a modified version of MZ, wherein the test statistic is based on angles rather than on Euclidean distances. While both approaches are viable on their own merits, we chose to merge them as they augment each other yielding a test statistic that, according to our results on raw ECG and PPG records, performs favorably compared to the test statistic constructed using either one on its own.In other words, we augment and improve upon the test statistic of MZ by making use of the information from the angles between and as well.
- Improved thresholding through Sequential Ranks CUSUMMZ provides further potential for improvement by employing a CUSUM-type control chart (see Equations (13) and (14)) whose control limit (or threshold) h is obtained through suitable normal approximation and asymptotic considerations (see [40] at 31; see also [41] at 8). The nuisance of having to properly normalize the test statistic (see Equation (12)) is a direct consequence of this design choice.We instead propose the use of McDonald’s Sequential Ranks CUSUM (SRC) [58] which we deem to be more appropriate and in line with the model-free nature of SSA.
- Restarting of SRC control chart after it signaledLastly, to allow for the detection of multiple and potentially nearby change-points we restart the SRC every time after it signaled an anomaly by exceeding the preset threshold .This is indicated since otherwise, depending on the extent of the anomaly (in terms of number of samples) and how it relates to the embedding dimension M as well as the number Q of columns in the Hankel matrix , it may take some time before the anomaly propagates through and clears (i.e., our sliding window) thereby resulting in a return of the test statistic to its ‘baseline level’. This is illustrated in Figure 3 where, as depicted in (a), three windows (differing in size) with are slid over an ECG containing a single PVC (highlighted in purple and marked with an arrow). As can be seen in (b), while is a feasible choice even without restarting the control chart after exceeding the threshold , since the respective SRC returns to values below after a relatively long but perhaps still acceptable amount of time, the same cannot be said for . Part (c) of Figure 3 illustrates the clear benefits of restarting the control charts, in that regardless of the choice of Q the PVC is detected and monitoring for further changes can swiftly resume. As was to be expected, is favorable in terms of detection delay.
3.2. Formal Description of l-SSA-CPD
- Initialization atSSA is applied on the interval to get , which akin to MZ involves:
- (a)
- Construction of the trajectory/base matrix , see Equation (8).
- (b)
- Singular Value Decomposition of
- (c)
- Selection of with
- 2.
- Construct test matrix on the interval , see Equation (9).
- 3.
- Compute the detection statisticswithtaking values in , accordingly , being the matrix of eigenvectors spanning , and ∘ denoting the Hadamard (element-wise) product.
- 4.
- Monitoring of using the Sequential Ranks CUSUM Control ChartLet us denote the sequential rank of asThe Sequential Ranks CUSUM is thenwith and being a reference constant.The SRC then signals and a change-point at n is declared ifholds, i.e., if exceeds a predetermined control limit .It can be shown [58] that, given that no change in the monitored signal occurred, the quantities are independent and discrete uniform onwhich represents a crucial advantage of the SRC in that it implies that for any we can obtain the control limit without the need for any historical training data or further assumptions through simulations as outlined in Algorithm 1.
Algorithm 1: Calculate for fixed (see Appendix A).
4. Performance Evaluation
4.1. Performance Metrics
4.2. Setup and l-SSA-CPD Parameters
- MZ would be computationally prohibitively expensive.Recall that the PC15 records are approximately 75 × 103 samples long, requiring computing the SVD of a 300 × 301 trajectory matrix, assuming about 74100 times as opposed to just once for l-SSA-CPD (see Figure 2).
- We aim to assess whether, based on its own merits, the performance of l-SSA-CPD suffices to be considered for potential real life applications such as the use case presented in this paper. To further this goal an in-depth comparative analysis to competing algorithms is not required and deemed to be beyond the scope of this paper.
4.3. Performance Evaluation and Comparison on PC15 Data
4.4. Performance Evaluation and Comparison on the St. Petersburg INCART Arrhythmia Database ECG Data
5. Discussion and Outlook
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ARL | Average Run Length |
| AV | Atrioventricular Node |
| CUSUM | Cumulative Sum Control Chart |
| ECG | Electrocardiography |
| HR | Heart Rate |
| INCART | St. Petersburg Institute of Cardiological Technics 12-Lead Arrhythmia Database |
| l-SSA-CPD | lightweight Singular Spectrum Analysis Change Point Detection |
| MEBD | Multimodal Ectopic Beat Detector |
| PAC | Premature Atrial Contraction |
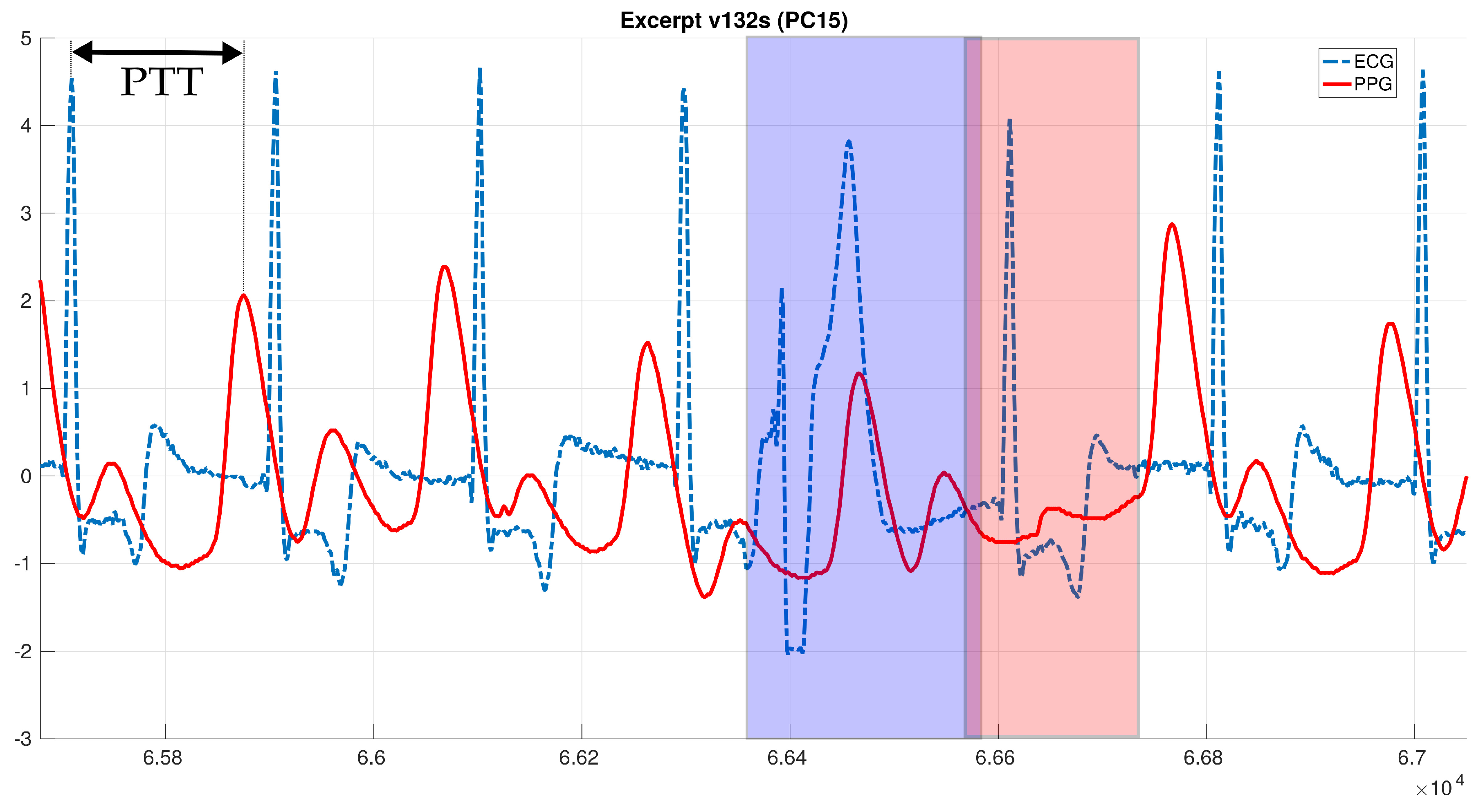
| PAT | Pulse Arrival Time |
| PC15 | Physionet Challenge 2015 Training Database |
| PCA | Principal Component Analysis |
| PPG | Photoplethysmography |
| PR | Pulse Rate |
| PTT | Pulse Transit Time |
| PVC | Premature Ventricular Contraction |
| SA | Sinoatrial Node |
| SRC | Sequential Ranks CUSUM Control Chart |
| SSA | Singular Spectrum Analysis |
| SVD | Singular Value Decomposition |
| TERMA | Two Event-Related Moving Averages |
Appendix A. CUSUM Control Charts
References
- Anindya, N.; Mukhopadhyay, S.C. Wearable Electronics Sensors: Current Status and Future Opportunities. In Wearable Electronics Sensors, 1st ed.; Mukhopadhyay, S.C., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–35. ISBN 978-3-31-918190-5. [Google Scholar]
- Selke, S. Introduction. In Lifelogging, 1st ed.; Selke, S., Ed.; Springer: Wiesbaden, Germany, 2016; pp. 1–21. ISBN 978-3-65-813136-4. [Google Scholar]
- Vieau, S.; Iaizzo, P.A. Basic ECG Theory, 12-Lead Recordings, and Their Interpretation. In Handbook of Cardiac Anatomy, Physiology, and Devices, 3rd ed.; Iaizzo, P.A., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 321–334. ISBN 978-3-31-919463-9. [Google Scholar]
- Gupta, R.; Mitra, M.; Bera, J. ECG Acquisition and Automated Remote Processing, 1st ed.; Springer India: New Delhi, India, 2014; ISBN 978-8-13-221556-1. [Google Scholar]
- Gacek, A.; Pedrycz, W. ECG Signal Processing, Classification and Interpretation, 1st ed.; Springer: London, UK, 2012; ISBN 978-0-85-729867-6. [Google Scholar]
- Kiasaleh, K. Biological Signals Classification and Analysis, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-64-254878-9. [Google Scholar]
- Webster, J.G. (Ed.) Design of Pulse Oximeters, 1st ed.; CRC Press: Boca Raton, FL, USA, 1997; ISBN 978-0-75-030467-2. [Google Scholar]
- Lemay, M.; Bertschi, M.; Sola, J.; Renevey, P.; Parak, J.; Korhonen, I. Application of Optical Heart Rate Monitoring. In Wearable Sensors, 1st ed.; Sazonov, E., Neuman, M., Eds.; Academic Press: Cambridge, MA, USA, 2014; pp. 105–129. ISBN 978-0-12-418662-0. [Google Scholar]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1. [Google Scholar] [CrossRef] [PubMed]
- Adibi, S. (Ed.) Mobile Health, 1st ed.; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-31-912816-0. [Google Scholar]
- Holzinger, A.; Röcker, C.; Ziefle, M. (Eds.) Smart Health, 1st ed.; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-31-916225-6. [Google Scholar]
- Malvey, D.; Slovensky, D.J. mHealth, 1st ed.; Springer: New York, NY, USA, 2014; ISBN 978-1-48-997456-3. [Google Scholar]
- Lang, M. Heart Rate Monitoring Apps: Information for Engineers and Researchers About the New European Medical Devices Regulation 2017/745. JMIR Biomed. Eng. 2017, 2, e2. [Google Scholar] [CrossRef]
- Quinn, P. The EU commission’s risky choice for a non-risk based strategy on assessment of medical devices. Comput. Law Secur. Rev. 2017, 33, 361–370. [Google Scholar] [CrossRef]
- Sperlich, B.; Holmberg, H.C. Wearable, yes, but able…? it is time for evidence-based marketing claims! Br. J. Sports. Med. 2017, 51, 1240. [Google Scholar] [CrossRef] [PubMed]
- Lang, M. Beyond Fitbit: A Critical Appraisal of Optical Heart Rate Monitoring Wearables and Apps, Their Current Limitations and Legal Implications. Albany Law J. Sci. Technol. 2017, 28, 39–72. [Google Scholar]
- Tripathi, O.N.; Ravens, U.; Sanguinetti, M.C. (Eds.) Heart Rate and Rhythm: Molecular Basis, Pharmacological Modulation and Clinical Implications, 1st ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-64-217574-9. [Google Scholar]
- Jangra, M.; Dhull, S.K.; Singh, K.K. Recent trends in arrhythmia beat detection: A review. In Communication and Computing Systems, 1st ed.; Prasad, B.M., Singh, K.K., Ruhil, N., Singh, K., O’Kennedy, R., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 177–183. ISBN 978-1-13-802952-1. [Google Scholar]
- Veeravalli, B.; Deepu, C.J.; Ngo, D. Real-Time, Personalized Anomaly Detection in Streaming Data for Wearable Healthcare Devices. In Handbook of Large-Scale Distributed Computing in Smart Healthcare, 1st ed.; Khan, S.U., Zomaya, A.Y., Abbas, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 403–426. ISBN 978-3-31-958280-1. [Google Scholar]
- Elgendi, M.; Eskofier, B.; Dokos, S.; Abbott, D. Revisiting QRS Detection Methodologies for Portable, Wearable, Battery-Operated, and Wireless ECG Systems. PLoS ONE 2014, 9, e84018. [Google Scholar] [CrossRef] [PubMed]
- Lemkaddem, A.; Proença, M.; Delgado-Gonzalo, R.; Renevey, P.; Oei, I.; Montano, G.; Martinez-Heras, J.A.; Donati, A.; Bertschi, M.; Lemay, M. An autonomous medical monitoring system: Validation on arrhythmia detection. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017; pp. 4553–4556. [Google Scholar]
- Ye, C.; Coimbra, M.T.; Vijaya Kumar, B.V.K. Arrhythmia detection and classification using morphological and dynamic features of ECG signals. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 1918–1921. [Google Scholar]
- Chang, R.C.H.; Lin, C.H.; Wei, M.F.; Lin, K.H.; Chen, S.R. High-precision real-time premature ventricular contraction (PVC) detection system based on wavelet transform. J. Sign. Process. Syst. 2014, 77, 289–296. [Google Scholar] [CrossRef]
- Yaghouby, F.; Ayatollahi, A.; Bahramali, R.; Yaghouby, M.; Alavi, A.H. Towards automatic detection of atrial fibrillation: a hybrid computational approach. Comput. Biol. Med. 2010, 40, 919–930. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Bhat, B.S.; Iyengar, S.S.; Rao, A.; Dua, S. Classification of heart rate data using artificial neural network and fuzzy equivalence relation. Pattern Recognit. 2003, 36, 61–68. [Google Scholar] [CrossRef]
- Kumar, S.; Bansal, A.; Tiwari, V.N.; Nayak, M.M.; Narayanan, R.V. Remote health monitoring system for detecting cardiac disorders. IET Syst. Biol. 2015, 9, 309–314. [Google Scholar] [CrossRef]
- Gradl, S.; Kugler, P.; Lohmüller, C.; Eskofier, B. Real-time ECG monitoring and arrhythmia detection using Android-based mobile devices. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 2452–2455. [Google Scholar]
- Luz, E.J.S.; Schwartz, W.R.; Cámara-Chávez, G.; Menotti, D. ECG-based heartbeat classification for arrhythmia detection: A survey. Comput. Methods Programs. Biomed. 2016, 127, 144–164. [Google Scholar] [CrossRef] [PubMed]
- Oresko, J.J.; Jin, Z.; Cheng, J.; Huang, S.; Sun, Y.; Duschl, H.; Cheng, A.C. A Wearable Smartphone-Based Platform for Real-Time Cardiovascular Disease Detection Via Electrocardiogram Processing. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 734–740. [Google Scholar] [CrossRef] [PubMed]
- Amiri, A.M.; Mankodiya, A.K. m-QRS: An efficient QRS detection algorithm for mobile health applications. In Proceedings of the 17th International Conference on E-health Networking, Application & Services (HealthCom), Boston, MA, USA, 14–17 October 2015; pp. 673–676. [Google Scholar]
- Kim, Y.J.; Heo, J.; Park, K.S.; Kim, S. Proposition of novel classification approach and features for improved real-time arrhythmia monitoring. Comput. Biol. Med. 2016, 75, 190–202. [Google Scholar] [CrossRef] [PubMed]
- Tsipouras, M.G.; Fotiadis, D.I. Automatic arrhythmia detection based on time and time-frequency analysis of heart rate variability. Comput. Methods Programs Biomed. 2004, 74, 95–108. [Google Scholar] [CrossRef]
- De Chazal, P.; O’Dwyer, M.; Reilly, R.B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2004, 51, 1196–1206. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. Fast QRS Detection with an Optimized Knowledge-Based Method: Evaluation on 11 Standard ECG Databases. PLoS ONE 2013, 8, e73557. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. TERMA Framework for Biomedical Signal Analysis: An Economic-Inspired Approach. Biosensors 2016, 6, 55. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Mohamed, A.; Ward, R. Efficient ECG Compression and QRS Detection for E-Health Applications. Sci. Rep. 2017, 7, 459. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Al-Ali, A.; Mohamed, A.; Ward, R. Improving Remote Health Monitoring: A Low-Complexity ECG Compression Approach. Diagnostics 2018, 8, 10. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Howard, N.; Lovell, N.; Cichocki, A.; Brearley, M.; Abbott, D.; Adatia, I. A Six-Step Framework on Biomedical Signal Analysis for Tackling Noncommunicable Diseases: Current and Future Perspectives. JMIR Biomed. Eng. 2016, 1, e1. [Google Scholar] [CrossRef]
- Moskvina, V. Application of the Singular Spectrum Analysis for Change-Point Detection in Time Series. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2001. [Google Scholar]
- Moskvina, V.; Zhigljavsky, A. An Algorithm Based on Singular Spectrum Analysis for Change-Point Detection. Commun. Stat. Simul. Comput. 2003, 32, 319–352. [Google Scholar] [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A. Analysis of Time Series Structure: SSA and Related Techniques, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2001; ISBN 978-1-58-488194-0. [Google Scholar]
- Dong, Q.; Yang, Z.; Chen, Y.; Li, X.; Zeng, K. Anomaly Detection in Cognitive Radio Networks Exploiting Singular Spectrum Analysis. In Computer Network Security. MMM-ACNS 2017. Lecture Notes in Computer Science; Rak, J., Bay, J., Kotenko, I., Popyack, L., Skormin, V., Szczypiorski, K., Eds.; Springer: Cham, Switzerland, 2017; pp. 321–334. ISBN 978-3-319-19463-9. [Google Scholar]
- Yang, Z.; Zhou, N.; Polunchenko, A.; Chen, Y. Singular Spectrum Analysis Based Quick Online Detection of Disturbance Start Time in Power Grid. In Proceedings of the IEEE Global Communications Conference (GLOBECOM) 2015, San Diego, CA, USA, 6–10 December 2015. [Google Scholar]
- Zhang, S.; Liu, Y.; Pei, D.; Chen, Y.; Qu, X.; Tao, S.; Zang, S.; Jing, X.; Feng, M. FUNNEL: Assessing Software Changes in Web-Based Services. IEEE Trans. Serv. Comput. 2018, 11, 34–48. [Google Scholar] [CrossRef]
- Georgescu, V.; Delureanu, S.M. Fuzzy-valued and complex-valued time series analysis using multivariate and complex extensions to singular spectrum analysis. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Istanbul, Turkey, 2–5 August 2015; pp. 1–8. [Google Scholar]
- Jarchi, D.; Lo, B.; Wong, C.; Ieong, E.; Nathwani, D.; Yang, G.Z. Gait Analysis From a Single Ear-Worn Sensor: Reliability and Clinical Evaluation for Orthopaedic Patients. IEEE Trans. Neural. Syst. Rehabil. Eng. 2016, 24, 882–892. [Google Scholar] [CrossRef] [PubMed]
- Uus, A.; Liatsis, P. Singular Spectrum Analysis for detection of abnormalities in periodic biosignals. In Proceedings of the 18th International Conference on Systems, Signals and Image Processing, Sarajevo, Bosnia and Hercegovina, 16–18 June 2011; pp. 1–4. [Google Scholar]
- Sanei, S.; Hassani, H. Singular Spectrum Analysis of Biomedical Signals, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015; ISBN 978-1-46-658927-8. [Google Scholar]
- Clifford, G.D.; Silva, I.; Moody, B.; Li, Q.; Kella, D.; Shahin, A.; Kooistra, T.; Perry, D.; Mark, R.G. The PhysioNet/Computing in Cardiology Challenge 2015: Reducing False Arrhythmia Alarms in the ICU. Comput. Cardiol. 2015, 42, 273–276. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. Physiobank, physiotoolkit, and physionet. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Pflugradt, M.; Geissdoerfer, K.; Goernig, M.; Orglmeister, R. Fast Multimodal Ectopic Beat Detection Method Applied for Blood Pressure Estimation Based on Pulse Wave Velocity Measurements in Wearable Sensors. Sensors 2017, 17, 158. [Google Scholar] [CrossRef] [PubMed]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-64-234912-6. [Google Scholar]
- Elsner, J.B.; Tsonis, A.A. Singular Spectrum Analysis: A New Tool in Time Series Analysis, 1st ed.; Springer: New York, NY, USA, 1996; ISBN 978-0-30-645472-1. [Google Scholar]
- Idé, T.; Inoue, K. Knowledge discovery from heterogeneous dynamic systems using change-point correlations. In Proceedings of the SIAM International Conference on Data Mining; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005; pp. 571–575. ISBN 0898715938. [Google Scholar]
- Mohammad, Y.; Nishida, T. Robust Singular Spectrum Transform. In Next-Generation Applied Intelligence: 22nd International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, IEA/AIE 2009, Tainan, Taiwan; Chien, B.C., Hong, T.P., Chen, S.M., Ali, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 123–132. ISBN 978-3-64-202568-6. [Google Scholar]
- Idé, T.; Tsuda, K. Change-Point Detection using Krylov Subspace Learning. In Proceedings of the SIAM International Conference on Data Mining; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 515–520. [Google Scholar]
- McDonald, D.R. A Cusum Procedure Based on Sequential Ranks. Laboratory for Research in Statistics and Probability; Carleton University: Ottawa, Canada, 1985. [Google Scholar]
- Salvi, P. Pulse Waves, 1st ed.; Springer: Milan, Italy, 2012; ISBN 978-8-84-702439-7. [Google Scholar]
- Page, E.S. Continuous Inspection Schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Lucas, J.M. The Design and Use of Cumulative Sum Control Schemes. Technometrics 1976, 14, 51–59. [Google Scholar]
- Chatterjee, S.; Qiu, P. Distribution-free cumulative sum control charts using bootstrap-based control limits. Ann. Appl. Stat. 2009, 3, 349–369. [Google Scholar] [CrossRef]
- Reynolds, M.R. Approximations to the average run length in cumulative sum control charts. Technometrics 1975, 17, 65–71. [Google Scholar] [CrossRef]


| Record | Q | 1 | 5 | 10 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Statistic | ||||||||||
| v132s | Se | 0.9677 | 0.9677 | 0.9677 | 0.9677 | 0.8710 | 0.9677 | 0.9677 | 0.6774 | 0.9677 |
| Sp | 0.9992 | 0.9991 | 0.9991 | 0.9992 | 0.9988 | 0.9992 | 0.9992 | 0.9997 | 0.9992 | |
| Acc | 0.9992 | 0.9991 | 0.9991 | 0.9992 | 0.9988 | 0.9991 | 0.9992 | 0.9996 | 0.9992 | |
| v253l | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.7922 | 1.0000 | 1.0000 | 0.3247 | 1.0000 |
| Sp | 0.9987 | 0.9988 | 0.9987 | 0.9987 | 0.9985 | 0.9987 | 0.9987 | 0.9999 | 0.9987 | |
| Acc | 0.9987 | 0.9988 | 0.9987 | 0.9987 | 0.9983 | 0.9987 | 0.9987 | 0.9993 | 0.9987 | |
| v255l | Se | 0.9844 | 0.9844 | 0.9844 | 0.9844 | 0.3906 | 0.9844 | 0.9844 | 0.6250 | 0.9844 |
| Sp | 0.9988 | 0.9988 | 0.9988 | 0.9988 | 0.9988 | 0.9988 | 0.9988 | 0.9999 | 0.9988 | |
| Acc | 0.9988 | 0.9988 | 0.9988 | 0.9988 | 0.9984 | 0.9988 | 0.9988 | 0.9996 | 0.9988 | |
| v368s | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.7143 | 1.0000 | 1.0000 | 0.7143 | 1.0000 |
| Sp | 0.9989 | 0.9985 | 0.9987 | 0.9989 | 0.9994 | 0.9990 | 0.9989 | 0.9995 | 0.9989 | |
| Acc | 0.9989 | 0.9985 | 0.9987 | 0.9989 | 0.9994 | 0.9990 | 0.9989 | 0.9995 | 0.9989 | |
| v557l | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.2500 | 1.0000 | 1.0000 | 0.0000 | 1.0000 |
| Sp | 0.9993 | 0.9991 | 0.9992 | 0.9993 | 0.9995 | 0.9993 | 0.9993 | 0.9997 | 0.9993 | |
| Acc | 0.9993 | 0.9991 | 0.9992 | 0.9993 | 0.9995 | 0.9993 | 0.9993 | 0.9996 | 0.9993 | |
| t662s | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 |
| Sp | 0.9988 | 0.9986 | 0.9987 | 0.9988 | 0.9984 | 0.9987 | 0.9988 | 0.9999 | 0.9988 | |
| Acc | 0.9988 | 0.9986 | 0.9987 | 0.9988 | 0.9984 | 0.9987 | 0.9988 | 0.9998 | 0.9988 | |
| a746s | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8333 | 1.0000 | 1.0000 | 0.6667 | 1.0000 |
| Sp | 0.9986 | 0.9987 | 0.9986 | 0.9986 | 0.9990 | 0.9986 | 0.9986 | 0.9997 | 0.9986 | |
| Acc | 0.9986 | 0.9987 | 0.9986 | 0.9986 | 0.9990 | 0.9986 | 0.9986 | 0.9997 | 0.9986 | |
| v831l | Se | 0.9583 | 0.9583 | 0.9583 | 0.9583 | 0.8750 | 0.9583 | 0.9167 | 0.0417 | 0.9167 |
| Sp | 0.9992 | 0.9991 | 0.9992 | 0.9992 | 0.9991 | 0.9992 | 0.9992 | 0.9998 | 0.9992 | |
| Acc | 0.9992 | 0.9991 | 0.9991 | 0.9992 | 0.9991 | 0.9992 | 0.9992 | 0.9995 | 0.9992 | |
| Se | 0.9888 | 0.9888 | 0.9888 | 0.9888 | 0.7158 | 0.9888 | 0.9836 | 0.3812 | 0.9836 | |
| Sp | 0.9989 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9989 | 0.9989 | 0.9997 | 0.9989 | |
| Acc | 0.9989 | 0.9988 | 0.9989 | 0.9989 | 0.9987 | 0.9989 | 0.9989 | 0.9996 | 0.9989 | |
| Record | Q | 1 | 5 | 10 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Statistic | ||||||||||
| v132s | Se | 0.7419 | 0.8387 | 0.8387 | 0.7419 | 0.0000 | 0.7419 | 0.7419 | 0.0000 | 0.7419 |
| Sp | 0.9994 | 0.9995 | 0.9995 | 0.9994 | 0.9999 | 0.9994 | 0.9994 | 0.9999 | 0.9994 | |
| Acc | 0.9993 | 0.9994 | 0.9994 | 0.9993 | 0.9995 | 0.9993 | 0.9993 | 0.9995 | 0.9993 | |
| v253l | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.3108 | 1.0000 | 1.0000 | 0.7432 | 1.0000 |
| Sp | 0.9992 | 0.9991 | 0.9991 | 0.9992 | 0.9999 | 0.9992 | 0.9991 | 0.9999 | 0.9991 | |
| Acc | 0.9992 | 0.9991 | 0.9991 | 0.9992 | 0.9993 | 0.9992 | 0.9991 | 0.9997 | 0.9991 | |
| v255l | Se | 0.9688 | 0.9688 | 0.9688 | 0.9688 | 0.4219 | 0.9688 | 0.9688 | 0.4062 | 0.9688 |
| Sp | 0.9993 | 0.9993 | 0.9993 | 0.9992 | 0.9999 | 0.9992 | 0.9992 | 0.9999 | 0.9992 | |
| Acc | 0.9992 | 0.9993 | 0.9993 | 0.9992 | 0.9995 | 0.9992 | 0.9992 | 0.9994 | 0.9992 | |
| v368s | Se | 0.0000 | 0.1667 | 0.1667 | 0.1667 | 0.1667 | 0.1667 | 0.0000 | 0.0000 | 0.0000 |
| Sp | 0.9978 | 0.9980 | 0.9979 | 0.9978 | 0.9997 | 0.9978 | 0.9977 | 0.9996 | 0.9977 | |
| Acc | 0.9978 | 0.9980 | 0.9979 | 0.9978 | 0.9997 | 0.9978 | 0.9977 | 0.9995 | 0.9977 | |
| v557l | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.2500 | 1.0000 | 1.0000 | 0.7500 | 1.0000 |
| Sp | 0.9990 | 0.9986 | 0.9988 | 0.9990 | 0.9999 | 0.9990 | 0.9990 | 0.9997 | 0.9990 | |
| Acc | 0.9990 | 0.9986 | 0.9988 | 0.9990 | 0.9998 | 0.9990 | 0.9990 | 0.9997 | 0.9990 | |
| t662s | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 |
| Sp | 0.9986 | 0.9986 | 0.9987 | 0.9986 | 0.9999 | 0.9986 | 0.9986 | 0.9998 | 0.9986 | |
| Acc | 0.9986 | 0.9986 | 0.9987 | 0.9986 | 0.9999 | 0.9986 | 0.9986 | 0.9997 | 0.9986 | |
| a746s | Se | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.1667 | 1.0000 | 1.0000 | 0.3333 | 1.0000 |
| Sp | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9998 | 0.9980 | 0.9980 | 0.9997 | 0.9980 | |
| Acc | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9998 | 0.9980 | 0.9980 | 0.9997 | 0.9980 | |
| v831l | Se | 0.9583 | 0.9583 | 0.9583 | 0.9583 | 0.1250 | 0.9583 | 0.9583 | 0.1667 | 0.9583 |
| Sp | 0.9984 | 0.9983 | 0.9983 | 0.9984 | 0.9997 | 0.9984 | 0.9984 | 0.9998 | 0.9984 | |
| Acc | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9995 | 0.9983 | 0.9983 | 0.9995 | 0.9983 | |
| Se | 0.8336 | 0.8666 | 0.8666 | 0.8545 | 0.1801 | 0.8545 | 0.8336 | 0.2999 | 0.8336 | |
| Sp | 0.9987 | 0.9987 | 0.9987 | 0.9987 | 0.9998 | 0.9987 | 0.9987 | 0.9998 | 0.9987 | |
| Acc | 0.9987 | 0.9987 | 0.9987 | 0.9987 | 0.9996 | 0.9987 | 0.9987 | 0.9996 | 0.9987 | |
| Method | ECG | PPG | ||
|---|---|---|---|---|
| Se | Sp | Se | Sp | |
| l-SSA-CPD | 0.989 | 0.999 | 0.867 | 0.998 |
| MEBD | 0.953 | 0.989 | 0.876 | 0.955 |
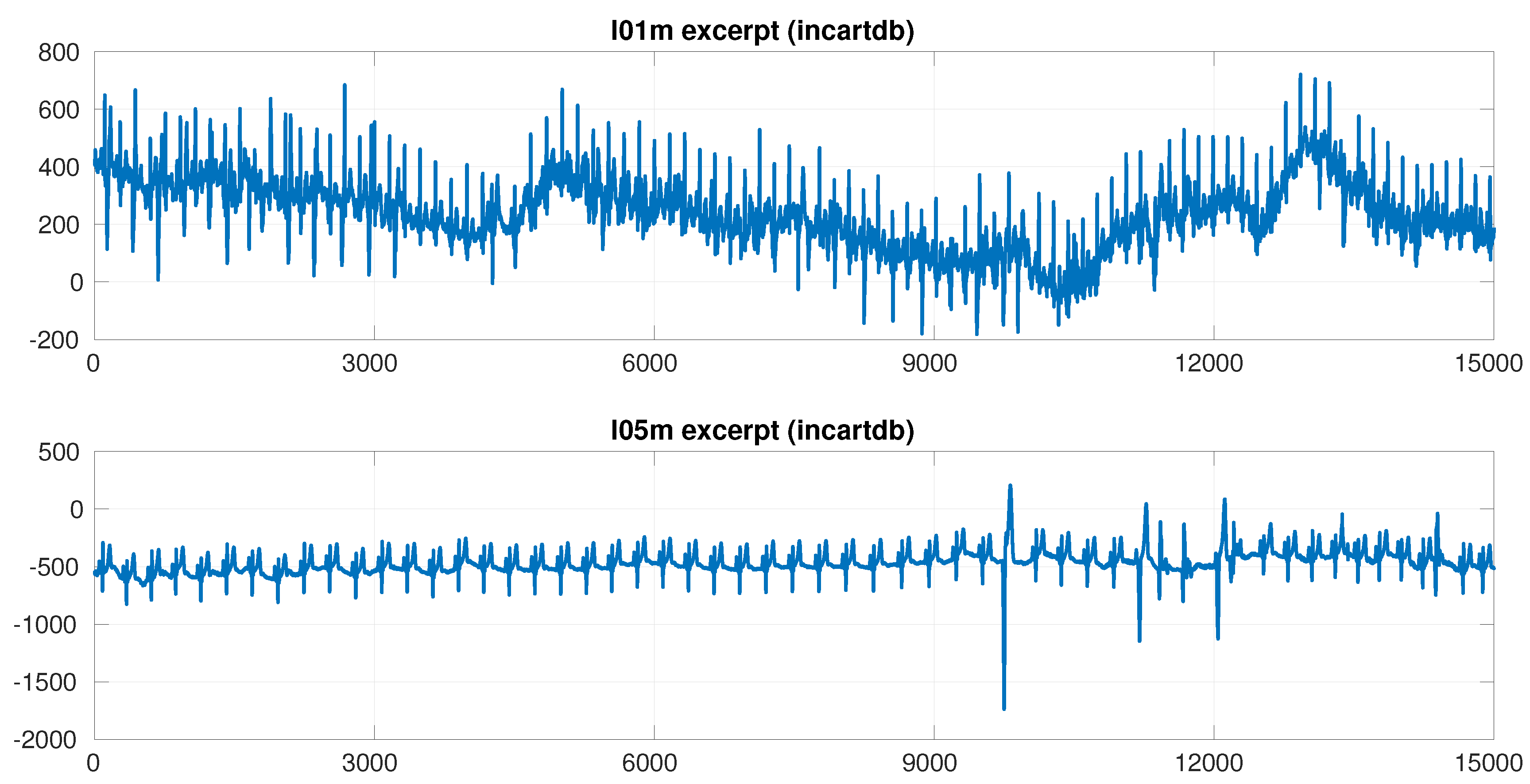
| Record | l-SSA-CPD (unfiltered) | l-SSA-CPD (BP-filtered) | Uus and Liatsis (man. par. adj.) | Uus and Liatsis (aut. par. adj.) | ||||
|---|---|---|---|---|---|---|---|---|
| Se | Sp | Se | Sp | Se | Sp | Se | Sp | |
| I01m | 0.25 | 0.99 | 0.34 | 0.99 | 0.99 | 0.95 | 0.94 | 0.84 |
| I02m | 0.43 | 0.99 | 0.24 | 0.99 | 0.97 | 0.93 | 0.92 | 0.86 |
| I03m | 0.98 | 0.99 | 1.00 | 0.99 | 0.96 | 0.95 | 0.90 | 0.85 |
| I04m | 0.23 | 0.99 | 0.58 | 0.99 | 0.97 | 0.92 | 0.91 | 0.89 |
| I05m | 0.82 | 0.99 | 0.99 | 0.99 | 0.98 | 0.94 | 0.92 | 0.88 |
| I06m | 0.86 | 0.99 | 0.97 | 0.99 | 0.97 | 0.96 | 0.92 | 0.85 |
| I07m | 0.57 | 0.99 | 0.74 | 0.99 | 0.98 | 0.93 | 0.90 | 0.83 |
| I08m | 0.92 | 0.99 | 0.99 | 0.99 | 0.97 | 0.91 | 0.92 | 0.91 |
| I09m | 0.83 | 0.99 | 0.89 | 0.99 | 0.98 | 0.91 | 0.89 | 0.89 |
| I10m | 0.93 | 0.99 | 0.98 | 0.99 | 0.98 | 0.93 | 0.93 | 0.88 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, M. A Low-Complexity Model-Free Approach for Real-Time Cardiac Anomaly Detection Based on Singular Spectrum Analysis and Nonparametric Control Charts. Technologies 2018, 6, 26. https://doi.org/10.3390/technologies6010026
Lang M. A Low-Complexity Model-Free Approach for Real-Time Cardiac Anomaly Detection Based on Singular Spectrum Analysis and Nonparametric Control Charts. Technologies. 2018; 6(1):26. https://doi.org/10.3390/technologies6010026
Chicago/Turabian StyleLang, Michael. 2018. "A Low-Complexity Model-Free Approach for Real-Time Cardiac Anomaly Detection Based on Singular Spectrum Analysis and Nonparametric Control Charts" Technologies 6, no. 1: 26. https://doi.org/10.3390/technologies6010026
APA StyleLang, M. (2018). A Low-Complexity Model-Free Approach for Real-Time Cardiac Anomaly Detection Based on Singular Spectrum Analysis and Nonparametric Control Charts. Technologies, 6(1), 26. https://doi.org/10.3390/technologies6010026






