The Physics of Turbulence-Free Ghost Imaging

Abstract

Since its first experimental demonstration, ghost imaging has attracted a great deal of attention due to interests in its fundamental nature and its potential applications. In terms of applications, the most interesting and useful feature, perhaps, is the turbulence insensitivity of thermal light ghost imaging, i.e., atmospheric turbulence would not have any influence on the ghost images of sunlight. Inspired by ghost imaging, a new type of camera is ready for turbulence-free imaging applications. This turbulence-free camera would be especially useful for long distance imaging, such as satellite imaging. How could fluctuations of thermal light produce an image? Why is it turbulence-free? This article addresses these questions.

1. Introduction

The first ghost imaging experiment was demonstrated in 1995 using entangled photon pairs [1,2]. The image was observed from the joint photo-detection events of two independent and spatially separated photon counting detectors, which is the result of a two-photon constructive–destructive superposition among a large number of biphoton amplitudes, a nonclassical entity corresponding to different yet indistinguishable alternative ways of producing a joint photo-detection event between two distant photo-detectors. Based on the two-photon interference picture, ten years later, in 2005, lensless ghost imaging experiments were designed and demonstrated with pseudo-thermal light [3,4,5,6]. The image was, again, observed in the correlation measurement of two independent and spatially separated photon counting detectors, but from their photon number fluctuations, which is the result of a superposition between two different yet indistinguishable alternative amplitudes for a random pair of photons, or subfields, to produce a joint photo-detection event. A number of classical simulations of ghost imaging, either based on the measurement of correlated laser beams or based on the measurement of correlated light speckles, have been introduced successfully since then [7,8,9]. It is necessary to emphasize that not all of these ghost imaging mechanisms produce turbulence-free images. The only turbulence-free ghost image is produced from a peculiar interference: the observed image is the result of a random pair of photons or subfields interfering with the pair itself. We may name it “two-photon interference”or “two-subfield interference”. The physics is simple: when the superposed two amplitudes “overlap”, i.e., experience the same optical path and thus the same turbulence, the turbulence-induced phase variations cancel each other in the cross interference term of the interference. In this type of ghost imaging, the ghost image is observed from the measurement of this cross interference term, i.e., the photon number fluctuation correlation or intensity fluctuation correlation. Therefore, the observed image would not be “blurred” by the turbulence-induced phase variations. Inspired by the turbulence-free ghost imaging experiment [10], based on the two-photon, or two-subfield, interference picture, a new type of turbulence-free camera is practically ready for applications. The turbulence-free camera would be especially useful for long distance imaging, such as satellite imaging.

2. Classical Imaging

Assume a target object is either self-luminous or externally illuminated, and imagine each point on the object surface is an independent point sub-source of radiation with amplitude proportional to the aperture-function of the object plane $A({\overrightarrow{\rho }}_o)$, where ${\overrightarrow{\rho }}_o$ is the transverse coordinate of the point sub-source. Each point sub-source emits spherical waves in all possible directions. Intuitively, we expect there is very little chance that a spherical wave emitted from a point sub-source will collapse to a point or a speckle again after its free propagation of a certain distance. It has been understood since early times that the chance is zero unless an imaging system is applied. A perfect imaging system makes sub-radiation that is either emitted, reflected or scattered from a point of the object plane observable only at a unique point on the image plane, thus producing a point-to-point relationship between the object plane and the image plane, i.e., an image of the object.

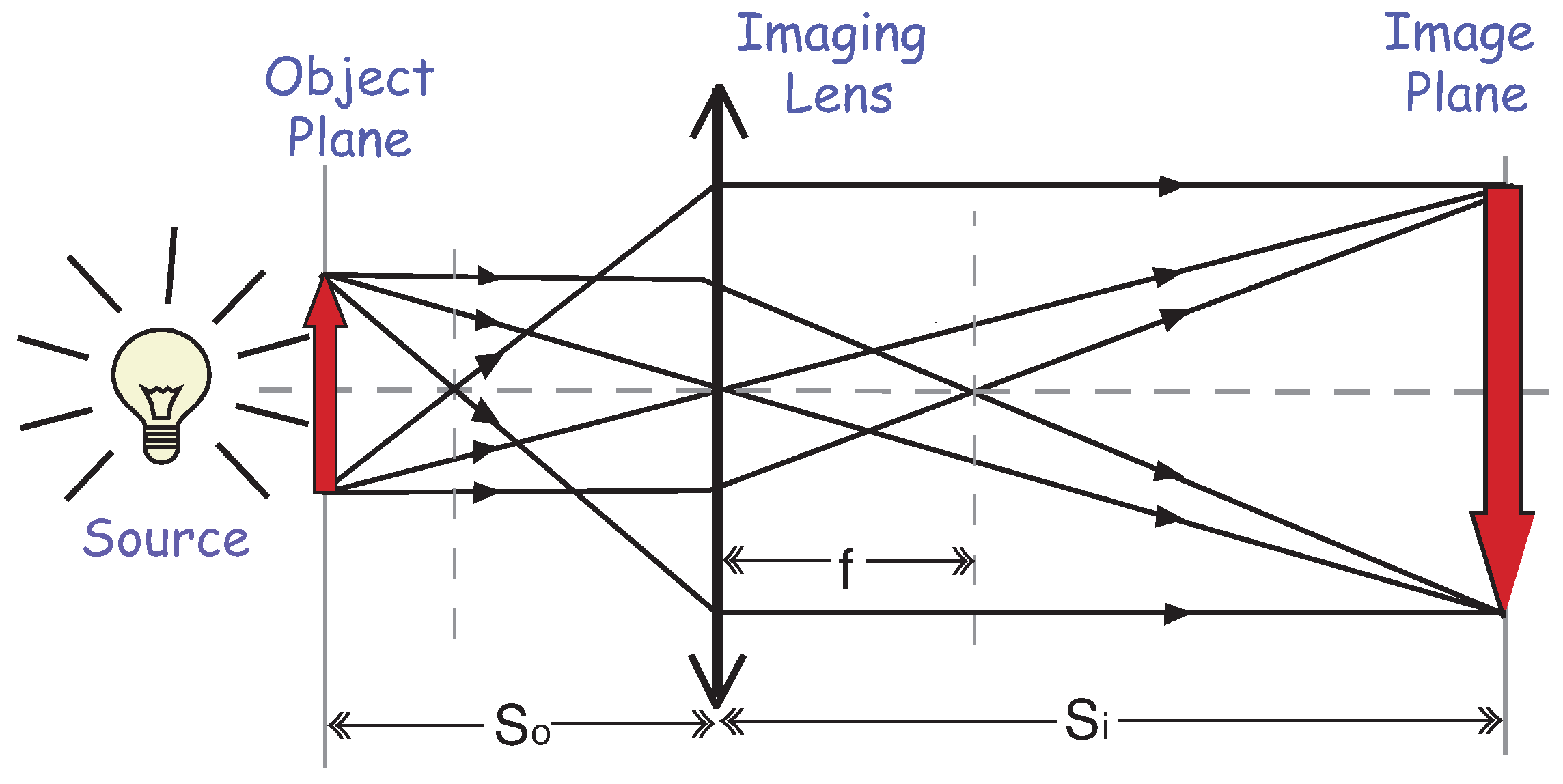
The concept of optical imaging is well developed in classical optics [11,12]. Figure 1 schematically illustrates a standard imaging setup. In this setup, an object is illuminated by a thermal radiation source, while an imaging lens focuses the scattered and reflected light from the object onto an image plane defined by the Gaussian thin lens equation

$$\frac{1}{s_i}+\frac{1}{s_o}=\frac{1}{f}$$

(1)

where $s_o$ is the distance between the object and the imaging lens, $s_i$ the distance between the imaging lens and the image plane, and f the focal length of the imaging lens. In an ideal situation, the imaging lens produces a point-to-point relationship between the object plane and the image plane: any radiation starting from a point on the object plane will collapse to a unique point on the image plane. It is not difficult to see from Figure 1 that the point-to-point relationship is the result of constructive–destructive interference. The radiation fields coming from a point on the object plane will experience equal distance propagation to superpose constructively at one unique point on the image plane, and experience unequal distance propagation to superpose destructively at all other points on the image plane. The use of the imaging lens makes this constructive–destructive interference possible.

Recall that Einstein introduced a granularity to radiation, abandoning the continuum interpretation of Maxwell [13]. This led to a statistical view of light: point sources of radiation emits photons, or subfields, randomly in all possible directions. The radiation measured at coordinate $(\mathbf{r},t)$ is the result of a superposition among a large number of random subfields, ${\sum }_{m=1}^{\infty }{E}_m(\mathbf{r},t)$, each emitted from a point source. The measured intensity, which is proportional to the number of photons, corresponds to the theoretical expectation of $\langle I(\mathbf{r},t)\rangle \propto \langle n(\mathbf{r},t)\rangle$,

$$\begin{array}{c}\langle I(\mathbf{r},t)\rangle =\langle E^{*}(\mathbf{r},t)E(\mathbf{r},t)\rangle =\langle \sum _m{E}_m^{*}(\mathbf{r},t)\sum _n{E}_n(\mathbf{r},t)\rangle \hfill \\ =\langle \sum _m|E_m(\mathbf{r},t){|}^2\rangle +\langle \sum _{m\ne n}{E}_m^{*}(\mathbf{r},t)E_n(\mathbf{r},t)\rangle \hfill \\ =\sum _m|E_m(\mathbf{r},t){|}^2+0\hfill \end{array}$$

(2)

It is clear that the mean intensity (or mean number of photons) is the result of the mth subfield interfering with the mth subfield itself; $\Delta I(\mathbf{r},t)$, the intensity fluctuation (or photon number fluctuation) is the result of the mth subfield interfering with the nth subfield, $m\ne n$. Due to the random phases associated with the subfields, $\Delta I(\mathbf{r},t)$ takes random values from time to time or from measurement to measurement. It is also easy to find that $\langle \Delta I(\mathbf{r},t)\rangle =0$ by taking into account all possible random phases of the subfields. It is understandable that $\Delta I(\mathbf{r},t)={\sum }_{m\ne n}{E}_m^{*}(\mathbf{r},t)E_n(\mathbf{r},t)$ does not have any significant contribution to the measurement of $\langle I(\mathbf{r},t)\rangle$, unless the measurement was too far from an ensemble average. Therefore, ${\sum }_{m\ne n}{E}_m^{*}(\mathbf{r},t)E_n(\mathbf{r},t)$ is usually considered random “noise” in the measurement of $\langle I(\mathbf{r},t)\rangle$.

To calculate the classical image, we model the thermal radiation source as a collection of a large number of independent and randomly radiating point-like sub-sources randomly distributed on a disk parallel to the object plane. A large number of subfields radiate from these sub-sources to all possible directions with random phases. In a natural thermal source, such as the sun, each sub-source corresponds to an atomic transition. A photon created from a transition corresponds to a subfield. In a pseudo-thermal source, such as a ground glass scattered laser beam, millions of tiny scattering diffusers on the rotating ground glass act as sub-sources. Each scattered radiation, containing a group of identical photons, plays the role of subfields. Each diffuser scatters a subfield to all possible directions, during which the subfields acquire random phases. To simplify the calculation, we assume the radiation is monochromatic, so that the calculation will focus on its spatial behavior. The measured intensity at transverse coordinate ${\overrightarrow{\rho }}_i$ of the image plane is calculated as follows:

$$\begin{array}{cc}\hfill \langle I({\overrightarrow{\rho }}_i)\rangle & =\langle \sum _m[E_m^{*}\int d{\overrightarrow{\rho }}_o{g}_m^{*}({\overrightarrow{\rho }}_o)A^{*}({\overrightarrow{\rho }}_o)g_o^{*}({\overrightarrow{\rho }}_i)]\sum _n[E_n\int d{\overrightarrow{\rho }}_{o^{\prime }}{g}_n({\overrightarrow{\rho }}_{o^{\prime }})A({\overrightarrow{\rho }}_{o^{\prime }})g_o({\overrightarrow{\rho }}_i)]\rangle \hfill \\ & =\langle \sum _m|E_m\int d{\overrightarrow{\rho }}_o{g}_m({\overrightarrow{\rho }}_o)A({\overrightarrow{\rho }}_o)g_o({\overrightarrow{\rho }}_i){|}^2\rangle \hfill \\ & +\langle \sum _{m\ne n}[E_m^{*}\int d{\overrightarrow{\rho }}_o{g}_m^{*}({\overrightarrow{\rho }}_o)A^{*}({\overrightarrow{\rho }}_o)g_o^{*}({\overrightarrow{\rho }}_i)][E_n\int d{\overrightarrow{\rho }}_{o^{\prime }}{g}_n({\overrightarrow{\rho }}_{o^{\prime }})A({\overrightarrow{\rho }}_{o^{\prime }})g_o({\overrightarrow{\rho }}_i)]\rangle \hfill \\ & =\sum _m|E_m\int d{\overrightarrow{\rho }}_o{g}_m({\overrightarrow{\rho }}_o)A({\overrightarrow{\rho }}_o)g_o({\overrightarrow{\rho }}_i){|}^2+0\hfill \end{array}$$

(3)

where $E_m$ is the mth subfield, ${\overrightarrow{\rho }}_o$ and ${\overrightarrow{\rho }}_i$ are the transverse coordinates in the object and image planes, respectively, $g_m({\overrightarrow{\rho }}_o)$ is the propagator, or Green’s function, which propagates the mth subfield from the mth sub-source (coordinate ${\overrightarrow{\rho }}_m$) to point ${\overrightarrow{\rho }}_o$ on the object plane, $A({\overrightarrow{\rho }}_o)$ is the aperture-function of the object including a real and positive amplitude and a phase, and $g_o({\overrightarrow{\rho }}_i)$. is Green’s function, which propagates the field from ${\overrightarrow{\rho }}_o$ to ${\overrightarrow{\rho }}_i$, (Note, the subindex of Green’s function indicates the plane and the coordinates in the plane. For example, the subindex of o in $g_o({\overrightarrow{\rho }}_i)$ indicates the object plane and the coordinates ${\overrightarrow{\rho }}_o$ in the plane), and $\langle I({\overrightarrow{\rho }}_i)\rangle$ is the mean value of the intensity. A classical image is measured and calculated from $\langle I({\overrightarrow{\rho }}_i)\rangle$. Since $\langle \Delta I\rangle =0$, the intensity fluctuation $\Delta I({\overrightarrow{\rho }}_i)$, which is randomly fluctuated in the neighborhood of $\langle I({\overrightarrow{\rho }}_i)\rangle$, can reasonably be considered noise. However, we will see in the next two sections that it is this “noise” $\Delta I({\overrightarrow{\rho }}_i)$ that produces the ghost image.

A perfect classical imaging system produces a perfect point-to-point image-forming function, and thus produces a perfect image. The observed image is a reproduction, either magnified or demagnified, of the illuminated object, mathematically corresponding to a convolution between the aperture function of the object $|A({\overrightarrow{\rho }}_o){|}^2$ and a δ-function-like image-forming function which characterizes the point-to-point relationship between the object plane and the image plane [12]:

$$\begin{array}{c}\hfill \langle I({\overrightarrow{\rho }}_i)\rangle =\sum _m|E_m\int d{\overrightarrow{\rho }}_o{g}_m({\overrightarrow{\rho }}_o)A({\overrightarrow{\rho }}_o)g_o({\overrightarrow{\rho }}_i){|}^2\propto {\int }_{obj}d{\overrightarrow{\rho }}_o|A({\overrightarrow{\rho }}_o){|}^2\delta ({\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_i}{\mu })={\left|A({\overrightarrow{\rho }}_i/\mu )\right|}^2\end{array}$$

(4)

where $\mu =s_i/s_o$ is the magnification factor.

In reality, limited by the finite size of the imaging system, we may never have a perfect point-to-point correspondence. The incomplete constructive–destructive interference turns the point-to-point correspondence into a point-to-”spot” relationship. The δ-function in the convolution of Equation (4) will be replaced by a point-to-”spot” image-forming function, or a point-spread function,

$$\langle I({\overrightarrow{\rho }}_i)\rangle ={\int }_{obj}d{\overrightarrow{\rho }}_o{\left|A({\overrightarrow{\rho }}_o)\right|}^2{\mathrm{somb}}^2[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_i}{\mu }|]$$

(5)

where the sombrero-like point-spread function is defined as $\mathrm{somb}(x)\equiv 2J_1(x)/x$, with $J_1(x)$ the first-order Bessel function, and D the diameter of the imaging lens. The finite size of the spot, which is defined by the point-spread function, determines the spatial resolution of the imaging setup. It is clear from Equation (5) that, for a chosen value of distance $s_o$, a larger imaging lens and shorter wavelength will result in a narrower point-spread function, and thus a higher spatial resolution of the image.

3. “Noise” Produced Image

In fact, the “noise” term $\Delta I({\overrightarrow{\rho }}_i)$ in Equation (2) may not be considered “noise” at all in the measurement of intensity fluctuation correlation $\langle \Delta I({\overrightarrow{\rho }}_{i1})\Delta I({\overrightarrow{\rho }}_{i2})\rangle$, or the photon number fluctuation correlation $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$. The correlated noises, if they exist, in $\langle \Delta I({\overrightarrow{\rho }}_{i1})\Delta I({\overrightarrow{\rho }}_{i2})\rangle$ or $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ may produce an image from the joint photo-detection of two independent and spatially separated photodetectors, $D_1$ and $D_2$. 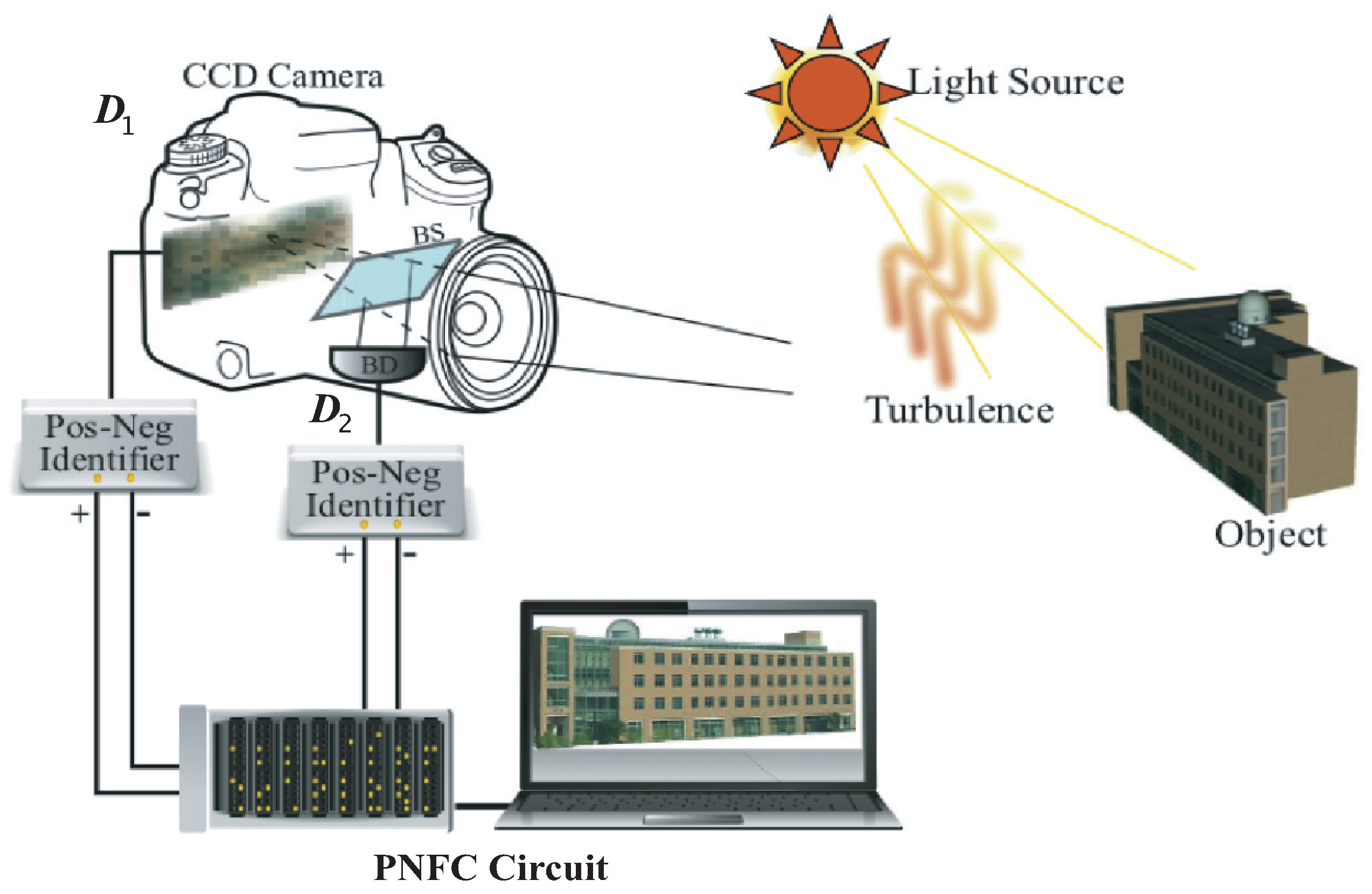Figure 2 schematically illustrates a camera that is able to observe the noise produced images from $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ and/or $\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle$. [Note, in Figure 2, $D_1$ is shown as a CCD array (Charge-Coupled Device) and $D_2$ is shown as a bucket detector. We will learn from later discussions that, in fact, $D_2$ can be replaced by a CCD array, too. In Figure 2, the turbulence-free image is observed from the photon number fluctuation correlation measurement by means of the PNFC (Photon Number Fluctuation Correlation) circuit. This circuit is especially designed for satellite imaging in which the complicated statistical calculations are performed on the ground. The hardware located in the satellite records two sets of data only: the counting numbers per time window of $D_1$ and $D_2$.] The most interesting feature of this camera is its turbulence-free nature: although its classical image observed in either $\langle I({\overrightarrow{\rho }}_{i1})\rangle$ or $\langle I({\overrightarrow{\rho }}_{i2})\rangle$ are both completely “blurred” due to the influence of the atmospheric turbulence, the image observed in $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$, and/or $\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle$, is unaffected.

The camera in Figure 2 is a standard CCD (Charge-Coupled Device) camera, except (1) the image is divided into two, path one and path two, by an optical beamsplitter, with two sets of CCD arrays, $D_1$ and $D_2$, respectively, placed on the two image planes; and (2) $D_1$ and $D_2$ measure the photon number fluctuations, $\Delta n({\overrightarrow{\rho }}_{i1})$ and $\Delta n({\overrightarrow{\rho }}_{i2})$. A novel PNFC circuit is designed for the measurement of $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$, and/or $\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ [14,15]. This circuit is especially useful for satellite imaging in which the complicated statistical calculations can be performed on the ground. The hardware located in the satellite records two sets of data only: the registration time of each photo-detection event of $D_1$ and $D_2$.

The PNFC protocol records the registration time of each photo-detection event of a CCD element, or unit, of $D_1$ and the corresponding element of $D_2$, or the integrated bucket detector $D_2$, by two independent yet synchronized “Event Timers” along their time axes, which are divided into sequences of short time windows. Then, the circuit and the associated software analyze the photon number fluctuations in each time window. The software first calculates the average counting numbers per short time window, ${\overline{n}}_1$, and ${\overline{n}}_2$. Two virtual logic circuits (“Pos-Neg identifiers”) classify the counting numbers per window as “positive” and “negative” fluctuations based on ${\overline{n}}_1$ and ${\overline{n}}_2$,

$$\begin{array}{ccc}\hfill \Delta n_{j\alpha }^{(+)}& =& \left\{\begin{array}{cc}{n}_{j\alpha }-{\overline{n}}_j,& \text{if }{n}_{j\alpha }>{\overline{n}}_j\hfill \\ 0,& \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \Delta n_{j\alpha }^{(-)}& =& \left\{\begin{array}{cc}{n}_{j\alpha }-{\overline{n}}_j,& \text{if }{n}_{j\alpha }<{\overline{n}}_j\hfill \\ 0,& \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(6)

where $j=1,2$, labeling $D_1$ and $D_2$, $\alpha =1$ to N labeling the αth short time window. N is the total number of time windows in a measurement. After synchronizing the two time windows, we define the following quantities for the statistical correlation calculation of $\langle \Delta n_1\Delta n_2\rangle$:

$$\begin{array}{cc}\hfill {(\Delta n_1\Delta n_2)}_{\alpha }^{(++)}& =|\Delta n_{1\alpha }^{(+)}\times \Delta n_{2\alpha }^{(+)}|{(\Delta n_1\Delta n_2)}_{\alpha }^{(--)}=|\Delta n_{1\alpha }^{(-)}\times \Delta n_{2\alpha }^{(-)}|\hfill \end{array}$$

$$\begin{array}{cc}\hfill {(\Delta n_1\Delta n_2)}_{\alpha }^{(+-)}& =|\Delta n_{1\alpha }^{(+)}\times \Delta n_{2\alpha }^{(-)}|{(\Delta n_1\Delta n_2)}_{\alpha }^{(-+)}=|\Delta n_{1\alpha }^{(-)}\times \Delta n_{2\alpha }^{(+)}|\hfill \end{array}$$

(7)

The corresponding statistical average of $\langle \Delta n_1\Delta n_2\rangle$ is thus

$$\begin{array}{cc}\langle \Delta n_1\Delta n_2\rangle & =\frac{1}{N}[\sum _{\alpha }{(\Delta n_1\Delta n_2)}_{\alpha }^{(++)}+\sum _{\beta }{(\Delta n_1\Delta n_2)}_{\beta }^{(--)}\hfill \\ & -\sum _{\gamma }{(\Delta n_1\Delta n_2)}_{\gamma }^{(+-)}-\sum _{\delta }{(\Delta n_1\Delta n_2)}_{\delta }^{(-+)}]\hfill \end{array}$$

(8)

The recorded data from the measurements include two sets of registration times of the photo-detection events of $D_1$ and $D_2$, along their time axes defined by the two synchronized event timers. The data may be analyzed simultaneously or at a later time. The software should be able to (1) evaluate $\Delta n_{1\alpha }$ and $\Delta n_{2\alpha }$ for each short time window; (2) calculate ${(\Delta n_1\Delta n_2)}_{\alpha }^{(++)}$, ${(\Delta n_1\Delta n_2)}_{\alpha }^{(--)}$, ${(\Delta n_1\Delta n_2)}_{\alpha }^{(+-)}$, and ${(\Delta n_1\Delta n_2)}_{\alpha }^{(-+)}$ for each short time window; and (3) calculate the statistical average of $\langle \Delta n_1\Delta n_2\rangle$ according to Equation (8). It should be emphasized that choosing an appropriate width of time window is important for achieving an efficient and accurate evaluation. For fluctuation measurements, although we know, in principle, the shorter the better, the width is limited by the response time of the photo-detector and by the statistics of ${\overline{n}}_1$ and ${\overline{n}}_2$.

To calculate the photon number fluctuation correlation, we start from examining the second-order coherence function $G^{(2)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2})$ [16,17], which is jointly measured by $D_1$ and $D_2$ on the two image planes:

$$\begin{array}{c}{G}^{(2)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2})\hfill \\ =\langle E^{*}({\overrightarrow{\rho }}_{i1})E({\overrightarrow{\rho }}_{i1})E^{*}({\overrightarrow{\rho }}_{i2})E({\overrightarrow{\rho }}_{i2})\rangle \hfill \\ =\langle \sum _m{E}_m^{*}({\overrightarrow{\rho }}_{i1})\sum _p{E}_p({\overrightarrow{\rho }}_{i1})\sum _n{E}_n^{*}({\overrightarrow{\rho }}_{i2})\sum _q{E}_q({\overrightarrow{\rho }}_{i2})\rangle \hfill \\ =\sum _m|E_m({\overrightarrow{\rho }}_{i1}){|}^2\sum _n{\left|E_n({\overrightarrow{\rho }}_{i2})\right|}^2+\sum _{m\ne n}{E}_m^{*}({\overrightarrow{\rho }}_{i1})E_n({\overrightarrow{\rho }}_{i1})E_n^{*}({\overrightarrow{\rho }}_{i2})E_m({\overrightarrow{\rho }}_{i2})\hfill \\ =\frac{1}{2}\sum _{m,n}|E_m({\overrightarrow{\rho }}_{i1})E_n({\overrightarrow{\rho }}_{i2})+E_n({\overrightarrow{\rho }}_{i1})E_m({\overrightarrow{\rho }}_{i2}){|}^2\hfill \\ =\langle n({\overrightarrow{\rho }}_{i1})\rangle \langle n({\overrightarrow{\rho }}_{i2})\rangle +\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle \hfill \end{array}$$

(9)

where we have completed the ensemble average by taking into account all possible random phases of a large number of subfields. The only surviving terms from the ensemble average are those terms satisfying (1) $p=m$, $q=n$, and (2) $q=m$, $p=n$. There is no doubt that the first term $\langle n({\overrightarrow{\rho }}_{i1})\rangle \langle n({\overrightarrow{\rho }}_{i2})\rangle$ corresponds to the product of two identical classical images measured by $D_1$ and $D_2$, respectively. The second term is the cross interference term between $E_m({\overrightarrow{\rho }}_{i1})E_n({\overrightarrow{\rho }}_{i2})$ and $E_n({\overrightarrow{\rho }}_{i1})E_m({\overrightarrow{\rho }}_{i2})$. It is this cross interference term that produces an image in the joint photon number fluctuation measurements of $D_1$ and $D_2$,

$$\begin{array}{c}\hfill \langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle =\sum _m{E}_m^{*}({\overrightarrow{\rho }}_{i1})E_m({\overrightarrow{\rho }}_{i2})\sum _{n\ne m}{E}_n^{*}({\overrightarrow{\rho }}_{i2})E_n({\overrightarrow{\rho }}_{i1})\simeq |\sum _m{E}_m^{*}({\overrightarrow{\rho }}_{i1})E_m({\overrightarrow{\rho }}_{i2}){|}^2\end{array}$$

(10)

where ${\sum }_m{E}_m^{*}({\overrightarrow{\rho }}_{i1})E_m({\overrightarrow{\rho }}_{i2})$ is usually defined as the first-order coherence function $G_{12}^{(1)}$. It is important, however, to keep in mind that $G_{12}^{(1)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2})$, here, is measured jointly by two detectors, $D_1$ and $D_2$, at spatially separated coordinates ${\overrightarrow{\rho }}_{i1}$ and ${\overrightarrow{\rho }}_{i2}$.

We now calculate $G_{12}^{(1)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2})$,

$$\begin{array}{c}{G}_{12}^{(1)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2})=\sum _m{E}_m^{*}({\overrightarrow{\rho }}_{i1})E_m({\overrightarrow{\rho }}_{i2})\hfill \\ =\sum _m[E_m^{*}\int d{\overrightarrow{\rho }}_o{g}_m^{*}({\overrightarrow{\rho }}_o)\int d\overrightarrow{\kappa }{A}^{*}({\overrightarrow{\rho }}_o)g_o^{*}(\overrightarrow{\kappa },{\overrightarrow{\rho }}_{i1})][E_m\int d{\overrightarrow{\rho }}_{o^{\prime }}{g}_m({\overrightarrow{\rho }}_{o^{\prime }})\int d{\overrightarrow{\kappa }}^{\prime }A({\overrightarrow{\rho }}_{o^{\prime }})g_{o^{\prime }}({\overrightarrow{\kappa }}^{\prime },{\overrightarrow{\rho }}_{i2})]\hfill \\ =\sum _m{E}_m^{*}\int d{\overrightarrow{\rho }}_o\int d{\overrightarrow{\rho }}_{o^{\prime }}{g}_m^{*}({\overrightarrow{\rho }}_o)E_m{g}_m({\overrightarrow{\rho }}_{o^{\prime }})[\int d\overrightarrow{\kappa }{A}^{*}({\overrightarrow{\rho }}_o)e^{i\overrightarrow{\kappa }·{\overrightarrow{\rho }}_o}\mathrm{somb}[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_{i1}}{\mu }|]]\hfill \\ \times [\int d{\overrightarrow{\kappa }}^{\prime }A({\overrightarrow{\rho }}_{o^{\prime }})e^{-i{\overrightarrow{\kappa }}^{\prime }·{\overrightarrow{\rho }}_{o^{\prime }}}\mathrm{somb}[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_{o^{\prime }}+\frac{{\overrightarrow{\rho }}_{i2}}{\mu }|]]\hfill \end{array}$$

(11)

where we have introduced Green’s function for propagating each $\mathbf{k}$ vector (transverse component is labeled as $\overrightarrow{\kappa }$) of the field from the object plane to the image plane, $g_o(\overrightarrow{\kappa },{\overrightarrow{\rho }}_{i1})$, and completed the integrals on the lens in $g_o(\overrightarrow{\kappa },{\overrightarrow{\rho }}_{i1})$ and $g_{o^{\prime }}({\overrightarrow{\kappa }}^{\prime },{\overrightarrow{\rho }}_{i2})$ [12].

Next, we complete the summation in terms of the subfields, or the sub-sources, by means of an integral over the entire source plane. This integral results in the well known Hanbury–Brown and Twiss (HBT) correlation [18,19,20]: ${\mathrm{somb}}^2[(\pi \Delta \theta )/\lambda ](|{\overrightarrow{\rho }}_o-{\overrightarrow{\rho }}_{o^{\prime }}|)$, where $\Delta \theta$ is the angular diameter of the light source relative to the object plane. To simplify further calculations, we assume a large value of $\Delta \theta$ and thus approximate the somb-function to a δ-function like function, i.e., ${\overrightarrow{\rho }}_o\simeq {\overrightarrow{\rho }}_{o^{\prime }}$. $G_{12}^{(1)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2})$ is therefore approximated in the following form,

$$\begin{array}{c}\hfill G_{12}^{(1)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2})\propto \int d{\overrightarrow{\rho }}_o{|A({\overrightarrow{\rho }}_o)|}^2\mathrm{somb}[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_{i1}}{\mu }|]\mathrm{somb}[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_{i2}}{\mu }|]\end{array}$$

(12)

We have two ways to observe an image: (1) from the measurement of $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$; and (2) from the measurement of $\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle$.

(1) Taking ${\overrightarrow{\rho }}_{i1}={\overrightarrow{\rho }}_{i2}$ in the joint measurement, i.e., calculating the joint photo-detection events only between a pair of the CCD elements corresponding to ${\overrightarrow{\rho }}_{i1}={\overrightarrow{\rho }}_{i2}$. In this approach, the measurement is equivalent to an “auto-correlation”. However, the “auto-correlation” is not based on the measurement of intensity or photon number, but their fluctuations, and the measurements are at two spatially separated image planes,

$$\begin{array}{c}\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle \propto |G_{12}^{(1)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2}){|}^2\hfill \\ \propto |\int d{\overrightarrow{\rho }}_o{\left|A({\overrightarrow{\rho }}_o)\right|}^2{\mathrm{somb}}^2[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_{i1}}{\mu }|]{|}^2\hfill \\ =|\int d{\overrightarrow{\rho }}_o{|A({\overrightarrow{\rho }}_o)|}^2{\mathrm{somb}}^2[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_{i2}}{\mu }|]{|}^2\hfill \end{array}$$

(13)

For a perfect imaging system, i.e., if the somb-function can be approximated to a δ-function-like image-forming function, two perfect turbulence-free images, $|A({\overrightarrow{\rho }}_{i1}/\mu ){|}^2$ and $|A({\overrightarrow{\rho }}_{i2}/\mu ){|}^2$, are observable from the joint photon number fluctuation measurement in terms of ${\overrightarrow{\rho }}_{i1}$ and ${\overrightarrow{\rho }}_{i2}$. We may name $|A({\overrightarrow{\rho }}_{i1}/\mu ){|}^2$ and $|A({\overrightarrow{\rho }}_{i2}/\mu ){|}^2$ “conditional” images by means of the joint fluctuation measurement with the other detector at ${\overrightarrow{\rho }}_{i1}={\overrightarrow{\rho }}_{i2}$.

(2) Summing over the fluctuations measured by all elements of a CCD, such as that of $D_2$, and using the integrated fluctuations for the joint measurement paired with that of each element of another CCD, such as that of $D_1$, results in the measurement of $\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle$:

$$\begin{array}{cc}\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle & \propto |\int d{\overrightarrow{\rho }}_{i2}{G}_{12}^{(1)}({\overrightarrow{\rho }}_{i1},{\overrightarrow{\rho }}_{i2}){|}^2\hfill \\ & =|\int d{\overrightarrow{\rho }}_o{\left|A({\overrightarrow{\rho }}_o)\right|}^2\mathrm{somb}[\frac{\pi }{\lambda }\frac{D}{s_o}|{\overrightarrow{\rho }}_o+\frac{{\overrightarrow{\rho }}_{i1}}{\mu }|]{|}^2\hfill \end{array}$$

(14)

For a perfect imaging system, i.e., if the somb-function can be approximated as δ-function, a perfect turbulence-free image, $|A({\overrightarrow{\rho }}_{i1}/\mu ){|}^2$, is observable from the joint photon number fluctuation measurement in terms of ${\overrightarrow{\rho }}_{i1}$. $|A({\overrightarrow{\rho }}_{i1}/\mu ){|}^2$ is “conditional” due to the joint fluctuation measurement of $D_1$ with the bucket detector $D_2$.

Based on Equation (9), we may conclude that the noise produced image is the result of a superposition between amplitudes $E_m({\overrightarrow{\rho }}_{i1})E_n({\overrightarrow{\rho }}_{i2})$ and $E_n({\overrightarrow{\rho }}_{i1})E_m({\overrightarrow{\rho }}_{i2})$, corresponding to two different yet indistinguishable ways for a random pair of photons or subfields (the mth and the nth) to produce a joint photo-detection event: (1) the mth subfield triggers $D_1$ at ${\overrightarrow{\rho }}_{i1}$ and the nth subfield triggers $D_2$ at ${\overrightarrow{\rho }}_{i2}$; (2) the nth subfield triggers $D_1$ at ${\overrightarrow{\rho }}_{i1}$ and the mth subfield triggers $D_2$ at ${\overrightarrow{\rho }}_{i2}$. It should not be difficult to see that a perfect constructive interference occurs at ${\overrightarrow{\rho }}_{i1}={\overrightarrow{\rho }}_{i2}$. When ${\overrightarrow{\rho }}_{i1}={\overrightarrow{\rho }}_{i2}$, all the $m\ne n$ amplitude pairs, corresponding to (1) and (2), overlap completely and are “in phase”.

Based on the two-photon or two-subfield interference picture, we found that the images observed from $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ and/or from $\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ are turbulence-free, even in the case in which the classic images in $\langle n({\overrightarrow{\rho }}_{i1})\rangle$ and $\langle n({\overrightarrow{\rho }}_{i2})\rangle$ are completely blurred due to the influence of atmospheric turbulence. Why is the image observed from $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ or from $\langle \Delta n({\overrightarrow{\rho }}_{i1})\int d{\overrightarrow{\rho }}_{i2}\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ turbulence-free? The answer is simple: when the superposed two amplitudes “overlap”, i.e., experience the same optical path and thus the same turbulence, the turbulence-induced phase variations cancel each other in the cross interference term of the two-photon interference. Therefore, the image observed from $\langle \Delta n({\overrightarrow{\rho }}_{i1})\Delta n({\overrightarrow{\rho }}_{i2})\rangle$ would not be “blurred” by the turbulence-induced phase variations.

To clarify this unusual interference picture, we start from analyzing a two-photon interference experiment. Figure 3 schematically illustrates a standard Young’s double-slit interferometer, except the measurement is $\langle \Delta I(x_1)\Delta I(x_2)\rangle$ by means of the use of two point-like scannable photodetectors $D_1$ and $D_2$, as well as the PNFC measurement circuit. We managed an experimental condition that satisfies $d\gg l_c$, where d is the separation between the double-slit A and B and $l_c$ is the coherence length of the thermal field. Consequently, no first-order interferences are observable from $\langle I(x_1)\rangle$ and $\langle I(x_2)\rangle$. The question is: do we observe interference from $\langle \Delta I(x_1)\Delta I(x_2)\rangle$? Many may respond with a straightforward answer: no! According to a well-accepted theory, thermal light correlation only occurs within its coherent area. Therefore, no correlation is observable behind the double-slit due to the experiment condition of $d\gg l_c$. The measured intensity fluctuation correlation $\langle \Delta I(x_1)\Delta I(x_2)\rangle$ should always be zero! From where does the interference pattern come? The experimental result, however, is quite different. We have observed an interference pattern from $\langle \Delta I(x_1)\Delta I(x_2)\rangle$ [21]. [Note, Recent repeating measurements using PNFC circuit have demonstrated interference pattern with ∼$100\%$ visibility. The hardware of the PNFC circuit recorded two sets of photo-detection events along the time axis of two independent event timers. The correlation calculation was usually made by a PC a few hours or a few days later.]

$$\begin{array}{c}\hfill \langle \Delta I(x_1)\Delta I(x_2)\rangle =1+\mathrm{sinc}\frac{\pi w}{\lambda z}(x_1-x_2)\cos \frac{\pi d}{\lambda z}(x_1-x_2)\end{array}$$

(15)

where w is the width of the single-slit, z is the distance between the double-slit plane and $D_1$–$D_2$ plane.

The observed interference is the result of a superposition between the following two different yet indistinguishable amplitudes for a random pair of photons to trigger a joint photo-detection event: (1) the mth photon, coming from the upper slit-A, is annihilated at $D_1$ and the nth photon, coming from the lower slit-B, is annihilated at $D_2$; and (2) the mth photon, coming from the upper slit-A, is annihilated at $D_2$ and the nth photon, coming from the lower slit-B, is annihilated at $D_1$.

The interference pattern observed in $\langle \Delta I(x_1)\Delta I(x_2)\rangle$ is turbulence-free in the neighborhood of $x_1\simeq x_2$. In fact, the physics is simple and straightforward: imagine that we move $D_1$ and $D_2$ closer to $x_1\simeq x_2$ and introduce turbulence into the interferometer. Even in the case of strong influence of turbulence, the above-mentioned two amplitudes (1) and (2) overlap, i.e., the paths of the two amplitudes are the same, and thus experience the same turbulence. The turbulence-induced phase variations in the interference cross term would “cancel” each other and consequently have no influence on the interference pattern,

$$\begin{array}{c}{G}^{(2)}(x_1,x_2\simeq x_1)\hfill \\ =\frac{1}{2}\sum _{m,n}|E_m{e}^{i\delta {\phi }_{m1}}{g}_m(x_1)E_n{e}^{i\delta {\phi }_{n2}}{g}_n(x_2\simeq x_1)+E_n{e}^{i\delta {\phi }_{n1}}{g}_n(x_1)E_m{e}^{i\delta {\phi }_{m2}}{g}_m(x_2\simeq x_1){|}^2\hfill \\ \simeq \frac{1}{2}\sum _{m,n}|E_m{g}_m(x_1)E_n{g}_n(x_2\simeq x_1)+E_n{g}_n(x_1)E_m{g}_m(x_2\simeq x_1){|}^2,\hfill \end{array}$$

(16)

where $e^{i\delta {\phi }_{m1}}$ stands for the turbulence-induced phase variations when the mth photon or subfield propagates from the upper slit to $D_1$. At $x_1=x_2$, $e^{-i\delta {\phi }_{m1}}{e}^{-i\delta {\phi }_{n2}}{e}^{i\delta {\phi }_{n1}}{e}^{i\delta {\phi }_{m2}}=1$, the cross interference term reaches its turbulence-free constructive maximum.

Next, we replace the double-slit with an object such as a distant building, as shown in Figure 2. Each random pair of thermal sub-radiations, either reflected or scattered from two randomly chosen points of the object, can be treated as subfields coming from a double-slit with a certain slit-separation. All pairs of subfields would have their constructive interferences at ${\overrightarrow{\rho }}_1\simeq {\overrightarrow{\rho }}_2$, and thus produce the maximum correlation of $\langle \Delta I({\overrightarrow{\rho }}_1)\Delta I({\overrightarrow{\rho }}_2\simeq {\overrightarrow{\rho }}_1)\rangle$. There would be no interference pattern observable due to the averaging effect when adding together all individual interference patterns of different spatial periods. However, the maximum value of $\langle \Delta I({\overrightarrow{\rho }}_1)\Delta I({\overrightarrow{\rho }}_2)\rangle$ is observable at ${\overrightarrow{\rho }}_1={\overrightarrow{\rho }}_2$. The calculation is complex yet straightforward. We need to modify Green’s functions with the appropriate experimental setup. For the turbulence-free camera of Figure 2, all of Green’s functions have been developed [12]. No matter how complicated the sum of $m\ne n$ and Green’s functions are, the superposed two-photon amplitudes with $\overrightarrow{\kappa }$ and ${\overrightarrow{\kappa }}^{\prime }$ would always experience the same paths and thus the same turbulence. Therefore, the turbulence effect of any phase variations would cancel each other in the measurement of $\langle \Delta I({\overrightarrow{\rho }}_1)\Delta I({\overrightarrow{\rho }}_2\simeq {\overrightarrow{\rho }}_1)\rangle$. In fact, a turbulence-free camera is ready for practical applications. [Note, commercial products based on such turbulence-free cameras are currently under development.]

It should be emphasized that the above calculation is based on monochromatic thermal radiation. For multi-wavelengths, such as sunlight, narrow spectral bandwidth filters, either in their optical path or in their electronic circuit, are necessary. The noise correlation is physically measured by $D_1$ in ${\sum }_{m\ne n}{E}_m^{*}({\overrightarrow{\rho }}_{i1})E_n({\overrightarrow{\rho }}_{i1})$ and by $D_2$ in ${\sum }_{m\ne n}{E}_n^{*}({\overrightarrow{\rho }}_{i2})E_m({\overrightarrow{\rho }}_{i2})$. Considering $E_m({\overrightarrow{\rho }}_{ij})$ and $E_n({\overrightarrow{\rho }}_{ij})$, $j=1,2$, randomly created and distributed wavepackets along the jth time axis, a monochromatic wavepacket has an infinite temporal width and always results in nonzero products of the two. However, a wavepacket with multi-wavelengths has a finite temporal dimension. The “correlation” requires a nonzero product of the two wavepackets within the chosen time window, i.e., the two wavepackets must “overlap” within the time window. The spectral filters make this “overlap” possible.

4. The Theory for Turbulence-Free Lensless Ghost Imaging

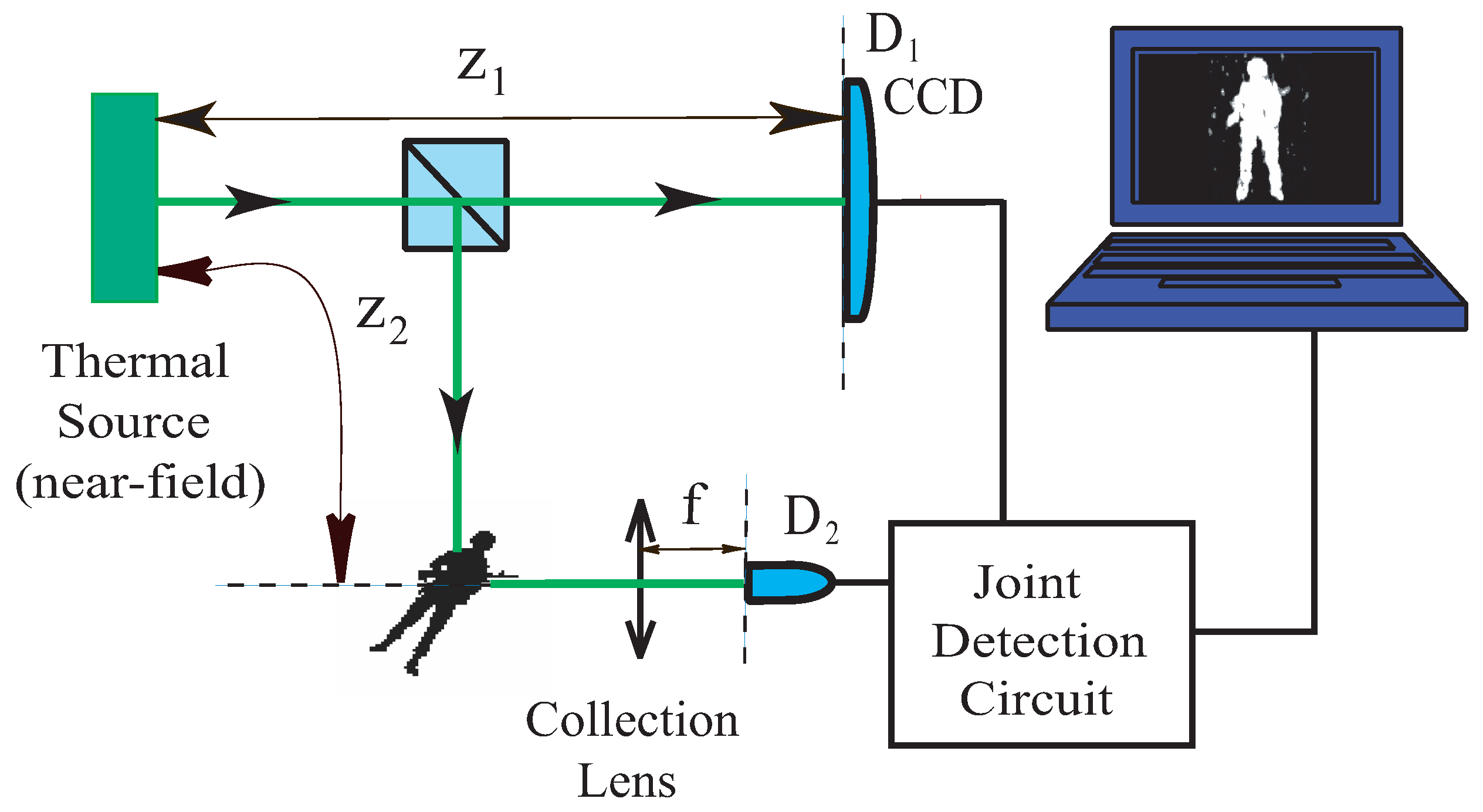
The lensless ghost imaging experiment was demonstrated by Valencia et al. in 2005 [3]. In the same year, Wang et al. [4] and Zhu et al. [5] demonstrated similar experiments. Figure 4 illustrates an improved experiment performed by Meyers et al. [22]. The pseudo-thermal radiation source [23] has a fairly large size in its transverse dimension. A beamsplitter divides the radiation into two beams of 50%–50%. One of the beams illuminates a toy soldier as shown in Figure 4. The scattered and reflected photons from the solider (object) are collected and counted by a “bucket” photon counting detector $D_2$. In the other beam, a high resolution CCD array, $D_1$, operated in the photon counting regime, is placed facing towards the radiation source for joint photo-detection with the “bucket” detector $D_2$. The photon number fluctuation correlation between $D_2$ and each element of the CCD array ($D_1$) is measured and calculated by a photon-counting-coincidence circuit, which is similar to the PNFC circuit described in the previous section. The counting rate of $D_2$ and each element of the CCD array ($D_1$) were both constants during the measurement (the constant value is mainly determined by the source intensity). Surprisingly, a ghost image of the toy soldier was captured in the photon number fluctuation correlation $\langle \Delta n({\overrightarrow{\rho }}_1)\int d{\overrightarrow{\rho }}_2\Delta n({\overrightarrow{\rho }}_2)\rangle$ between the CCD array ($D_1$) and $D_2$ when taking $z_1=z_2$, where the integral of ${\overrightarrow{\rho }}_2$ simulates the behavior of the “bucket” detector. The images “blurred” when the CCD was moved away from $z_1=z_2$, either to the direction of $z_1>z_2$ or $z_1<z_2$. [Note, on one hand, $D_1$ (CCD array) has the ability to resolve an image, however, it cannot “see” the object; on the other hand, $D_2$ (bucket detector) “saw” the object, however, it does not have ability to resolve any image. Perhaps, this is the reason to name it “Ghost Imaging”.]

Similar to classical imaging, mathematically, the observed ghost image from the photon number fluctuation correlation measurement corresponds to a convolution between the aperture function of the object and an image-forming function that can be approximated as δ-function in an ideal experimental condition

$$\begin{array}{c}\hfill \langle \Delta n({\overrightarrow{\rho }}_1)\int d{\overrightarrow{\rho }}_2\Delta n({\overrightarrow{\rho }}_2)\rangle =\int d{\overrightarrow{\rho }}_2|A({\overrightarrow{\rho }}_2){|}^2{\mathrm{somb}}^2[\frac{\pi \Delta \theta }{\lambda }|{\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_2|]\simeq |A({\overrightarrow{\rho }}_1){|}^2\end{array}$$

(17)

where $\Delta \theta$ is the angular diameter of the thermal light source. For a large value of $\Delta \theta$, the somb-function can be approximated as a point-to-point image-forming function. The convolution thus produces a perfect image of the object in $\langle \Delta n({\overrightarrow{\rho }}_1)\int d{\overrightarrow{\rho }}_2\Delta n({\overrightarrow{\rho }}_2)\rangle$.

There is no doubt that chaotic-thermal radiation propagates to any transverse plane in a random and chaotic manner. A large transverse sized chaotic-thermal source consists of a large number of independent point sub-sources randomly distributed on the source plane. Each point sub-source randomly radiates independent spherical waves freely propagating in all possible directions and may be observed at any transverse plane. Due to the chaotic nature of the source, there are no observable interference effects between these subfields. These independent sub-intensities simply add together, yielding a constant total intensity across the entire transverse plane. In particular, the lensless setup has no lens applied to force the spherical waves to collapse to a point or a “speckle”, and has no chance to have two identical copies of any “speckle” of the source onto the object and image planes. What is the cause of the point-to-point image-forming correlation?

4.1. An Interference Model Based on a Large Number of Random Radiation Subfields

Returning to our earlier discussion, Equation (9), we start from

$$\begin{array}{c}{G}^{(2)}({\overrightarrow{\rho }}_1,z_1;{\overrightarrow{\rho }}_2,z_2)\hfill \\ =\langle \sum _{m,\mathbf{k}}{E}_{m,\mathbf{k}}^{*}({\overrightarrow{\rho }}_1,z_1)\sum _{p,{\mathbf{k}}^{\prime \prime }}{E}_{p,{\mathbf{k}}^{\prime \prime }}({\overrightarrow{\rho }}_1,z_1)\sum _{n,{\mathbf{k}}^{\prime }}{E}_{n,{\mathbf{k}}^{\prime }}^{*}({\overrightarrow{\rho }}_2,z_2)\sum _{q,{\mathbf{k}}^{\prime \prime \prime }}{E}_{q,{\mathbf{k}}^{\prime \prime \prime }}({\overrightarrow{\rho }}_2,z_2)\rangle \hfill \\ =\sum _{m,n}\sum _{\mathbf{k},{\mathbf{k}}^{\prime }}|\frac{1}{\sqrt{2}}[E_{m,\mathbf{k}}({\overrightarrow{\rho }}_1,z_1)E_{n,{\mathbf{k}}^{\prime }}({\overrightarrow{\rho }}_2,z_2)+E_{n,{\mathbf{k}}^{\prime }}({\overrightarrow{\rho }}_1,z_1)E_{m,\mathbf{k}}({\overrightarrow{\rho }}_2,z_2)]{|}^2\hfill \\ =\langle n({\overrightarrow{\rho }}_1,z_1)\rangle \langle n({\overrightarrow{\rho }}_2,z_2)\rangle +\langle \Delta n({\overrightarrow{\rho }}_1,z_1)\Delta n({\overrightarrow{\rho }}_2,z_2)\rangle \hfill \end{array}$$

(18)

where the ensemble average is completed by taking into account all possible values of the phases associated with a large number of subfields and $\mathbf{k}$-vectors. Note that when we claim that the surviving terms $m=q,n=p$, we have assumed that the radiation fields of $E({\overrightarrow{\rho }}_1,z_1)$ and $E({\overrightarrow{\rho }}_2,z_2)$ are able to interfere through the measurement of independent and spatially separated photodetectors $D_1$ and $D_2$. This postulate is beyond the classical theory of light. In fact, the interference shown in Equation (18) is a nonlocal interference: a pair of subfields interferes with the pair itself. The pair has two different yet indistinguishable alternative ways, or probabilities, to produce a joint photo-detection event: (1) the mth subfield produces a photo-electron at $D_1$, and the nth subfield produces a photo-electron at $D_2$; (2) the nth subfield produces a photo-electron at $D_1$, and the mth subfield produces a photo-electron at $D_2$. The superposition of the above two different yet indistinguishable “probability amplitudes” produces a point-to-point correlation in the photon number fluctuations measurements of $D_1$ and $D_2$. The point-to-point correlation plays the role of image-forming function and thus produces the ghost image. In the following, we attempt a Fresnel near-field calculation to obtain the point-to-point image-forming function and the ghost image. We start from Equation (18) and focus on the transverse spatial correlation

$$\begin{array}{c}\hfill \langle \Delta n({\overrightarrow{\rho }}_1,z_1)\Delta n({\overrightarrow{\rho }}_2,z_2)\rangle =|\sum _{m,k}{E}_{m,\mathbf{k}}^{*}({\overrightarrow{\rho }}_1,z_1)E_{m,\mathbf{k}}({\overrightarrow{\rho }}_2,z_2){|}^2=|G_{12}^{(1)}({\overrightarrow{\rho }}_1,z_1;{\overrightarrow{\rho }}_2,z_2){|}^2\end{array}$$

(19)

In the near-field, we apply the Fresnel approximation to propagate each subfield from its transverse coordinate ${\overrightarrow{\rho }}_s$ of the source plane to the coordinate $({\overrightarrow{\rho }}_j,z_j)$, $j=1,2$ of the $D_1$ and $D_2$ planes [12],

$$\begin{array}{cc}{g}_{{\overrightarrow{\rho }}_s}(\overrightarrow{\kappa },{\overrightarrow{\rho }}_1,z_1)& =\frac{-i\omega }{2\pi c}\frac{e^{i\frac{\omega }{c}{z}_1}}{z_1}E({\overrightarrow{\rho }}_s)e^{i\overrightarrow{\kappa }·{\overrightarrow{\rho }}_s}{e}^{i\frac{\omega }{2c{z}_1}{|{\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_s|}^2}\hfill \\ g_{{\overrightarrow{\rho }}_s}(\overrightarrow{\kappa },{\overrightarrow{\rho }}_2,z_2)& =\frac{-i\omega }{2\pi c}\frac{e^{i\frac{\omega }{c}{z}_2}}{z_2}E({\overrightarrow{\rho }}_s)e^{i\overrightarrow{\kappa }·{\overrightarrow{\rho }}_s}{e}^{i\frac{\omega }{2c{z}_2}{|{\overrightarrow{\rho }}_2-{\overrightarrow{\rho }}_s|}^2}A({\overrightarrow{\rho }}_2)\hfill \end{array}$$

(20)

where $A({\overrightarrow{\rho }}_2)$ is the aperture function of the object plane. Substituting Green’s functions into Equation (19),

$$\begin{array}{c}\hfill \langle \Delta n({\overrightarrow{\rho }}_1,z_1)\Delta n({\overrightarrow{\rho }}_2.z_2)\rangle \propto |\frac{1}{z_1{z}_2}\int d{\overrightarrow{\rho }}_s{\left|E({\overrightarrow{\rho }}_s)\right|}^2{e}^{-i\frac{\omega }{c}{z}_1}{e}^{-i\frac{\omega }{2c{z}_1}{|{\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_s|}^2}{e}^{i\frac{\omega }{c}{z}_2}{e}^{i\frac{\omega }{2c{z}_2}{|{\overrightarrow{\rho }}_2-{\overrightarrow{\rho }}_s|}^2}A({\overrightarrow{\rho }}_2){|}^2\end{array}$$

Assuming $|E({\overrightarrow{\rho }}_s){|}^2\sim C\sim$ constant, and taking $z_1=z_2=d$, we obtain

$$\begin{array}{cc}\langle \Delta n({\overrightarrow{\rho }}_1)\Delta n({\overrightarrow{\rho }}_2)\rangle & \propto |A({\overrightarrow{\rho }}_2)\int d{\overrightarrow{\rho }}_{s}C{e}^{-i\frac{\omega }{2cd}{|{\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_s|}^2}{e}^{i\frac{\omega }{2cd}{|{\overrightarrow{\rho }}_2-{\overrightarrow{\rho }}_s|}^2}{|}^2\hfill \\ & \propto |A({\overrightarrow{\rho }}_2)e^{-i\frac{\omega }{2cd}(|{\overrightarrow{\rho }}_1{|}^2-|{\overrightarrow{\rho }}_2{|}^2)}\int d{\overrightarrow{\rho }}_s{e}^{i\frac{\omega }{cd}({\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_2)·{\overrightarrow{\rho }}_s}{|}^2\hfill \\ & \propto |A({\overrightarrow{\rho }}_2){|}^2{\mathrm{somb}}^2\left[\frac{\pi \Delta \theta }{\lambda }|{\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_2|\right]\hfill \end{array}$$

(21)

where we have assumed a disk-shaped light source with finite angular diameter $\Delta \theta$.

Now, we account for the “bucket” nature of $D_2$ by an integral of ${\overrightarrow{\rho }}_2$,

$$\begin{array}{c}\hfill \langle \Delta n({\overrightarrow{\rho }}_1)\int d{\overrightarrow{\rho }}_2\Delta n({\overrightarrow{\rho }}_2)\rangle =\int d{\overrightarrow{\rho }}_2|A({\overrightarrow{\rho }}_2){|}^2{\mathrm{somb}}^2[\frac{\pi \Delta \theta }{\lambda }|{\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_2|]\simeq |A({\overrightarrow{\rho }}_1){|}^2\end{array}$$

(22)

where we have assumed a large value of $\Delta \theta$ and approximated the somb-function to δ-function. For a perfect imaging system, i.e., if the somb-function can be approximated to a δ-function-like image-forming function, a perfect turbulence-free ghost image, $|A({\overrightarrow{\rho }}_1){|}^2$, is observable from the joint photon number fluctuation measurements of $D_1$ and $D_2$ in terms of ${\overrightarrow{\rho }}_1$.

From the above calculation, we may conclude again that the “noise” produced ghost image is the result of an interference involving a superposition between amplitudes $E_m(\overrightarrow{\kappa },{\overrightarrow{\rho }}_1)E_n({\overrightarrow{\kappa }}^{\prime },{\overrightarrow{\rho }}_2)$ and $E_n({\overrightarrow{\kappa }}^{\prime },{\overrightarrow{\rho }}_1)E_m(\overrightarrow{\kappa },{\overrightarrow{\rho }}_2)$, corresponding to two different yet indistinguishable ways for a random pair of subfields (the mth and the nth) to produce a joint photo-detection event: (1) the mth subfield triggers $D_1$ at ${\overrightarrow{\rho }}_1$ and the nth subfield triggers $D_2$ at ${\overrightarrow{\rho }}_2$; and (2) the nth subfield triggers $D_1$ at ${\overrightarrow{\rho }}_1$ and the mth subfield triggers $D_2$ at ${\overrightarrow{\rho }}_2$. We see that a perfect constructive interference occurs at ${\overrightarrow{\rho }}_1={\overrightarrow{\rho }}_2$. In this situation, all the $m\ne n$ and $\overrightarrow{\kappa }\ne {\overrightarrow{\kappa }}^{\prime }$ amplitude pairs experienced the same optical path and thus the same turbulence; any path and index variations are canceled out in the cross interference term ${\sum }_{m\ne n}{E}_m^{*}(\overrightarrow{\kappa },{\overrightarrow{\rho }}_1)E_m(\overrightarrow{\kappa },{\overrightarrow{\rho }}_2)E_n^{*}({\overrightarrow{\kappa }}^{\prime },{\overrightarrow{\rho }}_2)E_n({\overrightarrow{\kappa }}^{\prime },{\overrightarrow{\rho }}_1)$ and has no influence on the result of this constructive interference. From the viewpoint of two-subfield interference, the turbulence-free nature of ghost imaging is clear and understandable. In fact, a turbulence-free ghost imaging experiment was demonstrated by Meyers et al. in 2012 [10].

4.2. Quantum Theory of Lensless Light Ghost Imaging

It seems that we do not need quantum mechanics for the calculation of ghost imaging. All of the above calculations are based on the concept of classical radiation field, except the thermal field $E(\mathbf{r},t)$ is treated as a superposition of a large number of individual random subfields ${\sum }_{m}E(\mathbf{r},t)$, as Einstein introduced in 1905 [13]. The two-subfield interference picture is helpful in understanding the unusual phenomenon of ghost imaging, especially its turbulence-free nature. However, we have to face the issue that the two-subfield interference happens at two separated space-time points. In the theory of Maxwell, the radiation field cannot be superposed in such a manner. When the two detectors are separated by large distance, Einstein would certainly ask: how long does it take for this kind of interference to be completed? All experiments seem to show that the two-subfield superposition happens instantaneously. However, we know the electromagnetic field has a speed limit of c! On one hand, Einstein introduced a granularity to radiation, abandoning the continuum interpretation of Maxwell. On the other hand, he worried about the nonlocal problem, such as the nonlocal interference that we have discussed above, associated with his model. Bohr had a famous answer to Einstein’s question: wavefunction “collapses” instantaneously! Perhaps, we need to replace Einstein’s concept of subfield with Bohr’s concept of “wavefunction” for a philosophically “self-consistent” understanding of ghost imaging. The “nonlocal” problem has forced us to replace the classical concept of subfield with the quantum concept of photon. It is true, in quantum mechanics, that the superposition happens between probability amplitudes, and there is no need to define any speed limit on the probability amplitude propagation. Common sense dictates that a physical event can happen with simultaneous probabilities at distance.

In the following, we give a quantum mechanical treatment to obtain the ghost image from the two-photon interference produced photon number fluctuation correlation. The physical model of thermal radiation, either natural thermal light or pseudo-thermal light, is the same as that of the classical, except we write the state of the thermal radiation in the quantum coherent state representation [12,24]:

$$|\mathsf{\Psi }\rangle =\prod _m|\left\{{\alpha }_m\right\}\rangle =\prod _{m,\mathbf{k}}|{\alpha }_m(\mathbf{k})\rangle$$

(23)

where m labels the mth randomly radiated or scattered sub-radiation from the mth sub-source, and $\mathbf{k}$ is a wavevector. $|{\alpha }_m(\mathbf{k})\rangle$ is an eigenstate of the annihilation operator with an eigenvalue ${\alpha }_m(\mathbf{k})$,

$${\widehat{a}}_m(\mathbf{k})|{\alpha }_m(\mathbf{k})\rangle ={\alpha }_m(\mathbf{k})|{\alpha }_m(\mathbf{k})\rangle$$

(24)

Thus, we have,

$${\widehat{a}}_m(\mathbf{k})|\mathsf{\Psi }\rangle ={\alpha }_m(\mathbf{k})|\mathsf{\Psi }\rangle$$

(25)

The above model is reasonable for a natural thermal light source, such as the sun, or pseudo-thermal light source, such as a ground glass scattered laser beam in which a laser beam is scattered by millions of tiny diffusers. The coherent laser beam is scattered into millions of groups of identical photons propagating to all possible directions denoted by $\mathbf{k}$. The scattered subfields acquire random phases in the scattering process. $|{\alpha }_m(\mathbf{k})\rangle$ describes the state of a subfield that is scattered by the mth diffuser with a vector $\mathbf{k}$.

The field operator at detector $D_j$, $j=1,2$, can be written in the following form in terms of the subfields:

$$\begin{array}{c}\hfill {\widehat{E}}^{(+)}({\mathbf{r}}_j,t_j)=\sum _m\int d\mathbf{k}{\widehat{a}}_m(\mathbf{k})g_m(\mathbf{k};{\mathbf{r}}_j,t_j)\end{array}$$

(26)

where $g_m(\mathbf{k};{\mathbf{r}}_j,t_j)$ is Green’s function, which propagates the $\mathbf{k}$ mode of the mth subfield from the mth sub-source to space-time coordinate $({\mathbf{r}}_j,t_j)$.

Following Glauber’s theory, the second-order coherence function $G^{(2)}({\mathbf{r}}_1,t_1;{\mathbf{r}}_2,t_2)$ is calculated as follows [16]:

$$\begin{array}{c}{G}^{(2)}({\mathbf{r}}_1,t_1;{\mathbf{r}}_2,t_2)\hfill \\ =\langle \langle \mathsf{\Psi }\left|E^{(-)}({\mathbf{r}}_1,t_1)E^{(-)}({\mathbf{r}}_2,t_2)E^{(+)}({\mathbf{r}}_2,t_2)E^{(+)}({\mathbf{r}}_1,t_1)\right|\mathsf{\Psi }\rangle {\rangle }_{\mathrm{Es}}\hfill \\ =\langle \langle \mathsf{\Psi }\left|\sum _m{E}_m^{(-)}({\mathbf{r}}_1,t_1)\sum _n{E}_n^{(-)}({\mathbf{r}}_2,t_2)\sum _q{E}_q^{(+)}({\mathbf{r}}_2,t_2)\sum _p{E}_p^{(+)}({\mathbf{r}}_1,t_1)\right|\mathsf{\Psi }\rangle {\rangle }_{\mathrm{Es}}\hfill \\ =\sum _m{\psi }_m^{*}({\mathbf{r}}_1,t_1){\psi }_m({\mathbf{r}}_1,t_1)\sum _n{\psi }_n^{*}({\mathbf{r}}_2,t_2){\psi }_n({\mathbf{r}}_2,t_2)+\sum _{m\ne n}{\psi }_m^{*}({\mathbf{r}}_1,t_1){\psi }_n({\mathbf{r}}_1,t_1){\psi }_n^{*}({\mathbf{r}}_2,t_2){\psi }_m({\mathbf{r}}_2,t_2)\hfill \\ =\sum _{m,n}|\frac{1}{\sqrt{2}}[{\psi }_m({\mathbf{r}}_1,t_1){\psi }_n({\mathbf{r}}_2,t_2)+{\psi }_m({\mathbf{r}}_2,t_2){\psi }_n({\mathbf{r}}_1,t_1)]{|}^2\hfill \\ =\langle n_1({\mathbf{r}}_1,t_1)\rangle \langle n_2({\mathbf{r}}_2,t_2)\rangle +\langle \Delta n_1({\mathbf{r}}_1,t_1)\Delta n_2({\mathbf{r}}_2,t_2)\rangle \hfill \end{array}$$

(27)

Here, ${\psi }_m({\mathbf{r}}_j,t_j)$, $j=1,2$, is the effective wavefunction of the mth photon, or the mth group identical photons (so called “coherent photons”) at space-time coordinate $({\mathbf{r}}_j,t_j)$,

$$\begin{array}{c}\hfill {\psi }_m({\mathbf{r}}_j,t_j)=\int d\mathbf{k}{\alpha }_m(\mathbf{k})g_m(\mathbf{k};{\mathbf{r}}_j,t_j)\end{array}$$

(28)

The photon number fluctuation correlation is thus:

$$\begin{array}{c}\hfill \langle \Delta n_1\Delta n_2\rangle =\sum _m{\psi }_m^{*}({\mathbf{r}}_1,t_1){\psi }_m({\mathbf{r}}_2,t_2)\sum _n{\psi }_n^{*}({\mathbf{r}}_2,t_2){\psi }_n({\mathbf{r}}_1,t_1)=|G_{12}^{(1)}({\mathbf{r}}_1,t_1;{\mathbf{r}}_2,t_2){|}^2\end{array}$$

(29)

To simplify the calculation, we assume a monochromatic field and define the two observation planes parallel to the source plane. The calculation is thus concentrated on the transverse spatial behavior of the radiation,

$$\begin{array}{c}\hfill \langle \Delta n({\overrightarrow{\rho }}_1,z_1)\Delta n({\overrightarrow{\rho }}_2.z_2)\rangle =|\sum _m{\psi }_m^{*}({\overrightarrow{\rho }}_1,z_1){\psi }_m({\overrightarrow{\rho }}_2,z_2){|}^2=|G_{12}^{(1)}({\overrightarrow{\rho }}_1,z_1;{\overrightarrow{\rho }}_2,z_2){|}^2\end{array}$$

(30)

Comparing with the photon number fluctuation $\langle \Delta n({\overrightarrow{\rho }}_1,z_1)\Delta n({\overrightarrow{\rho }}_2.z_2)\rangle$ calculated in the previous section, we can see that the effective wavefunction of the mth photon, or the mth group identical photons (so called “coherent photons”), ${\psi }_m({\overrightarrow{\rho }}_j,z_j)$ plays the same role as that of the subfield $E_m({\overrightarrow{\rho }}_j,z_j)$. The rest of the calculation is the same as that shown in the last section. We thus have a ghost image in the photon number fluctuation correlation:

$$\begin{array}{c}\hfill \langle \Delta n({\overrightarrow{\rho }}_1)\int d{\overrightarrow{\rho }}_2\Delta n({\overrightarrow{\rho }}_2)\rangle =\int d{\overrightarrow{\rho }}_2|A({\overrightarrow{\rho }}_2){|}^2{\mathrm{somb}}^2[\frac{\pi \Delta \theta }{\lambda }|{\overrightarrow{\rho }}_1-{\overrightarrow{\rho }}_2|]\simeq |A({\overrightarrow{\rho }}_1){|}^2\end{array}$$

(31)

where we have assumed a large value of $\Delta \theta$ and approximated the somb-function to δ-function. For a perfect imaging system, i.e., if the somb-function can be approximated to a δ-function-like image-forming function, a perfect turbulence-free ghost image, $|A({\overrightarrow{\rho }}_1){|}^2$, is observable from the joint photon number fluctuation measurement in terms of ${\overrightarrow{\rho }}_1$.

From the above calculation, we may conclude again that the noise produced ghost image is the result of an interference involving a superposition between quantum amplitudes $A_1={\psi }_m({\overrightarrow{\rho }}_1){\psi }_n({\overrightarrow{\rho }}_2)$ and $A_2={\psi }_n({\overrightarrow{\rho }}_1){\psi }_m({\overrightarrow{\rho }}_2)$, corresponding to two different yet indistinguishable ways for two photons, or two groups of identical photons, or two wavepackets (the mth and the nth) to produce a joint photo-detection event: (1) the mth wavepacket triggers $D_1$ at ${\overrightarrow{\rho }}_1$ and the nth wavepacket triggers $D_2$ at ${\overrightarrow{\rho }}_2$; and (2) the nth wavepacket triggers $D_1$ at ${\overrightarrow{\rho }}_1$ and the mth wavepacket triggers $D_2$ at ${\overrightarrow{\rho }}_2$.

A perfect constructive interference occurs at ${\overrightarrow{\rho }}_1={\overrightarrow{\rho }}_2$. In this situation, the two two-photon amplitudes experienced the same optical path and thus the same turbulence. Basically, any path and index variations are canceled out in the cross interference term ${\sum }_{m\ne n}{\psi }_m^{*}({\overrightarrow{\rho }}_1){\psi }_m({\overrightarrow{\rho }}_2){\psi }_n^{*}({\overrightarrow{\rho }}_2){\psi }_n({\overrightarrow{\rho }}_1)$ and have no influences on the result of this constructive interference. From the viewpoint of two-photon interference, the turbulence-free nature of ghost imaging is also clear and understandable. Again, the turbulence-free ghost imaging experiment has been demonstrated by Meyers et al. in 2012 [10].