1. Introduction
Sustainability of fossil fuel-fired power generation plants require the removal of carbon in the form of carbon dioxide (CO
2) from either the fuel before combustion or flue gas after combustion. This becomes necessary because CO
2 emission, which is a consequence of combustion or oxidation of fossil fuel, has been identified as a main greenhouse gas [
1,
2]. Once the CO
2 is removed, it is usually compressed and transported to the point of storage away from the atmosphere. The point of CO
2 storage is usually far from the source of emission; hence, transportation over long distance is highly envisaged. As a result, the CO
2 is envisaged to be transported via pipelines, which primarily have gained wide acceptance for long-distance transportation [
2,
3,
4,
5]. Prior to transport, equipment driven by gas turbines is used to compress the captured CO
2 to a dense-phase state, which is said to be the most efficient and economical state for CO
2 pipeline transport [
3,
4]. The required power for compression or compression duty using appropriately sized GT is addressed in this paper.
It is worth mentioning that the quantification of compression duty has been conducted by many researchers, especially in areas that deal with cost prediction models of CO
2 pipeline transport [
6]. In such studies, the required energy for compression is either treated as an efficiency penalty on the overall power generation plant’s efficiency or assumed to be supplied from the grid [
7,
8,
9,
10]. The power consumption of the compression process is said to be about 40% of the auxiliary load and could constitute 7%–12% of the power plants output [
11,
12]. This energy consumption is huge in economic terms, and the need for a separate source of energy for compression becomes desirable. Similarly, the requirement for booster stations in remote locations along a trunk pipeline where the cost of transporting electricity becomes prohibitive necessitates a suitable prime mover. Thus, GTs being extensively used in pipelines to compress gas at suitable points becomes a prime mover of choice for this duty. While considerable operational experience has been gathered in natural gas transmission, the same is not true for CO
2 transmission, especially since the properties and behavior of the gases are quite different. The distinguishing feature of this work hinges on the close coupling of the compression system with the GT prime mover, with a view of assessing the CO
2 compression power requirement. Analysis of this kind becomes imperative to aid the techno-economic assessment of deploying this prime mover in a CO
2 pipeline transport.
2. The Pipeline Transmission of CO2
The economics for transporting large volumes of CO
2 over long distance in the gaseous phase is quite unfavorable [
13,
14]. This is because such pure gas phase transportation will be restricted to operate below 30–50 bar at which the densities and capacities will be too small. However, the pure gas phase will fit a system where the CO
2 is initially transported on gathering lines from low CO
2 producers for connection to larger trunk pipelines [
13]. Low-pressure liquid phase is not desirable either except for transportation in vessels, tanks, and barges. The liquid phase for pipeline transportation comes with problems of frost formation in cold climates and the need for pipeline material suitable for cryogenic application. Furthermore, unlike natural gas, the critical point of CO
2 is near the potential compressor (and pipeline) operating point such that slight changes in ambient temperature or soil temperature for a buried pipeline can result in two-phase flow [
3].
Abrupt pressure drops occasioned by two-phase flows and the detrimental effect of impurities must be avoided during CO
2 transmission in pipelines. Hence, the CO
2 is transported in the dense-phase state especially for onshore pipelines, as has been earlier highlighted [
3,
4]. In addition, the dense-phase transport gives an advantage for high delivery pressure at injection to sink [
2]. The pipeline operating pressure in this state is between 10 and 15 MPa [
5,
7,
15]. In general though, the CO
2 can be transported at temperature and pressure ranges of 12–44 °C and 85–150 bar, respectively [
5,
16]. The upper temperature limit is fixed by the compressor-station discharge temperature, while the lower limit is fixed by winter ground temperature for buried pipelines. The lower pressure limit is dictated by the phase behavior of CO
2, especially with impurities present and the need to maintain supercritical conditions, while the upper pressure limit is mostly due to economic concerns [
5].
Highly recommended within this pipeline operating conditions is the “API 5L X-70” line pipe specification in the US Code of Federal Regulations—CFR (the CFR regulates the design, construction and operation of CO
2 pipeline transport in the USA) [
8,
17]. Similarly, the ASME/ANSI class 900# flanges are quite suitable since they can tolerate an operating pressure of about 153 bar (15.3 MPa) at a temperature of about 311.15 K (38 °C) [
3,
16].
3. Methodology
This work was carried out by adapting the TERA (Techno-Economic and Environmental Risk Analysis) framework developed in Cranfield University, UK [
18,
19]. The core of the TERA is the performance module, which is a detailed and rigorous thermodynamic representation of the component parameters and power plant achieved by simulating the design, off-design, and degraded performance of the power plant. The economic, environmental, and risk modules are built around the performance module and integrated with an optimizer to compare power plants optimized for a particular duty such as fuel consumption and operating cost. Applying this to the GT-driven transmission of CO
2 in pipelines, the adapted framework consists of four sets of FORTRAN-coded integrated modules,
i.e., a compression module, an engine performance module, an emission module, and an economic module. The compression module addressed in this paper involved code development to simulate the centrifugal compressor power requirement using the Peng–Robinson equation of state (PR-EOS), said to be among the most precise and proper for engineering application [
4,
20]. The CO
2 is assumed to be compressed from atmospheric pressure (1 bar) to the pipeline intake pressure of 10 MPa (100 bars) using a centrifugal compressor. A maximum temperature of 40 °C was maintained at the suction end of the centrifugal compressor. Considering the limitation imposed by maximum head achievable and allowable temperature in the compressor, multistage compression with intercooling was simulated. The CO
2 was assumed to be pure and the required CO
2 properties of density and viscosity were calculated using the code developed by McCollum and Ogden [
9].
4. Physical Properties of Pure CO2
Since the captured CO
2 will be compressed to a dense-phase state, an insight into the phase behavior of pure CO
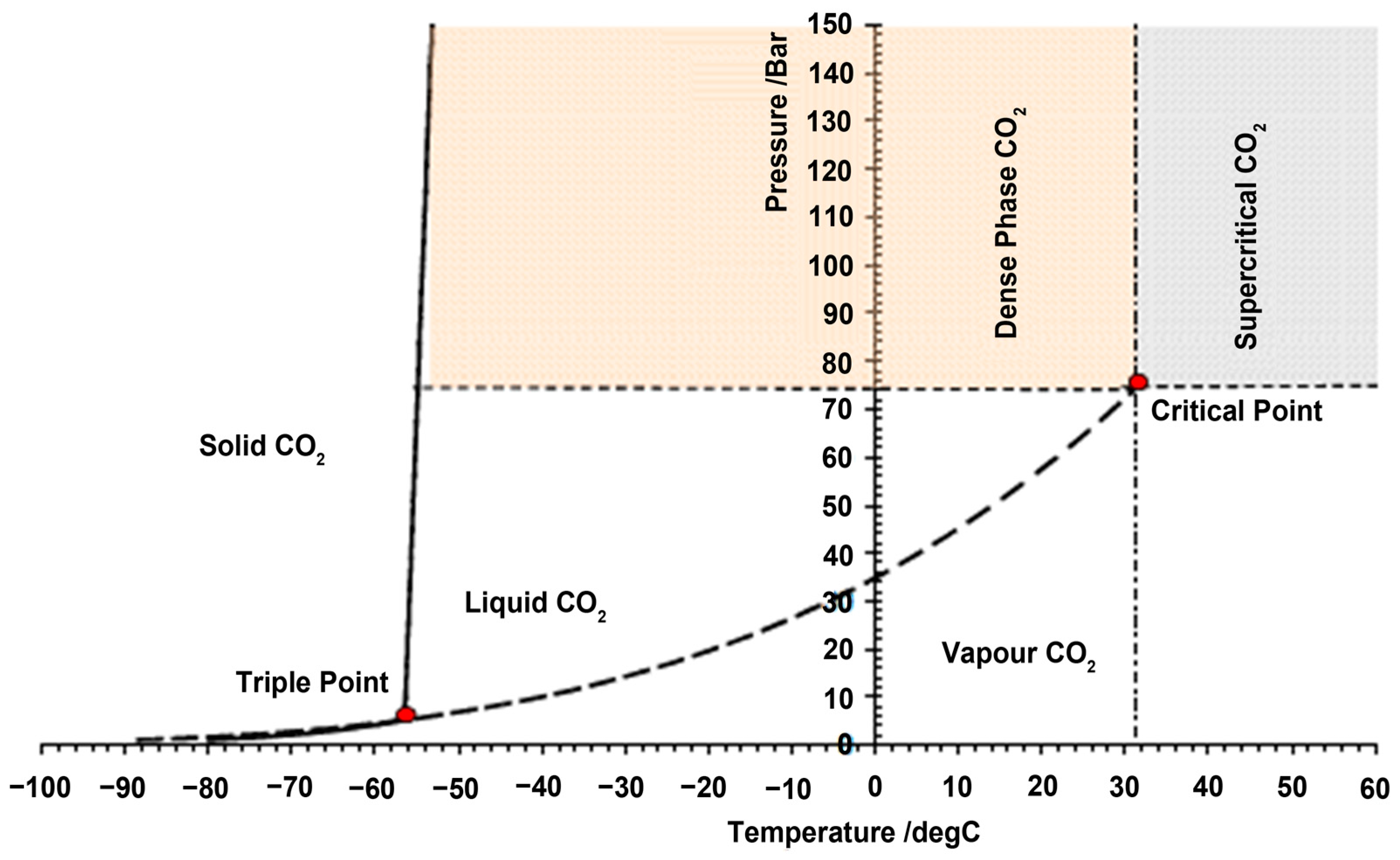
2 depicted by
Figure 1 is worthwhile. CO
2 in its pure state is colorless, odorless, and non-inflammable at ambient temperature and pressure [
5].
Two distinct points can be observed, namely the triple point (5 bar, −56 °C) and the critical point (74 bar, 31 °C). At the triple point, CO
2 can exist as solid, liquid, or gas. Above the critical point, the pure CO
2 is in a supercritical phase where it acts as neither gas nor liquid [
21]. At pressures above the critical pressure but below the critical temperature, a fluid is said to be in a dense phase; otherwise, it is in a non-dense phase. Note from
Figure 1 above that the dense phase could be achieved without passing the liquid area. The dense phase is a very peculiar state in that, on one hand, it is not a liquid because it has a viscosity similar to that of a gas while, on the other hand, its density is closer to that of a liquid and has similar flow conditions as that of a liquid [
13].
5. Modeling the Compressor Power (Head) Requirement
Equations for evaluating the head, work or power of a centrifugal compressor in units of Nm/kg, Nm or Nm/sec respectively have been presented in the literature. These equations are primarily used to evaluate the adiabatic head (H
ad) (Equation (1)) and, with slight modification, the polytropic head (H
poly) (Equation (2)) as expressed below [
22,
23,
24].
where
Ts is the suction temperature (K); Zave is the average compressibility factor; R is the specific gas constant (KJ/kg-K); Ro is the universal gas constant (KJ/Kmol-K); mw is the molecular weight (kg/Kmol); is ratio of specific heats; Pd and Ps are pressures at discharge and suction, respectively (MPa); Cp and Cv are specific heats at constant pressure and volume respectively (KJ/kg-K); n is the polytropic index; and is the polytropic efficiency.
Considering the “polytropic head”, the required compression power, or gas power (P
poly) as it is also called, is defined by Equation (5) as
Further, the shaft or prime mover power (P
shaft) is given by Equation (6) as
Mechanical efficiency () of about 87% was assumed in the simulation; m is the CO2 mass flow rate (kg/s).
In actual applications, the compression process is rarely polytropic or adiabatic. Thus, to achieve an estimate of the actual compression head, modifications such as the “Schultz polytropic head correction factor”, the Mollier diagrams, or the use of equations of state have been readily explored [
23,
24,
25].
In light of the above, the modeling of the centrifugal compressor power presented here was achieved using the PR-EOS [
20]. Further reading about other equations of states, the Mollier diagram and the Schultz polytropic factor can be found in [
23,
25].
Equations (1) and (2) can be re-cast in terms of the enthalpy difference between the suction and discharge states determined by two of the following given properties of the compressed gas: pressure, temperature, and entropy. Hence, the actual compressor head,
can be represented as [
23,
26]
This is further defined as
where
is change in enthalpy (KJ/kg); H
d and H
s are enthalpies at discharge and suction respectively (KJ/kg); and dT is change in temperature (K). The term
is called the enthalpy departure function defined by the PR-EOS as
The terms of this equation are fully defined in [
20]:
The mathematical expression for Equation (10) specifically for CO
2 is found in [
26]. T is temperature (K).
6. Modeling the PR-EOS for Compressibility Factor (Z)
To fully solve Equation (8) for the actual head, the CO
2 compressibility factor (Z) needs to be determined by using the PR-EOS to evaluate
. From [
20],
where
The terms A and B are fully defined in [
20].
7. The Simulation of the Required Compression Power
The power required for compression is evaluated for the CO
2 flow rate that will meet both available GT driver power and pipeline compressor actual suction capacity. Consideration was given to the range of CO
2 flow rates in million tonnes per year (MTPY), which are representative of the kilograms of CO
2 produced per kilowatt hour from conventional (subcritical), supercritical, and advanced steam coal power generation plants as well as a CCGT power plant. A typical CCGT power generation plant will give a CO
2 equivalence of 1.5 MTPY [
2,
27]. A maximum of 25 MW driver power is considered while the compressor is expected to operate at best efficiency over the chosen CO
2 flow range. An actual design CO
2 flow rate of 1.5 MTPY (~100,000 m
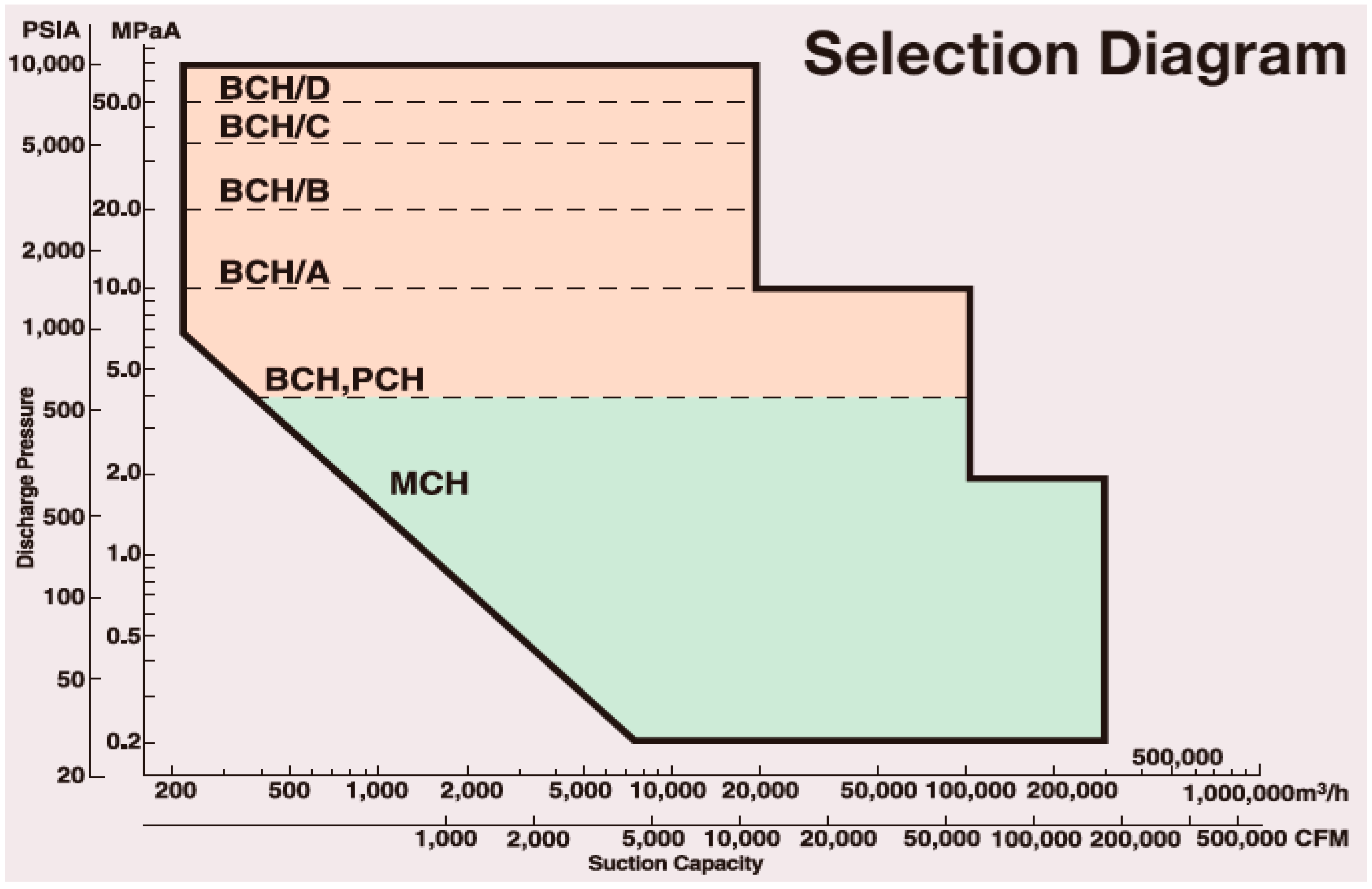
3/h) at design speed, which is within the operational limit specified for pipeline compressor (PCH) as shown in
Figure 2, is maintained. Inlet flows above and up to twice this capacity will be assumed driven by the same driver in a parallel flow arrangement. The simulation entails multistage compression power evaluation as well as consideration of pressure drop due to intercooling. All simulated results are assumed to be at a steady state.
A constant compressor polytropic efficiency value of 80% per stage was assumed for the simulation considering existing technology [
24]. However, it should be noted that the compressor efficiency value decreases in successive stages for multi-stage compression due to fouling, speed matching, and mechanical constraints. A polytropic efficiency value of 90% was also used in the simulation to evaluate the effect of change in efficiency on the compressor head. A 10% increment on simulated power is applied to meet the API 617 minimum power margin specification for GT driver selection.
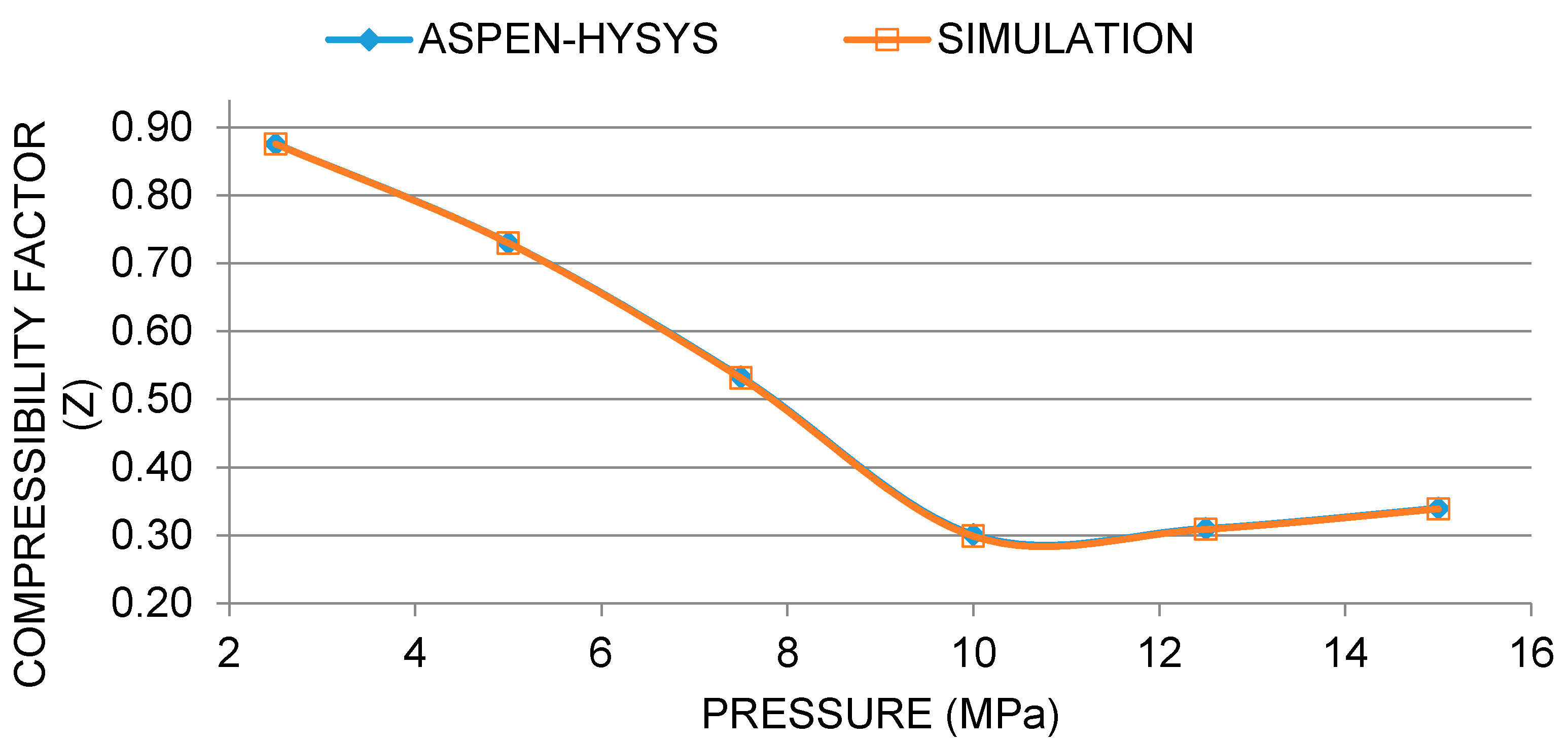
8. A Validation of the Simulated Compressibility Factor (Z)
The compressibility factor is crucial to the evaluation of required compression power. Therefore, the simulated CO
2 compressibility values from the code developed using the PR-EOS was validated against the values obtained using Aspen HYSYS—a commercial pipeline simulation software with a built-in PR-EOS library. The simulated values show a good agreement with Aspen-HYSYS, as is evident from the plot obtained in
Figure 3.
However, the PR-EOS like all other equations of state has limits of applicability. Thus, the code will give useful results from zero pressure and temperature to pressures and temperatures of about 30 MPa and 589.29 K, respectively. It is worth mentioning that the maximum pressure required for the CO2 pipeline is 15 MPa, which is within the EOS applicability range.
9. Results and Discussion
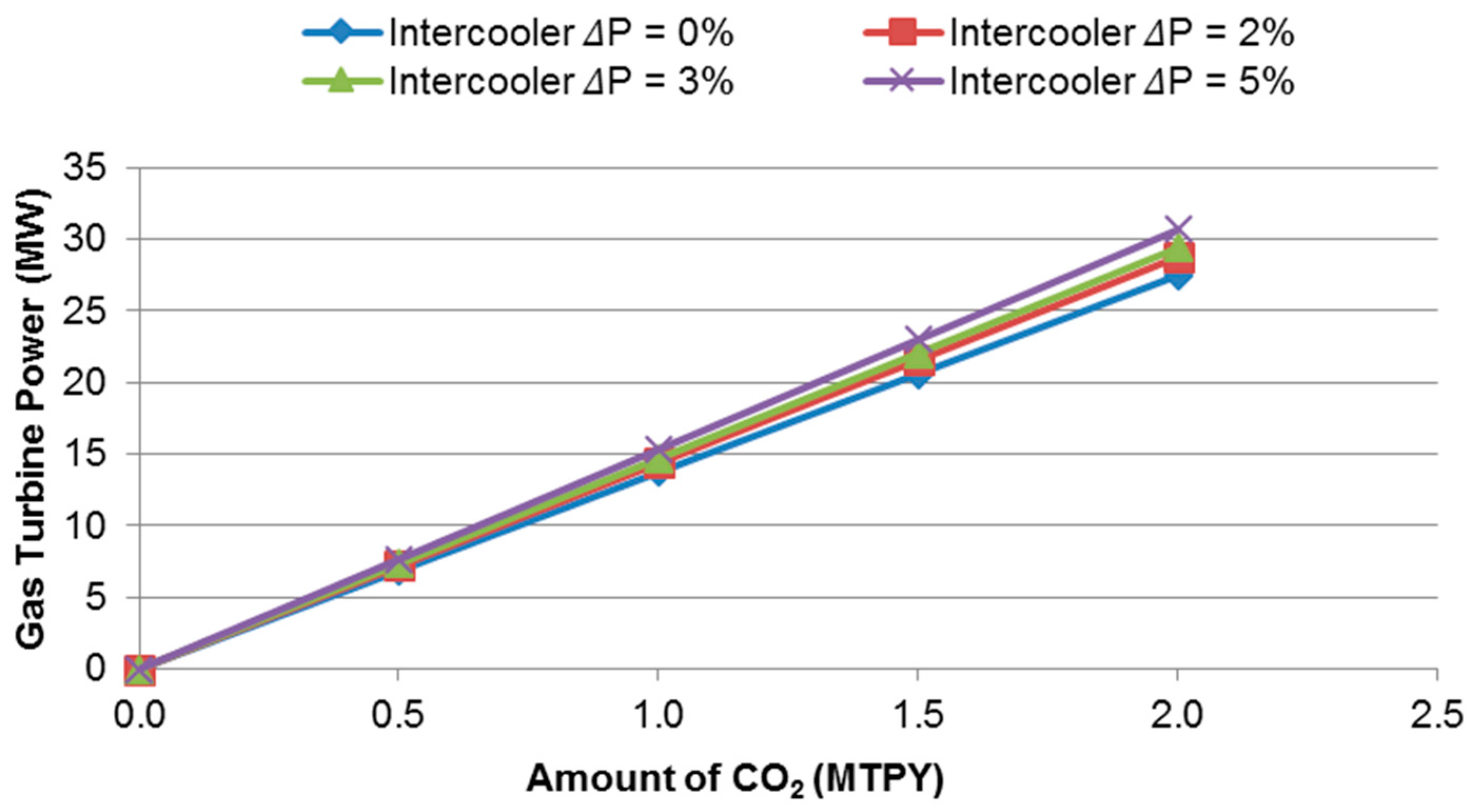
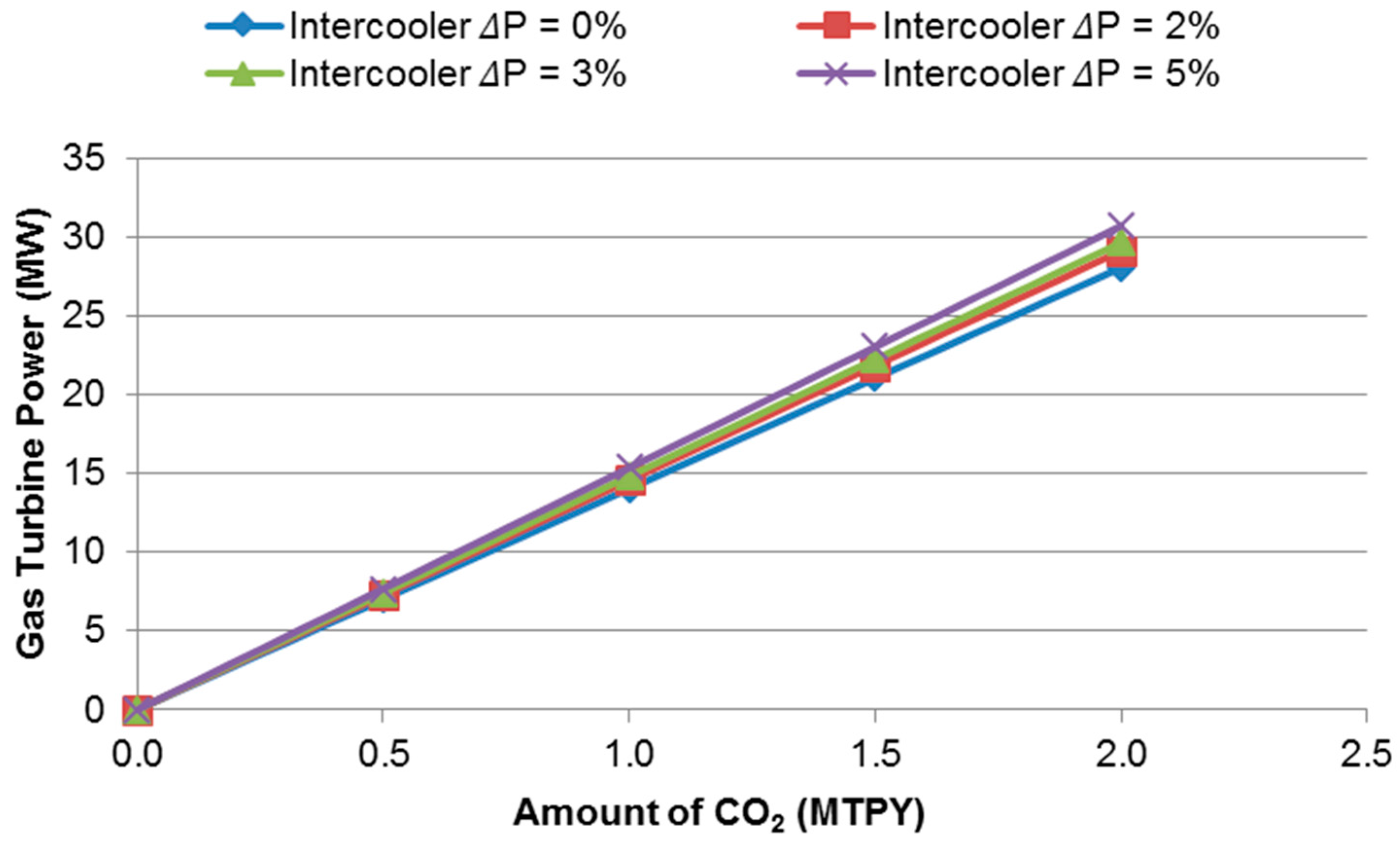
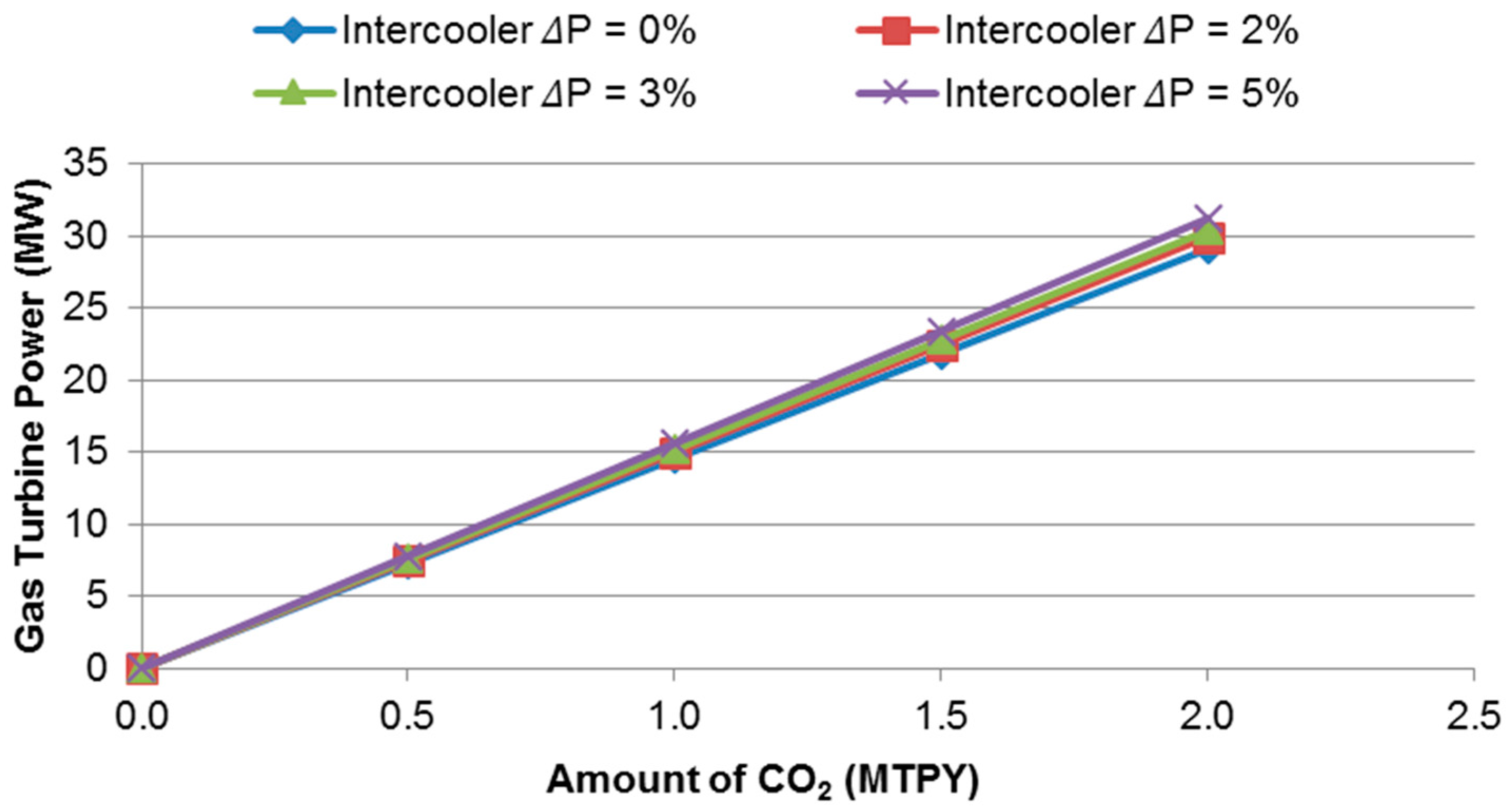
Figure 4,
Figure 5 and
Figure 6 depict the GT power required for 10, 8, and 6 compressor stages of CO
2 compression, respectively, within the operating conditions earlier highlighted. The process requirement is to give a constant discharge pressure which is accomplished by varying the speed of the GT driver. In so doing, the compressor efficiently develops a constant head by lowering its speed at flows below the rated flow. As a result, it can be observed from the graphs that, as the CO
2 mass flow rate increases, the power requirement increases.
Further deducible from the plots is the steady increase in compression power requirement as the intercooler pressure drop increases. This is necessary to ensure the required discharge pressure is attained during the compression process.
At the rated flow of 1.5 MTPY, the power required considering a 5% intercooler pressure drop is 22.98 MW, 23.03 MW, and 23.41 MW for the 10, 8, and 6 compression stages, respectively. The values indicate about a 2% increase in power requirement as the number of stages reduces from 10 to 6 (compression ratios varying from 1.58 to 2.26). The rise in compressor head or otherwise rise in stage compression ratio with fewer stages accounts for this development.
From the operational point of view, the increase in required power means an increase in energy cost. However, this is a trade-off for the compactness and comparative light weight of centrifugal compressors with fewer numbers of stages, which is advantageous during installation and scheduled maintenance. Another merit of the increase compressor head from the GT driver performance point of view is the ability to operate near design speed at a rated compressor operating point, thus minimizing part load operation. This is so considering the fact that higher head per stage is achieved at a higher compressor speed.
10. Conclusions
This paper has established the estimated power demand by the GT prime mover to compress typical CO2 flows within the limits of assumptions considered. The results have shown that about 23 MW of power will be required for the initial compression of the CO2 to pipeline operating pressure. This amount of power corresponds to 1.5 MTPY of CO2—a projected equivalent CO2 released from a 530-MW combined cycle gas turbine (CCGT) power generation plant. Future work will look at the off-design performance of a selected GT prime mover as well as cost implications.
Acknowledgments
The overseas study fellowship of the Federal Government of Nigeria is highly appreciated. Many thanks to Pericles Pilidis of the Centre for Propulsion Engineering, Cranfield University, UK for his candid support and supervision. The corresponding author is also grateful to Rahmatullah Yaqoob for proofreading this paper.
Author Contributions
Abdussalam El-Suleiman designed, run and analyzed the codes for the research; Nnamdi B. Anosike validated the codes; while Pericles Pilidis supervised and justified the results obtained. The paper was written by Abdussalam El-Suleiman. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Safdarnejad, S.M.; Hedengren, J.D.; Baxter, L.L. Dynamic Optimization of a Hybrid System of Energy-Storing Cryogenic Carbon Capture and a Baseline Power Generation Unit. Appl. Energy 2016, 172, 66–79. [Google Scholar] [CrossRef]
- IPCC. Special Report on Carbon Dioxide Capture and Storage; Prepared by Working Group III of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar]
- Kurz, R.; Ohanian, S.; Brun, K. Compressors in High Pressure Pipeline Applications. In Proceedings of the ASME Turbo Expo, Glasgow, UK, 14–18 June 2010; pp. 631–640.
- Li, H.; Yan, J. Impacts of Impurities in CO2-Fluids on CO2 Transport Process. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 367–375.
- Joana, S.; Joris, M.; Evangelos, T. Technical and Economic Characteristics of a CO2 Transmission Pipeline Infrastructure; EUR 24731 EN; European Commission Joint Research Centre, Institute for Energy: Petten, The Netherlands, 2011. [Google Scholar]
- Knoope, M.M.J.; Ramirez, A.; Faaij, A.P.C. A State-of-the-Art Review of Techno-Economic Models Predicting the Costs of CO2 Pipeline Transport. Int. J. Greenh. Gas Control 2013, 16, 241–270. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Wang, G.X.; Massarotto, P.; Rudolph, V. Optimization of Pipeline Transport for CO2 Sequestration. Energy Convers. Manag. 2006, 47, 702–715. [Google Scholar] [CrossRef]
- International Energy Agency Greenhouse Gas Programme (IEA GHG). CO2 Pipeline Infrastructure: An Analysis of Global Challenges and Opportunities; Element Energy Ltd.: Cambridge, UK, 2010. [Google Scholar]
- McCollum, D.L.; Ogden, J.M. Techno-Economic Models for Carbon Dioxide Compression, Transport, and Storage & Correlations for Estimating Carbon Dioxide Density and Viscosity; Institute of Transportation Studies, University of California: Davis, CA, USA, 2006. [Google Scholar]
- Chandel, M.K.; Pratson, L.F.; Williams, E. Potential Economies of Scale in CO2 Transport through Use of a Trunk Pipeline. Energy Convers. Manag. 2010, 51, 2825–2834. [Google Scholar] [CrossRef]
- Justin, Z.; Sara, T. CO2 Capture and Sequestration Options: Impact on Turbo-Machinery Design. In Proceedings of the ASME Turbo Expo, Berlin, Germany, 9–13 June 2008; pp. 945–963.
- Cohen, S.M.; Rochelle, G.T.; Webber, M.E. Optimizing Post-Combustion CO2 Capture in Response to Volatile Electricity Prices. Int. J. Greenh. Gas Control 2012, 8, 180–195. [Google Scholar] [CrossRef]
- Skovholt, O. CO2 Transportation System. Energy Convers. Manag. 1993, 34, 1095–1103. [Google Scholar] [CrossRef]
- Koornneef, J.; Ramírez, A.; Turkenburg, W.; Faaij, A. The Environmental Impact and Risk Assessment of CO2 Capture, Transport and Storage—An Evaluation of the Knowledge Base. Prog. Energy Combust. Sci. 2012, 38, 62–86. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Kennington, L.; Baxter, L.L.; Hedengren, J.D. Investigating the Impact of Cryogenic Carbon Capture on Power Plant Performance. In Proceedings of the American Control Conference, Palmer House Hilton, Chicago, IL, USA, 1–3 July 2015; pp. 5016–5021.
- Mohitpour, M.; Golshan, H.; Murray, A. Pipeline Design and Construction: A Practical Approach, 2nd ed.; ASME Press: New York, NY, USA, 2003. [Google Scholar]
- McCoy, S.T.; Rubin, E.S. An Engineering-Economic Model of Pipeline Transport of CO2 with Application to Carbon Capture and Storage. Int. J. Greenh. Gas Control 2008, 2, 219–229. [Google Scholar] [CrossRef]
- Ogaji, S.; Pilidis, P.; Sethi, V. Power Plant Selection in a Carbon Constrained World the TERA (Technoeconomic Environmental Risk Analysis). J. Aerosp. Power 2009, 24, 896–902. [Google Scholar]
- MacCapani, M.; Khan, R.S.R.; Burgmann, P.J.; Lorenzo, G.D.; Ogaji, S.O.T.; Pilidis, P.; Bennett, I. A TERA Based Comparison of Heavy Duty Engines and their Artificial Design Variants for Liquefied Natural Gas Service. J. Eng. Gas Turbines Power 2014, 136. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two—Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Maroto-Valer, M.M. Developments and Innovation in Carbon Dioxide (CO2) Capture and Storage Technology; CRC Press: Boca Raton, FL, USA; Oxford, UK, 2010. [Google Scholar]
- Kurz, R. The Physics of Centrifugal Compressor Performance; Pipeline Simulation Interest Group: Palm Springs, CA, USA, 2004. [Google Scholar]
- Paresh, G. Performance Evaluation of Pumps and Compressors, 1st ed.; Lulu.com: Raleigh, NC, USA, 2008. [Google Scholar]
- Boyce, M.P. Centrifugal Compressors: A Basic Guide; PennWell: Tulsa, OK, USA, 2003. [Google Scholar]
- Mokhatab, S.; Poe, W.A.; Speight, J.G. Natural Gas Compression. In Handbook of Natural Gas Transmission and Processing; Gulf Professional Pub.: Burlington, MA, USA, 2006; pp. 295–322. [Google Scholar]
- Walsh, P.P.; Fletcher, P. Gas Turbine Performance, 2nd ed.; Blackwell Science: Oxford, UK, 2004. [Google Scholar]
- Coal Industry Advisory Board (CIAB). Power Generation from Coal: Measuring and Reporting Efficiency Performance and CO2 Emissions; OECD/IEA: Paris, France, 2010. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).