Drilling of Copper Using a Dual-Pulse Femtosecond Laser
Abstract
:1. Introduction
2. Modeling
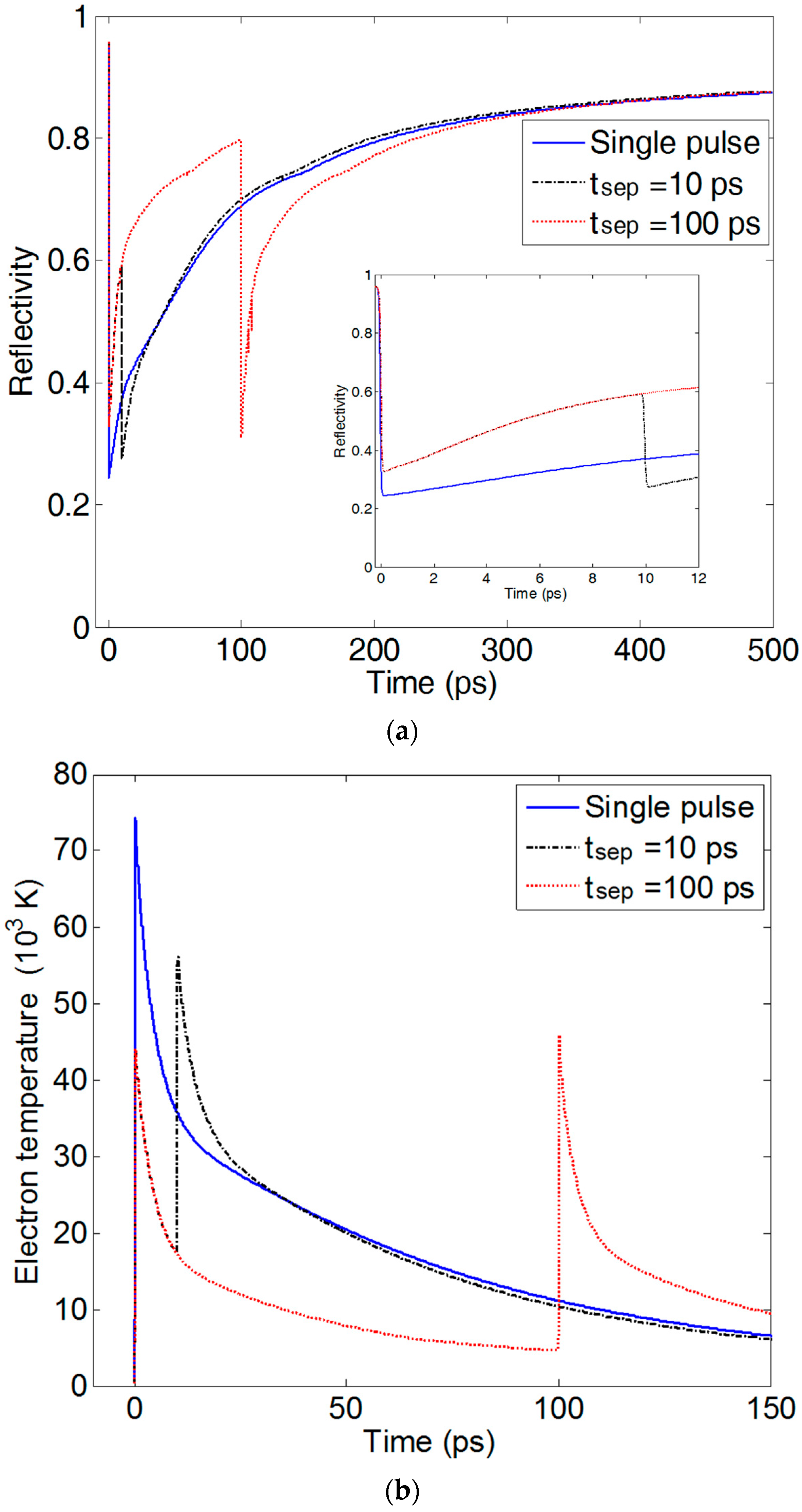
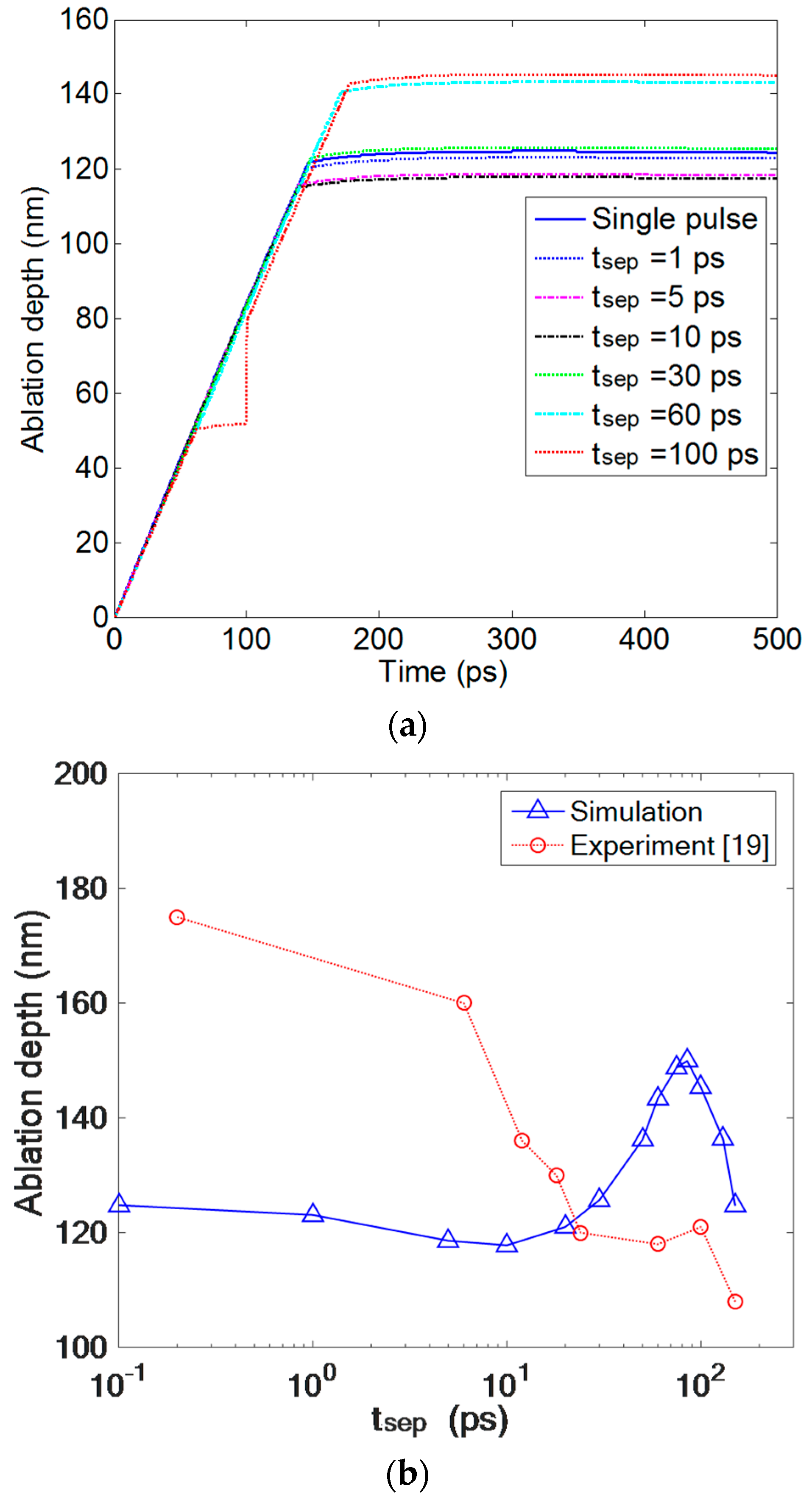
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nolte, S.; Momma, C.; Jacobs, H.; Tunnermann, A.; Chichkov, B.N.; Wellegehausen, B.; Welling, H. Ablation of metals by ultrashort laser pulses. J. Opt. Soc. Am. B 1997, 14, 2716–2722. [Google Scholar] [CrossRef]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.; Zhu, X. Theoretical studies of ultrafast ablation of metal targets dominated by phase explosion. Appl. Phys. A 2007, 89, 571–578. [Google Scholar] [CrossRef]
- Wu, B.; Shin, Y.C. A simple model for high fluence ultra-short pulsed laser metal ablation. Appl. Surf. Sci. 2007, 253, 4079–4084. [Google Scholar] [CrossRef]
- Byskov-Nielsen, J.; Savolainen, J.-M.; Christensen, M.S.; Balling, P. Ultra-short pulse laser ablation of copper, silver and tungsten: Experimental data and two-temperature model simulations. Appl. Phys. A 2011, 103, 447–453. [Google Scholar] [CrossRef]
- Colombier, J.P.; Combis, P.; Bonneau, F.; le Harzic, R.; Audouard, E. Hydrodynamic simulations of metal ablation by femtosecond laser irradiation. Phys. Rev. B 2005, 71, 165406. [Google Scholar] [CrossRef]
- Byskov-Nielsen, J.; Savolainen, J.M.; Christensen, M.S.; Balling, P. Ultra-short pulse laser ablation of metals: Threshold fluence, incubation coefficient and ablation rates. Appl. Phys. A 2010, 101, 97–101. [Google Scholar] [CrossRef]
- Hashida, M.; Semerok, A.F.; Gobert, O.; Petite, G.; Izawa, Y.; Wagner, J.F. Ablation threshold dependence on pulse duration for copper. Appl. Surf. Sci. 2002, 197, 862–867. [Google Scholar] [CrossRef]
- Kirkwood, S.E.; van Popta, A.C.; Tsui, Y.Y.; Fedosejevs, R. Single and multiple shot near-infrared femtosecond laser pulse ablation thresholds of copper. Appl. Phys. A 2005, 81, 729–735. [Google Scholar] [CrossRef]
- Le Harzic, R.; Breitling, D.; Weikert, M.; Sommer, S.; Fohl, C.; Valette, S.; Donnet, C.; Audouard, E.; Dausinger, F. Pulse width and energy influence on laser micromachining of metals in a range of 100 fs to 5 ps. Appl. Surf. Sci. 2005, 249, 322–331. [Google Scholar] [CrossRef]
- Weck, A.; Crawford, T.H.R.; Wilkinson, D.S.; Haugen, H.K.; Preston, J.S. Laser drilling of high aspect ratio holes in copper with femtosecond, picosecond and nanosecond pulses. Appl. Phys. A 2008, 90, 537–543. [Google Scholar] [CrossRef]
- Artyukov, I.A.; Zayarniy, D.A.; Ionin, A.A.; Kudryashov, S.I.; Makarov, S.V.; Saltuganov, P.N. Relaxation phenomena in electronic and lattice subsystems on iron surface during its ablation by ultrashort laser pulses. JETP Lett. 2014, 99, 51–55. [Google Scholar] [CrossRef]
- Wang, S.Y.; Ren, Y.; Cheng, C.W.; Chen, J.K.; Tzou, D.Y. Micromachining of copper by femtosecond laser pulses. Appl. Surf. Sci. 2013, 265, 302–308. [Google Scholar] [CrossRef]
- Cheng, C.W.; Wang, S.Y.; Chang, K.P.; Chen, J.K. Femtosecond laser ablation of copper at high laser fluence: Modeling and experimental comparison. Appl. Surf. Sci. 2016, 361, 41–48. [Google Scholar] [CrossRef]
- Lehane, C.; Kwok, H.S. Enhanced drilling using a dual-pulse Nd:YAG laser. Appl. Phys. A 2001, 73, 45–48. [Google Scholar] [CrossRef]
- Forsman, A.C.; Banks, P.S.; Perry, M.D.; Campbell, E.M.; Dodell, A.L.; Armas, M.S. Double-pulse machining as a technique for the enhancement of material removal rates in laser machining of metals. J. Appl. Phys. 2005, 98, 033302. [Google Scholar] [CrossRef]
- Wang, X.D.; Michalowski, A.; Walter, D.; Sommer, S.; Kraus, M.; Liu, J.S.; Dausinger, F. Laser drilling of stainless steel with nanosecond double-pulse. Opt. Laser Technol. 2009, 41, 148–153. [Google Scholar] [CrossRef]
- Semerok, A.; Dutouquet, C. Ultrashort double pulse laser ablation of metals. Thin Solid Films 2004, 453, 501–505. [Google Scholar] [CrossRef]
- Noël, S.; Hermann, J. Reducing nanoparticles in metal ablation plumes produced by two delayed short laser pulses. Appl. Phys. Lett. 2009, 94, 053120. [Google Scholar] [CrossRef]
- Amoruso, S.; Bruzzese, R.; Wang, X.; O’Connell, G.; Lunney, J.G. Multidiagnostic analysis of ultrafast laser ablation of metals with pulse pair irradiation. J. Appl. Phys. 2010, 108, 113302. [Google Scholar] [CrossRef]
- Liebig, C.; Srisungsitthisunti, P.; Weiner, A.M.; Xu, X. Enhanced machining of steel using femtosecond pulse pairs. Appl. Phys. A 2010, 101, 487–490. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Kapeliovich, B.L.; Perel’man, T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. J. Exp. Theor. Phys. 1974, 39, 375–377. [Google Scholar]
- Chen, J.K.; Beraun, J.E. Numerical study of ultrashort laser pulse interactions with metal films. Numer. Heat Transf. Part A 2001, 40, 1–20. [Google Scholar]
- Ren, Y.; Chen, J.K.; Zhang, Y. Optical properties and thermal response of copper films induced by ultrashort-pulsed lasers. J. Appl. Phys. 2011, 110, 113102. [Google Scholar] [CrossRef]
- Lin, Z.; Zhigilei, L.V.; Celli, V. Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Phys. Rev. B 2008, 77, 075133. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.O. Supersonic Flow and Shock Waves; Interscience Publishers: New York, NY, USA, 1976. [Google Scholar]
- Ionin, A.A.; Kudryashov, S.I.; Makarov, S.V.; Seleznev, L.V.; Sinitsyn, D.V. Generation and detection of superstrong shock waves during ablation of an aluminum surface by intense femtosecond laser pulses. JETP Lett. 2011, 94, 34–38. [Google Scholar] [CrossRef]
- Ren, Y.; Cheng, C.W.; Chen, J.K.; Zhang, Y.; Tzou, D.Y. Thermal ablation of metal films by femtosecond laser bursts. Int. J. Therm. Sci. 2013, 70, 32–40. [Google Scholar] [CrossRef]
- Kelly, R.; Miotello, A. Comments on explosive mechanisms of laser sputtering. Appl. Surf. Sci. 1996, 96–98, 205–215. [Google Scholar] [CrossRef]
- Hess, H. Critical data and vapor pressures of aluminium and copper. Z. Metallkunde 1998, 89, 388–393. [Google Scholar]
- Huang, J.; Zhang, Y.; Chen, J.K. Superheating in liquid and solid phases during femtosecond-laser pulse interaction with thin metal film. Appl. Phys. A 2011, 103, 113–121. [Google Scholar] [CrossRef]
- Sandhu, A.S.; Dharmadhikari, A.K.; Kumar, G.R. Time resolved evolution of structural, electrical, and thermal properties of copper irradiated by an intense ultrashort laser pulse. J. Appl. Phys. 2005, 97, 023526. [Google Scholar] [CrossRef]
- Roberts, D.E.; Plessis, A.d.; Botha, L.R. Femtosecond laser ablation of silver foil with single and double pulses. Appl. Surf. Sci. 2010, 256, 1784–1792. [Google Scholar] [CrossRef]



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.-W.; Chen, J.-K. Drilling of Copper Using a Dual-Pulse Femtosecond Laser. Technologies 2016, 4, 7. https://doi.org/10.3390/technologies4010007
Cheng C-W, Chen J-K. Drilling of Copper Using a Dual-Pulse Femtosecond Laser. Technologies. 2016; 4(1):7. https://doi.org/10.3390/technologies4010007
Chicago/Turabian StyleCheng, Chung-Wei, and Jinn-Kuen Chen. 2016. "Drilling of Copper Using a Dual-Pulse Femtosecond Laser" Technologies 4, no. 1: 7. https://doi.org/10.3390/technologies4010007
APA StyleCheng, C.-W., & Chen, J.-K. (2016). Drilling of Copper Using a Dual-Pulse Femtosecond Laser. Technologies, 4(1), 7. https://doi.org/10.3390/technologies4010007




