3D Localization of Near-Field Sources with Symmetric Enhanced Nested Arrays
Abstract
1. Introduction
- •
- A SENA array is proposed, which unfolds the nested array and introduces central symmetry, facilitating the elimination nonlinear range-related information inherent in the phase component of the steering matrix for NF signals. An analysis of the SENA array’s properties is provided, followed by a proposal of the optimal virtual array parameter configuration for the proposed SENA array.
- •
- The FOC calculation is applied to the SENA array’s output, which is vectorized to expand the virtual array aperture, enhancing the parameter estimation performance. Simulation results demonstrate the proposed algorithm’s superiority in parameter estimation accuracy and its abilities in underdetermined and mixed source estimation.
2. Signal Model
3. Proposed Algorithm
3.1. Construction of Virtual FF Data
3.2. 2D Angle Estimation
3.3. 2D Angle Pairing
3.4. Range Estimation
4. Property Analysis of the Proposed Array
4.1. Total Elements of Virtual Array
4.2. Design Optimization of Virtual Aperture
4.3. Complexity Analysis
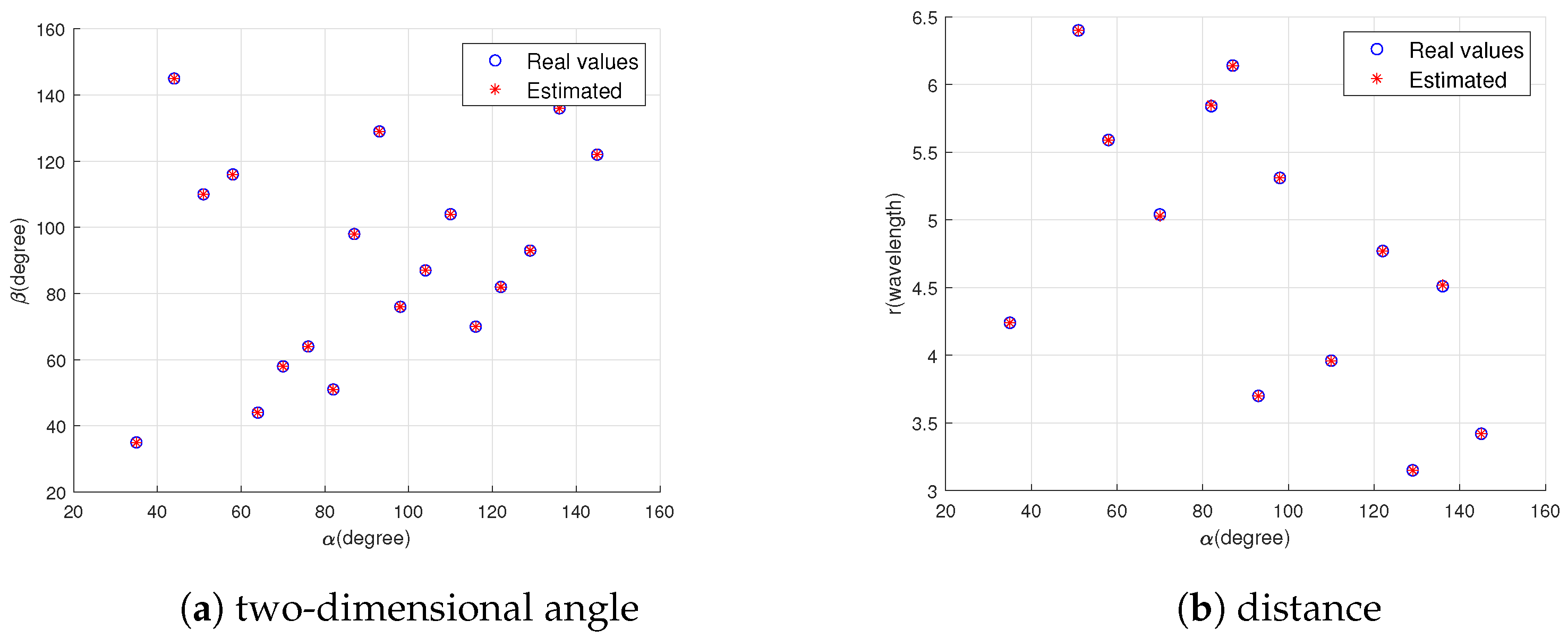
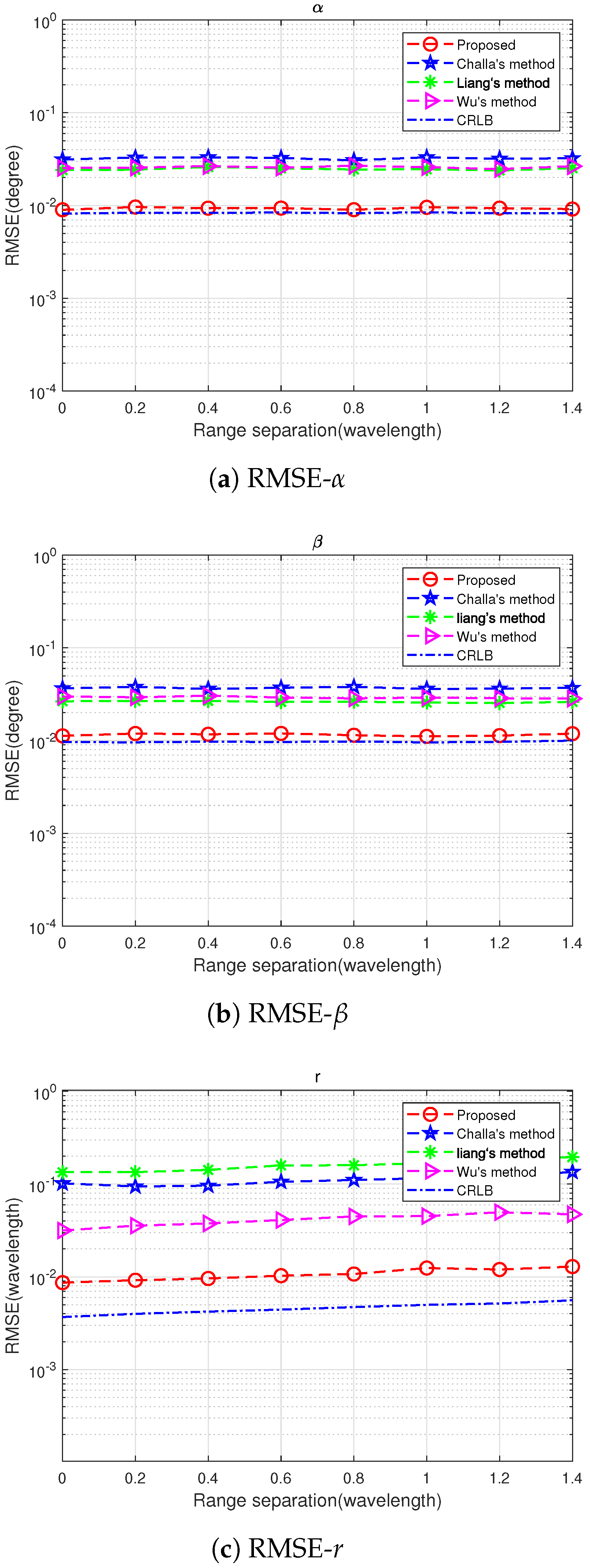
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Levy-Israel, M.; Bilik, I.; Tabrikian, J. MCRB on DOA Estimation for Automotive MIMO Radar in the Presence of Multipath. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4831–4843. [Google Scholar] [CrossRef]
- Sorkhabi, S.E.; Rambabu, K. Multi-Target DoA Estimation with mmWave MIMO Radar using Limited Number of Sensors. IEEE Trans. Veh. Technol. 2025, 1–13. [Google Scholar] [CrossRef]
- Pote, R.R.; Rao, B.D. Maximum Likelihood-Based Gridless DoA Estimation Using Structured Covariance Matrix Recovery and SBL With Grid Refinement. IEEE Trans. Signal Process. 2023, 71, 802–815. [Google Scholar] [CrossRef]
- Sakhnini, A.; Bourdoux, A.; Pollin, S. Estimation of Array Locations, Orientations, Timing Offsets and Target Locations in Bistatic Radars. IEEE Trans. Radar Syst. 2023, 1, 520–531. [Google Scholar] [CrossRef]
- Chen, H.; Fang, J.; Wang, W.; Liu, W.; Tian, Y.; Wang, Q.; Wang, G. Near-Field Target Localization for EMVS-MIMO Radar With Arbitrary Configuration. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 5406–5417. [Google Scholar] [CrossRef]
- Shamsian, M.R.; Sadeghi, M.; Behnia, F. Joint TDOA and DOA Single Site Localization in NLOS Environment Using Virtual Stations. IEEE Trans. Instrum. Meas. 2024, 73, 5500710. [Google Scholar] [CrossRef]
- Yuan, S.; Fioranelli, F.; Yarovoy, A.G. Vehicular-Motion-Based DOA Estimation With a Limited Amount of Snapshots for Automotive MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7611–7625. [Google Scholar] [CrossRef]
- He, J.; Swamy, M.N.S.; Ahmad, M.O. Efficient Application of MUSIC Algorithm Under the Coexistence of Far-Field and Near-Field Sources. IEEE Trans. Signal Process. 2012, 60, 2066–2070. [Google Scholar] [CrossRef]
- Liang, J.; Liu, D. Passive Localization of Mixed Near-Field and Far-Field Sources Using Two-stage MUSIC Algorithm. IEEE Trans. Signal Process. 2010, 58, 108–120. [Google Scholar] [CrossRef]
- Zhi, W.; Chia, M.Y.W. Near-Field Source Localization via Symmetric Subarrays. IEEE Signal Process. Lett. 2007, 14, 409–412. [Google Scholar] [CrossRef]
- Xie, J.; Tao, H.; Rao, X.; Su, J. Efficient Method of Passive Localization for Near-Field Noncircular Sources. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1223–1226. [Google Scholar] [CrossRef]
- Yan, H.; Chen, H.; Liu, W.; Yang, S.; Wang, G.; Yuen, C. RIS-Enabled Joint Near-Field 3D Localization and Synchronization in SISO Multipath Environments. IEEE Trans. Green Commun. Netw. 2025, 9, 367–379. [Google Scholar] [CrossRef]
- Wu, X. Localization of far-field and near-field signals with mixed sparse approach: A generalized symmetric arrays perspective. Signal Process. 2020, 175, 107665. [Google Scholar] [CrossRef]
- Guo, H.; Chen, H.; Liu, W.; Yang, S.; Yuen, C.; So, H.C. Third-Order Sum-Difference Expansion: An Array Extension Strategy Based on Third-Order Cumulants. IEEE Trans. Signal Process. 2025, 73, 2099–2109. [Google Scholar] [CrossRef]
- Leite, W.S.; Lamare, R.C.d.; Zakharov, Y.; Liu, W.; Haardt, M. Direction Finding With Sparse Subarrays: Design, Algorithms, and Analysis. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8149–8165. [Google Scholar] [CrossRef]
- Chen, H.; Lin, H.; Liu, W.; Wang, Q.; Shen, Q.; Wang, G. Augmented Multi-Subarray Dilated Nested Array With Enhanced Degrees of Freedom and Reduced Mutual Coupling. IEEE Trans. Signal Process. 2024, 72, 1387–1399. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing With Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing With Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Kulkarni, P.; Vaidyanathan, P.P. Weight-Constrained Sparse Arrays For Direction of Arrival Estimation Under High Mutual Coupling. IEEE Trans. Signal Process. 2024, 72, 4444–4462. [Google Scholar] [CrossRef]
- Sarangi, P.; Hücümenoğlu, M.C.; Rajamäki, R.; Pal, P. Super-Resolution With Sparse Arrays: A Nonasymptotic Analysis of Spatiotemporal Trade-Offs. IEEE Trans. Signal Process. 2023, 71, 4288–4302. [Google Scholar] [CrossRef]
- Chen, Y.P.; Liu, C.L. Half-Inverted Array Design Scheme for Large Hole-Free Fourth-Order Difference Co-Arrays. IEEE Trans. Signal Process. 2023, 71, 3296–3311. [Google Scholar] [CrossRef]
- Patra, R.K. A Novel Third-Order Nested Array for DOA Estimation With Increased Degrees of Freedom. IEEE Signal Process. Lett. 2025, 32, 1475–1479. [Google Scholar] [CrossRef]
- Shaikh, A.H.; Liu, X. Super Fragmented Coprime Arrays for DOA Estimation. IEEE Signal Process. Lett. 2025, 32, 1825–1829. [Google Scholar] [CrossRef]
- S., J.; Yadav, S.K.; George, N.V. Coarray LMS: Adaptive Underdetermined DOA Estimation With Increased Degrees of Freedom. IEEE Signal Process. Lett. 2024, 31, 591–595. [Google Scholar] [CrossRef]
- Sheng, X.; Lu, D.; Li, Y.; de Lamare, R.C. Enhanced MISC-Based Sparse Array With High uDOFs and Low Mutual Coupling. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 972–976. [Google Scholar] [CrossRef]
- Chen, H.; Guo, H.; Liu, W.; Shen, Q.; Wang, G.; So, H.C. Fourth-Order Sparse Array Design From a Sum-Difference Co-Array Perspective. IEEE Trans. Signal Process. 2025, 73, 2243–2254. [Google Scholar] [CrossRef]
- Ebadi, Z.; Molaei, A.M.; Alexandropoulos, G.C.; Abbasi, M.A.B.; Cotton, S.; Tukmanov, A.; Yurduseven, O. Near-Field Localization With Antenna Arrays in the Presence of Direction-Dependent Mutual Coupling. IEEE Trans. Veh. Technol. 2025, 74, 7033–7048. [Google Scholar] [CrossRef]
- Gast, A.; Le Magoarou, L.; Shlezinger, N. DCD-MUSIC: Deep-Learning-Aided Cascaded Differentiable MUSIC Algorithm for Near-Field Localization of Multiple Sources. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Fang, J.; Chen, H.; Liu, W.; Yang, S.; Yuen, C.; So, H.C. Three-Dimensional Localization of Mixed Near-Field and Far-Field Sources Based on a Unified Exact Propagation Model. IEEE Trans. Signal Process. 2025, 73, 245–258. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, M.; Wang, W.Q.; Zhang, S.; Liao, Y. Localization of Mixed Near-Field and Far-Field Sources Using Symmetric Double-Nested Arrays. IEEE Trans. Antennas Propag. 2019, 67, 7059–7070. [Google Scholar] [CrossRef]
- Wu, X.; Yan, J. A Second-Order Statistics-Based Mixed Sources Localization Method With Symmetric Sparse Arrays. IEEE Commun. Lett. 2020, 24, 1695–1699. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, X.; Jin, X.; Hou, Y. Near-field Source Location Estimation Algorithm Based on Coprime Array. In Proceedings of the 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, Chian, 25–27 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Su, X.; Hu, P.; Liu, Z.; Liu, T.; Peng, B.; Li, X. Mixed Near-Field and Far-Field Source Localization Based On Convolution Neural Networks via Symmetric Nested Array. IEEE Trans. Veh. Technol. 2021, 70, 7908–7920. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, M.; Wang, W.Q.; So, H.C. Symmetric Displaced Coprime Array Configurations for Mixed Near- and Far-Field Source Localization. IEEE Trans. Antennas Propag. 2021, 69, 465–477. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W.P. Single Far-Field or Near-Field Source Localization With Sparse or Uniform Cross Array. IEEE Trans. Veh. Technol. 2020, 69, 9135–9139. [Google Scholar] [CrossRef]
- Wu, X.; Yan, J. 3-D Mixed Far-Field and Near-Field Sources Localization With Cross Array. IEEE Trans. Veh. Technol. 2020, 69, 6833–6837. [Google Scholar] [CrossRef]
- Challa, R.N.; Shamsunder, S. Passive near-field localization of multiple non-Gaussian sources in 3-D using cumulants. Signal Process. 1998, 65, 39–53. [Google Scholar] [CrossRef]
- Chen, H.; Yi, Z.; Jiang, Z.; Liu, W.; Tian, Y.; Wang, Q.; Wang, G. Spatial-temporal-based Underdetermined Near-field 3-D Localization Employing a Nonuniform Cross Array. IEEE J. Sel. Top. Signal Process. 2024, 18, 561–571. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. A Discretization-Free Sparse and Parametric Approach for Linear Array Signal Processing. IEEE Trans. Signal Process. 2014, 62, 4959–4973. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Liu, W. Joint DOA, Range, and Polarization Estimation for Rectilinear Sources With a COLD Array. IEEE Wirel. Commun. Lett. 2019, 8, 1398–1401. [Google Scholar] [CrossRef]



| Proposed Method |
|---|
| Step 1 Construct the virtually extended receiving matrix using Equation (8). |
| Step 2 Obtain the noise free covariance matrix using Equation (13). |
| Step 3 Obtain estimated values and of angle parameters using the root MUSIC algorithm and Equation (3). |
| Step 4 Pair the electrical angles and through Equation (17). |
| Step 5 Construct received data containing only range information using Equation (22). |
| Step 6 Based on the MUSIC algorithm, for each execution, the distance parameter is obtained. |
| Number of Array Elements | Virtual Array Aperture | |||||
|---|---|---|---|---|---|---|
| even | even | all odd | ||||
| even | even | all even | ||||
| even | odd | all odd | ||||
| even | odd | all even | ||||
| odd | one odd, one even |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Wu, H.; Meng, H.; Zhou, Z.; Chen, H. 3D Localization of Near-Field Sources with Symmetric Enhanced Nested Arrays. Technologies 2025, 13, 415. https://doi.org/10.3390/technologies13090415
Yu L, Wu H, Meng H, Zhou Z, Chen H. 3D Localization of Near-Field Sources with Symmetric Enhanced Nested Arrays. Technologies. 2025; 13(9):415. https://doi.org/10.3390/technologies13090415
Chicago/Turabian StyleYu, Linke, Huayue Wu, Haifen Meng, Zheng Zhou, and Hua Chen. 2025. "3D Localization of Near-Field Sources with Symmetric Enhanced Nested Arrays" Technologies 13, no. 9: 415. https://doi.org/10.3390/technologies13090415
APA StyleYu, L., Wu, H., Meng, H., Zhou, Z., & Chen, H. (2025). 3D Localization of Near-Field Sources with Symmetric Enhanced Nested Arrays. Technologies, 13(9), 415. https://doi.org/10.3390/technologies13090415






