Using Solar Sails to Rendezvous with Asteroid 2024 YR4
Abstract
1. Introduction
- the numerical investigation of optimal performance, in terms of global minimum flight time, for orbit-to-orbit heliocentric transfers as a function of the sailcraft’s propulsive characteristics, namely its reference acceleration value;
- the analysis of potential rapid rendezvous trajectories constrained by actual planetary ephemerides, in which the launch date spans a time interval of approximately 10 years and the sailcraft’s propulsive characteristics are consistent with those considered in the previous point.
2. Numerical Results for Sailcraft Transfer Scenarios
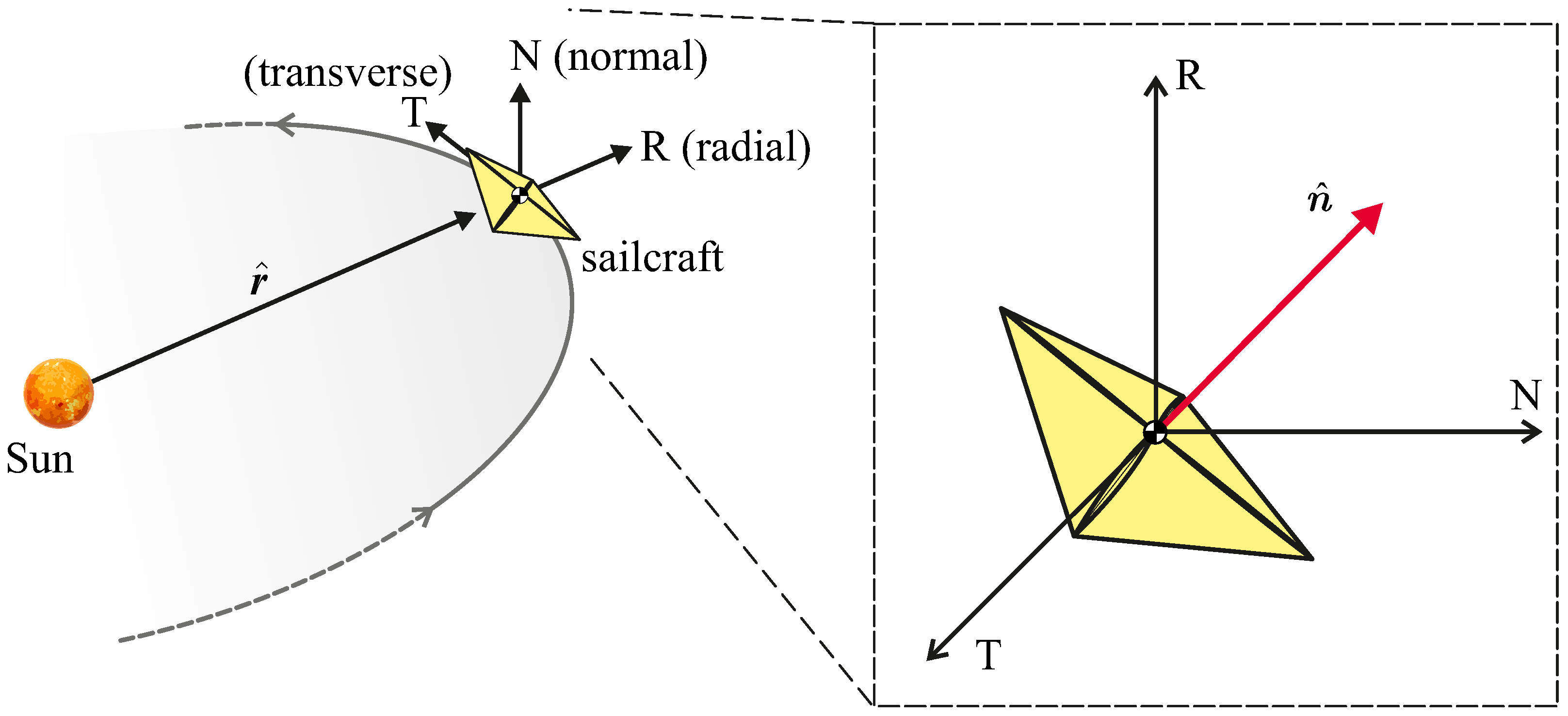
2.1. Thrust Vector Modeling and Trajectory Computation
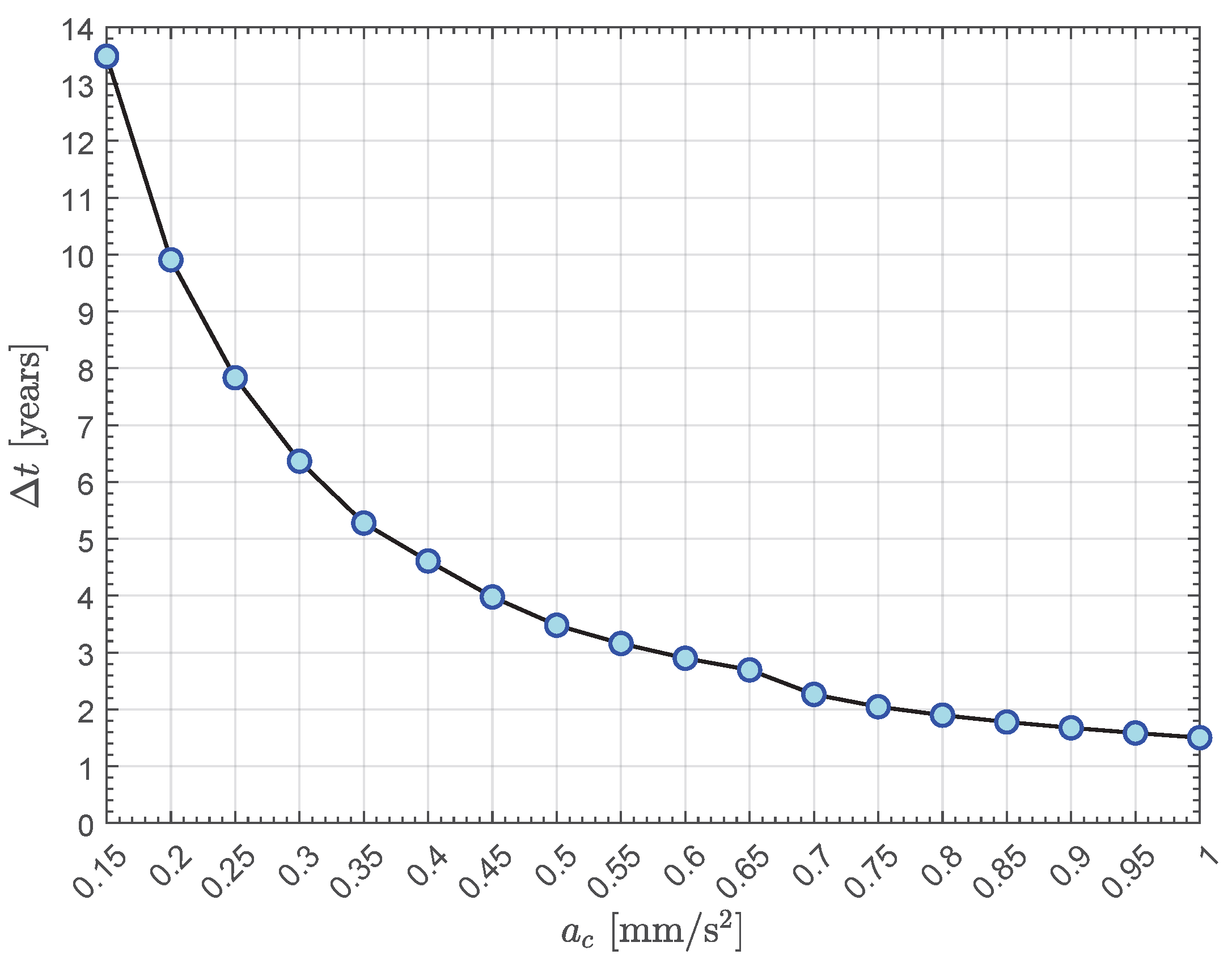
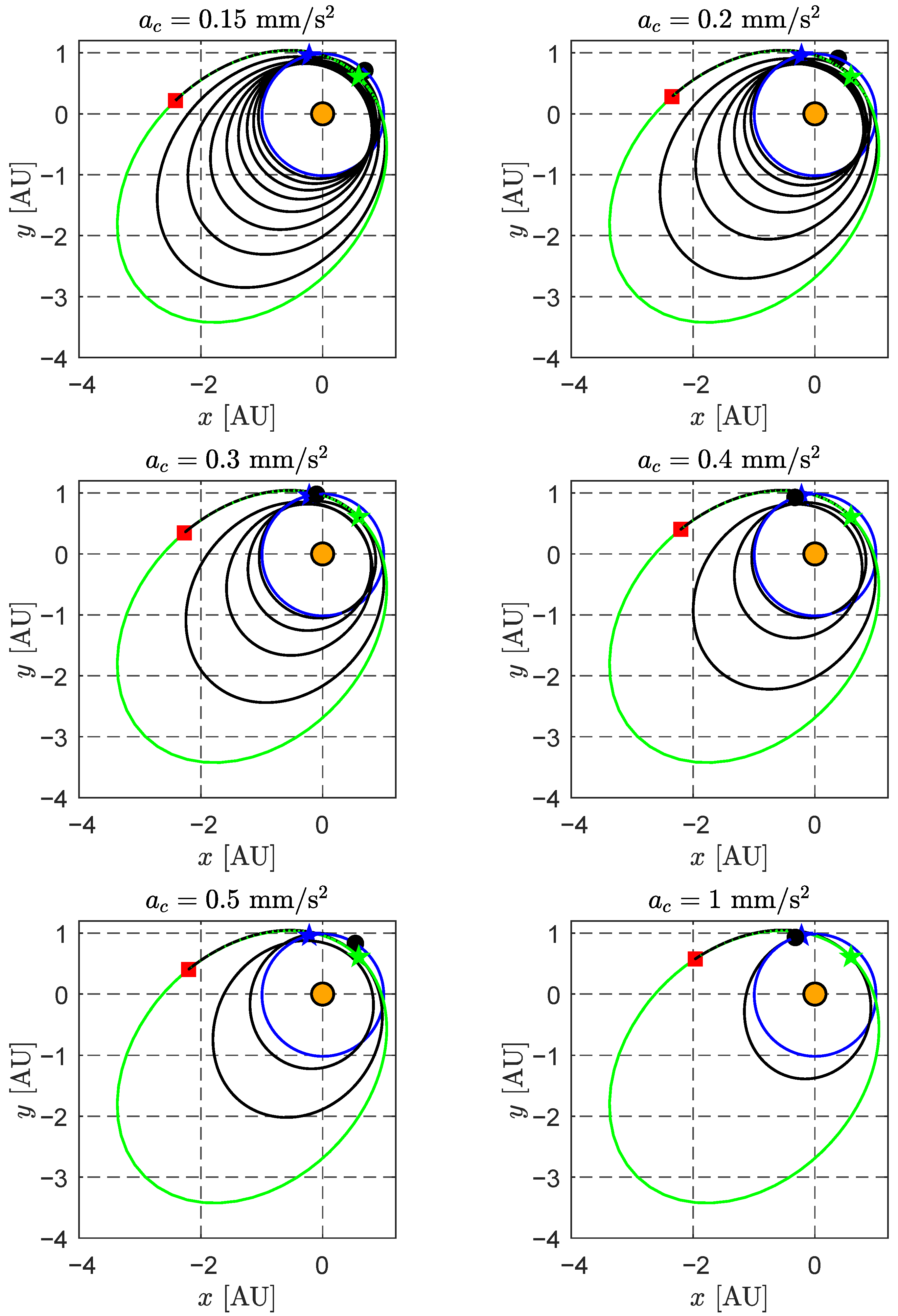
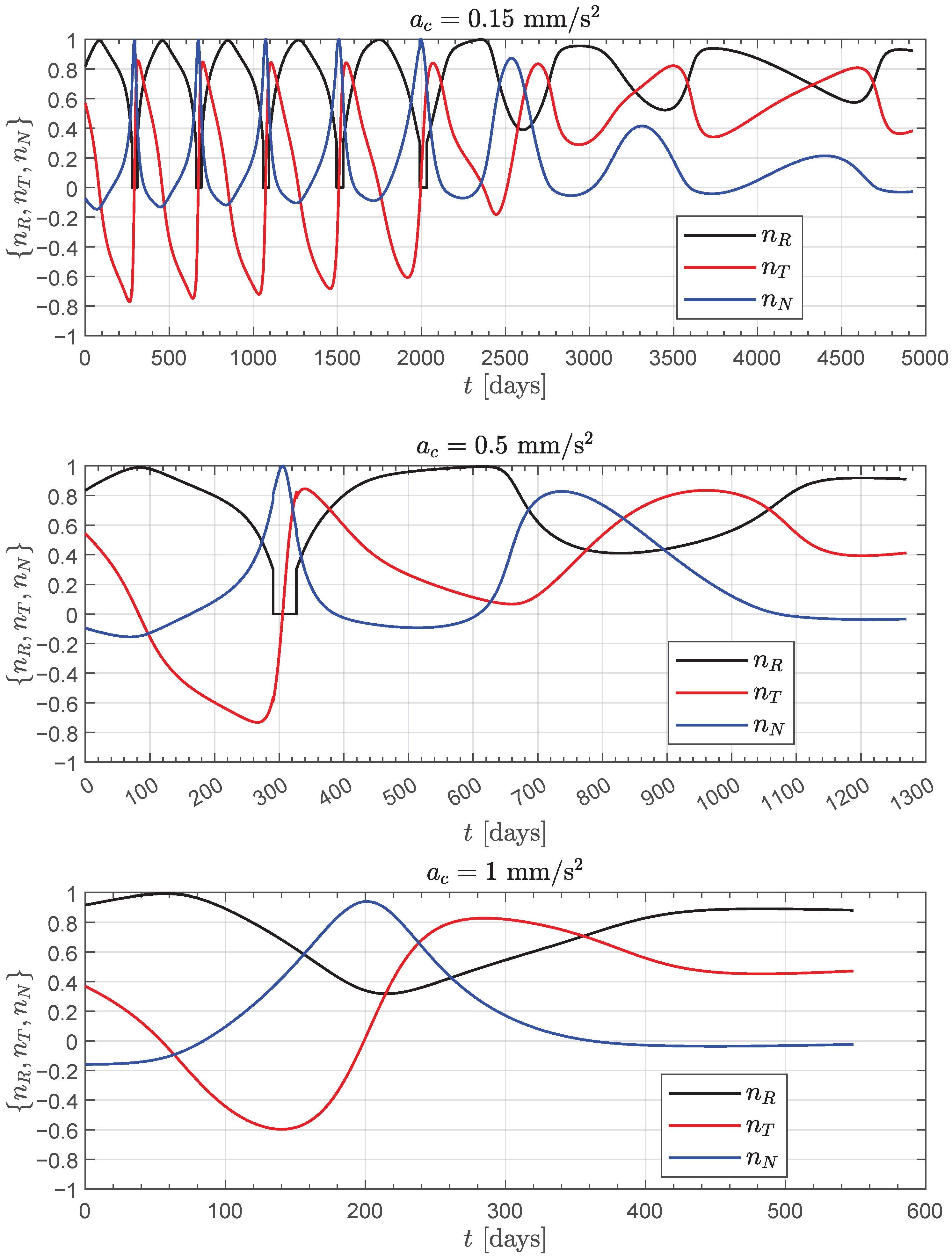
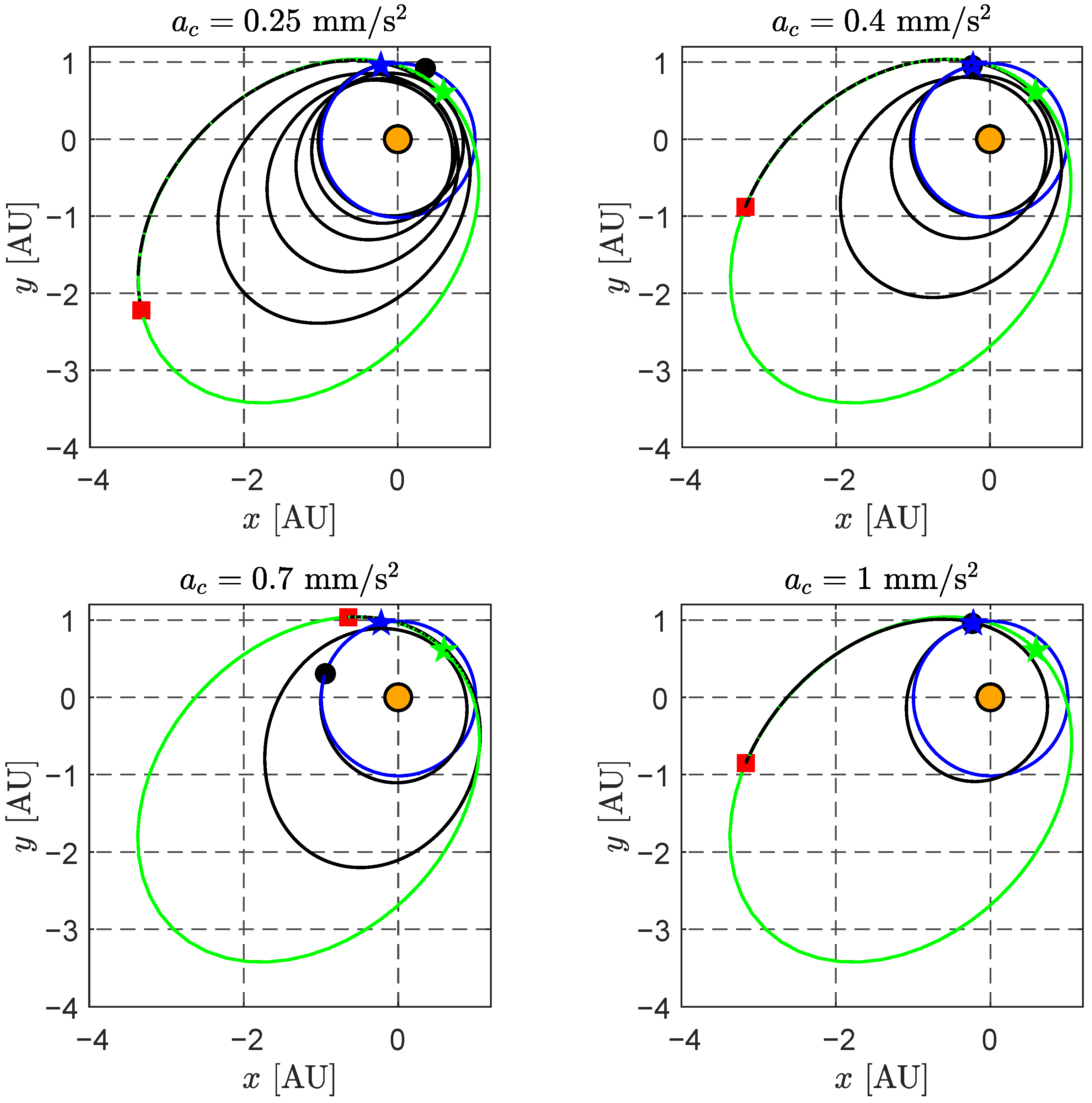
2.2. Optimized Trajectories in the EFT Scenario
2.3. Optimized Trajectories in the ECT Scenario
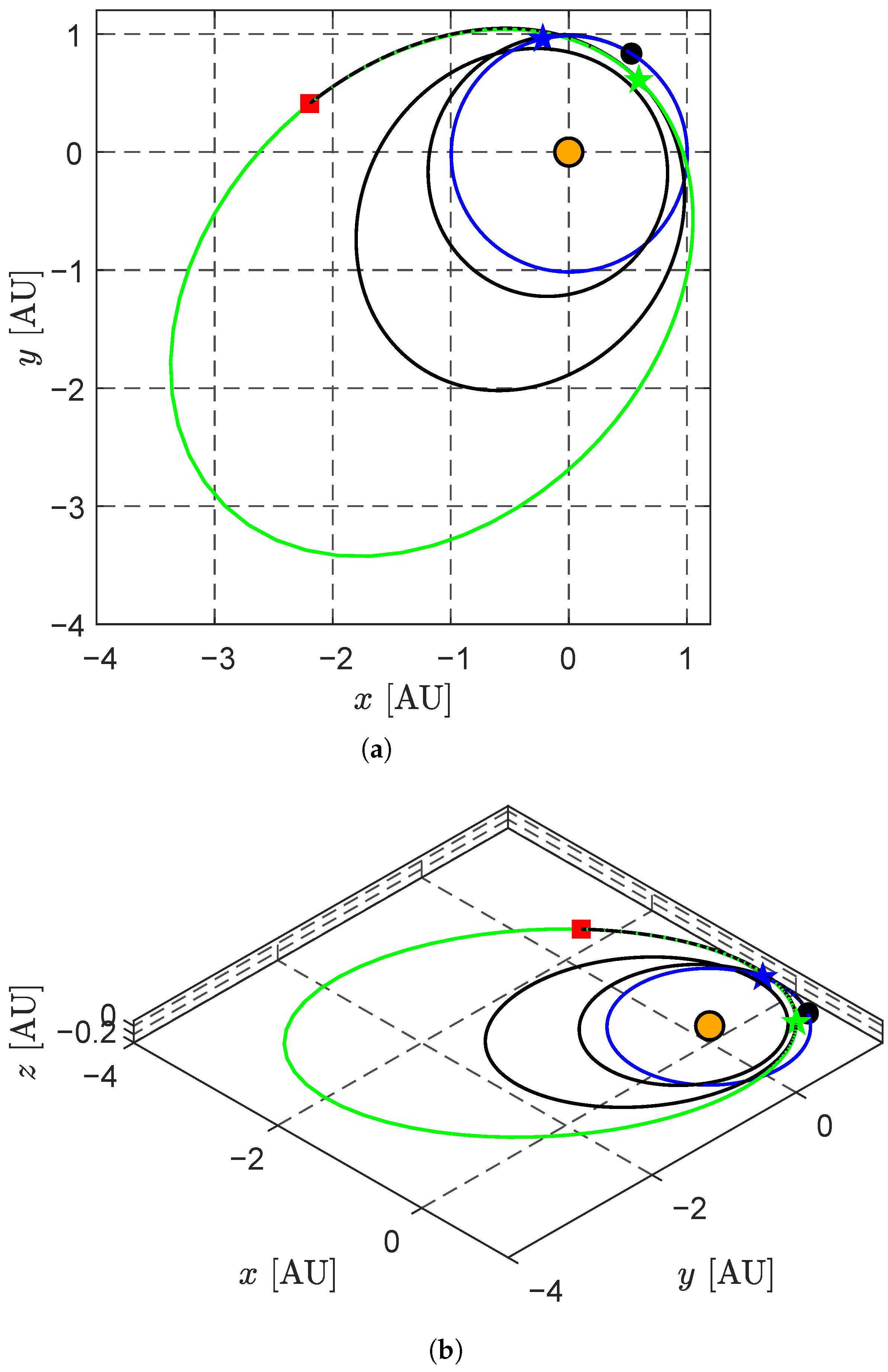
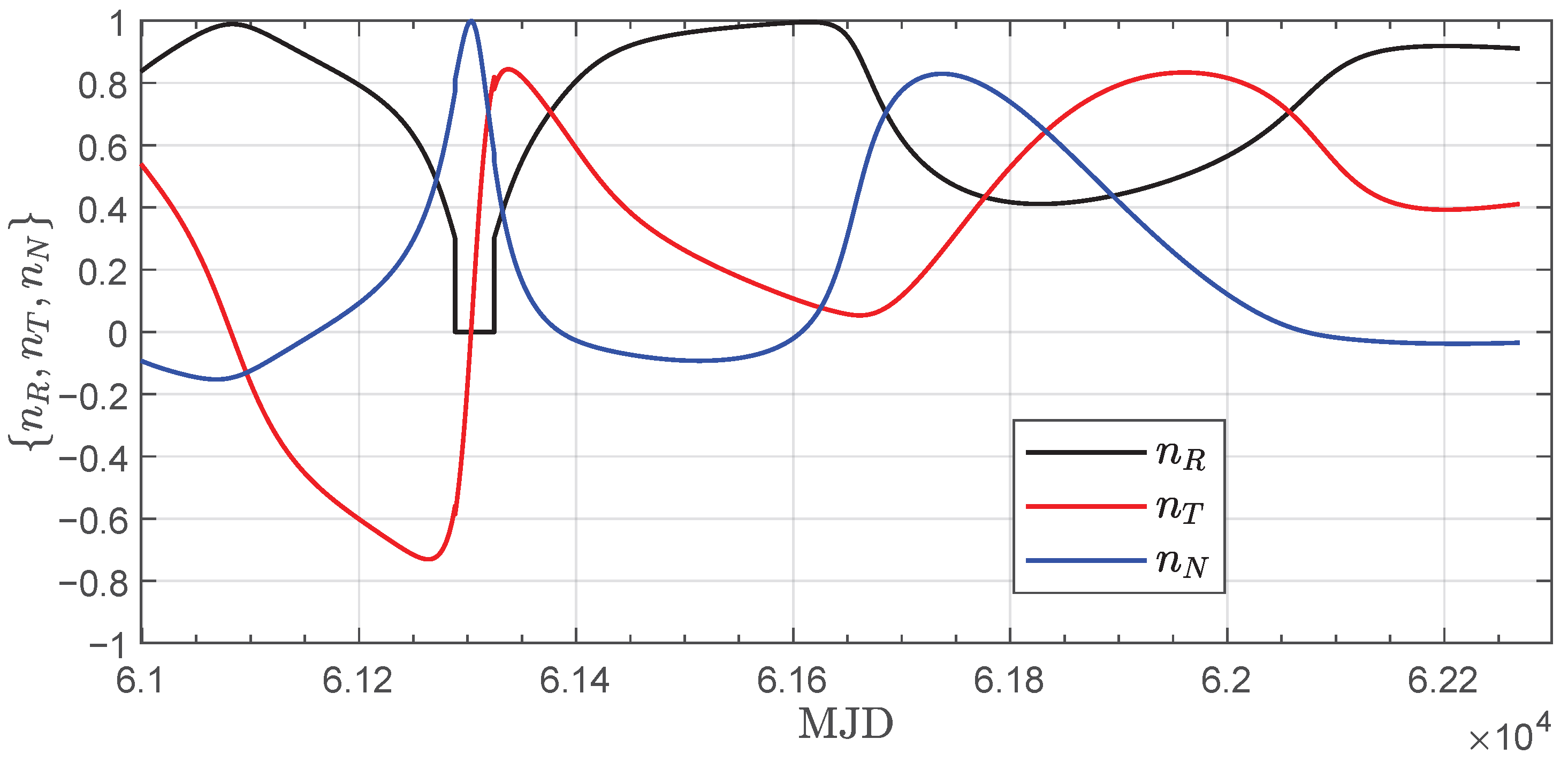
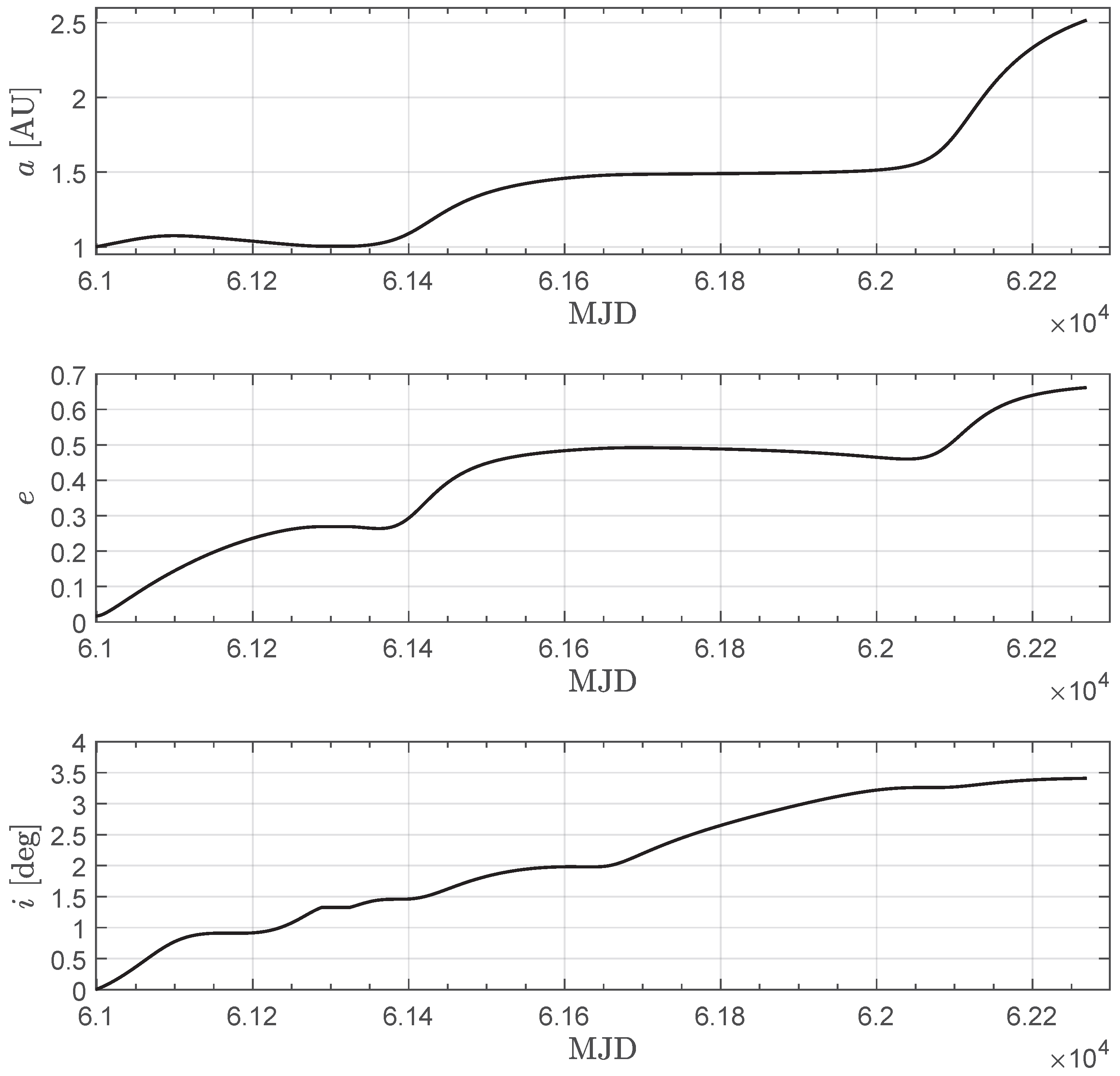
2.4. Representative Mission Scenario
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| ACS3 | Advanced Composite Solar Sail System |
| ECT | ephemeris-constrained transfer |
| EFT | ephemeris-free transfer |
| IKAROS | Interplanetary Kite-craft Accelerated by Radiation Of the Sun |
| JAXA | Japan Aerospace Exploration Agency |
| JPL | Jet Propulsion Laboratory |
| MEOE | modified equinoctial orbit element |
| MJD | modified Julian date |
| NASA | National Aeronautics and Space Administration |
| PHA | Potentially Hazardous Asteroid |
| RTN | radial-transverse-normal orbital reference frame |
| sailcraft | solar sail-propelled spacecraft |
| a | semimajor axis [AU] |
| characteristic acceleration [mm/s] | |
| propulsive acceleration vector [mm/s] | |
| vector; see Equation (A6) | |
| e | eccentricity |
| i | orbital inclination [deg] |
| M | mean anomaly [deg] |
| matrix; see Equation (A6) | |
| N | number of complete revolutions around the Sun |
| normal unit vector | |
| normal component of | |
| radial component of | |
| transverse component of | |
| modified equinoctial orbit elements | |
| sailcraft’s position vector [AU] | |
| radial unit vector | |
| r | Sun-sailcraft distance [AU] |
| t | time [days] |
| sailcraft’s velocity vector [km/s] | |
| minimum flight time [days] | |
| true anomaly [deg] | |
| adjoint vector | |
| argument of perihelion [deg] | |
| right ascension of the ascending node [deg] | |
| Subscripts | |
| 0 | initial |
| f | final |
| Superscripts | |
| ★ | optimal value |
| · | temporal derivative |
| ∧ | unit vector |
Appendix A
References
- Vichi, V.; Tommei, G. Exploring the potential of neural networks in early detection of potentially hazardous near-earth objects. Celest. Mech. Dyn. Astron. 2025, 137, 17. [Google Scholar] [CrossRef]
- Lay, O.; Masiero, J.; Grav, T.; Mainzer, A.; Masci, F.; Wright, E. Asteroid Impact Hazard Warning from the Near-Earth Object Surveyor Mission. Planet. Sci. J. 2024, 5, 149. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, R.; Gao, Y. Trajectory Design of Potentially Hazardous Asteroid Exploration with Reusable Probes from Cislunar Space. Aerospace 2024, 11, 546. [Google Scholar] [CrossRef]
- Sears, D.W.G. The Explored Asteroids: Science and Exploration in the Space Age. Space Sci. Rev. 2015, 194, 139–235. [Google Scholar] [CrossRef]
- Vardaxis, G.; Wie, B. Near-Earth object intercept trajectory design for planetary defense. Acta Astronaut. 2014, 101, 1–15. [Google Scholar] [CrossRef]
- Aslani Khiavi, S.; Jafari-Nadoushan, M. Efficient approach of painting asteroids for planetary defense using network data envelopment analysis. Adv. Space Res. 2025, 75, 3230–3241. [Google Scholar] [CrossRef]
- Bolin, B.T.; Hanuš, J.; Denneau, L.; Bonamico, R.; Abron, L.M.; Delbo, M.; Ďurech, J.; Jedicke, R.; Alcorn, L.Y.; Cikota, A.; et al. The Discovery and Characterization of Earth-crossing Asteroid 2024 YR4. Astrophys. J. Lett. 2025, 984, L25. [Google Scholar] [CrossRef]
- Binzel, R.P. The Torino Impact Hazard Scale. Planet. Space Sci. 2000, 48, 297–303. [Google Scholar] [CrossRef]
- Smirnov, E.A. Chaotic diffusion and transient resonance captures of the near-Earth asteroid 2024 YR4. Astron. Astrophys. 2025, 699, A26. [Google Scholar] [CrossRef]
- Reddy, V.; Kelley, M.S.; Dotson, J.; Farnocchia, D.; Erasmus, N.; Polishook, D.; Masiero, J.; Benner, L.A.M.; Bauer, J.; Alarcon, M.R.; et al. Apophis Planetary Defense Campaign. Planet. Sci. J. 2022, 3, 123. [Google Scholar] [CrossRef]
- Norwood, J.; Hammel, H.; Milam, S.; Stansberry, J.; Lunine, J.; Chanover, N.; Hines, D.; Sonneborn, G.; Tiscareno, M.; Brown, M.; et al. Solar System Observations with theJames Webb Space Telescope. Publ. Astron. Soc. Pac. 2016, 128, 025004. [Google Scholar] [CrossRef]
- Rivkin, A.S.; Marchis, F.; Stansberry, J.A.; Takir, D.; Thomas, C. Asteroids and the James Webb Space Telescope. Publ. Astron. Soc. Pac. 2016, 128, 018003. [Google Scholar] [CrossRef]
- Thomas, C.A.; Abell, P.; Castillo-Rogez, J.; Moskovitz, N.; Mueller, M.; Reddy, V.; Rivkin, A.; Ryan, E.; Stansberry, J. Observing Near-Earth Objects with the James Webb Space Telescope. Publ. Astron. Soc. Pac. 2016, 128, 018002. [Google Scholar] [CrossRef]
- Morelli, A.C.; Mannocchi, A.; Giordano, C.; Ferrari, F.; Topputo, F. Initial Trajectory Assessment of a low-thrust option for the RAMSES Mission to (99942) Apophis. Adv. Space Res. 2024, 73, 4241–4253. [Google Scholar] [CrossRef]
- Megia, V.H.; Ho, T.M.; Grundmann, J.T.; Noeker, M. Modeling and control techniques for landing on (99942) Apophis: An analysis of a mission scenario. Acta Astronaut. 2025, 235, 185–194. [Google Scholar] [CrossRef]
- Izzo, D. Optimization of Interplanetary Trajectories for Impulsive and Continuous Asteroid Deflection. J. Guid. Control Dyn. 2007, 30, 401–408. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Rapid Solar Sail Rendezvous Missions to Asteroid 99942 Apophis. J. Spacecr. Rocket. 2009, 46, 134–140. [Google Scholar] [CrossRef]
- Foster, C.; Bellerose, J.; Mauro, D.; Jaroux, B. Mission concepts and operations for asteroid mitigation involving multiple gravity tractors. Acta Astronaut. 2013, 90, 112–118. [Google Scholar] [CrossRef]
- Quarta, A.A. Thrust model and trajectory design of an interplanetary CubeSat with a hybrid propulsion system. Actuators 2024, 13, 384. [Google Scholar] [CrossRef]
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Gong, S.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Tsuda, Y.; Mori, O.; Funase, R.; Sawada, H.; Yamamoto, T.; Saiki, T.; Endo, T.; Yonekura, K.; Hoshino, H.; Kawaguchi, J. Achievement of IKAROS—Japanese deep space solar sail demonstration mission. Acta Astronaut. 2013, 82, 183–188. [Google Scholar] [CrossRef]
- Funase, R.; Kawaguchi, J.; Mori, O.; Sawada, H.; Tsuda, Y. IKAROS, A solar sail demonstrator and its application to trojan asteroid exploration. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Minervino Amodio, A.; Visser, P.; Heiligers, J. Dynamical modelling of NASA’s ACS3 solar sail mission. Aerosp. Sci. Technol. 2025, 161, 110146. [Google Scholar] [CrossRef]
- Wilkie, W.K.; Fernandez, J.M.; Stohlman, O.R.; Schneider, N.R.; Dean, G.D.; Kang, J.H.; Warren, J.E.; Cook, S.M.; Brown, P.L.; Denkins, T.C.; et al. An overview of the NASA advanced composite solar sail (ACS3) technology demonstration project. In Proceedings of the AIAA SciTech Forum, Virtual event, 11–21 January 2021. [Google Scholar] [CrossRef]
- Berthet, M.; Schalkwyk, J.; Çelik, O.; Sengupta, D.; Fujino, K.; Hein, A.M.; Tenorio, L.; Cardoso dos Santos, J.; Worden, S.P.; Mauskopf, P.D.; et al. Space sails for achieving major space exploration goals: Historical review and future outlook. Prog. Aerosp. Sci. 2024, 150, 101047. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, C.; Li, Y. Design and application of solar sailing: A review on key technologies. Chin. J. Aeronaut. 2023, 36, 125–144. [Google Scholar] [CrossRef]
- Pezent, J.B.; Sood, R.; Heaton, A.; Miller, K.; Johnson, L. Preliminary trajectory design for NASA’s Solar Cruiser: A technology demonstration mission. Acta Astronaut. 2021, 183, 134–140. [Google Scholar] [CrossRef]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer: Berlin, Germany, 1999; Chapter 2, pp. 46–53. [Google Scholar] [CrossRef]
- Quarta, A.A.; Abu Salem, K.; Palaia, G. Solar sail transfer trajectory design for comet 29P/Schwassmann-Wachmann 1 rendezvous. Appl. Sci. 2023, 13, 9590. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, Z.; He, G.; Yuan, H. Uncertainty characterization of solar sail thrust with a multiscale modeling method. Adv. Space Res. 2025, 75, 5640–5655. [Google Scholar] [CrossRef]
- Johnson, L.; Akhavan-Tafti, M.; Sood, R.; Szabo, A.; Thomas, H.D. Space Weather Investigation Frontier (SWIFT) Mission Concept: Continuous Distributed Observations of Geo-Effective, Heliospheric Structures from the Vantage Points of Sun-Earth L1 and Sub-L1. In Proceedings of the 75th International Astronautical Congress (IAC), Milan, Italy, 14–18 October 2024. [Google Scholar]
- Johnson, L.; Akhavan-Tafti, M.; Sood, R.; Szabo, A.; Thomas, H.D. Space Weather Investigation Frontier (SWIFT) Mission Concept: Continuous, Distributed Observations of Heliospheric Structures from the Vantage Points of Sun-Earth L1 and Sub-L1. Acta Astronaut. 2025, 236, 684–691. [Google Scholar] [CrossRef]
- Boni, L.; Bassetto, M.; Quarta, A.A. Characterization of a Solar Sail Membrane for Abaqus-Based Simulations. Aerospace 2024, 11, 151. [Google Scholar] [CrossRef]
- Luo, Y.z.; Yang, Z. A review of uncertainty propagation in orbital mechanics. Prog. Aerosp. Sci. 2017, 89, 23–39. [Google Scholar] [CrossRef]
- Niccolai, L.; Anderlini, A.; Mengali, G.; Quarta, A.A. Effects of optical parameter measurement uncertainties and solar irradiance fluctuations on solar sailing. Adv. Space Res. 2021, 67, 2784–2794. [Google Scholar] [CrossRef]
- Bate, R.R.; Mueller, D.D.; White, J.E. Fundamentals of Astrodynamics; Dover Publications: New York, NY, USA, 1971; Chapters 4 & 7, pp. 212–222 & 321–355. ISBN 0-486-60061-0. [Google Scholar]
- Moiseev, Y.A.; Emelyanov, N.V. Ephemeris Theories JPL DE, INPOP, and EPM. Astron. Rep. 2024, 68, 1098–1118. [Google Scholar] [CrossRef]
- Lisse, C.M.; Steckloff, J.K.; Prialnik, D.; Womack, M.; Harrington Pinto, O.; Sarid, G.; Fernandez, Y.R.; Schambeau, C.A.; Kareta, T.; Samarasinha, N.H.; et al. 29P/Schwassmann–Wachmann 1: A Rosetta Stone for Amorphous Water Ice and CO ↔ CO2 Conversion in Centaurs and Comets? Planet. Sci. J. 2022, 3, 251. [Google Scholar] [CrossRef]
- Georgevic, R.M. The solar radiation pressure force and torques model. In Proceedings of the Astrodynamics Specialists Conference, Ft. Lauderdale, FL, USA, 17–19 August 1971. [Google Scholar]
- Mengali, G.; Quarta, A.A. Optimal three-dimensional interplanetary rendezvous using nonideal solar sail. J. Guid. Control Dyn. 2005, 28, 173–177. [Google Scholar] [CrossRef]
- Heaton, A.F.; Artusio-Glimpse, A.B. An Update to the NASA Reference Solar Sail Thrust Model. In Proceedings of the AIAA Space and Astronautics Forum and Exposition (AIAA SPACE 2015), Pasadena, CA, USA, 31 August–2 September 2015. [Google Scholar]
- Stengel, R.F. Optimal Control and Estimation; Dover Books on Mathematics, Dover Publications, Inc.: New York, NY, USA, 1994; pp. 222–254. ISBN 978-0486682006. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Yang, W.Y.; Cao, W.; Kim, J.; Park, K.W.; Park, H.H.; Joung, J.; Ro, J.S.; Hong, C.H.; Im, T. Applied Numerical Methods Using MATLAB; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; Chapter 3 and 6, pp. 158–165, 312. [Google Scholar]
- Spencer, D.A.; Johnson, L.; Long, A.C. Solar sailing technology challenges. Aerosp. Sci. Technol. 2019, 93, 105276. [Google Scholar] [CrossRef]
- Walker, M.J.H.; Ireland, B.; Owens, J. A set of modified equinoctial orbit elements. Celest. Mech. 1985, 36, 409–419, Erratum in Celest. Mech. 1986, 38, 391–392. [Google Scholar] [CrossRef]
- Curtis, H.D. Orbital Mechanics for Engineering Students; Butterworth-Heinemann: Oxford, UK, 2020; Chapter 8, pp. 423–428. ISBN 978-0-08-102133-0. [Google Scholar] [CrossRef]
- Betts, J.T. Very low-thrust trajectory optimization using a direct SQP method. J. Comput. Appl. Math. 2000, 120, 27–40. [Google Scholar] [CrossRef]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: San Francisco, CA, USA, 2015; Chapter 2, pp. 127–129. [Google Scholar]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2, pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]

| Celestial Body | a [AU] | e | i [deg] | [deg] | [deg] | M [deg] |
|---|---|---|---|---|---|---|
| Earth | ||||||
| 2024 YR4 |
| [mm/s] | [Days] | N | [deg] | [deg] |
|---|---|---|---|---|
| 0.15 | 4923 | 8 | 303 | 129 |
| 0.2 | 3616 | 6 | 324 | 127 |
| 0.25 | 2859 | 5 | 7 | 126 |
| 0.3 | 2323 | 4 | 353 | 126 |
| 0.35 | 1926 | 3 | 296 | 127 |
| 0.4 | 1683 | 3 | 7 | 124 |
| 0.45 | 1452 | 2 | 263 | 132 |
| 0.5 | 1270 | 2 | 314 | 124 |
| 0.55 | 1153 | 2 | 350 | 122 |
| 0.6 | 1058 | 2 | 24 | 121 |
| 0.65 | 983 | 1 | 65 | 119 |
| 0.7 | 826 | 1 | 267 | 129 |
| 0.75 | 747 | 1 | 292 | 123 |
| 0.8 | 693 | 1 | 311 | 120 |
| 0.85 | 649 | 1 | 327 | 119 |
| 0.9 | 612 | 1 | 341 | 118 |
| 0.95 | 578 | 1 | 354 | 118 |
| 1 | 548 | 1 | 6 | 118 |
| [mm/s] | [days] | MJD Start | MJD Arrival | Start Date | Arrival Date |
|---|---|---|---|---|---|
| 0.25 | 3098 | 61,010 | 64,108 | 1 December 2025 | 26 May 2034 |
| 0.3 | 2324 | 61,408 | 63,732 | 3 January 2027 | 15 May 2033 |
| 0.4 | 1759 | 60,679 | 62,438 | 4 January 2025 | 29 October 2029 |
| 0.45 | 1566 | 60,947 | 62,513 | 29 September 2025 | 12 January 2030 |
| 0.5 | 1270 | 60,999 | 62,269 | 20 November 2025 | 13 May 2029 |
| 0.6 | 1130 | 61,046 | 62,176 | 6 January 2026 | 9 February 2029 |
| 0.7 | 1055 | 61,102 | 62,157 | 3 March 2026 | 21 January 2029 |
| 0.8 | 961 | 61,432 | 62,393 | 27 January 2027 | 14 September 2029 |
| 0.9 | 838 | 61,432 | 62,270 | 27 January 2027 | 14 May 2029 |
| 1 | 660 | 61,775 | 62,435 | 5 January 2028 | 26 October 2029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quarta, A.A. Using Solar Sails to Rendezvous with Asteroid 2024 YR4. Technologies 2025, 13, 373. https://doi.org/10.3390/technologies13080373
Quarta AA. Using Solar Sails to Rendezvous with Asteroid 2024 YR4. Technologies. 2025; 13(8):373. https://doi.org/10.3390/technologies13080373
Chicago/Turabian StyleQuarta, Alessandro A. 2025. "Using Solar Sails to Rendezvous with Asteroid 2024 YR4" Technologies 13, no. 8: 373. https://doi.org/10.3390/technologies13080373
APA StyleQuarta, A. A. (2025). Using Solar Sails to Rendezvous with Asteroid 2024 YR4. Technologies, 13(8), 373. https://doi.org/10.3390/technologies13080373






