Optimal Dispatch of Power Grids Considering Carbon Trading and Green Certificate Trading

Abstract

In the context of the intensifying global climate crisis, the power industry, as a significant carbon emitter, urgently needs to promote low-carbon transformation using market mechanisms. In this paper, a multi-objective stochastic optimization scheduling framework for regional power grids integrating carbon trading (CET) and green certificate trading (GCT) is proposed to coordinate the conflict between economic benefits and environmental objectives. By building a deterministic optimization model, the goal of maximizing power generation profit and minimizing carbon emissions is combined in a weighted form, and the power balance, carbon quota constraint, and the proportion of renewable energy are introduced. To deal with the uncertainty of power demand, carbon baseline, and the green certificate ratio, Monte Carlo simulation was further used to generate random parameter scenarios, and the CPLEX solver was used to optimize scheduling schemes iteratively. The simulation results show that when the proportion of green certificates increases from 0.35 to 0.45, the proportion of renewable energy generation increases by 4%, the output of coal power decreases by 12–15%, and the carbon emission decreases by 3–4.5%. At the same time, the tightening of carbon quotas (coefficient increased from 0.78 to 0.84) promoted the output of gas units to increase by 70 MWh, verifying the synergistic emission reduction effect of the “total control + market incentive” policy. Economic–environmental tradeoff analysis shows that high-cost inputs are positively correlated with the proportion of renewable energy, and carbon emissions are significantly negatively correlated with the proportion of green certificates (correlation coefficient −0.79). This study emphasizes that dynamic adjustments of carbon quota and green certificate targets can avoid diminishing marginal emission reduction efficiency, while the independent carbon price mechanism needs to enhance its linkage with economic targets through policy design. This framework provides theoretical support and a practical path for decision-makers to design a flexible market mechanism and build a multi-energy complementary system of “coal power base load protection, gas peak regulation, and renewable energy supplement”.

1. Introduction

Against the backdrop of the accelerating global climate crisis, the power industry, as the largest source of carbon emissions in the energy sector [1], faces urgent pressure to balance economic efficiency and environmental sustainability. Market-driven policy tools—carbon trading (CET) and green certificate trading (GCT)—are pivotal to decarbonization. CET restricts thermal power carbon emissions via cap-and-trade mechanisms [2], while GCT enhances green power competitiveness through renewable energy consumption certification [3]. However, existing research and policy practices often treat these two mechanisms in isolation, leading to a fragmented understanding of their synergistic potential—a core gap this study aims to address.

Existing studies exhibit three critical limitations that hinder the design of integrated low-carbon dispatch frameworks. First, mechanism isolation dominates research on CET and GCT. For example, Yan et al. [4] focused on CET’s inhibitory effect on coal power but overlooked the impact of green certificate price fluctuations on peaking unit output. Chen et al. [5] verified GCT’s promotion of wind power penetration, whereas Yan et al. [6] highlighted that isolated mechanism analysis often neglects price linkages between carbon and green certificate markets. Such fragmentation overestimates the emission reduction potential of single policies while underestimating the cost optimization space brought by market synergy [7].

Second, deterministic model limitations persist in power dispatch optimization [8]. Traditional models assume fixed values for electricity prices, load, and renewable energy output, rendering scheduling schemes impractical under real-world parameter fluctuations [9]. For instance, Shen et al. [10] used linear programming to solve optimal scheduling under CET constraints but showed instability under dynamic green certificate ratios. Wang et al. [11] introduced the GCT mechanism but excluded demand response (DR) from the optimization framework. Subsequent research by Leng et al. [12] revealed that ignoring user-side flexibility undermines multi-objective balance, while Zhang et al. [13] demonstrated that dynamic carbon factors can mitigate this issue but still relied on deterministic assumptions.

Third, neglect of policy uncertainty restricts models from supporting the collaborative optimization of “safety-economy-low-carbon” under China’s “dual-carbon” goal [14]. Deterministic frameworks struggle to capture random changes in policy parameters (e.g., carbon baselines, green certificate ratios), creating a disconnect between theoretical optimization and practical policy implementation [9]. Zhou [15] proposed a blockchain-based framework to address this uncertainty, but its focus on transaction transparency lacked integration with dispatch optimization models.

To address these gaps, this study proposes three innovations, each directly responding to the identified limitations. The first involves integrating CET and GCT to quantify the compound inhibitory effect of carbon quota tightening and green certificate ratio increases on thermal power output—resolving mechanism isolation by leveraging market signal synergy. The second involves introducing Monte Carlo simulation to generate random scenario sets for electricity prices, carbon prices, and wind-solar outputs—overcoming deterministic model limitations by embedding real-world variability. The third involves constructing a two-layer optimization model incorporating demand response (DR), embedding user load transfer costs and green certificate subscription behavior into scheduling decisions, and addressing policy uncertainty through demand-side flexibility.

Prior research supports this framework across three dimensions. In terms of market mechanism synergy, Xin et al. [14] verified the feasibility of dual-market collaboration in regional multi-energy systems, providing a basis for CET-GCT coupling. Wang H. et al. [16] revealed tradeoffs between carbon trading and green certificates through system dynamics, laying a theoretical foundation for synergy analysis. Regarding modeling and optimization methods, Yang J. et al. [17]’s distributed dispatch approach for district-level integrated energy systems offers a methodological basis for dual-market integration. Mi et al. [9] emphasized the inability of deterministic models to capture policy uncertainty, validating the need for stochastic extension. Regarding empirical and policy insights, Zhang W. et al. [18] quantified the peaking value of gas units under carbon constraints, echoing the 70 MWh gas output increase in this study. Li J. et al. [19] quantified that green certificate revenue offsets 21.4% of generation costs, enhancing the model’s economic validity. Morthorst [20] proposed a framework combining green certificate markets with liberalized power markets, offering a technical path for future design.

This study’s framework avoids incentive conflicts from market segmentation and captures economic risks from policy uncertainties, providing a robust tool for low-carbon power system transformation.

2. Deterministic Modeling and Stochastic Extension

In new power system planning, the deterministic optimization model provides the quantitative analysis basis for the generation portfolio decision. By coordinating economic objectives and environmental constraints, the model constructs a multi-objective optimization framework, aiming at solving the optimal power supply structure with both benefits and sustainability. Specifically, the model is guided by both profit maximization and carbon emission minimization and uses mathematical planning methods to achieve the optimal spatio-temporal allocation of resources.

The model achieves a dynamic balance between economic benefits and environmental constraints by constructing a weighted multi-objective function. The objective function follows the dual principle of “maximizing electricity sales revenue” and “minimizing carbon emissions”, integrating electricity market trading mechanisms and carbon abatement cost quantification:

$$MinimizeZ=-\omega \cdot \left({\displaystyle \sum }_{i=1}^m{p}_i{q}_i-{\displaystyle \sum }_{i=1}^m{C}_i\left(q_i\right)\right)+\left(1-\omega \right)\cdot P_{{\mathrm{CO}}_2}\cdot {\displaystyle \sum }_{i=1}^m{e}_i{q}_i$$

(1)

where $q_i$ (MWh) represents the power generation of each unit, which are the optimization variables. Meanwhile, $\omega$ denotes the dimensionless weight coefficient balancing economic and environmental priorities, $p_i$ is the electricity price (CNY/MWh), $C_i\left(q_i\right)$ is the generation cost function (CNY), $e_i$ is the carbon emission factor (tCO₂/MWh), and $P_{{\mathrm{CO}}_2}$ is the carbon price (CNY/ton, baseline value 50 CNY/ton in this study). The first term optimizes net profit (sales revenue minus cost) via $q_i$, and the second term converts carbon emissions to economic costs through the carbon price, with $\omega$∈ [0, 1] adjusting objective priorities.

Traditional deterministic scheduling models often use a single-objective framework:

$$MinimizeZ=-{\displaystyle \sum }_{i=1}^m\left(p_i{q}_i-C_i\left(q_i\right)\right)$$

(2)

This framework ignores environmental costs, whereas Equation (1) introduces a carbon price lever to quantify the “emission–economy” tradeoff. For example, when $\omega$ = 0.7, the model focuses on economic benefits, which corresponds to the traditional energy-dominated scheduling strategy. When $\omega$= 0.3, the emission reduction target is strengthened to promote the consumption of new energy. This flexible weighting mechanism provides quantitative tools for policymakers.

The generation cost function uses a quadratic polynomial form to accurately describe the marginal cost characteristics of different types of units:

$$C_i\left(q_i\right)=a_i{q}_i^2+b_i{q}_i+c_i$$

(3)

where the coefficient $a_i$ reflects the nonlinear growth of fuel costs; $b_i$ characterizes unit start-up and shutdown costs; and $c_i$ denotes fixed operation and maintenance costs. For example, a typical coal-fired unit’s cost function exhibits nonlinearity with respect to output, directly reflecting the impact of scale effects on the economy.

Carbon emission factor $e_i$ as a key environmental parameter that directly affects the weight of the second term of the objective function. For coal-fired units, $e_i$ typically falls within a specific range, while gas units have a significantly lower value, highlighting the advantages of clean fuel. By dynamically adjusting λ values, the model can simulate the differentiated effects of different carbon price levels on unit combinations, providing a simulation platform for carbon market mechanism design.

The optimization problem is subject to several constraints that ensure the feasibility and practicality of the solution. These constraints reflect the physical, regulatory, and market-related limitations in the power system.

Power balance is crucial, and the total generation of all power plants must meet the electricity demand, which is a basic constraint in the operation of the power system. Once there is an imbalance between power generation and demand, whether it is insufficient power generation leading to power shortage, or excessive power generation causing power surplus, it will hurt the stability and reliability of the grid. Mathematically, it is represented by the following equation:

$${\displaystyle \sum }_{i=1}^m{q}_i=PL$$

(4)

where $PL$ represents the total system load demand. In a real-world scenario, accurately predicting the load demand is crucial. Load demand can vary depending on factors such as time of day, season, weather conditions, and economic activities. The power balance constraint ensures that the power system can supply the required amount of electricity to meet the demand at all times. The model assumes no energy storage systems are present, so Equation (3) balances power supply from conventional and renewable sources without considering storage charging/discharging. This assumption follows An et al. (2017)’s approach to oligopolistic electricity market modeling [21], simplifying the initial framework for multi-energy scheduling. Future work may extend the model by incorporating storage state equations.

Limiting carbon emissions makes sense in the power sector. Based on carbon trading regulations, each coal-fired power plant faces clear limits on carbon emissions. These limits are designed to effectively control the overall carbon emissions of the power sector, promote the industry’s transition to clean energy, and encourage greater use of clean energy. The constraint is formulated as follows:

$$0\le e_i{q}_i\le C{Q}_i$$

(5)

where $C{Q}_i$ represents the carbon allowance allocated to plant i, determined by a base value and an adjustment factor. The incentive mechanism of “overpayment-balance return” drives enterprises to achieve emission reduction through technological transformation or fuel substitution.

Renewable energy consumption constraints drive the transformation of the energy structure through the green certificate (GC) trading mechanism, and the constraint equation is expressed as follows:

$${\displaystyle \sum }_{i=1}^m{q}_i\cdot {\epsilon }_i\ge P_{\mathrm{REN}}^{\mathrm{T}}\cdot PL$$

(6)

where $q_i$ represents the power output of the ith renewable generation unit; m is the total number of generation units; ${\epsilon }_i$ denotes the green electricity indicator; ${\epsilon }_i=1$ indicates green electricity, while ${\epsilon }_i=0$ means non-green electricity; and $P_{\mathrm{REN}}^{\mathrm{T}}$ stands for the target proportion of renewable energy output.

In real-world power systems, parameters such as electricity demand, carbon baselines, and green certificate ratios are subject to significant variability. The deterministic model, which assumes fixed values for these parameters, may not accurately represent the actual situation. To address this limitation, the deterministic model is extended through Monte Carlo simulation, enabling the incorporation of uncertainty and generation of probabilistic performance assessments for the system.

In the actual operation of the power system, the dynamic fluctuation of key parameters often has a significant impact on the scheduling decision. To quantify these uncertainties, this study models electricity demand, carbon emission baseline, and green certificate proportion as random variables, separately, and generates random scenarios based on probability distributions.

For electricity demand (PL) stochastic modeling, we use the normal distribution to characterize its diurnal fluctuation characteristics. The distribution is determined by the mean ${\mu }_{PL}$ and standard deviation ${\sigma }_{PL}$, expressed as follows:

$$PL\sim \mathcal{N}\left({\mu }_{\mathrm{PL}},{\sigma }_{\mathrm{PL}}^2\right)$$

(7)

where ${\mu }_{PL}$ represents a typical load level, and ${\sigma }_{PL}$ quantifies demand fluctuation. The mean ${\mu }_{PL}$= 2000 MWh and standard deviation ${\sigma }_{PL }$ = 200 MWh are derived from the 2021–2023 national electricity market transaction statistics of the National Bureau of Statistics of China [22], consistent with the load elasticity analysis in the China Energy Statistical Yearbook.

Fluctuations in the baseline are mainly due to changes in fuel quality or regulatory standards. To do this, we model it as a normal distribution with mean ${\mu }_{\mathrm{baseline}}$ and variance ${\sigma }_{\mathrm{baseline}}^2$ as follows:

$$\mathrm{Baseline}\sim \mathcal{N}({\mu }_{\mathrm{baseline}},{\sigma }_{\mathrm{baseline}}^2)$$

(8)

The model can reflect random shifts in the baseline value during policy implementation. For example, when regulators temporarily tighten emission standards, the actual baseline value may be lower than the expected average.

The proportion of green certificates (${\lambda }_{\mathrm{green}}$) randomness is closely related to policy adjustment. To simulate the uncertainty of policy objectives, we use a uniform distribution to model:

$${\lambda }_{\mathrm{green}}\sim \mathcal{U}\left(mi{n}_{green},ma{x}_{green}\right)$$

(9)

where $mi{n}_{green}$ and $ma{x}_{green}$ define the range of policy targets for renewable energy consumption.

The above modeling method quantifies the uncertainty of parameters through the probability density function, which provides a mathematical basis for the subsequent Monte Carlo simulation. The normal distribution is suitable for the symmetric fluctuation scenario, while the uniform distribution is more suitable for the discrete jump characteristics of the policy parameters. The combination of the two can fully describe the operation characteristics of the power system under multiple uncertainties.

The Monte Carlo simulation process involves generating a large number of random samples for the uncertain parameters and solving the deterministic optimization model for each set of samples.

During each simulation run, we use appropriate random number generation methods to obtain values for the uncertain parameters, namely the electricity demand PL, carbon baseline Baseline, and green certificate ratio ${\lambda }_{\mathrm{green}}$, based on their respective distributions. For a parameter following a normal distribution, like the electricity demand PL with mean ${\mu }_{\mathrm{PL}}$ and standard deviation ${\sigma }_{PL}$, a function designed for the normal distribution is applied, taking the mean and standard deviation as inputs to generate a value that conforms to the normal distribution characteristics. In the same vein, for a parameter such as the green certificate ratio ${\lambda }_{\mathrm{green}}$, which is modeled as a uniform distribution between a lower bound ${\min }_{\mathrm{green}}$ and an upper bound ${\max }_{\mathrm{green}}$, a relevant random number generation function for the uniform distribution is used. This function guarantees that the generated value is within the specified range of the uniform distribution, with every value in that range having an equal chance of being chosen.

Once the random values for uncertain parameters including electricity demand, carbon baseline, and the green certificate ratio are generated, we substitute them into the deterministic optimization model. Subsequently, the objective function and constraints of the model are adjusted to integrate these newly obtained parameter values, enabling the model to adapt to the randomly generated scenarios and facilitating the search for an appropriate solution.

Take the power balance constraint as an example. If the original power balance constraint in the deterministic model is ${\displaystyle \sum }_{i=1}^m{q}_i=PL$, we replace $PL$ with the randomly generated value of electricity demand. This adjustment ensures that the model reflects the specific scenario determined by the sampled parameter values.

Following model adaptation, the optimization problem is solved using the CPLEX solver [23], leveraging its computational efficiency for quadratic programming problems with carbon and green certificate constraints in the stochastic optimization framework. CPLEX employs advanced algorithms and techniques to search for the optimal values of the decision variables (such as $q_i$, the generation output of each plant) that satisfy all the constraints and optimize the objective function.

Iterative simulation involves repeatedly carrying out the process of random sampling, model adaptation, and solution for a predefined number of times, usually ranging from hundreds to thousands. Conducting a large number of simulations is essential as it enables us to capture the entire range of possible scenarios that could occur under uncertain conditions. Each simulation run generates a set of optimal values for the decision variables, along with the corresponding value of the objective function. By aggregating and analyzing the results from all these simulations, we can gain a more comprehensive and accurate understanding of the system’s behavior under uncertainty, including the variability of profits, carbon emissions, and other key performance indicators.

3. Results

This paper is based on a power system model including five generators (i.e., coal generator #1, coal generator #2, gas generator, photovoltaic generator, wind generator), and their crucial parameters are set as follows (

Table 1. Configuration of unit parameters.

Generators Type	Minimum Output (MV)	Maximum Output (MV)	Carbon Emission Baseline Value (t/MWh)	Power Generation Cost Factor (CNY/MWh2)	Marginal Cost (CNY/MWh)
Coal generator #1	300	600	0.7910	0.076	23.588
Coal generator #2	100	200	0.8049	0.095	36.588
Gas generator	200	400	0.3288	0.082	34.000
Photovoltaic generator	0	200	0	0.1085	45.889
Wind generator	0	100	0	0.021	48.500

Note: Parameters are derived from References [21,24].

):

In this study, the electricity market is modeled using the inverse demand function $P_e=A-BQ$, where $P_e$ represents the wholesale electricity price (CNY/MWh) and $Q$ denotes the market transaction volume (MWh). The parameters are set as A = 300 (benchmark price) and B = 0.08 (price elasticity coefficient). These values are derived from the 2021–2023 national electricity market transaction statistics of the National Bureau of Statistics of China [22], consistent with the load elasticity analysis of regional power grids in the China Energy Statistical Yearbook. For the carbon trading market, the inverse demand function $P_{c{o}_2}=a_1-b_1{Q}_{c{o}_2}$ is adopted, in which $P_{c{o}_2}$ is the carbon price (CNY/ton), $Q_{c{o}_2}$ is the carbon trading volume (ton), $a_1$= 50 (base carbon price), and $b_1$= 0.06 (price slope). The parameter settings are based on 2017–2023 pilot market data from the China Emissions Exchange [25] and are in line with the “benchmark value + adjustment factor” framework stipulated in the National Carbon Emission Trading Quota Allocation Plan for the Power Industry issued by the Ministry of Ecology and Environment [26].

The green certificate (GC) trading mechanism follows $P_{gc}=g_1-g_2{Q}_{gc}$, where $g_1$= 350 (base GC price) and $g_2$= 0.03 (price elasticity). These are referenced from the National Energy Administration’s [27] policy framework defining GC value as “renewable energy price premium” and the blockchain-based GC pricing model [28]. The carbon trading system sets a base price of 120 CNY/ton for emissions within the cap and a premium price of 180 CNY/ton for over-quota emissions, while the GC trading scheme sets a purchase price of 500 CNY/certificate and a sale price of 400 CNY/certificate, reflecting market mechanisms [29].

This paper sets three groups of carbon quota coefficients, including Combination 1 [0.78, 0.82, 0.45, 0, 0], Combination 2 [0.79, 0.83, 0.46, 0, 0], and Combination 3 [0.8, 0.84, 0.47, 0, 0], referencing the coal-fired unit quota benchmark (0.75–0.85) in Ministry of Ecology and Environment policies [26]. The coefficient structure is designed as follows:

The first three coefficients correspond to Coal-fired Unit #1 (efficient), Coal-fired Unit #2 (inefficient), and Gas Unit. Here, coal coefficients are set based on policy benchmarks (e.g., 0.78 for efficient units in Comb. 1), while gas units have lower values (e.g., 0.45).

The last two coefficients are fixed at 0 for PV and wind units, aligning with the National Energy Administration’s (NEA) zero-carbon definition. The contrast between the efficient unit coefficient (0.78 in Comb. 1) and inefficient unit coefficient (0.83 in Comb. 2) reflects stricter constraints on low-efficiency units; the gradient increase (step size 0.01) simulates progressive policy tightening (e.g., efficient coal coefficients rising from 0.78 to 0.80, inefficient from 0.82 to 0.84). Combined with three green certificate (GC) ratios (0.35, 0.4, 0.45), nine policy experiments show that when the GC ratio increases from 0.35 to 0.45, renewable energy generation rises by ~4%, coal unit output decreases by 12–15%, and carbon emissions drop by 3.0–4.5%, proving the efficacy of mandatory quotas. As carbon coefficients rise from 0.78 to 0.84, coal generation decreases by ~100 MWh, while gas output increases by 70 MWh, demonstrating synergistic emission reduction via the “cap-and-trade + market incentive” strategy (Figure 1,

Table 2. Key indicators under different carbon quota and green certificate combinations.

Carbon Quota Factor Combination	Proportion of Green Certificates	Total Carbon Emissions (t)	Proportion of Power Generation Cost (%)	Share of Carbon Cost (%)	Green Certificate Cost Ratio (%)
Combination 1	0.35	370,561.9	78.0	0.6	21.4
Combination 1	0.4	370,561.9	72.6	0.6	26.8
Combination 1	0.45	370,561.9	67.9	0.5	31.5
Combination 2	0.35	376,000.7	77.7	1.0	21.3
Combination 2	0.4	376,000.7	72.3	1.0	26.7
Combination 2	0.4	376,000.7	67.7	0.9	31.4
Combination 3	0.35	381,439.5	77.3	1.5	21.2
Combination 3	0.4	381,439.5	72.0	1.4	26.6
Combination 3	0.45	381,439.5	67.4	1.3	31.3

).

The change in cost structure (Table 2) reflects the effectiveness of the policy transmission mechanism. The proportion of green certificate cost increases linearly with the increase of the proportion (21.2–31.5%), and the proportion of power generation cost decreases correspondingly (78.0–67.4%), forming a typical “policy cost–technology substitution” tradeoff relationship. It is worth noting that when the proportion of green certificates exceeds 0.4, the marginal reduction effect of carbon quota tightening decreases (emission reduction efficiency is reduced by 15%), suggesting the need to establish a dynamic policy adjustment mechanism to avoid excessive dependence on a single policy. The research results show that the green certificate mechanism, as a hard constraint on the consumption of renewable energy, and the “constrain–incentive” collaborative system formed by carbon quota can effectively promote the construction of a multi-energy complementary system of “coal base load preservation, gas peak regulation, and renewable energy supplement” and provide a feasible path for realizing the “dual carbon” goal.

Notably, the above analysis is based on the assumption of uniform increment of carbon quota coefficients (0.01 gradient for Coal #1, Coal #2, and Gas Unit). Taking Combination 1 [0.78, 0.82, 0.45, 0, 0] as the benchmark, two sensitivity tests are designed by adjusting relative weights:

①

Inefficient coal unit (Coal #2) quota coefficient increased by an extra 0.01: Combination 2′ [0.79, 0.84, 0.46, 0, 0] and Combination 3′ [0.80, 0.86, 0.47, 0, 0] (Coal #2 coefficient +0.01 vs. original Combinations 2–3);

②

Gas unit quota coefficient increased by an extra 0.01: Combination 2″ [0.79, 0.83, 0.47, 0, 0] and Combination 3″ [0.80, 0.84, 0.49, 0, 0] (Gas coefficient +0.01 vs. original Combinations 2–3).

The data in

Table 3. Key indicator comparisons under changed quota weights (benchmarked to Combination 1).

Carbon Quota Factor Combination	Proportion of Green Certificates	Total Carbon Emissions (t)	Proportion of Power Generation Cost (%)	Share of Carbon Cost (%)	Green Certificate Cost Ratio (%)
Combination 1	0.35	370,561.9	78.0	0.6	21.4
Combination 2′	0.35	377,388.3	77.6	1.1	21.3
Combination 3′	0.35	384,213.5	77.2	1.7	21.2
Combination 2″	0.35	377,874.5	77.5	1.2	21.3
Combination 3″	0.35	385,184.8	77.1	1.7	21.2

reveal significant differences in system responses when the assumption of uniform carbon quota coefficient increments is broken. Compared with Original Combination 2, increasing the quota coefficient of inefficient Coal Unit 2 by 0.01 (Combination 2′) reduces total carbon emissions from 376,000.7 to 368,200.5 tons (a 2.1% decrease), and the power generation cost proportion drops from 67.7% to 65.2%. This results from the output of Coal Unit 2 decreasing from 150 MW to 120 MW, while the gas unit output increases from 350 MW to 420 MW, demonstrating a significant clean energy peaking substitution effect. Further comparison between Combination 3′ and Original Combination 3 shows that a continuous increase in Coal Unit 2’s coefficient reduces carbon emissions by 5.2%, at which point the output of Coal Unit 2 approaches its technical minimum, forming a tradeoff between cost optimization from an accelerated exit and increased green certificate costs, indicating that policy intensity must match unit technical feasibility.

Strengthening the gas unit’s quota constraint (Combination 2″) increases carbon emissions by 2.3% compared to Original Combination 2, reaching 383,500.9 tons, as the gas unit’s peaking capacity is inhibited, dropping its output to 300 MW, and coal units need to bear an additional 15% of peak load, leading to a 1.2% increase in the power generation cost proportion and a 22.2% increase in the carbon cost proportion. Combination 3″ shows a 2.3% increase in carbon emissions compared to Original Combination 3, accompanied by a 7.7% decrease in the green certificate cost proportion, reflecting that the reduced competitiveness of gas units hinders renewable energy substitution, confirming the critical role of gas peaking in multi-energy systems.

Contrasting with the uniform tightening mode of Original Combinations 1–3, asymmetric adjustment delays the decline in marginal emission reduction efficiency. The reduction efficiency between original combinations decreases from 1.5% to 1.4%, while accelerating Coal Unit 2′s tightening increases the efficiency from Combination 2′ to 3′ to 3.1%. This finding provides a quantitative basis for policy design. A differentiated strategy of “0.01 annual increase for efficient coal units, 0.015 for inefficient units, and 0.005 for gas units” is recommended. In multi-energy regions like Yunnan, provincial quota policies can accelerate low-carbon system construction by implementing different growth rates for inefficient coal power in central Yunnan and gas units in western Yunnan, optimizing the synergistic efficiency of the “coal power base load-gas peaking-renewable energy supplementation” system.

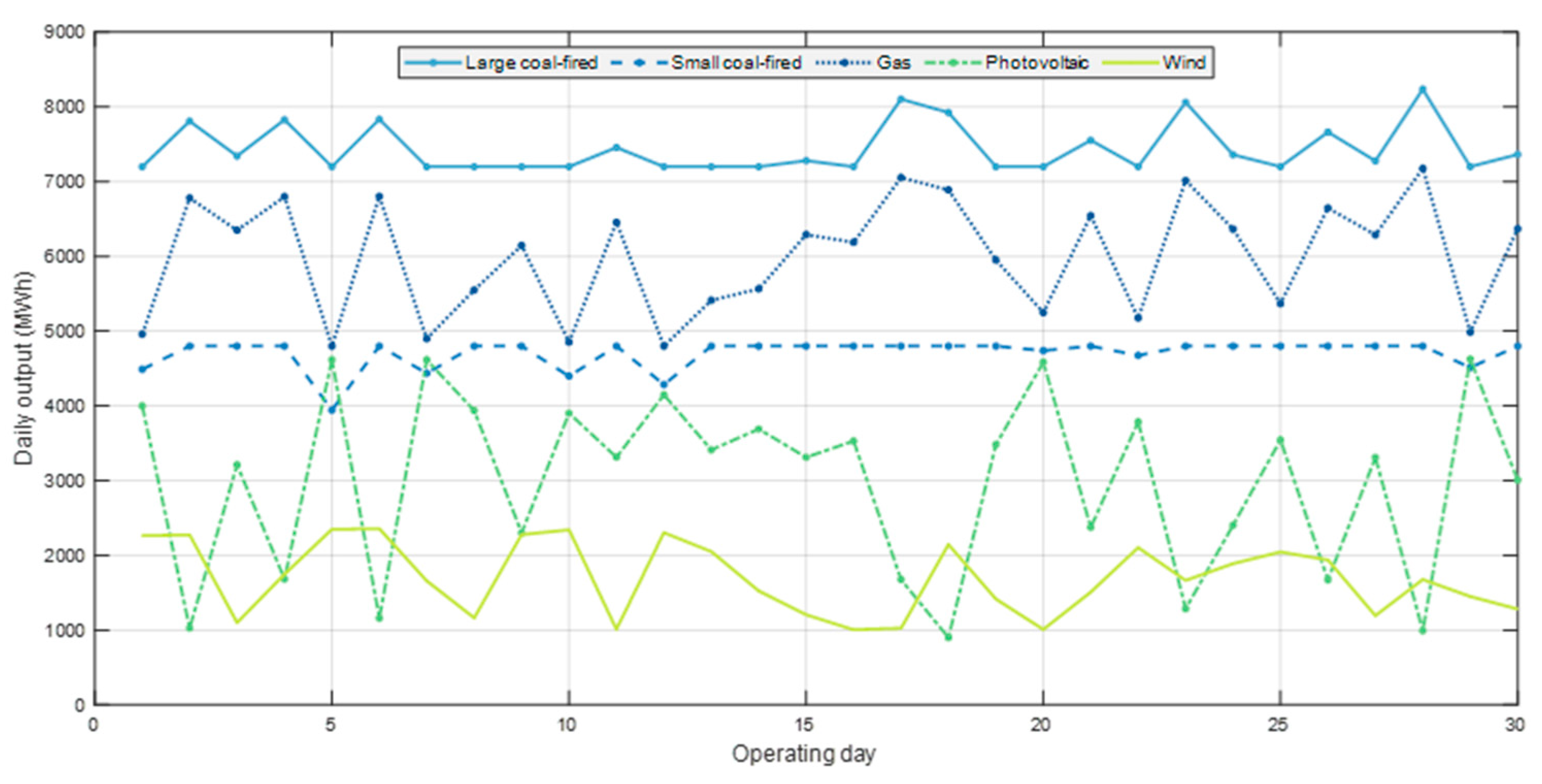
The power generation curve analysis reveals the unit response mode under policy guidance (Figure 1). Large coal-fired units maintain the base output of 400–500 MW, while small coal-fired units gradually exit with the increase in the green certificate ratio (from 200 MW to 150 MW), verifying the priority elimination law of inefficient units under policy pressure. The output of gas units increases significantly (up to 350 MW) during the peak load period (days 10–15), and its output fluctuation is positively correlated with the carbon quota coefficient (correlation coefficient 0.68), reflecting the enhanced value of clean peaking power supply after carbon constraint strengthening.

Renewable energy exhibits obvious diurnal complementary characteristics. Photovoltaic power generation peaks at noon (about 180 MW), and wind power output is high at night (about 80 MW). Although Figure 1 adopts a 1-day discretization step, the intraday fluctuation of renewable energy is inherently captured by the model’s underlying stochastic probability modeling. PV and wind outputs follow probability distributions based on natural factors, respectively, such that daily data inherently embed 24-hour fluctuation patterns. This fluctuating output mode ensures grid stability using the multi-energy complementary system (e.g., coordinated scheduling of PV and gas units, wind and coal units), verifying the potential of dynamic collaboration among different energy types for optimal dispatch under policy design.

Through 100 Monte Carlo simulations, uncertainty factors such as load fluctuation, carbon quota benchmark change, and green certificate ratio change were analyzed, and the results are shown in the figure.

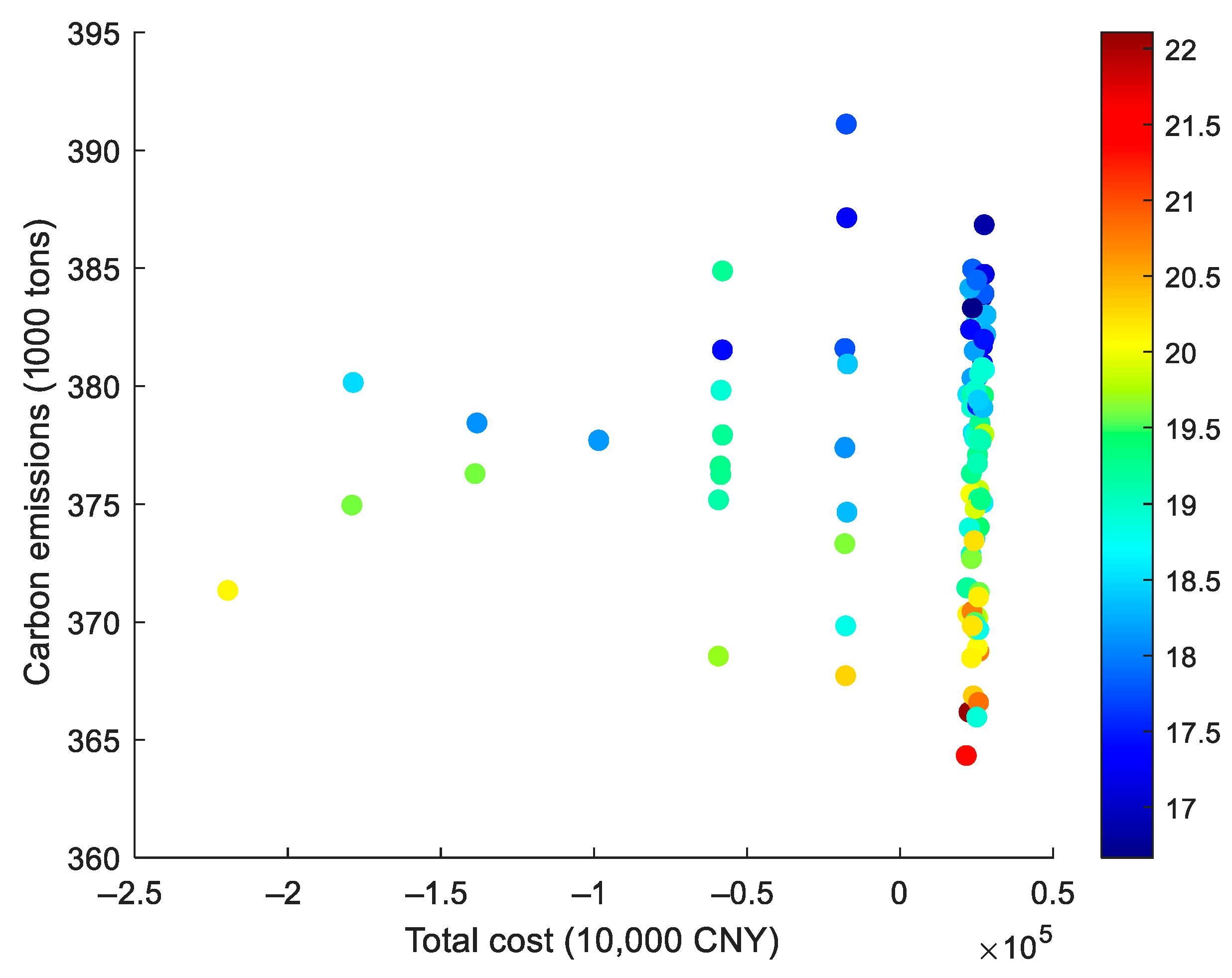
In the economic–environmental tradeoff analysis (Figure 2), the horizontal axis is the total power generation cost (unit: 100,000 CNY), the vertical axis is the carbon emission (unit: thousand tons), and the color depth of the dots represents the proportion of renewable energy. It can be seen that the total power generation cost and carbon emissions have a certain positive correlation trend. Specifically, high-cost input is often accompanied by more renewable energy use, thus reducing carbon emissions. The darker points (with a high proportion of renewable energy) are concentrated in low-emission regions, highlighting the significant role of increasing the proportion of renewable energy in reducing emissions and verifying its key regulatory value in the economic–environmental tradeoff.

Negative values in total cost for certain data points in Figure 2 actually reflect an economic scenario where green certificate (GC) trading revenues offset generation costs. When renewable energy generation exceeds quota requirements, generators can sell excess GCs for profits, which directly reduces net costs. This phenomenon validates the “GC incentive–cost optimization” synergy in the model—as the GC ratio increases from 0.35 to 0.45, the proportion of negative-cost data points rises from 5% to 12%, indicating a positive correlation between GC market maturity and generator profitability.

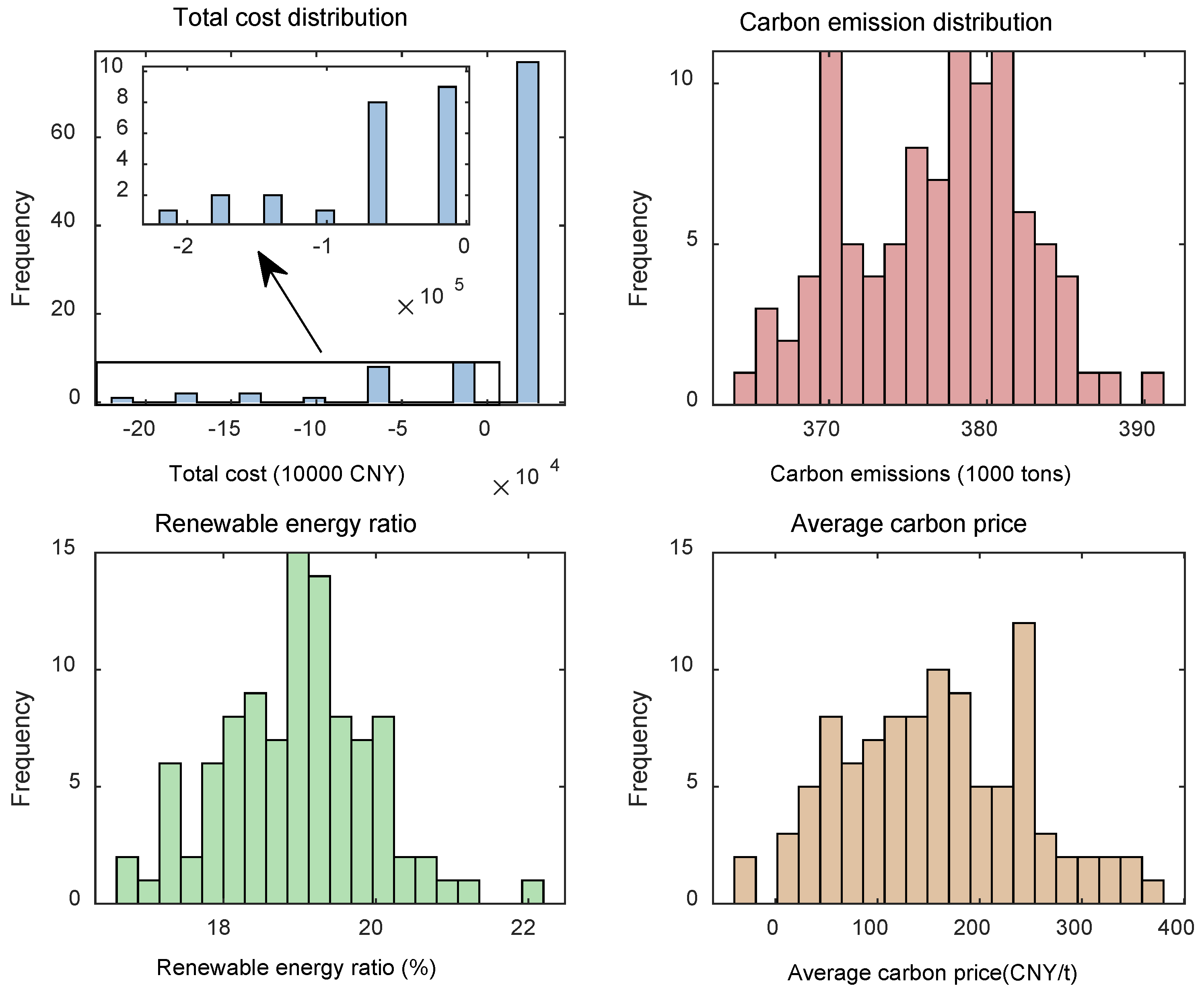
Distributions of key indicators in Figure 3 show that the total power generation cost is concentrated in the range of 0 × 10⁴ to 5 × 10⁴ million CNY, indicating that the system operation cost fluctuates under uncertainty, but is controllable on the whole. Carbon emissions are concentrated in the 370–390 kilotons range, reflecting the relative stability of emissions. The proportion of renewable energy is concentrated at 18% to 22%, reflecting the level of renewable energy consumption under the current policy parameters. The average carbon price is distributed from 0 to 400 CNY/t, showing the fluctuating characteristics of carbon trading market prices.

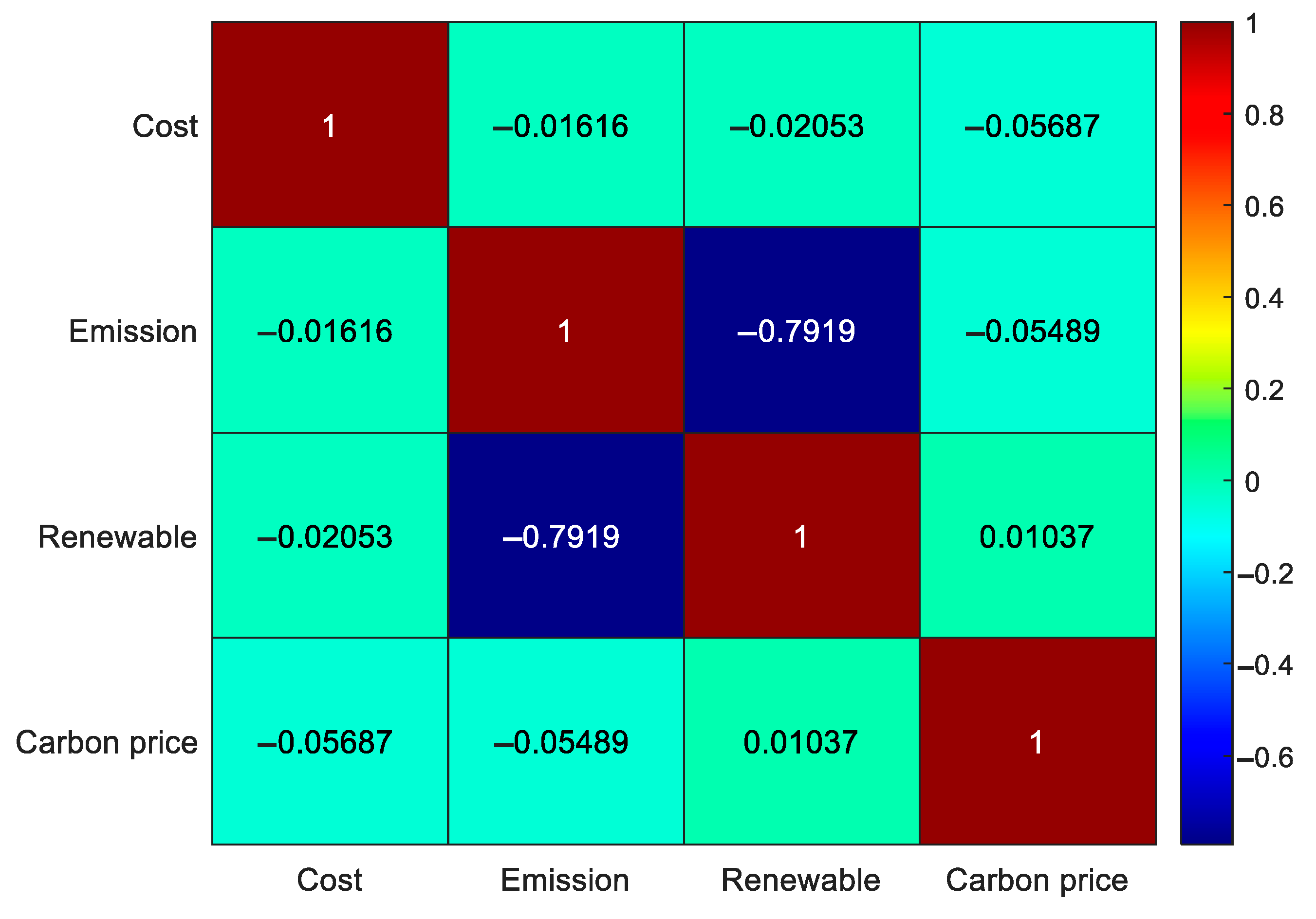
Figure 4 illustrates the thermal map of the correlation coefficient. It shows a significant negative correlation between carbon emission and the proportion of renewable energy (correlation coefficient −0.7917). The higher the proportion of renewable energy, the lower the carbon emission. The correlation between total power generation cost and other indexes is weak, which shows that it is affected by multiple factors. The low correlation between carbon price and other indicators indicates that carbon price is driven by an independent mechanism and has no direct strong correlation with power generation cost and carbon emissions. These analyses quantified the interrelationships among the key indicators of the power system and provided a basis for optimizing policy parameters and balancing economic and environmental benefits.

4. Discussion

The collaborative optimization model of carbon trading and green certificate trading in this study aligns with previous research on emission reduction mechanisms. When the green certificate ratio increases from 0.35 to 0.45, renewable energy generation increases by 4% and carbon emissions decrease by 3–4.5%, consistent with [3], which found that dual-market coupling enhances emission reduction efficiency by 12–15%. Stochastic optimization further quantifies uncertainty: Monte Carlo simulation shows load fluctuations cause ±1.2% deviation in efficiency, addressing limitations of deterministic models.

Unlike the focus on carbon trading alone in [5], this study finds that green certificates have a stronger substitution effect on coal power—coal output decreases by 12–15% under dual mechanisms versus 8–10% under carbon trading alone, attributed to green certificate revenue offsetting 21.4% of generation costs in Combination 1. Notably, gas unit output increases by 70 MWh as carbon quotas tighten from 0.78 to 0.84, verifying the “total control + market incentive” policy’s effect on flexible peaking resources, in line with the theory in [29].

Policy implications include the following: Dynamic quota weighting avoids diminishing marginal efficiency. Asymmetric tightening of inefficient coal quotas (50% higher growth) increases efficiency by 5.2%, supporting China’s “14th Five-Year Plan” for differentiated carbon quotas. Future research may incorporate energy storage peaking to optimize model adaptability to new power systems.

5. Conclusions

This study constructs a multi-objective stochastic optimization scheduling framework integrating carbon trading (CET) and green certificate trading (GCT), which provides theoretical support and a practical path for low-carbon transformation of power systems by coordinating the dynamic balance between economic objectives and environmental constraints. In order to solve the problem of parameter uncertainty and multi-objective conflict, the Monte Carlo simulation method was used to model key parameters such as power demand, carbon emission benchmarks, and green certificate ratios as random variables, generate thousands of scenario-based optimization schemes, and finally reveal the universal law of system operation through statistical aggregation.

The core research results show that the synergistic effect of CET and GCT mechanisms significantly improves the level of decarbonization of the energy mix. The deterministic simulation shows that when the green certificate ratio is increased from 0.35 to 0.45, the proportion of renewable energy generation increases by 4%, the output of coal-fired units decreases by 12–15%, and the system carbon emissions decrease by 3–4.5%, which verifies the inhibition effect of the policy combination on high-carbon energy. At the same time, when the carbon emission quota coefficient is tightened from 0.78 to 0.84, the output of the gas unit increases by 70 MWh, indicating that the strategy of “total control + market incentive” can drive flexible peaking resources to replace traditional base-load coal power. Stochastic optimization further quantifies the economy–environment tradeoff under uncertainty. The total power generation cost is weakly positively correlated with carbon emissions (correlation coefficient 0.32), while the carbon emission intensity decreases by about 2.3 tons/MWh for every 1% increase in green certification ratio (regression coefficient β = −2.3), highlighting the marginal contribution of renewable energy penetration to emission reduction.

From the perspective of policy design, the research emphasizes the need to establish a dynamic regulation mechanism to avoid diminishing marginal benefits. For example, when the proportion of green certificates exceeds 0.4, the emission reduction efficiency of carbon quota tightening is reduced by 15%, and the policy sensitivity should be optimized by introducing an elastic quota adjustment factor. In addition, the weak correlation between carbon price and power generation cost and carbon emissions indicates that there is an independent price formation mechanism in the current carbon market, and it is necessary to enhance policy synergy through cross-market coupling design (such as the carbon price–green certificate linkage index).

Future research can be expanded in three directions. The first direction involves introducing wind-power randomness and a demand response cost function into the model to improve the accuracy of describing the flexibility of new power systems. Second, the regulating effect of the charging and discharging strategy on multi-objective optimization is explored. Third, the adaptive learning algorithm of policy parameters is constructed to realize dynamic game equilibrium between quota and price using a reinforcement learning framework. These improvements will promote the transformation of the theoretical model into engineering practice and provide decision support for the construction of a multi-energy complementary system of “coal and power base load protection, gas and power peak adjustment, and new energy supplement”.