Performance Evaluation of IM/DD FSO Communication System Under Dust Storm Conditions
Abstract
1. Introduction
2. Dusty Channel Model
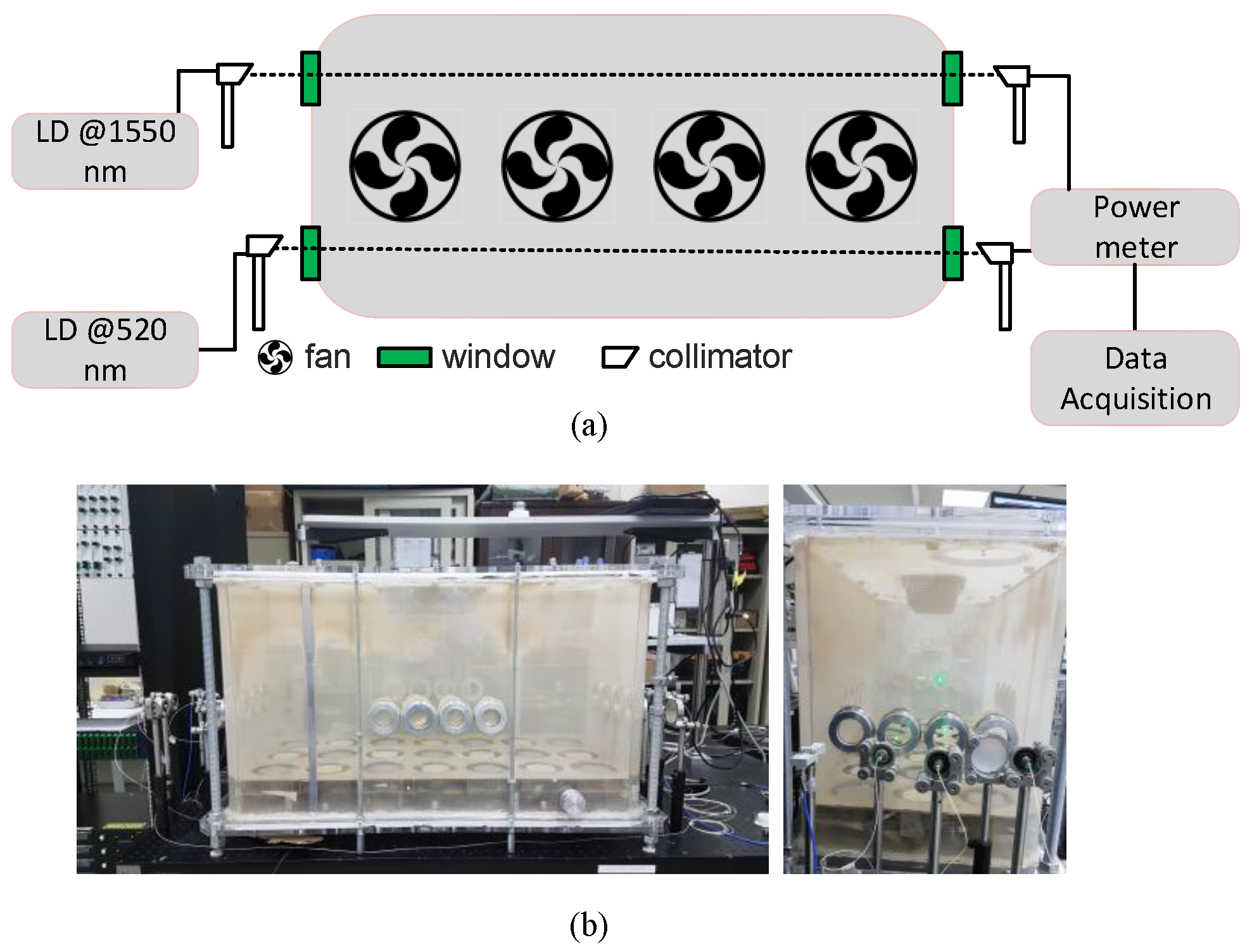
2.1. Experimental Setup
2.2. Dusty Channel Model
3. System Model and Performance Analysis
3.1. Average BER Analysis
3.2. Outage Probability Analysis
3.3. Average Channel Capacity Analysis
4. Results and Discussion
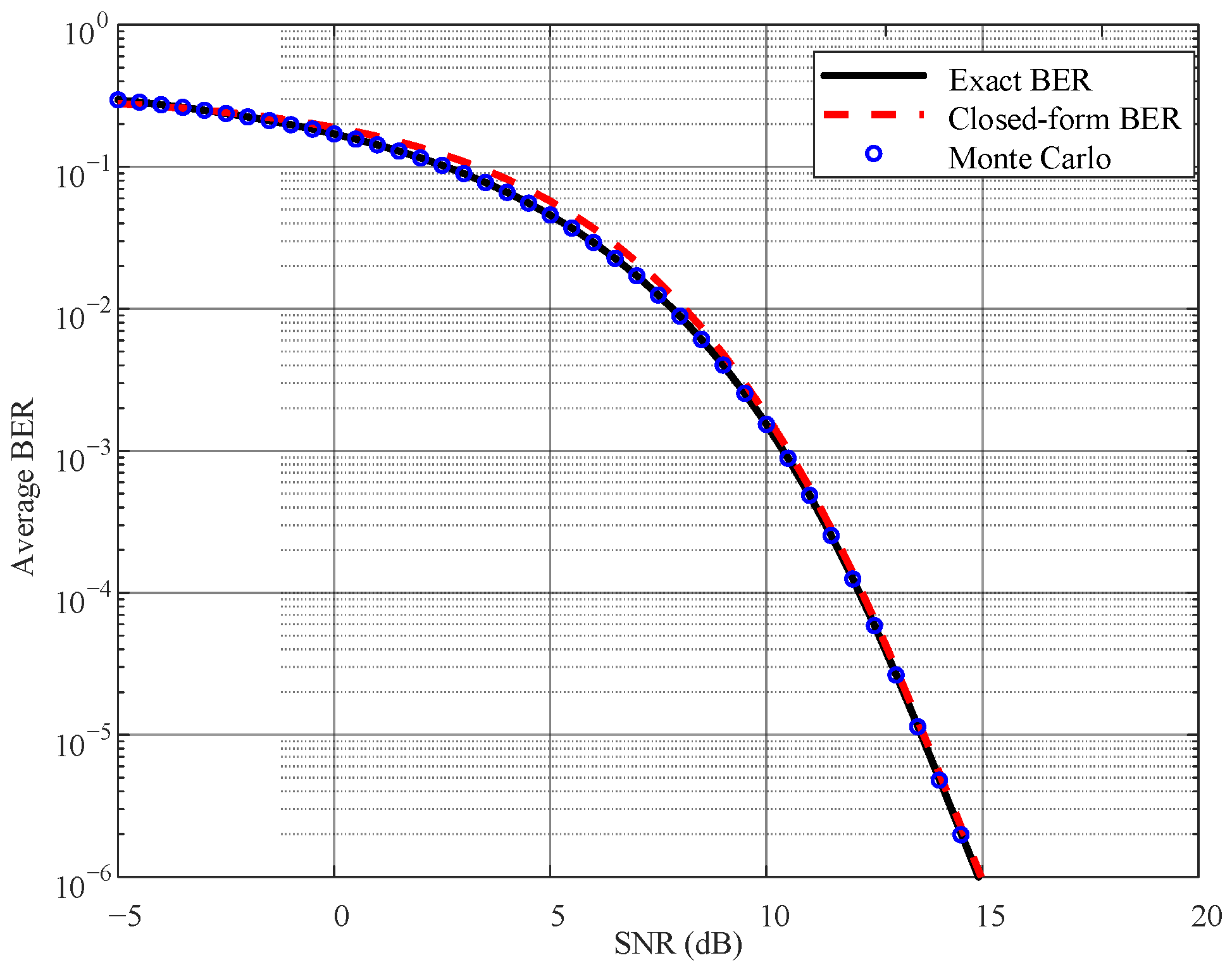
4.1. BER Simulation Results
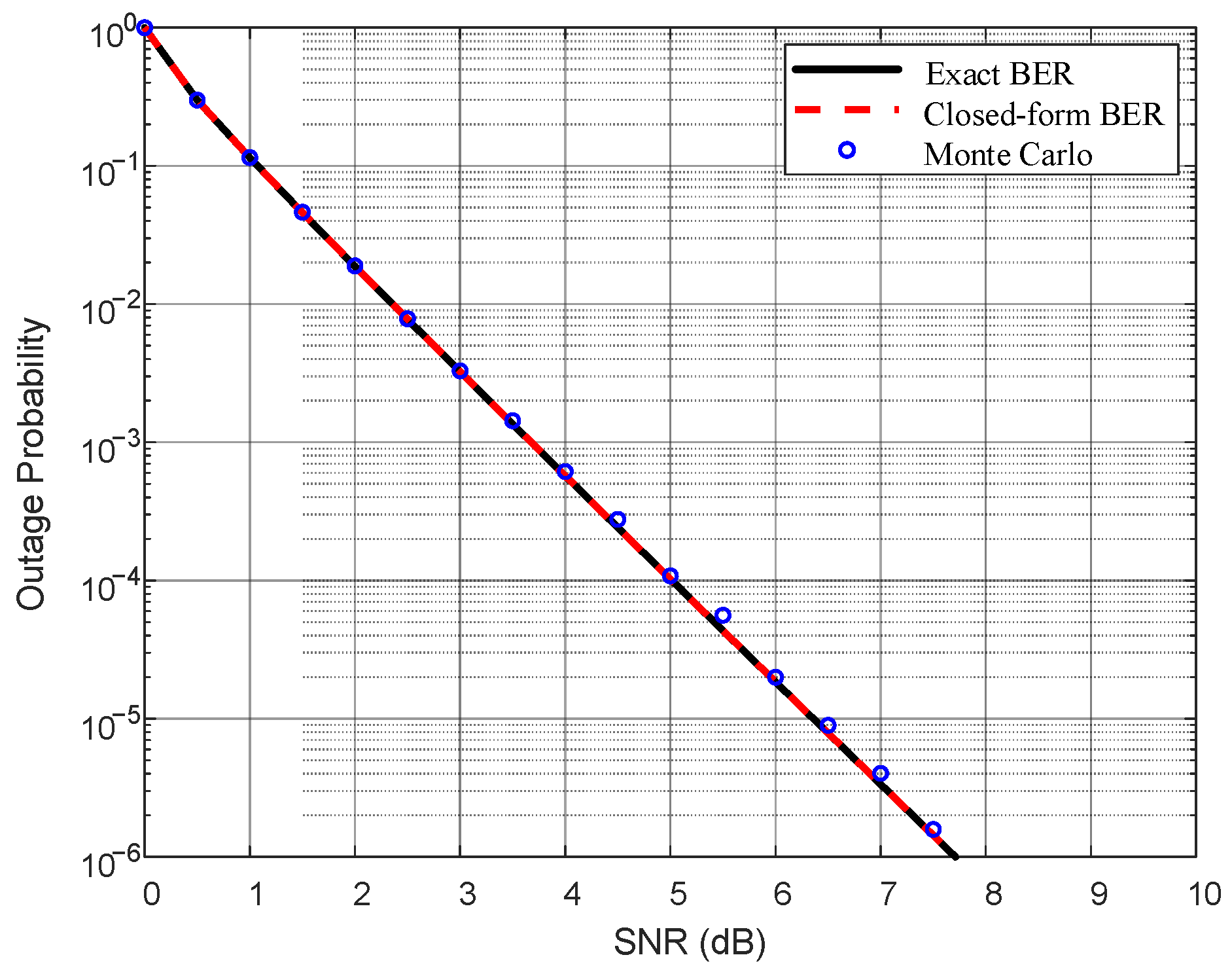
4.2. Outage Probability Simulation Results
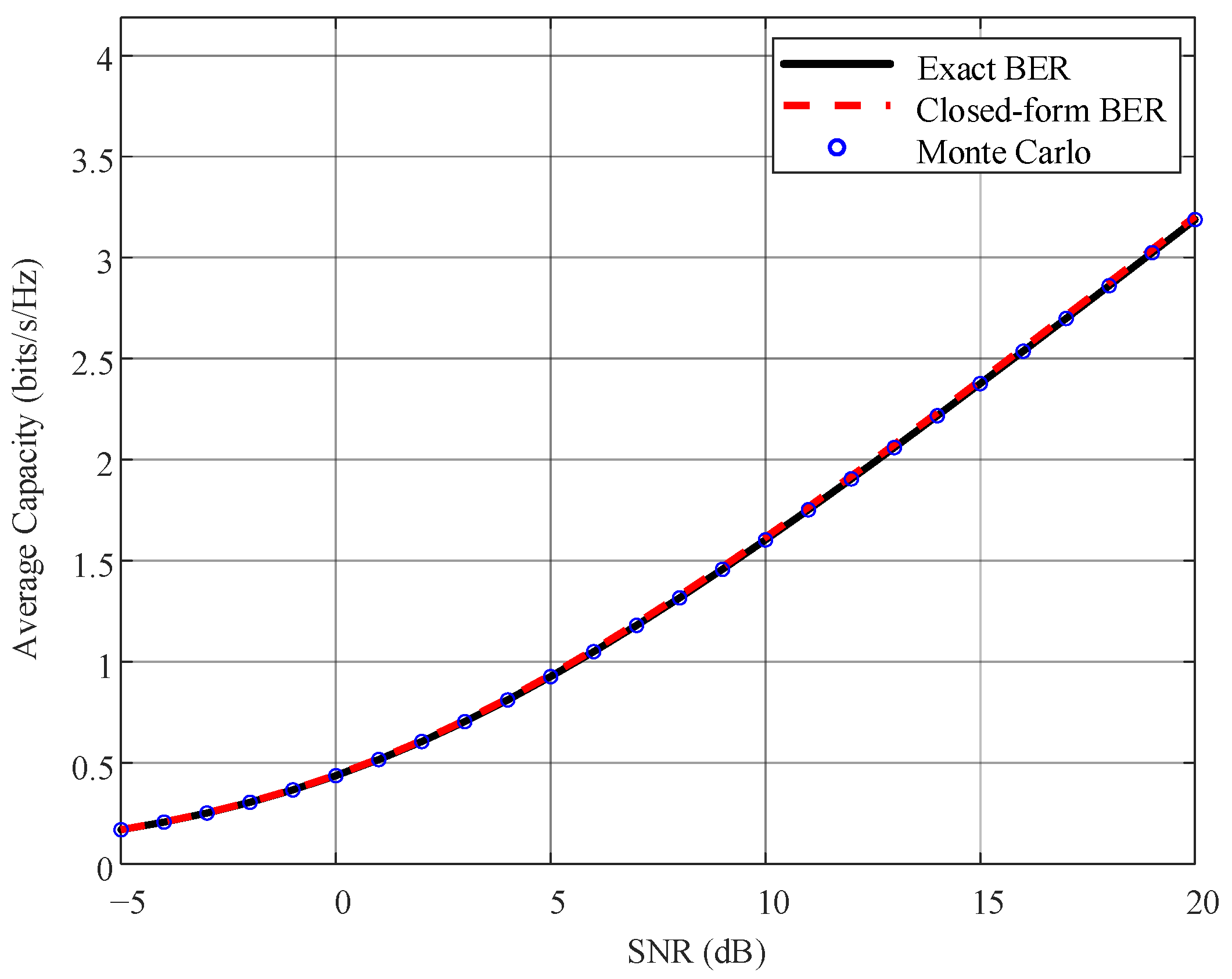
4.3. Average Channel Capacity Simulation Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Vliet, V.; Koelemeij, J.; Elschot, M.; van Groesen, H.; Koonen, T. 5.7 Tb/s Transmission Over a 4.6 km Field-Deployed Free-Space Optical Link in Urban Environment. arXiv 2025, arXiv:2503.21058. [Google Scholar] [CrossRef]
- Othman, W.M.; Ateya, A.A.; Nasr, M.E.; Muthanna, A.; ElAffendi, M.; Koucheryavy, A.; Hamdi, A.A. Key Enabling Technologies for 6G: The Role of UAVs, Terahertz Communication, and Intelligent Reconfigurable Surfaces in Shaping the Future of Wireless Networks. J. Sens. Actuator Netw. 2025, 14, 30. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Shahjalal, M.; Hasan, M.K.; Jang, Y.M. The Role of Optical Wireless Communication Technologies in 5G/6G and IoT Solutions: Prospects, Directions, and Challenges. Appl. Sci. 2019, 9, 4367. [Google Scholar] [CrossRef]
- El-Mottaleb, S.A.A.; Singh, M.; Alshathri, S.; El-Shafai, W.; Aly, M.H. Enhancing Security and Capacity in FSO Transmission for Next-Generation Networks Using OFDM/OCDMA-Based ICSM Codes. Front. Phys. 2023, 11, 1231025. [Google Scholar] [CrossRef]
- El-Meadawy, S.A.; Moneim, M.S.A.E.; Badawy, M.S.; El-Mahdy, M.A.; Shabayek, M.S.I. Performance Analysis of 3D Video Transmission Over Deep-Learning-Based Multi-Coded N-ary Orbital Angular Momentum FSO System. IEEE Access 2021, 9, 110116–110136. [Google Scholar] [CrossRef]
- Esmail, M.A.; Ragheb, A.; Fathallah, H.; Alouini, M.S. Investigation and Demonstration of High Speed Full-Optical Hybrid FSO/Fiber Communication System Under Light Sand Storm Condition. IEEE Photonics J. 2017, 9, 7900612. [Google Scholar] [CrossRef]
- Mohamed, P.H.; El-Shimy, M.A.; Shalaby, H.M.; Kheirallah, H.N. Hybrid FSO/RF system over proposed random dust attenuation model based on real-time data combined with G–G atmospheric turbulence. Opt. Commun. 2023, 549, 129891. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, W.; Liu, C.; Fang, D. Performance Evaluation of FSO Communications under Sand-Dust Conditions. Int. J. Antennas Propag. 2019, 2019, 2046896. [Google Scholar] [CrossRef]
- De, S.; Raj, A.A.B. Experimental Study of Sand-Storm Effect on Digital FSO Communication Link. In Proceedings of the 2020 International Conference on Recent Trends on Electronics, Information, Communication and Technology (RTEICT), Bangalore, India, 12–13 November 2020; pp. 35–40. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Perez, J.; Leitgeb, E. On the performance of FSO communications links under sandstorm conditions. In Proceedings of the 12th International Conference on Telecommunications, Zagreb, Croatia, 26–28 June 2013; pp. 53–58. [Google Scholar]
- Esmail, M.A.; Ragheb, A.M.; Fathallah, H.A.; Altamimi, M.; Alshebeili, S.A. 5G-28 GHz Signal Transmission Over Hybrid All-Optical FSO/RF Link in Dusty Weather Conditions. IEEE Access 2019, 7, 24404–24410. [Google Scholar] [CrossRef]
- Khan, A.N.; Saeed, S.; Naeem, Y.; Zubair, M.; Massoud, Y.; Younis, U. Atmospheric Turbulence and Fog Attenuation Effects in Controlled Environment FSO Communication Links. IEEE Photonics Technol. Lett. 2022, 34, 1341–1344. [Google Scholar] [CrossRef]
- Zedini, E.; Oubei, H.M.; Kammoun, A.; Hamdi, M.; Ooi, B.S.; Alouini, M.S. A New Simple Model for Underwater Wireless Optical Channels in the Presence of Air Bubbles. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Esmail, M.A.; Fathallah, H.; Alouini, M.S. An experimental study of FSO link performance in desert environment. IEEE Commun. Lett. 2016, 20, 1888–1891. [Google Scholar] [CrossRef]
- Farid, A.A.; Hranilovic, S. Outage Capacity Optimization for Free-Space Optical Links With Pointing Errors. J. Light. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Chiani, M.; Dardari, D.; Simon, M.K. New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels. IEEE Trans. Wirel. Commun. 2003, 2, 840–845. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Chapter 13: Confluent Hypergeometric Functions. In Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Applied Mathematics Series; National Bureau of Standards: Washington, DC, USA, 1964; Volume 55. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. Chapter 13: Confluent Hypergeometric Functions. In NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Wei, L.; Yuan, S.S.A.; Huang, C.; Zhang, J.; Bader, F.; Zhang, Z.; Muhaidat, S.; Debbah, M.; Yuen, C. Electromagnetic Channel Modeling and Capacity Analysis for HMIMO Communications. IEEE Trans. Wirel. Commun. 2025, 24, 4500–4514. [Google Scholar] [CrossRef]

| Distribution | RMSE | Estimated Parameters | |
|---|---|---|---|
| Beta | 0.85 | 1.30 | |
| Power | 0.76 | 1.63 | |
| Weibull | 0.44 | 2.48 | |
| Lognormal | 0.18 | 3.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmail, M.A. Performance Evaluation of IM/DD FSO Communication System Under Dust Storm Conditions. Technologies 2025, 13, 288. https://doi.org/10.3390/technologies13070288
Esmail MA. Performance Evaluation of IM/DD FSO Communication System Under Dust Storm Conditions. Technologies. 2025; 13(7):288. https://doi.org/10.3390/technologies13070288
Chicago/Turabian StyleEsmail, Maged Abdullah. 2025. "Performance Evaluation of IM/DD FSO Communication System Under Dust Storm Conditions" Technologies 13, no. 7: 288. https://doi.org/10.3390/technologies13070288
APA StyleEsmail, M. A. (2025). Performance Evaluation of IM/DD FSO Communication System Under Dust Storm Conditions. Technologies, 13(7), 288. https://doi.org/10.3390/technologies13070288






