A Logarithmic Compression Method for Magnitude-Rich Data: The LPPIE Approach
Abstract
1. Introduction
1.1. Previous Work
1.2. Contributions
- A condensed list of our contributions is presented below:
- The introduction of LPPIE, a logarithmic magnitude-driven encoder retaining bijection without context mixing.
- The demonstration of competitive ratios versus mainstream codecs across heterogeneous datasets, with the specific advantage on magnitude-rich streams.
- The presentation of three architectural pivots—adaptive partitioning, precision scheduling, and Golomb–Rice headers—each quantified through ablation.
- The provision of analytical complexity bounds, together with empirical runtime evidence, supporting scalability toward gigabyte archives.
2. Methodology
2.1. Quantitative Validation of Declarative Assertions
2.2. Environment of Experiments
2.3. Complexity
- Input byte stream B; concatenate into integer N.
- Partition N under the digit-entropy heuristic; impose constraints on the maximal substring length.
- For each substring, perform the consequent procedure:
- (a)
- Repeat until the value ; record depth r and terminal digit d.
- (b)
- Store pair using the Golomb–Rice code.
- Output the metadata buffer; terminate the operation.
2.4. Convergence and Termination
2.5. Entropy Bounds and Isometry
2.6. Comparative Perspective
2.7. Generalized Iterative Transform Encoding (GITE)
2.8. LPPIE Integrated with Entropy Encoding
| Algorithm 1 LPPIE-EE Encoding |
|
2.9. Complexity of Alternative Transforms
2.9.1. Iterated Roots
2.9.2. Modular Splits
2.9.3. Exponential Damping
2.10. Implementation Nuances
- A1 (Bijectivity): A decoding function D exists with for every admissible x.
- A2 (Termination): The iterative operator halts after a finite sequence whenever .
- A3 (Monotone Contraction): T remains strictly decreasing on the interval .
3. Explication of Iterative Logarithmic Transformation and Metadata Handling
3.1. Iterative Logarithmic Transformation of Extensive Numerals
3.2. Dynamic Precision Adjustment and Control Mechanism
3.3. Metadata Compaction via Golomb–Rice Encoding
3.4. Hybrid Entropy Coding Integration
3.5. Limitations
4. Results
5. Discussion
5.1. Observations
5.2. Future Work and Applications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miranda, L.C.; Lima, C.A. Trends and cycles of the internet evolution and worldwide impacts. Technol. Forecast. Soc. Change 2012, 79, 744–765. [Google Scholar] [CrossRef]
- Boughdiri, M.; Abdelattif, T.; Guegan, C.G. Integrating Onchain and Offchain for Blockchain Storage as a Service (BSaaS). In Proceedings of the 2024 IEEE/ACS 21st International Conference on Computer Systems and Applications (AICCSA), Sousse, Tunisia, 22–26 October 2024; pp. 1–2. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Zhou, K.; Cheng, H. ESS: An Efficient Storage Scheme for Improving the Scalability of Bitcoin Network. IEEE Trans. Netw. Serv. Manag. 2022, 19, 1191–1202. [Google Scholar] [CrossRef]
- Malathy, V.; Saritha, S.; Latha, M.; Hasmukhlal, D.J.; Rawat, S.; Tiwari, M. Implementation and Enabling Internet of Things (IoT) in Wireless communication Networks. In Proceedings of the 2023 Global Conference on Information Technologies and Communications (GCITC), Bangalore, India, 1–3 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Saidani, A.; Jianwen, X.; Mansouri, D. A lossless compression approach based on delta encoding and T-RLE in WSNs. Wirel. Commun. Mob. Comput. 2020, 2020, 8824954. [Google Scholar] [CrossRef]
- Levine, J. RFC 6713: The ’Application/Zlib’ and ’Application/Gzip’ Media Types. 2012. Available online: https://www.rfc-editor.org/rfc/rfc6713.html (accessed on 1 February 2025).
- Mochurad, L. A Comparison of Machine Learning-Based and Conventional Technologies for Video Compression. Technologies 2024, 12, 52. [Google Scholar] [CrossRef]
- Fitriya, L.A.; Purboyo, T.W.; Prasasti, A.L. A review of data compression techniques. Int. J. Appl. Eng. Res. 2017, 12, 8956–8963. [Google Scholar]
- Hanumanthaiah, A.; Gopinath, A.; Arun, C.; Hariharan, B.; Murugan, R. Comparison of lossless data compression techniques in low-cost low-power (LCLP) IoT systems. In Proceedings of the 2019 9th International Symposium on Embedded Computing and System Design (ISED), Kollam, India, 13–14 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Ma, Z.; Zhu, H.; He, Z.; Lu, Y.; Song, F. Deep Lossless Compression Algorithm Based on Arithmetic Coding for Power Data. Sensors 2022, 22, 5331. [Google Scholar] [CrossRef]
- Goyal, M.; Tatwawadi, K.; Chandak, S.; Ochoa, I. DZip: Improved general-purpose loss less compression based on novel neural network modeling. In Proceedings of the 2021 Data Compression Conference (DCC), Snowbird, UT, USA, 23–26 March 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 153–162. [Google Scholar]
- Matinyan, S.; Abrahams, J.P. TERSE/PROLIX (TRPX)—A new algorithm for fast and lossless compression and decompression of diffraction and cryo-EM data. Found. Crystallogr. 2023, 79, 536–541. [Google Scholar] [CrossRef]
- Lyu, F.; Xiong, Z.; Li, F.; Yue, Y.; Zhang, N. An effective lossless compression method for attitude data with implementation on FPGA. Sci. Rep. 2025, 15, 13809. [Google Scholar] [CrossRef]
- Agnihotri, S.; Rameshan, R.; Ghosal, R. Lossless Image Compression Using Multi-level Dictionaries: Binary Images. arXiv 2024, arXiv:2406.03087. [Google Scholar]
- Al-Okaily, A.; Tbakhi, A. A novel lossless encoding algorithm for data compression–genomics data as an exemplar. Front. Bioinform. 2025, 4, 1489704. [Google Scholar] [CrossRef]
- Wang, W.; Chen, W.; Yan, L.; Yang, Y.; Zhao, H. Heuristic genetic algorithm parameter optimizer: Making lossless compression algorithms efficient and flexible. Expert Syst. Appl. 2025, 272, 126693. [Google Scholar] [CrossRef]
- Wang, R.; Liu, J.; Sun, H.; Katto, J. Learned Lossless Image Compression With Combined Autoregressive Models And Attention Modules. arXiv 2022, arXiv:2208.13974. [Google Scholar]
- Kang, N.; Qiu, S.; Zhang, S.; Li, Z.; Xia, S.T. Pilc: Practical image lossless compression with an end-to-end gpu oriented neural framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3739–3748. [Google Scholar]
- Wyeth, C.; Bu, D.; Yu, Q.; Gao, W.; Liu, X.; Li, M. Lossless data compression by large models. arxiv 2025, arXiv:2407.07723. [Google Scholar]
- Liu, A.; Mandt, S.; Broeck, G.V.d. Lossless compression with probabilistic circuits. arXiv 2021, arXiv:2111.11632. [Google Scholar]
- Narashiman, S.S.; Chandrachoodan, N. AlphaZip: Neural Network-Enhanced Lossless Text Compression. arXiv 2024, arXiv:2409.15046. [Google Scholar]
- Zhang, J.; Cheng, Z.; Zhao, Y.; Wang, S.; Zhou, D.; Lu, G.; Song, L. L3TC: Leveraging RWKV for Learned Lossless Low-Complexity Text Compression. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 13251–13259. [Google Scholar]
- Carpentieri, B. Data Compression with a Time Limit. Algorithms 2025, 18, 135. [Google Scholar] [CrossRef]
- Alakuijala, J.; Farruggia, A.; Ferragina, P.; Kliuchnikov, E.; Obryk, R.; Szabadka, Z.; Vandevenne, L. Brotli: A general-purpose data compressor. ACM Trans. Inf. Syst. (TOIS) 2018, 37, 1–30. [Google Scholar] [CrossRef]
- Chen, J.; Daverveldt, M.; Al-Ars, Z. Fpga acceleration of zstd compression algorithm. In Proceedings of the 2021 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Portland, OR, USA, 17–21 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 188–191. [Google Scholar]
- Alakuijala, J.; Kliuchnikov, E.; Szabadka, Z.; Vandevenne, L. Comparison of Brotli, Deflate, Zopfli, Lzma, Lzham and Bzip2 Compression Algorithms; Google Inc.: Mountain View, CA, USA, 2015; pp. 1–6. [Google Scholar]
- Gilchrist, J. Parallel data compression with bzip2. In Proceedings of the 16th IASTED International Conference on Parallel and Distributed Computing and Systems, Cambridge, MA, USA, 9–11 November 2004; Citeseer: New York, NY, USA, 2004; Volume 16, pp. 559–564. [Google Scholar]
- Rauschert, P.; Klimets, Y.; Velten, J.; Kummert, A. Very fast gzip compression by means of content addressable memories. In Proceedings of the 2004 IEEE Region 10 Conference TENCON 2004, Chiang Mai, Thailand, 21–24 November 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 500, pp. 391–394. [Google Scholar]
- Almeida, S.; Oliveira, V.; Pina, A.; Melle-Franco, M. Two high-performance alternatives to ZLIB scientific-data compression. In Proceedings of the Computational Science and Its Applications–ICCSA 2014: 14th International Conference, Guimarães, Portugal, 30 June–3 July 2014; Proceedings, Part IV 14. Springer: Berlin/Heidelberg, Germany, 2014; pp. 623–638. [Google Scholar]
- Bharadwaj, S. Using convolutional neural networks to detect compression algorithms. In Proceedings of the International Conference on Communication and Computational Technologies: ICCCT 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 33–45. [Google Scholar]
- Čegan, L. Empirical study on effects of compression algorithms in web environment. J. Telecommun. Electron. Comput. Eng. (JTEC) 2017, 9, 69–72. [Google Scholar]
- Gæde, E.T.; van der Hoog, I.; Rotenberg, E.; Stordalen, T. Dynamic Indexing Through Learned Indices with Worst-case Guarantees. arXiv 2025, arXiv:2503.05007. [Google Scholar]
- Ryzhikov, V.; Walega, P.A.; Zakharyaschev, M. Data Complexity and Rewritability of Ontology-Mediated Queries in Metric Temporal Logic under the Event-Based Semantics (Full Version). arXiv 2019, arXiv:1905.12990. [Google Scholar]
- Frigo, M.; Strumpen, V. The cache complexity of multithreaded cache oblivious algorithms. In Proceedings of the Eighteenth Annual ACM Symposium on Parallelism in Algorithms and Architectures, Cambridge, MA, USA, 30 July–2 August 2006; pp. 271–280. [Google Scholar]
- Tang, Y.; Gao, W. Processor-Aware Cache-Oblivious Algorithms. In Proceedings of the 50th International Conference on Parallel Processing, Lemont, IL, USA, 9–12 August 2021; pp. 1–10. [Google Scholar]
- Sun, J.; Chowdhary, G. CoMusion: Towards Consistent Stochastic Human Motion Prediction via Motion Diffusion. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2024; pp. 18–36. [Google Scholar]
- Pan, R. Efficient stochastic human motion prediction via consistency model. In Proceedings of the Fourth International Conference on Computer Vision, Application, and Algorithm (CVAA 2024), Chengdu, China, 11–13 October 2024; SPIE: Bellingham, WA, USA, 2025; Volume 13486, pp. 821–826. [Google Scholar]
- Li, X.; Xiao, M.; Yu, D.; Lee, R.; Zhang, X. UltraPrecise: A GPU-Based Framework for Arbitrary-Precision Arithmetic in Database Systems. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), Utrecht, The Netherlands, 13–17 May 2024; pp. 3837–3850. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.H.; Kim, S.; Park, J.; Yoo, K.M.; Kwon, S.J.; Lee, D. Memory-efficient fine-tuning of compressed large language models via sub-4-bit integer quantization. Adv. Neural Inf. Process. Syst. 2023, 36, 36187–36207. [Google Scholar]
- Williams, A.; Ordaz, J.D.; Budnick, H.; Desai, V.R.; Bmbch, J.T.; Raskin, J.S. Accuracy of depth electrodes is not time-dependent in robot-assisted stereoelectroencephalography in a pediatric population. Oper. Neurosurg. 2023, 25, 269–277. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Zhou, H.; Wen, Y.; Wang, P. Accuracy Analysis of Interpolation Method for Abrupt Change of Seabed Water Depth. In Proceedings of the 2022 3rd International Conference on Geology, Mapping and Remote Sensing (ICGMRS), Zhoushan, China, 22–24 April 2022; pp. 818–821. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, L.; Chen, Y.; Yin, H. Finite-Precision Arithmetic Transceiver for Massive MIMO Systems. IEEE J. Sel. Areas Commun. 2025, 43, 688–704. [Google Scholar] [CrossRef]
- Kim, S.; Norris, C.J.; Oelund, J.I.; Rutenbar, R.A. Area-Efficient Iterative Logarithmic Approximate Multipliers for IEEE 754 and Posit Numbers. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2024, 32, 455–467. [Google Scholar] [CrossRef]
- Hao, Z.; Luo, Y.; Wang, Z.; Hu, H.; An, J. Model Compression via Collaborative Data-Free Knowledge Distillation for Edge Intelligence. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, Z.; Pan, W.D.; Shen, H. Universal Golomb–Rice Coding Parameter Estimation Using Deep Belief Networks for Hyperspectral Image Compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 3830–3840. [Google Scholar] [CrossRef]
- Hwang, I.; Yun, J.; Kim, C.G.; Park, W.C. A Memory Bandwidth-efficient Architecture for Lossless Compression Using Multiple DPCM Golomb-rice Algorithm. In Proceedings of the 2019 International Symposium on Multimedia and Communication Technology (ISMAC), Quezon City, Philippines, 19–21 August 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, Z.; Fang, P.; Liu, C.; Xiao, X.; Wen, Y.; Meng, D. DEPCOMM: Graph Summarization on System Audit Logs for Attack Investigation. In Proceedings of the 2022 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 23–26 May 2022; pp. 540–557. [Google Scholar] [CrossRef]
- Minnen, D.; Singh, S. Channel-Wise Autoregressive Entropy Models for Learned Image Compression. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Virtual, 25–28 October 2020; pp. 3339–3343. [Google Scholar] [CrossRef]
- Shekhara Kaushik Valmeekam, C.; Narayanan, K.; Kalathil, D.; Chamberland, J.F.; Shakkottai, S. LLMZip: Lossless Text Compression using Large Language Models. arXiv 2023, arXiv:2306.04050. [Google Scholar]
- Chang, B.; Wang, Z.; Li, S.; Zhou, F.; Wen, Y.; Zhang, B. TurboLog: A Turbocharged Lossless Compression Method for System Logs via Transformer. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; pp. 1–10. [Google Scholar] [CrossRef]
- Li, M.; Jin, R.; Xiang, L.; Shen, K.; Cui, S. Crossword: A semantic approach to data compression via masking. arXiv 2023, arXiv:2304.01106. [Google Scholar]
- Alevizos, V.; Yue, Z.; Edralin, S.; Xu, C.; Georlimos, N.; Papakostas, G.A. Biomimicry-Inspired Automated Machine Learning Fit-for-Purpose Wastewater Treatment for Sustainable Water Reuse. Water 2025, 17, 1395. [Google Scholar] [CrossRef]

| Metric | LPPIE | Zstd | Brotli |
|---|---|---|---|
| Speed | Moderate | Rapid | Rapid |
| Efficiency | High | Medium | Medium |
| Applicability | Numeric streams | General files | Web payload |
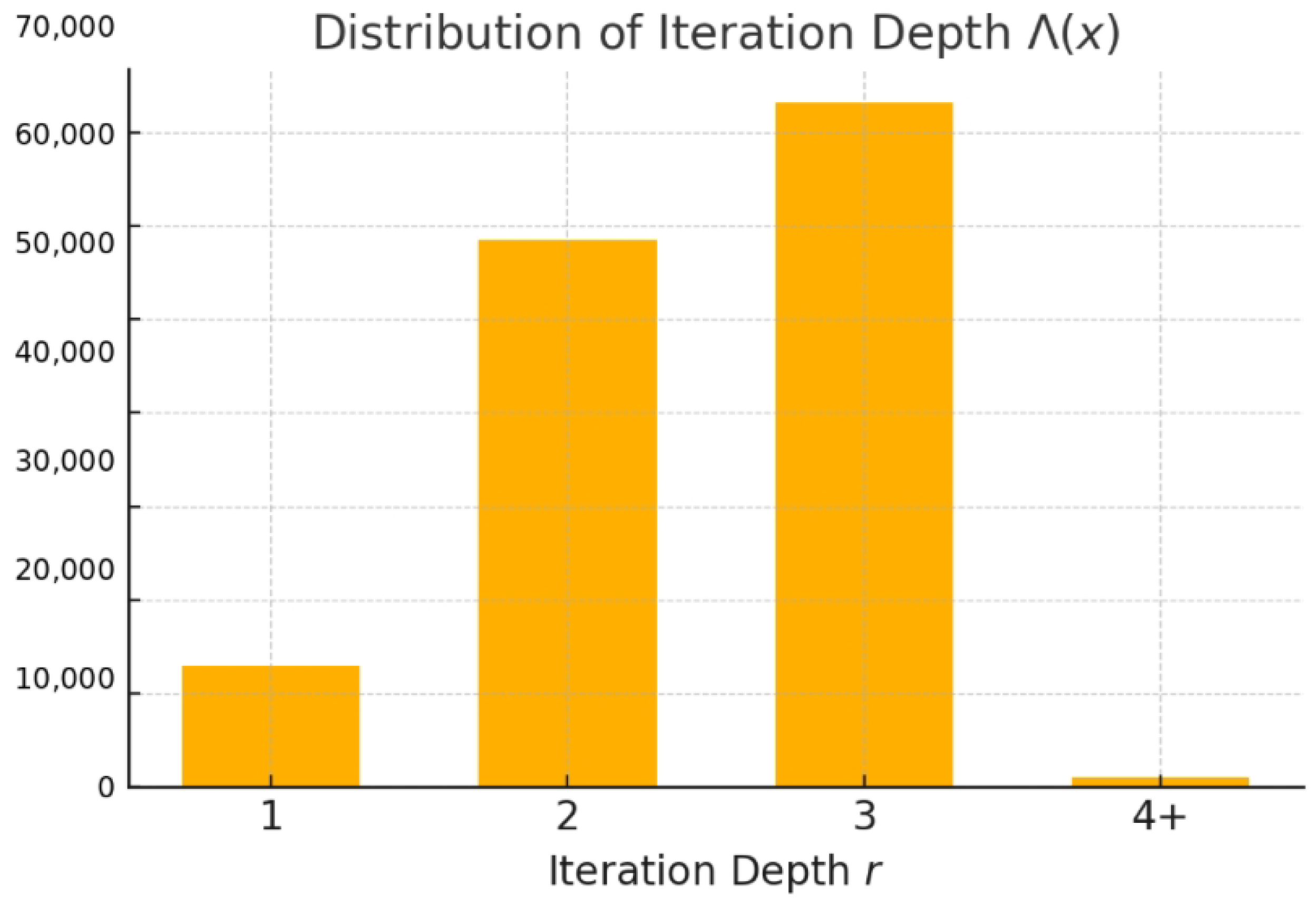
| r | 1 | 2 | 3 | 4+ |
|---|---|---|---|---|
| Count | 12,871 | 58,402 | 73,119 | 1066 |
| Ratio % | 7.4 | 33.6 | 42.1 | 0.6 |
| Strategy | RAM (MB) | CPU (ms) |
|---|---|---|
| Static FP64 (64-bit floating point) | 512 | 140 |
| Adaptive Mantissa | 256 | 90 |
| MTGP | 128 | 70 |
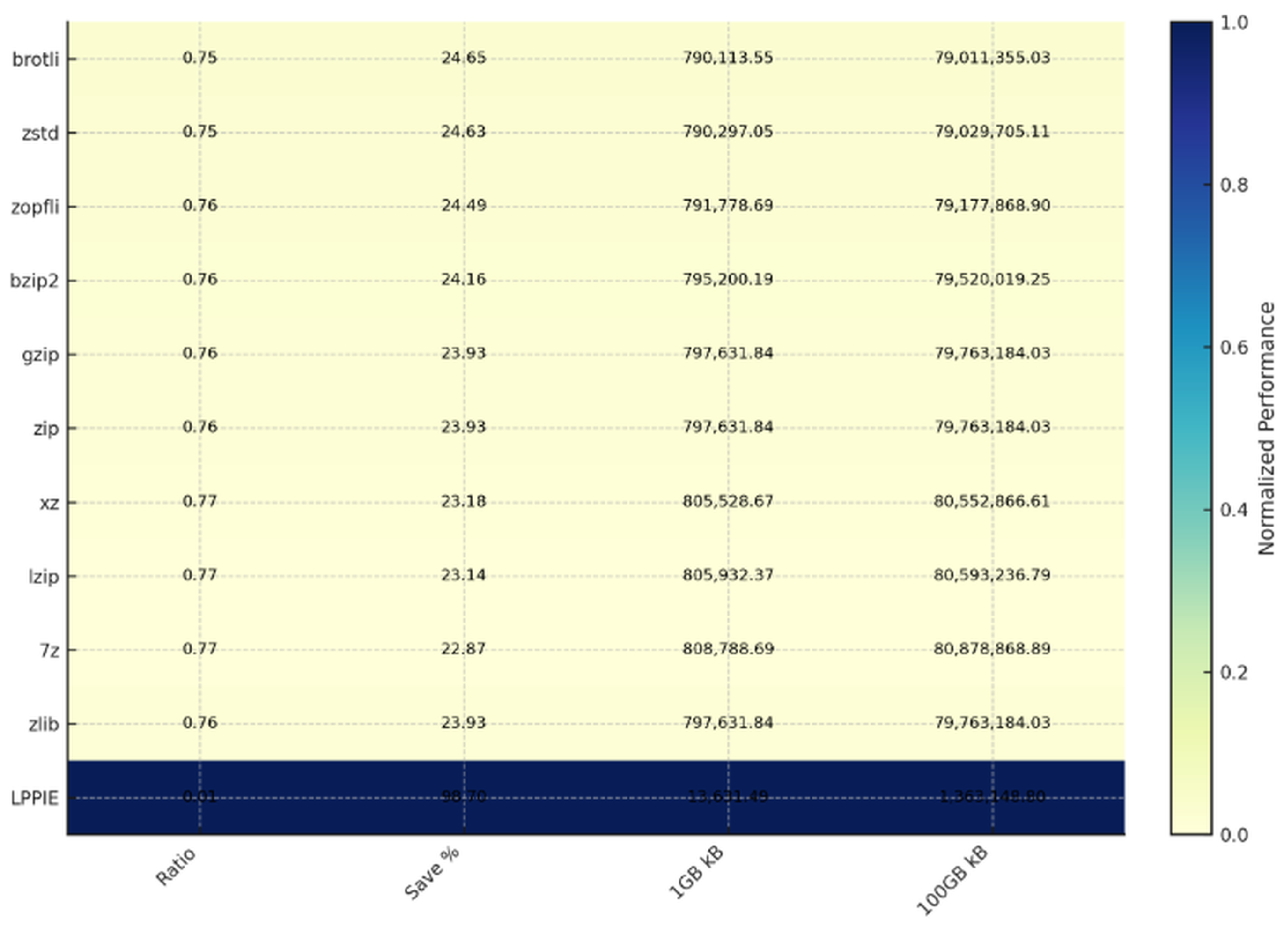
| Algorithm | Ratio | Save % | 1 GB kB | 100 GB kB |
|---|---|---|---|---|
| brotli | ||||
| zstd | ||||
| zopfli | ||||
| bzip2 | ||||
| gzip | ||||
| zip | ||||
| xz | ||||
| lzip | ||||
| 7z | ||||
| zlib | ||||
| LPPIE |
| Pivot | Ratio | Time | Memory |
|---|---|---|---|
| Partitioning | 0.18 | 1.0 | 1.2 |
| Precision scheduling | 0.22 | 0.9 | 1.1 |
| Golomb–Rice | 0.24 | 0.95 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alevizos, V.; Yue, Z.; Edralin, S.; Xu, C.; Gerolimos, N.; Papakostas, G.A. A Logarithmic Compression Method for Magnitude-Rich Data: The LPPIE Approach. Technologies 2025, 13, 278. https://doi.org/10.3390/technologies13070278
Alevizos V, Yue Z, Edralin S, Xu C, Gerolimos N, Papakostas GA. A Logarithmic Compression Method for Magnitude-Rich Data: The LPPIE Approach. Technologies. 2025; 13(7):278. https://doi.org/10.3390/technologies13070278
Chicago/Turabian StyleAlevizos, Vasileios, Zongliang Yue, Sabrina Edralin, Clark Xu, Nikitas Gerolimos, and George A. Papakostas. 2025. "A Logarithmic Compression Method for Magnitude-Rich Data: The LPPIE Approach" Technologies 13, no. 7: 278. https://doi.org/10.3390/technologies13070278
APA StyleAlevizos, V., Yue, Z., Edralin, S., Xu, C., Gerolimos, N., & Papakostas, G. A. (2025). A Logarithmic Compression Method for Magnitude-Rich Data: The LPPIE Approach. Technologies, 13(7), 278. https://doi.org/10.3390/technologies13070278








