1. Introduction
As the global population continues to increase, so does the energy demand; hence, this demand has placed significant pressure on existing energy resources and infrastructure [
1]. A significant portion of the global population experiences daily power outages due to insufficient electricity production, making it essential to discover and develop efficient technologies for harnessing electrical energy [
2]. Although conventional fossil fuels are most abundantly used for the generation of electric power, they are depleting at a fast pace and causing adverse environmental effects due to carbon emissions [
3]. At the current pace of consumption, fossil fuels will be depleted in the near future if rising energy demand is not taken into account [
4]. Renewable energy sources (RESs), particularly photovoltaic (PV), have emerged as a leading source of energy today, due to cost-effectiveness and environmental advantages [
5]. However, a study related to long-term monitoring of PV power plants reveals that first-tier PV panels, particularly in moderate climates, often begin to degrade or fail after approximately 10–12 years [
6]. Due to this, maximum power extraction from PV systems is necessary to make them more reliable, economically viable, and capable of compensating for the gradual degradation of panels over their operational lifespan.
Maximum power point tracking (MPPT) plays a substantial role in reducing inefficiencies associated with solar power systems. By continuously adjusting the operating point, MPPT ensures that the PV system generates maximum possible power, minimizing energy losses and enhancing overall system performance [
7]. To ensure the system operates at its maximum power point (MPP) under varying conditions, MPPT algorithms have been instrumental in optimizing energy harvesting from PV panels [
8]. These algorithms have played a significant role in harvesting energy and significantly improved the efficiency and reliability of solar energy systems [
9,
10]. However, despite their importance, conventional MPPT controllers still have limitations in terms of tracking speed and accuracy, requiring a viable solution that reduces the cost of solar power and enhances its efficiency [
11]. Researchers have developed a range of both simple and complex techniques to enhance energy harvesting, energy conversion, power tracking efficiency, etc. However, there remains significant potential for improvement [
12].
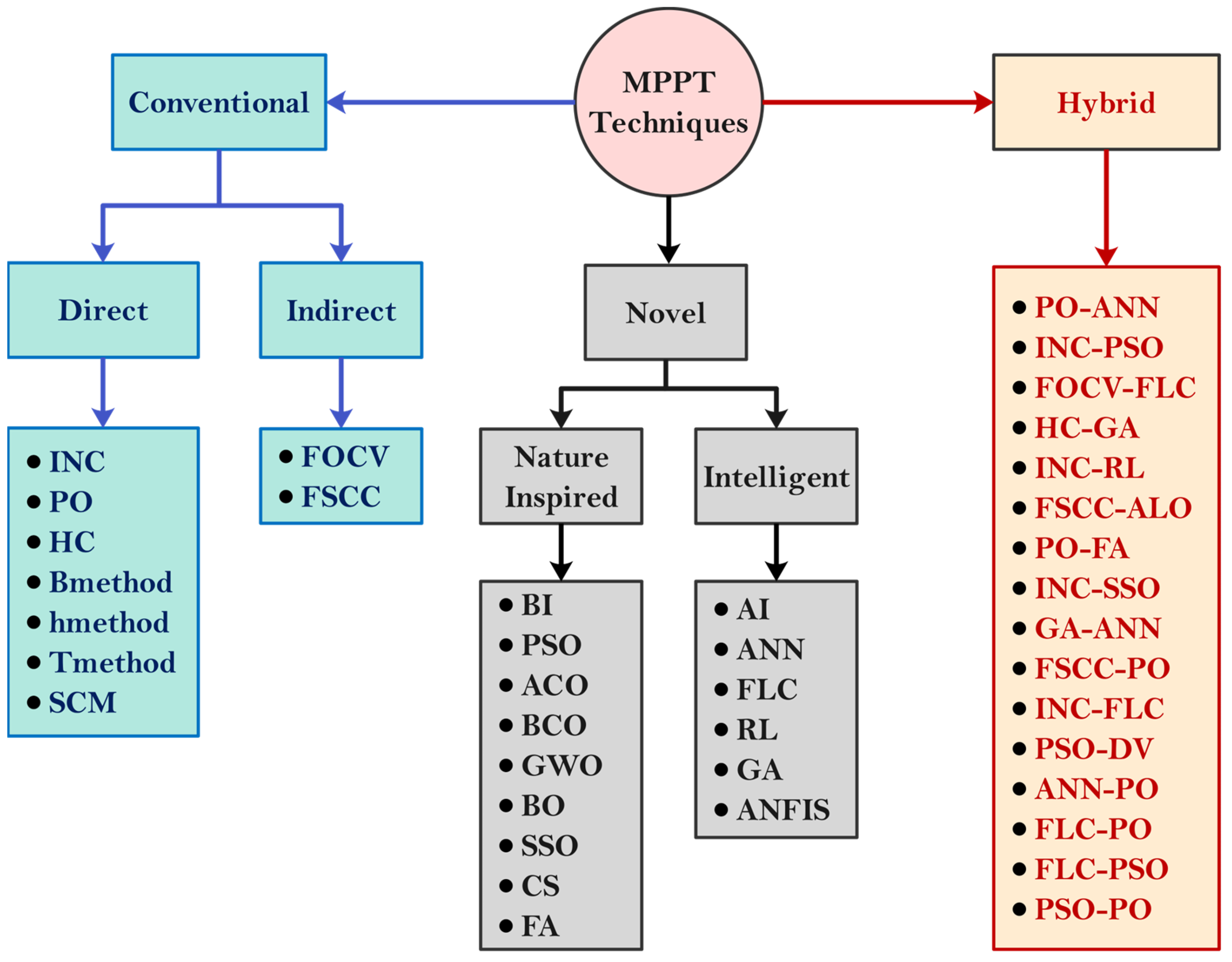
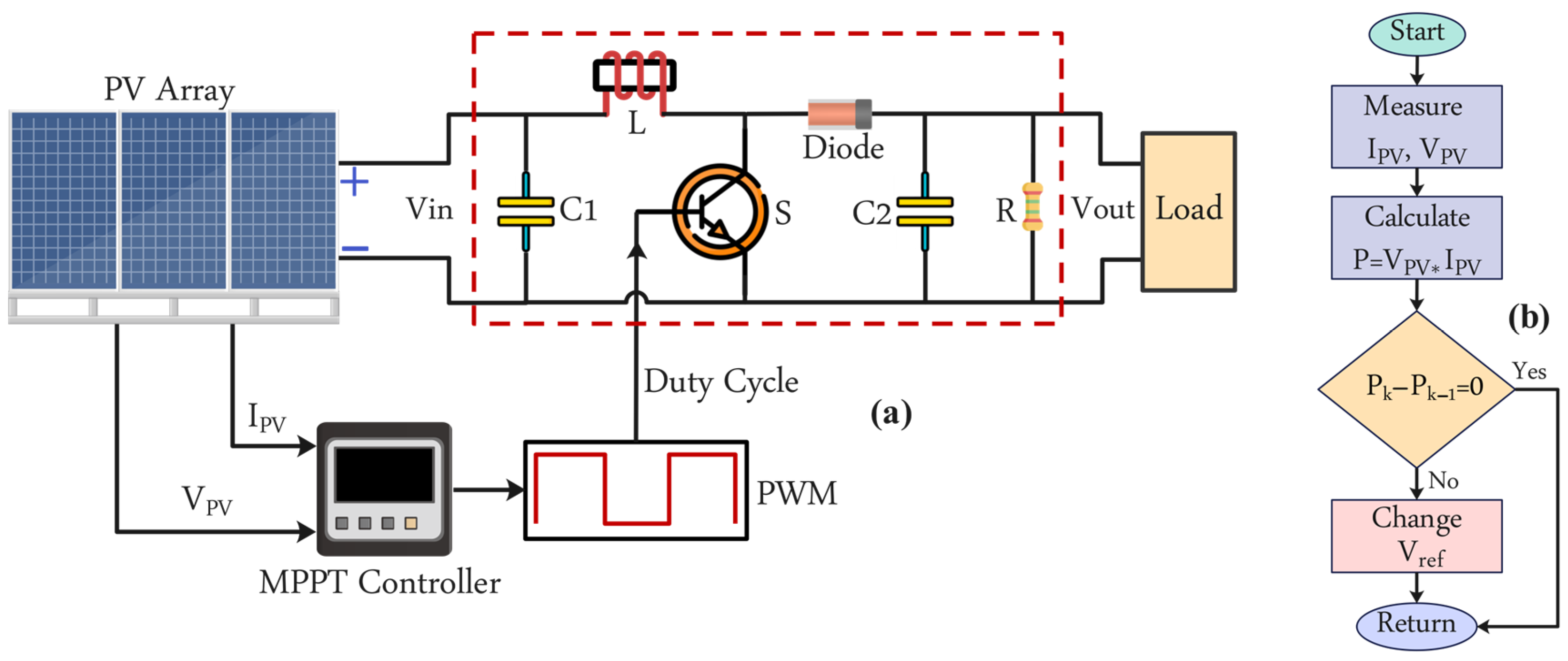
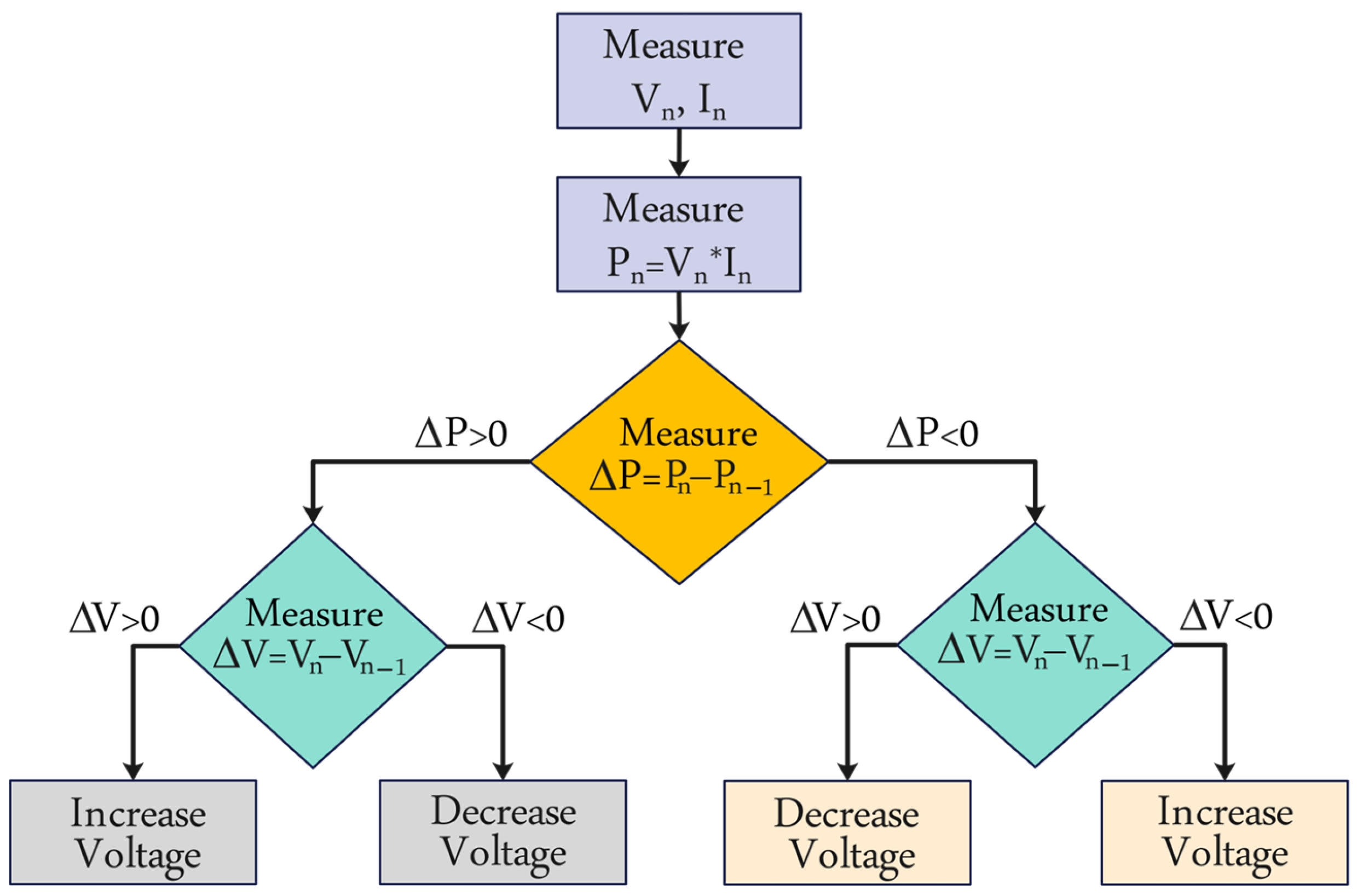
Conventional MPPT control methods are easy to implement due to the relative simplicity of these algorithms; one such algorithm is perturb and observe (P&O) [
13]. The P&O technique is more well-known because of its flexibility and adaptability [
14]. However, one of the principal disadvantages of this conventional MPPT technique is the sharp fluctuations around the MPP. These fluctuations can lead to power losses over time, and frequently overlook the impact of solar converters, making it difficult to accurately track the true MPP [
15].
Metaheuristic algorithms are advanced optimization techniques designed to address complex problems that are beyond the reach of traditional methods [
16]. They are particularly useful when the search space is large, complex, or contains diverse regions, which is often the case in PV systems. One major category of metaheuristic control algorithms is bio-inspired control algorithms [
17]. These algorithms draw inspiration from natural processes and systems to enhance their ability to extract electric power efficiently. By mimicking biological mechanisms and behaviors found in nature, bio-inspired control algorithms are designed to optimize performance and improve energy harvesting in PV systems [
18]. They can address the rapid irradiance fluctuations by replicating natural systems and processes. These controllers employ their own set of modern techniques to maximize energy collection and enhance the operational efficiency of the system [
19].
Nature-inspired algorithms have gained popularity over time due to their ability to solve several complex optimization issues efficiently. These algorithms represent biological processes such as natural selection, swarm behavior, and evolutionary adaptation to find optimal or near-optimal solutions under uncertain environmental conditions [
20]. The particle swarm optimization (PSO) algorithm is inspired by the social behavior of birds and fishes. Its main advantages include fast convergence and implementation simplicity. It can handle nonlinear and multidimensional optimization problems, which makes it suitable for using varying solar irradiance and temperature conditions. However, one of the disadvantages is that it may encounter premature convergence to local optima, necessitating careful parameter tuning to overcome this issue [
21].
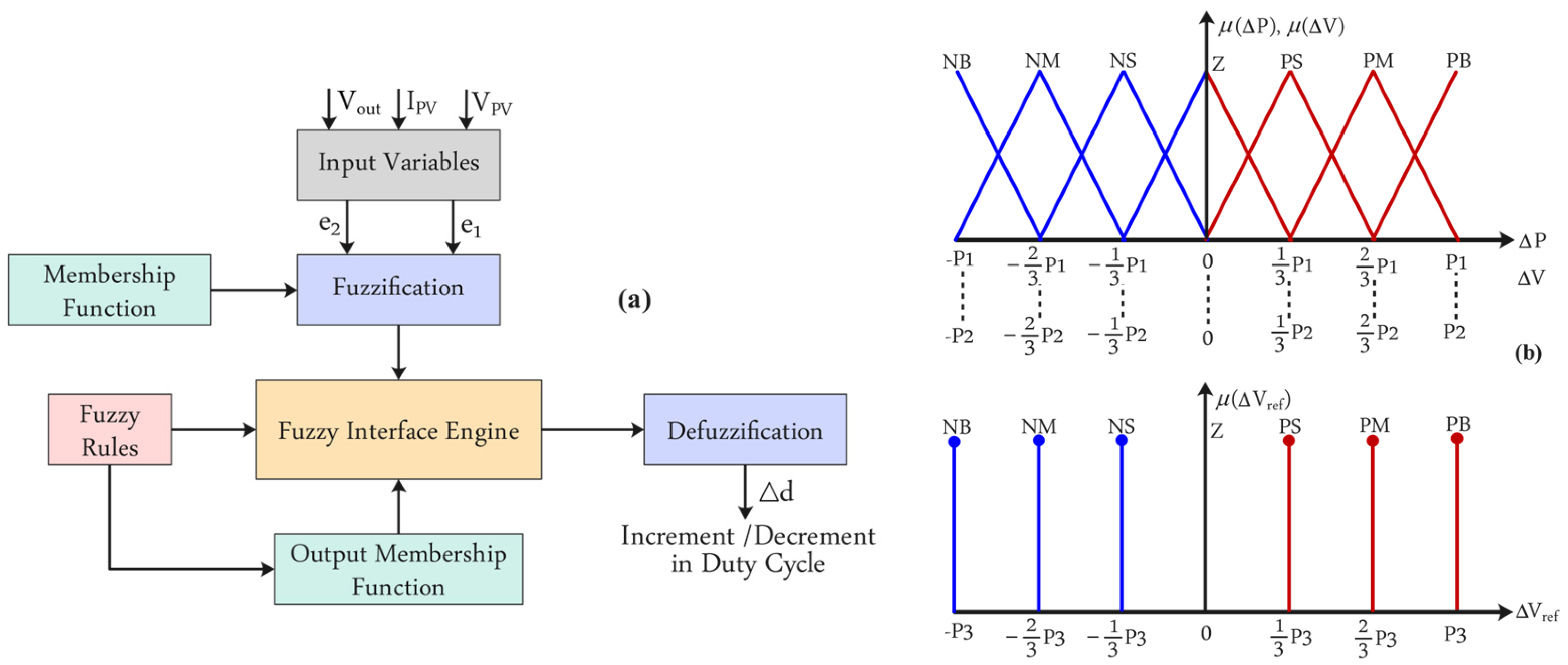
Intelligent MPPT controllers represent a significant advancement in improving the power tracking efficiency of PV systems. These controllers have better tracking speeds and power extraction capabilities compared with conventional MPPT controllers. Fuzzy logic (FL) control is a state-of-the-art technique widely utilized in this domain [
22]. It offers significant advantages, including adaptability to nonlinear behavior and varying environmental conditions. It is capable of providing fast and accurate power tracking without the need for a specified mathematical model, which has resulted in reducing power losses and improving overall system efficiency. However, designing an effective FL control system is challenging due to the need for precisely tuned fuzzy rules and membership functions. Despite these drawbacks, FL is widely applied in PV systems for enhancing power tracking performance.
Hybrid MPPT controllers combine multiple types of MPPT controllers into a single unit and incorporate the strengths of each to enhance energy extraction efficiency [
23]. Combining specific features of different controllers into a single unit can result in an effective hybrid MPPT controller, which offers enhanced power extraction for PV systems [
24]. Such advancement signifies the considerable effort to provide sustainable solutions that can address the energy imbalance that plagued world economies [
25]. Hybridization techniques are especially useful in cases where a single controller is less efficient in finding MPP. A study by [
26] proposed a hybrid MPPT method that integrates PSO and P&O (PSO-P&O) for PV systems to track the global maxima. Results obtained show that the hybrid method has a faster tacking speed than conventional PSO and converges more rapidly. A modified version of the P&O MPPT algorithm has been designed using an adaptive duty cycle PID (proportional-integral-derivative) controller that was tuned by genetic algorithms (GAs) [
27]. This approach has significantly improved the tracking efficiency and power extraction under dynamic environments.
A hybrid PSO–Incremental Conductance (PSO-INC)-based algorithm was designed by [
28] to obtain efficient solar power tracking for PV systems. The technique has demonstrated superior peak power tracking and performance. To help in navigating the system to its global MPP, ant colony optimization (ACO) and PSO (ACO-PSO) have been embedded to boost the efficiency of the PV systems [
29]. In a recent study, a hybrid MPPT method comprising PSO and an adaptive neuro-fuzzy inference system (PSO-ANFIS) was employed to achieve faster and more accurate tracking of maximum PV power, ensuring optimal energy extraction [
30]. A high-speed MPPT control approach using a hybrid PSO and PID (PSO-PID) controller has been used to enhance the tracking efficiency of PV systems [
31].
The study [
32] used a hybrid MPPT, i.e., GA-P&O, for analyzing performance factors like oscillations, power extraction, and implementation complexity. The modified grey wolf optimization-based adaptive neuro-fuzzy inference system (GWO-ANFIS) method demonstrates superior tracking speed and stability [
33]. The performance of the hybrid MPPT controller, i.e., artificial neural network and PSO (ANN-PSO), was investigated and compared with the P&O algorithm [
34]. The results obtained indicate that the PSO-trained ANN outperformed in terms of time response, oscillation minimization, and tracking speed. PSO with an FL (PSO-FL) approach for MPPT was employed for PV systems to address the limitations of traditional PSO. The results obtained indicate that the hybrid PSO-FL surpasses standard PSO in tracking efficiency, stability, and oscillation reduction, significantly enhancing the system’s overall performance under both normal and partial shading conditions [
35]. In [
36], the authors integrate the PSO and cuckoo search algorithm (PSO-CS) to harvest the possible maximum PV power. Furthermore, an FL and modified shuffled frog leaping algorithm (FL-MSFLA) has been developed by [
37] for MPPT. Compared to other techniques, the proposed system has shown better performance in both transient and steady-state conditions, providing effective power flow management between the grid and the combined energy system.
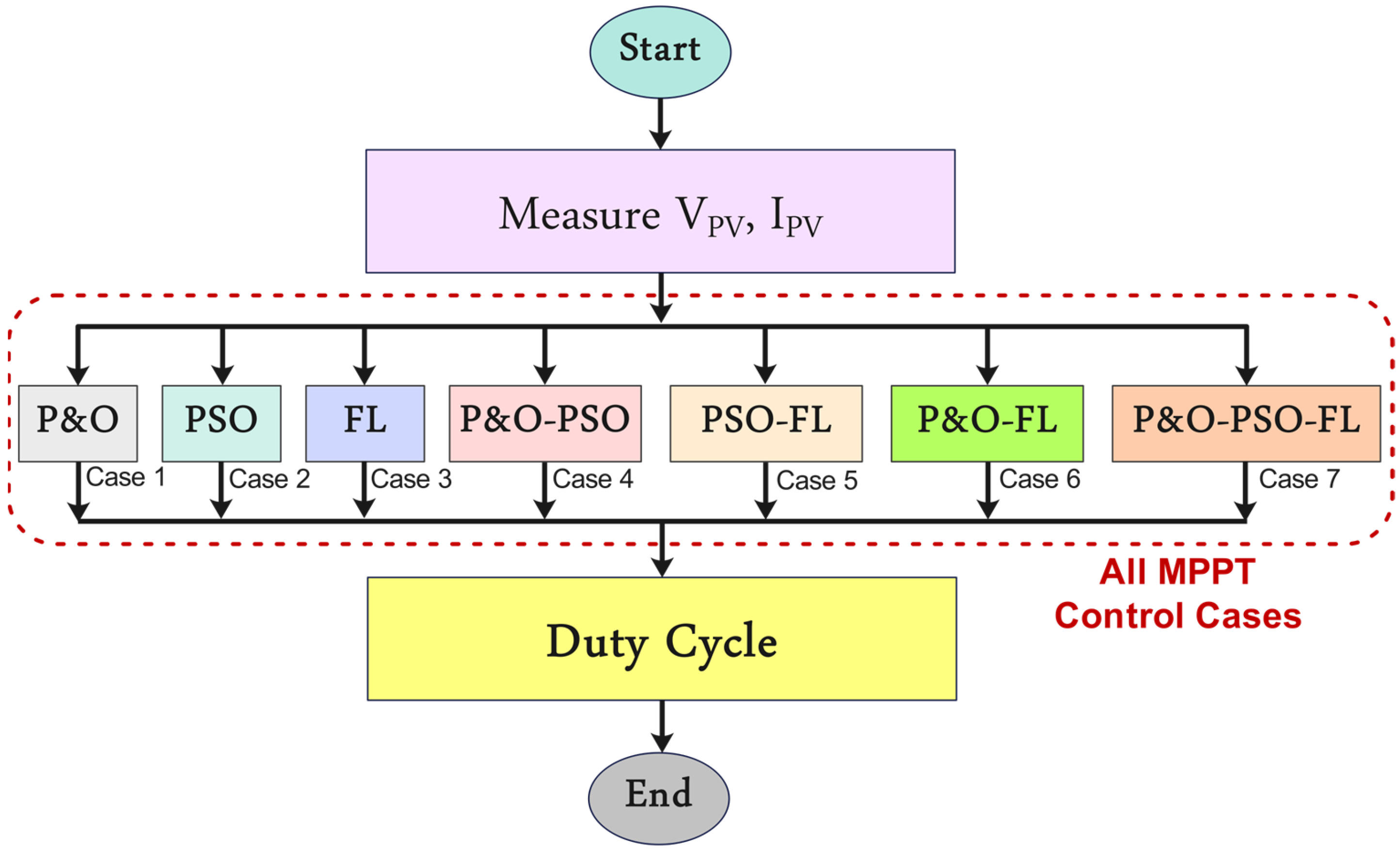
Although substantial research has been conducted on hybrid MPPT controllers combining two techniques, very few studies have explored the integration of more than two MPPT controllers. The main objective of this research is to optimize the performance of a standalone PV system and improve its output characteristics by utilizing both individual and hybrid MPPT algorithms. The proposed research aims to fill the gap by the utilization of individual as well as the combination of three distinct types of MPPT controllers, i.e., conventional (P&O), nature-inspired (PSO), and intelligent (FL). In addition to implementing individual and dual combinations of MPPT controllers, a hybrid P&O-PSO-FL controller is proposed and developed for a standalone PV system using MATLAB/SIMULINK, version R2022a. The primary goal is to capitalize on the strengths of each method to improve tracking speed, ensure faster convergence to the MPP, and increase overall power extraction efficiency. The novelty of this research lies in the development of a triple-hybrid MPPT controller (P&O-PSO-FL), which optimally integrates conventional, nature-inspired, and intelligent algorithms to enhance the efficiency of standalone PV systems. Unlike previous studies that focus on single or dual MPPT approaches, this research introduces a unique synergistic hybridization that capitalizes on the strengths of each algorithm while mitigating their limitations. This research offers a significant step forward in optimizing solar energy harvesting, particularly in standalone PV systems where efficiency and resilience are critical factors.
This research paper starts with an introduction that consists of the research background.
Section 2 presents the PV diode model configuration,
Section 3 discusses the MPPT classification, and
Section 4 provides an overview of the methodology used for this research work.
Section 5 presents the results, followed by the conclusion and references in the subsequent sections.
5. Results and Discussion
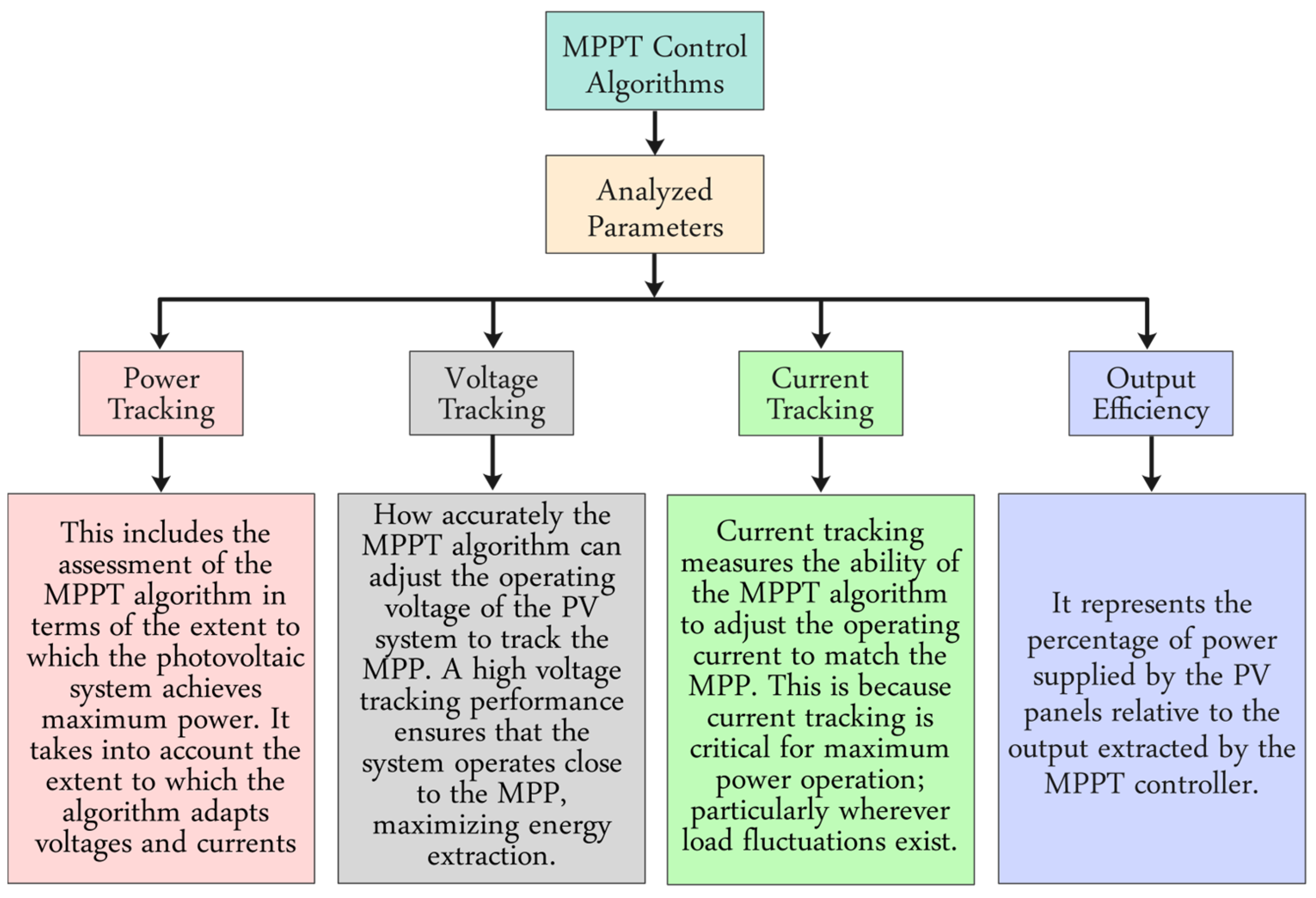
The proposed analysis assists in selecting the optimal MPPT algorithm for a PV system by evaluating parameters like power tracking, voltage tracking, current tracking, and output efficiency. By analyzing the results and evaluations of the outputs generated using P&O, PSO, and FL optimization algorithms, the most effective optimization approach can be easily determined. The performance of the designed system was assessed using two scenarios. Simulations were carried out under constant temperature and irradiance in the first scenario for power, voltage, current, and output efficiency as detailed in
Section 5.1,
Section 5.2 and
Section 5.3. In the second scenario, the power tracking results of all MPPT controllers at varying operating conditions are presented in
Section 5.4. The evaluation of MPPT algorithms in PV systems involves analyzing various key performance metrics, as illustrated in
Figure 9.
Table 4 provides the PV module specifications utilized in the proposed simulation models.
The tracking efficiency of the individual and hybrid MPPT controllers was evaluated by a MATLAB/SIMULINK model designed for a standalone PV system that consists of four PV panels with a rating of 213.15 watts each. The efficiency of each MPPT algorithm was calculated as the ratio of the MPP achieved by the algorithm to the total maximum power output of the four PV panels (852.6 W under standard test conditions). This method provides a standardized measure to compare the performance of different algorithms under the same conditions.
5.1. Simulated Results for Individual MPPT Controllers (P&O, PSO, and FL)
The tracking efficiencies of the individual MPPT controllers were evaluated by analyzing the output power, voltage, and current graphs for all the proposed cases. The tracking efficiencies of the P&O MPPT controller output power, voltage, and current are presented in
Figure 10a–c. The average value of the output power tracked for this controller was 832.5 watts (W). The corresponding output voltage and current when the system operates at MPP are 64.485 volts (V) and 12.91 amperes (A), respectively. These output parameters show that the controller can effectively control the power output of the PV system to the optimum level.
The tracking performances of the PSO MPPT controller output power, voltage, and current are shown in
Figure 11a–c. For a PSO-based MPPT controller, the average recorded output power is approximately 770 W. The output voltage and the output current at MPP are observed to be 61.0366 V and 12.407 A, respectively. These values show that the controller is capable of providing the desired power output of the PV system.
The tracking efficiencies of the FL MPPT controller are evaluated by determining the power, voltage, and current output graphs presented in
Figure 12a–c. It can be observed that the tracked output power is identified as 768.7 W, with a voltage of 62.03 V and a current of 12.39 A. The results indicate that the controller is useful in ensuring that the PV system harvests its maximum output. Although the P&O MPPT controller achieved a higher output power, it exhibited greater fluctuations compared to the FL & PSO MPPT, which provided a more stable power output. Stability in power delivery is crucial for system efficiency and overall performance.
For individual MPPT controllers, the P&O algorithm has a relatively quick response reaching the MPP at t = 0.1 s. However, it shows fluctuations in the power at MPP, which can result in reduced efficiency for this controller. PSO takes t = 0.22 s; it shows excellent performance in tracking the global MPP, which makes it best for use under dynamic conditions. The FL MPPT controller tracks the MPP much faster, at t = 0.006 s, and offers a more stable output. Keeping in view the limitations of the individual MPPT controllers, hybrid MPPT controllers were developed to gain improved performance and faster convergence.
5.2. Results for Dual-Hybrid MPPT Controllers (P&O-PSO, PSO-FL, and P&O-FL)
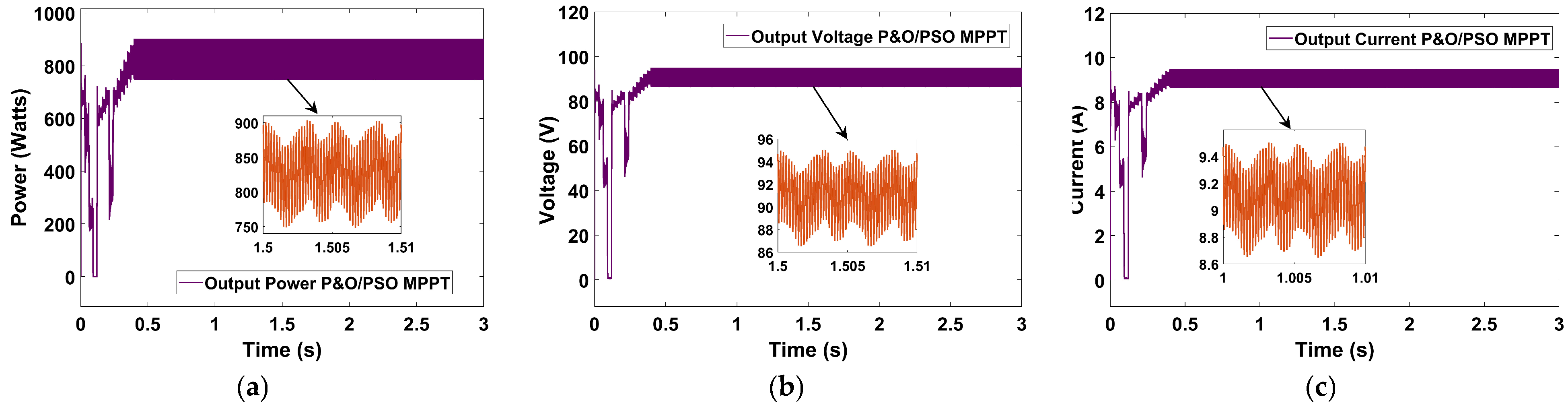
The performance of the proposed dual-hybrid MPPT controllers was evaluated by analyzing the tracking efficiencies in terms of output power, voltage, and current of the system. The tracking efficiencies of the P&O-PSO MPPT controller, namely, output power, voltage, and current, are illustrated in
Figure 13a–c. The controller results demonstrate that the tracked output power reached 825.58 W, having an output voltage of 90.8 V and a current of 9.09 A. The obtained results demonstrate the ability of the hybrid MPPT controller to effectively harvest the power output of the PV system. The achieved higher voltage and current confirmed the enhanced performance of the hybrid technique in delivering optimum output power.
The tracking efficiencies of the PSO-FL MPPT controller were assessed by computing the harvested power, voltage, and current, as displayed in
Figure 14a–c. The tracked harvested power was 822 W with an output voltage of 127. 75 V and an output current of 6.19 A. These results validate that the utilization of the PSO-FL MPPT controller contributes to higher energy conversion efficiency in contrast to the individual MPPT controller. It increases power extraction, which makes it an effective solution for increasing PV energy production.
The performance of the P&O-FL MPPT controller was also analyzed by the tracking efficiency of the output power, voltage, and current, as shown in
Figure 15a–c. The output power obtained was 823 W with a corresponding voltage of 128.2 V and a current of 6.42 A. Such values prove that the controller equally performs well in the maximum power extraction of the PV system from having a stable power output. This integration enhances the power output and system efficiency and is, therefore, a solution that can be used to maximize the utilization of solar energy.
The P&O-PSO hybrid controller reaches the MPP at t = 0.35 s, while the PSO-FL controller is faster, achieving it at t = 0.3 s. In comparison, the P&O-FL controller reaches the MPP at t = 0.045 s, considerably faster than both the P&O-PSO and PSO-FL controllers, ensuring stable power delivery. Although these hybrid MPPT controllers offer improved performance, further advancements are necessary to achieve optimal results. The limitations of both individual and dual-hybrid MPPT controllers highlight the need for more sophisticated solutions, paving the way for the development of triple-hybrid MPPT controllers.
5.3. Results for Proposed Hybrid Tri-MPPT Controller (P&O-PSO-FL)
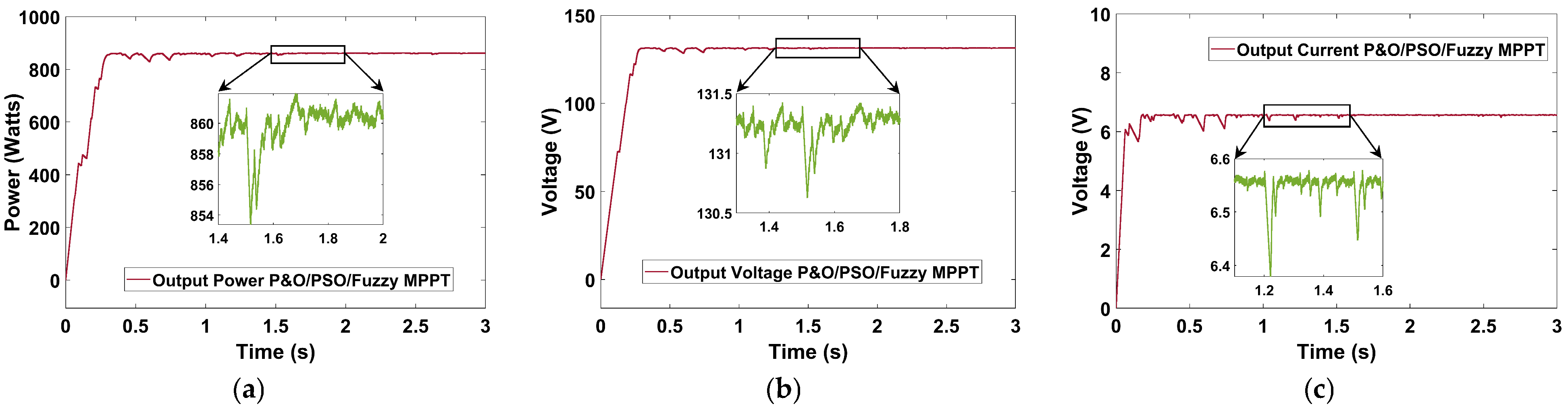
The efficiency of the proposed P&O-PSO-FL MPPT controller was evaluated through the tracked output power, voltage, and current of the PV system, as shown in
Figure 16a–c. The controller provides a tracked output power of 848.5 W with a corresponding output voltage of 130.75 V and a current of 6.49 A. The results confirm the improved efficiency of the triple-hybrid MPPT controller compared with the individual and dual-hybrid MPPT controllers. This combination significantly boosts power extraction, making it an excellent choice for optimizing solar energy extraction.
For triple-hybrid MPPT controllers, the P&O-PSO-FL combination offers the best performance. It reaches the MPP rapidly at t = 0.02 s and delivers stable output power at the MPP. By combining the global optimization of PSO, the adaptability of FL, and the simplicity of P&O, this triple-hybrid system addresses the limitations of individual and dual-hybrid controllers, achieving both fast convergence and stability. As a result, the P&O-PSO-FL hybrid emerges as the most efficient and stable configuration for maximizing PV system performance in the proposed study.
5.4. Power Tracking Results of MPPT Controllers at Varying Operating Conditions
The performance of the proposed MPPT controllers was also evaluated under varying operating conditions by introducing step variations in temperature and irradiance to assess power tracking efficiency. The temperature has been raised from 25 °C to 50 °C, and the irradiance has changed from 400 W/m
2 to 1000 W/m
2 in various steps, respectively. The introduced variations in irradiance and temperature are shown in
Figure 17.
The output power tracked by various MPPT controllers at varying operating conditions is shown in
Figure 18a–g. The results demonstrate how well the MPPT controllers tracked parameter variations, dynamically adjusting the MPP to ensure optimal power extraction. Despite the variations in temperature and irradiance, the controllers are able to maintain tracking efficiency levels similar to the uniform operating conditions.
A summary of the output parameters measured for both individual and hybrid MPPT controllers is provided in
Table 5. A graphical representation of this comparison is shown in
Figure 19a–d.
The P&O controller has produced an output power of 832.5 W with an efficiency of 97.6%. However, P&O has its limitations, including fluctuations around the MPP and a relatively slow response to dynamic conditions. On the other hand, the PSO MPPT controller produced an output power of 770 watts with an efficiency of 90.3%. In contrast to P&O, this control strategy’s convergence accuracy increased significantly. The results demonstrate that PSO is highly effective for global optimization and avoids becoming trapped in local minima. The FL MPPT controller, which extracted 768.7 W of power with an efficiency of 90.1%, was observed to adapt rapidly to dynamic conditions.
Comparing the performance of these individual MPPT controllers, the P&O controller provides high efficiency but is limited by fluctuations around the MPP. In contrast, the PSO controller offers better accuracy in convergence and effectively avoids local minima, although its efficiency is slightly lower. The FL controller excels in adapting quickly to dynamic conditions, providing greater flexibility, but it demands a more complex design approach. Combining FL with other MPPT control techniques could address these issues and improve its overall effectiveness.
It has been observed that hybrid MPPT controllers offer better power extraction performance compared to individual methods. The hybridization of P&O with PSO has an output power of 825.58 W and an efficiency of 96.8%. The technique successfully merged P&O’s rapid convergence capability with PSO’s global optimization characteristic to achieve better tracking performance. The hybrid controller consisting of PSO and FL has an output of 822 W and 96.4% efficiency, and integrates global search with adaptive control, proving its effectiveness. The P&O-FL method achieves an output of 823 W with 96.5% efficiency. This approach combines a systematic search approach with adaptable responsiveness for optimized performance.
The triple-hybrid MPPT controller achieved the highest performance, with an output power of 848.5 W and an efficiency of 99.5%. It demonstrated exceptional efficiency by combining the strengths of three different classes of MPPT controllers: P&O (conventional), PSO (nature-inspired), and FL (intelligent). This superior performance underscores the potential of hybrid methods for maximizing energy extraction in PV systems. Overall, this study confirms that hybrid MPPT controllers, particularly the P&O-PSO-FL method, offer the highest efficiency and performance for PV systems. While conventional and intelligent control methods are useful, hybrid techniques provide the best solution for optimizing power extraction and system performance.
Table 6 provides a comparison between the parameters calculated for various MPPT control techniques in this research.
6. Conclusions
The proposed study demonstrates that hybrid MPPT controllers significantly enhance the power tracking efficiency, stability, and overall performance in PV systems. Among the tested controllers, the triple-hybrid P&O-PSO-FL MPPT controller achieved the highest efficiency of 99.5%, outperforming both individual and dual-hybrid controllers. In contrast, the dual-hybrid P&O-PSO controller yielded an output power of 825.58 W with an efficiency of 96.8%, while the PSO-FL and P&O-FL hybrid controllers achieved efficiencies of 96.4% (822 W) and 96.5% (823 W), respectively. The individual MPPT controllers P&O, PSO, and FL exhibited efficiencies of 97.6%, 90.3%, and 90.1%, respectively. It was observed that while individual and dual hybrid controllers demonstrated good tracking performance, they produced fluctuations at the output. The P&O-PSO-FL controller also achieved the fastest convergence speed, just 0.02 s, a significantly quicker response compared with other methods. Furthermore, it minimized steady-state oscillations, reducing energy losses and ensuring stable power output. The superior tracking accuracy and efficiency of the P&O-PSO-FL hybrid MPPT make it an ideal solution for PV systems, ensuring optimized energy utilization and improved system reliability. These findings highlight the potential of hybrid MPPT approaches in enhancing PV system performance, offering faster convergence, greater stability, and reduced power losses. This research contributes to the development of more resilient and efficient solar energy systems, supporting the growing demand for renewable energy. This study reinforces solar energy’s critical role in sustainable energy solutions, paving the way for more advanced and adaptive MPPT strategies in future PV applications.