Enhancing Computational Efficiency of Network Reliability with a New Prime Shortest Path Algorithm

Abstract

To address the increasing demands of modern networks, evaluating computational efficiency of modified network reliability is essential, with minimal paths (MPs) serving as a critical factor. However, traditional approaches to assessing computational efficiency of network reliability often struggle with challenges such as duplicate MPs and sub-path identification, resulting in exponential computational time. In this study, we present a novel algorithm based on the Prime Shortest Path (PSP) approach, which efficiently resolves these challenges by self-detecting and eliminating duplication in polynomial time. This marks a significant improvement over existing methods. The algorithm’s correctness is rigorously validated, and its superior performance is confirmed through a detailed time complexity analysis and comparisons with the leading state-of-the-art algorithms.

1. Introduction

In the era of rapid technological advancements, the evaluation of network reliability has become increasingly crucial. These modern infrastructures rely heavily on the integrity and efficiency of their underlying networks, making reliability a key concern.

Network reliability, which measures the likelihood of a network remaining operational, is a crucial parameter for overseeing and evaluating a wide range of systems, such as power grids [1,2,3], computer and communication networks [4], transportation networks [5], and oil/gas production facilities [6].

In contemporary networked environments, a connected undirected network G(V, E) is commonly used to represent the structure of various infrastructures, as shown in Figure 1. Here, V = {1, 2, …, n} denotes the set of nodes that n = 6, E represents the set of arcs, node 1 (s) is identified as the source node, and node n (t) serves as the sink node.

In the context of networks, the nodes and arcs play a crucial role in forming the backbone of communication infrastructure. Nodes typically correspond to vital components such as base stations, while arcs represent the data links that facilitate communication between these stations. The reliability of these elements is paramount to ensure high-speed and seamless connectivity.

As networks evolve to meet growing demands, they often undergo modifications, such as the addition of paths or arcs for expansion or reinforcement. This results in what is termed a modified network. The challenge in evaluating the reliability of such networks lies in their NP-hard nature, necessitating efficient methods that can utilize existing information from the original networks without requiring a complete recalculation of reliability.

A critical aspect of network reliability evaluation is the consideration of MPs, which are extensively used as a metric in various research studies. However, a significant hurdle in this process is the identification and elimination of duplicate MPs or sub-paths, which can drastically increase the computational complexity of reliability assessments. Traditional methods for addressing this issue often require exponential time, making them impractical for large-scale applications.

To overcome this challenge, we introduce a novel algorithm that leverages the PSP approach. This innovative method is designed to efficiently prevent the duplication of MPs in polynomial time, marking a substantial improvement over existing techniques. The algorithm’s correctness is rigorously proven, and its superior performance is demonstrated through a time complexity analysis and comparative studies with the best-known algorithms. By ensuring network reliability and efficiency, our approach is essential for the seamless integration and operation of advanced technologies in urban and digital infrastructures, paving the way for more resilient and intelligent infrastructure development.

The organization of this paper is as follows: Section 2 provides an overview of the modified network and the concept of the MPs. Section 3 introduces the proposed Prime Shortest Path (PSP) method. Section 4 details the proposed algorithm, which integrates both the PSP and the self-test method, and discusses its time complexity. Additionally, this section includes a comprehensive example demonstrating the application of our proposed PSP-based self-test MP algorithm for identifying all new MPs in modified networks. Concluding remarks and a summary of the main contributions of this study are provided in Section 5.

2. Modified Network and MP

Before introducing our novel algorithm for the efficient identification of new MPs in networks, it is crucial to lay the groundwork with foundational concepts and known properties. Additionally, we will present the innovative PSP approach and the self-test method, which are central to our proposed solution.

2.1. Network Assumptions and Terminology

In this study, we use the acronyms MP to denote minimal path and PSP to represent Prime Shortest Path. All discussed networks must meet the following conditions, which are both required and reasonable [7,8,9]:

Each node is completely reliable: This assumption simplifies the analysis of network reliability. In the networks, where nodes represent crucial components such as base stations or routers, it allows us to focus on the connectivity provided by the links, which are more prone to be failures.

Each link can either be working or not working: This binary state simplifies the modeling of network reliability. In a network, links represent communication channels that can either be available for data transmission or not due to various factors such as interference, congestion, and physical damage.

The network is connected, with no loops or duplicate links: This assumption ensures that the network has a simple structure, essential for analyzing its reliability. In a network, the network’s connectivity is crucial for providing seamless communication services. Loops or duplicate links would complicate the analysis without adding significant value to the reliability assessment.

2.2. Scenario of Modified Network

Consider a bustling metropolis on the brink of a transformative technological revolution, eagerly poised to embrace the cutting-edge advancements of connectivity. This urban landscape, already teeming with digital activity, stands at the cusp of a new era, where the promise of ultra-fast, reliable, and seamless communication beckons.

To optimize the network, a multifaceted approach is required. New pathways must be meticulously crafted and added to the network to support the increased data speeds, bandwidth requirements, and low-latency demands. Additionally, some existing paths may require reinforcement or upgrading to handle the augmented data traffic and ensure robust and uninterrupted connectivity. This process of augmentation and reinforcement is not merely a technical exercise but a strategic endeavor to transform the original network into a modified network that is specifically tailored to accommodate the advanced features.

This modified network is a testament to the network’s commitment to embracing the future of connectivity. It is designed to unlock the full potential of network, paving the way for a host of innovative applications and services that promise to revolutionize the way the network lives, works, and interacts. As the network navigates this journey of technological transformation, the modified network stands as a symbol of progress, resilience, and the relentless pursuit of innovation.

2.3. Minimal Paths

In evaluating network reliability, we assume that each node within the network is perfectly reliable, and each arc can be in either a working or failed state. Furthermore, the network is considered to be connected, with no self-loops or parallel arcs, to enable the accurate assessment of MPs and the implementation of the PSP approach.

A minimal path is denoted as MP; this term refers to a simple path between two nodes in the network, which forms an arc set such that no proper subset of this set can be considered an MP.

A key property, as highlighted in prior research [10], clarifies the relationship between MPs in the original network and those in its modified form. This property asserts that every MP in the original network retains its status as an MP in the network modifications. Consequently, the primary focus of existing algorithms, including our proposed algorithm, is the identification of new MPs that emerge as a result of modifications in the networks.

In the network G(V, E), every MP continues to be recognized as a minimal path even when a new path, denoted as b_x,y, is integrated into the network. This new path links nodes x and y, yet it is designed in such a way that it does not share or intersect with any of the existing arcs in E. For instance, Figure 2 illustrates the modified network following the insertion of b2,4 (indicated by the dotted line) into Figure 1.

The reason for the persistence of the original MPs as minimal paths, despite the network modification, is that the newly added arcs are strategically placed so as not to interfere with the existing minimal paths. They neither cause any disruption in the connectivity of these paths nor do they introduce additional arcs into the paths’ structure. This ensures that the essential characteristics of the minimal paths, which are critical for network reliability assessments, remain intact even after the network undergoes modifications.

2.4. Principle of Separation

Our proposed algorithm is built upon the foundational principle of separation, as outlined in previous studies [10]. This principle involves categorizing the MPs in the network based on their traversal through one or both nodes in the set {x, y}. By doing so, we divide these MPs into four distinct subsets, each with its own unique characteristics:

The first subset includes all MPs that pass through either node x or y, represented as the union of four sets: Px\y = {all MPs that traverse node x but not node y in the original network}, Py\x = {all MPs that traverse node y but not node x in the original network}, Px,y = {all MPs that traverse at least one path from nodes x to y in the original network}, and Py,x = {all MPs that traverse at least one path from nodes y to x in the original network}. For instance, in Figure 1, p1 = {e1,2, e2,5, e5,6} is an MP in the set P2/4, and p2 = {e1,2, e2,5, e5,4, e4,6} is an MP in the set P2,4.

A crucial aspect of these subsets is their mutual exclusivity. That is, there is no overlap between any two sets among Px\y, Py\x, Px,y, and Py,x. This exclusivity ensures a clear and unambiguous classification of each MP.

The principle of exclusivity extends to subsets defined by paths connecting specific pairs of nodes. For example, the sets of paths from node s to x or from y to t are distinct, with no common paths between Πs,x(Px\y)⊗Πx,t(Px\y) and Πs,y(Py\x)⊗Πy,t(Py\x), where S ⊗ T = T ⊗ S = $\left\{\begin{array}{ll}{\displaystyle {\cup }_{i,j}\{S_i\cup T_j\}}\hfill & ,\mathrm{if}S\ne Ø\mathrm{and}T\ne Ø\hfill \\ Ø\hfill & ,\mathrm{if}S=Ø\mathrm{or}T=Ø\hfill \end{array}\right.$ for all S_i ⊆ S, T_j ⊆ T and S_i^T_j = { v∈V | all endpoints (nodes) v in e ∈ (S ∩ T)} = Ø.

This distinctness also applies to subsets of paths connecting other pairs of nodes, such as from s to x via y or from y to t via x. Here, no common paths exist between Πs,x(Px\y)⊗Πx,t(Px\y) and Πs,y(Py\x)⊗Πy,t(Py\x), where Πa,b(●) = {πa,b(p) | for all sub-paths from nodes a to v in path p∈●}.

When considering the union of paths from s to x via y and from y to t via x, there is no overlap with the union of paths from s to y via x and from x to t via y.

Furthermore, there are no shared paths between the set of paths from x to y via node y and the set of paths from y to x via node x.

Lastly, the set of paths from x to y via node y does not intersect with the combined sets of other paths mentioned in the two paragraphs above.

These properties and the clear separation of subsets are based on the definitions of the sets Px,y, Px\y, Py\x, Px,y, Py,x, and the path functions Πs,x(●), Πy,t(●), Πs,y(●), and Πx,t(●). This meticulous categorization and analysis of MPs form the core of our algorithm, ensuring that each path is accurately identified and evaluated without any redundancy or overlap.

A significant method for identifying new MPs in a modified network was initially proposed in [10]. This approach, which is foundational to the proposed PSP-based self-test MP algorithm, provides a systematic way to discover all new MPs accurately. While the detailed proof of this method is available in [10], the core idea is summarized as follows:

In a network G updated by adding a path bx,y, the complete set of new MPs can be determined through a combination of paths. Specifically, if bx,y is an undirected path connecting nodes x and y, the new MPs are found by uniting two sets: the first set is formed by concatenating paths from node s to x, paths within the set Px\y union Px,y, the path bx,y, and paths within the set Py\x union Py,x leading to node t; the second set is similarly constructed by starting from node s to y, through Py\x union Py,x, the path by,x, and concluding with paths in Px\y union Px,y leading to node t.

Furthermore, if bx,y is a directed path that only goes from node x to node y, the set of new MPs simplifies to just the first set mentioned above, where paths from s to x are concatenated with paths in Px\y union Px,y, followed by the directed path bx,y, and concluding with paths in Py\x union Py,x leading to node t.

This method provides a clear and effective way to identify all new MPs in a modified network, ensuring that the reliability evaluation is accurate and comprehensive.

2.5. Existing Algorithms

In a pioneering study presented in [11], a strategic approach was developed to enhance the identification of new MPs in networks that have undergone modifications. This approach is particularly focused on streamlining the process by eliminating redundant elements, specifically targeting the removal of duplicate elements within the sets {Πs,x(Px\y⊗Px,y)}, {Πy,t(Py\x⊗Py,x)}, {Πs,y(Py\x⊗Py,x)}, and {Πx,t(Px\y⊗Px,y)}. The essence of this method lies in ensuring that there are no duplicate elements across the sets {Πs,x(Px\y⊗Px,y)}, {Πy,t(Py\x⊗Py,x)}, {Πs,y(Py\x⊗Py,x)}, and {Πx,t(Px\yΠPx,y)}. When this condition is satisfied, the union of the sets {Πs,x(Px\y⊗Px,y) ⊗bx,y⊗Πy,t(Py\x⊗Py,x)} and {Πs,y(Py\x⊗Py,x)⊗by,x⊗Πx,t(Px\y⊗Px,y)} represents a comprehensive collection of all the new MPs within the modified network G = G union bx,y, devoid of any duplicates.

Moreover, scenarios where there are no duplicate elements specifically within {Πs,x(Px\y⊗Px,y)}, {Πy,t(Py\x⊗Py,x)}, and {Πs,x(Px\y⊗Px,y)⊗bx,y⊗Πy,t(Py\x⊗Py,x)} encompass all the new MPs within the network G = G union bx,y. This is applicable under the condition that bx,y represents a directed path that exclusively connects node x to node y.

The computational complexity associated with this method is also noteworthy. The total number of elements present within the sets {Πs,x(Px\y⊗Px,y) ⊗bx,y⊗Πy,t(Py\x⊗Py,x)} and {Πs,y(Py\x⊗Py,x)⊗by,x⊗Πx,t(Px\y⊗Px,y)} does not exceed the square of the total number of paths, denoted as |P|², where |•| the number of elements of •.

The process of verifying whether these elements qualify as new MPs within the modified network requires a computational time of O(|V|). Additionally, the conventional method of pairwise comparison, which involves a thorough comparison of each new MP against other newly generated MPs to eliminate any duplicates, demands a computational time of O(|V|∙|P|⁴). Consequently, the overall time complexity for the process of identifying new MPs and removing duplicates using this conventional method is calculated as O(|V|∙|P|² + |V|∙|P|⁴) = |V|∙|P|⁴.

Expanding upon this discussion, it has been established that the time complexity for obtaining a complete set of new MPs in modified networks, while employing the pairwise comparison method to exclude duplicates, is quantified as O(|V|∙|P|⁴). This insight is based on the best-known existing algorithm proposed in [11], which serves as a benchmark for evaluating the efficiency of this method.

3. Proposed Novel Prime Shortest Path

As we embrace the era of network technology, the need for optimized network structures becomes critical. To address the challenges of modifying existing networks, we propose a novel algorithm that leverages the unique properties of prime numbers to prevent duplicate MPs, ensuring a streamlined and efficient network.

3.1. Concept of PSP

The foundational element of our proposed methodology is the PSP, which capitalizes on a key attribute of prime numbers: the product of distinct prime numbers is invariably unique.

To illustrate this, let us consider a set of prime numbers smaller than 20, such as 1, 3, 5, 7, 11, 13, 17, and 19. When we select a subset of these numbers and calculate their product, for instance, 1 × 5 × 11 × 17, the result is a unique value that cannot be matched by the product of any other distinct combination of prime numbers, such as 3 × 7 × 13 × 19. This unique property, combined with the infinite nature of prime numbers, serves as a critical foundation for our algorithm.

In our approach, we define the PSP as the shortest path within a network where each arc is assigned a weight that is a distinct prime number. The total weight of the path is then determined by the minimal product of these prime numbers. To identify the PSP, we can utilize standard shortest path algorithms, such as Dijkstra’s algorithm, with a minor modification. Rather than adding the weights of the arcs, we multiply them. This adjustment ensures that the PSP between any two distinct nodes remains unique without impacting the time complexity of the algorithm.

The assignment of distinct prime numbers to network arcs is indeed a crucial aspect of our proposed algorithm. While it may initially appear that the choice of prime numbers is arbitrary, this methodology is designed to ensure the uniqueness and distinctiveness of each arc’s weight, which is fundamental to the algorithm’s functionality.

Arbitrary association of prime numbers: The assignment of prime numbers is not entirely arbitrary. By using prime numbers, we ensure that each arc has a unique weight, which helps in accurately identifying and differentiating paths in the network.

Effect on path finding: The algorithm’s ability to find the shortest path is indeed independent of the specific prime numbers assigned. The shortest path is determined based on the weights of the arcs, and since prime numbers are unique, they provide a consistent basis for comparison. The use of primes helps in maintaining the distinctiveness of paths without introducing biases that could result from using non-unique or non-distinct weights.

Potential overload of arcs with small prime numbers: While arcs associated with smaller prime numbers might seem to have an advantage due to their lower weights, the overall structure of the network and the distribution of prime numbers ensures that this does not lead to an overload. Each arc’s weight contributes to the path calculation, and since paths are composed of multiple arcs, the cumulative weight rather than individual arc weights determines the shortest path. Additionally, using consecutive prime numbers can help distribute the weights more evenly, minimizing the risk of overloading any particular arc.

Choosing consecutive prime numbers: Utilizing consecutive prime numbers is indeed a practical constraint that can help ensure a balanced and systematic assignment of weights. This approach not only simplifies the weight assignment process but also maintains the algorithm’s robustness and effectiveness in identifying the shortest path without introducing unnecessary complexity.

In summary, while the use of prime numbers is a deliberate choice to ensure distinctiveness, the specific values do not impact the shortest path calculation due to the cumulative nature of path weights. The potential for overloading is mitigated by the network’s structure and the distribution of weights. Nonetheless, adopting consecutive prime numbers can further enhance the method’s practicality and consistency.

Implementing this strategy not only guarantees the uniqueness of the PSP but also substantially simplifies the management of modified networks. By harnessing the properties of prime numbers, our algorithm effectively eliminates the occurrence of duplicate MPs. This results in a more streamlined network structure, enhancing both the efficiency and reliability of the network. In the evolving landscape of telecommunications, where the demand for high-speed and reliable connectivity is ever-increasing, our proposed algorithm offers a robust solution to ensure the seamless integration and optimal performance of networks.

3.2. PSP Pseudo Code

The process of finding the proposed PSP using Dijkstra’s algorithm (Algorithm 1) is outlined as follows:

Algorithm 1: Find the PSP from node α to node β in a network G(V, E).
Input:	A connected graph G(V, E) with a set of nodes V and a set of arcs E.
Output:	The PSP from node α to node β.
STEP 0:	Initialization: Assign a distinct prime number ni > 2 to each arc ei ∈ E, ensuring that ni ≠ nj for i ≠ j.
STEP 1:	Setup: For all nodes v in V except α, set W(v) = L(v) = Prec(v) = ∞. For node α, set W(α) = L(α) = 0, and let u = α.
STEP 2:	Relaxation: For each arc euv ∈ E with L(v) > 0, update W(v) = W(u) × W(euv) and Prec(v) = u if W(u) × W(euv) < W(v).
STEP 3:	Selection: Find a node u such that W(u) ≤ W(v) for all v ∈ V, and set L(u) = 0.
STEP 4:	Termination: If u = β, terminate the algorithm; otherwise, return to STEP 2.

This algorithm is a modified version of Dijkstra’s algorithm, where the addition of weights is replaced by multiplication. After implementing this algorithm, we can uniquely determine the PSP in the network, ensuring no duplication of paths.

In this algorithm, STEP 0 is executed once to assign a unique prime number to each arc initially. STEPs 1–4 are repeated each time when identifying the related PSP in the proposed PSP-based self-test MP algorithm. The key distinction from the original Dijkstra algorithm is the replacement of the condition W(u) + W(e_u,v) < W(v) with W(u) × W(e_u,v) < W(v).

3.3. Example

The PSP approach is based on a simple yet powerful principle: the multiplication of distinct prime numbers always yields a unique result. By assigning a unique prime number to each path in the network, we can ensure that the product of the numbers along any given path is unique. This uniqueness helps us identify and prevent the creation of duplicate MPs, thereby streamlining the network’s structure.

Let us illustrate this with an example. Suppose we have a network represented as a graph, with nodes connected by arcs (paths). Each arc is assigned a weight, which is a distinct prime number. When we apply Dijkstra’s algorithm to find the shortest path between two nodes, we modify the algorithm to use multiplication of weights instead of their summation. This way, the shortest path calculated (the PSP) has a unique product of prime numbers as its weight.

In our network, this approach ensures that each MP is distinct, making the network more efficient and easier to manage. The PSP-based algorithm becomes a key tool in the networks, ensuring that the network is not only faster but also smarter and more reliable. The modified network, optimized with the PSP approach, stands as a testament to the power of innovation in overcoming the challenges of modern technology.

For example, consider a network as shown in Figure 3 where each arc is labeled with a distinct prime number greater than 2. After applying Dijkstra’s algorithm, the PSP from nodes s to t is uniquely determined to be the path from nodes 1 to 2 to 5 to 6, with a total weight of 285, as listed in

Table 1. Network labeled with distinct prime numbers on each arc.

	Weight	s = 1	2	3	4	5	6
STEP
0		00	∞	∞	∞	∞	∞
1			31	11	∞	∞	∞
2				111	∞	15	∞
3					143	152	∞
4					1433		285
5							2854

. This path is the only PSP with a weight lower than or equal to 285, demonstrating the uniqueness and effectiveness of our proposed approach.

4. The Proposed Algorithm and Example

This section introduces the pseudocode for our proposed PSP-based algorithm and demonstrates its application using a medium-sized network depicted in Figure 1 (Data Availability Statements are available in Figure 1 and Table 1).

4.1. The Pseudocode of the Proposed PSP-Based Self-Test MP Algorithm

Our PSP-based algorithm for identifying all new MPs in modified networks is detailed below (Algorithm 2). This approach eliminates the need to remove duplicate and infeasible new MPs, streamlining the process:

Algorithm 2: The Pseudocode of the Proposed PSP-Based Self-Test MP Algorithm
STEP 0:	Initialize Ωs,x, Ωy,t, Ωs,y, and Ωx,t as empty sets. Set i = 1, and assign a distinct prime number ni > 2 to each arc ei ∈ E, ensuring ni ≠ nj for i ≠ j.
STEP 1:	Check if the MP pi is in Px,y, Py,x, Px/y, or Py/x. Based on this, set α and β accordingly to determine πα,t(pi) and πs,β(pi). If none of these conditions are met, proceed to STEP 4.
STEP 2:	If πα,t(pi) is equal to pi, update Ωs,α by adding πs,α(pi).
STEP 3:	If πs,β(pi) is equal to pi, update Ωβ,t by adding πβ,t(pi).
STEP 4:	If i is less than the total number of MPs (N), increment i by 1 and return to STEP 1.
STEP 5:	Combine the sets {Ωs,x⊗bx,y⊗Ωy,t} and {Ωs,y⊗by,x⊗Ωx,t} to form the set of all new MPs in the modified network.

In this pseudocode, the PSP concept is applied in STEP 0 to uniquely label each arc with a prime number. STEP 1 evaluates whether the MP pi belongs to specific subsets of MPs and sets the parameters α and β accordingly. STEPs 2 and 3 utilize these parameters to simplify the process of identifying PSPs. The final step, STEP 5, generates all new MPs in the modified network using the results obtained in the previous steps.

The proposed algorithm runs STEPs 1–3 once for each MP, with the worst-case scenario requiring three iterations for MPs in Px,y ∪ Py,x and two iterations for MPs in Px/y ∪ Py/x. The time complexity for finding PSPs for all MPs (STEPs 0–3) is O(3∙|P|∙[|E| + |V|∙log|V|]), where O(|E| + |V| log |V|) is the time complexity for finding a single PSP. The majority of time complexity arises in STEP 5, which requires O(|V|∙|P|²/2) if the sizes of Ωs,x, Ωy,t, Ωs,y, and Ωx,t are equal to |P|/4. Therefore, the total time complexity for the proposed algorithm is approximately O(|V|∙|P|²/2).

Therefore, the proposed algorithm demonstrates theoretical superiority in efficiency compared to the existing algorithms presented in references [10,11,12].

4.2. Example

To illustrate the proposed algorithm, we use a medium-sized benchmark network shown in Figure 1. The network contains several MPs between the source node (node 1) and the sink node (node 6): p1 = {e1,2, e2,5, e5,6}, p2 = {e1,2, e2,5, e5,4, e4,6}, p3 = {e1,2, e2,3, e3,4, e4,6}, p4 = {e1,2, e2,3, e3,4, e4,5, e5,6}, p5 = {e1,3, e3,4, e4,6}, p6 = {e1,3, e3,4, e4,5, e5,6}, p7 = {e1,3, e3,2, e2,5, e5,6}, p8 = {e1,3, e3,2, e2,5, e5,4, e4,6}. The procedure for searching for all new MPs in the modified network (Figure 2), which includes an undirected branch string {e2,7, e7,4}, is outlined step by step. The detailed process and the final result of finding all new MPs without duplicates using the proposed algorithm are presented in

Table 2. Procedure for the proposed algorithm to solve MP problems in Figure 2.

p	π1,2(p)	π2,4(p)	π4,6(p)	π1,4(p)	π2,6(p)	Remark
p1∈P2/4	{e1,2}*				{e2,5, e5,6}*	Ω1,2 = {{e1,2}} Ω2,6 = {{e2,5, e5,6}}
p2∈P2,4	{e1,2}	{e2,5, e5,4}*	{e4,6}	{e1,2, e2,5, e5,4}	{e2,5, e5,4, e4,6}
p3∈P2,4	{e1,2}	{e2,3, e3,4}	{e4,6}
p4∈P2,4	{e1,2}	{e2,3, e3,4}*	{e4,5, e5,6}	{e1,2, e2,3, e3,4}	{e2,3, e3,4, e4,5, e5,6}
p5∈P4/2			{e4,6}*	{e1,3, e3,4}*		Ω1,4 = {{e1,3, e3,4}} Ω4,6 = {{e4,6}}
p6∈P4/2			{e4,5, e4,6}	{e1,3, e3,4}*		Ω4,6 = {{e4,6},{e4,5,e4,6}}
p7∈P2/4	{e1,3, e3,2}				{e2,5, e5,6}*	Ω1,2 = {{e1,2},{e1,3,e3,2}}
p8∈P2,4	{e1,3, e3,2}	{e2,5, e5,4}	{e4,6}	{e1,3, e3,2, e2,5, e5,4}	{e2,5, e5,4, e4,6}

.

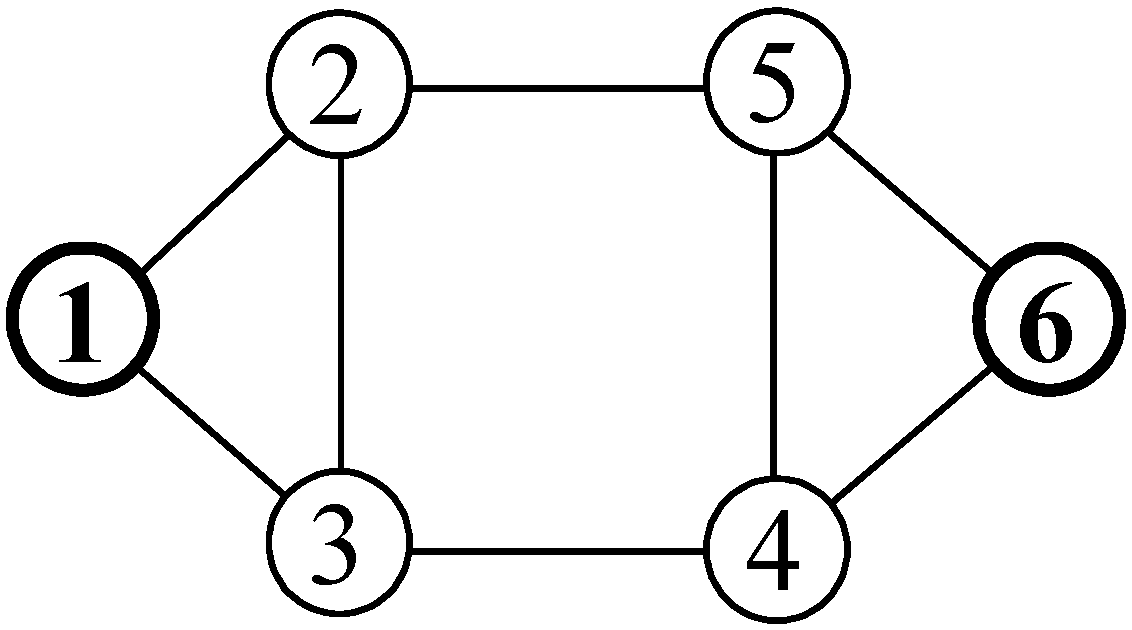
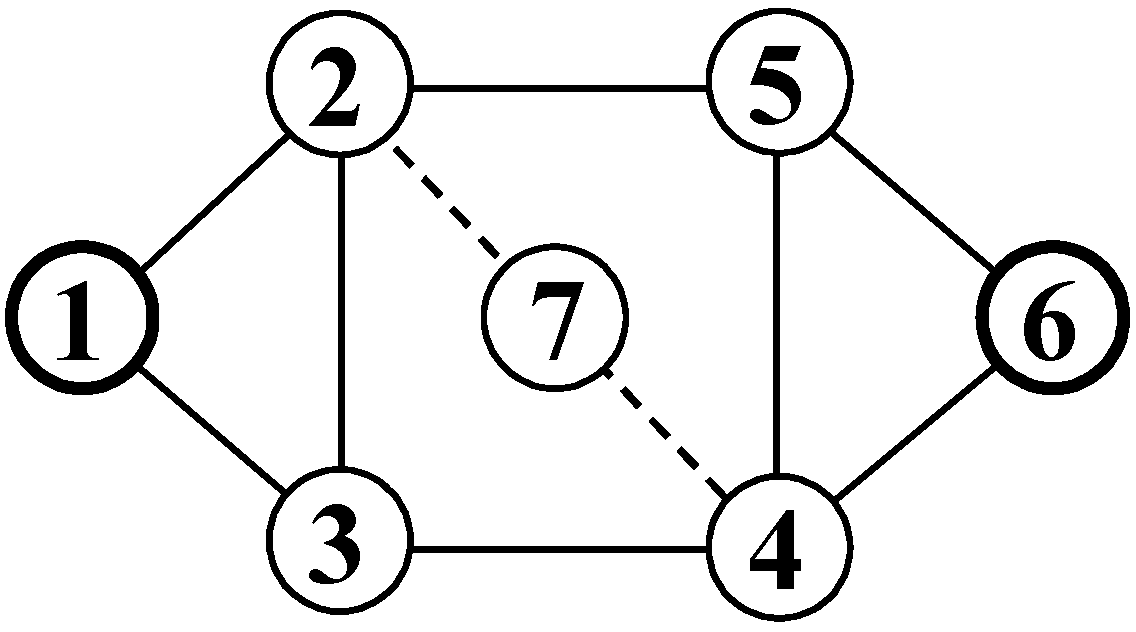
Solution: An illustration of the proposed algorithm by a medium-sized benchmark network shown in Figure 1.

STEP 0. Let Ω1,2 = Ω4,6 = Ω1,4 = Ω2,6 = Ø and i = 1. STEP 1. Because pi = p1 = {e1,2, e2,5, e5,6}∈P2/4, let α = β = 2. STEP 2. Because πα,t(pi) = π2,6(p1) = {e2,5, e5,6} = ${\mathsf{\pi }}_{2,6}^{*}$(p1), let Ωs,β = Ω1,2∪{{e1,2}} = {{e1,2}}. STEP 3. Because πs,β(pi) = π1,2(p1) = {e1,2} = ${\mathsf{\pi }}_{1,2}^{*}$(p1), let Ωα,t = Ω2,6∪{{e2,5, e5,6}} = {{e2,5, e5,6}}. STEP 4. Because i = 1 < (the number of MPs) = 8, let i = i + 1 = 2 and go to STEP 1. STEP 1. Because pi = p2 = {e1,2, e2,5, e5,4, e4,6}∈P2,4 and π2,4(p2) = {e2,5, e5,4} = ${\mathsf{\pi }}_{2,4}^{*}$(p2), let α = 2 and β = 4. STEP 2. Because πα,t(pi) = π2,6(p2) = {e2,5, e4,5, e4,6} ≠ ${\mathsf{\pi }}_{2,6}^{*}$(p2), go to STEP 3. STEP 3. Because πs,β(pi) = π1,4(p2) = {e1,2, e2,5, e5,4} ≠ ${\mathsf{\pi }}_{1,4}^{*}$(p2), go to STEP 4. STEP 4. Because i = 2 < (the number of MPs) = 8, let i = i + 1 = 3 and go to STEP 1. STEP 1. Because pi = p3 = {e1,2, e2,3, e3,4, e4,6}∈P2,4 and π2,4(p3) = {e23, e34} ≠ ${\mathsf{\pi }}_{2,4}^{*}$(p3), go to STEP 4. STEP 4. Because i = 3 < (the number of MPs) = 8, let i = i + 1 = 4 and go to STEP 1. STEP 1. Because pi = p4 = {e1,2, e2,3, e3,4, e4,5, e5,6}∈P2,4 and π2,4(p4) = {e2,3, e3,4} = ${\mathsf{\pi }}_{2,4}^{*}$(p4), let α = 2 and β = 4. STEP 2. Because πα,t(pi) = π2,6(p4) = {e2,3, e3,4, e4,5, e5,6} ≠ ${\mathsf{\pi }}_{2,6}^{*}$(p4), go to STEP 3. STEP 3. Because πs,β(pi) = π1,4(p4) = {e1,2, e2,3, e3,4} ≠ ${\mathsf{\pi }}_{1,4}^{*}$(p4), go to STEP 4. STEP 4. Because i = 4 < (the number of MPs) = 8, let i = i + 1 = 5 and go to STEP 1. STEP 1. Because pi = p5 = {e1,3, e3,4, e4,6}∈P4/2, let α = β = 4. STEP 2. Because πα,t(pi) = π4,6(p5) = {e4,6} = ${\mathsf{\pi }}_{4,6}^{*}$(p5), let Ωs,β = Ω1,4∪{{e1,3, e3,4}} = {{e1,3, e3,4}}. STEP 3. Because πs,β(pi) = π1,4(p5) = {e1,3, e3,4} = ${\mathsf{\pi }}_{1,4}^{*}$(p5), let Ωα,t = Ω4,6∪{{e4,6}} = {{e4,6}}. STEP 4. Because i = 5 < (the number of MPs) = 8, let i = i + 1 = 6 and go to STEP 1. STEP 1. Because pi = p6 = {e1,3, e3,4, e4,5, e5,6}∈P4/2, let α = β = 4. STEP 2. Because πα,t(pi) = π4,6(p6) = {e4,5, e5,6} ≠ ${\mathsf{\pi }}_{4,6}^{*}$(p6), go to STEP 3. STEP 3. Because πs,β(pi) = π1,4(p6) = {e1,3, e3,4} = ${\mathsf{\pi }}_{1,4}^{*}$(p6), let Ωα,t = Ω4,6∪{{e4,5, e5,6}} = {{e4,5, e5,6}, {e4,6}}. STEP 4. Because i = 6 < (the number of MPs) = 8, let i = i + 1 = 7 and go to STEP 1. STEP 1. Because pi = p7 = {e1,3, e3,2, e2,5, e5,6}∈P2/4, let α = β = 2. STEP 2. Because πα,t(pi) = π2,6(p7) = {e2,5, e5,6} = ${\mathsf{\pi }}_{2,6}^{*}$(p7), let Ωs,β = Ω1,2∪{{e1,3, e3,2}} = {{e1,2}, {e1,3, e3,2}}. STEP 3. Because πs,β(pi) = π1,2(p7) = {e1,3, e3,2} ≠ ${\mathsf{\pi }}_{1,2}^{*}$(p1), go to STEP 4. STEP 4. Because i = 7 < (the number of MPs) = 8, let i = i + 1 = 8 and go to STEP 1. STEP 1. Because pi = p8 = {e1,3, e3,2, e2,5, e5,4, e4,6}∈P2,4 and π2,4(p8) = {e2,5, e5,4} = ${\mathsf{\pi }}_{2,4}^{*}$(p8), let α = 2 and β = 4. STEP 2. Because πα,t(pi) = π2,6(p8) = {e2,5, e5,4, e4,6} ≠ ${\mathsf{\pi }}_{2,6}^{*}$(p8), go to STEP 3. STEP 3. Because πs,β(pi) = π1,4(p8) = {e1,3, e3,2, e2,5, e5,4} ≠ ${\mathsf{\pi }}_{1,4}^{*}$(p9), go to STEP 4. STEP 4. Because i = |P| = 8, go to STEP 5. STEP 5. [Ω1,2⊗{{e2,7, e7,4}}⊗Ω4,6]∪[Ω1,4⊗{{e4,7, e7,2}}⊗Ω2,6]                = [{{e1,2}, {e1,3, e3,2}}⊗{{e2,7, e7,4}}⊗{{e4,5, e5,6},{e4,6}}]∪                {{e1,3, e3,4}}⊗{{e4,7, e7,2}}⊗{{e2,5, e5,6}}                = {{e1,2, e2,7, e7,4 e4,5, e5,6}, {e1,2, e2,7, e7,4 e4,6}, {e1,3, e3,2, e2,7, e7,4 e4,5, e5,6},                {e1,3, e3,2, e2,7, e7,4 e4,6}}∪{{e1,3, e3,4, e4,7, e7,2, e2,5, e5,6}}.

The ultimate outcome of the algorithm, which identifies all new MPs without any duplicates, is displayed in Table 2. In this table, terms marked with an asterisk (*) indicate that the corresponding item is a PSP.

4.3. Computational Experiments

In this study, an experimental evaluation was conducted to assess the efficacy of our newly proposed algorithm in comparison to the state-of-the-art algorithm delineated in reference [11]. Both algorithms were meticulously implemented utilizing the C programming language and executed on a high-performance computing platform equipped with an Intel Core i7-5960X 3.00 GHz CPU, boasting 16 GB of RAM and running the Windows 10 64-bit operating system.

The experimental setup involved testing the algorithms on a diverse set of randomly generated network topologies, with the size of the networks (|V|) varying from 5 vertices (denoting a small network) to 50 vertices (representing a medium-sized network). To ensure robustness in the evaluation, each network size was subjected to five distinct trials, culminating in a comprehensive analysis of 50 randomly generated networks.

The results of the experiment are systematically summarized in

Table 3. Runtime comparison for solving MP problems using both algorithms.

K = |V|	|Ek|	|Pk|	${\mathit{T}}_{\mathit{k}}^{*}$	Tk
5	15	61.04	0.0101	0.0908
10	30	1845.60	0.0436	0.0799
15	45	65,545.67	0.3054	1.1198
20	60	5,625,891.49	4.0845	4.2153
25	75	97,745,622.73	16.5051	34.8428
30	90	1,198,096,571.07	66.3704	267.7001
35	105	15,678,565,410.66	270.0127	2934.3659
40	120	133,915,691,581.97	1191.0334	12,342.3152
45	135	2,743,769,009,302.40	5120.5834	165,360.2595
50	150	15,049,530,474,939.80	22,804.5198	1,206,765.7107

, which presents the average runtime for each network size, measured in CPU seconds. The notation T_5, T_10, …, T_50 is employed to denote the average runtime corresponding to networks with |V| = 5, 10, …, 50 vertices, respectively. The notation in Table 3 has been defined as follows: k = |V| is the size of the networks, |E_k| is the number of arcs of the networks, |P_k| is the number of MPs of the networks, $T_k^{*}$ is average runtime for each network size measured in CPU seconds and terms marked with an asterisk (*) indicate that the corresponding item is a PSP, and T_k is the average runtime for each network size measured in CPU seconds. According to the experimental results in Table 3, for the most complex network, the last line in the table, the run time is 1206765.7107 s, which is about 14 days. If you run each network size five times (line 386), the total run time will be 70 days.

As anticipated in the context of NP-hard problems, the computational runtime exhibits a direct correlation with the increase in the size of the network |V|. Notably, the performance improvement offered by the proposed algorithm is marginally superior to that of the best-known algorithm for networks with |V| = 5 vertices. This modest enhancement can be attributed to the fact that the average number of minimal paths (MPs) for this network size is relatively low, at approximately 61.04.

Consequently, the distinction in runtime between the PSP-based self-test method and the pairwise comparison method, both employed to prevent or eliminate the occurrence of duplicate new MPs, is not markedly pronounced. This analysis underscores the nuanced performance dynamics of the proposed algorithm in comparison to existing methodologies, particularly in scenarios characterized by varying network complexities and minimal path distributions.

5. Conclusions

In conclusion, this paper presents a novel algorithm based on the PSP approach, specifically designed to address the challenge of redundant MPs in network reliability assessments. The process of modifying, upgrading, and reconfiguring the network requires a thorough assessment of the network’s architecture. Our algorithm is particularly critical for the evaluation and optimization of networks, where robust and efficient connectivity is paramount.

Our proposed algorithm significantly enhances the efficiency of existing methods by effectively eliminating redundant MPs. A theoretical analysis of time complexity indicates that our algorithm is superior to traditional approaches in identifying all new MPs within modified networks. This is further supported by comprehensive experimental results, which demonstrate the superior performance of our algorithm, particularly in larger networks with more than 10 nodes.

Overall, both theoretical and empirical evidence confirm the effectiveness and efficiency of our proposed algorithm in improving network reliability assessments. This contribution is expected to have a significant impact on the ongoing development and optimization of networks and related technologies.

In future work, we will evaluate the PSP algorithm’s robustness in a dynamic smart city network with n nodes. Each node will have a d% chance of going offline every 10 min for 1 to 5 min. The PSP algorithm will adapt by identifying PSPs when all nodes are online and eliminating those where nodes go offline every minute. This will help us calculate the network’s functional probability. We will also measure adaptation time, path change frequency, and network efficiency to assess the algorithm’s performance under fluctuating node availability. Additionally, a breadth search algorithm considering unity as a weight in network figure can be considered in a future study, and the shortest path with a graph with positive weights like a phasor measurement unit (PMU) and a phasor data concentrator (PDC), as in references [1,2,3], can be confirmed. Exactly how the proposed PSP approach can be used, instead of Dijkstra’s algorithm as proposed in [1,2,3], will be analyzed in future work. Whether the proposed algorithm can be used for optimal placement of phasor measurement units (PMUs) and a phasor data concentrator (PDC), as well as their associated communication infrastructure (CI), will be analyzed in future work. In addition, a comparative study with references [1,2,3] and a simple Dijkstra’s single-source shortest path algorithm will be analyzed in future work.