Abstract
Artificial Intelligence (AI) has brought a revolution in many areas, including the education sector. It has the potential to improve learning practices, innovate teaching, and accelerate the path towards personalized learning. This work introduces Reinforcement Learning (RL) methods to develop a personalized examination scheduling system at a university level. We use two widely established RL algorithms, Q-Learning and Proximal Policy Optimization (PPO), for the task of personalized exam scheduling. We consider several key points, including learning efficiency, the quality of the personalized educational path, adaptability to changes in student performance, scalability with increasing numbers of students and courses, and implementation complexity. Experimental results, based on case studies conducted within a single degree program at a university, demonstrate that, while Q-Learning offers simplicity and greater interpretability, PPO offers superior performance in handling the complex and stochastic nature of students’ learning trajectories. Experimental results, conducted on a dataset of 391 students and 5700 exam records from a single degree program, demonstrate that PPO achieved a 42.0% success rate in improving student scheduling compared to Q-Learning’s 26.3%, with particularly strong performance on problematic students (41.3% vs 18.0% improvement rate). The average delay reduction was 5.5 months per student with PPO versus 3.0 months with Q-Learning, highlighting the critical role of algorithmic design in shaping educational outcomes. This work contributes to the growing field of AI-based instructional support systems and offers practical guidance for the implementation of intelligent tutoring systems.
1. Introduction
The integration of Artificial Intelligence (AI) and Machine Learning (ML) is being driven by significant investments from public–private partnerships, highlighting the growing use and potential of AI advancements in educational settings. Europe has spent up to 700 million euros on AI for robotics and public–private partnerships [1]. Moreover, the European research and innovation funding program, Horizon Europe, has prioritized AI as a key enabling technology [2]. Additionally, the European Union High-Level Expert Group on AI has given policy and investment guidelines for trustworthy AI, making a comprehensive, risk-based policy framework in Europe [3]. The scope of AI applications in education is diverse, starting from personalized learning systems to smart tutoring platforms. AI tools revolutionize the conventional education system by providing dynamic and adaptive learning solutions.
There are various factors on the need and growing use of AI in education, including edutainment acceptance. The increasing investments in AI and EdTech by the public and commercial sectors are driven by these factors. Although industries and companies were severely affected by the COVID-19 outbreak, the pandemic led to a marked increase in demand for creative AI-based teaching solutions. According to a poll held in 2021 conducted by the University Professional and Continuing Education, 51% of American professors are more optimistic about online education now than they were before the pandemic [3].
Personalized learning approaches have been gaining significant attention in the education sector in recent years, as institutions begin to recognize the importance of tailoring learning experiences to the individual needs of students [4]. Personalized learning is one of the significant and innovative uses of AI in education. The concept of personalized learning can be realized with the help of modern AI and ML tools. Personalized learning is a learning method to employ AI and ML, especially Reinforcement Learning (RL), that considers the requirements of every individual student [5]. With the help of personalized learning, each student’s learning experience and skills are customized to meet their needs, and it provides an opportunity to grow using their own skills and learning experience.
The issue in some personalized educational platforms is that they lack the methods to effectively assist the needs of students who are normally heterogeneous in terms of academic background, preferences, learning pace, and intellectual abilities [6]. It is necessary to have a defined personalized or digital learning environment on the concept of a learning ecosystem [7]. The model should analyze the interactions occurring among its components during automatic assessment activities. The AI method of RL has the ability to tailor instructions by utilizing learners’ emotional experiences and learning behaviors. The RL in intelligent tutoring and personalized learning, affective vocational learning, and social engagement training [8].
The contribution of this work is the development of an RL-based personalized examination system. We formulate the complex exam scheduling scenario as a Markov Decision Process (MDP) and then use two RL algorithms, i.e., Proximal Policy Optimization (PPO) and Q-learning, to solve the formulated MDP problem. We analyze the performance of both methods using various metrics and highlight the strengths and weaknesses. The proposed system provides valuable insights for education professionals and institutions that wish to develop AI-based learning support systems. Understanding the relative advantages of value-based methods (Q-Learning) versus policy-based approaches (PPO) in educational settings can inform future implementations and research directions. Furthermore, this research contributes to the broader field of AI in education by demonstrating how different algorithmic approaches impact learning outcomes.
The rest of the paper is organized into five sections. Section 2 provides an overview of the existing relevant works and their limitations with respect to our work. Section 3 gives a brief technical introduction to the methods that we use in our work. Section 4 presents our system model and experimental setup. We present the results in Section 5 and the conclusion in Section 6.
2. Related Work
This section overviews the state of the art from the perspective of our work.
A tutoring system is developed in [9] using the actor-critic method, where the teacher is modeled as an RL agent. The tutoring system presents a question to the students then records the students, and at the end, presents the solution to enable the students to learn. The objective of the model is to maximize the students’ potential, but it cannot be usedto help the students in examination scheduling. A similar work was also conducted by [10], where the authors utilized a Deep Q-Network RL and an online rule-based decision-making model for the learning of school students. A deep RL model was introduced in [11] for instructional sequencing. The proposed system suggests personalized learning exercises in both classrooms and MOOCs. A deep RL agent was employed to induce adaptive, efficient learning sequences for students. The results suggest that the use of AI methods like RL can be useful for other educational processes, such as an examination schedule.
A real-time recommendation system based on RL is proposed in [12] to assist individual learners online. The given model is developed to help students online in content selection. A similar system with more features is presented in [13] using the Q-learning method. The system adaptively helps students in course assignments and educational activities based on the students’ characteristics, skills, and preferences. The proposed work considers different student-centered academic factors to recommend a suitable learning path that maximizes the students’ overall performance. However, neither of these systems considers the issue of examination scheduling. A deep RL method was used in [14] for adaptive pedagogical support for students learning about the idea of volume in a narrative storyline software. The authors also utilized explainable AI schemes for the extraction of interpretable insights about the learned and demonstrated pedagogical policy. It is observed that the RL narrative system had the most significant advantage for the students with the minimum starting pretest scores, indicating the need for AI to adapt and provide support for those students most in need.
An intelligent adaptive e-learning framework is introduced in [15] using machine learning and RL. The authors first create a deep profile of a user by using K-means and linear regression, and the recommendation of adaptive learning by utilizing the Q-learning algorithm. Moreover, in another interesting work [16], RL is used to create comfortable and smart learning in a classroom. The RL-based technique analyses students’ learning materials, behavior change, and technologies to improve their overall learning efficiency. The created smart learning classroom achieves a benefit of e-learning like flexibility, interactions, and experience.
While previous works applied multi-agent deep Reinforcement Learning for adaptive course sequencing and personalized curriculum generation, our RL-based framework focuses specifically on exam-level scheduling optimization. Our work addresses the complex problem of examination at the university level. We formulate this educational problem as an MDP and then use PPO and Q-learning to solve the formulated MDP problem. We analyze the performance of both methods using various metrics and highlight the strengths and weaknesses.
3. Technical Background
Artificial Intelligence (AI) represents the capability to develop computational systems able to emulate human cognitive processes, including reasoning, learning, and problem-solving, thereby creating intelligent machines that can process information and make autonomous decisions [17].
Machine Learning (ML) constitutes a fundamental subfield of AI, focusing on the development of algorithms and statistical models that enable software systems to automatically improve their performance through experience, without being explicitly programmed for every specific task. ML allows for computers to identify complex patterns in data and leverage this information to make informed predictions or decisions.
The ML paradigm is traditionally structured into three main categories, each addressing different types of learning problems. The first one is Supervised Learning, which operates on labeled datasets where the correct output is known for each input. A domain expert provides the training data, assuming the role of an external supervisor. The primary objective is to construct models capable of generalizing the underlying relationship between inputs and outputs, thereby enabling accurate predictions on previously unseen data. Common applications include classification tasks and regression problems. The second type of ML is Unsupervised Learning, which differs fundamentally by analyzing unlabeled datasets without any supervisory help. This approach aims to discover hidden structures, patterns, and intrinsic relationships within the data. Typical applications include clustering algorithms and dimensionality reduction techniques.
The third and advanced type of ML is Reinforcement Learning (RL), which distinguishes itself through a fundamentally different learning mechanism based on continuous interaction with an environment. In RL, an agent learns optimal behavior through a trial-and-error process, similar to how humans learn from experience [18]. The agent receives feedback from the environment in the form of rewards for beneficial actions and penalties for detrimental ones, as demonstrated in Figure 1. Through this iterative feedback mechanism, the agent progressively accumulates knowledge about the environment dynamics and develops optimal policies to maximize long-term cumulative rewards [19]. Unlike supervised learning, RL does not require labeled examples; instead, the agent discovers effective strategies through autonomous exploration and exploitation of the environment.
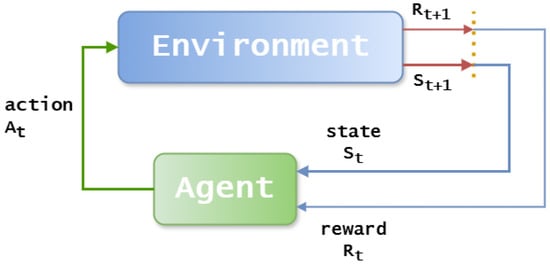
Figure 1.
Reinforcement learning problem.
Similarly, another modern type of ML is Deep Learning (DL), which is transforming the way machines learn from complex data. DL mimics the Neural Networks (NNs) of the human brain, thus enabling computers to autonomously discover patterns and make informed decisions from the huge volumes of unstructured data [20]. NNs are networks of interconnected neurons that collaborate to process input data. For instance, in a fully connected deep NN, data flows via multiple layers, and every neuron performs nonlinear transformations. This enables a model to learn.
Reinforcement Learning for Educational Applications
Within the landscape of AI and ML algorithms, Reinforcement Learning has emerged as a particularly powerful paradigm for personalized education systems. RL naturally models the complex learning process as a sequential decision-making problem, where decisions made at each time step influence future educational outcomes and overall student success.
The concept of personalized learning is receiving attention worldwide, and it can be realized with the help of modern AI and ML tools. Personalized learning is a learning method that employs AI and ML, especially RL, that considers the requirements of every individual student. Personalized learning means that each student’s learning experience and skills are customized to meet their needs. Moreover, it provides an opportunity to grow using their own skills and learning experience. AI-powered personalized learning gives flexibility to students in various aspects aspects, like the use of material, quality of material, speed to learn, and way of teaching. Furthermore, RL algorithms can be utilized for various education applications including task automation, smart content creation, data-based feedback, and secure and decentralized learning systems.
The application of RL to educational scheduling and planning offers several advantages over traditional rule-based systems: (1) adaptability to individual student characteristics and evolving performance patterns, (2) optimization of complex, long-term objectives rather than myopic short-term goals, (3) ability to handle the inherent uncertainty and variability in student learning trajectories, and (4) continuous improvement through interaction with real student data.
4. System Model and Dataset
This section presents the details about the proposed system model, characteristics of the dataset, and RL algorithms. The university ecosystem related to exam planning is modeled as a Markov Decision Process (MDP), and then applying Reinforcement Learning algorithms to recommend an optimal examination calendar to students based on specific parameters, as also demonstrated in Figure 2.
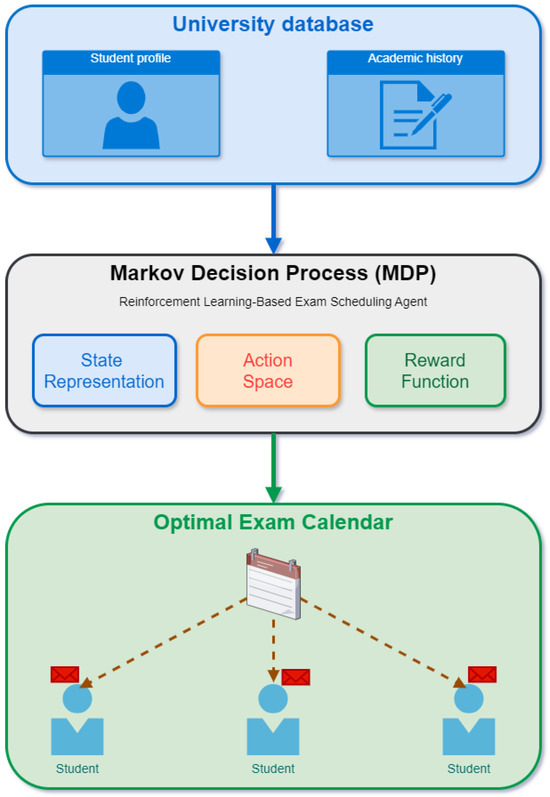
Figure 2.
The proposed system model.
First, the examination calendar is modeled as a Markov Decision Process (MDP) by defining states, actions, and reward. Then, an RL agent continuously interacts with the educational environment comprising student performance data, curriculum structure, and learning objectives. The agent observes the current state, selects appropriate actions, and receives rewards reflecting educational outcomes. Through this iterative process, the system learns to optimize long-term objectives, such as maximizing student achievement while minimizing time to graduation. The following sections explain the process and functioning of the proposed system.
4.1. Algorithm Selection
There is a potential of applying RL for personalized exam scheduling [21], but it is important to address the critical issue of algorithm selection. Different RL algorithms offer different tradeoffs in terms of performance, implementation complexity, and suitability for specific applications. The education domain presents unique challenges due to its stochastic nature and the high dimensionality of student data. In our work, among the RL algorithms, Q-Learning and Proximal Policy Optimization are used.
Q-Learning is a model-independent and off-policy Reinforcement Learning algorithm [22] that learns a value function Q(s, a) to estimate the expected utility of performing an action a in a state s, following an optimal policy. It uses a Q-table to store the expected future rewards for each state-action combination. The Q-function is updated iteratively according to the Bellman Equation (1):
where
- is the Q-value for state s and action a;
- is the learning rate;
- r is the immediate reward;
- is the discount factor;
- is the next state;
- is the maximum possible Q-value in state .
Due to its characteristics, Q-Learning is particularly suitable for the educational context: simplicity of implementation and intuitive understanding of the learned decisions, low computational requirements for problems with discrete spaces and moderate dimensions, and convergence to the optimal policy in deterministic environments under theoretical conditions.
However, Q-Learning presents limitations in large state spaces due to the exponential growth of the Q-table, and has difficulties with continuous action spaces, which could limit its applicability to complex educational scenarios, with possible potential loss of relevant information through discretization of continuous variables.
The Proximal Policy Optimization (PPO) algorithm is a policy gradient algorithm that belongs to the family of on-policy and model-free approaches [23]. Unlike Q-Learning, PPO directly optimizes an objective function based on the current policy through an iterative update of the parameters of the Neural Network representing the policy. The goal of PPO is to maximize the expected benefit function, while ensuring stable updates thanks to a clipping mechanism of the likelihood ratio between the new and the old policy, as demonstrated in Equation (2):
where is the likelihood ratio according to the new and the old policy;
- is the estimate of the advantage at time t;
- is a hyperparameter that regulates the size of the update window.
It also offers several advantages for educational applications and contexts, such as stability and efficiency during learning, adaptability to state spaces and continuous actions, avoiding discretizations, and good scalability on high-dimensional problems.
On the other hand, PPO implementations are typically more complex than Q-Learning ones and may require more computational resources.
From a theoretical perspective, we anticipate several key differences between Q-Learning and PPO in the context of personalized exam scheduling:
- State space representation: Q-Learning may require discretizations of continuous student parameters (such as performance metrics or time preferences), potentially losing important information, while PPO can work directly with continuous representations.
- Policy complexity: PPO should be able to capture more complex relationships between student characteristics and optimal planning decisions than Q-Learning, but requires more data.
- Sample efficiency: Q-Learning may require fewer samples to learn effective policies in simpler scenarios, while PPO typically requires more data but can perform better in complex environments.
- Adaptation to changing conditions: PPO is expected to adapt more quickly to changes in student performance or curricular requirements due to its straightforward approach to policy optimization.
4.2. Dataset Description
This subsection presents details about the dataset and key variables. Our experimental evaluation is based on real academic data from a single degree program at our reference university. The dataset provides a comprehensive view of student exam performance and timing patterns.
The main characteristics of the used dataset are outlined below:
- Total exam records: 5700 completed exams.
- Unique students: 391 students.
- Time period: Multi-year academic data.
- Average exams per student: 14.6 exams.
- Data source: University information system.
In addition, there are several variables such as student identifier and exam completion dates, planned year vs. actual year of exam completion, exam outcomes, academic progression, course load, and timing patterns.
4.3. Problem Formulation
A key contribution of this work is the formulation of this complex educational scenario into a solvable RL problem. We model the personalized exam scheduling problem as a sequential decision-making process where an intelligent agent must learn optimal scheduling policies for different student profiles. The formulation includes the definition of a set of states, a set of actions, and the reward function. These key parameters are described below:
State Representation: Each student’s state includes their current academic progress, historical exam timing patterns, and remaining course requirements.
Action Space: The agent can recommend different scheduling strategies (actions), including maintaining planned timing, deferring exams, or accelerating the schedule based on student performance patterns.
Reward Function: The reward function is the critical part of an RL problem, and we define a reward function that incentivizes timely exam completion and penalizes delays.
4.4. Student Classification and Target Definition
This subsection presents the definition of different categories of students and the target for the RL agent.
Based on temporal analysis of exam completion patterns, we established a threshold-based classification system to identify the students who would benefit from RL-based scheduling assistance.
First, we compute the delay for each examination and we calculate the temporal delay as given in Equation (3).
The exam delay is calculated for each student to capture individual variability in the learning path and planning dynamics. This choice allows us to more accurately represent differences in course completion times, linked to personal factors such as study pace, external commitments, or specific subject difficulties. Excessive deviations from the planned study plan represent cases in which students accumulate significant delays, compromising the coherence of the learning path.
The university’s exam scheduling framework, considered in our case study, includes sessions in which students may take exams during which students can take exams based on exam availability and academic prerequisites. This operational context forms the basis on which our RL agent learns optimal scheduling policies.
Furthermore, we divide the students into three categories with specific characteristics as explained below:
- Virtuous Students: ≤20% of exams delayed (60 students, 15.3%).
- Moderate Students: 20–50% of exams delayed (159 students, 40.7%).
- Problematic Students: >50% of exams delayed (172 students, 44.0%).
As a result of this division, we can set the target for our RL agent. Therefore, the students with >20% exam delays were identified as the target population that would benefit from intelligent scheduling assistance, representing 331 students (84.7% of the dataset).
4.5. Algorithm Implementation
In this subsection, we present the main hyperparameters that we used during our experiments.
4.5.1. Q-Learning Configuration
The learning parameters used for Q-learning algorithm are given below:
- Learning rate: 0.1 with gradual decay.
- Exploration strategy: -greedy starting at 0.9, ending at 0.01.
- Discount factor: 0.95.
The main component of the state space are delay percentage, academic year and course requirements. We discretized the continuous state space into manageable categories, as explained below:
- Delay percentage: 5 bins (0–20%, 20–40%, 40–60%, 60–80%, >80%).
- Academic year: 4 categories (1st, 2nd, 3rd, beyond normal duration).
- Course load: 3 levels (low, medium, high).
4.5.2. PPO Configuration
The second RL algorithm that we use is PPO. The parameters used for Neural Network architecture are given below:
- Input layer: 12 features representing continuous student state.
- Hidden layers: 128 and 64 neurons with ReLU activation.
- Output layer: Action probability distribution.
Similarly, the parameters used for learning are outlined below:
- Learning rate: 0.0003.
- Batch size: 64 training samples.
- Training epochs: 10 per update cycle.
- Clipping parameter: 0.2 for stable policy updates.
5. Experiments and Results
This section details the experiments, their performance metrics, and the resulting data.
Delay represents the temporal deviation between the academic year in which an exam should be taken according to the official study plan, Planned Exam Year, and the academic year in which the student actually completes that exam, Student Current Year, as given in Equation (3).
A positive delay indicates late completion, and zero indicates on-time completion.
The delay is initially calculated in academic years and then converted to months for all reported metrics to provide greater granularity in evaluating algorithm performance.
For each student, the cumulative delay is the sum of the delays of all their exams. This metric is directly correlated with the time required to complete the degree program: a student with high cumulative delay will tend to graduate beyond the normal duration of the degree.
When we report that PPO reduces the average delay, we refer to the reduction in average cumulative delay obtained by applying the RL agent’s scheduling recommendations. In practical terms, this means the following:
- The student completes exams closer to the planned schedule;
- The study path aligns better with the ideal curriculum plan;
- The overall time required to obtain the degree is reduced.
5.1. Performance Metrics
The choice of performance metrics is important in the evaluation of any system. We used many metrics to evaluate the performance of our proposed personalized examination scheduling system, and we divided the metrics into primary metrics and secondary metrics. Each category includes specific metrics, detailed below.
Primary Metrics:
- Algorithm Effectiveness: Percentage of target students showing scheduling improvement.
- Delay Reduction: Average decrease in exam delays (measured in months).
- Convergence Time: Training duration required for stable performance.
Secondary Metrics:
- Solution Stability: Consistency of recommendations over time.
- Adaptability: Performance when student patterns change.
- Implementation Complexity: Development and maintenance requirements.
5.2. Experimental Protocol
This section presents details about experimental protocol including data used for training and testing, evaluation method, performance assessment and software setup.
The data distribution for experiments are given below:
- Training data: 70% of students (274 students).
- Testing data: 30% of students (117 students).
- Maintained proportional representation of all student categories.
Moreover, both algorithms were trained on the same training set and evaluated on identical test conditions to ensure a fair comparison between the Q-learning algorithm and the PPO algorithm. Scheduling efficiency was assessed by comparing the proportion of students in each category who showed reduced exam delays after applying the RL recommendations.
Next, we present some details about software setup and computational time, as highlighted below:
- Programming language: Python 3.9.
- Computational environment: Standard consumer-grade hardware.
- Training time: Approximately two days for PPO and half a day for Q-Learning.
This experimental setup is instrumental for a comparative analysis of Q-Learning and PPO algorithms in personalized university exam scheduling, prioritizing metrics that quantify the effective educational benefit.
5.3. Dataset Analysis and Student Classification
This subsection presents a detailed analysis of the dataset and classification of students. The analysis of our dataset revealed significant patterns in student exam timing behavior that justify the application of Reinforcement Learning for personalized scheduling.
Below are the details about the temporal distribution of examinations:
- Examinations completed on time (delay = 0): 2620 exams (46.0%)
- Examinations completed with delay (>0): 3034 exams (53.3%).
- Examinations completed early (delay < 0): 42 exams (0.7%).
- Average delay across all exams: 0.52 years.
- Average delay for delayed exams only: 1.00 years.
There is a high percentage of delayed examinations (53.3%), and this high proportion of delayed examinations signifies the need for improved scheduling assistance, validating our research approach.
Therefore, we make a classification of students based on the percentage of examinations performed with delay as indicated in Figure 3. This classification is further elaborated in the Table 1.
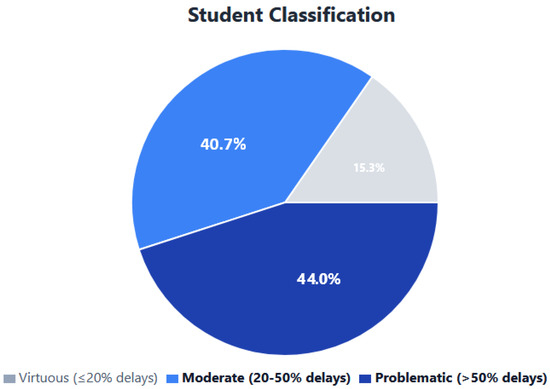
Figure 3.
Distribution of students by delay category and RL intervention target groups.

Table 1.
Student classification based on exam delay patterns.
The classification reveals that 331 students (84.7% of the dataset) would benefit from RL-based scheduling assistance, representing a substantial target population with high potential for the use of AI methods in education.
5.4. Algorithm Performance Comparison
This subsection presents the results of experiments conducted against Q-learning and PPO algorithms.
The Table 2 presents the performance of the Q-learning method. We can see that the percentage of moderate students is , the percentage of problematic students is , and the percentage of total students is , respectively. Q-Learning demonstrated effectiveness, particularly with students showing regular, predictable delay patterns.

Table 2.
Performance of Q-learning algorithm.
Similarly, Table 3 presents the performance of the Q-learning algorithm in terms of secondary metrics. We can see from Table 3 that the average delay reduction is 3 months per student, while the convergence time is 12–16 weeks. The stability is and the implementation complexity is low.

Table 3.
Performance of Q-learning algorithm for secondary metrics.
The Table 4 shows the performance of the PPO algorithm. We can see that the PPO performance is superior than that of Q-learning (Table 2 across all student categories, with particularly strong results for students with complex, irregular delay patterns.

Table 4.
Performance of PPO algorithm.
Similarly, Table 5 presented the performance of the PPO algorithm in terms of secondary metrics. We can see from Table 5 that the average delay reduction is 5.5 months per student while the convergence time is 8–12 weeks. The stability is and the implementation complexity is high.

Table 5.
Performance of PPO algorithm for secondary metrics.
Finally, we put all results together in Table 6 and in Figure 3 to present a comparison between Q-learning and PPO algorithms across all evaluation metrics. It is evident that PPO has better performance than Q-learning for most of the metrics.

Table 6.
Comprehensive algorithm comparison.
In addition, we demonstrated the performance of RL algorithms and their impact on personalized examination scheduling with the help of charts. For example, Figure 4 presents the improvement rates for each category and for each algorithm, i.e., Q-learning and PPO algorithm. Similarly, Figure 5 highlights how many students are improved with respect to the problem of examination scheduling using Q-learning and PPO methods.
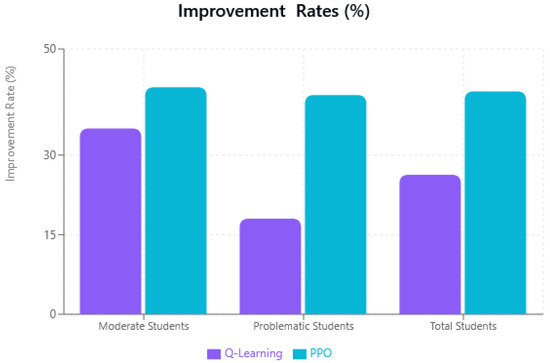
Figure 4.
Improvement rates by category and algorithm.
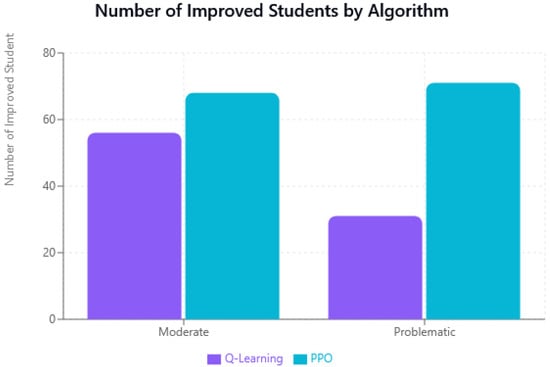
Figure 5.
Absolute count of students showing improvement in each category.
6. Conclusions
We present an RL-based personalized exam scheduling in higher education based on real academic data from 391 students across 5700 exam records. Our experimental results provide quantitative evidence that PPO outperforms Q-Learning by 59.8% in terms of students helped, with particularly strong advantages (129.4% improvement) for students with complex scheduling challenges. We establish a threshold-based approach using 20% exam delays as the criterion for identifying students who benefit from RL assistance, achieving 84.7% coverage of the target population while efficiently excluding students who do not require intervention. Our findings demonstrate that PPO achieves 5.5 months of average delay reduction compared to 3.0 months for Q-Learning, representing substantial practical value for student academic progression.
Based on our findings, educational institutions should choose PPO for personalized exam scheduling systems, particularly in environments with diverse student populations and complex scheduling constraints. The threshold-based student identification approach we developed provides a practical deployment strategy that focuses on students with irregular scheduling patterns, where PPO demonstrates maximum effectiveness. While PPO requires higher implementation complexity than Q-Learning, the substantial performance advantages justify the additional development effort, particularly for institutions with significant numbers of students experiencing scheduling difficulties.
This research demonstrates the practical viability and substantial benefits of applying Reinforcement Learning to personalized educational scheduling. These findings underscore the importance of algorithm selection in educational AI systems. The clear superiority of PPO over Q-Learning, particularly for students most in need of assistance, provides actionable guidance for educational institutions seeking to improve student outcomes through intelligent scheduling systems. The 42.0% success rate achieved by PPO in helping students improve their scheduling, combined with the 5.5-month average delay reduction, represents meaningful progress toward more personalized and effective educational support systems.
The threshold-based approach we developed offers a scalable framework for identifying students who would benefit most from such systems, ensuring efficient resource allocation and maximum educational impact. This work contributes to the growing field of AI in education by demonstrating how algorithmic choice significantly impacts real-world educational outcomes, providing both theoretical understanding and practical guidance for implementing RL-based solutions in academic environments.
In light of our evidence, several future research directions naturally emerge from the current results. First, since our threshold-based approach achieved great coverage of students requiring intervention, it would be valuable to extend this method to all degree programs within the reference university. This would allow us to verify its effectiveness across different academic disciplines and educational pathways. Secondly, although PPO clearly outperformed Q-Learning in terms of delay reduction and student support rate, it also showed higher implementation complexity. Exploring hybrid approaches that combine Q-Learning’s stability with PPO’s adaptability could potentially reduce implementation complexity while maintaining strong performance levels. Third, our current model focuses primarily on scheduling data. Incorporating additional features, such as student learning styles, course difficulty, prerequisite relationships, and perceived workload, could enhance personalization and improve the accuracy of scheduling recommendations. Finally, transparency could be a key element for the effective integration of AI-based systems in education. Future research should therefore explore Explainable AI (XAI) techniques to make Reinforcement Learning-based recommendations more understandable for students and academic tutors. Improving system interpretability would increase user trust, foster decision-making accountability, and facilitate broader institutional adoption. Overall, these directions represent a coherent extension of the study findings, aimed at enhancing the scalability and practical applicability of Reinforcement Learning in personalized educational planning.
Author Contributions
Conceptualization, M.N.; Methodology, M.B. and M.N.; Software, M.B. and G.T.; Validation, M.B. and G.T.; Formal analysis, M.C.; Investigation, M.C.; Data curation, M.C.; Writing—original draft, M.B. and M.N.; Writing—review & editing, M.N.; Visualization, G.T.; Supervision, A.C.; Project administration, A.C.; Funding acquisition, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
The funding is provided by Università di Foggia under PhD Program in Learning Sciences and Digital Technologies 38th cycle.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding The data is the ownership of a university and cannot be shared publically.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, C.; Teo, T.S.; Janssen, M. Public and private value creation using artificial intelligence: An empirical study of AI voice robot users in Chinese public sector. Int. J. Inf. Manag. 2021, 61, 102401. [Google Scholar] [CrossRef]
- Ahern, M.; O’sullivan, D.T.; Bruton, K. Development of a framework to aid the transition from reactive to proactive maintenance approaches to enable energy reduction. Appl. Sci. 2022, 12, 6704. [Google Scholar] [CrossRef]
- Digital Learning Pulse Surveys. 2021. Available online: https://www.bayviewanalytics.com/pulse.html (accessed on 15 September 2025).
- Ouyang, F.; Zheng, L.; Jiao, P. Artificial intelligence in online higher education: A systematic review of empirical research from 2011 to 2020. Educ. Inf. Technol. 2022, 27, 7893–7925. [Google Scholar] [CrossRef]
- Ismail, A.; Naeem, M.; Syed, M.H.; Abbas, M.; Coronato, A. Advancing Patient Care with an Intelligent and Personalized Medication Engagement System. Information 2024, 15, 609. [Google Scholar] [CrossRef]
- Fernandes, C.W.; Rafatirad, S.; Sayadi, H. Advancing personalized and adaptive learning experience in education with artificial intelligence. In Proceedings of the 2023 32nd Annual Conference of the European Association for Education in Electrical and Information Engineering (EAEEIE), Eindhoven, The Netherlands, 14–16 June 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Barana, A.; Marchisio, M. Analyzing interactions in automatic formative assessment activities for mathematics in digital learning environments. In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021), Virtual Event, 23–25 April 2021. [Google Scholar]
- Ouyang, F.; Zheng, L.; Jiao, P. The role of reinforcement learning in enhancing education: Applications in psychological education and intelligent tutoring systems. Highlights Sci. Eng. Technol. 2025, 124, 123–131. [Google Scholar] [CrossRef]
- Malpani, A.; Ravindran, B.; Murthy, H. Personalized Intelligent Tutoring System Using Reinforcement Learning. In Proceedings of the Twenty-Fourth International Florida Artificial Intelligence Research Society Conference, Palm Beach, FL, USA, 18–20 May 2011. [Google Scholar]
- Sayed, W.; Noeman, A.; Abdellatif, A.; Abdelrazek, M.; Badawy, M.; Hamed, A.; El-Tantawy, S. AI-based adaptive personalized content presentation and exercises navigation for an effective and engaging E-learning platform. Multimed. Tools Appl. 2022, 82, 3303–3333. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y.; Wang, C.; Wu, W. A deep reinforcement learning framework for instructional sequencing. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; IEEE: New York, NY, USA, 2020; pp. 5201–5208. [Google Scholar]
- Intayoad, W.; Kamyod, C.; Temdee, P. Reinforcement Learning for Online Learning Recommendation System. In Proceedings of the 2018 Global Wireless Summit (GWS), Chiang Rai, Thailand, 25–28 November 2018; pp. 167–170. [Google Scholar] [CrossRef]
- Fernandes, C.W.; Miari, T.; Rafatirad, S.; Sayadi, H. Unleashing the Potential of Reinforcement Learning for Enhanced Personalized Education. In Proceedings of the 2023 IEEE Frontiers in Education Conference (FIE), College Station, TX, USA, 18–21 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Ruan, S.; Nie, A.; Steenbergen, W.; He, J.; Zhang, J.; Guo, M.; Liu, Y.; Dang Nguyen, K.; Wang, C.Y.; Ying, R.; et al. Reinforcement learning tutor better supported lower performers in a math task. Mach. Learn. 2024, 113, 3023–3048. [Google Scholar] [CrossRef]
- Mustapha, R.; Soukaina, G.; Mohammed, Q.; Es-Sâadia, A. Towards an Adaptive e-Learning System Based on Deep Learner Profile, Machine Learning Approach, and Reinforcement Learning. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 265–274. [Google Scholar] [CrossRef]
- Fu, S. A Reinforcement Learning-Based Smart Educational Environment for Higher Education. Int. J. E-Collab. 2023, 19, 1–17. [Google Scholar] [CrossRef]
- Zhou, Z.; Tian, Y.; Khan, A.; Liu, J.; Hameed, N. An Enhanced Pavement Crack Detection Approach Using Improved YOLOv8 Model. In Proceedings of the 2025 5th International Symposium on Computer Technology and Information Science (ISCTIS), Xi’an, China, 16–18 May 2025; IEEE: New York, NY, USA, 2025; pp. 1184–1188. [Google Scholar]
- Jamal, M.; Ullah, Z.; Naeem, M.; Abbas, M.; Coronato, A. A hybrid multi-agent reinforcement learning approach for spectrum sharing in vehicular networks. Future Internet 2024, 16, 152. [Google Scholar] [CrossRef]
- Fiorino, M.; Naeem, M.; Ciampi, M.; Coronato, A. Defining a Metric-Driven Approach for Learning Hazardous Situations. Technologies 2024, 12, 103. [Google Scholar] [CrossRef]
- Ullah, A.; Sun, Z.; Mohsan, S.A.H.; Khatoon, A.; Khan, A.; Ahmad, S. Spliced Multimodal Residual18 Neural Network: A breakthrough in pavement crack recognition and categorization. IEEE Access 2024, 12, 110781–110797. [Google Scholar] [CrossRef]
- Barone, M.; Ciaschi, M.; Ullah, Z.; Piccardi, A. Reinforcement Learning based Intelligent System for Personalized Exam Schedule. In Proceedings of the 2024 19th Conference on Computer Science and Intelligence Systems (FedCSIS), Belgrade, Serbia, 8–11 September 2024; pp. 549–553. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, UK, 2018. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).