Quantum Security Multi-Party Extremum Protocol with Greenberger–Horne–Zeilinger States

Abstract

Secure multi-party extremum, as a significant offshoot of secure multi-party computation, has extensive applications in various domains, including healthcare, financial transactions, market analysis, sports events, etc. Nevertheless, most existing secure multi-party extremum protocols rely on computational hard problems and are thus vulnerable to quantum algorithms. This paper presents a quantum secure multi-party extremum protocol that is built upon the correlations of Greenberger–Horne–Zeilinger (GHZ) states. Within this protocol, multiple participants, with the aid of a semi-honest third party, can obtain the maximum and minimum values of their secret inputs. GHZ states act as the information carriers and are transmitted among the participants and the third party. Their unique correlations ensure the secure transmission of quantum particles. The analysis demonstrates that the proposed protocol is capable of not only warding off common external attacks but also resisting internal attacks launched by dishonest participants and the semi-honest third party. Moreover, the protocol boasts correctness and high scalability.

1. Introduction

Quantum cryptography is an innovative integration of quantum mechanics and cryptography. Unlike traditional cryptography, which hinges on computational complexity, quantum cryptography is built on the fundamental principles of quantum mechanics, providing significantly enhanced security. Since Bennett and Brassard introduced the pioneering quantum key distribution protocol (BB84 protocol) [1], researchers have developed a wide array of quantum cryptographic protocols. These protocols address complex security tasks that are challenging for traditional cryptography, such as quantum key distribution (QKD) [2,3,4,5], quantum secret sharing (QSS) [6,7,8,9], quantum secure direct communication (QSDC) [10,11,12], and more.

Secure multi-party computation (SMPC), a major branch of cryptography, has extensive applications across various fields, including finance, healthcare, social networking, data analysis, and beyond. Quantum secure multi-party computation, which harnesses the unique properties of quantum mechanics to effectively solve some SMPC tasks, has made remarkable research progress in recent years. It has established a relatively comprehensive theoretical framework and has been applied to address numerous practical privacy-preservation challenges in the information age, such as private comparison problems [13,14,15], private query problems [16,17,18], private set computation problems [19,20,21,22], private scientific computing problems [23,24,25,26,27], private geometric computation problems [28], and other practical SMPC issues. Moreover, to deepen understanding of the quantum-classical boundary and lower the barriers to entry for quantum technology, a series of semi-quantum SMPC protocols [29,30,31,32,33,34,35,36] have been proposed, meaning the gradual practicalization of quantum secure multi-party computation. Calculating the minimum (or maximum) value of multiple private inputs is a highly significant problem in private scientific computing. In 2022, Shi et al. proposed the first quantum protocol for privately computing the logical OR [37]. Based on this work, the secure task of privately computing the maximum value was accomplished using single particles. Subsequently, Kong et al. introduced the first protocol for privately computing the minimum value [38]. To achieve this, they designed two quantum-secure MPC protocols for the logical AND operation, which can respectively resist collective dephasing noise and collective rotation noise. In 2024, Lu and Ding proposed two quantum secure extremum protocols utilizing d-dimensional particles [39]. One protocol is for privately computing the maximum and minimum values, while the other protocol is for privately computing the sum and difference of extremums. Inspired by these works, we propose a quantum-secure MPC extremum protocol based on GHZ states, in which multiple participants compute the maximum and minimum values of their private inputs with the assistance of a semi-honest third party. In this protocol, the GHZ states are prepared by the third party and distributed to each participant. The correlation properties of GHZ states are utilized to design an eavesdropping detection process, ensuring the security of particle transmission. At the end of the protocol, all participants simultaneously obtain the maximum and minimum values, keeping these results and the private inputs confidential from others, including the third party.

The remainder of this paper is organized as follows. The relevant preliminary knowledge related to this paper is introduced in Section 2. Subsequently, the proposed three-party quantum private extremum protocol is presented in Section 3. The proposed protocol’s security, scalability, and correctness are analyzed in Section 4, Section 5, and Section 6, respectively. After that, the performance of this protocol is discussed in Section 7. Finally, Section 8 provides a short conclusion.

2. Preliminary

2.1. Security Multi-Party Extremum

Secure multi-party computation refers to a scenario where two or more mutually distrustful participants collaborate to solve a computational problem. After the computation is completed, each participant only obtains the result without gaining any private information about the other participants’ inputs. Since Yao proposed the two-party secure computation problem, known as Yao’s Millionaires’ Problem, in 1982, numerous scholars have conducted research on secure multi-party computation, which has now become an important research hotspot in the field of cryptography. Secure multi-party extremum (SME) is a new research branch within secure multi-party computation that has wide applications in fields such as healthcare, financial transactions, market analysis, sports events, and so on. For instance, in psychology, the difference between the maximum and minimum values is known as the total range. It is an important measurement indicator in psychology, and utilizing this range helps in the early detection of psychological disorders, enabling preventive measures to be taken. Meanwhile, to protect user privacy, specific user data should not be disclosed.

In a secure multi-party extremum protocol, there are multiple participants, each possessing a private data value. They wish to securely compute the extrema of these values, such as the maximum and minimum, without revealing any other information about the values. For a security multi-party extremum protocol, it is commonly required to meet the following criteria:

R1: Correctness. The protocol should ensure that, as long as participants follow the protocol steps, the computation process can be completed smoothly. Moreover, all participants should obtain the same accurate computation result after the protocol execution.

R2: Security. Each participant’s input must be strictly protected throughout the computation process. No participant should be able to obtain any information about the inputs of other participants except for the final extremum result.

R3: Scalability. The protocol should be easily extendable to scenarios involving multiple parties without a significant decrease in protocol efficiency due to an increase in the number of participants.

However, the advent of cutting-edge quantum algorithms [40,41,42,43,44] has placed traditional SMC protocols—whose security rests on the computational hardness of mathematical problems—under unprecedented pressure. To break the impasse, researchers are turning to the fundamental effects of quantum mechanics itself, seeking to design quantum SMC protocols that will preserve the frontiers of privacy in the quantum era.

2.2. Greenberger–Horne–Zeilinger States

Quantum entanglement, a unique characteristic in quantum mechanics, refers to the phenomenon where the state of the remaining subsystems in a composite system can be determined based on the measurement outcomes of some of its subsystems. The GHZ state is an important class of multi-particle entangled states, boasting excellent entanglement properties. It is frequently chosen as an information carrier and finds extensive applications in the field of quantum cryptography.

For example, in 1999, Hillery et al. [7] designed the first (2,2) quantum secret-sharing protocol utilizing the three-particle GHZ state,

$$\begin{array}{c}\hfill |GH{Z}_3^2\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|000\rangle +|111\rangle ).\end{array}$$

(1)

Here, the subscript denotes the number of particles, while the superscript indicates the dimension of the particles. In this protocol, the security is ensured by the correlations among the measurement outcomes of the three particles in this state. Subsequently, Xiao et al. [8] extended this protocol to a multi-party scenario, implementing a (m, m) quantum secret-sharing protocol using the m-particle GHZ state,

$$\begin{array}{c}\hfill |GH{Z}_m^2\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|\stackrel{m}{\overbrace{00\cdots 0}}\rangle +|\stackrel{m}{\overbrace{11\cdots 1}}\rangle ).\end{array}$$

(2)

Each particle of these two quantum states depicted in Equations (1) and (2) is two-dimensional. Namely, it exists in a state of two-dimensional Hilbert space $H^2$, whose computational basis is $\left\{\right|0\rangle ,|1\rangle \}$.

Furthermore, we can consider a more general scenario where each particle resides in a d-dimensional Hilbert space $H^d$. In this case, this class of GHZ states can be represented as

$$\begin{array}{c}\hfill |GH{Z}_m^d\rangle ={\displaystyle \frac{1}{\sqrt{d}}}\left(\right|\stackrel{m}{\overbrace{00\cdots 0}}\rangle +|\stackrel{m}{\overbrace{11\cdots 1}}\rangle +|\stackrel{m}{\overbrace{d-1d-1\cdots d-1}}\rangle .\end{array}$$

(3)

where $C{B}_d=\left\{\right|0\rangle ,|1\rangle ,\cdots ,|d-1\rangle \}$ is a set of computational basis vectors for $H^d$. Obviously, when a computational basis measurement is performed on these m particles, the measurement results $r_1,r_2,\cdots ,r_m$ satisfy the following correlation,

$$\begin{array}{c}\hfill r_1=r_2=\cdots =r_m.\end{array}$$

(4)

Moreover, when a Fourier transform $F_d:|j\rangle \to {\displaystyle \frac{1}{\sqrt{d}}}{\sum }_{k=0}^{d-1}{e}^{2\pi \mathrm{i}jk/d}|k\rangle$ ($\mathrm{i}=\sqrt{-1}$) is applied to each particle of state $|GH{Z}_m^d\rangle$, this quantum state is transformed into the following state,

$$\begin{array}{c}\hfill \stackrel{m}{\overbrace{F_d\otimes F_d\otimes \cdots \otimes F_d}}|GH{Z}_m^d\rangle =|FGH{Z}_m^d\rangle ={({\displaystyle \frac{1}{\sqrt{d}}})}^{m-1}\sum _{i_1+i_2+\cdots +i_m=0\mathrm{mod}d}|i_1\rangle |i_2\rangle \cdots |i_m\rangle .\end{array}$$

(5)

At this point, if a computational basis measurement is applied on these particles again, the sum of these measurement results is equal to zero. In other words, if a measurement is performed on a Fourier basis $F{B}_d=\left\{F_d\right|0\rangle ,F_d|1\rangle ,\cdots ,F_d|d-1\rangle \}$ on the quantum state $|GH{Z}_m^d\rangle$, the measurement results satisfy the following correlation:

$$\begin{array}{c}\hfill r_1+r_2+\cdots +r_m=0\mathrm{mod}d.\end{array}$$

(6)

Based on Equations (4) and (6), it is guaranteed that these particles are in the state $|GH{Z}_m^d\rangle$. In Ref. [45], Huang et al. proved that these particles are in the state $|GH{Z}_m^d\rangle$ when the measurement results meet these two equations; this proof is shown below.

Theorem 1.

An m-particle d-level state is in the form of the state $|GH{Z}_m^d\rangle$, if and only if it satisfies both the following conditions:

(C1) When each particle is measured on the basis of $C{B}_d$, the m measurement results are the same, i.e., Equation (4).

(C2) When each particle is measured on the basis of $F{B}_d$, the sum of the m measurement results is 0 modulo d, i.e., Equation (6).

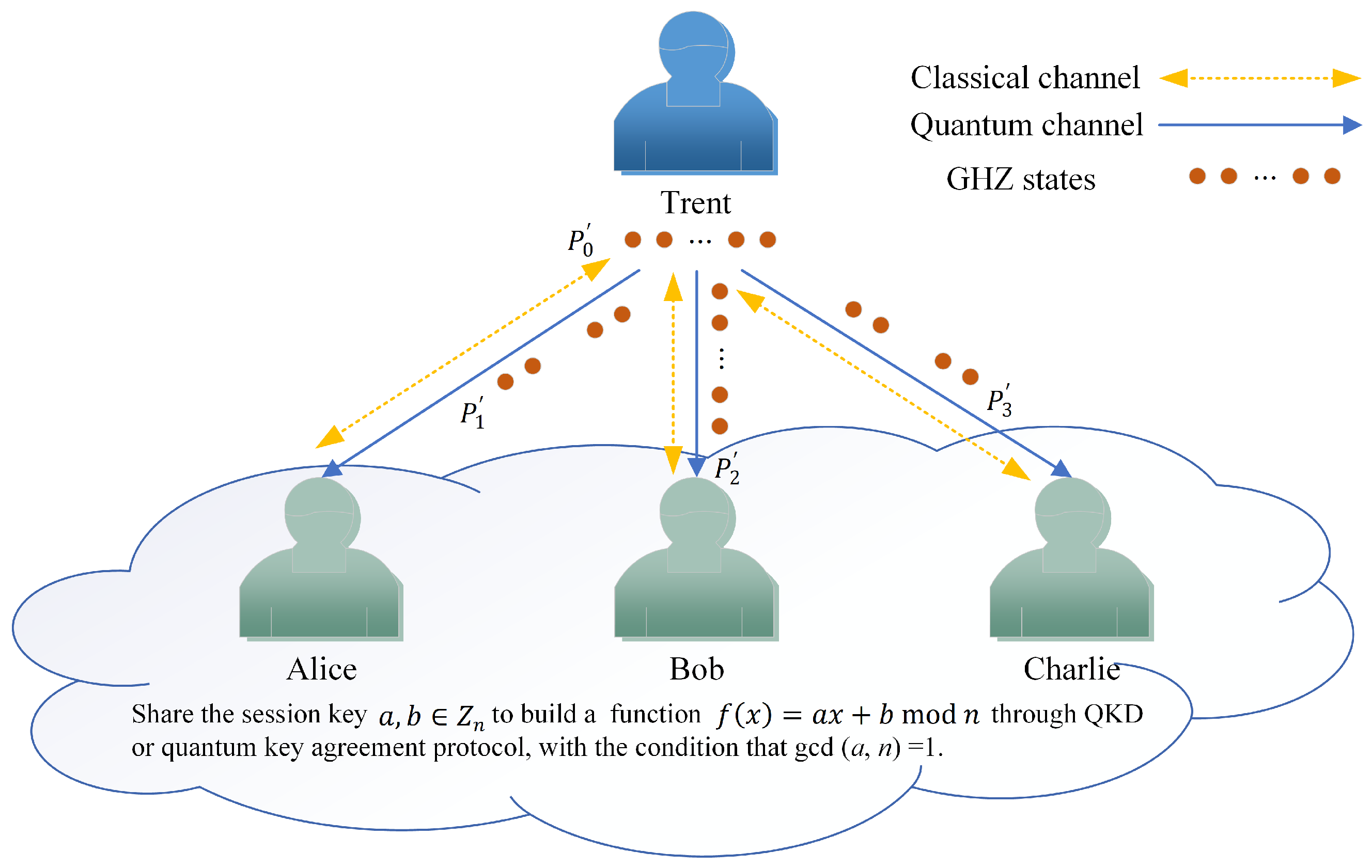
3. Three-Party Protocol

In this section, we propose a three-party quantum security extremum protocol with GHZ states. For generality, we consider three participants, Alice, Bob, and Charlie, who hold three private numbers $s_1,s_2,s_3\in X=\{x_0,x_1,\cdots ,x_{n-1}\}$, respectively. They hope to securely compute the maximum and minimum values of these three private numbers with the assistance of a semi-honest third party, Trent. The specific steps are as follows (also see Figure 1).

Protocol 1

Step 1. Three participants share a session key $a,b\in Z_n=\{0,1,\cdots ,n-1\}$ through a secure quantum key distribution or quantum key agreement protocol (e.g., BB84 protocol), with the condition that $\gcd (a,n)=1$. In this way, Alice, Bob, and Charlie can obtain a one-to-one mapping function $f\left(x\right)=ax+b\mathrm{mod}n$ over the set $Z_n$. Moreover, this function is kept confidential from anyone else, including Trent.

Step 2. Trent prepares $n^{\prime }=n+3\eta$ four-particle four-level GHZ states $|GH{Z}_4^4\rangle ={\displaystyle \frac{1}{2}}\left(\right|0000\rangle +|1111\rangle +|2222\rangle +|3333\rangle )$. Then, he organizes the four particles of each quantum state into four ordered sequences of $n^{\prime }$-length particle sequences, denoted as $P_0^{\prime },P_1^{\prime },P_2^{\prime },P_3^{\prime }$. Finally, Trent respectively sends $P_1^{\prime },P_2^{\prime },P_3^{\prime }$ to Alice, Bob, and Charlie, while keeping $P_0^{\prime }$ himself.

Step 3. After all three participants confirm receipt of the particle sequence, they respectively execute an eavesdropping detection process. The specific detection process is described as follows. Alice (Bob, Charlie) randomly selects $\eta$ particles from the particle sequence as samples and measures these sample particles in the computational basis or Fourier basis at random. Then, Alice (Bob, Charlie) requires Trent plus Bob and Charlie (Charlie and Alice, Alice and Bob) to measure the corresponding particles in the same bases and announce their measurement results accordingly. In terms of Theorem 1, if the sample particles are in the state $|GH{Z}_4^4\rangle$, the measurement result must satisfy the conditions (C1) and (C2). Therefore, Alice (Bob, Charlie) can calculate the error rate based on these measurement results. If the error rate is higher than the pre-set threshold, there is an eavesdropping termination protocol, otherwise the protocol continues.

Step 4. Trent and the three participants discard the sample particles and are left with four new n-length particle sequences, denoted as $P_0,P_1,P_2,P_3$, respectively. After that, they perform Fourier basis measurements on the remaining n particles in their possession and record the measurement outcomes $R_i=(r_i^1,r_i^2,\cdots ,r_i^n)$, where $i=0,1,2,3$.

Step 5. Based on her/his own private data $s_1$ ($s_2$, $s_3$) and the set X, Alice (Bob, Charlie) obtains an n-length bit string $Y_1=(y_1^1,y_1^2,\cdots ,y_1^n)$($Y_2$, $Y_3$). The specific calculation formula is described as follows:

$$\begin{array}{c}\hfill y_i^j=\left\{\begin{array}{cc}\hfill 1,& \hfill x_j\le s_i\\ \hfill 0,& \hfill x_j>s_i\end{array}\right.,\end{array}$$

(7)

where $i=1,2,3$ and $j=1,2,\cdots ,n$. Then, according to $Y_1$ ($Y_2$, $Y_3$) and the function $f\left(x\right)$, Alice (Bob, Charlie) derives a new n-length bit string $Z_1=(z_1^1,z_1^2,\cdots ,z_1^n)$ ($Z_2=(z_2^1,z_2^2,\cdots ,z_2^n)$, $Z_3=(z_3^1,z_3^2,\cdots ,z_3^n)$), where $z_i^{f\left(j\right)}=y_i^j$. Finally, Alice (Bob, Charlie) calculates $O_1=(o_1^1,o_1^2,\cdots ,o_1^n)$ ($O_2=(o_2^1,o_2^2,\cdots ,o_2^n)$, $O_3=(o_3^1,o_3^2,\cdots ,o_3^n)$), where $o_i^j=z_i^j\oplus r_i^j$, and publicly announces the result $O_1$ ($O_2$, $O_3$).

Step 6. According to the messages announced by the three participants and his own measurement results, Trent can calculate $T=(t^1,t^2,\cdots ,t^n)$, where $t^j=o_1^j\oplus o_2^j\oplus o_3^j\oplus r_0^j$. Then, he infers the message $O_0=(o_0^1,o_0^2,\cdots ,o_0^n)$ from T as follows: for each $j=1,2,\cdots ,n$, set $o_0^j=0$ if $t^j=0$ or $t^j=3$; otherwise, set $o_0^j=1$. Finally, Trent publicly declares this message to the three participants.

Step 7. The Three participants, based on the public message $O_0$ and the function $f\left(x\right)$, obtain a new n-length bit string $V=(v^1,v^2,\cdots ,v^n)$, where $v^j=o_0^{f\left(j\right)}$. If the bit string does not contain consecutive “1”s, it indicates an error in the protocol and the protocol is restarted. Otherwise, the positions of the first “1” and the last “1” in the string V are recorded as $k_1$ and $k_2$, respectively. In this way, the participants can obtain the minimum and maximum values of their private numbers, which are $x_{k_1-1}$ and $x_{k_2}$, respectively.

Next, we will further elaborate on the execution process of the protocol through a simple example. In this example, we can assume three private numbers, $s_1=255$, $s_2=4100,s_3=30$, and the set $X=\{1,16,30,255,512,1025,4100,15000,32767\}(n=9)$. Some classical sequences in this example are depicted in

Table 1. Some classical sequences in the presented example.

	Trent	Alice	Bob	Charlie
Step 1		$a=5,b=2$	$a=5,b=2$	$a=5,b=2$
Step 4	$R_0=3,3,0,2,1,2,0,3,1$	$R_1=1,2,1,0,1,1,0,0,3$	$R_2=1,2,2,0,1,2,2,3,3$	$R_3=3,1,1,2,1,3,2,2,1$
Step 5		$Y_1=1,1,1,1,0,0,0,0,0$, $Z_1=0,0,1,1,0,0,0,1,1$, $O_1=1,2,2,1,1,1,0,1,0$	$Y_2=1,1,1,1,1,1,1,0,0$, $Z_2=1,0,1,1,1,1,0,1,1$, $O_2=2,2,3,1,2,3,2,0,0$	$Y_3=1,1,1,0,0,0,0,0,0$, $Z_3=0,0,1,1,0,0,0,1,0$, $O_3=3,1,2,3,1,3,2,3,1$
Step 6	$T=1,0,3,3,1,1,0,3,2$, $O_0=1,0,0,0,1,1,0,0,1$
Step 7		$V=0,0,0,1,1,1,1,0,0$, $x_2=30$, $x_6=4100$	$V=0,0,0,1,1,1,1,0,0$, $x_2=30$, $x_6=4100$	$V=0,0,0,1,1,1,1,0,0$, $x_2=30$, $x_6=4100$

.

In Step 1, Alice, Bob, and Charlie negotiate and agree on a secret affine function $f\left(x\right)=5x+2\mathrm{mod}9$, where $a=5$ and $b=2$. In Step 2, Trent prepares nine four-particle, four-level GHZ states $|GH{Z}_4^4\rangle$. Here, our focus is on discussing the correctness of the protocol under ideal conditions, so we will temporarily disregard the eavesdropping detection process. In Step 4, Trent and the three participants each perform a measurement on the particles in their possession using the Fourier basis. The measurement results obtained are $R_0=(3,3,0,2,1,2,0,3,1)$, $R_1=(1,2,1,0,1,1,0,0,3)$, and $R_2=(1,2,2,0,1,2,2,3,3)$, $R_3=(3,1,1,2,1,3,2,2,1)$.

In Step 5, Alice obtains $Y_1=(1,1,1,1,0,0,0,0,0)$ based on Equation (7) and her secret number $s_1=255$. Then, by utilizing the function $f\left(x\right)$, she derives $Z_1=(0,0,1,1,0,0,0,1,1)$. Finally, she performs a bitwise modulo 4 addition on these two values $R_1$ and $Z_1$ to obtain a result $O_1=(1,2,2,1,1,1,0,1,0)$. Similarly, Bob and Charlie each calculate their respective values, $O_2=(2,2,3,1,2,3,2,0,0)$ and $O_3=(3,1,2,3,1,3,2,3,1)$. These three messages are told to Trent publicly. In Step 6, Trent performs a bitwise modulo 4 addition on these three open messages and his own measurement results $R_0$ to obtain $T=(1,0,3,3,1,1,0,3,2)$, according to which he announces $O_0=(1,0,0,0,1,1,0,0,1)$.

At the end of the protocol, the three participants derive $V=(0,0,0,1,1,1,1,0,0)$ based on the open message $O_0$ and the secret function $f\left(x\right)$. Specifically, they obtain $k_1=3$ and $k_2=6$. In this way, they are able to simultaneously determine both the minimum value $x_{k_1-1}=30$ and the maximum value $x_{k_2}=4100$.

4. Security

Before presenting the security analysis, let us first briefly discuss the security model of the protocol. In the realm of SMPC, there are two common security models: the semi-honest model and the malicious model. In the semi-honest model, it is postulated that one or more parties engaged in the computation are semi-honest. These parties comply with the protocol yet endeavor to deduce information about others through their interactions. In contrast, in the malicious model, the parties may be malicious. They have the capacity to arbitrarily deviate from the protocol and even initiate active attacks. Obviously, in comparison to the semi-honest model, the malicious model that constitutes the strongest security assumption in MPC provides a higher level of security and is more apt for high-risk scenarios, including finance, healthcare, and government affairs, thereby rendering it more practical. The protocol proposed in this paper is based on the assumption of the malicious model.

On the other hand, owing to the limitations imposed by the no-go theorem [46,47], most quantum SMPC protocols require the introduction of a semi-honest third party. This third party will strictly adhere to the protocol procedures but may passively attempt to infer the private information of other participating parties through protocol interactions, a behavior characterized as “honest but curious”. Introducing a semi-honest third party under the malicious model represents a compromise solution. It enables us to harness the semi-honest third party to enhance efficiency while still shielding the protocol from attacks by malicious parties. Nevertheless, it is imperative to rigorously restrict the volume of information accessible to the third party and assume that the third party does not collude with malicious parties. Therefore, in addition to external attacks, the security of the proposed protocol is analyzed under some common types of internal attacks.

4.1. External Attack

Suppose that there is an external attacker named Eve, whose goal is to eavesdrop on the secret input of one of the participants (e.g., Bob, $s_2$). Based on the publicly available messages $O_1$ and $O_0$, Eve cannot obtain any information about $s_2$. Therefore, she must target the traveling particle sequence $P_2^{\prime }$, which is transmitted from Trent to Bob. Common attack strategies could be the intercept–measure–resend attack, the entanglement–measure attack, etc. However, these attacks can be detected by Bob when he performs his eavesdropping detection process in Step 3. From Theorem 1, we can deduce that there are no errors introduced only when the traveling particles are in the state $|GH{Z}_4^4\rangle$. In other words, as long as Eve attempts to attack the traveling particles during their transmission, her actions will be detected because the traveling particles are not in the state $|GH{Z}_4^4\rangle$. Consequently, the proposed protocol is secure against such external attacks.

4.2. Internal Attack

4.2.1. Dishonest Participant’s Attack

Since the three participating parties play identical roles in the protocol and perform the same operations without the loss of generality, we can assume that participant Alice is dishonest, denoted as Alice*. She attempts to steal the secret input of participant Bob, $s_2$. To this end, she may adopt the following common attack strategy.

In this attack, Alice intercepts the signal particle sequence $P_2^{\prime }$. For each particle in this sequence, she prepares two fake particles ($f_1$, $f_2$) in a quantum state $|\psi \rangle ={\displaystyle \frac{1}{2}}\left(\right|00\rangle +|11\rangle +|22\rangle +|33\rangle )$ and substitutes the fake particle $f_1$ for the signal particle to be transmitted to Bob. After Bob performs a Fourier basis measurement on the fake particle $f_1$, Alice* also measures the particle $f_2$ in the Fourier basis. Consequently, Alice* can infer Bob’s measurement result from her own measurement outcome. Using this information along with Bob’s public disclosures $O_2$, she can deduce Bob’s private data. However, this attack will be detected by Bob’s eavesdropping detection process in Step 3. When the fake particle $f_1$ is selected as the sample, Bob measures this particle using a randomly chosen computational basis or Fourier basis. With a probability of 1/2, Bob selects the computational basis, resulting in a random measurement outcome. According to the eavesdropping detection process, Bob then requests for Trent and the other two participants to measure their corresponding particles. Since the fake particles are not entangled with the four genuine particles in the GHZ state $|GH{Z}_4^4\rangle$, there is no correlation between the measurement results of these particles. Alice* is also unable to forge the measurement results of Trent and Charlie. Therefore, the probability of obtaining different measurement results is ${\displaystyle \frac{3}{4}}$. Clearly, this attack will be easily detected by Bob.

Moreover, it is not difficult to see that even if Charlie is also dishonest and conspires with Alice to attack the protocol, they will not succeed. The reason is that they cannot forge Trent’s measurement results, and the selection of sample particles is entirely determined by Bob, something they cannot predict in advance. In summary, the proposed protocol can resist attacks from dishonest participants.

4.2.2. Semi-Honest Third Party’s Attack

Similarly to most quantum secure multi-party computation protocols, the proposed protocol requires the introduction of a third party, Trent, to assist the participants in completing secure computation tasks. Here, the requirement for Trent is that he is semi-honest. It means that he will correctly follow the protocol steps and will not collude with other participants, but he may attempt to obtain participants’ privacy numbers or computation results (i.e., the maximum and minimum values) from the protocol execution process.

In the protocol, although Trent calculates $O_0$ based on the public messages $O_1$, $O_2$, and $O_3$, he does not know the function $f\left(x\right)$, and thus cannot deduce the participants’ secret inputs solely from these messages. Since the initial quantum states are prepared by Trent and sent to each participant, Trent might attempt to exploit this convenience to launch an attack. For example, he could prepare multiple two-particle entangled states $|\psi \rangle$ and distribute them to each participant instead of the GHZ state $|GH{Z}_4^4\rangle$. However, according to Theorem 1 and the analysis above, such behavior will inevitably introduce errors during the eavesdropping detection process in Step 3, which will be detected by the participants. Therefore, the proposed protocol is secure against this type of attack.

5. Scalability

In this section, we can directly generate the three-party quantum security extremum protocol presented in Section 3 to the multi-party case. In the multi-party protocol, there are m participants and User_i ($i=1,2,\cdots m$), who holds a private numbers $s_i\in X=\{x_0,x_1,\cdots ,x_{n-1}\}$. They can securely compute the maximum and minimum values of these m private numbers by executing the following steps:

Protocol 2

Step 2.1. The m participants securely agree on a session key $a,b\in Z_n$ and obtain a one-to-one mapping function $f\left(x\right)=ax+b\mathrm{mod}n$.

Step 2.2. Trent prepares $n^{\prime }=n+m\eta$   $m+1$-particle d-level GHZ states $|GH{Z}_{m+1}^d\rangle$ ($d>m$). Then, he selects the $m+1$ particles from each quantum state and obtains $m+1$ ordered sequences of $n^{\prime }$-length particle sequences, denoted as $P_0^{\prime },P_1^{\prime },\cdots ,P_m^{\prime }$. Finally, Trent distributes these sequences, sending $P_i$ to User_i for $i=1,2,\cdots ,m$, while retaining $P_0^{\prime }$.

Step 2.3. After confirming receipt of the particle sequence, each User_i ($i=1,2,\cdots ,m$) chooses $\eta$ samples and performs their eavesdropping detection process. The specific detection process is the same as that in Step 3 of Protocol 1.

Step 2.4. Following the discarding of sample particles, Trent and m participants obtain $m+1$ new n-length particle sequences, denoted as $P_0,P_1,\cdots ,P_m$. After that, Fourier basis measurements are performed on the remaining particles, yielding the measurement outcomes $R_i=(r_i^1,r_i^2,\cdots ,r_i^n)$ for $i=0,1,\cdots ,m$.

Step 2.5. Based on his private data $s_i$ and Equation (9), each participant User_i ($i=1,2,\cdots ,m$) generates an n-length bit string $Y_i=(y_i^1,y_i^2,\cdots ,y_i^n)$. Then, according to $Y_i$ and the function $f\left(x\right)$, User_i derives a new n-length bit string $Z_i=(z_i^1,z_i^2,\cdots ,z_i^n)$, where $z_i^{f\left(j\right)}=y_i^j$. Finally, User_i computes $O_i=(o_i^1,o_i^2,\cdots ,o_i^n)$, with $o_i^j=z_i^j\oplus r_i^j$, and sends it to Trent.

Step 2.6. Trent combines the messages $O_1,O_2,\cdots ,O_m$ and his own measurement results to calculate $T=(t^1,t^2,\cdots ,t^n)$, where $t^j=o_1^j\oplus o_2^j\oplus o_3^j\oplus r_0^j$. After that, he can obtain the message $O_0=(o_0^1,o_0^2,\cdots ,o_0^n)$ and publicly announce it to all participants. Here, the calculation formula for $o_0^j$ is as follows:

$$\begin{array}{c}\hfill o_0^j=\left\{\begin{array}{cc}\hfill 0,& \mathrm{if}{t}^j=0\mathrm{or}{t}^j=m\hfill \\ \hfill 1,& \mathrm{otherwise}\hfill \end{array}\right.,\end{array}$$

(8)

Step 2.7. In terms of the public message $O_0$ and $f\left(x\right)$, each User_i ($i=1,2,\cdots ,m$) obtains a new n-length bit string $V=(v^1,v^2,\cdots ,v^n)$, where $v^j=o_0^{f\left(j\right)}$. He then identifies the positions of the first “1” ($k_1$) and the last “1” ($k_2$) in the string V. These positions allow all participants to determine the minimum and maximum values of their private numbers, $x_{k_1-1}$ and $x_{k_2}$, respectively.

It is not hard to see that the amounts of classical and quantum bits that need to be transmitted in Protocol 2 are $mn(1+{log}_{2}d)$ and $(m+1)n{log}_{2}d$, respectively. This implies that the communication complexity of the protocol, $O\left(mn{log}_{2}m\right)$ ($d=m+1$), increases approximately linearly, rather than exponentially, with the growth in the number of participants m and the size of the dataset n. Moreover, since each participant only needs to perform single-particle measurements n times, the computational complexity of the protocol is $O\left(n\alpha \right)$, where $\alpha$ is the cost of a single-particle operation. This implies that its computational complexity remains unchanged as the number of participants increases. For Trent, he is required to prepare GHZ entangled states comprising $m+1$ particles, which is quite challenging under current technological conditions. However, it is believed that with continuous breakthroughs in quantum technology, especially in quantum entanglement in recent years, this issue can be resolved in the near future. Therefore, the protocol proposed in this paper is not only theoretically scalable but also practically feasible.

6. Correctness

Suppose that the minimum value of the set $\{s_1,s_2,\cdots ,s_m\}$ is $x_{min}$, the maximum value is $x_{max}$, the secret number of $m_1$ participants is $x_{min}$, and the secret number of $m_2$ participants is $x_{max}$ ($0<m_1,m_2<m$). From the protocol, it is evident that each participant performs the same operation in the protocol. Therefore, for simplicity, we assume that the secret number of the first $m_1$ participants is $x_{min}$, and that of the last $m_2$ participants is $x_{max}$. That is,

$$\begin{array}{c}\hfill s_1=\cdots =s_{m_1}=x_{min},s_m=\cdots =s_{m-m_2+1}=x_{max}.\end{array}$$

(9)

In this case, the secret numbers of the remaining $m-m_1-m_2$ participants lie between $x_{min}$ and $x_{max}$, namely,

$$\begin{array}{c}\hfill x_{min}<s_{m_1+1},\cdots ,s_{m-m_2}<x_{max}.\end{array}$$

(10)

According to Equations (7) and (9), we can obtain,

$$\begin{array}{c}\hfill Y_1=\cdots =Y_{m_1}=(\stackrel{min}{\overbrace{1,\cdots ,1}},\stackrel{n-min}{\overbrace{0,\cdots ,0}}),Y_{m-m_2+1}=\cdots =Y_m=(\stackrel{max}{\overbrace{1,\cdots ,1}},\stackrel{n-max}{\overbrace{0,\cdots ,0}})\end{array}$$

(11)

Similarly, the corresponding bit string of the remaining participant User_i ($m_1<i<m-m_2+1$) is

$$\begin{array}{c}\hfill Y_i=(\stackrel{min}{\overbrace{1,\cdots ,1}},\stackrel{j-min}{\overbrace{1,\cdots ,1}},\stackrel{n-max-j}{\overbrace{0,\cdots ,0}},\stackrel{n-max}{\overbrace{0,\cdots ,0}}),\end{array}$$

(12)

where $s_i=x_j$.

In the protocol, the affine function $f\left(x\right)$ is employed to prevent Trent from obtaining the computation result. Since an inverse transformation is applied to it in subsequent steps, this function has no impact on the correctness of the protocol. For simplicity, we assume that $f\left(x\right)=x$, i.e., $Z_i=Y_i$. In this case, the concrete value of $T=(t^1,t^2,\cdots ,t^n)$ calculated by Trent in Step 6 is depicted as follows. For $1\le j\le m_1$, in terms of Equation (7) and $z_i^j=y_i^j=1(i=1,2,\cdots m)$, the value of $t^j$ is obtained,

$$\begin{array}{c}\hfill t^j=\sum _{i=1}^m{o}_i^j=\sum _{i=1}^m(y_i^j+r_i^j)=\sum _{i=1}^m{y}_i^j+\sum _{i=1}^m{r}_i^j=\sum _{i=1}^m{y}_i^j=m.\end{array}$$

(13)

For $j>m-m_2+1$, in terms of Equation (7) and $z_i^j=y_i^j=0(i=1,2,\cdots m)$, the value of $t^j$ is obtained,

$$\begin{array}{c}\hfill t^j=\sum _{i=1}^m{o}_i^j=0.\end{array}$$

(14)

In the same way, for $m_1<j\le m-m_2+1$, $1<t^j<m$ can be derived from Equation (12). Based on T and Equation (8), we obtain $O_0$,

$$\begin{array}{c}\hfill O_0=(\stackrel{min}{\overbrace{0,\cdots ,0}},\stackrel{max-min}{\overbrace{1,\cdots ,1}},\stackrel{n-max}{\overbrace{0,\cdots ,0}}).\end{array}$$

(15)

From this public message, all participants deduce that $k_1=min+1$ and $k_2=max$, namely, the minimum and maximum values of their private numbers are, respectively, $x_{k_1-1}=x_{min}$ and $x_{k_2}=x_{max}$. Hence, the proposed protocol is correct.

7. Performance Evaluation

In this section, we briefly discuss other performance aspects of the proposed protocol, aside from its security, correctness, and scalability. To better illustrate the performance characteristics of our protocol, we compare it with two other existing protocols [37,39], with the specific comparison results presented in

Table 2. A performance comparison between the proposed protocol and the existing QSME protocol is presented, covering comparative analysis across 11 aspects including quantum resources. A detailed discussion is provided in Section 4 of the main text.

Protocols	Ref. [37]	Ref. [39]	The Proposed Protocol
Quantum resource	single particles	single particles	multi-particle GHZ states
Quantum bits	$2kmn{log}_{2}m$	$mn{log}_{2}d$	$(m+1)n{log}_{2}d$
Classical bits	$2kmn{log}_{2}m$	0	$mn(1+{log}_{2}d)$
Communication complexity	$O\left(kmn{log}_{2}m\right)$	$O\left(mn{log}_{2}m\right)$	$O\left(mn{log}_{2}m\right)$
Quantum operation	Single-particle operation	Single-particle operation	Single-particle measurement
Computation task	Maximum	Maximum and Minimum	Maximum and Minimum
Resistant to external attacks	Yes	Yes	Yes
Resistant to internal attacks	Yes	No	Yes
Security model	Semi-honest model	Malicious model	Malicious model with a semi-honest third party
Deterministic or probabilistic	Probabilistic	Deterministic	Deterministic
Other requirement	Authenticated quantum channels	Decoy qudits	No

m = number of parties, n = cardinality of the dataset, d = dimension of signal particle > m, ${\left({\displaystyle \frac{1}{2}}\right)}^k$ = probability of obtaining wrong calculation results.

.

Communication complexity serves as a crucial indicator representing the efficiency of the proposed protocol. In our protocol, Trent prepares n $m+1$-particle d-level GHZ states and respectively sends n particles to all m participants. In Step 5, each participant, User_i, sends a classical message $O_i$ to Trent. In Step 8, Trent announces his result $O_0$ to all participants, which consumes $mn$ classical bits. In total, the communication overhead comprises $(m+1)n{log}_{2}d$ qubits and $mn(1+{log}_{2}d)$ classical bits. Given that $d=m+1$, the overall communication complexity of the proposed protocol is $O\left(mn{log}_{2}m\right)$.

In the protocol presented in Ref. [37], the maximum of all private inputs is obtained through multiple executions OR computations, which has a certain probability of yielding incorrect results, meaning that the computation is probabilistic. To reduce the error probability, the protocol needs to be executed k times so that the error probability ${\left({\displaystyle \frac{1}{2}}\right)}^k$ approaches zero. Consequently, this protocol incurs a relatively high communication complexity. As for the protocol presented in Ref. [39], d-level single particles are utilized as information carriers and the computation is deterministic, resulting in a low communication complexity, which is the same as in our proposed protocol. However, in this protocol, the decoy method is employed to ensure the security of signal particle transmission between two adjacent participants, but it cannot withstand collusion attacks from multiple dishonest participants [9]. Moreover, at the end of the protocol, only the first participant obtains the computation result, which makes it unsuitable for some application scenarios that require fairness, where each participant is expected to obtain the result simultaneously. A detailed performance comparison between the proposed protocol and these two protocols is presented in Table 2. The comparison is based on various factors, including communication complexity, quantum resources, security model, etc.

Certainly, from the perspective of near-term deployment, semi-quantum secure multi-party computation [29,30,31,32,33,34,35,36] is more feasible. Such protocols only require one party among the communicating parties to possess quantum capabilities, while the other party only needs to perform classical operations to complete secure computation tasks. This significantly reduces the demand for quantum devices, making them easier to deploy and apply in practical communication networks. However, most current semi-quantum cryptographic protocols are designed for two-party or three-party scenarios and have poor scalability for arbitrary multi-party scenarios. A common solution is to achieve multi-party secure computation by conducting semi-quantum two-party secure communication between the third party with each participant. This, however, requires the expenditure of a substantial amount of quantum resources and increases communication complexity. Furthermore, compared to quantum participants, classical participants require more quantum states for measurement and reflecting transmission. Therefore, the efficiency of such semi-quantum multi-party secure computation protocols is generally low.

8. Conclusions

This paper presents a quantum secure multi-party computation protocol for finding the maximum and minimum values based on GHZ states. The protocol involves multiple participants and a semi-honest third party. By leveraging the correlations inherent in GHZ states, the participants can simultaneously obtain the final computational results, namely, the maximum and minimum values of their secret inputs, with the assistance of the third party. Meanwhile, the correlations of GHZ states are also employed to ensure the secure transmission of signal particles. Security analysis demonstrates that the protocol can not only withstand common external attacks but also resist internal attacks from dishonest participants and the semi-honest third party. Furthermore, the correctness and scalability of the protocol are analyzed, showing that it is both correct and scalable. Additionally, it is straightforward to compute the sum and difference of the extremum values using this protocol. Compared with Refs. [37,39], although our protocol adopts GHZ states, it offers distinct advantages, including that it does not require decoy particles or authenticated quantum channels and it places lower demands on participants’ quantum capabilities, thereby improving both feasibility and practicality. Notably, Refs. [48,49] demonstrate that the preparation of GHZ states is no longer experimentally prohibitive. In future work, we will attempt to construct multi-particle GHZ states on existing quantum cloud platforms to further evaluate the practical potential of the protocol. Additionally, since the protocol requires the assistance of a semi-honest third party, this imposes certain limitations on its practical applications. Therefore, we will also explore how to achieve secure computation of multi-party extremum values in scenarios without third-party involvement or when the third party is untrusted.