A Formal Verification Approach for Linux Kernel Designing

Abstract

Although the Linux kernel is widely used, its complexity makes errors common and potentially serious. Traditional formal verification methods often have high overhead and rely heavily on manual coding. They typically verify only specific functionalities of the kernel or target microkernels and do not support continuous verification of the entire kernel. To address these limitations, we introduce LMVM (Linux Kernel Modeling and Verification Method), a formal method based on type theory that ensures the correct design of the Linux architecture. In the model, the kernel is treated as a top-level type, subdivided into the following sublevels: subsystem, dentry, file, struct, function, and base. These types are defined in the structure and relationships. The verification process includes checking the design specifications for both type relationships and the presence of each type. Our contribution lies primarily in the following two points: 1. This is a lightweight verification. As long as the modeling is complete, architectural errors in the design phase can be identified promptly. 2. The designed “model refactor” module supports kernel updating, and the kernel can be continuously verified by extending the kernel model. To test its usefulness, we develop a set of security communication mechanisms in the kernel, which are verified using our method.

1. Introduction

Linux is widely adopted across various environments, leading to numerous development versions. Consequently, demands for its reliability and correctness have become increasingly stringent. Given the complexity of the kernel, a key method to ensure its correctness is through formal verification, employing various tools to specify and prove its behavior. However, formal verification requires significant expertise and proficiency in both tools and languages. The workload for kernel modeling and verification is substantial, which complicates comprehensive and continuous kernel verification. Numerous studies have focused on specifying and verifying Unix-like kernels. These research efforts include the verification of the UCLA security kernel [1], verification for multilevel security of operating system designs [2], and the KIT operating system verification project [3]. A comprehensive review of related studies can be found in [4]. Recent research includes the design of an automated verification method using restricted SMT for Unix-like systems in Hyperkernel [5], the certification of concurrent OS kernels with multi-core support in CertiKOS [6], and the development of a verification framework for reasoning about interrupts in preemptive kernels [7].

Each constructs code-level proofs using an interactive theorem prover, with the microkernel as the study object. The following two issues should be considered: 1. Code Size and Manual Overhead: The verification code is often several times larger than the code being verified and requires significant human involvement. This makes code-level verification of kernels with a large amount of code impractical, particularly for monolithic kernels. As a result, comprehensive studies tend to focus on microkernels, while research on monolithic kernels typically examines specific subsets or aspects. 2. Technical Challenges: Verification at the code level can lead to problems such as state explosion [8], difficulty in solving invariants, and low automation levels, requiring substantial human participation to complete verification. While many studies have attempted to optimize verification algorithms [9,10,11], the practicality of these approaches remains uncertain.

Based on the above issues, we propose a formal verification methodology for kernel designs in the architecture. According to a National Institute of Standards & Technology (NIST) report, over half of errors occur during the design phase [12]. In kernel research, avoiding most potential problems during the design phase can significantly reduce verification costs. Design verification has the advantage of high granularity and lower labor intensity. Compared to traditional methods that prescribe rules at the code level (e.g., seL4), our approach only requires developers to adhere to the kernel specifications during the design phase. This eliminates the complexity of code-level verification, significantly enhancing the efficiency of the verification process. As a result, it becomes feasible to ensure the correctness of the entire kernel. Moreover, verification of kernel increments can yield results quickly. This allows kernel verification and design to proceed almost concurrently, greatly enhancing the practicality of the formal method. In summary, our focus in verification research is on design correctness.

In terms of a detailed verification approach, traditional formal verification typically involves specifying the behavior or model of the kernel, followed by theorem proving or model checking for verification. This approach requires manual specification and, therefore, does not support automatic, continuous verification. Therefore, we opt to specify the kernel in the architecture. This is a general, structure-based specification, which can be automatically applied to the kernel and its increments. For our methodology, we choose a lightweight formal method based on type theory [13,14,15]. As a formal language, the core idea of type theory is to treat all objects as types. Using this theory, we can describe and specify software hierarchically. Based on this theory, we build a model based on kernel features and provide corresponding specifications (Section 3), such as the organization structures of functions and data structures.

In the kernel, the types encompass objects ranging from variables to subsystems. We focus on the correctness of these types to maintain the reliability of the kernel design. Verification is performed through specifications that include type structures and relationships. To reduce the overhead, we do not conduct reasoning in the code layer. Instead, we verify the existence of types and the correctness of type relationships during the design phase. The main contribution of this paper are summarized as follows:

• We describe the demand in a tree structure that can be disassembled down to the function level, allowing us to pinpoint errors.
• We provide a modeling methodology that decomposes the kernel architectures hierarchically to specify each level’s design accurately.
• We provide a verification approach for type and inter-type relationships to effectively verify the design’s correctness.
• We propose an implementation that includes modeling, verification, and refactoring to verify the kernel continuously.

The rest of this paper is arranged as follows. Section 2 introduces the definition and expression for the kernel model. Section 3 elaborates on the design specifications of the model. Section 4 explains the rules of verification and the reasoning process of an invocable relationship. Section 5 discusses the limitations of our method. Section 6 presents the “model refactor” module, error codes, and the processes of implementation algorithms. Section 7 elaborates upon applications verified by LMVM, including parts of functions in VFS and a set of security communications developed for businesses. Section 8 introduces the related works. Finally, we conclude with Section 9 and look forward to further research in Section 10.

2. Methodology

In this section, we introduce the basic concepts of our approach to help the reader better understand we build models and verify properties. An indispensable aspect of testing the kernel for the developer is ensuring that the design meets the proposed requirements. Therefore, the demand and design must be clearly defined. Below, we provide essential concepts and expressions related to demands and kernel design.

2.1. Demand

The demand is the function we want the software to perform. To describe the demand accurately, we define it at the func level. The demand consists of multiple demanding functions, and each function consists of multiple demanding paths. A demanding path can be split into several demanding invocations. Each invocation contains an invoking relationship and two participating funcs. The funcs depend on several types. Therefore, the demand property can be transformed into a sequence containing multiple types and constraint relationships, called the type sequence.

Expression 1.

Demand $D::=(D{F}_1,D{F}_2,\dots ,$$D{F}_n)$.

The big demand is composed of multiple small demands called a demanding function (DF), which is the list of the demanding path. DF ::= (Id, Name, Exp, State). Here, the Id and Name are the identification. The state describes whether the list is valid. Exp ::= (${\mathrm{DP}}_1$, ${\mathrm{DP}}_2$,…, ${\mathrm{DP}}_n$), where DP is the demanding path implemented by funcs.

Expression 2.

Demanding path $DP::=(Id,Name,Exp,State)$.

The demanding path is an invoking chain. Exp ::= (${\mathrm{DI}}_1$, ${\mathrm{DI}}_2$, …, ${\mathrm{DI}}_n$). DI is an invocation. DI ::= (${\mathrm{F}}_1$, ${\mathrm{F}}_2$), where ${\mathrm{F}}_i$ is a func. The meaning of DI is that ${\mathrm{F}}_1$ invokes ${\mathrm{F}}_2$.

2.2. Design

Design involves the formulation of the key points of software according to demands before implementing them in the programming language. This paper uses type theory to model kernel design based on architecture. The central idea of type theory is to view all objects as types. Type is a generalization of “class” in a high-level programming language. In a system, types are organized through inter-type relationships. Below, we introduce the critical concepts and expressions.

Definition 1.

Type Sequence: $TS::=(T_{list},R_{list})$ If $T_k$ (k = 1, …, n) is one of seven types with the constraint of R($T_i$, $T_j$) (1 ≤ i, j ≤ n) belonging to relationships between types (called inter-type relationship), $T_1$; …; $T_n$ is a type sequence.

Therefore, the type sequence is specified in ${\mathrm{T}}_{list}$ and ${\mathrm{R}}_{list}$ which are the lists of type T and inter-type relationships R respectively.

Expression 3.

Type List $Tlist::=(Id,Exp,Compound)$

Here, Exp represents Exp ::= (${\mathrm{T}}_1$,${\mathrm{T}}_2$, …, ${\mathrm{T}}_n$), where T is the type that makes up the composite type. Compound represents the composite mode of T, such as MultiList, ListAgg, etc. (details in

Table 1. Structural Relationship. Here, the associated types are the relations between the member type and the aggregated relationship type.

Category of Aggregated Relationship	Level Status	Relationship	Associated Types (Type-Aggregated Type)
Level type–list type List type–list type	Within level	MultiList	input parameter–input parameter list, member variable–member variable list, member func–member func list, global func–global func list, struct–struct list, file–file list, dentry–dentry list, subsys–subsys list
List type–level type		ListAgg	Input parameter list–func, member variable list–struct, member func list–struct, global func list–file, struct list–file, file list–dentry, dentry list–dentry, file list–subsys, dentry list–subsys
Level type–level type	Between levels	ParamIn	input parameter–func
		ParamOut	output parameter–func
		VarStruct	member variable–struct
		FuncStruct	member func–struct
		FuncFile	global func–file
		StructFile	struct–file
		Agg	file–dentry, dentry–dentry, file–subsys, dentry–subsys

). Since T can be a composite type, ${\mathrm{T}}_{list}$ can be composed of multiple levels.

Expression 4.

level Type $T::=(ID,Name,Level,Scope,Exp)$

Here, the type specifically refers to the level type. ID and Name are unique identifiers for each type. The level includes base, func, struct, file, dentry, and subsystem. Scope indicates the type scopes used exclusively to restrict base, func, and struct types. Exp ::= (Father, Lis${\mathrm{t}}_1$, Lis${\mathrm{t}}_2$), which identifies the upper and lower types. Father is the upper type, just as struct/file is the father of a func. Lis${\mathrm{t}}_1$/Lis${\mathrm{t}}_2$ is the low-level list that makes up the current type. Exp values in different levels are presented in

Table 2. Constraints in different levels.

Type Level	Member 1	Member 2	Relationship
Base	Null		Null
Func	${\mathrm{list}}_1$ = input parameter list	${\mathrm{type}}_{out}$ = output parameter type	${\mathrm{t}}_i$-T:ParamIn    ${\mathrm{type}}_{out}$-T:ParamOut    ${\mathrm{list}}_1$-T:ListAgg    ${\mathrm{t}}_1$/${\mathrm{t}}_2$-${\mathrm{list}}_1$/${\mathrm{list}}_2$:MultiList    ${\mathrm{t}}_3$/${\mathrm{t}}_4$-${\mathrm{t}}_2$:MultiList    ${\mathrm{t}}_5$/${\mathrm{t}}_6$-${\mathrm{t}}_4$:MultiList    …    ${\mathrm{t}}_{i+1}$-${\mathrm{t}}_i$:MultiList
	${\mathrm{list}}_1$.member_type = {${\mathrm{t}}_1$:Base|Func|Struct}    ${\mathsf{list}}_{\mathbf{1}}$.member_list = {${\mathsf{t}}_2$:List}    ${\mathrm{t}}_2$.member_type = {${\mathrm{t}}_3$:Base|Func|Struct}    ${\mathsf{t}}_2$.member_list = {${\mathsf{t}}_4$:List}   …    ${\mathrm{t}}_i$.member_type = {${\mathrm{t}}_{i+1}$:Base|Func|Struct}    ${\mathrm{t}}_i$.member_list = Null	${\mathrm{type}}_{out}$:Base|Func|Struct|List
Struct	${\mathrm{list}}_1$ = member variable list	${\mathrm{list}}_2$ = member function list	${\mathrm{t}}_i$-T:VarStruct    f-T:FuncStruct    ${\mathrm{list}}_1$/${\mathrm{list}}_2$-T:ListAgg    ${\mathrm{t}}_1$/${\mathrm{t}}_2$-${\mathrm{list}}_1$:MultiList    f-${\mathrm{list}}_2$:MultiList    ${\mathrm{t}}_3$/${\mathrm{t}}_4$-${\mathrm{t}}_2$:MultiList    ${\mathrm{t}}_5$/${\mathrm{t}}_6$-${\mathrm{t}}_4$:MultiList    …    ${\mathrm{t}}_{i+1}$-${\mathrm{t}}_i$:MultiList
	${\mathrm{list}}_1$.member_type = {${\mathrm{t}}_1$:Base/Struct}    ${\mathsf{list}}_{\mathbf{1}}$.member_list = {${\mathsf{t}}_{\mathbf{2}}$:List}    ${\mathrm{t}}_2$.member_type = {${\mathrm{t}}_3$:Base/Struct}    ${\mathsf{t}}_{\mathbf{2}}$.member_list = {${\mathsf{t}}_{\mathbf{4}}$:List}   …    ${\mathrm{t}}_i$.member_type = {${\mathrm{t}}_{i+1}$:Base/Struct}    ${\mathrm{t}}_i$.member_list = Null	${\mathrm{list}}_2$.member_type = {f:Func}    ${\mathrm{list}}_2$.member_list = Null
File	${\mathrm{list}}_1$ = global func list	${\mathrm{list}}_2$ = struct list	f-T:FuncFile    s-T:StructFile    ${\mathrm{list}}_1$/${\mathrm{list}}_2$-T:ListAgg    f-${\mathrm{list}}_1$:MultiList    s-${\mathrm{list}}_2$:MultiList
	${\mathrm{list}}_1$.member_type = {f:Func}    ${\mathrm{list}}_1$.member_list = Null	${\mathrm{list}}_2$.member_type = {s:Struct}    ${\mathrm{list}}_2$.member_list = Null
Dentry/ Subsys	${\mathrm{list}}_1$ = file list	${\mathrm{list}}_2$ = dentry list	f/d-T:Agg    ${\mathrm{list}}_1$/${\mathrm{list}}_2$-T:ListAgg    f-${\mathrm{list}}_1$:MultiList    d-${\mathrm{list}}_2$:MultiList
	${\mathrm{list}}_1$.member_type = {f:File}    ${\mathrm{list}}_1$.member_list = Null	${\mathrm{list}}_2$.member_type = {d:Dentry}    ${\mathrm{list}}_2$.member_list = Null

.

Expression 5.

Inter-type Relationship  $R::=(Id,RelationClassify,Exp)$

RelationClassify is the category of the type relationship. There are 11 classes in total, including 9 structural relationships (Table 1) and 2 invoking relationships (invocable and accessible relationships). Exp ::= (${\mathrm{T}}_1$, ${\mathrm{T}}_2$, Classify). Classify is the category of T, where 0 means both are level types and 1 means that at least one is of the list type.

Definition 2.

Correctness of type sequence. $\left\{R_1;\dots ;R_k\right\}$ is a set of relationships of the sequence type {$T_1$; …; $T_n$}. If $T_1\wedge \dots \wedge$ $T_n\wedge$ $R_1\wedge \dots \wedge$ $R_k$ is valid, the type sequence $T_1$; …; $T_n$ is correct. When we process verification, each T and R is matched and justified in the specification of the responding type and the specification of the inter-type relationship. If all types and relationships meet their specifications, it can be stated that the sequence is correct.

Based on the above definition of type, we propose the following paradigm of the kernel model.

Definition 3.

Kernel Paradigm.

M is the modeling paradigm. If $M_{kernel}$ = ${\mathrm{M}}_{base}\cup$ ${\mathrm{M}}_{func}\cup$ ${\mathrm{M}}_{struct}\cup$ ${\mathrm{M}}_{file}\cup$ ${\mathrm{M}}_{dentry}\cup$ ${\mathrm{M}}_{subsys}$, each level is defined as follows ($\left[T\right]\ast$ is the aggregation of types. The involved signs are listed in

Table 3. Signs and their meanings.

Sign	Meaning	Example
:	Sign defining type	t:Base means that the type of t is base.
⊢	Sign of deducing	A ⊢ B means A can deduce B.
$\Gamma$	System environment	$\Gamma$⊢ T means T exists in the system
environment.
${\mathrm{T}}_1$→${\mathrm{T}}_2$	“→” is the sign of map. If input
parameter type is ${\mathrm{T}}_1$ and output
parameter type is ${\mathrm{T}}_2$, ${\mathrm{T}}_1$ → ${\mathrm{T}}_2$
represents the func type.	f = t(x): ${\mathrm{T}}_1$ → ${\mathrm{T}}_2$ means f = t(x)
type is func ${\mathrm{T}}_1$ → ${\mathrm{T}}_2$.
[${\mathrm{T}}_i]$*	[${\mathrm{T}}_i]$ means that the list consists of several
types.	[${\mathrm{T}}_i]$* = {${\mathrm{T}}_1,\dots$, ${\mathrm{T}}_i,\dots$, ${\mathrm{T}}_n$}
= ${\mathrm{T}}_1\times \dots \times$ ${\mathrm{T}}_i\times \dots \times$ ${\mathrm{T}}_n$.

):

$$M_{Base}=\left\{\left[T_i\right]\ast =T_1,\dots ,T_i,\dots ,T_n,with〈1\le i\le n,T_i:Base〉\right\},$$

$$M_{Func}=\left\{\begin{array}{c}\left[T_i\right]\ast =\left\{T_1,\dots ,T_i,\dots ,T_n\right\},with〈1\le i\le n,T_i:Func〉\\ R\left(T_p,T_q\right),with〈\begin{array}{c}{T}_p,T_q:Base\left|Func\right|Struct|List,\\ R:ParamIn\left|ParamOut\right|MultiList|ListAgg\\ \left|Invokable\right|Accessible\end{array}〉\end{array}\right\},$$

$$M_{Struct}=\left\{\begin{array}{c}\left[T_i\right]\ast =\left\{T_1,\dots ,T_i,\dots ,T_n\right\},with〈1\le i\le n,T_i:Struct〉\\ R\left(T_p,T_q\right),with〈\begin{array}{c}{T}_p:Base\left|Func\right|Struct|List,T_q:Struct|List,\\ R:VarStruct\left|FuncStruct\right|MultiList|ListAgg\end{array}〉\end{array}\right\},$$

$$M_{File}=\left\{\begin{array}{c}\left[T_i\right]\ast =\left\{T_1,\dots ,T_i,\dots ,T_n\right\},with〈1\le i\le n,T_i:File〉\\ R\left(T_p,T_q\right),with〈\begin{array}{c}{T}_p:Func\left|Struct\right|List,T_q:File|List,\\ R:FuncFile\left|StructFile\right|MultiList|ListAgg\end{array}〉\end{array}\right\},$$

$$M_{Dentry}=\left\{\begin{array}{c}\left[T_i\right]\ast =\left\{T_1,\dots ,T_i,\dots ,T_n\right\},with〈1\le i\le n,T_i:Dentry〉\\ R\left(T_p,T_q\right),with〈\begin{array}{c}{T}_p:File\left|Dentry\right|List,T_q:Dentry|List,\\ R:Agg\left|MultiList\right|ListAgg\end{array}〉\end{array}\right\},$$

$$M_{Subsys}=\left\{\begin{array}{c}\left[T_i\right]\ast =\left\{T_1,\dots ,T_i,\dots ,T_n\right\},with〈1\le i\le n,T_i:Subsys〉\\ R\left(T_p,T_q\right),with〈\begin{array}{c}{T}_p:File\left|Dentry\right|List,T_q:Subsys|List,\\ R:Agg\left|MultiList\right|ListAgg\end{array}〉\end{array}\right\}$$

Here, T and R are the types and the relationship of types, respectively. Each level type is constrained by its type structure and inter-type relationships.

3. Design Specification

In this section, we elaborate on the specific rules. We specify the design in terms of type organizational structures and inter-type relationships. The definitions and equations of structures and relationships are extracted according to the characteristics of the Linux kernel.

Considering directory order, the Linux kernel is modeled with the following six levels from top to bottom: subsystem; dentry; file; and members of file, including struct, function, and base. These correspond to the following six types: Subsys, Dentry, File, Struct, Func, and Base.

3.1. Type Specification

The type structure specifies its types and its constituent members. We use preconditions and postconditions to represent these specifications. For an equation, if the preconditions (numerator) are met, the type (denominator) is valid.

3.1.1. Type Structure Specification

There are six level types and one list type. The list type is the middleware used to bridge level types. The type structure is specified as follows (the signs’ meanings are listed in Table 3):

Base Type

$${\displaystyle \frac{\Gamma ⊢T,T\in “void”,“\_Bool”,“char”,“short”,“int”,“long”}{t:Base}}$$

(1)

Data classes in Linux include numeric classes, void classes, and derived classes. In C programming language, the numeric class involves integer and floating-point classes. Since there is no floating-point number in Linux, our discussion only involves integers. _Bool, char, short, int, and long are basic integers. Sign, unsign, short, and long are qualifiers used to define the int. Float and double are basic floating-point classes. The void class cannot be separated (atomic class) and is always used as the parameter or returned value of funcs. The derived classes further include pointers, arrays, funcs, and constructed classes. A pointer is used to point to an address. With “*”, any type has properties of the pointer. An array is similar to a pointer. If the original type of members in the array exists and is correct, the array is available. Therefore, the array is treated as the original type. This section discusses Funcs and constructed classes in the “func type” and “struct type”.

In summary, the base type is the atomic type that cannot be separated. It should include the basic types of Linux. According to the above analysis, _Bool, char, short, int, long, float, double, and void belong to this type. As shown in Equation (1), if a type (t) is the member listed in the numerator, it is the base type.

Func Type

$${\displaystyle \frac{x:T_1,t:T_2,Func=\{T_1\to T_2\}}{f=\{\lambda ((x:T_1).(t:T_2)\}:Func}}$$

(2)

Func is the type composed of the mapping from input to output and has two subtypes. The one defined in a file directly is the global func. The other, used in a struct, is member func of struct, which is a pointer (details are introduced in relation to the struct type). In type theory, the concerned points of funcs are name, input/output parameter type, and list type (also introduced in this section). In Equation (2), we define t as the output parameter. If the input parameter (x) us of type ${\mathrm{T}}_1$ and the output parameter (t) is of type ${\mathrm{T}}_2$, the mapping from x to t is a func-type Func.

Struct Type

$${\displaystyle \frac{{\left[t_i:T\right]}^{\ast },{\left[f_j:Func\right]}^{\ast },Struct=\left\{vars:{\left[l:T\right]}^{\ast },funcs:\left\{{\left[l:Func\right]}^{\ast }\right\}\right\}}{s=\left\{vars=\left\{{\left[l=t_i\right]}^{\ast }\right\},funcs=\left\{{\left[l=f_j\right]}^{\ast }\right\}\right\}:Struct}}$$

(3)

The struct is a constructed type, similar to “class” in an object-oriented language. Func in struct only has a declaration but no definition. The pointer defined by struct is used to implement the member func by pointing to a global func.

Here, we focus on struct name, member variable-type list, and member func-type list. The member func has a pointer to point to a global func in the struct, and its implementation is achieved in the global func. Therefore, the member function belongs to a pointer, but the member variable could be a pointer or base/struct/list type. In Equation (3), if member variable ${\mathrm{t}}_i$ is of type T and the type of member func ${\mathrm{f}}_j$ is Func, the combined variable ($s=\{\left[t_i\right]\ast ,\left[f_j\right]\ast \}$) is a struct-type Struct.

File Type

$${\displaystyle \frac{{[f_i:Func]}^{\ast },{\left[t_j:Struct\right]}^{\ast },File=\left\{funcs:\left\{{\left[l:Func\right]}^{\ast }\right\},structs:\left\{{\left[l:Struct\right]}^{\ast }\right\}\right\}}{fls=\left\{funcs=\left\{{\left[l=f_i\right]}^{\ast }\right\},structs=\left\{{\left[l=t_j\right]}^{\ast }\right\}\right\}:File}}$$

(4)

Marco, declarations, and definitions consist of files. Macro a is a detailed implementation and, therefore, not included in the design phase. As for “declaration”, we need to define it first; then, we can use it at any time after declaring it. The declarations are checked and stored in a list to verify the accessible scope (Section 3.2). For the definition, we focus on its name, structs, and global funcs. In the specification of file type (Equation (4)), if the type of global funcs (${\mathrm{f}}_i$) is Func and the type of struct (${\mathrm{t}}_j$) is Struct, the composite type of file = $\left\{\left[f_i\right]\ast ,\left[t_j\right]\ast \right\}$ is a file-type File.

Dentry Type

$${\displaystyle \frac{{\left[f_i:File\right]}^{\ast },{\left[d_j:Dentry\right]}^{\ast },Dentry=\left\{files:\left\{{\left[l:File\right]}^{\ast }\right\},dentrys:\left\{{\left[l:Dentry\right]}^{\ast }\right\}\right\}}{d=\left\{files=\left\{{\left[l=f_i\right]}^{\ast }\right\},dentrys=\left\{{\left[l=d_j\right]}^{\ast }\right\}\right\}:Dentry}}$$

(5)

Dentry is for directories, which store files and dentries. In Equation (5), the dentry (d) comprises a file list (${\mathrm{f}}_i$) and a dentry list (${\mathrm{d}}_j$) in the current directory. The type of ${\mathrm{f}}_i$ is File, and the type of ${\mathrm{d}}_j$ is Dentry; then, the type of $d=\{\left[f_i\right]\ast ,\left[d_i\right]\ast \}$ is a dentry type Dentry.

Subsys Type

$$\begin{array}{c}{\displaystyle \frac{{\left[f_i:File\right]}^{\ast },{\left[d_j:Dentry\right]}^{\ast },Subsys=\{files:\left\{{\left[l:File\right]}^{\ast }\right\},dentrys:\left\{{[l:Dentry]}^{\ast }\right\}\},with<T^{subsys}.father=“/”>}{s=\left\{files=\left\{{\left[l=f_i\right]}^{\ast }\right\},dentrys=\left\{{\left[l=d_j\right]}^{\ast }\right\}\right\}:Subsys}}\end{array}$$

(6)

Subsys represents the subsystem in the root directory of Linux. Its structure is similar to that of dentry, comprising a file list and a dentry list. The only difference between dentry and subsys is that the father of subsys is “/”. Thus, the subsys type can be treated as a particular dentry type. In Equation (6), the only modified part modified the constraint Subsys.father = “/”, and the remaining are the same as in Equation (5).

List Type

$${\displaystyle \frac{a_1:T_1,\dots ,a_n:T_n,List=T_1\times \dots \times T_i\times \dots T_{n}for\forall n\ge 1}{l=(a_1,\dots ,a_n):List}}$$

(7)

The list type is always aggregated from multiple level types and list types. Parameter list, func list, and member variable-type list all belong to the list type. The list type involves two sub-relationships, MultiList and ListAgg, connecting the level and its father level. In Equation (7), “×” is the Cartesian product, which says that if several types aggregate to an object in the way of the tuple, the composite is of the list type, as ${\mathrm{T}}_1$$\times \dots \times T_n$ or [${\mathrm{T}}_i$]∗.

3.1.2. Other Specifications

In addition to the above types and levels, types are always organized on the grounds of the following rule:

$${\displaystyle \frac{\Gamma ⊢t:T,lisalabel}{\{l=t\}:\{l:T\}}}$$

(8)

Equation (8) is the definition of a label. As a label, l represents the purpose of a type, just like an integer for counting, such as {count:int}. In nature, a variable can be considered a label. The domain of l is $\left|\right|\{l:T\}\left|\right|=\left\{\right\{l=a\left\}\right|a\in \left|\right|T\left|\right|\}$.

$$\begin{array}{c}{\displaystyle \frac{\Gamma ⊢T_2,t:T_1,T_1<:T_2}{t:T_2}}\end{array}$$

(9a)

$$\begin{array}{c}{\displaystyle \frac{t:T_1}{t:\{T_1+T_2\}}}\end{array}$$

(9b)

Equation (9a) is an application rule for subtype expansion. ${\mathrm{T}}_1<:$ ${\mathrm{T}}_2$ indicates that ${\mathrm{T}}_1$ is a subtype of ${\mathrm{T}}_2$, where ${\mathrm{T}}_1$ has a smaller scope than ${\mathrm{T}}_2$. If type ${\mathrm{T}}_1$ is a subtype of type ${\mathrm{T}}_2$, t, as the term of ${\mathrm{T}}_1$, is also the term of type ${\mathrm{T}}_2$. In Equation (9b), the further reduction of Equation (9a), the term of ${\mathrm{T}}_1$ is also be the term of possible a large-scope {${\mathrm{T}}_1$ + ${\mathrm{T}}_2$}.

$$\Gamma ⊢error:T$$

(10)

Exceptions are also a type (Equation (10)). According to the verification requirements, we design several error exceptions related to type verification, structure verification, and invoking relationship verification. Each exception corresponds to its own exception item, including response error, database error, parameter error, and file type error (

Table 4. Error code in the LAMVs.

ID	Explanation
00x_1	Level type x exists
00x_2	Level type x does not exist
50x_1	Level type x is correct
50x_2	Level type x is incorrect
400_1	Demand is correct (all invocations and their dependent types are correct)
400_2	Demand is incorrect
401_1	Demanding paths are correct
401_2	Demanding paths are incorrect
402_1	Dependent types are correct
402_2	Dependent types are incorrect
403_1	Invocation of func is correct (only for invocation)
403_2	Invocation of func is incorrect

).

3.2. Inter-Type Relationship Specification

After specifying the components of types, we standardize the relationships between different types. The specification of inter-type relationships includes the following two categories: structural relationships and invoking relationships. Structural relationships describe how to organize types, including parameter association, member association, file composition, special aggregation, and list composition. The invoking relationship indicates the relationship between func and invoked/accessed type, including the invocable relationship of funcs and the accessible relationship of variables. The former is the relationship among funcs, and the latter is the relationship between func and struct/base.

3.2.1. Structural Relationships

This generalized aggregated relationship constitutes the type within or between the father–child levels. According to the associated types and corresponding levels, type structural relationships are divided into nine categories, as presented in Table 1.

MultiList and ListAgg are list composition relationships. MultiList says level types aggregate the list type. ListAgg indicates the level type comprising list types and level types. The rest of the structural relationships are between level types, which include parameter input(ParamIn), parameter output(ParamOut), variable-struct(VarStruct), func-struct(FuncStruct), func-file(FuncFile), struct-file(StructFile), and file–dentry or file–subsys(Agg).

Except for ParamOut, the relationships between levels can be decomposed into two relationships within levels. As mentioned above, the list is medium between father and child levels to combine relationships within levels conveniently. Therefore, the relationships between levels equal two relationships within levels (details in

Table 5. The correspondence of relationships within levels and between levels.

Relationship between Levels	MultiList	ListAgg
ParamIn	Input parameter–input parameter list	Input parameter list–func
ParamOut	-	-
VarStruct	Member variable–member variable list	Member variable list–struct
FuncStruct	Member func–member func list	Member func list–struct
FuncFile	Global func–global func list	Global func list–file
StructFile	Struct–struct list	Struct list–file
Agg (file–dentry)	File–file list	File list–dentry
Agg (dentry-dentry)	Dentry–dentry list	Dentry list–dentry
Agg (file–subsys)	File–file list	File list–subsys
Agg (dentry–subsys)	Dentry–dentry list	Dentry list–subsys

). This result is used to verify the correctness of structural relationships.

$$\begin{array}{c}{\displaystyle \frac{\Gamma ⊢T_i,\Gamma ⊢T_2,Func=\{\left[T_i\right]\ast \to T_2\}}{T_i\stackrel{\ll ParamIn\gg }{\to }Func,T_2\stackrel{\ll ParamOut\gg }{\to }Func}}\end{array}$$

(11a)

$$\begin{array}{c}{\displaystyle \frac{\Gamma ⊢T_i,\Gamma ⊢T_2,Func=\left[T_i\right]\ast \to T_2}{T_i\stackrel{\ll ParamIn\gg }{\to }Funcor{T}_i=Func.param\_in}}\end{array}$$

(11b)

$$\begin{array}{c}{\displaystyle \frac{\Gamma ⊢T_i,\Gamma ⊢T_2,f=\left[T_i\right]\ast \to T_2}{T_2\stackrel{\ll ParamOut\gg }{\to }Funcor{T}_2=Func.param\_out}}\end{array}$$

(11c)

Parameter Association Relationship

The relationship includes the input parameter association relationship (ParamIn) and the output parameter association relationship (ParamOut). The former represents the relationship between the input parameter list [${\mathrm{T}}_i$]* and the func (f), while the latter is the relationship between the output parameter list (${\mathrm{T}}_2$) and the func (f). For clarity, Equation (11a) is divided into the following two formulas: the input parameter relationship (Equation (11b)) and output parameter relationship (Equation (11c)).

$$\begin{array}{c}\hfill {\displaystyle \frac{\Gamma ⊢T,Struct=\{vars:{[l:T]}^{\ast },funcs:{\left[l:Func\right]}^{\ast }\}}{T\stackrel{\ll VarStruct\gg }{\to }Struct,Func\stackrel{\ll FuncStruct\gg }{\to }Struct}}\end{array}$$

(12a)

$$\begin{array}{c}\hfill {\displaystyle \frac{\Gamma ⊢T,Struct=\{vars:{[l:T]}^{\ast },funcs:{\left[l:Func\right]}^{\ast }\}}{T\stackrel{\ll VarStruct\gg }{\to }Struct}}\end{array}$$

(12b)

$$\begin{array}{c}\hfill {\displaystyle \frac{\Gamma ⊢T,Struct=\{vars:{[l:T]}^{\ast },funcs:{\left[l:Func\right]}^{\ast }\}}{Func\stackrel{\ll FuncStruct\gg }{\to }Struct}}\end{array}$$

(12c)

Member Association Relationship

This relationship includes an association relationship of member variable VarStruct and an association relationship of member func FuncStruct. The former is the relationship between member variables and the struct. The latter is the relationship between member funcs and the struct. In Equation (12a), vars and funcs represent the member variable list and member func list in the struct, respectively. Equation (12a) is also divided into the following two formulas: the member variable relationship (Equation (12b)) and the member func relationship (Equation (12c)):

$$\begin{array}{c}{\displaystyle \frac{File=\{funcs={[l:Func]}^{\ast },structs={\left[l:Struct\right]}^{\ast }\}}{Func\stackrel{\ll FunctFile\gg }{\to }File,Struct\stackrel{\ll StructFile\gg }{\to }File}}\end{array}$$

(13a)

$$\begin{array}{c}{\displaystyle \frac{File=\{funcs={[l:Func]}^{\ast },structs={\left[l:Struct\right]}^{\ast }\}}{Func\stackrel{\ll FunctFile\gg }{\to }File}}\end{array}$$

(13b)

$$\begin{array}{c}{\displaystyle \frac{File=\{funcs={[l:Func]}^{\ast },structs={\left[l:Struct\right]}^{\ast }\}}{Struct\stackrel{\ll StructFile\gg }{\to }File}}\end{array}$$

(13c)

File Composition Relationship

The file composition relationship (Equation (13a)) is the relationship between a file and its main component, including the func–file relationship (FuncFile, Equation (13b)) and the struct–file relationship (StructFile, Equation (13c)). The former, designed for global funcs, is the relationship between the global func and the file. The latter is the relationship between the struct and the file. A file type is composed of global funcs and structs defined locally without “include” and “extern” funcs and structs defined in other files. Only the “include” and “extern” parts can be used and considered in the invoking relationship (Section 3.2.3).

Special Aggregation Relationship

This signifies the relationship between levels beyond the file level. Since the types outside a file only indicate the level path, these types cannot be distinguished. File and dentry have a similar relationship of special aggregation. This paper considers the following four cases: file–dentry, dentry–dentry, file–subsys, and dentry–subsys. In Equation (14), T is a type in the upper level. ${\mathrm{T}}_i$ and ${\mathrm{T}}_j$ are types in the lower level. When T is a dentry, ${\mathrm{T}}_i$ and ${\mathrm{T}}_j$ are file and dentry, respectively. Files = [${\mathrm{T}}_i$]* and dentrys = [${\mathrm{T}}_j$]* are the file list and the dentry list, respectively.

$$\begin{array}{c}{\displaystyle \frac{\Gamma ⊢T_i,\Gamma ⊢T_{j}T=\left\{{files=[l:T_i}^{\ast }\right],dentrys={[l:T_j]}^{\ast }\}}{T_i\stackrel{\ll Agg\gg }{\to }T,T_j\stackrel{\ll Agg\gg }{\to }T}}\end{array}$$

(14)

List Composition Relationship

As analyzed above, the list is the medium for level types. Based on the aggregation result, the relationship can be divided into multiple-list relationships (MultiList) and list aggregation relationships (ListAgg). The former denotes the list type aggregated by level types or list types. The latter indicates level types aggregated by lists. If T=$T_1\times \dots \times T_i\times \dots \times T_n,1\le i\le n$, ${\mathrm{T}}_i$ and T satisfy the list composition relationship, as ${\mathrm{T}}_i\stackrel{\ll List\gg }{\to }$T (corresponding to Equation (15)).

Adding the constraints, Equation (15a) turns into a MultiList relationship (Equation (15b)) and ListAgg relationship (Equation (15c)). The two relationships correspond to eight and nine sub-relationships respectively, which are listed in Table 1.

$$\begin{array}{c}{\displaystyle \frac{T=T_1\times \dots \times T_i\times \dots \times T_n,1\le i\le n}{T_i\stackrel{\ll List\gg }{\to }Tor{T}_i=T.memberorEquation\left(15\right)\left(T_i,T\right)}}\\ {\displaystyle \frac{T=T_1\times \dots \times T_i\times \dots \times T_n,1\le i\le n,}{ }}\end{array}$$

(15a)

$$\begin{array}{c}{\displaystyle \frac{with<T_i:Base\left|Func\right|Struct\left|File\right|Dentry|List,T:List>}{T_i\stackrel{\ll MultiList\gg }{\to }T}}\\ {\displaystyle \frac{T=T_1\times \dots \times T_i\times \dots \times T_n,1\le i\le n,}{ }}\end{array}$$

(15b)

$$\begin{array}{c}{\displaystyle \frac{with<T_i:List,T:Func\left|Struct\right|File\left|Dentry\right|Subsys>}{T_i\stackrel{\ll ListAgg\gg }{\to }T}}\end{array}$$

(15c)

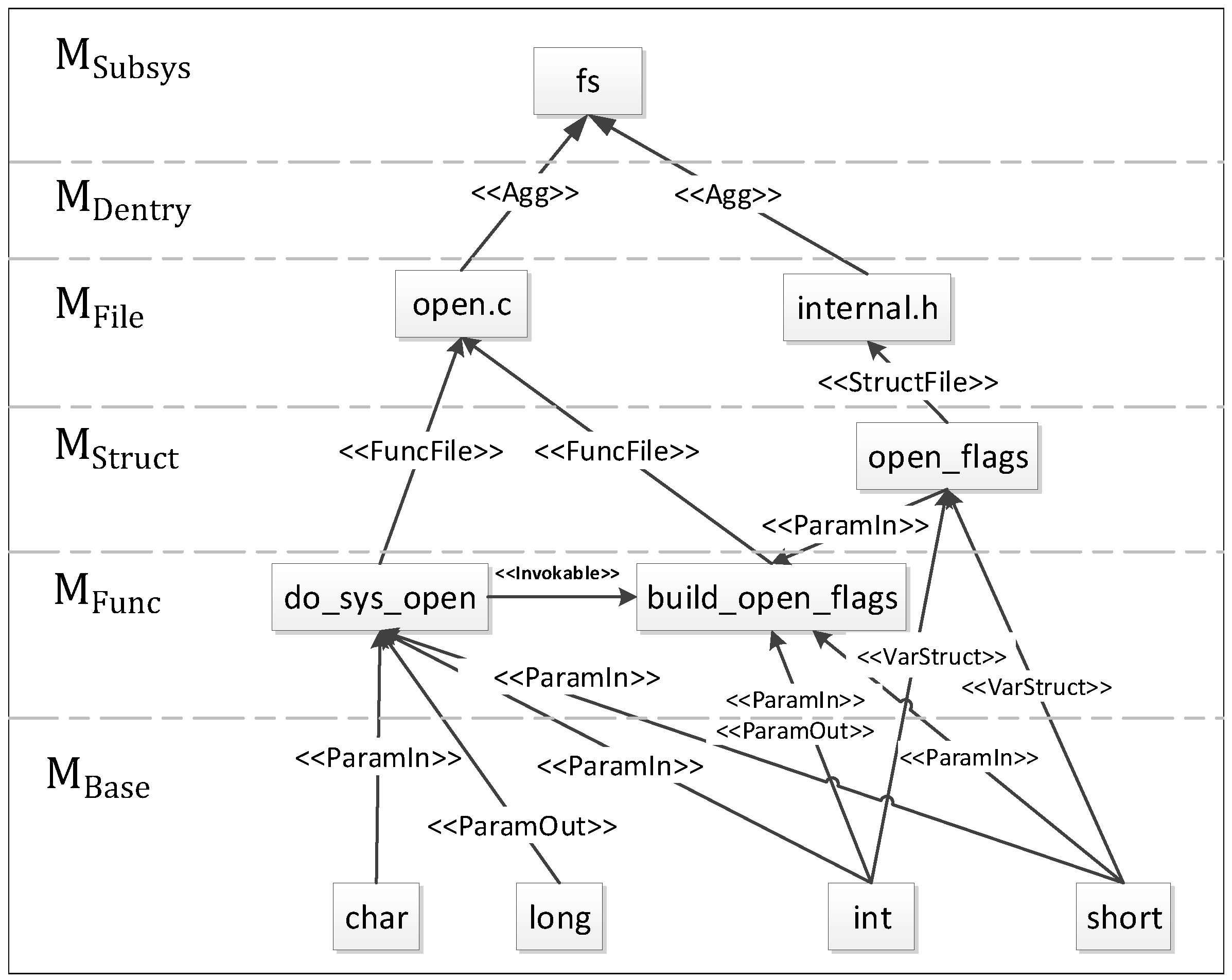
3.2.2. An Example

For example, for subsys fs, the file and file list meet the MultiList relationship. File list and fs satisfy the ListAgg relationship. Thus, we can conclude that file and fs satisfy the following Agg relationship:

fs:   files = {internal.h, open.c, …}, dentrys = {pguestfs, …}

Agg: R1 = internal.h$\stackrel{\ll Agg\gg }{\to }$fs, R2 = open.c$\stackrel{\ll Agg\gg }{\to }$fs,

         R3 = pguestfs$\stackrel{\ll Agg\gg }{\to }$fs

MultiList: R4 = internal.h$\stackrel{\ll MultiList\gg }{\to }$files,

              R5 = open.c$\stackrel{\ll MultiList\gg }{\to }$ files,

              R6 = pguestfs$\stackrel{\ll MultiList\gg }{\to }$dentrys

ListAgg: R7 = files$\stackrel{\ll ListAgg\gg }{\to }$fs,

              R8 = dentrys$\stackrel{\ll ListAgg\gg }{\to }$fs

3.2.3. Invoking Relationship

In this section, we analyze the properties of func invocation and introduce two invoking relationships. The scope is imported to illustrate the invocation. Only if the scope of an accessing/invoking subject is greater than or equal to the scope of an object can the access/invocation be implemented.

The Feature of Invocation in Linux

Invocation is the act of having one func invoke another. The initiator of invocation must be the global func. This is because invocation is implemented in the func definition. According to the analysis of struct type (Section Struct Type), the definition of member funcs can only be completed in global funcs. At the same time, the main func serves as the entrance of a program that can call any func. Therefore, a calling func can only be a main or global func. However, compared with the main funcs, there are multiple and complex mutual calls by global funcs. To simplify verification, we define the invoking subject as a global func. The receiver in the invoking relationship is the invoked func. It can be a global func or member func. Global funcs are invoked using “f()” directly, while member funcs are invoked through the struct member variable or pointer using “t2.f2()” or “${\mathrm{p}}_2\to$${\mathrm{f}}_2$()”.

To determine whether accesses and calls can be executed correctly, we list the scopes of func types, struct types, and variable types in

Table 6. Scopes for func, struct, and variable.

Name	Scope for Local Definition	Scope for Global Definition
func	Local (struct, func, variable)	File (static), Global (no prefix)
struct	Local (struct, func, variable)	Global (no prefix)
file	Local (struct, func, variable)	File (no prefix), Global (extern)

. For all locally declared types, the scope covers the currently declared type (struct, func, or parameter). External access requires permission of this scope to use the relevant type. For types declared in a file, the scope of a function type is global by default. When the prefix ’static’ is added, the scope of the func is restricted to the current file. The struct has no prefix, and the scope defaults to global. Variables declared in a file default to the current file and become global variables with the extern prefix.

Accessibility Scope

With the above analysis, we can define the accessibility scope of a global func in the accessible domain.

Table 7. Accessible scopes of func, struct, and variable.

Class	Accessible Domain
f1.FuncAccess	1. Defined global func in the same file; 2. Declared external global func (no static prefix); 3. Defined external global funcs (no static prefix) in the included (nested) file; 4. Declared external global funcs (no static prefix) in the included (nested) file.
f1.StructAccess	1. Defined struct in the same file; 2. Declared external struct; 3. Defined struct in the included (nested) file; 4. Declared external struct in the included file.
f1.VarAccess	1. Defined local variable in the same file; 2. Defined global variable in the same file; 3. Declared external global variable; 4. Defined global variable in the included (nested) file; 5. Declared external global variable in the included (nested) file

lists all the accessible domains of an invoking func. F1 is the file in which the invoking func (f1) resides and is the parent type of f1. FuncAccess, StructAccess, and VarAccess are classes within the accessible scope corresponding to the accessed funcs, structs, and variables, respectively. Scenarios in the FuncAccess accessible domain encompass defined global funcs, declared global external funcs, and external funcs in the ’include’ file. Scenarios in the StructAccess accessible domain include structs in this file and included files that can be defined or declared. Scenarios of VarAccess include local variables defined within the current func and declared/defined variables within the current file or nested ’include’ file. The variable can be a base type or a struct type. For the accessed struct and variable, if it is in the accessible domain of f1, f1 can access it. For the accessed func, if it is in the accessible domain of f1, f1 can invoke this func. In summary, Equation (17) relates to the accessible domain.

Accessible Relationship

Using the accessible scope, we define the accessible relationship. If the accessed type is in the accessible scope of the accessing type, the relationship is available. As per the above analysis, the initiator (accessing type) must be a global func, and the accessed type can be a struct (Equation (16a)) or variable (Equation (16b)). The variable can be a base or struct type. If the accessed type matches the corresponding type and meets the requirements of the accessible domain, an accessible relationship is established (Table 7).

$$\begin{array}{c}{\displaystyle \frac{T_2\in f_1.StructAccess,with<f_1:Func,f_1.father:File,T_2:Struct>}{f_1\stackrel{\ll accessible\gg }{\to }{T}_2}}\end{array}$$

(16a)

$$\begin{array}{c}{\displaystyle \frac{t_2\in f_1.VarAccess,with<f_1:Func,f_1.father:File,t_2:T_2,T_2:Base|Struct>}{f_1\stackrel{\ll accessible\gg }{\to }{t}_2}}\end{array}$$

(16b)

The accessible scopes of global func to access func, struct, and variable are presented in Equation (17a), Equation (17b), and Equation (17c) separately.

$$\begin{array}{c}{f}_1.FuncAccess=\{F_1.FuncDef+{(F}_1.FuncDecl+F_1.include.Func).notstatic\}\end{array}$$

(17a)

$$\begin{array}{c}{f}_1.StructAccess=\{(F_1+F_1.include).Struct\}\end{array}$$

(17b)

$$\begin{array}{c}{f}_1.VarAccess=\{(f_1+F_1).VarDef+{(F}_1.VarDecl+F_1.include.Var).extern\}\end{array}$$

(17c)

Invocable Relationship

The invocable relationship specifies the invocable func type, which includes the invoked global func and the struct member func defined in Equation (18a) and Equation (18b). If the called object is a global func, the called func and its file meet accessible scenarios of the FuncAccess. If the invoked object is a member func, the invoking func (f1) requires access to the struct or struct variable of the invoked member func. Meanwhile, the member function and struct should satisfy the member association relationship. Then, the invoking relationship is established.

$$\begin{array}{c}{\displaystyle \frac{f_2\in f_1.FuncAccess,with<f_1:Func,f_1.father:File,f_2:Func,f_2.father:File>}{f_1\stackrel{\ll Invocable\gg }{\to }{f}_2}}\end{array}$$

(18a)

$$\begin{array}{c}{\displaystyle \frac{f_1\stackrel{\ll Accessible\gg }{\to }{t}_2:T_2,f_1\stackrel{\ll Accessible\gg }{\to }{T}_2,with<f_1:Func,f_2:Func,T_2:Struct,f_2:Func\stackrel{\ll FuncStruct\gg }{\to }{T}_2>}{f_1\stackrel{\ll Invocable\gg }{\to }{t}_2.f_2}}\end{array}$$

(18b)

3.2.4. An Example

The inter-type relationship in the open function is presented in Figure 1.

4. Verification

In this section, we introduce the method for verifying whether the design is correct based on the kernel model. The verification involves judging the correctness of the type sequence. If all required types and relationships are valid, the design is correct.

4.1. Overview

The verification process is as follows:

• To verify whether the demand can be met, the demand list is extracted. Each demand consists of multiple funcs. As indicated by the expression in Section 2, the demand comprises the invocations to funcs. A func has a sequence of dependent types.
• The list of dependent types and is then extracted, and each type in the list is verified. If every type passes structural verification, the demand passes type verification. Invocable relationship verification is then performed.
• Invocable relationship verification is performed to verify the existence and correctness of each node in the func invocation chain. If all funcs pass verification, the business represented by the demanding list is satisfied.

In the pseudo-code of Algorithm 1 VERI_DP_LIST, we demonstrate the verification process for a requirement. Before verification, a large demand is broken down into smaller invocations, which are stored in the demand list to check individually. First, the existence and relationships of the involved funcs are verified. Secondly, the types that the func depends on are inspected in turn. Inspection encompasses structural and invoking verification and is performed by invoking the DV_SR (Demand Verification for Structure Relationship) and DV_IR (Demand Verification for Invoking Relationship) algorithms sequentially.

Algorithm 1 VERI_D_FUNC

Input:  demandList /* List of demands to be verified*/ Output:  dList_flag, R /*Verify the design correctness and generate a verification report*/   1: function VERI_D_FUNC(demandList):   2:     recordReport(); //Start recording the verification report   3:     dList_flag = true;   4:     for d in demandList do   5:         funcList = getFuncListFromDemand(d);   6:         fList_flag = true;   7:         for f do in funcList:   8:              f_flag = true;   9:              typeList = getDependTypeList(f); /*Getting the dependency type, including recursive father types, parameter types, and return value types.*/ 10:            for t do in typeList: 11:                t_flag = DV_SR(t); 12:                f_flag = f_flag && t_flag; 13:                fList_flag = fList_flag && f_flag; 14:                d_flag = fList_flag && DV_IR(d); /* If fList_flag is false, the program do not perform DV_IR*/ 15:                dList_flag = dList_flag && d_flag; 16:                R = printReport(); /* Print verification report */ 17:                return dList_flag, R; 18:            end for 19:         end for 20:     end for 21: end function

4.2. Structural Verification

Type structure verification can be transformed into the judgment of the following propositions:

• Whether the dependent types exist; (Equations (1)–(7))?
• Whether the structural relationship of the types is correct (Equations (11)–(15)).

The types at different levels involve different structural relationships (

Table 8. The relationship to be verified at different type levels.

Type Level	Relationship
func	ParamIn, ParamOut, MultiList, subtype
struct	VarStruct, FuncStruct, MultiList, typeAssociation
file	FuncFile, StructFile, MultiList
dentry	ListAgg, MultiList
subsystem	ListAgg, MultiList

), so the corresponding verification algorithms are also different. The algorithm for each level is derived from a judgment of its properties (akin to the structural relationship of func A being correct). These properties can be formalized using type constraints and subsequently translated into logical formulas (such as Equation (11)) to yield a definitive result (true or false). Given the properties at each level, we merely need to ascertain the level of the type under verification and process it according to the corresponding algorithm to obtain the final verification outcome.

The pseudo-code of type structural verification (DV_SR) is presented in Algorithm 2. According to the hierarchy, structural verification proceeds sequentially from the base level (TR_base ) to the subsystem level (TR_subsys), corresponding to the implementation from Equation (11) to Equation (15) (for space reasons, the detailed algorithms for each level are not listed). For the base type, since it is atomic, the correctness can be determined by verifying whether the type exists and is, indeed, a base type. The verification result can then be obtained directly. For higher-level types, the existence of dependent types, the correctness of inter-type relationships, and whether the type list is empty are considered. Table 2 describes the dependent types and constrained relationships for level types. The “Member_type” column indicates the level type of a member, including base, func, struct, file, and dentry type. “Member_list” represents the list type of a member. The list members can also be a list type to form a nested list, necessitating iterative processing. The bold parts in Table 2 signify recursive processing for the list type. The process continues until the “Member_list” is null.

Algorithm 2 DV_SR

Input:  t /* Type to be verified */ Output:  flag /*Check whether the structure of t is correct*/   1: function boolean DV_SR(Type t):   2:     recordReport(); //Start recording the verification report   3:     dList_flag = true;   4:     for d in demandList do   5:           boolean t_flag;   6:           if ruleExistService.Equation (1)(t) then   7:              t_flag = ruleStructService.TR_base(t);   8:           else if ruleExistService.Equation (2)(t) then   9:              t_flag = ruleStructService.TR_func(t); 10:         else if ruleExistService.Equation (3)(t) then 11:            t_flag = ruleStructService.TR_struct(t); 12:         else if ruleExistService.Equation (4)(t) then 13:            t_flag = ruleStructService.TR_file(t); 14:         else if ruleExistService.Equation (5)(t) then 15:            t_flag = ruleStructService.TR_dentry(t); 16:         else if ruleExistService.Equation (6)(t) then 17:            t_flag = ruleStructService.TR_subsys(t); 18:         end if 19:         return t_flag; 20:     end for 21: end function

4.3. Invoking Verification

Invoking verification involves checking whether the invocation satisfies the invocable relationship specification (Equation (18)) and the accessible relationship specification (Equation (16)). In the pseudo-code of Algorithm 3 (DV_IR), judgments regarding callability and accessibility are executed sequentially, serving as an entry for iterative verification of relationships. Subsequently, we introduce the notion of exit and complete verification by inference.

4.4. Reasoning Exit and Reasoning Process

Reasoning exit is the termination of inference. When encountering the exit discriminant, we can determine whether it is true or false based on the database or the current value. The reasoning exit discriminant includes type structure specifications (Equations (1)–(6)), exception rules (Equation (10)), and structural relationship specifications (Equations (11)–(15)), which can return results directly. Therefore, for the verification of invoking relationships, only Equations (16) and (18) need to be deduced.

Algorithm 3 DV_IR

Input:  di /* func Invocation to be verified */ Output:  flag /* verification result */   1: function boolean DV_IR(Type di):   2:     boolean flag;   3:     int classify = di.getRelationClassify();   4:     if classify == Data.Invocable then   5:         flag = Equation (18a)(di) ∥ Equation (18b)(di);   6:     else if classify==Data.Accessible then   7:         flag = Equation (16b)(di) ∥ Equation (16a)(di);   8:     else   9:         flag=false; 10:   end if 11:   return flag; 12: end function

The inference process involves recursively retrieving the discriminant that needs to be brought in by matching the precondition until the reasoning exit is found. The result obtained from each exit discriminant is used to determine whether the invocation satisfies the specification. An example is presented to illustrate the process of verifying logic. Given the term $f_1\stackrel{\ll invocable\gg }{\to }{f}_2$, to prove that $f_1$ can invoke $f_2$, the term is matched by Equations (18a) and (18b). Here, we do not specify whether the invoked func is a member func or a global func, so if any return results are true, the invoking relationship is established. The precondition of Equation (18a) is taken as a conclusion to match rules and determine the scope of FuncAccess (Equation (17a)) and the constraints of the func type (Equation (2)) and file type (Equation (4)). Similarly, the precondition of Equation (18b) can match rules of accessible relationships (Equations (16a) and (16b)) and the constraints of the func type (Equation (2)), struct type (Equation (3)), and member association relationship (Equations (12b) and (12c)). Furthermore, we can ascertain the precondition of accessible relationships (Equation (16a)) as the next conclusion to match. Matching continues until an exit of reasoning is found. Feedback is achieved with a value of true or false. Afterward, the value returns along the recursive stack, and calculations are performed. Finally, the invocation result from ${\mathrm{f}}_1$ to ${\mathrm{f}}_2$ is received.

4.5. An Example

Let us still use the “open system call” example. First, a list refined down to the function level is extracted to represent the full functionality. For example, at the function level, consider the following Func list: do_truncate();; vfs_truncate();; do_sys_truncate();; SYSCALL_DEFINE2;; COMPAT_SYSCALL_DEFINE2();; do_sys_ftruncate();; vfs_fallocate();; ksys_fallocate();; do_faccessat();; ksys_chroot;; do_fchownat();; vfs_open();; do_sys_open();; filp_close();; nonseekable_open(). Each func in the list is verified. Here, take $do\_sys\_open\left(\right)$$\stackrel{\ll invocable\gg }{\to }getname\left(\right)$, for example. As a func type, Equations (2) and (11b) are matched to specify the dependent type and structural relationship. The types that do_sys_open depends on include int:dfd;; char:__user;; int:flags;; umode_t:mode. These types are searched for in the database to determine their existence. Then, the structural relationship is checked. Types such as dfd (Equation (1)) are then matched to check whether they conform to the convention for the type. If correct, validation proceeds according to the type–structure relationship rule (Equation (11b)). After all the dependent types pass the above verification, $do\_sys\_open\left(\right)\stackrel{\ll invocable\gg }{\to }getname\left(\right)$ are deduced to determined whether they conform to the invoking relationship rules (Equation (18a)). According to the rules, the scopes of $do\_sys\_open\left(\right)$ and $getname\left(\right)$ are compared to determine the success of the invocation. If all funcs are correct, the design is considered to meet the requirements.

5. Discussion and Limitations

It should be noted that the correctness of design is not equivalent to the correctness of behavior. The kernel verification carried out here is from the perspective of the system architecture. Thus, we can use the abstract notion of type to verify the entire system. In contrast, behavior verification typically requires consideration of specific usage scenarios, in addition to modeling and verification of the specific properties that are important to us. The overhead of such verification is typically high. Therefore, existing work can usually only verify a small portion of the impact of system functionality on demand rather than consistently verifying large general-purpose cores.

Therefore, in this paper, we only perform static verification based on the built Linux model. Type theory is used to check the developers’ possible structural errors against the architecture but not to justify the other properties for behaviors or traces. In future work, we will consider using AI techniques such as neural networks to improve the efficiency of behavioral verification so that it can better support and guide developers.

6. Implementation

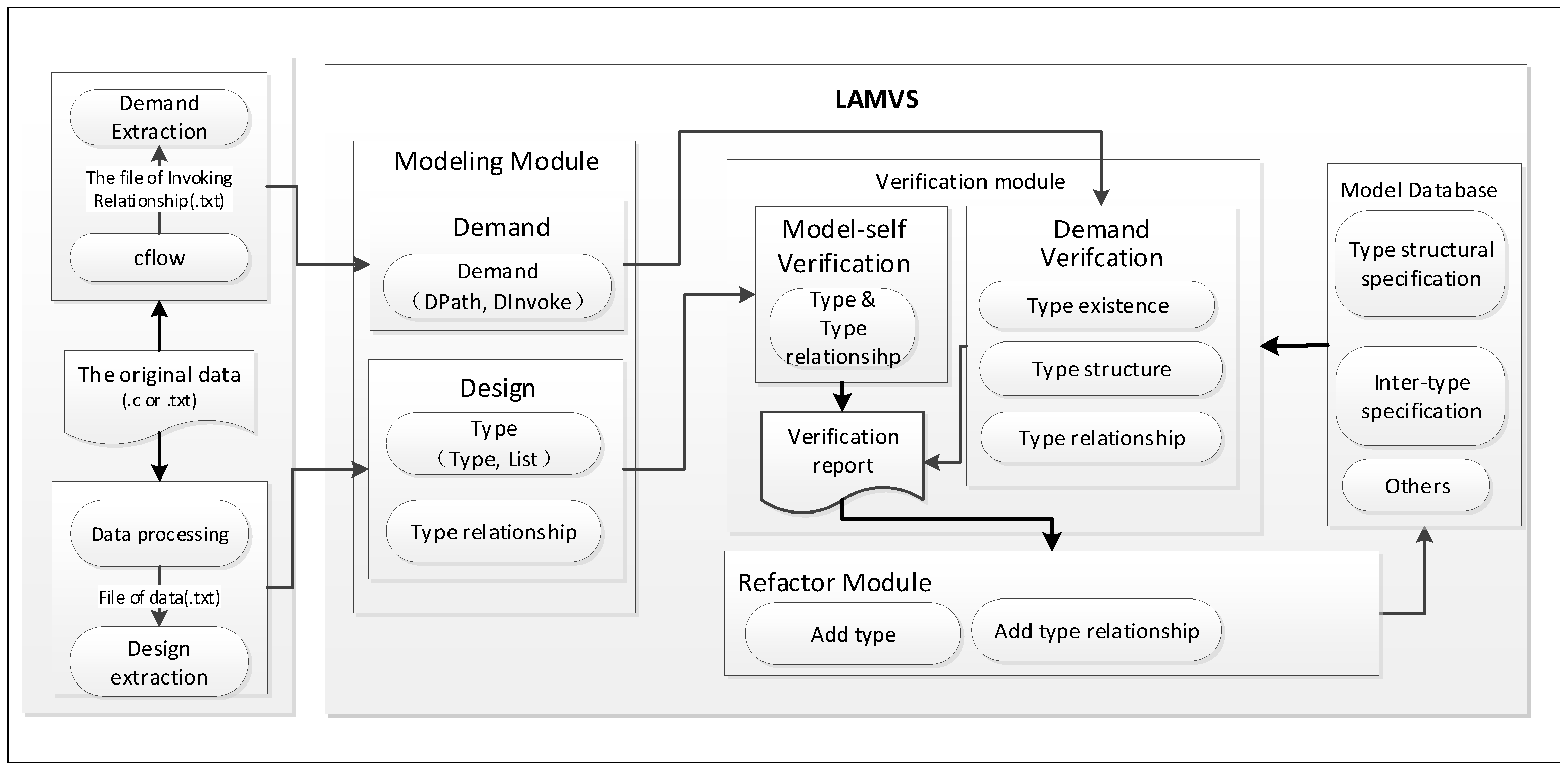
In this section, we introduce the detailed implementation of our proposed LAMVs (Linux kernel architecture modeling and verification system) Figure 2). The functions of LAMVs include modeling, verification, and refactoring of the kernel. After importing the raw data, the modeling module extracts the demand and design data. The data are then transferred to the verification module, which invokes the model database to execute model self-testing and demand verification and generate a verification report. Based on the report, users can extend the model and reconstruct the design by modifying the demand and design.

6.1. Modeling Module

The inputs to LAMVs are demand and design data, mainly extracted from specification-compliant raw data using GNU cflow and home-grown tools. The modeling is divided into the following two parts: data processing and the model database. Data processing is used to filter and pre-process the raw input data. For example, a pointer of type T is represented by “T*”. However, from a type dependency point of view, if T does not exist or is wrong, then T* is certainly the same. Therefore, T and “T*” are not distinguished in the type system. The pointer type (T*) is uniformly treated as T. For the array type (“T[]”) of type T, “[]” is also directly ignored and processed as type T. Further processing details are not described here. The model database stores the types and type relations according to the specification, and the extracted design data are stored in the model database after verification.

6.2. Verification Module

The verification module includes model self-testing and demand verification. Model self-testing involves testing the model’s capabilities and filling in the parts that are designed but not modeled. Demand verification is the core function of LAMVs. Users can find and improve problems in the design according to the report, mainly for the implementation of Algorithm 1. The detailed demands and design documents serve as input. The output is the verification report including the error code and its location.

6.3. Refactor Module

Due to the large size and complex characteristics of the Linux macro kernel, the verification model needs to be gradually expanded. Although the function of the open system call is relatively independent, there is no clear boundary between the implemented types. If a type is reported as missing, (1) this may indicate that we still need to model the demanded part, or (2) the developer may omit the required type or incorrectly construct the relationship between types. Therefore, we add a refactor module to the LAMVs for model refactoring. This module allows all missing types to be supplemented into the verification model so that additional kernel functions can be verified. The developer can also use this module to reconstruct and re-check the design.

It should be acknowledged that the refactor module is original. The missing types must be identified and added to the model manually. This slows down the modeling process and results in us only verifying part of the VFS. In future work, we will consider adding an automatic search and auto-complete feature for missing correct types.

6.4. Error Code

For the exception item in Equation (10), we designed the right and error code shown in Table 4. x is 1–7, corresponding to the seven level types. 00x_1/00x_2 is used to check the existence of level types. 50x_1/50x_2 is intended to check the correctness of level types based on the results of Equations (1)–(7) (algorithm DV_SR). 400_x expresses the correctness of the whole function. 401, 402, and 403 are used to verify the correctness of the demand, demanding path, and func invocation, respectively. When an error occurs, it is possible to pinpoint its location according to its name and the level to which it belongs, making it easy to modify errors in the design.

6.5. Effort

The verification algorithms and tools are developed in JAVA and HTML languages. The line of code is presented in

Table 9. System implementation.

Language	Files	Sum Lines	Blank	Comment	Code	Code/Sum Lines
.java	109	13,052	1947	1340	9765	74.82%
.html	56	13,266	1502	546	11,218	84.56%
SUM	165	26,318	3449	1886	20,983	79.43%

.

All codes can be found on GitHub at https://github.com/ssyybbiill/LAMVs (accessed on 27 April 2024).

7. Application

In the LAMVs, verification includes model self-checking and demand verification. The model of self-checking is mainly for kernel modeling. The goal is to ensure the integrity of the model. Demand verification is the core function of the whole system and is used to verify the correctness of the design.

To test its usefulness, we verify the open functionality of VFS in the kernel. The partial functionality of the kernel we designed is then verified. The complete modeling and verification cycle tale half to one person month, improving kernel security at a low manual cost.

7.1. Open System Call

In this section, we first test the validity of LAMVs. Since we designed a refactor module to extend the model gradually, here, we take the open function of VFS as an example to illustrate the modeling process.

7.1.1. Demand Extraction

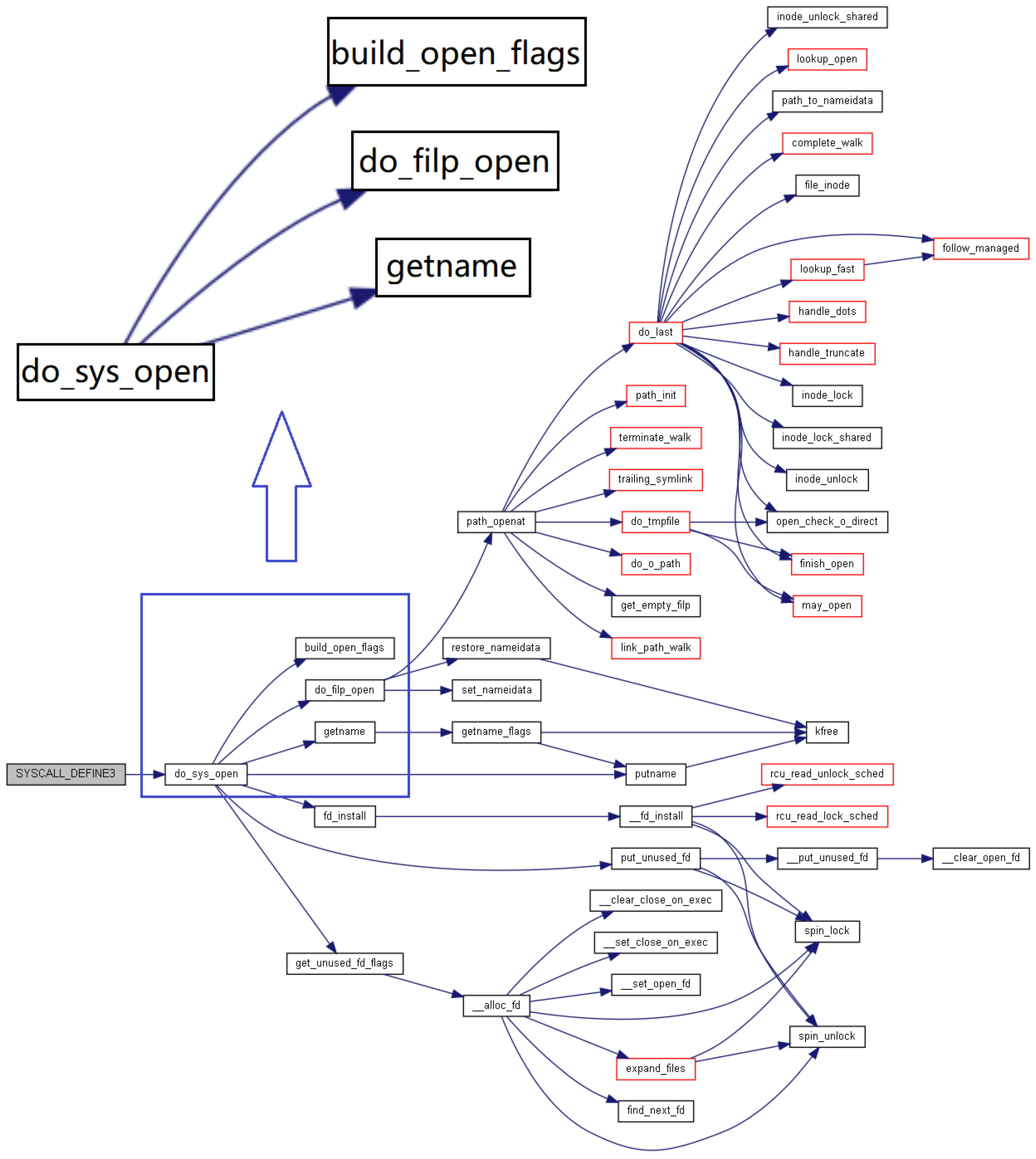
Through system calls, the open function traps the kernel to implement the entire business. Since we do not have detailed requirements, we need to reverse code transfer to the requirement. The entrance of the open system call is SYSCALL_DEFINE3. We present the code as follows.

• SYSCALL_DEFINE3(open, const char _user *, filename, int, flags, umode_t, mode)
• { /* fs/open.c*/
• if (force_o_largefile()) /* macro*/
• flags = O_LARGEFILE;
• return do_sys_open(AT_FDCWD, filename, flags, mode); /* fs/open.c*/
• }

Here, force_o_largefile() is a macro that is not pursued further. do_sys_open is a function. In addition, we extract the involved funcs using the doxygen [16] and cflow [17] tools and present the invoking tree in Figure 3. A total of 47 invoking relationships are extracted. The red box indicates cross-file invocation.

7.1.2. Modeling

We use the Linux source code to build the verification model backward. As the name suggests, the open system call can open files and is part of VFS. Therefore, we extract types and relationships as models from VFS. The main directories of VFS are linux/fs, linux/include, linux/kernel, and linux/mm. However, since the dependent types include 7018 files, a total of 35,699 types are extracted.

7.1.3. Model Self-Checking

It is important to note that since we chose to build the kernel gradually, the model we initially built is incomplete. As mentioned in the Refactor module, importing insufficient raw data leads to unsuccessful modeling, since there are no boundaries for called types. Therefore, we need to perform the self-checking type before requirement verification. This is a check to maintain the integrity of the model. The missing types in the model can be found. After completing this part with the Refactor module, the built model enables verification of demand (Figure 4).

7.2. Multi-Domain Kernel

We develop a secure kernel (QhOS) based on Linux-4.19 with multi-domain isolation architecture. Using LAMVs, we verify the partial functions in QhOS.

7.2.1. Overview

To improve kernel security, QhOS implements “domains” with solid isolation, which enable read/write functions between kernels. The kernel running in the virtual support environment is called the “domain” or “guest kernel” and initiates or accepts access. The kernel running on the physical machine is called the “host kernel”; it receives the request from the guest kernel and judges whether to fulfill the request. Here, we verify the correctness of the communication design in the guest kernel.

7.2.2. Model and Demand

The demand and design must be adopted from the detailed specification document for modeling and verification in the design phase. As part of the security kernel, the guest kernel supports the security communication mechanism between domains. We design the communication interface, session management, data transfer module, and pseudo file system in the guest kernel to implement communication. The communication interface is used for data transmission via I/O device. Data include the memory address and length, read and write properties, etc. Session management involves publishing/unpublishing or subscribing/unsubscribing to a file. Data transmission involves the use of a series of processing methods to send data. The pseudo file system is used to delete and create files by managing a black read tree called Proc. The initial model’s folders are linux/fs, linux/include, linux/kernel, linux/mm, and /guest/.

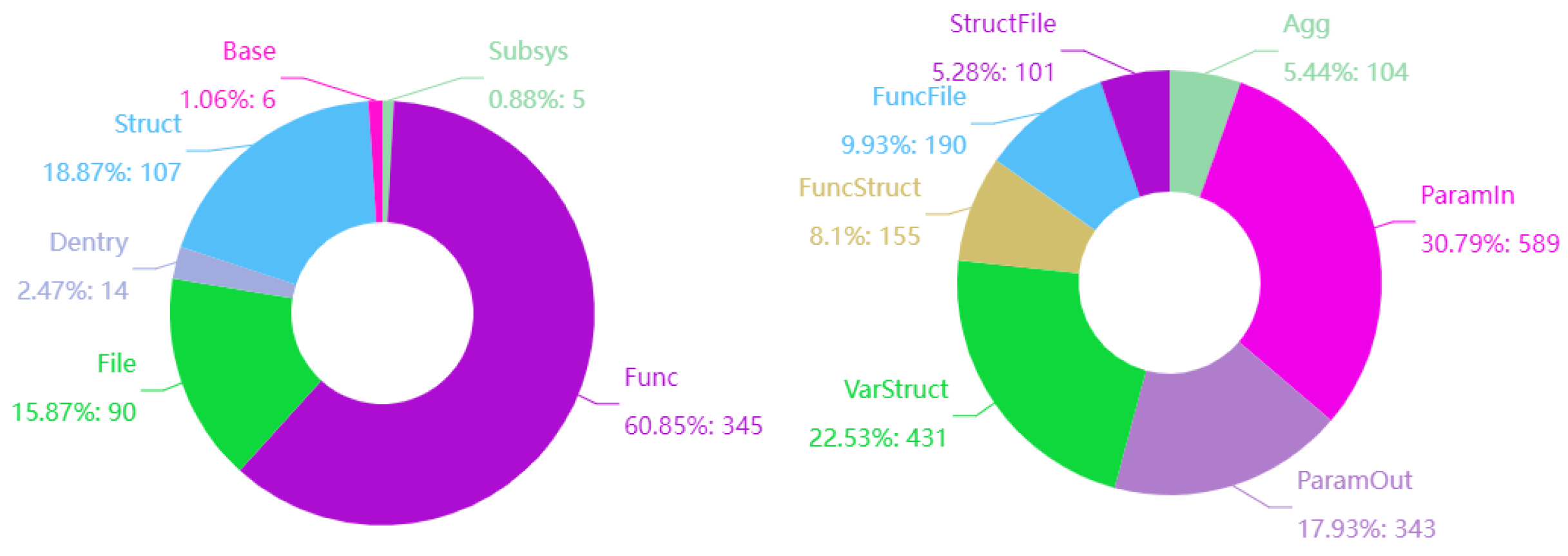
Figure 5 shows the parts of the demand (the invocations). The main structs designed according to demand include protocol_header, pguest_ring, and file. After importing the system design into the model, we complement the missing parent type and dependent list type to build the demand/design model. For the design, 44,548 types are extracted, including 8 base types, 29,899 func types, 11,020 struct types, 3472 file types, 144 dentry types, and 5 subsys types. For demand, 344 invocations are extracted, including 567 dependent types and 1881 dependent relationships. The ratio is presented in Figure 6.

7.2.3. Verification

As described in the Verification Section, verification includes in the confirmation of structural relationships and invoking relationships. For a demand, the system finds all invocation and dependent types. DV_SR and DV_IR are performed to verify the type and inter-type relationship. In demand verification, we check the correctness of the dependent type, structural relationship, and invoking relationship. 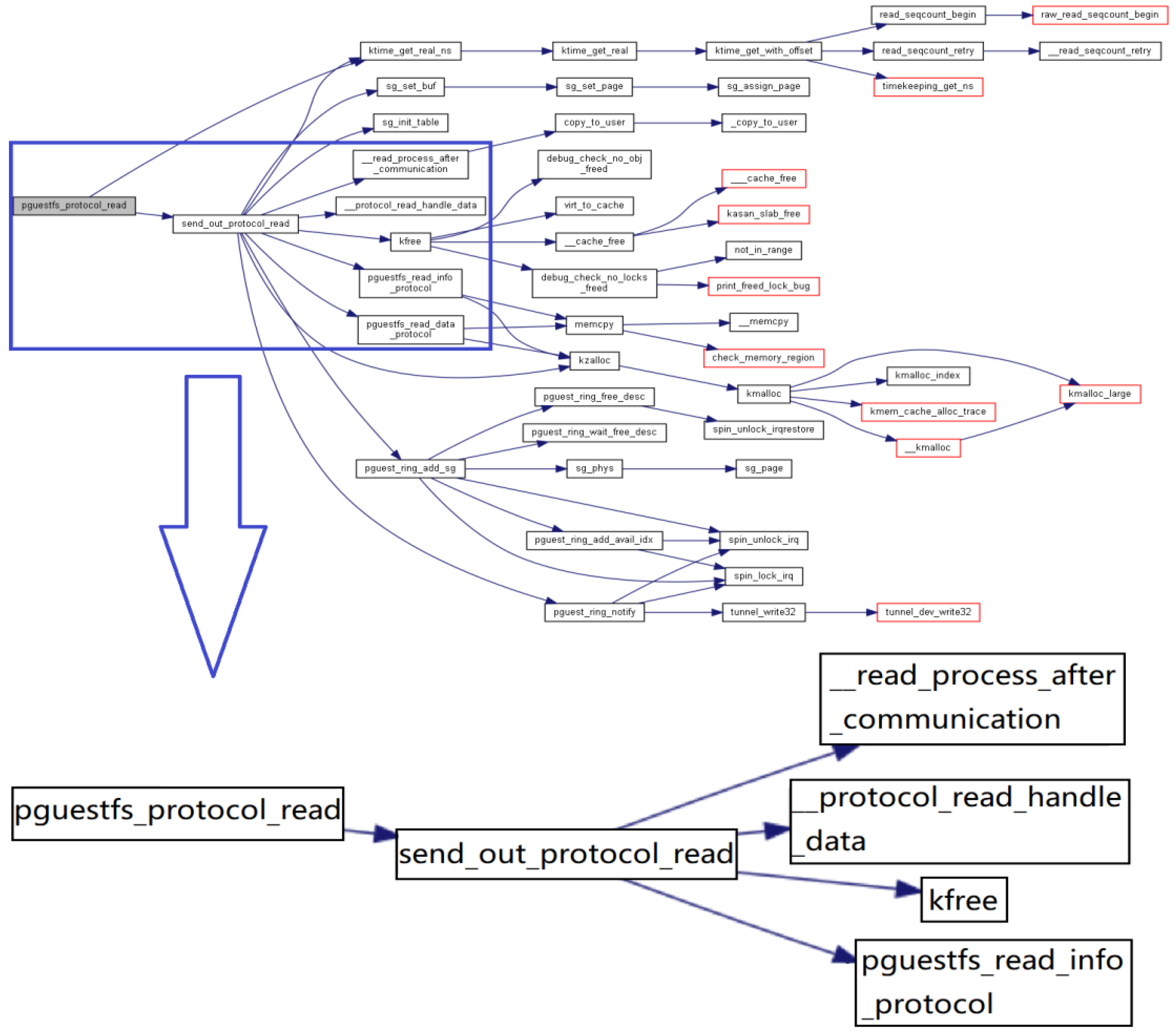Figure 7 shows a portion of the verification results. The correctness of each demand invocation is clearly listed. Furthermore, we present the verification process for the invocation. In Figure 8, we present the detailed results of pguestfs_protocol_read; ktime_get_ real_ns. On the first line, 4732 denotes the ID of the currently verified invocation, and 402_1 represents the verification type. Following this, the participation of functions in the invocation is indicated. The label “RIGHT” signifies that the verification result is correct. Subsequently, more detailed verification results are presented. First, the correctness of the participating functions is verified, encompassing their existence and relationships with different level types. Secondly, the correctness of the dependent types is verified, which, similarly, includes existence and relationship correctness. Finally, the invocation relationship is verified.

7.2.4. Discussion

In kernel design and verification, we identified two types of errors that occur most frequently. Here, we discuss the causes of these errors and the potential negative impacts on kernel stability and security.

Missing Level Type Errors (020_2)

One of the most prevalent errors found in the kernel design is the 020_2 error, which indicates missing level types. This suggests that types defined by the tested designer are often overlooked or incorrectly designed. These errors, if present at the code stage, would result in compilation failures. Addressing these issues later takes more time than solving them during the design phase.

Invocation Verification Errors (404_2)

Another significant category of errors pertains to invocation verification. Specifically, 404_2 errors arise when external functions defined in other files are called without proper declaration in the current file. This is a human-induced error, likely due to oversight or misunderstanding of the kernel function. However, further testing reveals that the GCC compiler can sometimes compile code even when functions are undeclared. While the compiler may not report an error and return an integer or pointer value to continue running, these undeclared invocations can lead to unpredictable behavior. Such errors undermine the consistency of the kernel, making it harder to maintain and extend over time. Moreover, they introduce security vulnerabilities, as incorrect or missing declarations can lead to unexpected behavior and potential exploits.

8. Related Work

8.1. Formal Kernel Verification

Depending on the code size and functionality, kernels can be divided into microkernels and monolithic kernels. Work on the verification of microkernels, such as sel4 [18] and certiKOS [6], has enriched the field of kernel verification. Other studies of formal kernel verification have mainly concerned kernel function correctness [19,20,21] and specific security properties [22,23,24,25]. In contrast to a microkernel, with about 10,000 code lines, the code of a monolithic kernel (such as the Linux kernel) is more than 10 million lines. Therefore, verification of a monolithic kernel is generally limited to its partial functionality. Penninckx proposed an approach to verify the USB keyboard driver [26]. This work verified the complete USB keyboard driver based on separation logic, considering dynamic memory allocation and concurrency. Sanjit Bhat [27] proposed a verification framework for the eBPF verifier of the Linux kernel. Through range analysis, security-critical bugs were found in the verifier. Luke Nelson [28] proposed a formal method for BPF just-in-time compilers in the Linux kernel. This approach applies precise step-wise specification and automatic proof strategies to compiler implementations. Li proposed an approach to verify the Linux KVM Hypervisor [29], ensuring the security of the entire KVM by verifying the key components. To enable real-time verification, Bristot proposed a formal verification method for the Linux kernel using automata models [30]. The automation description file can generate the verification code and be added to the kernel using in-kernel tracing features. Such studies typically take several person years and require continuous human involvement. The size and complexity of the kernel make such costly validation unsustainable, especially for monolith kernels with more significant amounts of code. This paper focuses on a general validation method for the monolithic Linux kernel. Our approach does not guarantee kernel soundness like the code-level validation efforts described above. Still, we significantly reduce human involvement, allowing our engineering team to apply it to their Linux development practice.

To reduce manual costs, Easterbrook discussed several formal modeling cases of the requirements in the early engineering process [31]. This paper clarifies the goal of lightweight verification; it is not necessary to guarantee the absolute correctness of the verification target but to reveal the missing errors in the non-formal requirements and improve the security level, providing a consistent requirement model to detect errors. The selection of requirement properties and error analysis are performed by a professional according to the requirements of the specific problem. As a formal analysis method relies on experience, more case studies were investigated in [32,33]. Betarte introduced a formal method to verify the Android access control policy [34]. The implementation was tested using lightweight model-based techniques. Bornholt developed a lightweight formal validation method for key-value storage that considers the automation and sustainability of validation [35]. While these studies only address a part of the kernel or reduce the effort of a single step, this paper focuses on architecturally verifying the whole Linux kernel.

8.2. Formal Modeling Method

We investigate the current main modeling methods for complex systems to model the kernel better. The ER model is an early modeling method that can describe entities, attributes, and relationships [36]. It has become the starting point for the design and development of relational databases, but the model mainly focuses on the key value relationship between entities. The product of object-oriented modeling, Unified Modeling Language (UML), can describe rich relationships in modeling, but its description is relatively complex [37]. A descriptive logical modeling method [38] expands the explanatory ability of the ER model and provides basic reasoning functions. However, the logical symbols are also complex, focusing more on checking the consistency verification of schema in the database. A multi-dimensional modeling method is mainly used to model complex data in Online Analytical Processing (OLAP) [39]. In addition, PCT, a type description language, can describe types, semantic features, and integrity constraints in models using high-level programming languages and first-order predicate logic [40], but its descriptive ability and application scale are limited. Many theoretical modeling and verification methods exist, but few can briefly and accurately describe a giant monolithic kernel’s construction process and relationships.

8.3. Type Theory

Type theory is closely related to mathematical methods and logical reasoning, such as set theory [41], and is widely used in program verification [41,42,43,44,45]. Filliatre applied type theory to non-functional programs to annotate logical interpretations [46]. Nanevski proposed an access control policy and information flow verification method [47]. Huang presented a verification framework for the cloud computing software environment based on type theory. The theory accurately describes the relationship of information transmission [48]. Unlike these researchers, our goal is to create a specification to verify the correctness of the kernel design. The structured nature of type theory allows us to model a complete kernel.

9. Conclusions

We propose a formal verification approach, LMVM, which uses type and type relationships to specify and verify the kernel design. Through structural and invoking verification, we can justify the functional correctness of the complete Linux kernel design in terms of architecture. At the same time, our experiment for “Open system call” shows that the refactor module can evolve the model to solve the problem of continuous kernel verification. We leverage the method to design “multi-domain kernel”, which shows it can find security-hazardous errors effectively. One cycle of modeling and verification takes a few person days, which greatly improves the method’s practicality. Compared to other formal verification efforts, our work improves the kernel’s security with a lower labor cost.

10. Further Works

In the future, we plan to conduct further research on the following two aspects. First, in terms of research content, we will attempt to use structured and typed approaches to standardize and verify the behavior of the kernel, thereby improving verification efficiency while ensuring the kernel’s security. Secondly, in terms of technology, we will try to automate the modeling, verification, and refactoring process with the help of artificial intelligence. For example, when the system detects a missing type, it could automatically rectify the design based on previously encountered error cases.