Abstract
Today, the field of biomedical engineering spans numerous areas of scientific research that grapple with the challenges of intelligent analysis of small datasets. Analyzing such datasets with existing artificial intelligence tools is a complex task, often complicated by issues like overfitting and other challenges inherent to machine learning methods and artificial neural networks. These challenges impose significant constraints on the practical application of these tools to the problem at hand. While data augmentation can offer some mitigation, existing methods often introduce their own set of limitations, reducing their overall effectiveness in solving the problem. In this paper, the authors present an improved neural network-based technology for predicting outcomes when analyzing small and extremely small datasets. This approach builds on the input doubling method, leveraging response surface linearization principles to improve performance. Detailed flowcharts of the improved technology’s operations are provided, alongside descriptions of new preparation and application algorithms for the proposed solution. The modeling, conducted using two biomedical datasets with optimal parameters selected via differential evolution, demonstrated high prediction accuracy. A comparison with several existing methods revealed a significant reduction in various errors, underscoring the advantages of the improved neural network technology, which does not require training, for the analysis of extremely small biomedical datasets.
1. Introduction
Today, there is a rapid development of various directions in biomedical engineering [1,2]. This is largely due to the advancements in artificial intelligence. However, existing machine learning (ML) methods or artificial neural networks (ANNs) primarily operate with large datasets [3,4]. The toolkit for the intelligent analysis of small biomedical data is currently significantly limited [5].
Despite this, the task of intelligent analysis of extremely small biomedical datasets is very relevant nowadays [5]. This relevance can be attributed to various reasons. Specifically, with technological advances in genomics and medical diagnostics, there are increasing opportunities to obtain biomedical data, including short DNA and RNA sequences, as well as other “extremely small” data types [6,7]. Analyzing these data can aid in understanding the causes of various diseases, their progression, and response to treatment. Enhancing the accuracy of diagnostics and treatment through the analysis of small biomedical data can promote the development of personalized medicine, where treatments are tailored to the specific characteristics of a patient and their disease. Additionally, effective intelligent analysis of small biomedical data can reveal new connections and discoveries in medical science, potentially leading to the development of new treatment and diagnostic methods [8].
Considering all the aforementioned points, the task of intelligent analysis of extremely small biomedical datasets remains important and relevant in the context of the development of medical science and practice. However, the intelligent analysis of such data presents several significant challenges and issues [9]. Specifically, small biomedical datasets often contain a high level of noise or a relatively small amount of useful information compared to the overall data volume. This can complicate the identification of true signals or patterns within the data. Moreover, extremely small datasets are very limited in size, making them less representative and potentially hindering the application of many standard data analysis methods (such as machine learning methods or artificial neural networks), which require large datasets for effective performance. Missing values and anomalies in such data, which further reduce the dataset size, critically affect subsequent intelligent analysis [10].
Additionally, a distinctive feature of small biomedical datasets is the large number of features or independent variables that characterize each individual observation in the set. This leads to the issue of high dimensionality, which in turn can reduce the generalization capabilities of the artificial intelligence tools used [11]. Consequently, this often leads to the overfitting of methods or ANN models and difficulties in identifying important relationships between independent features and the outcome [12]. Another characteristic of such data can be their heterogeneity or instability due to various technical limitations in the data collection process, which can affect data representativeness and complicate analysis [13]. Given their limited size, these constraints make analysis using existing machine-learning methods unfeasible [8]. Therefore, addressing all the above-mentioned problems requires the development of specialized methods and technologies for analyzing extremely small biomedical datasets, and careful preparation and processing of such data prior to analysis.
The objective of this paper is to improve the ANN-based prediction technology without training for extremely small biomedical data analysis (less than 100 observations).
The main contributions of this paper are the following:
- We improved the neural network-based technology without training for solving regression tasks in the case of the analysis of extremely small datasets using response surface linearization principles, which significantly increased prediction accuracy.
- We optimized the parameters of the improved technology using the Differential Evolution method, which substantially reduced both its operation time and approximation errors in solving the stated tasks.
- We validate the improved prediction technology on two extremely small datasets in the field of biomedical engineering and, through comparison with well-known methods, established its highest accuracy.
The paper is organized as follows: Section 2 provides an overview and critical analysis of existing approaches to small data analysis. Section 3 describes the operation of the improved neural network-based technology without training for prediction in the case of extremely small dataset analysis. It includes a description of the data augmentation procedure and the preparation and application algorithms of the improved technology. Section 4 provides a description of the datasets used for modeling, a mathematical description of the performance metrics for evaluating the improved technology, as well as the optimization procedure for selecting optimal parameters and the obtained results. Section 5 contains the results of comparisons with existing methods and a detailed discussion of the obtained results.
2. State-of-the-Arts
As mentioned above, there is currently a problem with the existing methodology for analyzing small and extremely small datasets [14]. The previous section lists the main reasons for the inefficiency of existing machine learning methods or artificial neural networks in analyzing such data.
Given the great variety of ML or ANN methods for analyzing tabular datasets, one of the first solutions to improve the efficiency of analyzing limited datasets is to increase the size of the small or extremely small dataset [15]. In a number of cases, biomedical engineering tasks are characterized by small data volumes, and increasing the size of the dataset is time-consuming, resource-intensive, or simply impossible at a given point in time. In this case, an intuitive approach would be to use methods of artificial data expansion or data augmentation.
Today, there are many methods for augmenting various types of datasets (text, images, and tabular data) [15]. In particular, in [16], the authors developed a whole framework with simple methods for augmenting tabular datasets. Despite the numerous arsenal of such methods, most of them, which are based on determining the distribution of the data, are not suitable for augmentation in the case of an extremely small dataset. This is due to the non-trivial nature of the task of determining the distribution of an extremely small dataset.
Among the more modern and promising neural network methods for data augmentation in the case of extremely small datasets, two main ones should be highlighted: (i) an autoencoder-based data augmentation procedure [17]; (ii) a Generative Adversarial Network (GAN)-based data augmentation procedure [18]. The fundamentals of these methods are thoroughly examined in [19]. In this article, we conducted an experimental analysis of the effectiveness of various machine learning classifiers when using both of the aforementioned data augmentation methods. A well-known small dataset [20] was selected for modeling.
Figure 1 shows the modeling results with a change in the % of synthetic vectors added to the training dataset, obtained using an autoencoder-based data augmentation procedure. The effectiveness of using this approach was evaluated by assessing the classification accuracy using four different machine-learning methods.
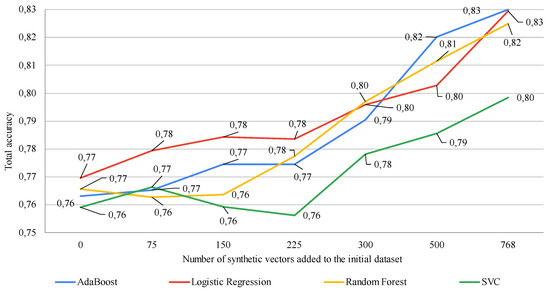
Figure 1.
Study of the impact of adding various numbers of synthetic vectors on the classification accuracy of different machine learning algorithms using an autoencoder-based data augmentation procedure (on the x-axis, zero denotes the classification results based on using the original dataset from [20] (768 vectors) without augmentation. The subsequent numbers denote the quantity of synthetic vectors added to the original dataset). Data augmentation ranged from 10% to 100% of the size of the original dataset.
As seen in Figure 1, in general, increasing the number of vectors in the training sample, which are generated using an autoencoder-based data augmentation procedure, shows an increase in the accuracy of almost all machine learning methods. The accuracy of their work increased by about 5%. However, as demonstrated using SVR, selecting the correct number of synthetic vectors to add to the initial training dataset plays an important role in the performance of this machine-learning method. In particular, the accuracy of SVR decreased when 225 artificial vectors were added compared to the accuracy of this method on the initial dataset. However, further increasing the number of vectors leads to an improvement in the accuracy of this machine learning method, although it also increases the amount of resources, especially time, required for model training.
The general conclusion from the results of evaluating the use of an autoencoder-based data augmentation procedure in the analysis of small datasets is that, in this case, an optimal complexity model should be sought. That is, one should experimentally determine the number of artificially created vectors that will enhance the accuracy of the classifiers while minimizing the resources required for model training.
Figure 2 shows the modeling results when varying the percentage of synthetic vectors added to the training dataset using a GAN-based data augmentation procedure. The effectiveness of this approach was assessed by evaluating the classification accuracy of four different machine learning methods.
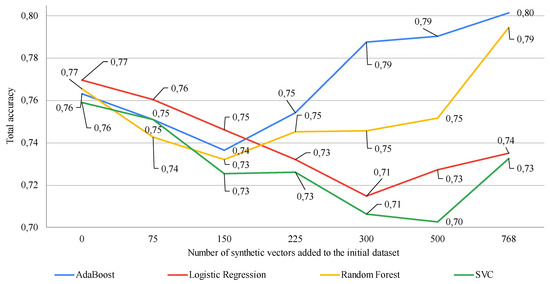
Figure 2.
Study of the impact of adding various numbers of synthetic vectors on the classification accuracy of different machine learning algorithms using a GAN-based data augmentation procedure (on the x-axis, zero denotes the classification results based on using the original dataset from [20] (768 vectors) without augmentation. The subsequent numbers denote the quantity of synthetic vectors added to the original dataset). Data augmentation ranged from 10% to 100% of the size of the original dataset.
As shown in Figure 2, using a GAN-based data augmentation procedure to augment the training dataset results in a significant decrease in the accuracy of all four classifiers when the size of the training sample is increased by less than double. Further increases in the training sample size also significantly affect the performance of machine learning methods. For two of them, the results significantly deteriorate, while for the other two, they significantly improve. The use of a GAN-based data augmentation procedure for augmenting the training dataset showed an improvement in accuracy by 2–3% for only two classifiers with 100% augmentation, meaning doubling the size of the training sample. The other two classifiers demonstrated significantly worse results compared to using the initial dataset for the training procedure.
The general conclusion from the results of evaluating the use of a GAN-based data augmentation procedure in the analysis of small datasets is that, in this case, it is also necessary to search for optimal model complexity. Moreover, this approach requires identifying the method or machine learning model that will ensure a potential increase in the accuracy of solving the given task.
Summarizing the conducted research, it should be stated that applying existing augmentation methods to tabular data has limitations and drawbacks that can impact machine learning outcomes. Among these, the following should be highlighted [8,9,10,15,21,22,23]:
- Excessive data augmentation can lead to the creation of a dataset that appears larger but actually contains a significant number of duplicate or similar records, which can increase the risk of model overfitting.
- Augmented data may not reflect the real data distribution. In particular, randomly adding or removing values can create inadequate or non-existent correlations, leading to bias in analysis and deterioration of model performance.
- Augmentation methods can generate inconsistent data that do not correspond to real situations (generated samples may not adhere to real physical or logical constraints), which can mislead the model.
- Data augmentation can significantly increase the volume of data, resulting in higher time and resource costs required for model training, which can be critical for systems with limited computational capabilities.
- Methods such as adding noise or altering values may create samples that are very similar to existing ones, significantly reducing the effectiveness of training since the model learns from practically identical examples.
- Increasing the data volume through augmentation can lead to the model becoming too specific to the training dataset and poorly transferring to new data or other domains.
- Tabular data often contain complex dependencies between features, and augmentation may disrupt these dependencies, leading to incorrect data interpretation by the model and, consequently, decreased prediction accuracy.
- During augmentation, errors or anomalies can be introduced into the data, which can lead to incorrect model training and reduced accuracy.
- There are many data augmentation methods, and selecting the best one for a specific dataset can be challenging. Improper selection of the method can reduce data quality and model efficiency.
- There are no universally accepted standards or criteria for evaluating the quality of augmented data, making it difficult to assess their impact on model performance.
Therefore, while data augmentation of tabular data can significantly improve machine learning model accuracy with limited data [15], users should approach the selection and application of augmentation methods carefully to avoid potential drawbacks and ensure optimal model efficiency.
To address several of the aforementioned limitations, a new method for analyzing short and extremely short datasets was developed in [24]. It involves increasing the size of the training data sample without creating entirely new samples and uses ensemble averaging principles with only one non-linear artificial intelligence tool to perform prediction procedures. The main steps of the basic input-doubling method can be described as follows [24]:
- Form a new augmented support dataset based on the existing vectors for which the output signal is known. Perform a data augmentation procedure by pairwise concatenating all possible pairs of vectors, including each vector with itself. The output signals are generated as the difference between the outputs of the two concatenated vectors.
In this case, augmentation occurs within the available dataset and is independent of the data distribution or other dataset characteristics that are important when using classical data augmentation methods. Thus, a quadratically increased or augmented dataset is formed with doubled feature counts in each vector from the dataset.
- 2.
- For a test vector with an unknown output signal, create a new temporary dataset by concatenating it with all vectors from the initial training set.
- 3.
- Predict the output signals for this temporary dataset using a General Regression Neural Network (GRNN), which has the highest generalization properties among existing artificial neural network (ANN) topologies [24]. Use the new augmented dataset from Step 1 as the support dataset.
- 4.
- Make the final prediction by adding the sum of the predictions obtained in the previous step to the sum of all output signals from the initial training set and then divide this sum by the number of vectors in the initial training set. This follows ensemble principles, specifically averaging the results, to ensure improved prediction accuracy.
- 5.
- Repeat Steps 2–4 for all vectors with unknown output signals.
However, a drawback of this method is the modest increase in prediction accuracy compared to the significant increase in the duration of applying the method due to the execution of augmentation procedures. This imposes several constraints on the practical application of the basic input-doubling method for solving various applied tasks.
3. Materials and Methods
This section describes an improved neural network-based technology without training for prediction extremely small datasets based on the principles of response surface linearization and ensemble learning elements. The main steps of the algorithms’ preparation and application are detailed. Structural–functional diagrams of the operation of the improved neural-network-based technology are provided for both preparation and application modes.
3.1. Data Augmentation Procedure of the Improved ANN-Based Technology without Training
The improved neural network-based technology without training for enhancing prediction accuracy of extremely small data analyses is based on the foundational input doubling method from [24]. It relies on four main steps: (i) forming an augmented dataset (quadratic increase by pairwise concatenation of all vectors from the available training dataset), which serves as the supporting dataset for GRNN; (ii) forming an augmented temporary dataset for each vector with unknown output; (iii) applying GRNN to predict preliminary results; and (iv) synthesizing the desired value using ensemble principles (averaging the result between predicted values and the original signals of all vectors from the initial training dataset). The visualization of this method in the data preparation and augmentation mode is presented in Figure 3. It is worth noting that the red circles denote enhancements to this method and should not be considered in the baseline approach.
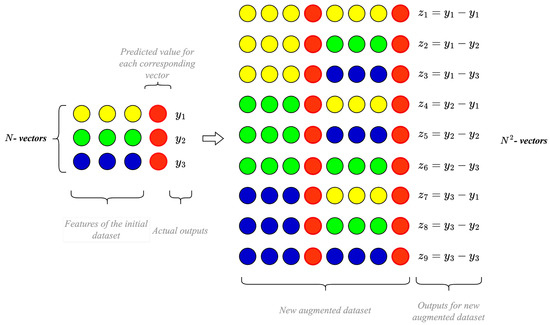
Figure 3.
Visualization of an augmentation procedure for the improved ANN-based prediction technology.
Unfortunately, the approach described above did not yield a significant increase in prediction accuracy under conditions of analyzing limited data volumes [24]. Additionally, the quadratic increase in the augmented dataset, as prescribed by the method, substantially increases the duration of GRNN operation, which is intended for short dataset analysis. Nevertheless, it shows promise specifically for analyzing short and extremely short datasets [10].
Therefore, this paper proposes an improvement to this method based on response surface linearization principles. Thus, the main steps of the quadratic increase (augmentation) procedure according to the improved neural network-based technology will be as follows:
Step 1: Use GRNN_1 to predict the output value for the entire training dataset. Add the obtained prediction to each corresponding data vector as a new additional feature. Since GRNN does not undergo a training procedure typical of other types of artificial neural networks, the prediction of the output signal for the current vector from the initial support dataset was performed by excluding the current vector from it at the time of prediction. This process was carried out sequentially for all vectors in the initial support training dataset, ensuring relevant predicted variable values for the entire initial support dataset.
Step 2: Pairwise concatenates all previously expanded vectors from the initial support training dataset formed in the previous step, thereby forming a quadratically increased, augmented support dataset where each vector contains a doubled number of features. The output signal for each such expanded vector is formed as the difference between the outputs of the two corresponding vectors that are concatenated.
Step 3: Use the augmented dataset as a support dataset during the implementation of the method application procedure using GRNN_2.
The sequence of steps outlined above is illustrated in Figure 3 for clarity. Notably, the changes and improvements discussed in this paper are highlighted in red in Figure 3. Without these enhancements, Figure 3 would represent the basic input-doubling method. The improvements we introduce align with the principles of response surface linearization, significantly boosting prediction accuracy with a minimal increase in the duration of the preparation and application procedures of the enhanced neural network-based technology described in this paper.
3.2. General Regression Neural Network
At the core of both the basic method of input doubling and the enhanced unsupervised neural network technology proposed in this work lies the use of a General Regression Neural Network (GRNN). This choice is justified by the fact that GRNN is one of the best neural network models for handling short tabular datasets [24]. The selection of this artificial neural network model (ANN) for implementing the enhanced technology proposed in this work is explained by several reasons, including [24,25]:
- It possesses the highest generalization properties among existing NNM topologies.
- It does not require a training procedure.
- Only one hyperparameter needs to be tuned.
- It operates with high speed.
- It is straightforward to implement.
The topology of this ANN is illustrated in Figure 4.
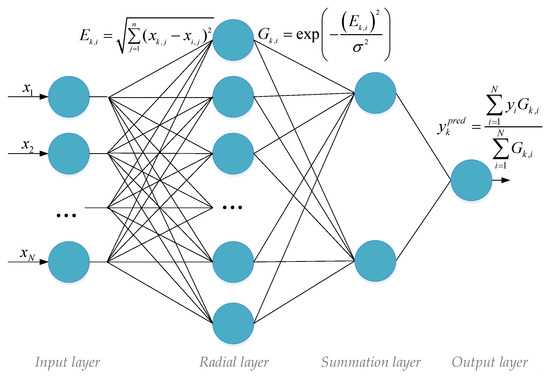
Figure 4.
ANN without training (General Regression Neural Network—GRNN).
The operation of GRNN can be described using the following main steps [26,27]:
- Calculation of Euclidean distances between the current vector and all vectors in the reference training set;
- Computation of Gaussian distances from the Euclidean distances;
- Prediction of the desired value;
Mathematically, all the steps described above are presented in Figure 4. Therefore, this type of neural network was used in the application mode of the enhanced neural network technology for analyzing extremely short datasets.
3.3. Application Procedure of the Improved ANN-Based Technology without Training
The application mode of the improved neural network-based technology requires the use of two GRNNs and the availability of an augmented dataset. The primary steps for applying the improved technology to one vector with an unknown output signal (one vector from the test dataset) are as follows:
Step 1: Use GRNN_1 to predict the output value for each vector in the test dataset. Add this predicted value as an additional feature to each corresponding data vector. The reference dataset for GRNN_1, in this case, is the initial extremely small dataset.
Step 2: Form a temporary dataset for each vector in the test dataset by pairwise concatenation of this vector with all vectors from the initial extremely small dataset.
Step 3: Use GRNN_2 and the augmented dataset (the quadratically increased dataset) as the reference dataset to predict a set of preliminary results for the temporary dataset formed in Step 2.
Step 4: Synthesize the predicted value for the current vector with an unknown output signal using the formula provided in Figure 4, which is based on ensemble learning principles, specifically averaging the results.
Step 5: Sequentially execute Step 1 through Step 4 for each vector in the test dataset (each data vector has an unknown output signal).
For clarity, the sequence of performing all these steps is depicted in Figure 5 where the improvements are highlighted in red. Without these improvements, Figure 5 would represent the application procedure of the basic input-doubling method. The improvements we introduce align with the principles of response surface linearization and significantly enhance prediction accuracy with a minimal increase in the duration of the preparation and application procedure.
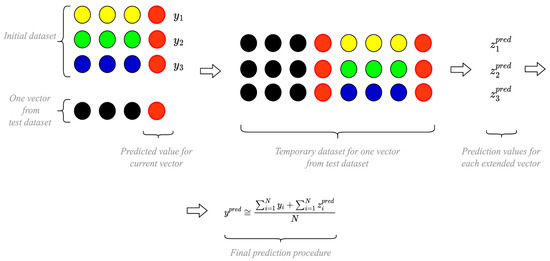
Figure 5.
Visualization of an application procedure for the improved ANN-based prediction technology.
4. Modeling and Results
The authors have developed their own software to implement an enhanced non-iterative technology for the intelligent analysis of extremely small biomedical datasets. Python programming language was used for this purpose. All experimental studies were conducted on a computer with the following specifications: CPU Intel Core i5-2500 K 3.3 GHz/6 MB, RAM 12 GB, HDD 2 TB, OS Windows 10.
4.1. Dataset Descriptions
To assess the efficacy of the improved technology in analyzing extremely small datasets, we employed two real, publicly available datasets from the field of biomedical engineering. Table 1 provides references to these datasets, details of the practical tasks addressed using them, and the number of instances and attributes for each dataset utilized.

Table 1.
Dataset’s descriptions.
Each of the investigated datasets contains a different number of instances and attributes.
4.2. Performance Indicators
Performance evaluation of the enhanced technology for analyzing small biomedical datasets was conducted using various metrics:
- ME (Maximum residual error):
- MedAE (Median absolute error):
- MAE (Mean absolute error):
- MSE (Mean square error):
- MAPE (Mean absolute percentage error):
- RMSE (Root mean square error):
- R2 (Coefficient of determination):
Since the improved technology does not require a training procedure, this paper will also assess the time required for its application to each investigated dataset.
4.3. Results
4.3.1. Optimal Parameter Selection
The improved technology for analyzing extremely small biomedical datasets in this work includes two GRNNs. Each requires the optimization of a single parameter value: the Gaussian function bandwidth (σ1 for the first GRNN and σ2 for the second GRNN of the improved technology). This parameter is crucial for obtaining prediction results.
In [24], it was demonstrated that during the analysis of short biomedical datasets, the parameter σ significantly affects the GRNN prediction results. Specifically, the search for σ values in [24] was conducted using a complete grid search method over the interval [0.01, 10] with a step of 0.01. Depending on the size and dimensionality of the dataset and the methodology of augmentation underlying the technology, such an approach can require considerable time and memory resources for proper implementation. For instance, with an input dataset of 100 instances, the augmented dataset contains 10,000 instances, and the aforementioned interval necessitates approximately 10,000 method runs to find the optimal parameter value (as conducted in [24]). This assumes the search is conducted for only one σ. In our case, we need to determine optimal values for both σ1 and σ2.
To save the aforementioned resources, the search for optimal parameters for the technology proposed in this article was conducted using the Differential Evolution optimization method over the interval [0.01, 10]. The accuracy results of the GRNN method during the parameter search for σ1 and σ2 of the improved technology in this work, utilizing both exhaustive search and Differential Evolution methods, for dataset #1 from Table 1, are presented in Figure 6.
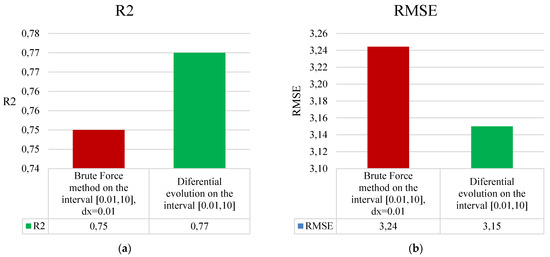
Figure 6.
Results of comparing two methods for finding optimal values of parameters σ1 and σ2 of the enhanced technology for analyzing short datasets based on (a) R2 and (b) RMSE.
This approach ensured a significant reduction in the application time of the improved technology (by more than 9500 times). Additionally, the search for values of σ1 and σ2 using the Differential Evolution optimization method used a significantly larger step size compared to the step size of 0.01 used in the exhaustive search method described in [24]. Therefore, this also ensured the search for truly optimal values for σ1 and σ2, which in turn significantly improved the overall accuracy of the improved technology’s predictions (Figure 6).
4.3.2. Results
In Table 2, the results of all performance indicators for the two studied biomedical datasets after applying the improved technology for analyzing extremely small biomedical datasets with optimized parameters are summarized. Table 2 also includes the optimal values of the smooth factor (σ) parameter for both GRNNs used in the improved technology presented in this paper (σ1 for the first GRNN and σ2 for the second GRNN of the improver technology).

Table 2.
Values of the performance indicators for all investigated datasets after applying the improved prediction technology for analyzing extremely small biomedical data analysis.
As seen in Table 2, the improved technology for analyzing extremely small biomedical datasets achieves sufficiently high accuracy. Specifically, the coefficient of determination for both datasets is quite high.
5. Comparison and Discussion
In this paper, we improved the ANN-based prediction technology for extremely small biomedical data analysis. This technology does not require training due to the use of GRNN for implementing the prediction procedure. Additionally, GRNN ensures high generalization and easy implementation. Furthermore, the improved technology modifies the augmentation procedure described in [24]. Therefore, to evaluate the effectiveness of the improved ANN-based prediction technology, we compared its results with those of well-known methods:
- Classical GRNN [29];
- Input-doubling method from [24].
The optimal parameter selection for both methods in this article was also performed using the Differential Evolution method.
Table 3 summarizes the optimal parameter values for all investigated methods.

Table 3.
Optimal parameters for the investigated methods, obtained using the Differential Evolution method.
A comparison of the results of the three methods based on three different performance indicators for dataset 1 is summarized in Figure 7.
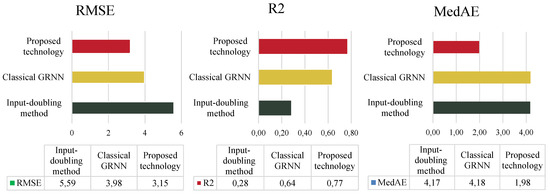
Figure 7.
Comparison of the accuracy of all investigated methods using dataset 1 from Table 1.
As seen in Figure 7, the classical GRNN demonstrates the lowest prediction accuracy. The input-doubling method [24] shows significantly better results. Specifically, it improves prediction accuracy by more than two times compared to the classical GRNN based on the coefficient of determination. However, achieving 64% prediction accuracy is still unsatisfactory for solving the stated task.
The improved technology in this study improves accuracy (based on the coefficient of determination) by 13% compared to [24] and by 49% compared to [29]. Furthermore, the increase in the number of features in the augmented dataset has a negligible impact on the duration of the technology compared to the input-doubling method [24].
A comparison of the results of the three methods based on three different performance indicators for dataset 2 is summarized in Figure 8.
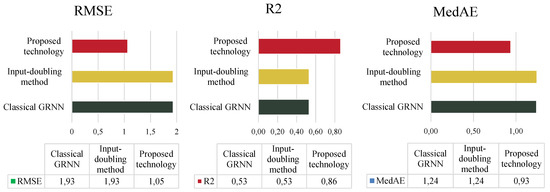
Figure 8.
Comparison of the accuracy of all investigated methods using dataset 2 from Table 1.
In this case, the results differ somewhat. Specifically, analysis of all investigated performance indicators shows that the use of classical GRNN and the input-doubling method [24] demonstrate similar and unsatisfactory accuracy performance (53% according to the coefficient of determination). It should also be noted that due to this low accuracy, the use of the method from [24] is not appropriate in this case, as it significantly increases the duration of the application procedure due to quadratic augmentation compared to classical GRNN. However, the improved technology presented in this paper achieved a 33% increase in accuracy based on the coefficient of determination compared to [24,29].
The results indicated the significant practical value of applying improved neural network-based technology without training, which is presented in this paper, particularly for predictive tasks involving the analysis of extremely small datasets. However, in addition to the prediction tasks discussed in this paper, future research prospects should consider adapting and enhancing this technology for classification tasks under limited data volumes. Such tasks are common in the field of biomedical engineering, where rapid diagnosis based on such solutions can provide additional information to physicians needing to make quick and accurate decisions.
The differences between a similar technology for solving classification tasks lie in the following aspects:
- Formation of the final class label value after applying improved technology using ensemble learning principles, specifically majority voting (rather than averaging the result, as performed in this study).
- The principle of response surface linearization, which underpins the improved technology in this paper, can be implemented differently in solving classification tasks. In the first case, one can expand the initial extremely small dataset with the predicted class label value to which the corresponding data vector belongs (similar to this study). In the second, more interesting case, such a process can be implemented using a set of probabilities of belonging to each class, predicted by the specific task. This approach provides the model with more information, especially in cases where more than three classes exist, which can further enhance the accuracy of solving express diagnostic tasks in the analysis of extremely small datasets. This implementation is possible using a Probabilistic Neural Network [11].
These aforementioned directions will form the basis for further scientific research on the development of AI-based Small Data Approaches in different application areas.
6. Conclusions
The domain of biomedical engineering increasingly encounters significant challenges in the intelligent analysis of small datasets. Traditional artificial intelligence tools, including machine learning methods and neural networks, face substantial issues such as overfitting when applied to these limited data scenarios, thereby imposing considerable constraints on their practical application. While data augmentation techniques can alleviate these challenges, they are often accompanied by inherent limitations that diminish their effectiveness.
In this study, we improved neural network-based technology with non-iterative training designed for the prediction of outcomes from extremely small datasets. The proposed technology is based on response surface linearization principles and ensemble learning techniques (but based on only one ANN). The primary steps of the proposed technology involve expanding the dataset with predicted output signals from an initial General Regression Neural Network (GRNN), augmenting the dataset through pairwise concatenation of existing data vectors, creating an augmented temporary data sample for each unknown output vector, utilizing a second GRNN to predict preliminary results, and synthesizing the desired output through ensemble averaging of the predictions and initial data signals from the initial support dataset. The improved technology’s performance was simulated using two distinct datasets and evaluated based on various performance metrics. The results indicate that the improved neural network-based technology achieves a 13% to 33% increase in accuracy, as measured using the coefficient of determination, compared to the baseline method.
These findings underscore the significant practical value of the improved technology presented in this paper, particularly for solving prediction tasks involving the analysis of extremely small datasets. However, beyond the prediction tasks examined in this research, future studies should consider adapting and refining this technology to address classification tasks in contexts with limited data volumes. Such challenges frequently arise in the field of biomedical engineering, where rapid diagnostics based on similar solutions can provide valuable information to physicians who must make quick and accurate decisions. These directions will serve as a foundation for future research aimed at advancing AI-based Small Data Approaches across various application domains.
Author Contributions
Conceptualization, I.I. and R.T.; methodology, I.I.; software, M.F.; validation, I.K., O.B. and M.K.; formal analysis, O.B.; investigation, I.I.; resources, I.I.; data curation, I.I. and M.F.; writing—original draft preparation, I.I. and R.T.; writing—review and editing, I.I. and R.T.; visualization, M.F.; supervision, R.T.; project administration, M.K.; funding acquisition, I.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union (through the EURIZON H2020 project, grant agreement 871072).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in this study are available here: Refs. [9,28].
Acknowledgments
Michal Kovac was supported by the APVV grant No. 21-0448 and received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie COFUND SASPro2 grant agreement No. 2207/02/01.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tranquillo, J.V.; Goldberg, J.; Allen, R. Biomedical Engineering Design; Academic Press Series in Biomedical Engineering; Academic Press: London, UK, 2023; ISBN 978-0-12-816444-0. [Google Scholar]
- Berezsky, O.; Pitsun, O.; Liashchynskyi, P.; Derysh, B.; Batryn, N. Computational Intelligence in Medicine. In Lecture Notes in Data Engineering, Computational Intelligence, and Decision Making; Babichev, S., Lytvynenko, V., Eds.; Lecture Notes on Data Engineering and Communications Technologies; Springer International Publishing: Cham, Switzerland, 2023; Volume 149, pp. 488–510. ISBN 978-3-031-16202-2. [Google Scholar]
- Babichev, S.; Škvor, J. Technique of Gene Expression Profiles Extraction Based on the Complex Use of Clustering and Classification Methods. Diagnostics 2020, 10, 584. [Google Scholar] [CrossRef] [PubMed]
- Bodyanskiy, Y.; Vynokurova, O.; Savvo, V.; Tverdokhlib, T.; Mulesa, P. Hybrid Clustering-Classification Neural Network in the Medical Diagnostics of the Reactive Arthritis. IJISA 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Hekler, E.B.; Klasnja, P.; Chevance, G.; Golaszewski, N.M.; Lewis, D.; Sim, I. Why We Need a Small Data Paradigm. BMC Med. 2019, 17, 133. [Google Scholar] [CrossRef] [PubMed]
- Babichev, S. An Evaluation of the Information Technology of Gene Expression Profiles Processing Stability for Different Levels of Noise Components. Data 2018, 3, 48. [Google Scholar] [CrossRef]
- Voronenko, M.A.; Zhunissova, U.M.; Smailova, S.S.; Lytvynenko, L.N.; Savina, N.B.; Mulesa, P.P.; Lytvynenko, V.I. Using Bayesian Methods in the Task of Modeling the Patients’ Pharmacoresistance Development. IAPGOS 2022, 12, 77–82. [Google Scholar] [CrossRef]
- Huang, S.; Deng, H. Data Analytics: A Small Data Approach, 1st ed.; CRC Press: Boca Raton, FL, USA, 2021; ISBN 978-0-367-60950-4. [Google Scholar]
- Shaikhina, T.; Khovanova, N.A. Handling Limited Datasets with Neural Networks in Medical Applications: A Small-Data Approach. Artif. Intell. Med. 2017, 75, 51–63. [Google Scholar] [CrossRef] [PubMed]
- Izonin, I.; Tkachenko, R. Universal Intraensemble Method Using Nonlinear AI Techniques for Regression Modeling of Small Medical Data Sets. In Cognitive and Soft Computing Techniques for the Analysis of Healthcare Data; Elsevier: Amsterdam, The Netherlands, 2022; pp. 123–150. ISBN 978-0-323-85751-2. [Google Scholar]
- Havryliuk, M.; Hovdysh, N.; Tolstyak, Y.; Chopyak, V.; Kustra, N. Investigation of PNN Optimization Methods to Improve Classification Performance in Transplantation Medicine. In Proceedings of the 6th International Conference on Informatics & Data-Driven Medicine, Bratislava, Slovakia, 17–19 November 2023; pp. 338–345. [Google Scholar]
- Mulesa, O.; Geche, F.; Batyuk, A.; Buchok, V. Development of combined information technology for time series prediction. In Advances in Intelligent Systems and Computing II; Shakhovska, N., Stepashko, V., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 689, pp. 361–373. ISBN 978-3-319-70580-4. [Google Scholar]
- Tolstyak, Y.; Chopyak, V.; Havryliuk, M. An Investigation of the Primary Immunosuppressive Therapy’s Influence on Kidney Transplant Survival at One Month after Transplantation. Transpl. Immunol. 2023, 78, 101832. [Google Scholar] [CrossRef] [PubMed]
- Bodyanskiy, Y.; Chala, O.; Kasatkina, N.; Pliss, I. Modified Generalized Neo-Fuzzy System with Combined Online Fast Learning in Medical Diagnostic Task for Situations of Information Deficit. MBE 2022, 19, 8003–8018. [Google Scholar] [CrossRef] [PubMed]
- Mumuni, A.; Mumuni, F. Data Augmentation: A Comprehensive Survey of Modern Approaches. Array 2022, 16, 100258. [Google Scholar] [CrossRef]
- Snow, D. DeltaPy: A Framework for Tabular Data Augmentation in Python; Social Science Research Network: Rochester, NY, USA, 2020. [Google Scholar]
- Deep Learning for Tabular Data Augmentation. Available online: https://lschmiddey.github.io/fastpages_/2021/04/10/DeepLearning_TabularDataAugmentation.html (accessed on 16 May 2021).
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling tabular data using conditional GAN. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada, 8–14 December 2019. [Google Scholar]
- Izonin, I.; Tkachenko, R.; Pidkostelnyi, R.; Pavliuk, O.; Khavalko, V.; Batyuk, A. Experimental Evaluation of the Effectiveness of ANN-Based Numerical Data Augmentation Methods for Diagnostics Tasks. In Proceedings of the 4th International Conference on Informatics & Data-Driven Medicine, CEUR Workshop Proceedings 2021, 3038, Valencia, Spain, 19–21 November 2021; pp. 223–232. [Google Scholar]
- Pima Indians Diabetes Database. Available online: https://kaggle.com/uciml/pima-indians-diabetes-database (accessed on 16 May 2021).
- Arora, A.; Shoeibi, N.; Sati, V.; González-Briones, A.; Chamoso, P.; Corchado, E. Data Augmentation Using Gaussian Mixture Model on CSV Files. In Proceedings of the Distributed Computing and Artificial Intelligence, 17th International Conference, L’Aquila, Italy, 17–19 June 2020; Springer: Cham, Switzerland, 2020; pp. 258–265. [Google Scholar]
- Guilhaumon, C.; Hascoët, N.; Chinesta, F.; Lavarde, M.; Daim, F. Data Augmentation for Regression Machine Learning Problems in High Dimensions. Computation 2024, 12, 24. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R.; Vitynskyi, P.; Zub, K.; Tkachenko, P.; Dronyuk, I. Stacking-Based GRNN-SGTM Ensemble Model for Prediction Tasks. In Proceedings of the 2020 International Conference on Decision Aid Sciences and Application (DASA), Sakheer, Bahrain, 8–9 November 2020; pp. 326–330. [Google Scholar]
- Izonin, I.; Tkachenko, R.; Gregus, M.M.; Zub, K.; Tkachenko, P. A GRNN-Based Approach towards Prediction from Small Datasets in Medical Application. Procedia Comput. Sci. 2021, 184, 242–249. [Google Scholar] [CrossRef]
- Bodyanskiy, Y.V.; Deineko, A.O.; Kutsenko, Y.V. On-Line Kernel Clustering Based on the General Regression Neural Network and T. Kohonen’s Self-Organizing Map. Autom. Control. Comput. Sci. 2017, 51, 55–62. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, Y.; Zhu, J. Application of Generalized Regression Neural Network Optimized by Fruit Fly Optimization Algorithm for Fracture Toughness in a Pearlitic Steel. Eng. Fract. Mech. 2020, 235, 107105. [Google Scholar] [CrossRef]
- Bani-Hani, D.; Khasawneh, M. A Recursive General Regression Neural Network (R-GRNN) Oracle for Classification Problems. Expert Syst. Appl. 2019, 135, 273–286. [Google Scholar] [CrossRef]
- Body Fat Percentage of Women. Available online: https://www.kaggle.com/datasets/vishweshsalodkar/body-fat-percentage (accessed on 23 July 2023).
- Specht, D.F. A General Regression Neural Network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).