Abstract
Code conversion, encompassing translation, optimization, and generation, is becoming increasingly critical in information systems and the software industry. Traditional validation methods, such as test cases and code coverage metrics, often fail to ensure the correctness, completeness, and equivalence of converted code to its original form. Formal verification emerges as a crucial methodology to address these limitations. Although numerous surveys have explored formal verification in various contexts, a significant research gap exists in pinpointing appropriate formal verification approaches to code conversion tasks. This paper provides a detailed survey of formal verification techniques applicable to code conversion. This survey identifies the strengths and limitations of contemporary adopted approaches while outlining a trajectory for future research, emphasizing the need for automated and scalable verification tools. The novel categorization of formal verification methods provided in this paper serves as a foundational guide for researchers seeking to enhance the reliability of code conversion processes.
1. Introduction
Code conversion, which encompasses code transformation, translation, and generation, is becoming crucial in the software and technological industry. Code conversion refers to the process of modifying, translating, or generating code to ensure compatibility, efficiency, and performance across different programming environments. Code transformation or optimization is essential for enhancing the efficiency and performance of programs through techniques like parallelization and code refactoring. This is crucial not only for execution speed but also for the reliability and maintainability of enterprise systems. Translating code from one high-level language to another is useful for migrating software systems from old, poorly performing languages to new, memory-efficient, and modern languages. It is also beneficial for translating an application from one platform to another. Model-based code generation automates the creation of system code from high-level models, significantly speeding up the development process and reducing human error. Trans-compilers [,,,,,,,], large language models LLMs [,,,,,,,], and model-based code generation [,,] are some of the approaches used in the domain of code conversion.
Functional validation with test cases, like functional testing, is one of the ways to validate code conversion. Functional validation ensures that the software performs its intended functions as specified in the development documentation or user requirements by using test cases to compare outputs from different code versions. However, it only concludes that, for a certain test case, the code and its model or unoptimized version have the same output. This might be biased according to the selection of the test cases []. On the other hand, tools like BLEU [] and CODE BLEU [] compare the generated code with a reference code and produce a score that represents how much the generated code syntactically matches its reference. There is no guarantee that the generated code is semantically correct since the reference code is also human-generated [,].
Functional validation and comparison with reference translations are not enough to address the challenges of code conversion verification. Code conversion faces numerous challenges that underscore the necessity of robust validation and verification techniques. Code optimization often grapples with the complexity of maintaining semantic equivalence while optimizing code, especially in systems that are highly reliant on concurrent processes []. Code translation requires syntactic adaptations, but it also demands a deep semantic understanding to preserve functional behaviors across language barriers. The different structures and natures of different programming languages make this task very challenging since some languages are weakly typed, like JavaScript and Python, and others are strongly typed, like Java, Swift, and C++ []. Lastly, code generation from high-level models introduces another layer of complexity, as it requires the generated code to be syntactically and semantically correct and adhere to the verified original model and its specifications [,,]. These challenges highlight the critical need for advanced verification methods, such as formal verification, to ensure that the converted code adheres rigorously to its intended functionality and performance criteria. Moreover, with the increasing use of large language models (LLMs) for code translation and generation, formal verification becomes crucial to ensure the integrity of output code. Since LLMs can sometimes generate misleading or incorrect code—often referred to as “hallucinations”—formal verification is essential to confirm that the neural-based generated code is syntactically correct and strictly adheres to the specified functional and security requirements.
Formal verification is the process of verifying that a system follows certain specifications. Formal verification is needed to guarantee code translation and generation correctness. For instance, a typical application of formal verification in code conversion can be observed in the verification of a code optimizer or code translator. The formal verification process involves defining a formal specification for the input and output codes, like security specification; for example, variable x must be less than y for all cases. Then, the verification ensures that the output code symbolically adheres to these specifications; i.e., for any possible input to this code, the specifications are still satisfied in the optimized or translated version of the code. Another way to conduct verification would be to express the input and output codes in a formal representation like first-order logic, Hoare logic (higher-order logic) [,], or state machine representation. Then, these formal representations are proved to be equivalent and to adhere to the same specifications using theorem provers, bisimulation, and/or the alignment of state machines [,].
This is particularly crucial in the aerospace, automotive, healthcare, and finance industries, where software failures can result in catastrophic outcomes or significant financial and reputational damage. For instance, in the aerospace industry [], ensuring that control software translated from one language to another or optimized maintains exact execution behaviors in all cases is vital to avoid failures that could endanger lives. Moreover, the increasing use of Internet of Things (IoT) devices and smart infrastructure necessitates rigorous formal verification [] to ensure that the autonomous, real-time interactions of these systems are defect-free after code conversion. In the automotive industry, formal verification is used to validate software that controls safety-critical functions such as braking and steering systems, ensuring compliance with stringent safety standards like ISO 26262 []. In the context of mobile application translation, there is a need for a verified tool that can convert an application from one language to another, preserving the application’s specifications and user interface across different platforms []. In the hardware industry, companies like Intel and ARM have long relied on formal techniques to verify the correctness of processors and chips, using tools like model checkers and SMT solvers to prove the properties of their designs [].
Formal verification can guarantee converted code’s correctness, completeness, and equivalence to its original. Correctness means the generated code is syntactically correct in terms of the grammar rules of the target language. Completeness means it is semantically complete; if the input or source performs three functions, for example, the output code also performs three functions. Equivalence means the output code is functionally equivalent to the input code; i.e., for any input variable that is processed via the input code and that gives an output, the same output should eventually be reached whenever the same input variable is given to the generated code.
Our main motivation for this survey was to find a suitable approach to formally verifying code translation and code translators from one language to another. Previous work by some of the authors of this survey included the trans-compiler-based translation of mobile application code from one high-level language to another [,,]. Therefore, we are interested in exploring the approaches to formally verifying code translation. Since code optimization and code generation are closely related to code translation, we included these forms of code conversion in our survey. Current formal verification surveys categorize formal verification according to the type of software being verified. Various surveys exist on formally verifying software-defined networks [,,], safety-critical systems [,,], smart contracts [,,], and model transformations [,,,]. However, there is a lack of recent overviews on the formal verification of code conversion. Therefore, in addition to our research interest in formal code translation verification, this survey fills the gap in code conversion verification surveys.
The main contribution of this survey is that it categorizes formal verification approaches from two perspectives: (1) the form of code conversion and whether it entails code optimization or translation from one language to another or one model-to-code generation and (2) the approach to verification, namely whether it depends on theorem proving, equivalence checking, assertions, or model checking. The categorization offered here is the first one to categorize formal verification approaches used for code conversions. This survey highlights the strengths and limitations of these approaches. In addition, it focuses on highlighting which methods can be used for code translation tasks specifically since it is our main research interest and one of the rarely formally verified code conversions. This survey paper is organized as follows: Section 2 presents an overview of the relevant research and the topics researched through earlier surveys in the field of the formal verification of software in general. Section 3 presents the methodology of this survey and how we collected the research related to code conversion. Section 4 categorizes code conversions into three main categories based on the source and generated code, with each category further divided into subcategories according to the formal verification approach. Section 5 elaborates on the strengths and limitations of the identified approaches. Finally, Section 6 presents the conclusion and lists the directions for future research.
2. Related Work
The literature most pertinent to our survey is systematic literature reviews on the formal verification of model transformations [,,,]. Model transformation is a process used in software engineering and systems engineering to convert one model into another. It is a key technique in model-driven engineering (MDE) and model-driven architecture (MDA) approaches, where abstract models are systematically transformed into more concrete models or implementation-specific code. These reviews critically assess methods to ensure that transformations of models preserve intended behaviors without introducing errors. Model transformations are a broad category encompassing all types of software models, with model-to-code conversion being one subset. Despite their relevance, these reviews typically cover a wide range of transformation types, like translating from one UML view to another UML or translating a UML model to a Petri net graph.These surveys rarely focus exclusively on code conversion. Furthermore, the most recent reviews in this area are more than five years old, suggesting a gap in the current literature concerning up-to-date verification techniques and their evolution in the context of recent technological advancements in code conversion.
Other surveys on formal verification have predominantly focused on general software systems [,] or specific applications such as software-defined networks (SDNs) [,,], security systems [,,], and smart contracts [,,]. These surveys have provided comprehensive insights into various verification techniques and their applicability across different software architectures and domains. However, they often do not address the unique challenges and methodologies associated with code conversion tasks, including translation, transformation, and generation.
The survey in this paper aims to fill this gap by focusing on formal verification techniques applicable to code conversions. By focusing on this narrower field, we provide a detailed exploration of the state-of-the-art methods for verifying the correctness, completeness, and equivalence of converted code to its original state, which is increasingly critical in today’s software development landscape. This focus allows for a deeper understanding of the specific challenges and solutions in code conversion verification, distinguishing our work from broader surveys and outdated reviews.
3. Methodology
The target of this survey is to present the formal verification approaches used in code conversion and their different forms. The perspective of the survey contains two main research points: (1) surveying the current formal verification methods applied to the different code conversions, and (2) highlighting the suitable formal verification methods that can be used for code translation. We are specifically interested in the category of code-to-code translation to explore approaches that could be applied to our previous research in code translation using trans-compilers [,,]. In addition, code translation is the most challenging code conversion form to be formally verified. This is due to the different forms of code structure for the source and target language. It is difficult to formally represent a program written in two different languages with the same formal representation to verify their equivalence. On the other hand, verifying a code translator is also challenging. It requires the availability of the translator model and the feasibility of describing it formally to be verified or proved correct.
The literature review followed a structured approach, guided by Preferred Reporting Items for Systematic Reviews and Meta-analysis Protocols (PRISMA) [] and principles outlined in ”Empirical Research in Software Engineering” by Malhotra []. We initiated our search by identifying relevant databases, including Google Scholar, Scopus, and ACM Digital Library, ensuring a comprehensive coverage of scholarly articles. Our search strategy involved the use of multiple search strings tailored to uncover articles addressing the formal verification of code conversions. These search strings included: “formal verification of code translation or Conversion”, “Equivalence checking of code transformation or translation”, “model and code equivalence verification”, and “model-based code generation verification”.
The search was restricted to the most recent decade (2014–2024) to focus on contemporary approaches and advancements. Filters applied during the searches included setting the publication year range from 2014 to 2024, selecting only documents written in English, and prioritizing articles based on relevance. This temporal limitation to the last decade ensures relevance, as the field of code conversion has undergone significant and rapid changes due to technological advancements, making older studies potentially outdated in terms of the technologies and methodologies they cover. The last search update was conducted on 10 June 2024. An example of a search process conducted used the Google Scholar library with the search string ”formal verification of code translation” and the most relevant filter checked, with year limits of 2014 to 2024 and in the English language.
Inclusion criteria were defined to select studies that specifically focus on the formal verification of code converters published in respected academic venues within the specified date range. We excluded any works published before 2014, dissertations, and studies not related to computer science or written in languages other than English. While the main focus was on recent studies, seminal works predating 2014 were occasionally cited to provide historical context or foundational knowledge. Subsequently, we performed a manual selection based on reading the title and abstract to check their relevance to our topic. References that included the formal verification process and methodology of code conversion were selected. The reference had to include the code verification of a software program. For example, references that focused on the verification of software requirements specifications or model-to-model verification were excluded, as they were out of the scope of this review. References that focused on code validation using conventional software testing were also excluded, as they are not considered to use formal verification. The number of initially collected articles resulting from the manual screening process was 82. Then, we applied the relevance selection criteria and qualitative assessment of the references mentioned previously. The total number of articles, after these filters were applied, was 31. Figure 1. displays a chart of the main categories and subcategories that are explained in the survey. We used Microsoft Excel tables to document the sources included, their categorization, and the year of publication. These tables were later used to chart the results.
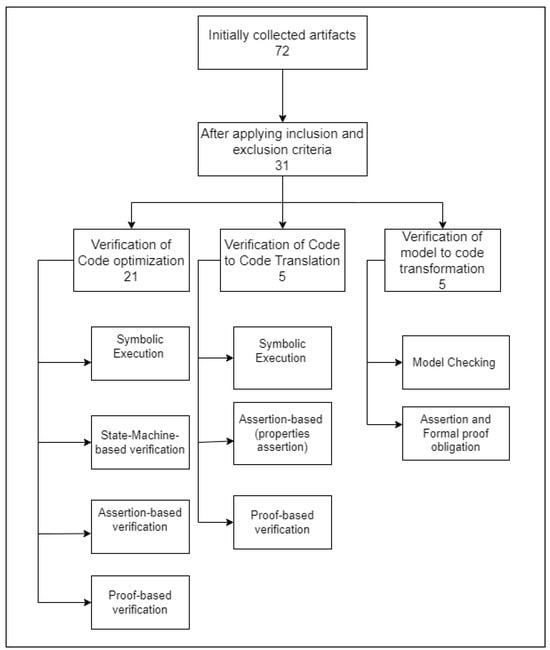
Figure 1.
Survey flow diagram with the number of sources in each stage and categorization of code conversion showing verification approaches applied in each category.
Since we focused on code conversion problems, we categorized the survey according to the form of code conversion that was being verified. In each category, we identified the different methods of formal verification applied. We identified three main forms of code conversion. The three categories are presented in Section 4, with the formal verification methods used for each included as subsections. The formal verification approaches identified in this survey reflect our perspective on categorizing formal verification methods and approaches in the context of code conversion. Each article surveyed was first identified under one of the three main categories of code conversion (optimization, translation, or model-to-code generation). Afterward, the type of formal verification applied was identified and categorized. If the method identified was new, then a new category was created since this paper also describes a categorization of the previous work done in the formal verification of code conversion. The advantages and disadvantages of the method used were also extracted from the article and used for the current study’s qualitative assessment. In the synthesis of results, the articles that used similar methodologies were grouped under the same category of formal verification in the tables that we used in summarizing. From these tables, we extracted charts that illustrate the yearly percentage distribution of each method.
4. Formal Verification Categories for Different Forms of Code Conversion
This section explains the formal verification methods applied to different categories of code conversion. The three main categories or forms of code conversion according to the source and destination are (1) code transformation or optimization, (2) code-to-code translation, and (3) code generation or model-to-code conversion.
4.1. Formal Verification of Code Optimization
This category includes formal verification approaches applied to code transformation that involve conversion between different forms of the same program, preserving the same programming language. For example, code optimization, parallelization, or vectorization are all applications of transforming code from one version to another or to an extended version with the same high-level language.
4.1.1. Symbolic Execution for Equivalence Checking
Symbolic execution is a method for exhaustively exploring the execution paths of a program where inputs are not assigned specific values. Instead, they are treated as symbols representing a range of possible values. An SMT (satisfiable modulo theory) solver checks the feasibility of each value through an exploration of all execution paths for a given predicate. This process is repeated to cover all possible program behaviors, ensuring a thorough exploration of all execution paths. Finally, the predicate is satisfied. In the other case, the predicate is not satisfied, and the solver provides a counter-example that violates the predicate, as shown in Figure 2.
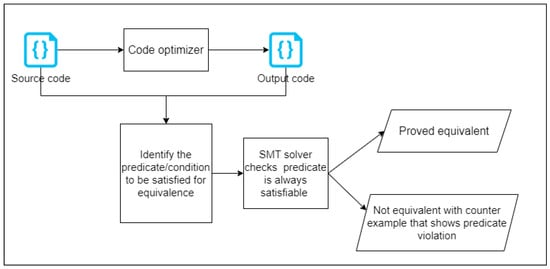
Figure 2.
The general flow of symbolic execution and theorem proving for proving equivalence between source and optimized code.
One of the most powerful and most used SMT solvers is Z3. Z3 is an efficient SMT solver that is freely available via Microsoft Research, and it can be used in various software verification and analysis applications []. To use the Z3 SMT solver for equivalence checking, input code and converted code can be expressed in first-order logic (FOL); then, Z3 would check for all cases to ensure that FOL expressions of input and converted code are equivalent. For example, for a simple multiply-by-two function and its equivalent version by shifting one bit , the Z3 solver will prove that all possible integer values of are equivalent to using the following predicate: . This simple illustrative example was implemented using the Python Z3 library, as shown in Figure 3 where the asterisk sign denotes multiply in Python language. The output of this run will be “The functions are equivalent for all integer values of x”. If we change the multiply-by-two, for example, in , to be three, the output will be “The functions are not equivalent”, and it will also print a random counter-example, which is any integer value in this case.

Figure 3.
Z3 SMT solver example to check equivalence between two functions.
Felsing et al. [] and Gupta et al. [] indicated that SMT solvers play a crucial role in program equivalence checking by providing a robust framework for discharging proof obligations, inferring invariants, handling complex transformations, generating counter-examples, and efficiently-processing queries. The symbolic execution approach can be reported later as a merged step with the other approaches. However, in this section, we list the verification approaches that strictly require symbolic execution.
The research completed by Sugawara et al. [] combines symbolic checking with a numerical evaluation to perform equivalence checking for code transformations. The check is performed using the Xevolver code transformation tool []; the check is conducted on the code transformation rules defined by the Fortran language to check the equivalence of C/C++ codes. The equivalence check is performed with the assistance of the CIVL (Concurrency Intermediate Verification Language) tool [] for equivalence checking using symbolic execution.
CIVL is a program-checking tool that supports multiple parallel execution environments, such as OpenMP and CUDA. It can identify various bugs, such as deadlocks, memory leaks, and division by zero. For equivalence checking, the input variables of the code are given the $input keyword. CIVL treats these variables as symbolic values. Also, the output variable is annotated using the $output keyword. This keyword directs CIVL to symbolically check whether the two codes generate the same value for the output variable. Listing 1 shows the original code and Listing 2 shows the transformed code to be verified through CIVL. Then, the command “civl compare”, shown in Figure 4, verifies whether both codes generate the same output value for the output variable. The results of checking program equivalence for two equivalent codes are indicated as “The standard properties hold for all executions”.
| Listing 1. civil_test_orig.c. |
 |
| Listing 2. civil_test_trans.c. |
 |

Figure 4.
Result of applying CIVL using the Z3 solver and symbolic execution. This figure was extracted from Figure 4 in [].
CIVL uses the Z3 SMT solver for the properties check. The proposed approach enhanced the use of CIVL by adding notations for programmers to specify the inputs and outputs of a code pattern to be transformed. The approach was evaluated using various optimization rules, demonstrating its capability to cover a wider range of application codes. However, this approach is not without hurdles, such as the need for more user-provided information and the time-consuming nature of the numerical comparison.
Kolesar et al. [] used symbolic execution with Coinduction for the equivalence checking of Haskell programs. Haskell is a functional programming language known for its strong static typing, immutability, and lazy evaluation. Coinduction is a proof technique for deriving conclusions about infinite data structures from cyclic patterns in their behavior []. It relies on proving that an object upholds a property and then deconstructs the object to show that each of its parts satisfies the same property. Coinduction uses a bisimulation to prove two states’ equivalence. The states are formal representations of two programs. A bisimulation is a relation between states in which two states are related only if they are still related after being reduced. The limitation of the used approach is that it poorly functions with code involving finite input only.
Symbolic execution was used by Badihi et al. [] in an approach named ARDiff for improving the scalability of symbolic-execution-based equivalence-checking techniques when comparing syntactically similar versions of a program. This is typically achieved through proof by contradiction, meaning that the predicate given to the SMT solver states that two versions, m and m’, of a function are not equivalent: . If the SMT solver finds this predicate unsatisfied (UNSAT), this means there exists no input that can make these two functions not equivalent, meaning that they are equivalent. Their approach relies on a set of novel heuristics to determine which parts of the versions’ common code can be effectively pruned during the equivalence analysis. Their results on Java program optimization demonstrate that ARDiff provides a substantial advancement, offering a more scalable, efficient, and effective approach than previously available methods. However, the scalability challenges were not completely eliminated. Large code bases or deeply nested loops remain a concern. In addition, the iterative process of refinement and abstraction can become computationally expensive as the size and complexity of the code increases.
While symbolic execution is widely used in equivalence checking for code transformation, it faces the challenges of scalability and dealing with complex code like nested loops, for which the SMT solver tries to iterate over the entire natural numbers. These limitations can lead to longer solving times or “unknown” results, requiring careful interpretation. However, it is a promising approach due to the technological improvements of SMT solvers, on which symbolic execution depends. There are now APIs and libraries for Z3 solvers that make them more user-friendly for developers.
4.1.2. State-Machine-Based Equivalence Checking
This approach depends on the graphical and mathematical representation of code in the form of states and data paths. In this approach, we can find the usage of state machines, control flow graphs, and data paths to prove the equivalence of two programs. State-machine-based equivalence checking is sometimes used with symbolic analysis, which is similar to the symbolic execution explained in the previous approach. However, we classify the use of the state-machine representation of code structure as a separate approach since it is widely used in code optimization verification. In addition, state machines are not exclusively used for symbolic execution. After the graphical representation of both source and target code is generated, usually, a sort of alignment is applied to both graphs, in addition to variables checking, for the SMT solver or input/output compatibility check, as shown in Figure 5. Further elaboration on each method is provided in the following paragraphs.
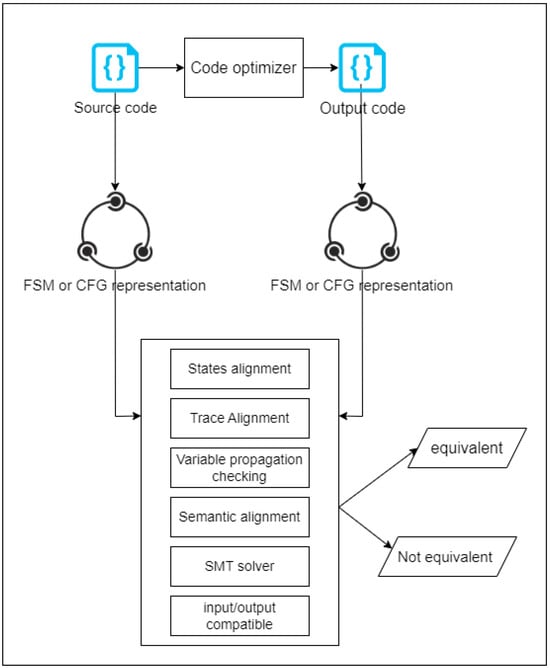
Figure 5.
The general flow of state-machine-based equivalence checking for the formal verification of code optimization.
A finite state machine with a data path (FSMD) and variable propagation (VP) is one of the approaches used in equivalence checking. The work done in [,] used FSMDs to ensure code equivalence between a C code and its optimized version. Banerjee et al. [] and Chouksey et al. [] specifically deal with invariant code motion, in which certain pieces of code can be moved outside the boundaries of a loop without affecting the code’s functionality. An example of the motion of the loop invariant is shown in Listings 3 and 4. The FSMDs of both codes before and after optimization are shown in Figure 6.
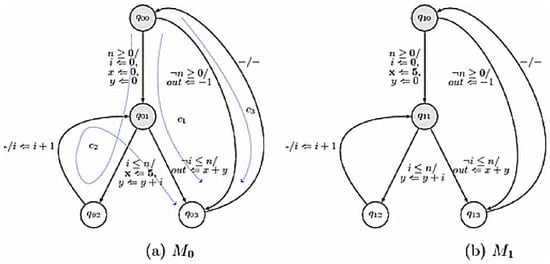
Figure 6.
The FSMDs of behaviors before and after the motion of loop invariant [].
This loop-invariant motion aims to produce faster code. The equivalence check is performed through three algorithms in which the states and paths of the FSMD are checked. In addition, the variable propagation vector is checked along with the path checker to ensure code equivalence. Again, in reference [], Banerjee et al. used the same method for FSMDs with VP to ensure code equivalence in compiler-based code transformation. The limitation reported for this method is that it cannot handle arrays containing other arrays in their subscripts.
More recent work by Hu et al. [] used the FSMD approach with the deep state sequence (DSS) strategy. DSS is symbolically simulated and converted into a static single-assignment (SSA) form. SMT (satisfiable modulo theory) formulas are generated from the SSA expressions and solved using the Z3 SMT solver to check for equivalence. An SMT solver checks the feasibility of each value based on the accumulated conditions. The tool’s ability to handle complex transformations, such as code motion across loops, and its use of deep state sequences and SMT solving make it a robust solution for ensuring the correctness of compiler optimizations. However, the tool faces scalability limitations due to the potentially large number of DSSs generated, suggesting that future work could focus on optimizing path generation.
| Listing 3. Original code before moving loop invariant. |
 |
| Listing 4. Code after moving loop invariant. |
 |
The research conducted by Pouchet et al. [] used computation-directed acyclic graphs (CDAGs) as a representation of two C/C++ programs, Pa and Pb. Every variable in the program that can be concretely evaluated, that is, expressions such as + j, are replaced with their result during CDAG interpretation, yielding values of 0, 1, …, which are used to identify the memory cells being addressed via the program. Pouchet et al. [] computed the equivalence between Pa and Pb by checking, cell by cell, whether the CDAGs were fully isomorphic. If so, the programs were proved to be equivalent. The approach is used to prove equivalence between two versions of C/C++ programs. The programs are specific for high-level synthesis (HLS) programs. HLS facilitates the description of complex hardware implementations. The approach used was novel and robust, but it required detailed knowledge of the transformations applied. This dependency on comprehensive understanding and the accurate modeling of transformations may pose challenges for users not deeply familiar with the specific HLS optimizations and their implications.
Semantic program alignment was used in [] for equivalence checking between the C program code and its vectorized or optimized version. Those authors introduced a technique for constructing product programs driven by semantics, rather than syntax, with trace alignment. The technique requires as input a set of test cases, . Churchill et al. executed the programs Pa and Pb on each test case to obtain traces. Then, the alignment predicate, , was guessed over pairs of machine states from Pa and Pb that would help align traces of Pa and Pb. The alignment predicate involved the variables of the program and the property they should hold. From the traces alignment, they obtained a program alignment automaton (PAA) that overapproximated the behaviors of both programs. If this PAA, with the aligned states it has, achieves consistent propagation and can always reach an acceptance state for all paths, then the codes are proved to be equivalent. The limitations of this approach arise when the program transformation includes reordering an unbounded number of memory writes, such as in loop splitting or loop fusion. It also fails when the control flow of programs depends on unbounded input, i.e., the number of loops in one program version becomes equivalent to a different number of loops in the equivalent version.
Similar to [], the work done in [] by Goyal et al. used the same product program technique. However, since it is difficult to obtain trace alignment, the authors introduced a predicate-guided semantic program alignment instead. The limitation of this approach is that, depending on the predicate, alignment might not be feasible in some cases. As stated in Goyal et al.’s research, their future work might include discarding states, transitions, and predicates that do not lead to an efficient alignment of an automaton.
In the same context of semantic equivalence, Malik et al. [] introduced the DIFFKEMP tool, which seeks to ensure equivalence checking for different versions of Linux kernels. The authors’ goal was to achieve a lightweight and scalable approach towards equivalence checking based on semantic-preserving change patterns (SPCPs). These patterns are used to identify and handle changes at a granular level. Functions under comparison are represented using control flow graphs (CFGs), leveraging the LLVM Intermediate Representation (LLVM IR) []. LLVM is a collection of modular and reusable compiler and toolchain technologies. This representation allows the tool to handle a function as a single CFG, facilitating a more straightforward comparison between source and target functions to be proved equivalent. The main idea is to find so-called synchronization points in both functions and to check that the code between pairs of corresponding synchronization points is semantically equal. Semantically equal means that the input–output at each synchronization point is the same for both functions. DIFFKEMP offers a highly scalable and practical approach to checking semantic equivalence in large-scale C projects. However, its limitations in handling very complex refactorings, indirect function calls, inline assembly, and the potential for false results highlight the need for complementary approaches or further enhancements to improve its completeness and correctness.
Other authors’ research, such as that of Bandopadhyay et al. [,,], depended on PRES+ models (Petri net-based representation of embedded systems) in addition to the more recent work, by the same authors, in [] that used CPN (colored Petri net), which is also a class of Petri net models. These models encompass data processing used to model parallel behaviors in a state machine-like structure. They used this model to compare code versus parallelized versions of the same C code. The equivalence between two CPN models is proven if they are input/output-compatible; that is, there is a bijection between their in-ports and out-ports. The major limitation of these models is that they cannot handle array-handling programs; therefore, several loop transformations, such as loop merging, loop distribution, etc., cannot be validated through this method, in which case the tool also fails to validate loop-shifting transformations.
The limitation of state machines and control flow graphs for equivalence checking arises when automata alignment is not possible. This might occur for several different reasons, depending on the approach used, for example, if the code being checked involves nested array structures, loop shifting and/or transformation, unbounded memory writes, or loops depending on unbounded inputs. However, the verification approach using state machines and control flow graphs is considered suitable for code transformation in which the source and destination languages are similar. Expressing codes that have a similar language structure using state machines can be flexible and feasible.
4.1.3. Assertion-Based Equivalence Checking
Assertion-based equivalence depends on the functional equivalence between code versions. The assertion is made on the input–output of the codes in the form of a formal predicate to be asserted. We do not consider assertion a form of validation. On the contrary, it is a formal verification since it asserts formal predicates and properties and not simply test cases. The general flow of assertion-based equivalence is shown in Figure 7.
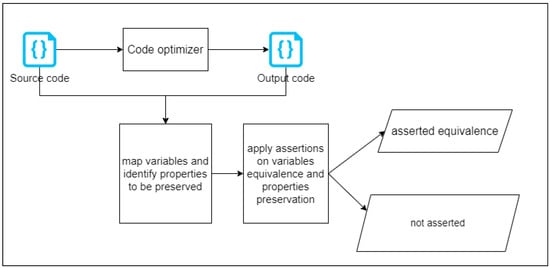
Figure 7.
The general flow of assertion-based equivalence checking.
In the context of code parallelization, Abadi et al. [] used assertion-based equivalence. The authors aimed to formally verify the equivalence between sequential and parallelized versions of C/C++ code. Suppose that is the set of variables of the source code and that is the set of variables of the output or optimized code. Then, comparing the output values is implemented as a series of assertions for each pair of matched variables: . The equivalence of variables is determined with symbolic analysis and not certain test cases. In a way, it is very similar to symbolic execution, but it uses assertions of variables without SMT solvers. Similarly, the work done in [] by Jakobs et al. performed localized equivalence checking between sequential and parallelized versions of C code using assertions. The authors introduced a tool called PEQCHECK that generates verification tasks. These verification tasks include only live variables, which helps in reducing the complexity of equivalence checking. Then, they use assertions to ensure that the outputs of the sequential and parallel code segments are equivalent. The same authors of PEQCHECK introduced another tool, the PaTech (pattern-based equivalence check) tool []. They used a similar approach to [], though specific to parallel design patterns. They divided the equivalence checking task into smaller sub-tasks based on these patterns and achieved better results compared to the first tool.
In general, assertion-based equivalence checking is very similar to symbolic execution. However, it requires certain assertions and variables to be symbolically checked and proved equivalent. Usually, these variables represent the inputs and outputs of code. This approach might face the same limitations as symbolic execution, like scalability and difficulty in dealing with complex code.
4.1.4. Proof-Based Verification (Optimizer Verification)
Proof-based verification or theorem proving is one of the approaches used to verify the correct behavior of a system, i.e., that a system conforms to its specifications. We surveyed code optimization verification, and compiler optimization verification is indeed one of the most important categories in verifying code optimization. Compiler optimization verification is performed by formally expressing a compiler in Hoare logic (higher-order logic) or logical predicates and proving the correctness of this logic. This verification is considered to have been completed once and for all, as the verification is performed on the code converter itself, as shown in Figure 8, unlike equivalence checking, which must be conducted for each translation.
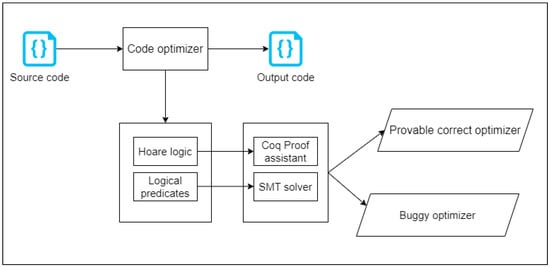
Figure 8.
The general flow of proof-based code optimizer verification.
Gourdin et al. [] discussed the extension of translation validation techniques within the CompCert compiler [,], the first formally verified realistic compiler. Compcert was verified using Coq proof assistant and Hoare logic (higher-order logic). Coq is a proof assistant for a logical framework known as the Calculus of Inductive Constructions. It allows for the interactive construction of formal proofs, as well as the manipulation of functional programs consistently with their specifications. The extension introduced in [] supported a broader range of optimizations to RTL (Register Transfer Language) code. A new intermediate representation (IR), called Block Transfer Language (BTL), was introduced, which was specifically designed to facilitate the formal verification of the inter-block transformations of a compiler. This representation, alongside a symbolic simulation validator, allows for the verification of more complex transformations between blocks of code.
The work presented in [] designed and developed a logic and a proof checker for reasoning about LLVM optimizations called Extensible Relational Hoare Logic (ERHL) using the proof assistant Coq to formally verify the LLVM compiler. Alive [] is one of the formally verified compiler optimizers for LLVM. Unlike CompCert, Alive depends on an SMT solver instead of Coq proof and a Hoare-logic representation of the compiler. Alive’s idea is based on representing compiler optimization logic with a domain-specific language (DSL). Lopes et al. [] defined the general constraints that should be satisfied for each optimization transformation done via the compiler. These constraints are applied to the SMT solver and are either satisfied or unsatisfied (UNSAT), and a counterexample is produced. Alive succeeded in representing certain kinds of optimizations, but it was not used for complex optimizations. It appears that it is more challenging to translate the implementation of complex optimizations using this method.
Compiler verification through theorem proving is the only identified optimizer verification approach in this survey for the category of code optimization. The reliance on formal proofs, while beneficial for the correctness of any transformation or optimization, also means that any new optimization strategies require corresponding updates to the formal models and proofs. Table 1 shows a summary of the code transformation verification approaches that were discussed in this section.

Table 1.
Summary of code optimization formal verification approaches.
4.2. Formal Verification of Code-to-Code Translation
This category involves formally verifying the code equivalence between two different source and target programming languages. The target is not necessarily a high-level language; sometimes, the translation switches from a high-level to intermediate or low-level language. Code translation is now used in many applications like cross-platform mobile application development, porting old code bases to new frameworks, or high-level (but slow) languages to low-level (and fast) ones. In the following subsections, we discuss the formal verification methods of code-to-code translation that involves porting code from one programming language to another.
4.2.1. Symbolic Execution for Equivalence Checking
Symbolic execution with animation representation was used in [] by Sneed et al. to prove the equivalence between COBOL and Java code. The core idea is to compare the symbolic execution paths of the COBOL code and the converted Java code. This comparison aims to ensure that, despite the potential static reordering of statements due to the conversion process, the dynamic execution sequence remains unchanged, thus preserving functional equivalence. Both the original and translated codes are animated through control flow sequence and symbolic execution, allowing a step-by-step comparison of execution paths. In this paper, this approach was not considered state-machine-based equivalence since it did not include any formal representation of nodes and transitions. Instead, paths traversed during the symbolic execution were documented and compared. Differing from the symbolic execution used in code equivalence checking after optimization, Sneed et al. [] did not use SMT solvers to check all possible paths. Instead, they performed manual checks of the aligned paths between original and translated codes.
4.2.2. Assertions (K-Safety Property-Based Translation Verification)
Interesting work was conducted by Eniser et al. [] to validate large language models (LLMs) used in code-to-code translation. The models translate between Java, C++, and Python codes. The methodology depended on specifying the k-safety properties that the translator should cover, ranging from syntactic to semantic properties. For example, the number of loops in the output code should be the same as in the input code, which is syntactic. On the other hand, the return values of a function in the input code should be the same for the function in the output code, which is purely semantic. In addition, this study presented a property-driven search process designed to enhance the model output based on the number of violated properties. The authors intended to extend this concept to various facets of the model in order to enforce quality criteria on the model output. Properties are used to test the equivalence of code-to-code translation through asserting. Based on the properties’ specification, test-case generation is performed, which asserts the properties’ coverage. Although it can be considered validation and not formal verification, relying on property preservation can be considered an assertion-based verification approach, according to the categorization presented in our paper.
4.2.3. Proof-Based (Translator Verification)
In this subsection, we present the work conducted on translator verification. The translator is represented in Hoare logic. Then, a proof assistant is used to prove the correctness of this logic. For compiler-based translators, the compiler is formally proved correct via formal proof assistants.
When investigating formal verification of compilers as code translators, most of the work was conducted decades ago [,,,]. Compiler verification was recently tackled in [], where Krijnen et al. introduced a novel architecture for a translation certifier based on translation relations. The approach is implemented in Coq, and it targets the translation from a high-level smart contract language (Plutus Intermediate Representation, PIR) to a low-level execution environment (Plutus Core, PLC). Each compiler translation step from PIR to PLC is modeled as a pure function that translates one abstract syntax tree (AST) into another. The Coq proof assistant is used to generate proof objects (translation certificates) that validate these translations by ensuring that they preserve the intended program semantics. The use of translation relations allows the verification process to be broken down into smaller, manageable parts corresponding to each translation step in the compilation process. However, the approach might be complex and time-consuming. Proofs written using such Coq’s tactics quickly become slow for large terms.
A formal verification of just-in-time compilers, JITs, was presented in recent works like [,]. Brown et al. [] focused on JavaScript JIT verification for certain compiler optimization. The latest work done by Barri et al. [] presents FM-JIT that used a free monad formalism in the Coq proof assistant. A free monad is a construction in category theory used extensively in functional programming and type theory to represent and manage computational effects in a purely functional way. In the context of the Coq proof assistant, free monads provide a flexible framework to formally model and verify various aspects of program behavior and conversion. The verification process involves proving the equivalence between the source program and the output program, ensuring that the compiled program’s behavior matches its source program’s behavior. This is achieved by reusing Compcert [,], where forward and backward simulations are used to prove equivalence. The JIT presented in this work compiles CoreIR, which is a low-level intermediate representation, to native x86 machine code.
Further research that involved compiler verification was presented in [], where the authors similarly modified Compcert to formally verify constant-time property preservation for cryptographic C programs. The presented work was considered translator verification since it represents the compiler model in Coq and formally proves its correctness. This method cannot be applied easily to production compilers because it necessitates that the compilers be written in the language of a proof assistant like Coq. Table 2 shows a summary of code translation verification approaches that were explained in this section.

Table 2.
Summary of formal verification approaches to code translation.
4.3. Formal Verification of Model-Based Code Generation
Model-based code generation is widely used by software developers to generate code from UML diagrams. Many tools generate code from UML diagrams, software specifications, or even sketches. “Correct code by design” is an approach used in model-based development tools like Event-B and Simulink, which have built-in model checkers. Code generators were also built for these tools. Event-B is a formal modeling language based on set theory and predicate logic for modeling and reasoning about systems, introduced by Abrial []. Event-B is greatly dependent on the B-Method []. Modeling in Event-B is facilitated via an extensible platform called Rodin []. The Rodin platform is an Eclipse-based IDE for Event-B that provides effective support for refinement and mathematical proof. The platform is open-source, it contributes to the Eclipse framework, and it is further extendible with plugins.
We present the two main methodologies used in the formal verification of model-based code generation. These approaches are (1) model checking and (2) assertion and proof obligation.
4.3.1. Model Checking
Model checking is a collection of techniques for analyzing an abstract representation of a system to determine the validity of one or more properties of interest []. State-space exploration is performed to evaluate large numbers of potential program executions. In theory, a model checker can exhaustively search the entire state space of the system and verify whether certain properties are satisfied. If these properties are not satisfied, a counter-example is produced. Previous research that used model checking to verify equivalence between code and its model includes the work done in []. Sampath et al. used the CBMC (C Bounded Model Checker ) [] to validate the equivalence between a Stateflow model and its corresponding C code. Simulink/Stateflow is a standard in the automotive and aerospace domains. Simulink generates the conditions and predicates that are passed to the C code model checker to verify the equivalence between the generated code and the model.
UML to code generation is one of the most famous model-driven development approaches in software engineering. In this context, Tong Ye et al. [] implemented the MDSSED (ModelDriven Safety and Security Enhanced Development) tool for generating formally verified smart home applications from their UML representations. The idea is based on modeling the behavior of the application in the form of a UML model. Then, the MDSSED tool generates the formal model from the UML. In addition, it extracts the safety properties that must be satisfied via the smart home application. This formal model is formally checked using the NuSMV (New Symbolic Model Verifier) tool []. Finally, the MDSSED generates the formally verified application code in the Groovy programming language. Currently, the MDSSED tool supports automatic app code generation for the Samsung SmartThings platform. In the future, it will support code generation for other smart home platforms.
The work done by Besnard et al. [] also verified UML-based C code generation through a UML interpreter. For formal verification of equivalence between the C code and the UML model, the authors depended on the concept of runtime validation: “What is verified is what is executed.” This is categorized as model checking since the verification is done on the model level using the UML interpreter they introduced. This was similar to the work done by Mery et al. [], who also depended on model checking the code generated from a model. However, they used the Event-B model-to-C code generator. The generated C code was model-checked using the BLAST model checker [], which acts as a complementary tool to receive the safety properties checked from Event-B.
4.3.2. Assertions and Formal Proof Obligation for Equivalence Checking
In this subcategory, the formal verification of Event-B to code generation is conducted through assertion. The work conducted by Catano et al. [] presented an approach to generating source code for architectural tactics in order to enhance cyber-resilience in safety and mission-critical systems. This method leverages the Event-B formal method and the EVENTB2JAVA code generation tool to create certified code, ensuring that the software can effectively detect and recover from cyber incidents. A notable innovation in this work is the introduction of a linear temporal logic (LTL) extension for Event-B, which allows for the modeling of both safety and liveness properties that are crucial for resilience. The correctness of the generated code is validated through both formal proof obligations and assertions within the Rodin platform and extensive unit testing. We classified this approach under assertion-based verification and not proof-based verification since the verification applied to the generated code depends on assertions. Those assertions are formulated from the proof obligation of the Event-B model. However, the assertions are the verification method applied to the generated code.
Dalvandi et al. [] used assertion-based verification to prove the correctness of the Dafny code generated via the Event-B model. Dafny is an imperative, class-based language that allows for strongly and weakly typed variables. The assertion is also considered a proof obligation in which the verification depends on assertion statements in the output code that ensure the satisfiability of certain model specifications. Table 3 shows a summary of formal verification approaches applied to model-based code generation.

Table 3.
Summary of formal verification approaches to model-based code generation.
5. Discussion
Our survey points out a real research gap in the formal verification of code conversion, especially for code-to-code translation tasks and model-based code generation. This review was limited to code conversion only, and it did not include general model conversion verification. There are two main ways to verify code conversion: translation or optimization verification (equivalence checking) and translator or optimizer verification. Translation verification is a part of formal verification that uses mathematical or graphical modeling of code to prove that two representations of code exhibit the same behavior and are, therefore, equivalent, and this is performed per translation or optimization.
Translator verification is based on applying program verification techniques to prove the correctness of a code translator or code optimizer. This is usually achieved by formally describing the specification of the translator and then proving its correctness. This should be performed once, and it does not imply verification for each translated code. Applying translator verification is theoretically difficult and very limited due to the difficulty of describing translator software in a formal way that enables it to be proved correct. Moreover, any change in the translation rules will imply changes in the proof of the translator.
Most of the work surveyed focused on code optimization verification, which usually checks the equivalence between two versions of code written in the same programming language. Surprisingly, formal verification is not found in new software development based on mobile and web programming, especially in trans-compilers that implement the conversion between native languages that support multiple platforms or from a cross-platform language to a native one in order to ensure higher performance. We also noticed that, regarding the programming languages, the previous work done mostly focused on C and C++, and then Java in a few articles. Very few articles included other programming languages.
The number of research articles in the domain of code conversion verification has stagnated since the year 2017, with a slight decline, as shown in Figure 9. The figure also shows that there was a large increase in interest for the years 2017–2019 compared to the previous three years, 2014–2016. This indicates advances and improvements in the software industry’s formal verification tools. The figure also shows the distribution of the formal verification approach used in the articles within each year range. In Figure 10, we can see the distribution of formal verification approaches to each code conversion category by percentage. We discuss the two main perspectives of this survey in the following subsections.
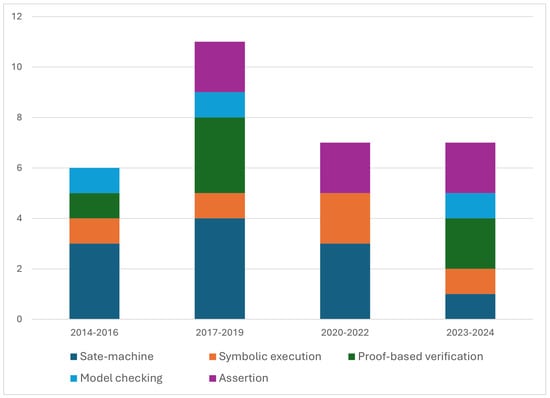
Figure 9.
Number of articles on formal verification for code conversion versus time expressed as the publication year, highlighting the approaches used.
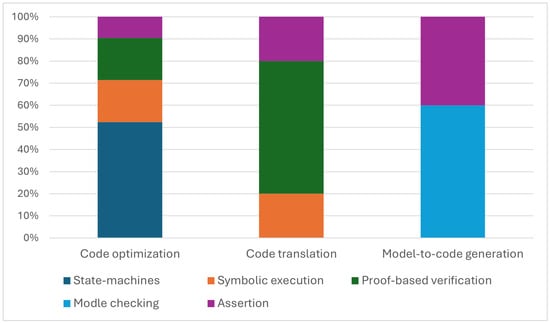
Figure 10.
Approach distribution for different categories of code conversion.
5.1. Approaches of Current Formal Verification Techniques Applied to Code-to-Code Conversion and Code Generation
Regarding the verification approaches reviewed in this article, our survey identified five different approaches. We can report many findings about the dominant methods used and those that are used for the different categories of code conversion. Table 4 shows a comparison of the five identified approaches.

Table 4.
Comparison of formal verification approaches to code conversion.
5.1.1. State-Machines and Graph-Based Equivalence Checking
Although state-machine and control-flow graph-based equivalence checking is the most reported approach, it is used only for code optimization, as shown in Figure 10.
The main idea of this approach is aligning states, checking variables’ propagation, and comparing memory conditions. This alignment task is not always feasible for complex code structures, and it faces limitations in achieving scalability. It is also clear that it was rarely used for different source and target languages or model and code equivalence verification. This necessitates further innovations to make this approach more flexible and usable.
5.1.2. Proof-Based Verification
The proof-based verification approach was the second most used approach in terms of the number of articles after the state-machines approach. It was used for code optimizers’ and code translators’ verification Figure 10. Proof-based verification was used as a compiler verification approach to both compiler optimization and compiler translation. Compiler verification is used to prove that, once and for all, any translation produced via this compiler is valid. However, this kind of verification depends on formally describing the compiler, which is a very difficult task, to the extent that it might be partial. However, only the compiler verification is considered to achieve once-and-for-all results. Other methods verify equivalence and must be applied to each conversion process.
5.1.3. Symbolic Execution
Symbolic execution was used as a stand-alone approach in both categories of code optimization and code translation. The timeline figure shown in Figure 9 depicts an increase in the use of this approach. This is due to the improvement and availability of efficient SMT solvers like Z3. Symbolic execution was also reported as a complementary approach to other approaches. For example, [] used state machine-based equivalence checking with symbolic analysis. The assertion-based equivalence by [] Abadi et al. also combined symbolic execution with assertions.
It can be assumed that symbolic execution with an SMT solver is a cornerstone and a main future path in the domain of equivalence checking of code conversion. The main limitations reported for symbolic execution are scalability and the fear of state-space explosion.
5.1.4. Assertion
Assertion-based equivalence was used in all code conversion categories (optimization, translation, and model-based generation), as shown in Figure 10. In the presented work like [,], assertions constituted more of a functional equivalence check since they checked the output of the different versions of code to be proved equivalent. However, assertions of the properties of code were presented in [], which included syntactic and semantic equivalence assertions of formal properties. Property-based checking was used with the LLM-based translator. The idea of making the LLM constrained by and tested with the equivalence properties enhanced the validity and reliability of this kind of translator. Assertion-based verification is a user-friendly approach. It can be a good starting point for developers seeking to apply a form of verification on the code conversion process they are interested in. Expressing the properties that should be preserved after code conversion in the form of assertions is feasible and flexible. Sometimes, assertions can be extracted from formal models, like in the work presented in [,].
5.1.5. Model Checking
Model checking is lightly used in code conversion verification. It was used for model-to-code generation verification only. It is the most frequently used approach for this category compared to assertion. UML model checking and software model checkers were used under the model checking approach. The UML model checker approach was applied to model-based code generation in order to formally verify the correctness of code behavior generated from UML. We noticed that software model checkers were used to check the equivalence between C code and its model. These software model checkers act as complementary tools to the model used in code generation as they are configured to receive the conditions and predicates to be checked in the target code.
Model checking in general is a concrete approach based on checking the correctness of formal specifications. The UML checking and software model checkers act strictly as equivalence checkers only. One of the most important insights here is that both the correctness and completeness of the transformer that generates code from models were not addressed in any of the surveyed articles.
5.2. Formal Verification Techniques for Code Translation Between Two Different Programming Languages
The current work conducted in the formal verification of code translation is summarized in Table 2, and it is also shown as the percentages of each code conversion category in Figure 11. Code translation is much less prevalent than code optimization, which previous researchers have tried to formally verify. This is due to the challenge of formally representing two programs written with different programming structures to prove their equivalence. In addition, concerning the translator verification process, formally representing the translator system is a complex process, and it is sometimes impossible for non-deterministic systems like LLM-based translators.
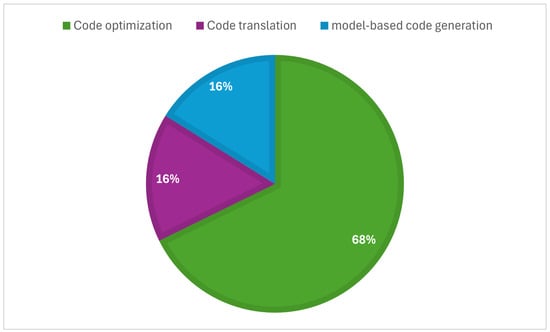
Figure 11.
Percentage of articles in each code conversion category.
The current approaches used to formally verify code translation are proof-based verification for translator verification, symbolic execution, and assertions for translation verification. In the following points, we summarize our findings and intuitions for formally verifying code translation.
- 1
- The proof-based verification method used takes the form of translator verification. The translator verification reported in the survey was a compiler verification approach. The compiler, as a translator, is described formally to be proved correct. Compiler verification is used for code-to-native code translation verification in order to verify JITs [,]. Compiler verification might be an applicable approach to verifying code translators. However, as mentioned in [,], some parts of the compiler cannot be modeled through formal languages. Those authors had to divide the compiler processes into small parts to be modeled, and they also added a sort of equivalence checking to the parts that cannot be formally modeled. Proof-based verification, in general, is important for verifying code translators, as it is considered to be done once and for all. However, the complexity of formally modeling a translator remains a challenge. In addition, any modification in the translator rules will have to be formally proved to ensure that it remains effective and reliable across future updates and iterations.
- 2
- Symbolic execution was used in only one article [] to check code-to-code translation equivalence. However, it was used without an SMT solver. Instead, the paths’ equivalence was checked manually. There is a possibility of enhancing this idea and using a solver for the checks. For example, we can get the first-order logic or FOL representation of a function written in two different programming languages. Then, we can pass the FOL predicate that checks whether they are equivalent to the SMT solver. We suggest that future research examine the use of this combination with code translation verification, as it was successfully used for the equivalence checking of code optimization.
- 3
- Assertions were used as property-based verification for code equivalence. Property-based verification was used with LLM-based code translation, and it can be extended to other translation approaches like compiler-based translation. In addition, the traditional assertion-based verification that relies on functional equivalence used in code optimization can be adapted to the task of code translation.
- 4
- In our scope of knowledge, state-machine-based verification has never been used for the code translation verification category. This proves that enhancements to this approach are needed.
We can infer that symbolic checking or assertion approaches can be used to check the equivalence of code translation tasks. However, equivalence checking, in general, proves translation correctness, and it must be applied to every translation process and every translated code with its source. On the other hand, proof-based verification, which aims at translator verification, might be difficult and incomplete. Therefore, integrating both translator verification through formal proofs and translation verification through symbolic execution and/or assertions is a promising solution to achieve a formally verified code translation system. The automation of both approaches might be a solution to guarantee reliability and continuous verification.
6. Conclusions
This comprehensive survey paper has highlighted the dynamic field of formal verification in code conversion, underscoring its vital role in ensuring the reliability and correctness of software conversion. This survey also presents the first categorization of formal verification methods used in code conversion. Throughout the exploration of various verification methods, we have seen an evolving landscape where traditional techniques are being adapted to meet the complexities of modern software development. Our analysis revealed a prevalent reliance on equivalence checking using state-machine representations, especially in code optimization scenarios. Formal verification of code-to-code optimization is substantially utilized more extensively than verification of translation or code generation from models, which highlights a real research gap in this domain.
Current code-to-code translation approaches involve equivalence checking through symbolic execution or assertions and translator verification through formal proofs. Our conclusion states that automated solutions and more user-friendly tools should be instantiated to ensure the reliability and consistency of these approaches. There is a critical need for verification tools that can be easily integrated into existing development pipelines. We encourage future researchers to investigate the possibility of developing such tools in order to increase the adoption of formal verification for code translation tasks and general code conversion tasks.
Our future research, given our interest in verifying code translation and code translators, will focus on two main strategies. First, we plan to apply equivalence-checking techniques like symbolic execution and assertion to verify code translations facilitated via trans-compilers and large language models (LLMs). This approach aims to ensure that translations preserve functional equivalence despite the complexities introduced via different programming languages and the nuances of neural-based code generation. This formal verification will guarantee the functional equivalence of two code pieces symbolically and not just for finite test cases. This will increase these translators’ reliability and encourage their use in industry.
Additionally, we intend to explore the application of model-checking techniques identified in this survey to verify model-based code generation. This will include testing the feasibility of using model checking to verify translators by comparing translator code against its model. The translator model will be represented as the grammar files of the input and the target languages. These efforts will refine current verification practices and attempt to more seamlessly integrate these advanced verification techniques into development pipelines. By doing so, we hope to enhance the adoption of formal verification methods, particularly for code translation and code generation tasks, ensuring that software conversions are performed with the highest standards of accuracy and reliability.
Author Contributions
Conceptualization, A.T.M. and N.E.; methodology, A.T.M.; validation, A.T.M. and N.E.; formal analysis, A.T.M.; investigation, A.T.M.; resources, A.T.M., A.A.M. and M.A.; data curation, A.T.M., A.A.M. and M.A.; writing—original draft preparation, A.T.M.; writing—review and editing, S.S., N.E., W.M., H.Z. and A.H.Y.; visualization, A.T.M., A.H.Y. and W.M.; supervision, N.E, W.M., S.S., A.H.Y. and H.Z.; project administration, W.M. and N.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
This work was supported in part by OEAD organization project No. P017-2022. The authors of this paper express their gratitude to Jens Knoop, Head of Research Unit Compilers and Languages at TU Wien, for his valuable review of this article. Open Access Funding by Technische Universität Wien.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Leopoldseder, D.; Stadler, L.; Wimmer, C.; Mössenböck, H. Java-to-JavaScript translation via structured control flow reconstruction of compiler IR. In DLS 2015, Proceedings of the 11th Symposium on Dynamic Languages, Pittsburgh, PA, USA, 25–30 October 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 91–103. [Google Scholar] [CrossRef]
- Shigenobu, K.; Ootsu, K.; Ohkawa, T.; Yokota, T. A Translation Method of ARM Machine Code to LLVM-IR for Binary Code Parallelization and Optimization. In Proceedings of the 2017 Fifth International Symposium on Computing and Networking (CANDAR), Aomori, Japan, 19–22 November 2017; Volume 2018, pp. 575–579. [Google Scholar] [CrossRef]
- Salama, D.I.; Hamza, R.B.; Kamel, M.I.; Muhammad, A.A.; Yousef, A.H. TCAIOSC: Trans-Compiler Based Android to iOS Converter. Adv. Intell. Syst. Comput. 2019, 1058, 842–851. [Google Scholar] [CrossRef]
- Hamza, R.B.; Salama, D.I.; Kamel, M.I.; Yousef, A.H. TCAIOSC: Application Code Conversion. In Proceedings of the 2019 Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 28–30 October 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 230–234. [Google Scholar] [CrossRef]
- Muhammad, A.A.; Mahmoud, A.T.; Elkalyouby, S.S.; Hamza, R.B.; Yousef, A.H. Trans-Compiler based Mobile Applications code converter: Swift to java. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 247–252. [Google Scholar] [CrossRef]
- Barakat, R.; Radwan, M.B.A.; Medhat, W.M.; Yousef, A.H. Trans-Compiler-Based Database Code Conversion Model for Native Platforms and Languages. In Model and Data Engineering; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2023; Volume 13761 LNAI, pp. 162–175. [Google Scholar] [CrossRef]
- Mahmoud, A.T.; Muhammad, A.A.; Yousef, A.H.; Medhat, W.; Zayed, H.H.; Selim, S. Compiler-based Web Services code conversion model for different languages of mobile application. In Proceedings of the 1st International Conference of Intelligent Methods, Systems and Applications, IMSA 2023, Cairo, Egypt, 15–16 July 2023; pp. 464–469. [Google Scholar] [CrossRef]
- El-Kaliouby, S.S.; Selim, S.; Yousef, A.H. Native Mobile Applications UI Code Conversion. In Proceedings of the 2021 16th International Conference on Computer Engineering and Systems, ICCES 2021, Cairo, Egypt, 15–16 December 2021. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Joty, S.; Hoi, S.C. CodeT5: Identifier-Aware Unified Pre-Trained Encoder-Decoder Models for Code Understanding and Generation, Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, Punta Cana, Dominican Republic, 7–11 November 2021; Moens, M.F., Huang, X., Specia, L., Yih, S.W.T., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; pp. 8696–8708. [Google Scholar] [CrossRef]
- Li, R.; Allal, L.B.; Zi, Y.; Muennighoff, N.; Kocetkov, D.; Mou, C.; Marone, M.; Akiki, C.; Li, J.; Chim, J.; et al. Starcoder: May the source be with you! arXiv 2023, arXiv:2305.06161. [Google Scholar]
- Wang, Y.; Wang, W.; Joty, S.; Hoi, S.C. Codet5: Identifier-aware unified pre-trained encoder-decoder models for code understanding and generation. arXiv 2021, arXiv:2109.00859. [Google Scholar]
- Ahmad, W.U.; Chakraborty, S.; Ray, B.; Chang, K.W. Unified pre-training for program understanding and generation. arXiv 2021, arXiv:2103.06333. [Google Scholar]
- Roziere, B.; Zhang, J.; Charton, F.; Harman, M.; Synnaeve, G.; Lample, G. Leveraging Automated Unit Tests for Unsupervised Code Translation. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Rajathi, V.; Harishankar, M.; DS, J.S. Origin-The Transcoder. In Proceedings of the 2022 1st International Conference on Computational Science and Technology (ICCST), Chennai, India, 9–10 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 179–182. [Google Scholar]
- Liu, F.; Li, J.; Zhang, L. Syntax and Domain Aware Model for Unsupervised Program Translation. In Proceedings of the 2023 IEEE/ACM 45th International Conference on Software Engineering (ICSE), Melbourne, Australia, 14–20 May 2023. [Google Scholar] [CrossRef]
- Tiwari, S.P.; Prasad, S.; Thushara, M.G. Machine Learning for Translating Pseudocode to Python: A Comprehensive Review. In Proceedings of the 2023 7th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 17–19 May 2023. [Google Scholar] [CrossRef]
- Falzone, E.; Bernaschina, C. Intelligent code generation for model driven web development. In Current Trends in Web Engineering; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2018; Volume 11153 LNCS, pp. 5–13. [Google Scholar] [CrossRef]
- Castro, O.J.; Vega, I.F. Automated Generation of Optimized Code Implementing SVM models on GPUs. IEEE Lat. Am. Trans. 2021, 19, 413–420. [Google Scholar] [CrossRef]
- Mehmood, A.; Jawawi, D.N. AJFCode: An Approach for Full Aspect-Oriented Code Generation from Reusable Aspect Models. KSII Trans. Internet Inf. Syst. 2022, 16, 1973–1993. [Google Scholar] [CrossRef]
- Vujošević-Janičić, M.; Nikolić, M.; Tošić, D.; Kuncak, V. Software verification and graph similarity for automated evaluation of students’ assignments. Inf. Softw. Technol. 2013, 55, 1004–1016. [Google Scholar] [CrossRef]
- Papineni, K.; Roukos, S.; Ward, T.; Zhu, W.J. BLEU: A method for automatic evaluation of machine translation. In Proceedings of the 40th Annual Meeting of the Association for Computational Linguistics, Philadelphia, PA, USA, 7–12 July 2002; pp. 311–318. [Google Scholar] [CrossRef]
- Ren, S.; Guo, D.; Lu, S.; Zhou, L.; Liu, S.; Tang, D.; Sundaresan, N.; Zhou, M.; Blanco, A.; Ma, S. Codebleu: A method for automatic evaluation of code synthesis. arXiv 2020, arXiv:2009.10297. [Google Scholar]
- Qi, M.; Huang, Y.; Wang, M.; Yao, Y.; Liu, Z.; Gu, B.; Clement, C.; Sundaresan, N. SUT: Active Defects Probing for Transcompiler Models. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, Singapore, 6–10 December 2023. [Google Scholar] [CrossRef]
- Evtikhiev, M.; Bogomolov, E.; Sokolov, Y.; Bryksin, T. Out of the BLEU: How should we assess quality of the Code Generation models? J. Syst. Softw. 2023, 203, 111741. [Google Scholar] [CrossRef]
- Pouchet, L.N.; Tucker, E.; Zhang, N.; Chen, H.; Pal, D.; Rodríguez, G.; Zhang, Z. Formal Verification of Source-to-Source Transformations for HLS. In Proceedings of the 2024 ACM/SIGDA International Symposium on Field Programmable Gate Arrays, FPGA ’24, New York, NY, USA, 3–5 March 2024; pp. 97–107. [Google Scholar] [CrossRef]
- Mahmoud, A.T.; Radwan, M.; Soliman, A.M.; Youssef, A.H.; Zayed, H.H.; Medhat, W. Trans-Compiler-Based Conversion from Cross-Platform Applications to Native Applications. Ann. Emerg. Technol. Comput. (AETiC) 2024, 8. [Google Scholar] [CrossRef]
- Sampath, P.; Rajeev, A.; Ramesh, S. Translation validation for Stateflow to C. In Proceedings of the 51st Annual Design Automation Conference, San Francisco, CA, USA, 1–5 June 2014; pp. 1–6. [Google Scholar]
- Ye, T.; Zhuang, Y.; Qiao, G. MDSSED: A safety and security enhanced model-driven development approach for smart home apps. Inf. Softw. Technol. 2023, 163, 107287. [Google Scholar] [CrossRef]
- Besnard, V.; Brun, M.; Jouault, F.; Teodorov, C.; Dhaussy, P. Unified LTL verification and embedded execution of UML models. In Proceedings of the 21th ACM/IEEE International Conference on Model Driven Engineering Languages and Systems, Copenhagen, Denmark, 14–19 October 2018; pp. 112–122. [Google Scholar]
- Kang, J.; Kim, Y.; Song, Y.; Lee, J.; Park, S.; Shin, M.D.; Kim, Y.; Cho, S.; Choi, J.; Hur, C.K.; et al. Crellvm: Verified credible compilation for LLVM. In Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, Philadelphia, PA, USA, 18–22 June 2018; Volume 53, pp. 631–645. [Google Scholar] [CrossRef]
- Gourdin, L.; Bonneau, B.; Boulmé, S.; Monniaux, D.; Bérard, A. Formally Verifying Optimizations with Block Simulations. Proc. ACM Program. Lang. 2023, 7, 59–88. [Google Scholar] [CrossRef]
- Chouksey, R.; Karfa, C.; Bhaduri, P. Translation validation of loop invariant code optimizations involving false computations. In Communications in Computer and Information Science; Springer: Singapore, 2017; Volume 711. [Google Scholar] [CrossRef]
- Sugawara, S.; Takahashi, K.; Shimomura, Y.; Egawa, R.; Takizawa, H. Equivalence Checking of Code Transformation by Numerical and Symbolic Approaches. In Parallel and Distributed Computing, Applications and Technologies; Takizawa, H., Shen, H., Hanawa, T., Hyuk Park, J., Tian, H., Egawa, R., Eds.; Springer: Cham, Switzerland, 2023; pp. 373–386. [Google Scholar]
- Bedin França, R.; Favre-Felix, D.; Leroy, X.; Pantel, M.; Souyris, J. Towards Formally Verified Optimizing Compilation in Flight Control Software. In Proceedings of the PPES 2011: Predictability and Performance in Embedded Systems, Grenoble, France, 18 March 2011; Volume 18, pp. 59–68. [Google Scholar] [CrossRef]
- Nenchev, V.; Imrie, C.; Gerasimou, S.; Calinescu, R. Code-Level Safety Verification for Automated Driving: A Case Study. In Formal Methods; Platzer, A., Rozier, K.Y., Pradella, M., Rossi, M., Eds.; Springer: Cham, Switzerland, 2025; pp. 356–372. [Google Scholar]
- Grimm, T.; Lettnin, D.; Hübner, M. A survey on formal verification techniques for safety-critical systems-on-chip. Electronics 2018, 7, 81. [Google Scholar] [CrossRef]
- Mahmoud, A.T.; Muhammad, A.A.; Yousef, A.H.; Zayed, H.H.; Medhat, W.; Selim, S. Industrial Practitioner Perspective of Mobile Applications Programming Languages and Systems. (IJACSA) Int. J. Adv. Comput. Sci. Appl. 2023, 14, 275–285. [Google Scholar] [CrossRef]
- ter Beek, M.H.; Chapman, R.; Cleaveland, R.; Garavel, H.; Gu, R.; ter Horst, I.; Keiren, J.J.A.; Lecomte, T.; Leuschel, M.; Rozier, K.Y.; et al. Formal Methods in Industry. Form. Asp. Comput. 2024, accepted. [Google Scholar] [CrossRef]
- Souri, A.; Norouzi, M.; Asghari, P.; Rahmani, A.M.; Emadi, G. A systematic literature review on formal verification of software-defined networks. Trans. Emerg. Telecommun. Technol. 2020, 31, e3788. [Google Scholar] [CrossRef]
- Shukla, N.; Pandey, M.; Srivastava, S. Formal modeling and verification of software-defined networks: A survey. Int. J. Netw. Manag. 2019, 29, e2082. [Google Scholar] [CrossRef]
- Yao, J.; Jing, M.; Lin, S.; Li, D.; Cao, X. Formal Verification and Testing of Data Plane in Software-Defined Networks: A Survey. In Advances in Artificial Intelligence and Security; Sun, X., Zhang, X., Xia, Z., Bertino, E., Eds.; Springer: Cham, Switzerland, 2022; pp. 134–144. [Google Scholar]
- Avalle, M.; Pironti, A.; Sisto, R. Formal verification of security protocol implementations: A survey. Form. Asp. Comput. 2014, 26, 99–123. [Google Scholar] [CrossRef]
- Erata, F.; Deng, S.; Zaghloul, F.; Xiong, W.; Demir, O.; Szefer, J. Survey of Approaches and Techniques for Security Verification of Computer Systems. J. Emerg. Technol. Comput. Syst. 2023, 19, 6. [Google Scholar] [CrossRef]
- Garfatta, I.; Klai, K.; Gaaloul, W.; Graiet, M. A Survey on Formal Verification for Solidity Smart Contracts. In Proceedings of the 2021 Australasian Computer Science Week Multiconference, ACSW ’21, New York, NY, USA, 1–5 February 2021. [Google Scholar] [CrossRef]
- Murray, Y.; Anisi, D.A. Survey of Formal Verification Methods for Smart Contracts on Blockchain. In Proceedings of the 2019 10th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Canary Islands, Spain, 24–26 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Tolmach, P.; Li, Y.; Lin, S.W.; Liu, Y.; Li, Z. A Survey of Smart Contract Formal Specification and Verification. ACM Comput. Surv. 2021, 54, 148. [Google Scholar] [CrossRef]
- Gabmeyer, S.; Kaufmann, P.; Seidl, M.; Gogolla, M.; Kappel, G. A feature-based classification of formal verification techniques for software models. Softw. Syst. Model. 2019, 18, 473–498. [Google Scholar] [CrossRef]
- Ab. Rahim, L.; Whittle, J. A survey of approaches for verifying model transformations. Softw. Syst. Model. 2015, 14, 1003–1028. [Google Scholar] [CrossRef]
- Amrani, M.; Combemale, B.; Lúcio, L.; Selim, G.; Dingel, J.; Le Traon, Y.; Vangheluwe, H.; Cordy, J.R. Formal verification techniques for model transformations: A tridimensional classification. J. Object Technol. 2015, 14, 1–43. [Google Scholar] [CrossRef]
- Calegari, D.; Szasz, N. Verification of model transformations: A survey of the state-of-the-art. Electron. Notes Theor. Comput. Sci. 2013, 292, 5–25. [Google Scholar] [CrossRef]
- Davis, N.A.; Berger, T.E.; McDonald, A.; Ingram, J.B.; Foster, J.D.; Sanchez, K. Software Verification Toolkit (SVT): Survey on Available Software Verification Tools and Future Direction; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2022. [Google Scholar] [CrossRef]
- Altaie, A.M.; Alsarraj, R.G.; Al-Bayati, A.H. Verification and validation of a software: A review of the literature. Iraqi J. Comput. Inform. 2020, 46, 40–47. [Google Scholar] [CrossRef]
- Tricco, A.C.; Lillie, E.; Zarin, W.; O’Brien, K.K.; Colquhoun, H.; Levac, D.; Moher, D.; Peters, M.D.; Horsley, T.; Weeks, L.; et al. PRISMA extension for scoping reviews (PRISMA-ScR): Checklist and explanation. Ann. Intern. Med. 2018, 169, 467–473. [Google Scholar] [CrossRef]
- Malhotra, R. Empirical Research in Software Engineering: Concepts, Analysis, and Applications; Taylor & Francis: Abingdon, UK, 2016; p. 498. [Google Scholar]
- De Moura, L.; Bjørner, N. Z3: An efficient SMT solver. In Tools and Algorithms for the Construction and Analysis of Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 337–340. [Google Scholar]
- Felsing, D.; Grebing, S.; Klebanov, V.; Rümmer, P.; Ulbrich, M. Automating regression verification. In Proceedings of the 29th ACM/IEEE International Conference on Automated Software Engineering, Sacramento, CA, USA, 29 September–4 October 2024; pp. 349–360. [Google Scholar]
- Gupta, S.; Saxena, A.; Mahajan, A.; Bansal, S. Effective use of SMT solvers for program equivalence checking through invariant-sketching and query-decomposition. In Theory and Applications of Satisfiability Testing–SAT 2018, Proceedings of the 21st International Conference, SAT 2018, Held as Part of the Federated Logic Conference, FloC 2018, Oxford, UK, 9–12 July 2018, Proceedings 21; Springer: Berlin/Heidelberg, Germany, 2018; pp. 365–382. [Google Scholar]
- Takizawa, H.; Hirasawa, S.; Hayashi, Y.; Egawa, R.; Kobayashi, H. Xevolver: An XML-based code translation framework for supporting HPC application migration. In Proceedings of the 2014 21st International Conference on High Performance Computing (HiPC), Goa, India, 17–20 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–11. [Google Scholar]
- Siegel, S.F.; Zheng, M.; Luo, Z.; Zirkel, T.K.; Marianiello, A.V.; Edenhofner, J.G.; Dwyer, M.B.; Rogers, M.S. CIVL: The concurrency intermediate verification language. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Austin, TX, USA, 15–20 November 2015; pp. 1–12. [Google Scholar]
- Kolesar, J.C.; Piskac, R.; Hallahan, W.T. Checking equivalence in a non-strict language. Proc. ACM Program. Lang. 2022, 6, 28. [Google Scholar] [CrossRef]
- Badihi, S.; Akinotcho, F.; Li, Y.; Rubin, J. ARDiff: Scaling program equivalence checking via iterative abstraction and refinement of common code. In Proceedings of the 28th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Sacramento, CA, USA, 6–16 November 2020; pp. 13–24. [Google Scholar]
- Banerjee, K.; Karfa, C.; Sarkar, D.; Mandal, C. Verification of code motion techniques using value propagation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2014, 33, 1180–1193. [Google Scholar] [CrossRef]
- Banerjee, K.; Mandal, C.; Sarkar, D. A translation validation framework for symbolic value propagation based equivalence checking of FSMDAs. In Proceedings of the 2015 IEEE 15th International Working Conference on Source Code Analysis and Manipulation (SCAM), Bremen, Germany, 27–28 September 2015. [Google Scholar] [CrossRef]
- Hu, J.; Kang, Y.; Hu, Y.; Yang, H.; Tong, L.; Cheng, J.; Deng, J. DssEC: A Deep State Sequence Based Equivalence Checker. In Proceedings of the 5th International Conference on Computer Science and Application Engineering, CSAE ’21, Sanya, China, 19–21 October 2021; Association for Computing Machinery: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Churchill, B.; Padon, O.; Sharma, R.; Aiken, A. Semantic program alignment for equivalence checking. In Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), Phoenix, AZ, USA, 22–26 June 2019; pp. 1027–1040. [Google Scholar] [CrossRef]
- Goyal, M.; Azeem, M.; Madhukar, K.; Venkatesh, R. Direct Construction of Program Alignment Automata for Equivalence Checking. arXiv 2021, arXiv:2109.01864. [Google Scholar]
- Malík, V.; Vojnar, T. Automatically checking semantic equivalence between versions of large-scale C projects. In Proceedings of the 2021 14th IEEE Conference on Software Testing, Verification and Validation (ICST), Virtual, 12–16 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 329–339. [Google Scholar]
- LLVM. Available online: https://llvm.org/ (accessed on 8 June 2012).
- Bandyopadhyay, S.; Sarkar, D.; Mandal, C. Samatulyataone: A path based equivalence checker. In Proceedings of the 12th Innovations in Software Engineering Conference (formerly known as India Software Engineering Conference), Pune, India, 14–16 February 2019. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Sarkar, S.; Sarkar, D.; Mandal, C. SamaTulyata: An efficient path based equivalence checking tool. In Automated Technology for Verification and Analysis; Springer: Cham, Switzerland, 2017; Volume 10482 LNCS. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Sarkar, D.; Mandal, C. An efficient path based equivalence checking for Petri net based models of programs. In Proceedings of the ISEC ’16: Proceedings of the 9th India Software Engineering Conference, Goa, India, 18–20 February 2016. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Sarkar, D.; Mandal, C. Equivalence checking of petri net models of programs using static and dynamic cut-points. Acta Inform. 2019, 56, 321–383. [Google Scholar] [CrossRef]
- Abadi, M.; Keidar-Barner, S.; Pidan, D.; Veksler, T. Verifying Parallel Code After Refactoring Using Equivalence Checking. Int. J. Parallel Program. 2019, 47, 59–73. [Google Scholar] [CrossRef]
- Jakobs, M.C. PEQcheck: Localized and context-aware checking of functional equivalence. In Proceedings of the 2021 IEEE/ACM 9th International Conference on Formal Methods in Software Engineering (FormaliSE), Madrid, Spain, 17–21 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 130–140. [Google Scholar]
- Jakobs, M.C. PatEC: Pattern-based equivalence checking. In Model Checking Software, Proceedings of the 27th International Symposium, SPIN 2021, Virtual, 12 July 2021, Proceedings 27; Springer: Cham, Switzerland, 2021; pp. 120–139. [Google Scholar]
- Leroy, X. Formal certification of a compiler back-end or: Programming a compiler with a proof assistant. In Proceedings of the Conference Record of the 33rd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Charleston, SC, USA, 11–13 January 2006; pp. 42–54. [Google Scholar]
- Leroy, X.; Blazy, S.; Kästner, D.; Schommer, B.; Pister, M.; Ferdinand, C. CompCert-a formally verified optimizing compiler. In Proceedings of the ERTS 2016: Embedded Real Time Software and Systems, 8th European Congress, Toulouse, France, 27–29 January 2016. [Google Scholar]
- Lopes, N.P.; Menendez, D.; Nagarakatte, S.; Regehr, J. Provably correct peephole optimizations with alive. In Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation, Portland, OR, USA, 13–17 June 2015; pp. 22–32. [Google Scholar]
- Sneed, H.M.; Verhoef, C. Validating Converted Java Code via Symbolic Execution. In Software Quality. Complexity and Challenges of Software Engineering in Emerging Technologies, Proceedings of the International Conference, SWQD 2017, Vienna, Austria, 17–20 January 2017, Proceedings 9; Springer: Cham, Switzerland, 2017; pp. 70–83. [Google Scholar]
- Eniser, H.F.; Wüstholz, V.; Christakis, M. Automatically Testing Functional Properties of Code Translation Models. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 21055–21062. [Google Scholar]
- Chirica, L.M.; Martin, D.F. Toward compiler implementation correctness proofs. ACM Trans. Program. Lang. Syst. (TOPLAS) 1986, 8, 185–214. [Google Scholar] [CrossRef]
- Buth, B.; Buth, K.H.; Fränzle, M.; v Karger, B.; Lakhneche, Y.; Langmaack, H.; Müller-Olm, M. Provably correct compiler development and implementation. In Compiler Construction, Proceedings of the 4th International Conference, CC’92 Paderborn, FRG, Paderborn, Germany, 5–7 October 1992, Proceedings 4; Springer: Cham, Switzerland, 1992; pp. 141–155. [Google Scholar]
- Zimmermann, W.; Gaul, T. On the Construction of Correct Compiler Back-Ends: An ASM-Approach. J. Univ. Comput. Sci. 1997, 3, 504–567. [Google Scholar]
- Gaulz, W.G.A.D.T.; Goosz, G.; Zimmermannz, H.P.H.R.W. Compiler Correctness and Implementation Verification: The Veri x Approach. Available online: https://www.uni-ulm.de/fileadmin/website_uni_ulm/iui.inst.090/Publikationen/1996/Goerigk96Verifix.pdf (accessed on 6 November 2024).
- Krijnen, J.O.; Chakravarty, M.M.; Keller, G.; Swierstra, W. Translation certification for smart contracts. Sci. Comput. Program. 2024, 233, 103051. [Google Scholar] [CrossRef]
- Brown, F.; Renner, J.; Nötzli, A.; Lerner, S.; Shacham, H.; Stefan, D. Towards a verified range analysis for JavaScript JITs. In Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation, London, UK, 15–20 June 2020; pp. 135–150. [Google Scholar]
- Barrière, A.; Blazy, S.; Pichardie, D. Formally Verified Native Code Generation in an Effectful JIT: Turning the CompCert Backend into a Formally Verified JIT Compiler. Proc. ACM Program. Lang. 2023, 7, 9. [Google Scholar] [CrossRef]
- Barthe, G.; Blazy, S.; Grégoire, B.; Hutin, R.; Laporte, V.; Pichardie, D.; Trieu, A. Formal verification of a constant-time preserving C compiler. Proc. ACM Program. Lang. 2019, 4, 7. [Google Scholar] [CrossRef]
- Abrial, J.R. Modeling in Event-B: System and Software Engineering; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Abrial, J.R.; Lee, M.K.; Neilson, D.; Scharbach, P.; Sørensen, I.H. The B-method. In Proceedings of the International Symposium of VDM Europe, Noordwijkerhout, The Netherlands, 21–25 October 1991; Springer: Berlin/Heidelberg, Germany, 1991; pp. 398–405. [Google Scholar]
- Abrial, J.R.; Butler, M.; Hallerstede, S.; Hoang, T.S.; Mehta, F.; Voisin, L. Rodin: An open toolset for modelling and reasoning in Event-B. Int. J. Softw. Tools Technol. Transf. 2010, 12, 447–466. [Google Scholar] [CrossRef]
- Clarke, E.M.; Emerson, E.A.; Sifakis, J. Model checking: Algorithmic verification and debugging. Commun. ACM 2009, 52, 74–84. [Google Scholar] [CrossRef]
- Clarke, E.; Kroening, D.; Lerda, F. A tool for checking ANSI-C programs. In Tools and Algorithms for the Construction and Analysis of Systems, Proceedings of the 10th International Conference, TACAS 2004, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2004, Barcelona, Spain, 29 March–2 April 2004, Proceedings 10; Springer: Cham, Switzerland, 2004; pp. 168–176. [Google Scholar]
- Cimatti, A.; Clarke, E.; Giunchiglia, F.; Roveri, M. NuSMV: A new symbolic model verifier. In Computer Aided Verification, Proceedings of the 11th International Conference, CAV’99, Trento, Italy, 6–10 July 1999, Proceedings 11; Springer: Berlin/Heidelberg, Germany, 1999; pp. 495–499. [Google Scholar]
- Méry, D.; Singh, N.K. Automatic code generation from Event-B models. In Proceedings of the 2nd Symposium on Information and Communication Technology, Hanoi, Vietnam, 13–14 October 2011; pp. 179–188. [Google Scholar]
- Beyer, D.; Henzinger, T.A.; Jhala, R.; Majumdar, R. The software model checker b last: Applications to software engineering. Int. J. Softw. Tools Technol. Transf. 2007, 9, 505–525. [Google Scholar] [CrossRef]
- Catano, N. Program Synthesis for Cyber-Resilience. IEEE Trans. Softw. Eng. 2023, 49, 962–972. [Google Scholar] [CrossRef]
- Dalvandi, M.; Butler, M.; Rezazadeh, A.; Salehi Fathabadi, A. Verifiable code generation from scheduled Event-B models. In Abstract State Machines, Alloy, B, TLA, VDM, and Z, Proceedings of the 6th International Conference, ABZ 2018, Southampton, UK, 5–8 June 2018, Proceedings 6; Springer: Cham, Switzerland, 2018; pp. 234–248. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).