Particle Size Distribution in Holby–Morgan Degradation Model of Platinum on Carbon Catalyst in Fuel Cell: Normal Distribution
Abstract
1. Introduction
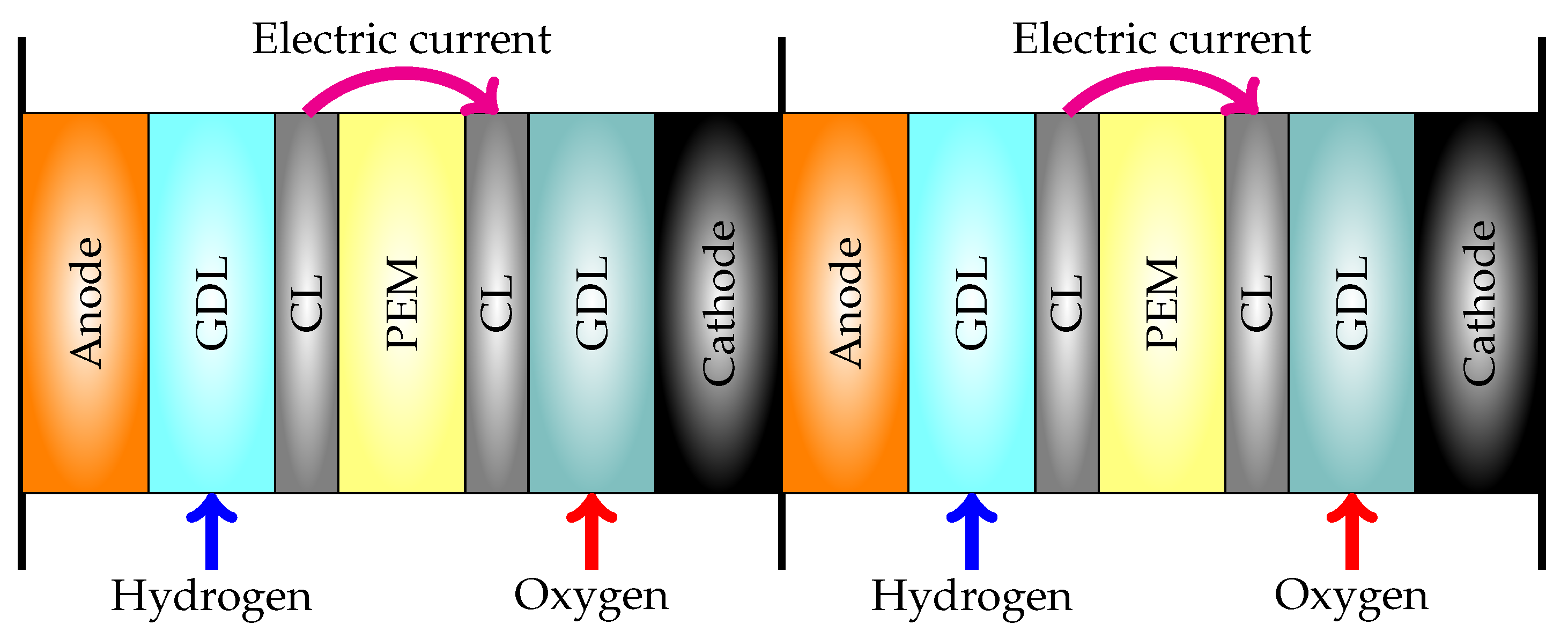
2. Materials and Methods
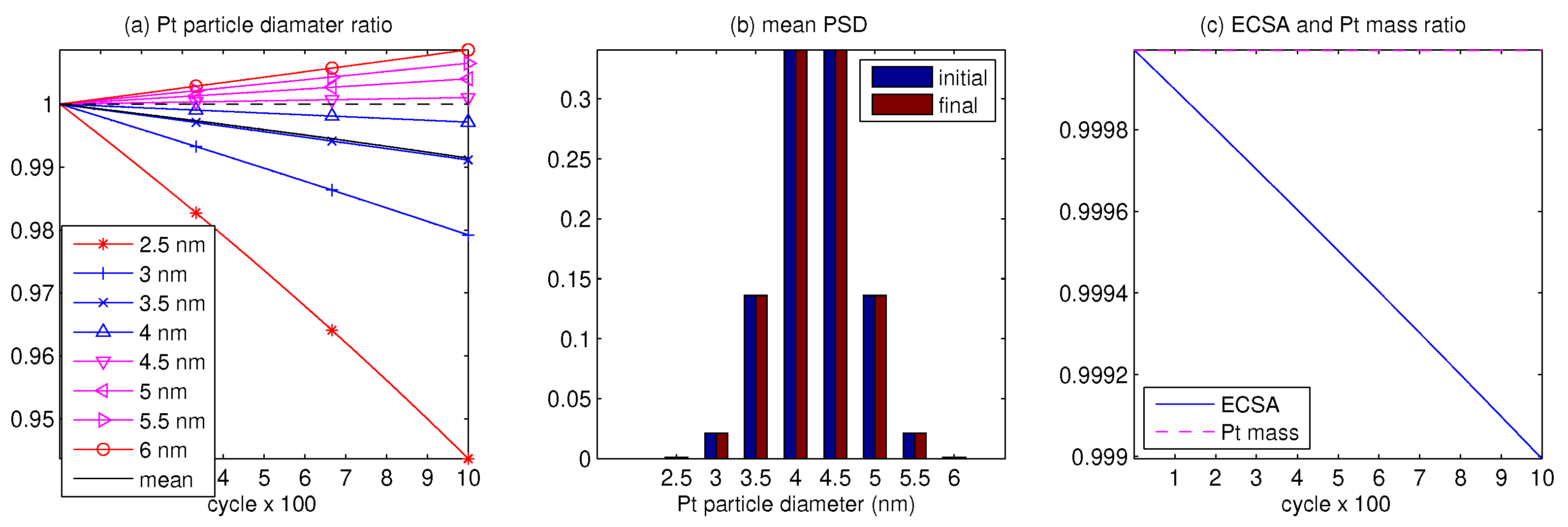
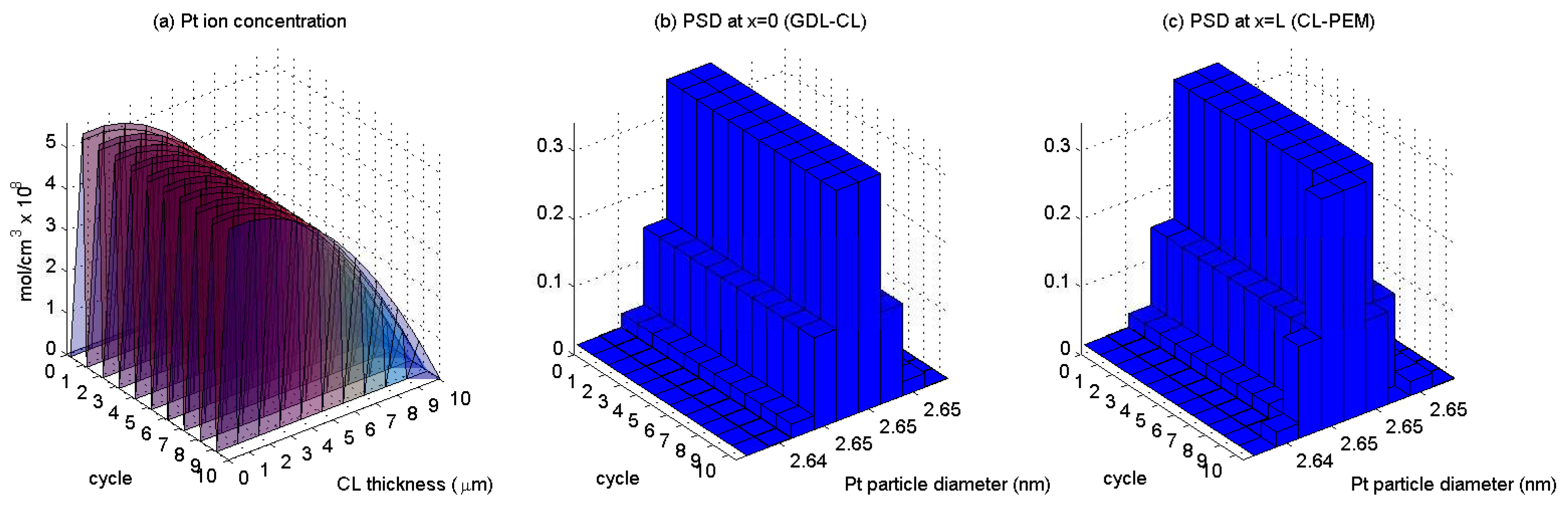
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AST | accelerated stress test |
| BoL/EoL | beginning/end of life |
| CNT | carbon nanotube |
| CCM | catalyst-coated membrane |
| CL | catalyst layer |
| CV | cyclic voltammetry |
| DDM | data-driven model |
| DOF | degree of freedom |
| DOE | design of experiments |
| ECSA | electrochemical surface area |
| FC | fuel cell |
| FCH JU2 | fuel cell and hydrogen joint undertaking |
| GDL | gas diffusion layer |
| HOR | hydrogen oxidation reaction |
| LPL/UPL | lower/upper potential level |
| MEA | membrane electrode assembly |
| MPC | model predictive control |
| ODE | ordinary differential equation |
| ORR | oxygen reduction reaction |
| PDE | partial differential equation |
| PSD | particle size distribution |
| Pt/C | platinum on carbon |
| Pt/PtO | platinum/platinum oxide |
| PEMFC | polymer electrolyte fuel cell |
| PEM | polymer electrolyte membrane/proton exchange membrane |
| pH | potential of hydrogen |
| SW/TW | square/triangle wave |
| TEM | transmission electron microscopy |
References
- Ball, M.; Basile, A.; Veziroǧlu, T.N. Compendium of Hydrogen Energy: Hydrogen Use, Safety and the Hydrogen Economy; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Hacker, V.; Mitsushima, S. (Eds.) Fuel Cells and Hydrogen: From Fundamentals to Applied Research; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Eikerling, M.; Kulikovsky, A. Polymer Electrolyte Fuel Cells: Physical Principles of Materials and Operation; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Kulikovsky, A. Analytical Modeling of Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Basile, A.; Lipnizki, F.; Rahimpour, M.R.; Piemonte, V. (Eds.) Current Trends and Future Developments on (Bio-) Membranes: Advances on Membrane Engineering; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Guerrero-Rodríguez, N.F.; De La Rosa-Leonardo, D.A.; Tapia-Marte, R.; Ramírez-Rivera, F.A.; Faxas-Guzmán, J.; Rey-Boué, A.B.; Reyes-Archundia, E. An overview of the efficiency and long-term viability of powered hydrogen production. Sustainability 2024, 16, 5569. [Google Scholar] [CrossRef]
- Gohar, O.; Khan, M.Z.; Saleem, M.; Chun, O.; Babar, Z.U.D.; Rehman, M.M.U.; Hussain, A.; Zheng, K.; Koh, J.-H.; Ghaffar, A.; et al. Navigating the future of solid oxide fuel cell: Comprehensive insights into fuel electrode related degradation mechanisms and mitigation strategies. Adv. Colloid Interface Sci. 2024, 331, 103241. [Google Scholar] [CrossRef]
- Padgett, E.; Yarlagadda, V.; Holtz, M.E.; Ko, M.; Levin, B.D.A.; Kukreja, R.S.; Ziegelbauer, J.M.; Andrews, R.N.; Ilavsky, J.; Kongkanand, A.; et al. Mitigation of PEM fuel cell catalyst degradation with porous carbon supports. J. Electrochem. Soc. 2019, 166, F198–F207. [Google Scholar] [CrossRef]
- Ding, Y.; Luo, X.; Chang, L.; Dong, C. Response characteristics of platinum coated titanium bipolar plates for proton exchange membrane water electrolysis under fluctuating conditions. Electrochem. Commun. 2024, 168, 107819. [Google Scholar] [CrossRef]
- Tian, H.; Wang, X.; Ge, J.; Wan, H.; Ma, W.; Xie, G.; Ge, J. Pt-based intermetallic compound catalysts for the oxygen reduction reaction: From problems to recent developments. J. Energy Chem. 2024, 99, 302–324. [Google Scholar] [CrossRef]
- Jithul, K.P.; Tamilarasi, B.; Pandey, J. Electrocatalyst for the oxygen reduction reaction (ORR): Towards an active and stable electrocatalyst for low-temperature PEM fuel cell. Ionics 2024. [Google Scholar] [CrossRef]
- Fuhrmann, J. A numerical strategy for Nernst–Planck systems with solvation effect. Fuel Cells 2016, 16, 704–714. [Google Scholar] [CrossRef]
- Fellner, K.; Kovtunenko, V.A. A singularly perturbed nonlinear Poisson–Boltzmann equation: Uniform and super-asymptotic expansions. Math. Meth. Appl. Sci. 2015, 38, 3575–3586. [Google Scholar] [CrossRef]
- González-Granada, J.R.; Kovtunenko, V.A. Entropy method for generalized Poisson–Nernst–Planck equations. Anal. Math. Phys. 2018, 8, 603–619. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Zubkova, A.V. Mathematical modeling of a discontinuous solution of the generalized Poisson–Nernst–Planck problem in a two-phase medium. Kinet. Relat. Mod. 2018, 11, 119–135. [Google Scholar] [CrossRef]
- Alekseev, G.V.; Spivak, Y.E. Stability estimates of optimal solutions for the steady magnetohydrodynamics-Boussinesq equations. Mathematics 2024, 12, 1912. [Google Scholar] [CrossRef]
- González-Durán, J.E.E.; Olivares-Ramírez, J.M.; Luján-Vega, M.A.; Soto-Osornio, J.E.; García-Guendulain, J.M.; Rodriguez-Resendiz, J. Experimental and numerical analysis of a novel cycloid-type rotor versus S-type rotor for vertical-axis wind turbine. Technologies 2024, 12, 54. [Google Scholar] [CrossRef]
- Khludnev, A.M.; Kovtunenko, V.A. Analysis of Cracks in Solids; WIT-Press: Southampton, UK, 2000. [Google Scholar]
- Efendiev, M. Evolution Equations Arising in the Modelling of Life Sciences; Springer: Basel, Switzerland, 2013. [Google Scholar]
- Khajavian, M.; Haseli, A. Modeling the adsorption of ibuprofen on the Zn-decorated S,P,B co-doped C2N nanosheet: Machine learning and central composite design approaches. J. Ind. Eng. Chem. 2024, 137, 583–592. [Google Scholar]
- Khatun, M.; Litagin, H.; Jung, R.; Glaß, M. Safe scenario boundaries determination by parameter variation for an automated driving system. In Proceedings of the IEEE 11th Conference on Systems, Process & Control (ICSPC), Malacca, Malaysia, 16 December 2023; pp. 22–27. [Google Scholar]
- Sevjidsuren, G.; Zils, S.; Kaserer, S.; Wolz, A.; Ettingshausen, F.; Dixon, D.; Schoekel, A.; Roth, C.; Altantsog, P.; Sangaa, D.; et al. Effect of different support morphologies and Pt particle sizes in electrocatalysts for fuel cell applications. J. Nanomater. 2010, 2010, 852786. [Google Scholar] [CrossRef]
- Ostwald, W. Lehrbruck der Allgemeinen Chemie; W. Engelmann: Leipzig, Germany, 1896. [Google Scholar]
- Mensharapov, R.M.; Ivanova, N.A.; Zasypkina, A.A.; Spasov, D.D.; Sinyakov, M.V.; Grigoriev, S.A.; Fateev, V.N. Model study of CNT-based PEMFCs’ electrocatalytic layers. Catalysts 2022, 12, 1227. [Google Scholar] [CrossRef]
- Sakurai, S.; Nishino, H.; Futaba, D.N.; Yasuda, S.; Yamada, T.; Maigne, A.; Matsuo, Y.; Nakamura, E.; Yumura, M.; Hata, K. Role of subsurface diffusion and Ostwald ripening in catalyst formation for single-walled carbon nanotube forest growth. J. Am. Chem. Soc. 2012, 134, 2148–2153. [Google Scholar]
- Jahnke, T.; Futter, G.; Latz, A.; Malkow, T.; Papakonstantinou, G.; Tsotridis, G.; Schott, P.; Gérard, M.; Quinaud, M.; Quiroga, M.; et al. Performance and degradation of Proton Exchange Membrane Fuel Cells: State of the art in modeling from atomistic to system scale. J. Power Sources 2016, 304, 207–233. [Google Scholar] [CrossRef]
- Darling, R.M.; Meyers, J.P. Kinetic model of platinum dissolution in PEMFCs. J. Electrochem. Soc. 2003, 150, A1523–A1527. [Google Scholar] [CrossRef]
- Holby, E.F.; Morgan, D. Application of Pt nanoparticle dissolution and oxidation modeling to understanding degradation in PEM fuel cells. J. Electrochem. Soc. 2012, 159, B578–B591. [Google Scholar] [CrossRef]
- Holby, E.F.; Sheng, W.; Shao-Horn, Y.; Morgan, D. Pt nanoparticle stability in PEM fuel cells: Influence of particle size distribution and crossover hydrogen. Energy Environ. Sci. 2009, 2, 865–871. [Google Scholar] [CrossRef]
- Li, Y.; Moriyama, K.; Gu, W.; Arisetty, S.; Wang, C.Y. A one-dimensional Pt degradation model for polymer electrolyte fuel cells. J. Electrochem. Soc. 2015, 162, F834–F842. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Karpenko-Jereb, L. Study of voltage cycling conditions on Pt oxidation and dissolution in polymer electrolyte fuel cells. J. Power Sources 2021, 493, 229693. [Google Scholar] [CrossRef]
- Kovtunenko, V.A.; Karpenko-Jereb, L. Lifetime of catalyst under voltage cycling in polymer electrolyte fuel cell due to platinum oxidation and dissolution. Technologies 2021, 9, 80. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Kovtunenko, V.A. Modeling of the impact of cycling operating conditions on durability of polymer electrolyte fuel cells and its sensitivity analysis. Int. J. Hydrog. Energy 2023, 48, 15646–15656. [Google Scholar] [CrossRef]
- Kovtunenko, V.A. Variance-based sensitivity analysis of fitting parameters to impact on cycling durability of polymer electrolyte fuel cells. Technologies 2022, 9, 111. [Google Scholar] [CrossRef]
- Kovtunenko, V.A. The Holby–Morgan model of platinum catalyst degradation in PEM fuel cells: Range of feasible parameters achieved using voltage cycling. Technologies 2023, 11, 184. [Google Scholar] [CrossRef]
- Kovtunenko, V.A. Feasible domain of cycling operating conditions and model parameters for Holby–Morgan model of platinum catalyst degradation in PEMFC. Int. J. Hydrog. Energy 2024, 51C, 1518–1526. [Google Scholar] [CrossRef]
- Cherevko, S. Stability and dissolution of electrocatalysts: Building the bridge between model and “real world” systems. Curr. Opin. Electrochem. 2018, 8, 118–125. [Google Scholar] [CrossRef]
- Kravos, A.; Ritzberger, D.; Tavčar, G.; Hametner, C.; Jakubek, S.; Katrašnik, T. Thermodynamically consistent reduced dimensionality electrochemical model for proton exchange membrane fuel cell performance modelling and control. J. Power Sources 2020, 454, 227930. [Google Scholar] [CrossRef]
- Vrlić, M.; Ritzberger, D.; Jakubek, S. Safe and efficient polymer electrolyte membrane fuel cell control using successive linearization based model predictive control validated on real vehicle data. Energies 2020, 13, 5353. [Google Scholar] [CrossRef]
- Bi, W.; Fuller, T.F. Modeling of PEM fuel cell Pt/C catalyst degradation. J. Power Sources 2008, 178, 188–196. [Google Scholar] [CrossRef]
- Schröder, J.; Pittkowski, R.K.; Martens, I.; Chattot, R.; Drnec, J.; Quinson, J.; Kirkensgaard, J.J.K.; Arenz, M. Tracking the catalyst layer depth-dependent electrochemical degradation of a bimodal Pt/C fuel cell catalyst: A combined operando small- and wide-angle X-ray scattering study. ACS Catal. 2022, 12, 2077–2085. [Google Scholar] [CrossRef]
- Kregar, A.; Katrašnik, T. Theoretical analysis of particle size re-distribution due to Ostwald ripening in the fuel cell catalyst layer. Open Phys. 2019, 17, 779–789. [Google Scholar] [CrossRef]
- Kregar, A.; Kravos, A.; Katrašnik, T. Methodology for evaluation of contributions of Ostwald ripening and particle agglomeration to growth of catalyst particles in PEM fuel cells. Fuel Cells 2020, 20, 487–498. [Google Scholar] [CrossRef]
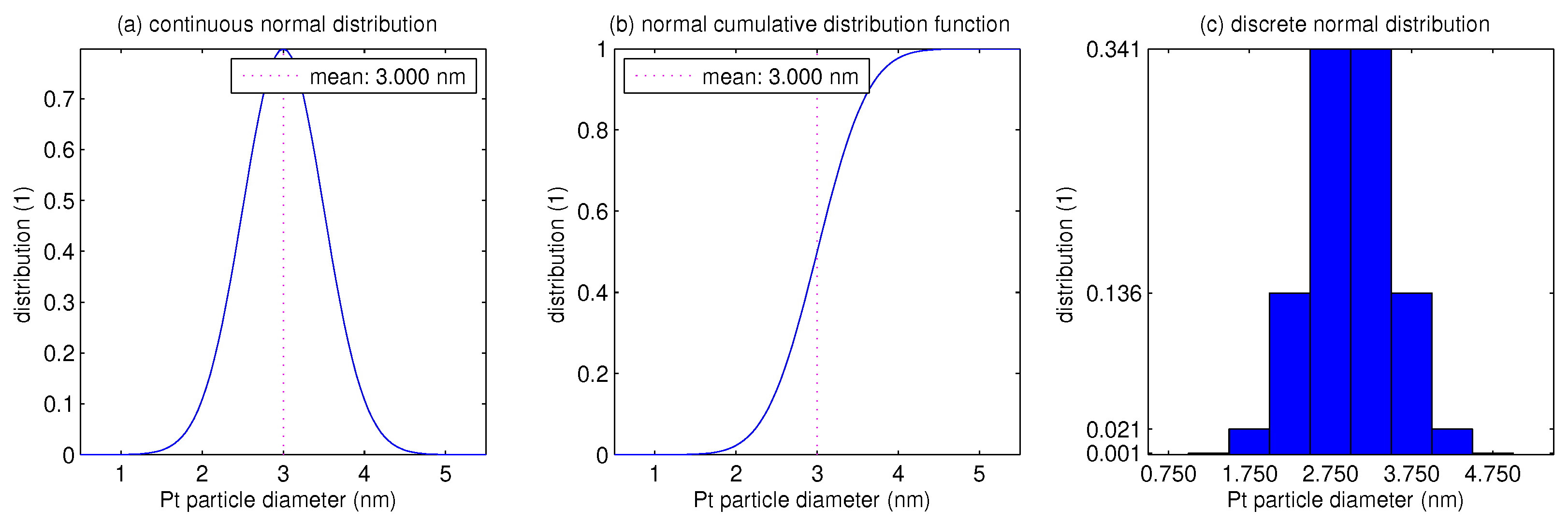


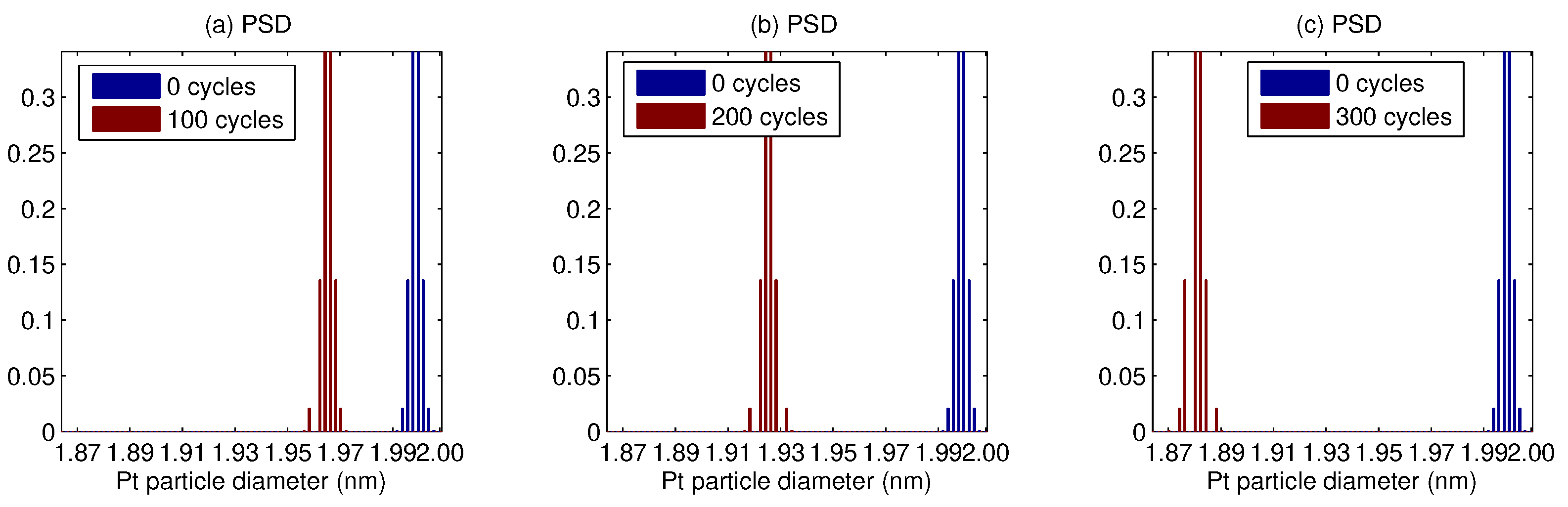
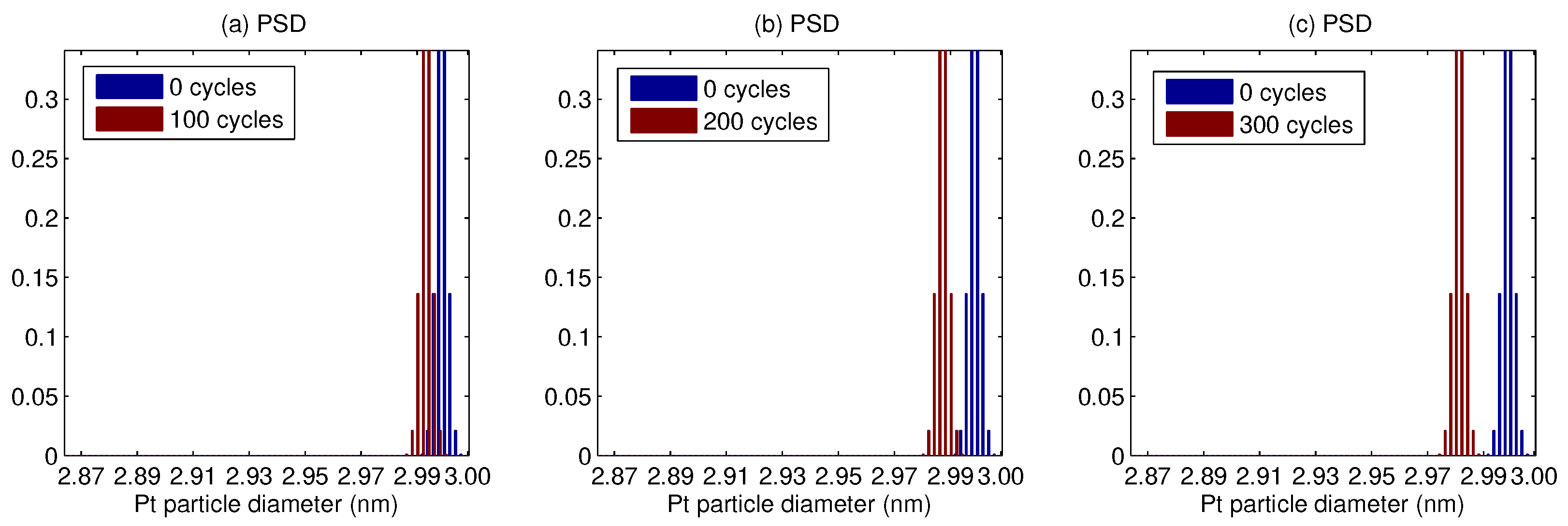

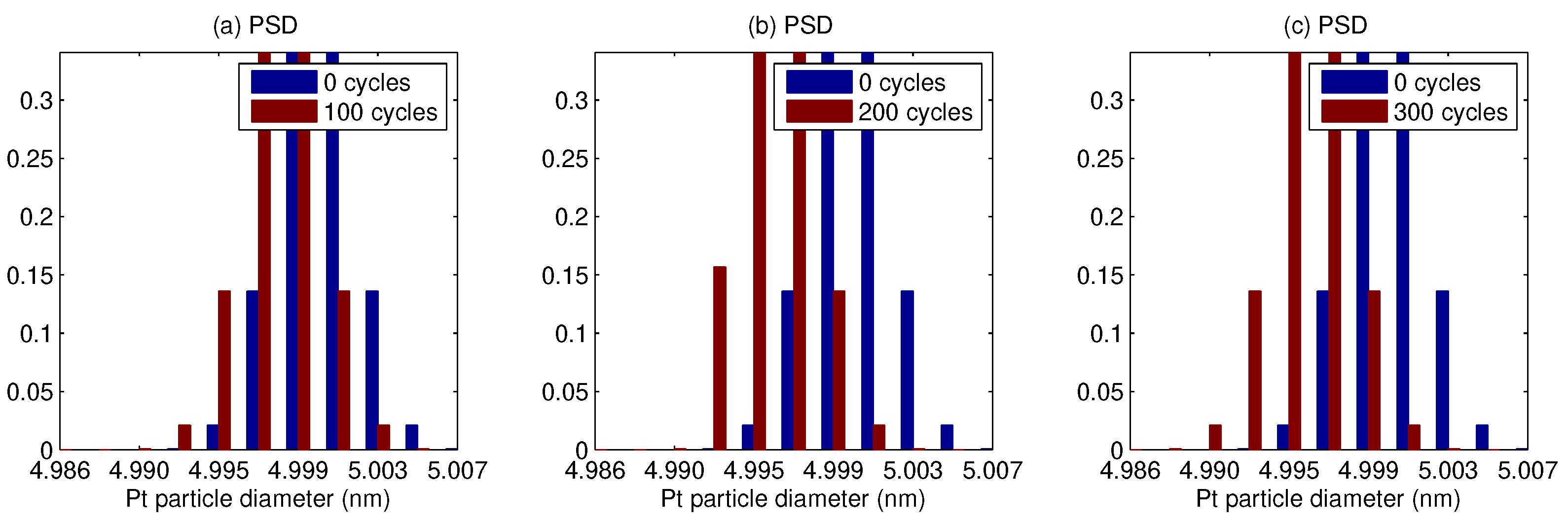
| Particle Size | Range | Probability |
|---|---|---|
| Symbol | Value | Units | Description |
|---|---|---|---|
| Hz | dissolution attempt frequency | ||
| Hz | backward dissolution rate factor | ||
| 0.5 | Butler transfer coefficient for Pt dissolution | ||
| n | 2 | electrons transferred during Pt dissolution | |
| 1.118 | V | Pt dissolution bulk equilibrium voltage | |
| 9.09 | /mol | molar volume of Pt | |
| J/ | Pt [1 1 1] surface tension | ||
| 1 | mol/ | reference Pt ion concentration | |
| J/mol | partial molar Pt dissolution activation enthalpy | ||
| /s | diffusion coefficient of Pt ion in the membrane | ||
| Hz | forward Pt oxide formation rate constant | ||
| Hz | backward Pt oxide formation rate constant | ||
| mol/ | Pt surface site density | ||
| 0.5 | Butler transfer coefficient for PtO formation | ||
| 2 | electrons transferred during Pt oxide formation | ||
| 0.8 | V | Pt oxide formation bulk equilibrium voltage | |
| J/mol | Pt oxide dependent kinetic barrier constant | ||
| J/mol | Pt oxide–oxide interaction energy | ||
| J/mol | partial molar oxide formation activation enthalpy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovtunenko, V.A. Particle Size Distribution in Holby–Morgan Degradation Model of Platinum on Carbon Catalyst in Fuel Cell: Normal Distribution. Technologies 2024, 12, 202. https://doi.org/10.3390/technologies12100202
Kovtunenko VA. Particle Size Distribution in Holby–Morgan Degradation Model of Platinum on Carbon Catalyst in Fuel Cell: Normal Distribution. Technologies. 2024; 12(10):202. https://doi.org/10.3390/technologies12100202
Chicago/Turabian StyleKovtunenko, Victor A. 2024. "Particle Size Distribution in Holby–Morgan Degradation Model of Platinum on Carbon Catalyst in Fuel Cell: Normal Distribution" Technologies 12, no. 10: 202. https://doi.org/10.3390/technologies12100202
APA StyleKovtunenko, V. A. (2024). Particle Size Distribution in Holby–Morgan Degradation Model of Platinum on Carbon Catalyst in Fuel Cell: Normal Distribution. Technologies, 12(10), 202. https://doi.org/10.3390/technologies12100202







