Abstract
Credit card fraud detection is a critical challenge in the financial industry, with substantial economic implications. Conventional machine learning (ML) techniques often fail to adapt to evolving fraud patterns and underperform with imbalanced datasets. This study proposes a hybrid deep learning framework that integrates Generative Adversarial Networks (GANs) with Recurrent Neural Networks (RNNs) to enhance fraud detection capabilities. The GAN component generates realistic synthetic fraudulent transactions, addressing data imbalance and enhancing the training set. The discriminator, implemented using various DL architectures, including Simple RNN, Long Short-Term Memory (LSTM) networks, and Gated Recurrent Units (GRUs), is trained to distinguish between real and synthetic transactions and further fine-tuned to classify transactions as fraudulent or legitimate. Experimental results demonstrate significant improvements over traditional methods, with the GAN-GRU model achieving a sensitivity of 0.992 and specificity of 1.000 on the European credit card dataset. This work highlights the potential of GANs combined with deep learning architectures to provide a more effective and adaptable solution for credit card fraud detection.
1. Introduction
Credit card fraud detection is a critical issue in the financial industry, with substantial economic implications [1,2,3]. According to recent reports, financial institutions worldwide lose over USD 32 billion annually due to fraudulent activities [2,4]. Additionally, the COVID-19 pandemic has led to a rise in online transactions, which further increased the risk of fraud [5]. Therefore, effective fraud detection systems are essential to mitigate these losses and protect consumers.
However, credit card fraud detection presents several challenges that traditional methods and even some DL techniques struggle to address effectively. For instance, fraud patterns constantly evolve as perpetrators develop new strategies to bypass detection systems [6,7]. This continuous evolution requires adaptive models that can learn from new and unseen fraudulent activities in real-time, a task which traditional rule-based systems and even some classical ML models find challenging [8,9,10]. Additionally, credit card fraud is typically a rare event, accounting for a tiny fraction of overall transactions [11]. This leads to highly imbalanced datasets where legitimate transactions significantly outnumber fraudulent ones. Such imbalanced data causes difficulties in training models that can effectively detect the minority class (fraudulent transactions) without overfitting to the majority class [1].
Furthermore, fraudulent behavior is often hidden within sequences of transactions over time. Thus, credit card fraud detection requires models capable of capturing temporal dependencies across sequential data. Fraudulent transactions may exhibit temporal relationships, such as multiple small transactions over a short period or patterns based on transaction time. Recurrent Neural Network (RNN)-based architectures like Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs) can model these temporal dependencies effectively. However, even these models face limitations when dealing with extreme data imbalance and complex, evolving fraud patterns that require synthetic data to enhance training.
Therefore, to overcome these challenges, the integration of Generative Adversarial Networks (GANs) into the fraud detection framework introduces a promising solution. GANs can generate realistic synthetic fraudulent transactions to augment the training data, addressing the imbalance issue directly [12]. They can enhance the model’s ability to detect rare events without overfitting the majority class by augmenting the dataset with synthetic examples. Furthermore, combining GANs with RNNs such as LSTM and GRU utilizes the strengths of both models, allowing the model to not only generate realistic synthetic data but also capture temporal dependencies in transaction patterns.
GANs consist of a generator and a discriminator that compete in a zero-sum game. The generator creates synthetic data, while the discriminator attempts to distinguish between real and fake data [13,14]. GANs have achieved improved performance in different applications, including image generation, natural language processing, and anomaly detection [15,16,17]. Therefore, this study aims to employ the robustness of the GAN framework and deep learning (DL) architectures to enhance credit card fraud detection. In the proposed credit card fraud detection approach, the GAN’s generator aims to create synthetic fraudulent transactions. The discriminator, using various architectures such as a Simple RNN, an LSTM, and a GRU, will initially distinguish between real and synthetic transactions. Through this adversarial training process, the discriminator will learn to identify realistic patterns of fraudulent activity. After this initial phase, the discriminator is further fine-tuned to directly classify transactions as fraudulent or legitimate. This dual-phase training process has proven to be effective in different applications [18,19,20]. The rationale for using GANs in conjunction with RNNs is that while RNNs capture temporal dependencies, GANs help balance imbalanced datasets and enhance model generalization by generating synthetic fraudulent transactions.
The main contributions of this study are threefold:
- First, the study proposes a hybrid DL framework that integrates GANs with RNNs to enhance credit card fraud detection. The proposed approach addresses the critical challenge of data imbalance by generating realistic synthetic fraudulent transactions, augmenting the training data and enabling more robust fraud detection.
- Second, the study evaluates multiple RNN architectures, including Simple RNN, LSTM, and GRU, as discriminators within the GAN structure to capture the temporal dependencies inherent in transaction sequences.
- Third, a performance evaluation is conducted on two widely used public datasets to demonstrate the robustness of the proposed framework.
The remainder of this paper is structured as follows: Section 2 reviews related works. Section 3 describes the dataset used in the study, the different DL architecture and the training procedures of the proposed hybrid GAN-RNN models. Section 4 presents the experimental results and discusses the implications of our findings, and Section 5 concludes the paper with suggestions for future work.
2. Related Works
The field of credit card fraud detection has seen significant advancements with the advent of machine learning. Traditional ML techniques, such as decision trees, logistic regression, and support vector machines (SVMs), have been widely applied in predicting credit card fraud. However, they are inefficient in capturing complex, non-linear patterns in transaction data [9,21]. Meanwhile, deep learning has revolutionized many fields due to its ability to model complex data distributions and uncover hidden patterns [22,23,24]. For instance, CNNs have been effectively used to capture spatial features in transaction data, while RNNs and their variants, such as LSTM networks and GRUs, are excellent at modeling temporal dependencies [25]. These approaches have demonstrated significant improvements in detection accuracy compared to traditional methods. However, deep learning models often require large amounts of balanced data for training, which is a common challenge in fraud detection since legitimate transactions often outnumber fraudulent transactions.
Recent advancements in deep learning have led to innovative architectures tailored for specific challenges in image and pattern recognition. For instance, Tao [26] and Tao et al. [27] presented the principles of enhanced deformable convolutions and channel-enhanced networks, respectively, and how they could be adapted to improve the feature extraction capabilities of neural networks used in fraud detection. These studies demonstrate how specialized neural network modifications can significantly enhance detection capabilities in complex environments. Additionally, these adaptations could potentially address the unique challenges of transaction data, which is often non-linear and temporally complex.
Furthermore, a GAN, introduced by Goodfellow et al. [28], has shown remarkable capabilities in generating realistic synthetic data. It consists of two neural networks: a generator, which creates synthetic samples, and a discriminator, which attempts to distinguish between real and synthetic samples. The adversarial training process enables the generator to produce highly realistic data, making GANs useful for tasks such as data augmentation and anomaly detection [17,29,30]. GANs address the problem of imbalanced datasets by generating synthetic fraudulent transactions, providing more training examples for fraud detection models. Recent studies have explored the application of GANs in fraud detection. For instance, Fiore et al. [31] utilized GANs to generate synthetic fraudulent transactions, demonstrating improved detection performance. Similarly, Chen et al. [32] proposed the use of InfoGANs for enhancing fraud detection by generating interpretable synthetic data.
Ding et al. [33] proposed a robust credit card fraud detection system using a hybrid model combining GANs and variational autoencoders (VAEs). The authors generated synthetic fraudulent transactions with a GAN to address the issue of imbalanced datasets, while an autoencoder was employed to reconstruct transaction data and detect anomalies. Their model significantly improved detection performance, especially in terms of recall, compared to other baseline models. Similarly, Wu et al. [34] introduced a GAN-based approach for credit card fraud detection, where the GAN generates synthetic fraudulent transactions, and two autoencoders are used to detect the anomalies, enhancing the model’s ability to detect fraudulent patterns over time. Their results demonstrated that the GAN-autoencoder framework outperformed conventional methods.
Additionally, Banu et al. [35] developed a deep neural network architecture specifically designed for credit card fraud detection by integrating a convolutional neural network (CNN) and an LSTM network. The CNN was employed to capture spatial correlations within transaction features, while the LSTM was used to detect temporal patterns over sequences of transactions. This combination allowed the model to detect fraudulent behavior across both short and long time horizons. Their experimental results demonstrated that this hybrid approach achieved higher accuracy and area under the receiver characteristic curve (AUC) compared to baseline models like random forests and SVMs.
These studies highlight the potential of GANs to improve the robustness and accuracy of fraud detection systems by augmenting the training data with realistic synthetic examples. Furthermore, the combination of GANs and RNNs presents a promising approach to fraud detection by utilizing the strengths of both techniques. GANs can generate synthetic fraudulent transactions that mimic real-world patterns, while RNN models can effectively process and analyze complex transaction data. Few studies have explored this hybrid approach in different applications. For example, Gupta et al. [36] used the GAN-RNN architecture for video generation, while Yang et al. [37] utilized it for health data augmentation.
Therefore, in this study, a hybrid GAN-RNN framework is proposed for effective credit card fraud detection. The framework explores multiple RNN architectures (Simple RNN, LSTM, and GRU) as discriminators within the GAN framework. This study aims to identify the most effective combination for enhancing fraud detection performance by systematically evaluating these architectures.
3. Materials and Methods
3.1. Datasets
In this study, we utilized two widely recognized datasets in the field of credit card fraud detection: the European credit card dataset and the Brazilian credit card dataset. Both datasets are known for their imbalanced nature, with fraudulent transactions constituting a small fraction of the total transactions, which poses a critical challenge for effective fraud detection.
3.1.1. European Credit Card Dataset
The European credit card dataset contains transactions made by European cardholders over a two-day period. This dataset comprises 284,807 transactions, of which only 492 are fraudulent, representing approximately 0.17% of the total transactions [25]. The dataset includes 30 features, such as transaction time, amount, and anonymized principal component analysis (PCA) transformed features. Due to privacy concerns, the actual features are masked, and the anonymized features make it difficult to interpret specific fraud patterns. The highly imbalanced nature of this dataset makes it challenging for ML models to accurately identify fraudulent transactions without overfitting to the majority class. This imbalance highlights the need for approaches like GANs to generate synthetic fraudulent samples for more balanced training data. The dataset is described in Table 1.

Table 1.
European credit card dataset features.
3.1.2. Brazilian Credit Card Dataset
The Brazilian credit card dataset was obtained from a large Brazilian bank. This dataset comprises 374,823 transactions, with fraudulent transactions constituting 3.74% of the total [38]. Each transaction includes 17 numerical features, providing detailed transactional information that could aid in fraud detection. The features are shown in Table 2. Meanwhile, the imbalance ratio, although lower than the European dataset, still poses a challenge for ML models. The dataset is summarized in Table 2.

Table 2.
Brazilian credit card dataset features.
Both datasets are extensively used in the research community to benchmark and compare the performance of different fraud detection methods. Their imbalanced nature necessitates the use of advanced techniques such as GANs and DL architectures to effectively learn from the minority class and improve classification performance. Table 3 compares and summarizes both datasets.

Table 3.
Summary of the credit card datasets.
3.2. Deep Learning Architectures
3.2.1. Simple RNN
A Simple RNN is a type of neural network designed for processing sequential data. Simple RNNs maintain a hidden state that captures information from previous time steps, allowing the network to learn temporal dependencies [39]. The hidden state at each time step t is computed as
where is the hidden state, is the input at time step t, and are weight matrices, is the bias term, and is the activation function [40]. Simple RNNs are useful for tasks that involve time-series or sequential data because they can retain information from previous inputs to inform future predictions. However, they are limited by the vanishing gradient problem, which makes it difficult for them to learn long-term dependencies [41,42]. Despite this limitation, Simple RNNs can be effective for shorter sequences or when combined with other architectures that mitigate their weaknesses.
3.2.2. LSTM
The LSTM network, shown in Figure 1, is an advanced type of RNN designed to overcome the vanishing gradient problem, enabling them to learn long-term dependencies [43]. An LSTM cell contains a cell state and three gates: an input gate , a forget gate , and an output gate . The operations within an LSTM cell are defined as follows:
where W matrices are weights, b terms are biases, and and tanh are activation functions [43]. LSTMs are well suited for tasks that require learning long-term dependencies, such as natural language processing and time-series forecasting. Their ability to retain and update information over long sequences makes them ideal for complex sequential patterns where important information might be separated by many time steps [44].

Figure 1.
LSTM architecture [45].
3.2.3. GRU
GRUs are a simplified variant of LSTM networks that also aim to capture long-term dependencies without having the vanishing gradient problem [46]. The GRU architecture is shown in Figure 2. It combines the input and forget gates into a single update gate and uses a reset gate . The GRU operations are
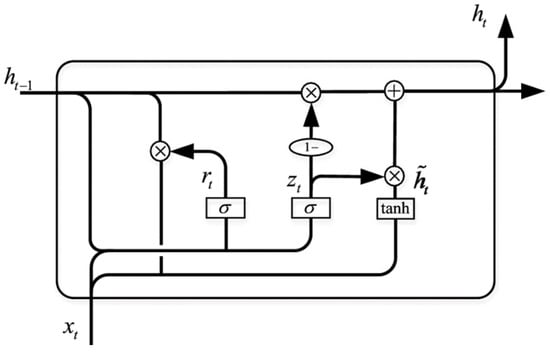
Figure 2.
GRU architecture [8].
By simplifying the forget and input gates into a single gate, the number of parameters and computational complexity are also reduced. This makes GRUs computationally more efficient while still maintaining the ability to capture long-term dependencies [47,48]. They are useful in applications where training time and computational resources are limited, and they often perform comparably to LSTMs on a variety of tasks.
3.3. Generative Adversarial Networks
GANs consist of two neural networks: a generator G and a discriminator D, which compete in a zero-sum game [16]. The generator creates synthetic data, while the discriminator distinguishes between real and fake data. The generator G is designed to produce realistic synthetic fraudulent transactions from a noise vector z:
The generator is trained to minimize the loss:
Different neural networks can be used as generators, including fully connected neural networks (FCNNs), CNNs, and RNNs. Meanwhile, the discriminator D is trained to classify transactions as real or fake, using architectures such as Simple RNN, LSTM, GRU, and CNN:
The training alternates between updating the discriminator and the generator using stochastic gradient descent. This adversarial training continues until the generator produces highly realistic synthetic transactions and the discriminator accurately distinguishes real from synthetic transactions.
3.4. Proposed Hybrid Deep Learning Framework
The proposed hybrid GAN-RNN framework leverages the generative capabilities of GANs and the sequential modeling strengths of RNNs to enhance credit card fraud detection. The hybrid GAN-RNN framework consists of two main components: the generator and the discriminator. In this study, the generator is implemented using an FCNN. This choice is motivated by the need to effectively generate realistic synthetic fraudulent transactions from tabular credit card transaction data. The FCNN generator starts with a random noise vector and passes it through multiple layers of neurons with ReLU activations to produce synthetic transactions.
Secondly, the discriminator is implemented using different architectures, including Simple RNN, LSTM, and GRU, to evaluate their effectiveness in detecting fraudulent activities. Meanwhile, the discriminator initially focuses on differentiating between real and synthetic transactions. This adversarial process forces the generator to create increasingly realistic fraudulent transactions. Once proficient, the discriminator is fine-tuned to classify transactions as fraudulent or legitimate, utilizing the detailed patterns learned during the adversarial training. The detailed algorithm is shown as Algorithm 1.
| Algorithm 1 Hybrid GAN-RNN framework training algorithm. |
|
3.5. Evaluation Metrics
This study uses a variety of metrics that provide a comprehensive assessment of the model’s performance. The metrics used are sensitivity, specificity, precision, F-measure, receiver operating characteristic (ROC) curve, and area under the ROC curve (AUC). Sensitivity, also known as recall, measures the proportion of actual fraudulent transactions that the model correctly identifies [49]. It is defined as
where is the number of true positives and is the number of false negatives. A higher sensitivity indicates that the model is effective in detecting fraudulent transactions [50]. Meanwhile, specificity measures the proportion of actual legitimate transactions that the model correctly identifies [51]:
where is the number of true negatives and is the number of false positives. The F-measure is the harmonic mean of precision and recall. It provides a single metric that balances the trade-off between precision and recall. Meanwhile, precision is the proportion of predicted fraudulent transactions that are actually fraudulent:
where
The ROC curve is a graphical plot that illustrates the diagnostic ability of the model by plotting the true positive rate against the false positive rate at various threshold settings [3,52]. The AUC provides a single scalar value to summarize the model’s performance. An AUC value closer to 1 indicates a better-performing model.
4. Results and Discussion
This section presents the experimental results and discussion. In the experimental setup of the proposed hybrid GAN-RNN framework, the data are split into training, validation, and test sets using a stratified k-fold cross-validation approach, which is suitable for handling imbalanced datasets. This method ensures that each fold has an equal proportion of fraudulent and legitimate transactions, providing a balanced representation across all splits. Specifically, the data are divided into , where folds are used for training, and the remaining fold is used for validation. During the training phase, the GAN’s generator and discriminator are trained iteratively using folds in an adversarial manner.
Once the adversarial training is complete, the discriminator is fine-tuned to classify transactions directly as fraudulent or legitimate using the same folds. This process is repeated k times, with each fold being used as the validation set once. The final model evaluation is performed on an independent test set, which is not used during the training and validation phases. This approach aims to mitigate overfitting and ensures that the model generalizes well to unseen data. Meanwhile, the parameters of the different models used in this study are shown in Table 4. These parameters were chosen as they are the commonly used default values in several ML and DL studies, known for their stability and effectiveness in similar binary classification tasks, such as fraud detection [33,53].

Table 4.
Model parameters.
4.1. Model Performance Using European Credit Card Dataset
The performance of various models using the European credit card dataset is evaluated and summarized in Table 5 and Figure 3. The models tested include GAN combined with LSTM, GRU, and Simple RNN, as well as standalone LSTM, GRU, and Simple RNN models. The GAN-GRU model achieved the highest performance among all models, with a sensitivity of 0.992, specificity of 1.000, precision of 1.000, and an F-measure of 0.996. This model’s robustness is further shown by its highest AUC of 0.997, as shown in the ROC curves. These results indicate that the GAN-GRU combination is highly effective in distinguishing between fraudulent and legitimate transactions.

Table 5.
Performance of the models based on the European dataset.
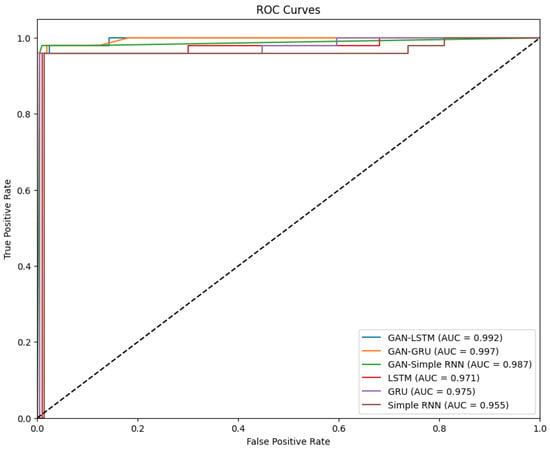
Figure 3.
ROC curves—European dataset.
The GAN-LSTM model also performed exceptionally well, with a sensitivity of 0.990, specificity of 0.995, precision of 0.979, an F-measure of 0.984, and AUC of 0.992, demonstrating the effectiveness of combining GAN with LSTM for this application. Meanwhile, the GAN-Simple RNN model, although slightly less effective, still achieved impressive results with a sensitivity of 0.960, specificity of 0.991, precision of 0.962, and an F-measure of 0.961, along with an AUC of 0.987. In contrast, the standalone models (LSTM, GRU, and Simple RNN) showed lower performance. The LSTM model achieved a sensitivity of 0.901, specificity of 0.990, precision of 0.912, and an F-measure of 0.906, with an AUC of 0.971. The GRU model followed closely with a sensitivity of 0.897, specificity of 0.990, precision of 0.850, an F-measure of 0.873, and an AUC of 0.975. The Simple RNN model had the lowest performance, with a sensitivity of 0.884, specificity of 0.989, precision of 0.870, an F-measure of 0.877, and an AUC of 0.955.
Furthermore, the best-performing model (i.e., GAN-GRU) is compared with widely used ML models, including random forest, logistic regression, SVM, multi-layer perceptron (MLP), and extreme gradient boosting (XGBoost). The proposed GAN-GRU is benchmarked against these classifiers in Table 6.

Table 6.
Comparison with baseline models using the European dataset.
The results in Table 6 demonstrate the superior performance of the proposed GAN-GRU model compared to widely used ML classifiers. The GAN-GRU model achieved the highest sensitivity, specificity, precision, and F-measure, significantly outperforming traditional models. Among the baseline models, XGBoost showed the best performance, with a sensitivity of 0.824, a specificity of 0.961, and an F-measure of 0.854. However, even XGBoost falls short when compared to GAN-GRU, particularly in terms of sensitivity and precision. Other models, such as random forest and MLP, performed reasonably well but struggled with lower sensitivity values, indicating difficulties in accurately detecting fraudulent transactions. Furthermore, SVM and decision tree showed lower performance in terms of sensitivity and F-measure, highlighting their limited ability to handle the imbalanced nature of the dataset. In contrast, the GAN-GRU model addressed the class imbalance effectively through the generation of synthetic fraudulent transactions, leading to its superior performance across all metrics.
4.2. Model Performance Using the Brazilian Dataset
The performance of the various models using the Brazilian dataset is summarized in Table 7 and illustrated by the ROC curves in Figure 4. The results consistently demonstrate the superior performance of the GAN-integrated models over their standalone counterparts. Among the tested models, GAN-LSTM obtained the best performance, achieving a sensitivity of 0.920, specificity of 0.965, precision of 0.988, and an F-measure of 0.953. Its AUC of 0.923 further confirms its effectiveness in accurately distinguishing fraudulent transactions from legitimate ones. Similarly, the GAN-GRU model also exhibited strong performance with a sensitivity of 0.903, specificity of 0.929, precision of 0.951, and an F-measure of 0.926, supported by an AUC of 0.913. The GAN-Simple RNN, while slightly behind, still achieved impressive results with a sensitivity of 0.898, specificity of 0.910, precision of 0.924, an F-measure of 0.911, and an AUC of 0.901.

Table 7.
Performance of the models using the Brazilian dataset.
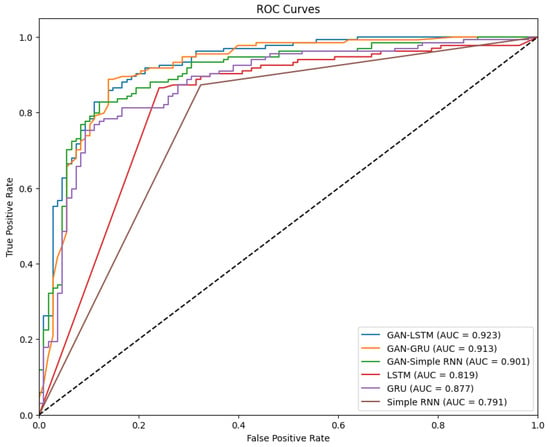
Figure 4.
ROC curves—Brazilian dataset.
In comparison, the standalone models demonstrated lower performance. The LSTM model recorded a sensitivity of 0.715, a specificity of 0.894, a precision of 0.881, an F-measure of 0.789, and an AUC of 0.819. The GRU model followed with a sensitivity of 0.690, specificity of 0.918, precision of 0.817, and an F-measure of 0.748, alongside an AUC of 0.877. The Simple RNN model scored the lowest in performance, with a sensitivity of 0.579, specificity of 0.864, precision of 0.703, an F-measure of 0.625, and an AUC of 0.791.
Furthermore, the performance of the proposed GAN-LSTM approach is benchmarked with baseline models in Table 8. The proposed GAN-LSTM model demonstrates a superior performance compared to the baseline models. The GAN-LSTM achieved the highest sensitivity, specificity, precision, and F-measure, outperforming all the baseline models. Meanwhile, among the baseline models, XGBoost achieved the best performance, with a sensitivity of 0.764, specificity of 0.899, and an F-measure of 0.833. While XGBoost outperforms other baselines in terms of precision, it still falls short compared to GAN-LSTM. Meanwhile, random forest also performed well with a sensitivity of 0.709 and an F-measure of 0.790, but it could not match the overall performance of the GAN-LSTM. The substantial gap in sensitivity and F-measure between the GAN-LSTM and the baseline models demonstrates the effectiveness of combining GANs with RNN architectures. This combination allows the model to better handle imbalanced datasets and capture long-term temporal dependencies, both of which are crucial for detecting fraudulent transactions in highly complex credit card transaction datasets.

Table 8.
Comparison with baseline models using the Brazilian dataset.
4.3. Performance Comparison with Other Scholarly Works
While the proposed approach achieved superior performance compared to the standalone DL and baseline models, it is necessary to compare its performance with state-of-the-art methods in the literature. A comparison is thus tabulated in Table 9, and it is based on studies that used the European dataset. It can be seen that the proposed GAN-GRU model outperformed several models presented in recent studies. The superior performance of our GAN-GRU model, as compared to these recent studies, validates the effectiveness of integrating GANs with the DL architectures to address the challenges of credit card fraud detection, particularly in handling class imbalance and improving model robustness.

Table 9.
Comparison with other recent studies.
4.4. Discussion
The proposed hybrid GAN-RNN framework demonstrated significant improvements in fraud detection performance across the two datasets. The results consistently show that integrating GANs with RNNs, particularly GRUs, enhances the model’s ability to distinguish between fraudulent and legitimate transactions. This can be attributed to the GAN’s capacity to generate realistic synthetic fraudulent transactions, which helps in balancing the training dataset and mitigating the class imbalance issues. The combination of GANs with RNN architectures leverages the strengths of both models. GANs excel in generating realistic data, while RNNs are proficient at capturing temporal dependencies in sequential data. This dual approach allows the model to learn complex patterns associated with fraudulent activities, which standalone models or traditional ML techniques might miss.
Furthermore, our findings align with and exceed the results reported in the existing literature. The superior performance of the GAN-GRU model on the European dataset, with its high sensitivity, specificity, and F-measure, highlights its practical applicability in real-world fraud detection scenarios. The GAN-GRU’s effectiveness on the European dataset can be attributed to its ability to capture short-term dependencies and effectively handle the subtle patterns in the transaction data, which are crucial for this dataset. Conversely, the GAN-LSTM model showed the best performance on the Brazilian dataset. LSTM networks are known for their capability to learn long-term dependencies, which might be more significant given the diverse and detailed features in the Brazilian dataset. The longer period over which transactions were recorded in the Brazilian dataset may benefit more from LSTM’s ability to retain information over extended sequences, helping to identify fraudulent patterns that span over longer periods.
5. Conclusions and Future Research Directions
This study proposed a hybrid DL framework that combines GANs with RNN architectures for credit card fraud detection. The experimental results on two datasets demonstrated the superior performance of the proposed approach, which outperformed other models using the European and Brazilian datasets. This highlights the robustness and effectiveness of the proposed approach in handling class imbalance and enhancing model performance. Our findings indicate that the integration of GANs with DL architectures significantly improves the ability to detect fraudulent transactions, providing a more reliable solution for credit card fraud detection. The dual-phase training process, where the GAN generates synthetic data and the RNN learns from it, proves to be highly effective.
Future research should focus on exploring other GAN configurations and incorporating additional DL models to further enhance the detection capabilities. Moreover, implementing and testing the proposed approach in real-world environments will be essential to validate its practical applicability and operational efficiency. Therefore, addressing challenges related to computational efficiency and scalability will be crucial for deploying these models in large-scale, real-time fraud detection systems.
Author Contributions
Conceptualization, I.D.M. and T.G.S.; methodology, I.D.M. and T.G.S.; software, I.D.M.; validation, I.D.M. and T.G.S.; formal analysis, I.D.M. and T.G.S.; investigation, I.D.M. and T.G.S.; resources, T.G.S.; data curation, I.D.M.; writing—original draft preparation, I.D.M.; writing—review and editing, I.D.M. and T.G.S.; visualization, I.D.M.; supervision, T.G.S.; project administration, T.G.S.; funding acquisition, T.G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GAN | Generative Adversarial Network |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| CNN | Convolutional Neural Network |
| FCNN | Fully Connected Neural Network |
| ML | Machine Learning |
| AUC | Area Under the Curve |
| PCA | Principal Component Analysis |
| SMOTE | Synthetic Minority Over-sampling Technique |
| MLP | Multi-Layer Perceptron |
| ROC | Receiver Operating Characteristic |
References
- Makki, S.; Assaghir, Z.; Taher, Y.; Haque, R.; Hacid, M.S.; Zeineddine, H. An Experimental Study With Imbalanced Classification Approaches for Credit Card Fraud Detection. IEEE Access 2019, 7, 93010–93022. [Google Scholar] [CrossRef]
- Forough, J.; Momtazi, S. Ensemble of deep sequential models for credit card fraud detection. Appl. Soft Comput. 2021, 99, 106883. [Google Scholar] [CrossRef]
- Mienye, I.D.; Obaido, G.; Emmanuel, I.D.; Ajani, A.A. A Survey of Bias and Fairness in Healthcare AI. In Proceedings of the 2024 IEEE 12th International Conference on Healthcare Informatics (ICHI), Orlando, FL, USA, 3–6 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 642–650. [Google Scholar]
- El Hlouli, F.Z.; Riffi, J.; Mahraz, M.A.; Yahyaouy, A.; El Fazazy, K.; Tairi, H. Credit Card Fraud Detection: Addressing Imbalanced Datasets with a Multi-phase Approach. SN Comput. Sci. 2024, 5, 173. [Google Scholar] [CrossRef]
- Zhu, X.; Ao, X.; Qin, Z.; Chang, Y.; Liu, Y.; He, Q.; Li, J. Intelligent financial fraud detection practices in post-pandemic era. Innovation 2021, 2, 100176. [Google Scholar] [CrossRef]
- Chatterjee, P.; Das, D.; Rawat, D.B. Digital twin for credit card fraud detection: Opportunities, challenges, and fraud detection advancements. Future Gener. Comput. Syst. 2024, 158, 410–426. [Google Scholar] [CrossRef]
- Cherif, A.; Badhib, A.; Ammar, H.; Alshehri, S.; Kalkatawi, M.; Imine, A. Credit card fraud detection in the era of disruptive technologies: A systematic review. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 145–174. [Google Scholar] [CrossRef]
- Mienye, I.D.; Jere, N. Deep Learning for Credit Card Fraud Detection: A Review of Algorithms, Challenges, and Solutions. IEEE Access 2024, 12, 96893–96910. [Google Scholar] [CrossRef]
- Malekloo, A.; Ozer, E.; AlHamaydeh, M.; Girolami, M. Machine learning and structural health monitoring overview with emerging technology and high-dimensional data source highlights. Struct. Health Monit. 2022, 21, 1906–1955. [Google Scholar] [CrossRef]
- Wang, T.; Gault, R.; Greer, D. Cutting down high dimensional data with Fuzzy weighted forests (FWF). In Proceedings of the 2022 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Seera, M.; Lim, C.P.; Kumar, A.; Dhamotharan, L.; Tan, K.H. An intelligent payment card fraud detection system. Ann. Oper. Res. 2024, 334, 445–467. [Google Scholar] [CrossRef]
- Strelcenia, E.; Prakoonwit, S. A survey on gan techniques for data augmentation to address the imbalanced data issues in credit card fraud detection. Mach. Learn. Knowl. Extr. 2023, 5, 304–329. [Google Scholar] [CrossRef]
- Mohebbi Moghaddam, M.; Boroomand, B.; Jalali, M.; Zareian, A.; Daeijavad, A.; Manshaei, M.H.; Krunz, M. Games of GANs: Game-theoretical models for generative adversarial networks. Artif. Intell. Rev. 2023, 56, 9771–9807. [Google Scholar] [CrossRef]
- O’Halloran, T.; Obaido, G.; Otegbade, B.; Mienye, I.D. A deep learning approach for Maize Lethal Necrosis and Maize Streak Virus disease detection. Mach. Learn. Appl. 2024, 16, 100556. [Google Scholar] [CrossRef]
- Sabuhi, M.; Zhou, M.; Bezemer, C.P.; Musilek, P. Applications of generative adversarial networks in anomaly detection: A systematic literature review. IEEE Access 2021, 9, 161003–161029. [Google Scholar] [CrossRef]
- Dash, A.; Ye, J.; Wang, G. A review of generative adversarial networks (GANs) and its applications in a wide variety of disciplines: From medical to remote sensing. IEEE Access 2023, 12, 18330–18357. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, D.; Olaniyi, E.; Huang, Y. Generative adversarial networks (GANs) for image augmentation in agriculture: A systematic review. Comput. Electron. Agric. 2022, 200, 107208. [Google Scholar] [CrossRef]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Tao, A.; Kautz, J.; Catanzaro, B. High-resolution image synthesis and semantic manipulation with conditional gans. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8798–8807. [Google Scholar]
- Kang, M.; Zhu, J.Y.; Zhang, R.; Park, J.; Shechtman, E.; Paris, S.; Park, T. Scaling up gans for text-to-image synthesis. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 10124–10134. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Roseline, J.F.; Naidu, G.; Pandi, V.S.; alias Rajasree, S.A.; Mageswari, N. Autonomous credit card fraud detection using machine learning approach✩. Comput. Electr. Eng. 2022, 102, 108132. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep learning: A comprehensive overview on techniques, taxonomy, applications and research directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hatcher, W.G.; Yu, W. A survey of deep learning: Platforms, applications and emerging research trends. IEEE Access 2018, 6, 24411–24432. [Google Scholar] [CrossRef]
- Esenogho, E.; Mienye, I.D.; Swart, T.G.; Aruleba, K.; Obaido, G. A Neural Network Ensemble With Feature Engineering for Improved Credit Card Fraud Detection. IEEE Access 2022, 10, 16400–16407. [Google Scholar] [CrossRef]
- Tao, H. A label-relevance multi-direction interaction network with enhanced deformable convolution for forest smoke recognition. Expert Syst. Appl. 2024, 236, 121383. [Google Scholar] [CrossRef]
- Tao, H.; Xie, C.; Wang, J.; Xin, Z. CENet: A channel-enhanced spatiotemporal network with sufficient supervision information for recognizing industrial smoke emissions. IEEE Internet Things J. 2022, 9, 18749–18759. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Xia, X.; Pan, X.; Li, N.; He, X.; Ma, L.; Zhang, X.; Ding, N. GAN-based anomaly detection: A review. Neurocomputing 2022, 493, 497–535. [Google Scholar] [CrossRef]
- Tang, T.W.; Kuo, W.H.; Lan, J.H.; Ding, C.F.; Hsu, H.; Young, H.T. Anomaly detection neural network with dual auto-encoders GAN and its industrial inspection applications. Sensors 2020, 20, 3336. [Google Scholar] [CrossRef]
- Fiore, U.; De Santis, A.; Perla, F.; Zanetti, P.; Palmieri, F. Using generative adversarial networks for improving classification effectiveness in credit card fraud detection. Inf. Sci. 2019, 479, 448–455. [Google Scholar] [CrossRef]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. Infogan: Interpretable representation learning by information maximizing generative adversarial nets. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Ding, Y.; Kang, W.; Feng, J.; Peng, B.; Yang, A. Credit card fraud detection based on improved Variational Autoencoder Generative Adversarial Network. IEEE Access 2023, 11, 83680–83691. [Google Scholar] [CrossRef]
- Wu, E.; Cui, H.; Welsch, R.E. Dual autoencoders generative adversarial network for imbalanced classification problem. IEEE Access 2020, 8, 91265–91275. [Google Scholar] [CrossRef]
- Banu, S.R.; Gongada, T.N.; Santosh, K.; Chowdhary, H.; Sabareesh, R.; Muthuperumal, S. Financial Fraud Detection Using Hybrid Convolutional and Recurrent Neural Networks: An Analysis of Unstructured Data in Banking. In Proceedings of the 2024 10th International Conference on Communication and Signal Processing (ICCSP), Sanya, China, 20–22 December 2024; pp. 1027–1031. [Google Scholar] [CrossRef]
- Gupta, S.; Keshari, A.; Das, S. Rv-gan: Recurrent gan for unconditional video generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2024–2033. [Google Scholar]
- Yang, Z.; Li, Y.; Zhou, G. Ts-gan: Time-series gan for sensor-based health data augmentation. ACM Trans. Comput. Healthc. 2023, 4, 1–21. [Google Scholar] [CrossRef]
- Forough, J.; Momtazi, S. Sequential credit card fraud detection: A joint deep neural network and probabilistic graphical model approach. Expert Syst. 2021, 39, 1–13. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent Neural Networks: A Comprehensive Review of Architectures, Variants, and Applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Rusch, T.K.; Mishra, S. Unicornn: A recurrent model for learning very long time dependencies. In Proceedings of the International Conference on Machine Learning. PMLR, Online, 18–24 July 2021; pp. 9168–9178. [Google Scholar]
- Obaido, G.; Mienye, I.D.; Egbelowo, O.F.; Emmanuel, I.D.; Ogunleye, A.; Ogbuokiri, B.; Mienye, P.; Aruleba, K. Supervised machine learning in drug discovery and development: Algorithms, applications, challenges, and prospects. Mach. Learn. Appl. 2024, 17, 100576. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, S.; Jin, B. Sequential fault diagnosis based on LSTM neural network. IEEE Access 2018, 6, 12929–12939. [Google Scholar] [CrossRef]
- Oliveira, P.; Fernandes, B.; Analide, C.; Novais, P. Forecasting energy consumption of wastewater treatment plants with a transfer learning approach for sustainable cities. Electronics 2021, 10, 1149. [Google Scholar] [CrossRef]
- Yiğit, G.; Amasyali, M.F. Simple but effective GRU variants. In Proceedings of the 2021 International Conference on Innovations in Intelligent systems and Applications (INISTA), Kocaeli, Turkey, 25–27 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Jia, P.; Liu, H.; Wang, S.; Wang, P. Research on a mine gas concentration forecasting model based on a GRU network. IEEE Access 2020, 8, 38023–38031. [Google Scholar] [CrossRef]
- Zheng, W.; Chen, G. An accurate GRU-based power time-series prediction approach with selective state updating and stochastic optimization. IEEE Trans. Cybern. 2021, 52, 13902–13914. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. A Machine Learning Method with Hybrid Feature Selection for Improved Credit Card Fraud Detection. Appl. Sci. 2023, 13, 7254. [Google Scholar] [CrossRef]
- Mienye, I.D.; Jere, N. Optimized Ensemble Learning Approach with Explainable AI for Improved Heart Disease Prediction. Information 2024, 15, 394. [Google Scholar] [CrossRef]
- Aniceto, M.C.; Barboza, F.; Kimura, H. Machine learning predictivity applied to consumer creditworthiness. Future Bus. J. 2020, 6, 37. [Google Scholar] [CrossRef]
- Hoo, Z.H.; Candlish, J.; Teare, D. What is an ROC curve? Emerg. Med. J. 2017, 34, 357–359. [Google Scholar] [CrossRef] [PubMed]
- Gandhar, A.; Gupta, K.; Pandey, A.K.; Raj, D. Fraud Detection Using Machine Learning and Deep Learning. SN Comput. Sci. 2024, 5, 453. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Y.; Xu, W.; Wang, Q. HOBA: A novel feature engineering methodology for credit card fraud detection with a deep learning architecture. Inf. Sci. 2021, 557, 302–316. [Google Scholar] [CrossRef]
- Madhurya, M.J.; Gururaj, H.L.; Soundarya, B.C.; Vidyashree, K.P.; Rajendra, A.B. Exploratory analysis of credit card fraud detection using machine learning techniques. Glob. Transitions Proc. 2022, 3, 31–37. [Google Scholar] [CrossRef]
- Varmedja, D.; Karanovic, M.; Sladojevic, S.; Arsenovic, M.; Anderla, A. Credit Card Fraud Detection - Machine Learning methods. In Proceedings of the 2019 18th International Symposium INFOTEH-JAHORINA (INFOTEH), Jahorina, Republic of Srpska, 20–21 March 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Awoyemi, J.O.; Adetunmbi, A.O.; Oluwadare, S.A. Credit card fraud detection using machine learning techniques: A comparative analysis. In Proceedings of the 2017 International Conference on Computing Networking and Informatics (ICCNI), Lagos, Nigeria, 29–31 October 2017; pp. 1–9. [Google Scholar] [CrossRef]
- Alarfaj, F.K.; Malik, I.; Khan, H.U.; Almusallam, N.; Ramzan, M.; Ahmed, M. Credit Card Fraud Detection Using State-of-the-Art Machine Learning and Deep Learning Algorithms. IEEE Access 2022, 10, 39700–39715. [Google Scholar] [CrossRef]
- Mrozek, P.; Panneerselvam, J.; Bagdasar, O. Efficient Resampling for Fraud Detection During Anonymised Credit Card Transactions with Unbalanced Datasets. In Proceedings of the 2020 IEEE/ACM 13th International Conference on Utility and Cloud Computing (UCC), Leicester, UK, 7–10 December 2020; pp. 426–433. [Google Scholar] [CrossRef]
- Almarshad, F.A.; Gashgari, G.A.; Alzahrani, A.I.A. Generative Adversarial Networks-Based Novel Approach for Fraud Detection for the European Cardholders 2013 Dataset. IEEE Access 2023, 11, 107348–107368. [Google Scholar] [CrossRef]
- Khalid, A.R.; Owoh, N.; Uthmani, O.; Ashawa, M.; Osamor, J.; Adejoh, J. Enhancing Credit Card Fraud Detection: An Ensemble Machine Learning Approach. Big Data Cogn. Comput. 2024, 8, 6. [Google Scholar] [CrossRef]
- Jain, V.; Kavitha, H.; Mohana Kumar, S. Credit Card Fraud Detection Web Application using Streamlit and Machine Learning. In Proceedings of the 2022 IEEE International Conference on Data Science and Information System (ICDSIS), Hassan, India, 29–30 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Lin, T.H.; Jiang, J.R. Credit Card Fraud Detection with Autoencoder and Probabilistic Random Forest. Mathematics 2021, 9, 2683. [Google Scholar] [CrossRef]
- Najadat, H.; Altiti, O.; Aqouleh, A.A.; Younes, M. Credit card fraud detection based on machine and deep learning. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Online, 7–9 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 204–208. [Google Scholar]
- Alwan, R.H.; Hamad, M.M.; Dawood, O.A. Credit Card Fraud Detection in Financial Transactions Using Data Mining Techniques. In Proceedings of the 2021 7th International Conference on Contemporary Information Technology and Mathematics (ICCITM), Mosul, Iraq, 25–26 August 2021; IEEE: Piscataway, NJ, USA, 2021; Volume 8. [Google Scholar] [CrossRef]
- RB, A.; KR, S.K. Credit card fraud detection using artificial neural network. Glob. Transitions Proc. 2021, 2, 35–41. [Google Scholar] [CrossRef]
- Dhankhad, S.; Mohammed, E.; Far, B. Supervised Machine Learning Algorithms for Credit Card Fraudulent Transaction Detection: A Comparative Study. In Proceedings of the 2018 IEEE International Conference on Information Reuse and Integration for Data Science (IRI), Salt Lake City, UT, USA, 6–9 July 2018; IEEE: Piscataway, NJ, USA, 2018; Volume 7. [Google Scholar] [CrossRef]
- Alfaiz, N.S.; Fati, S.M. Enhanced Credit Card Fraud Detection Model Using Machine Learning. Electronics 2022, 11, 662. [Google Scholar] [CrossRef]
- Dighe, D.; Patil, S.; Kokate, S. Detection of Credit Card Fraud Transactions Using Machine Learning Algorithms and Neural Networks: A Comparative Study. In Proceedings of the 2018 Fourth International Conference on Computing Communication Control and Automation (ICCUBEA), Pune, India, 16–18 August 2018; IEEE: Piscataway, NJ, USA, 2018; Volume 8. [Google Scholar] [CrossRef]
- Nadim, A.H.; Sayem, I.M.; Mutsuddy, A.; Chowdhury, M.S. Analysis of Machine Learning Techniques for Credit Card Fraud Detection. In Proceedings of the 2019 International Conference on Machine Learning and Data Engineering (iCMLDE), Taipei, Taiwan, 2–4 December 2019; IEEE: Piscataway, NJ, USA, 2019; Volume 12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).