Ant Colony Algorithm for Energy Saving to Optimize Three-Dimensional Bonding Chips’ Thermal Layout
Abstract
:1. Introduction
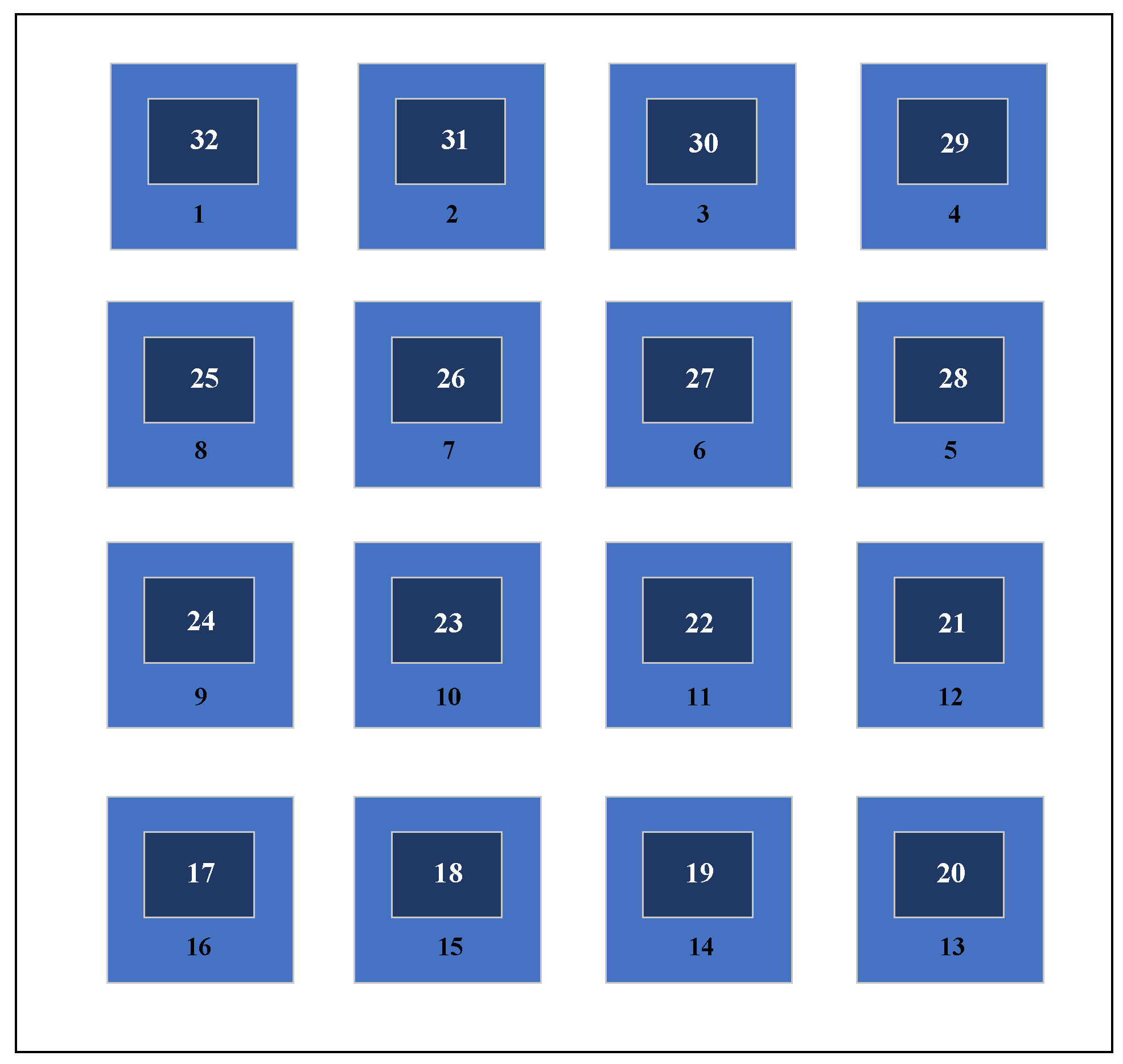
2. Description of Chip Layout
2.1. Establishment of Ant Colony Optimization Model
2.2. The Selection of Fitness Function
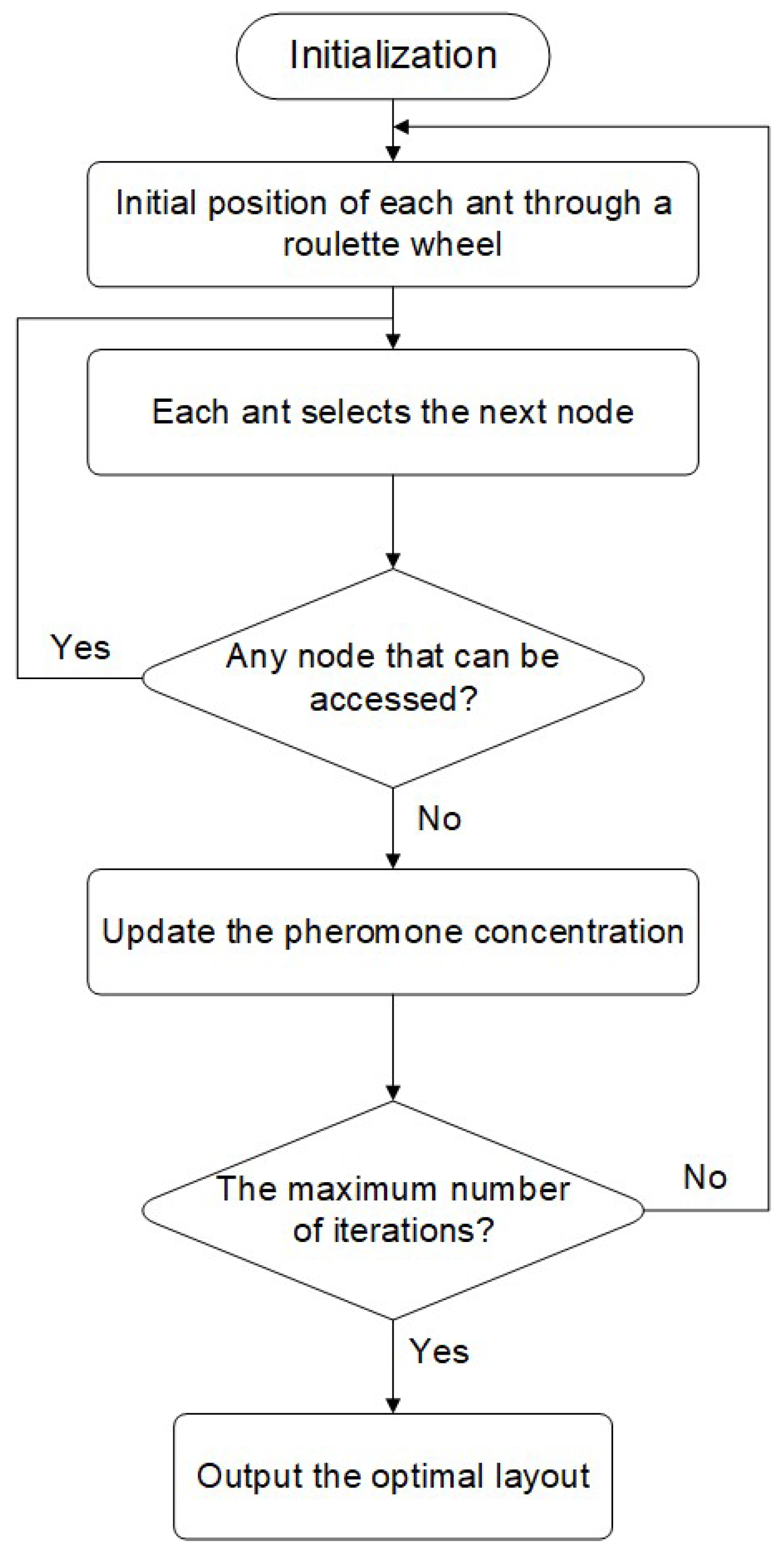
2.3. Algorithm Steps
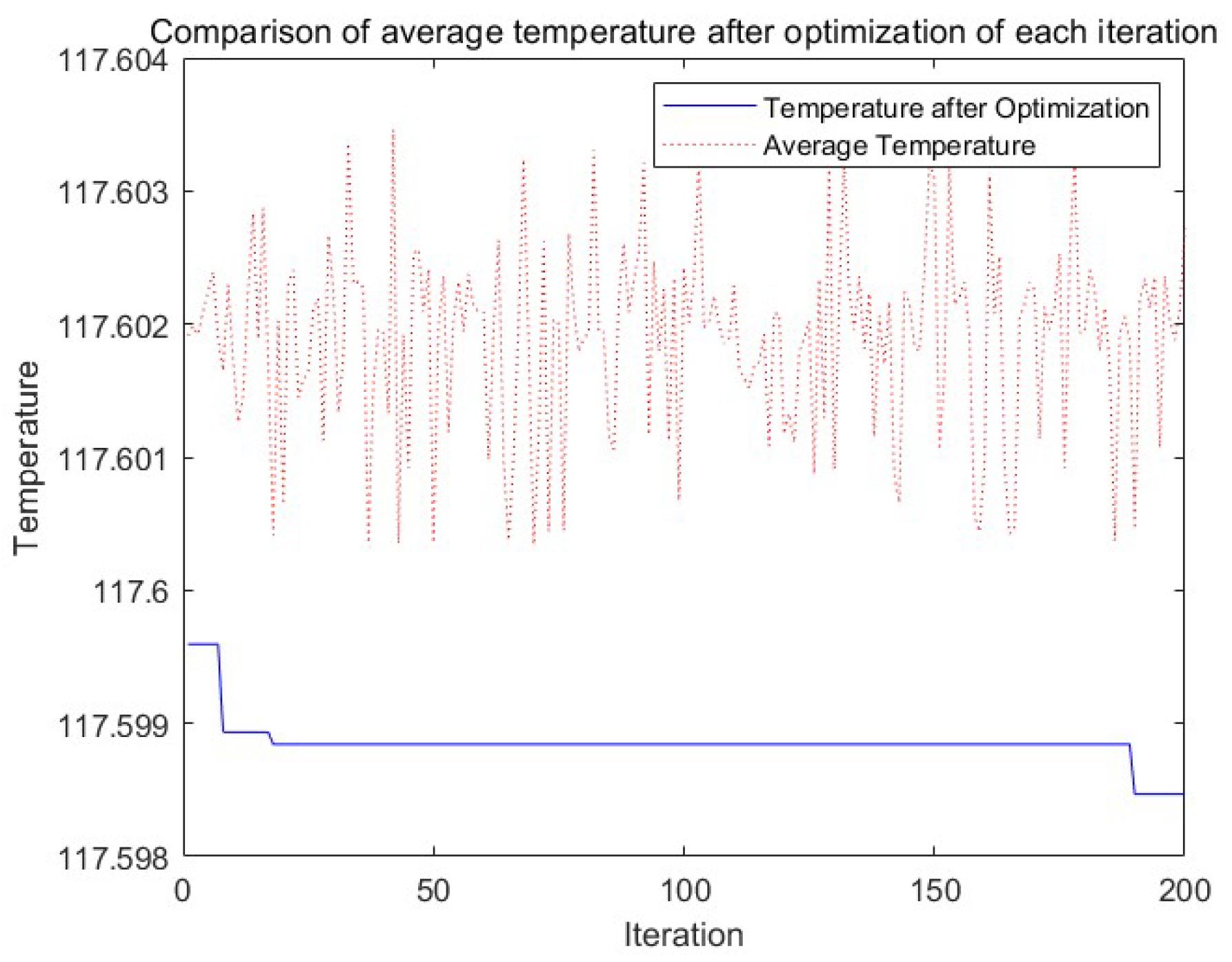
3. Simulation Results and Analysis of the Algorithm
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chung, W.C.; Cheng, P.Y.; Li, Z.; Ho, T.Y. Module Placement under Completion Time Uncertainty in Micro-Electrode-Dot-Array Digital Microfluidic Biochips. IEEE Trans. Multi-Scale Comput. Syst. 2018, 4, 811–821. [Google Scholar] [CrossRef]
- Arpan, C.; Piyali, D.; Rajat, K.P. A New Fluid-Chip Co-Design for Digital Microfluidic Biochips Considering Cost Drivers and Design Convergence. IEEE Trans. Multi-Scale Comput. Syst. 2018, 4, 548–564. [Google Scholar]
- Sung, T.T.; Ryu, B. SoC RATES: System-on-Chip Resource Adaptive Scheduling using Deep Reinforcement Learning. arXiv 2021, arXiv:2104.14354. [Google Scholar] [CrossRef]
- Ning, Y.; Jie, Y.; Ye, T. Thermal Chips Layout Method in MCM Based on an Improved Particle Swarm Algorithm. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Y.; Gao, H.; Li, C.; Luo, H.; Li, W.; He, X. A Layout Optimization Method to Reduce Commutation Inductance of Multi-Chip Power Module Based on Genetic Algorithm. In Proceedings of the 2021 IEEE Workshop on Wide Bandgap Power Devices and Applications in Asia (WiPDA Asia), Wuhan, China, 25–27 August 2021; pp. 247–252. [Google Scholar] [CrossRef]
- Al Razi, I.; Le, Q.; Evans, T.M.; Mukherjee, S.; Mantooth, H.A.; Peng, Y. PowerSynth Design Automation Flow for Hierarchical and Heterogeneous 2.5-D Multichip Power Modules. IEEE Trans. Power Electron. 2021, 36, 8919–8933. [Google Scholar] [CrossRef]
- Chung-Kuan, C.; Kahng, A.B.; Kang, I.; Wang, L. RePlAce: Advancing Solution Quality and Routability Validation in Global Placement. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 38, 1717–1730. [Google Scholar] [CrossRef]
- Lu, J.; Chen, P.; Chang, C.C.; Sha, L.; Huang, D.J.H.; Teng, C.C.; Cheng, C.K. ePlace: Electrostatics based placement using Nesterov’s method. In Proceedings of the 2014 51st ACM/EDAC/IEEE Design Automation Conference, San Francisco, CA, USA, 1–5 June 2014. [Google Scholar]
- Fukushima, T.; Bea, J.; Mariappan, M.; Koyanagi, M.; Son, H.-Y.; Suh, M.-S.; Byun, K.-Y.; Kim, N.-S.; Lee, K.-W.; Koyanagi, M. 3D memory chip stacking by multi-layer self-assembly technology. In Proceedings of the 2013 IEEE International 3D Systems Integration Conference (3DIC), San Francisco, CA, USA, 2–4 October 2013. [Google Scholar]
- Nayini, M.; Questad, D.; Farooq, M. Finite Element Method (FEM) simulation based analysis for optimal chip layout of a 2.5D flip chip package. In Proceedings of the 2018 IEEE SOI-3D-Subthreshold Microelectronics Technology Unified Conference (S3S), Burlingame, CA, USA, 15–18 October 2018. [Google Scholar]
- Budhathoki, P.; Knechtel, J.; Henschel, A.; Elfadel, I.A.M. Integration of thermal management and floorplanning based on three-dimensional layout representations. In Proceedings of the 2013 IEEE 20th International Conference on Electronics, Circuits, and Systems (ICECS), Abu Dhabi, United Arab Emirates, 8–11 December 2013. [Google Scholar]
- Doan, N.A.V.; Robert, F.; Smety, Y.D.; Milojevic, D. MCDA-based methodology for efficient 3D-design space exploration and decision. In Proceedings of the 2010 International Symposium on System on Chip, Tampere, Finland, 29–30 September 2010. [Google Scholar]
- Beura, S.; Majhi, B.; Dash, R. Mammogram classification using two dimensional discrete wavelet transform and gray-level co-occurrence matrix for detection of breast cancer. Neurocomputing 2015, 154, 1–14. [Google Scholar] [CrossRef]
- Jiao, Z.; Gao, X.; Wang, Y.; Li, J. A deep feature based framework for breast masses classification. Neurocomputing 2016, 197, 221–231. [Google Scholar] [CrossRef]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed event-triggered control for multi-agent systems. IEEE Trans. Autom. Control. 2011, 57, 1291–1297. [Google Scholar] [CrossRef]
- Li, W.; Gao, S. Prospective on energy related carbon emissions peak integrating optimized intelligent algorithm with dry process technique application for China’s cement industry. Energy 2018, 165, 33–54. [Google Scholar] [CrossRef]
- Guo, W.; Deng, F.; Meng, Z.; Hua, L.; Mao, H.; Su, J. A hybrid back-propagation neural network and intelligent algorithm combined algorithm for optimizing microcellular foaming injection molding process parameters. J. Manuf. Process. 2020, 50, 528–538. [Google Scholar] [CrossRef]
- Kim, J.; Schoeller, H.; Cho, J.; Park, S. Effect of oxidation on indium solderability. J. Electron. Mater. 2008, 37, 483–489. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar]
- Sivanandam, S.N.; Deepa, S.N. Genetic algorithm optimization problems. In Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 165–209. [Google Scholar]
- Qasim, T.; Zia, M.; Minhas, Q.A.; Bhatti, N.; Saleem, K.; Qasima, T.; Mahmood, H. An ant colony optimization based approach for minimum cost coverage on 3-D grid in wireless sensor networks. IEEE Commun. Lett. 2018, 22, 1140–1143. [Google Scholar] [CrossRef]
- Tibaldi, M.; Pilato, C.; Ferrandi, F. Automatic Generation of Heterogeneous SoC Architectures with Secure Communications. IEEE Embed. Syst. Lett. 2021, 13, 61–64. [Google Scholar] [CrossRef]
- Manogaran, G.; Alazab, M. Ant-inspired recurrent deep learning model for improving the service flow of intelligent transportation systems. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3654–3663. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Pan, Z.L. Optimization of 3D Stacking Chip Thermal Layout Based on Genetic Particle Swarm Algorithm. Electron. Process Technol. 2019, 5, 249–252, 260. (In Chinese) [Google Scholar] [CrossRef]
- Mishra, S. A hybrid least square-fuzzy bacterial foraging strategy for harmonic estimation. IEEE Trans. Evol. Comput. 2005, 9, 61–73. [Google Scholar] [CrossRef]
- Cheng, H.C. Thermal Chip Placement in MCMs Using a Novel Hybrid Optimization Algorithm. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 764–774. [Google Scholar] [CrossRef]
- Lee, J. A reliability-driven placement procedure based on thermal-force model. Microelectron. Reliab. 2006, 46, 973–983. [Google Scholar] [CrossRef]
- Lall, B.S.; Ortega, A.; Kabir, H. Thermal design rules for electronic components on conducting boards in passively cooled enclosures. In Proceedings of the 1994 4th Intersociety Conference on Thermal Phenomena in Electronic Systems (I-THERM), Washington, DC, USA, 4–7 May 1994; pp. 50–61. [Google Scholar]
- Rencz, M. Thermal issues in stacked die packages. In Proceedings of the Semiconductor Thermal Measurement and Management IEEE Twenty First Annual IEEE Symposium, San Jose, CA, USA, 15–17 March 2005; pp. 307–312. [Google Scholar]
- Szabo, P.; Poppe, A.; Farkas, G.; Szekely, V.; Courtois, B.; Rencz, M. Thermal characterization and compact modeling of stacked die packages. In Proceedings of the Thermal and Thermomechanical Proceedings 10th Intersociety Conference on Phenomena in Electronics Systems, 2006, ITHERM 2006, San Diego, CA, USA, 30 May–2 June 2006; pp. 251–257. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Yang, P.; Zhu, Z. Ant Colony Algorithm for Energy Saving to Optimize Three-Dimensional Bonding Chips’ Thermal Layout. Technologies 2023, 11, 122. https://doi.org/10.3390/technologies11050122
Sun B, Yang P, Zhu Z. Ant Colony Algorithm for Energy Saving to Optimize Three-Dimensional Bonding Chips’ Thermal Layout. Technologies. 2023; 11(5):122. https://doi.org/10.3390/technologies11050122
Chicago/Turabian StyleSun, Bihao, Peizhi Yang, and Zhiyuan Zhu. 2023. "Ant Colony Algorithm for Energy Saving to Optimize Three-Dimensional Bonding Chips’ Thermal Layout" Technologies 11, no. 5: 122. https://doi.org/10.3390/technologies11050122
APA StyleSun, B., Yang, P., & Zhu, Z. (2023). Ant Colony Algorithm for Energy Saving to Optimize Three-Dimensional Bonding Chips’ Thermal Layout. Technologies, 11(5), 122. https://doi.org/10.3390/technologies11050122





