FPGA-Based Implementation of a New 3-D Multistable Chaotic Jerk System with Two Unstable Balance Points
Abstract
1. Introduction
- (1)
- We propose a new dissipative chaotic jerk system having three quadratic nonlinear terms.
- (2)
- We establish that the new chaotic jerk system has two unstable equilibrium points, which implies that the new system exhibits a self-excited chaotic attractor.
- (3)
- We carry out a detailed bifurcation analysis of the new jerk system which shows the changes in the dynamic behavior of the jerk system with respect to changes in the system parameters.
- (4)
- We establish that the new jerk system has multistability with coexisting chaotic attractors.
- (5)
- We provide a control application of the new jerk system, viz. complete synchronization of the new jerk systems via backstepping control.
- (6)
- We design an FPGA implementation of the new chaotic jerk system.
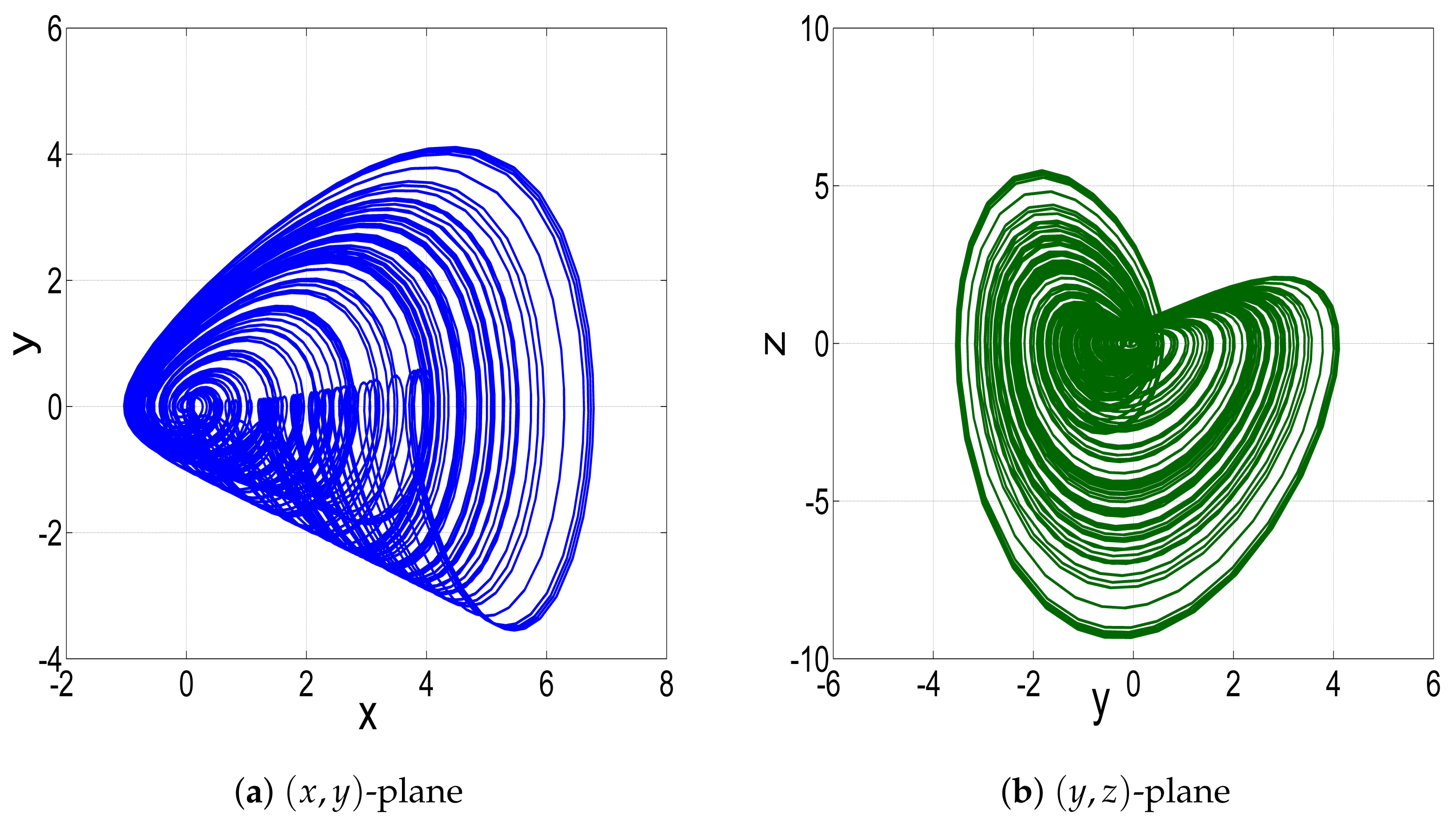
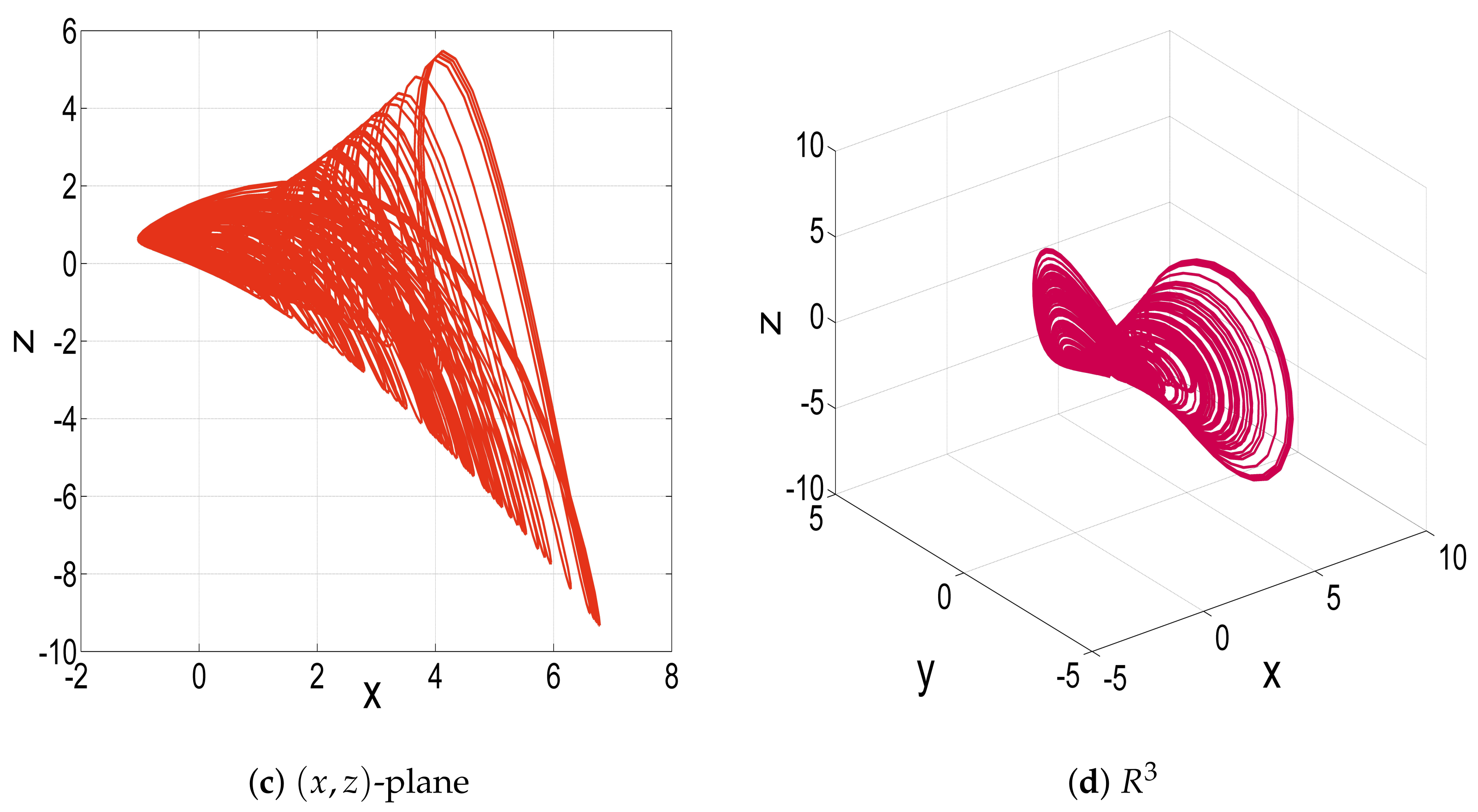
2. A New 3-D Jerk System
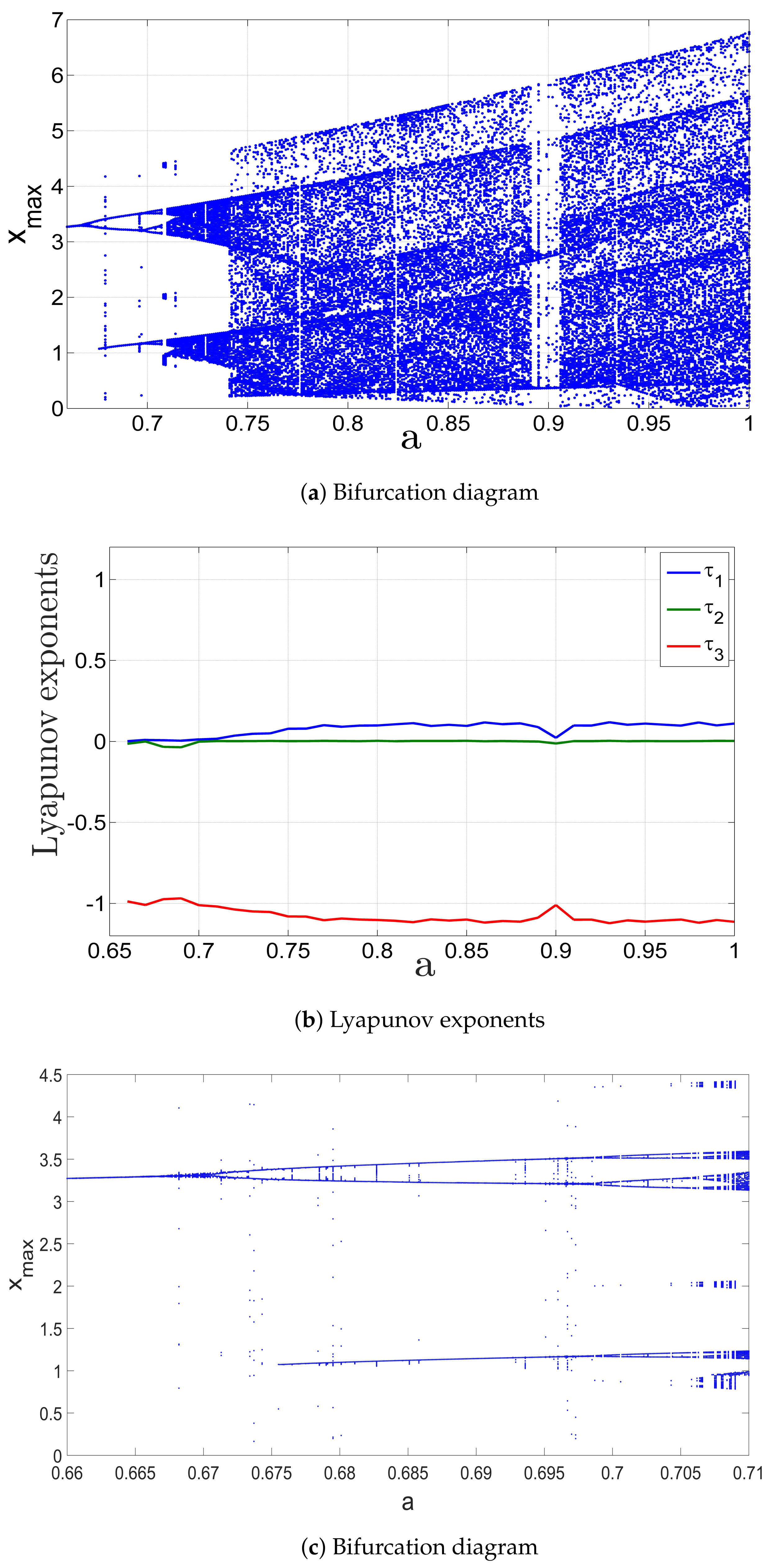
3. Bifurcation Analysis for the New 3-D Jerk System
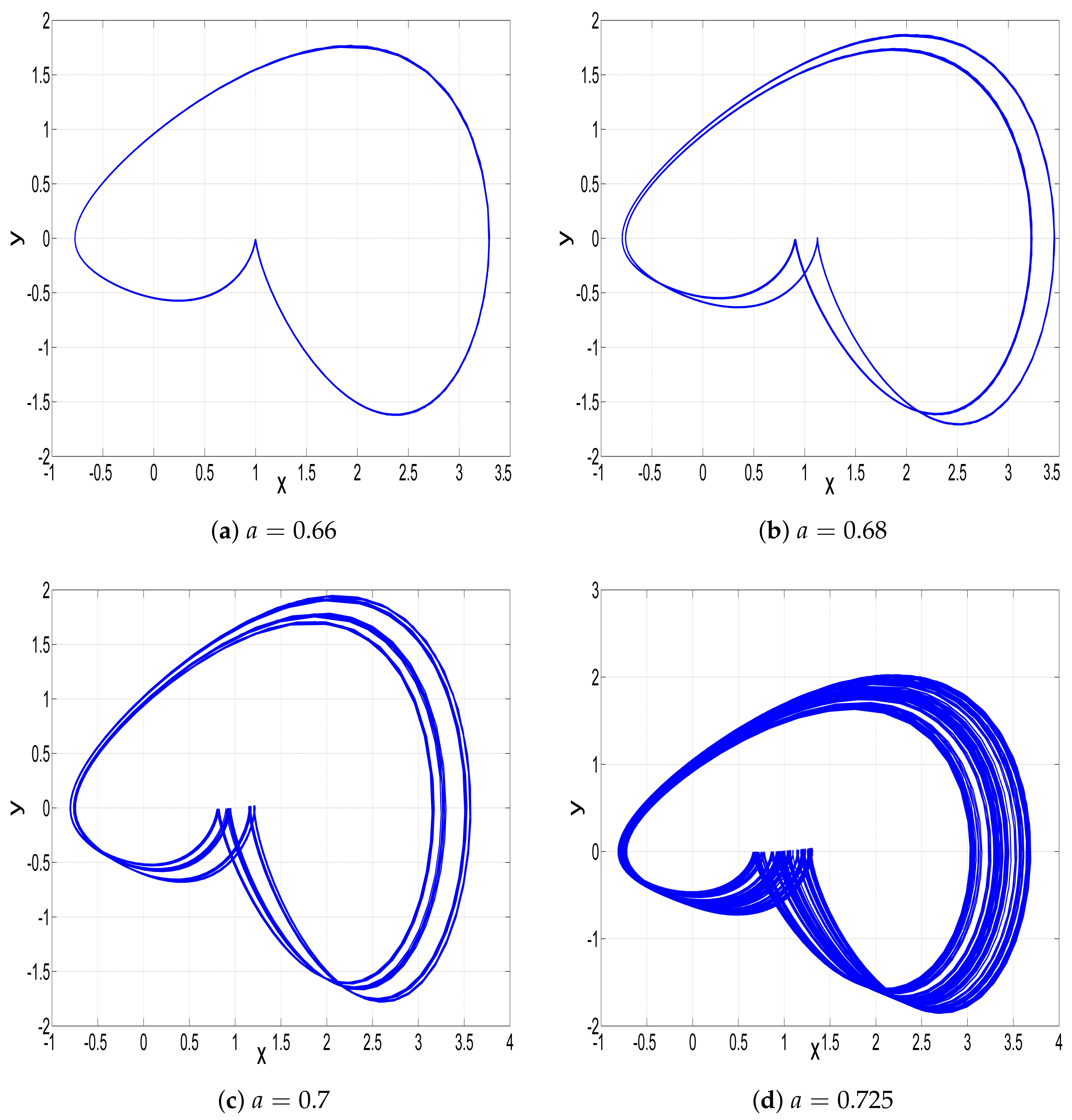
3.1. When the Parameter a Varies
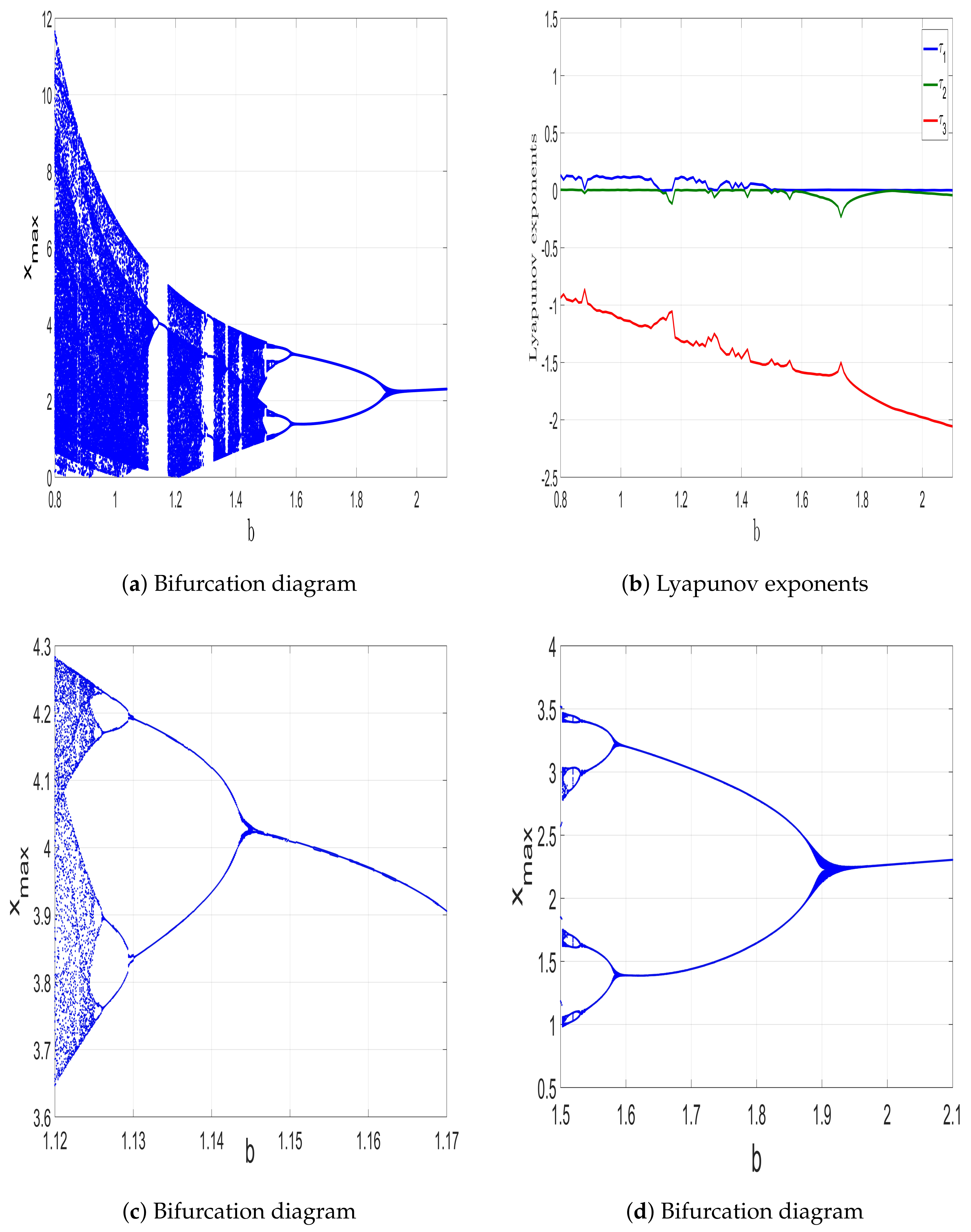
3.2. When the Parameter b Varies
3.3. When the Parameter c Varies
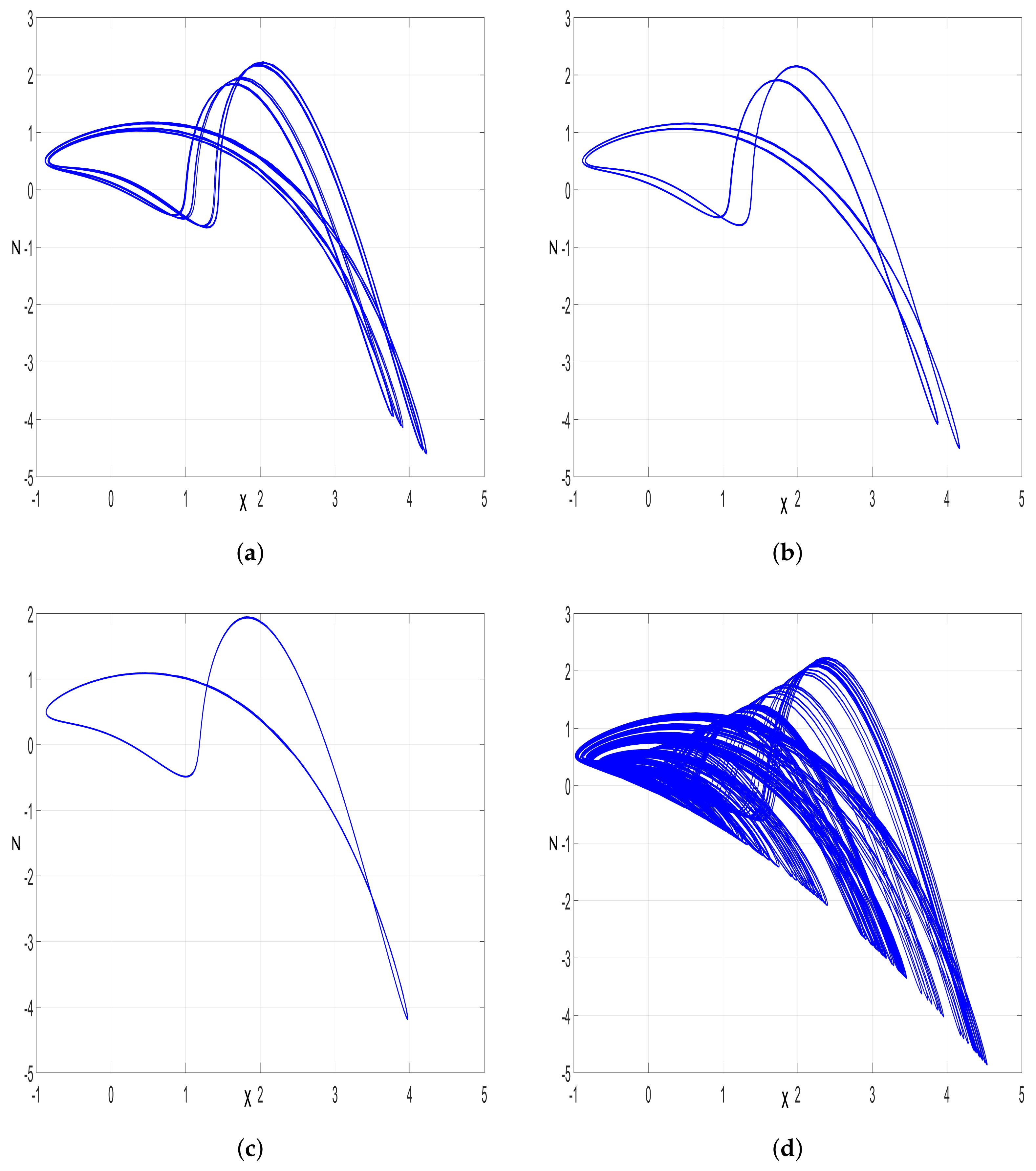
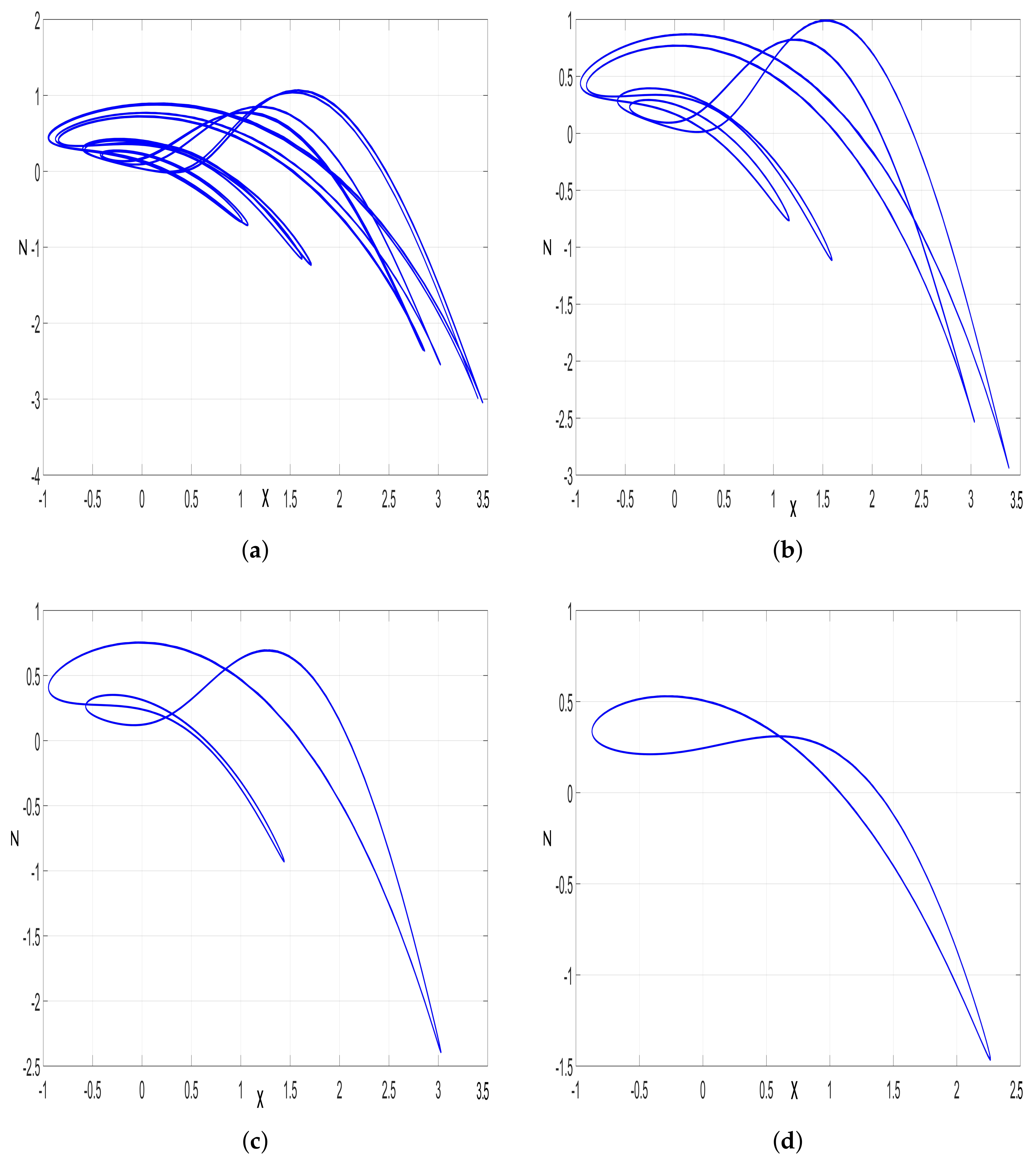
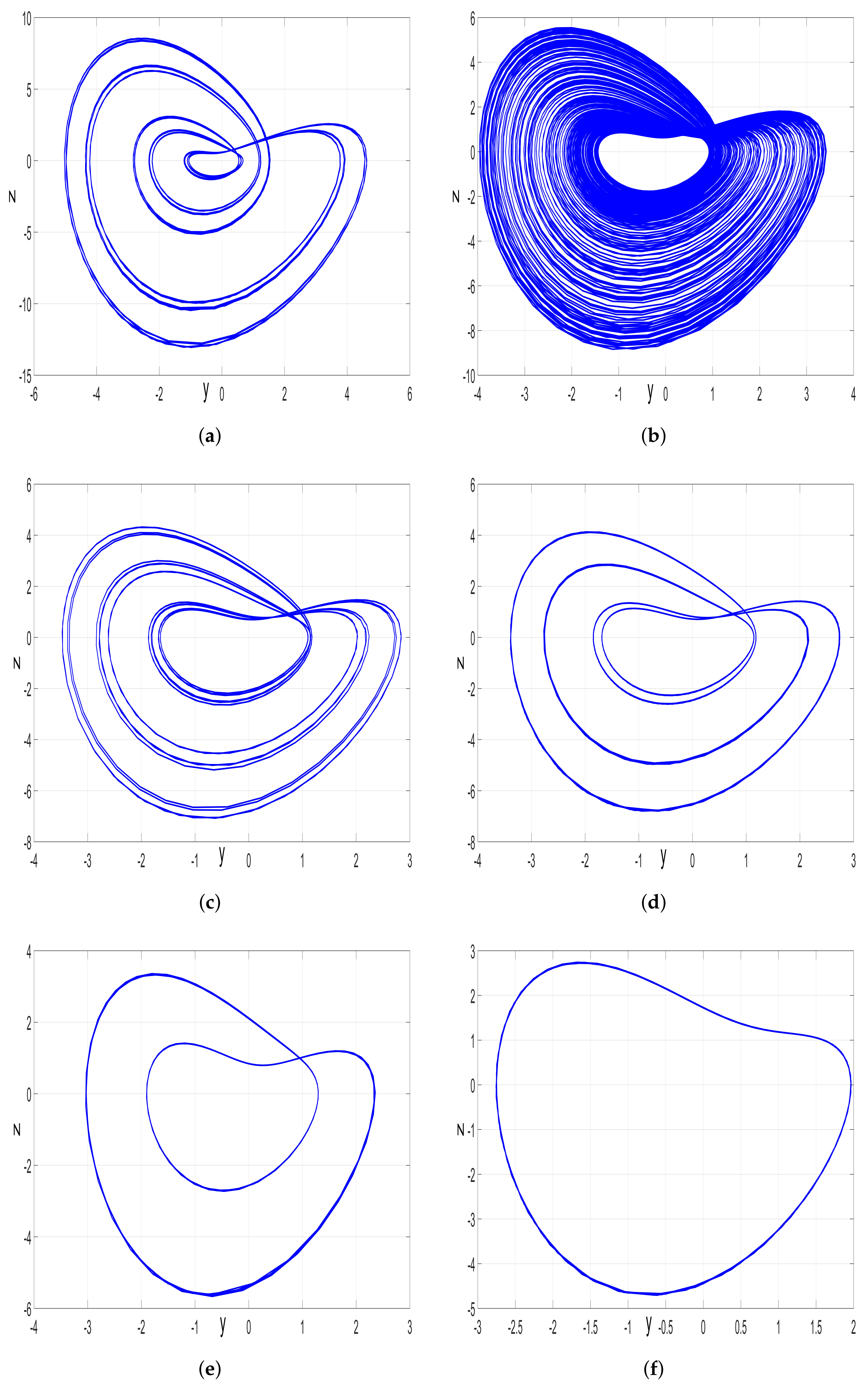
4. Multistability of the Jerk System
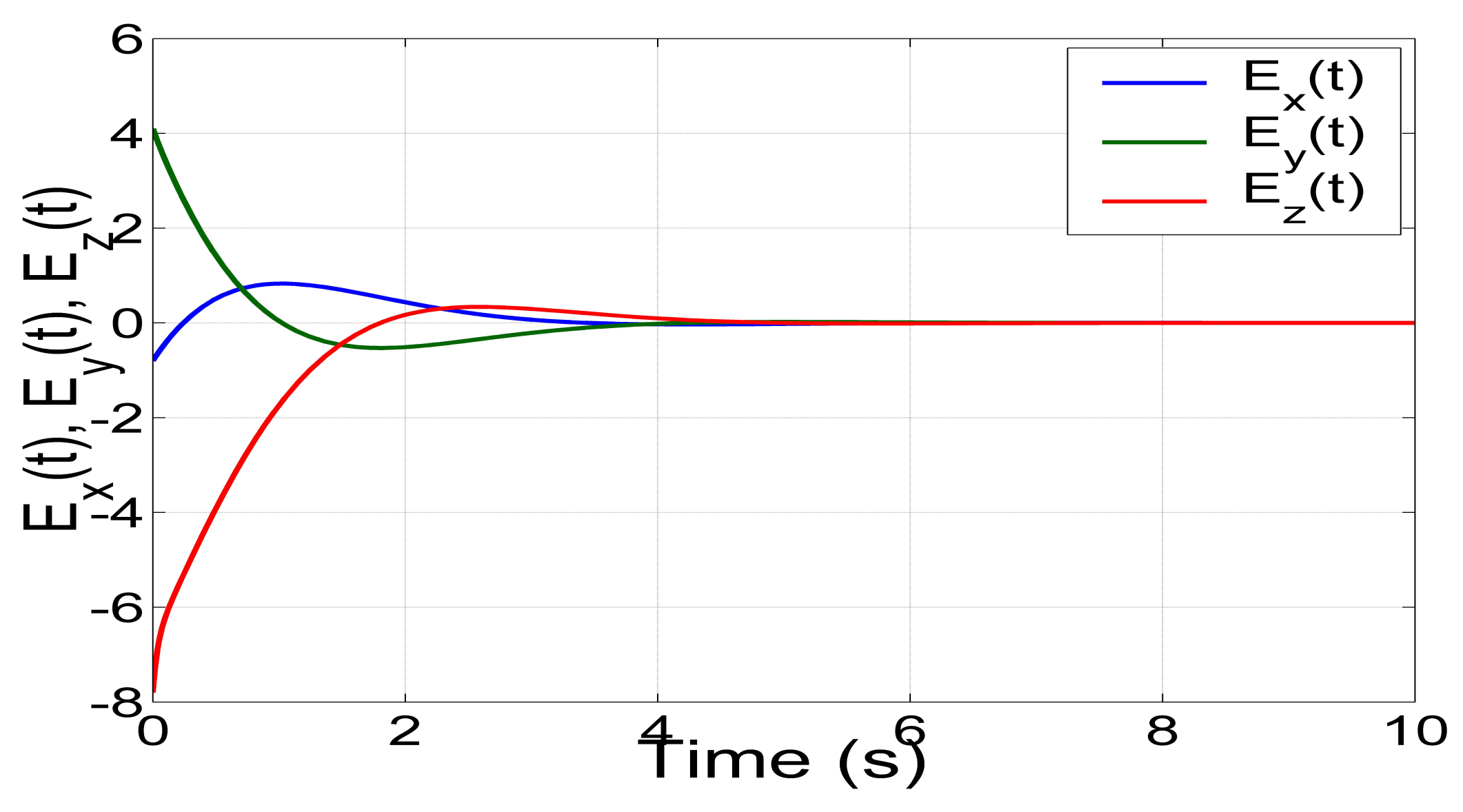
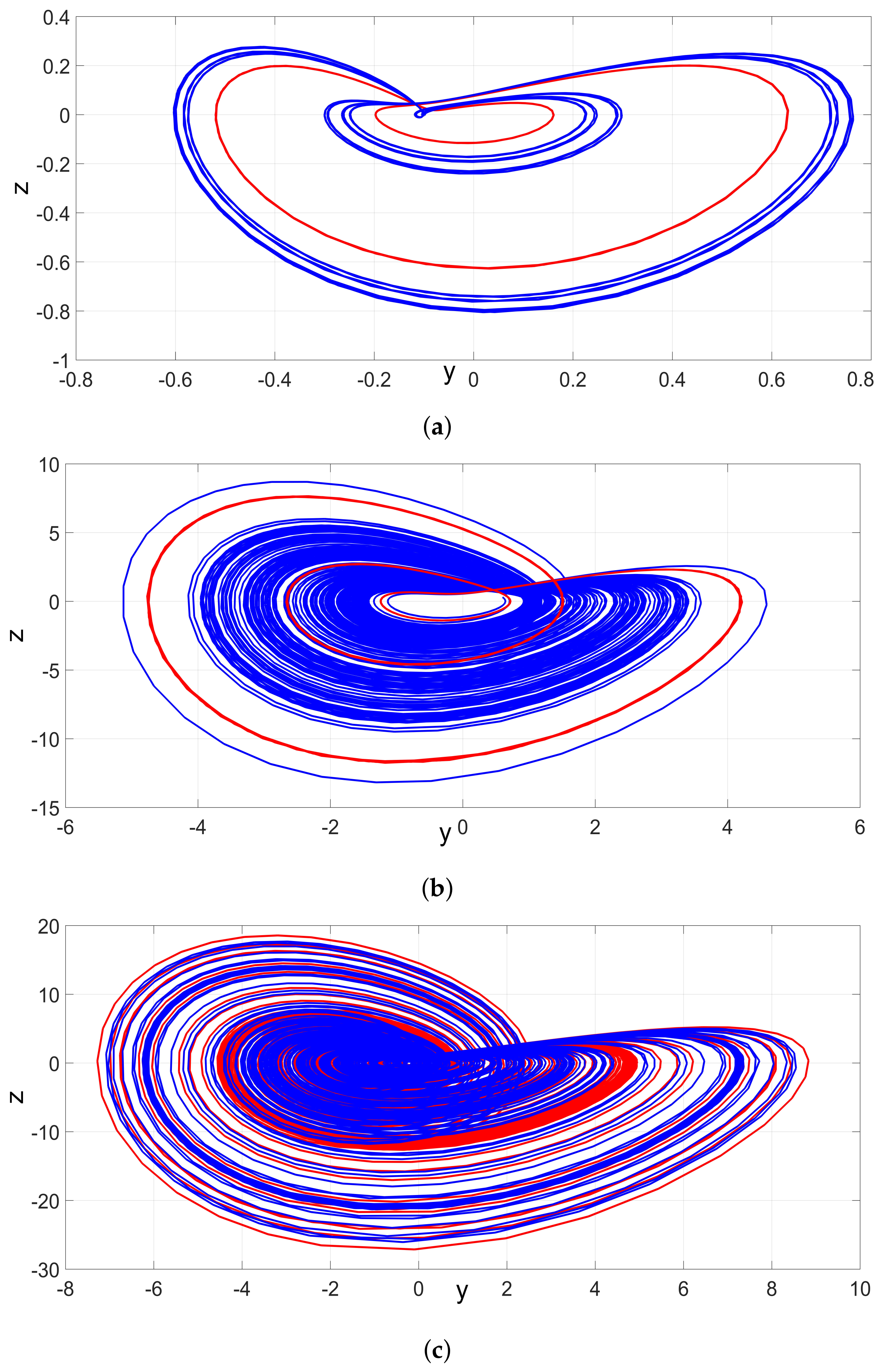
5. Complete Synchronization of the New Jerk Systems Using Backstepping Control
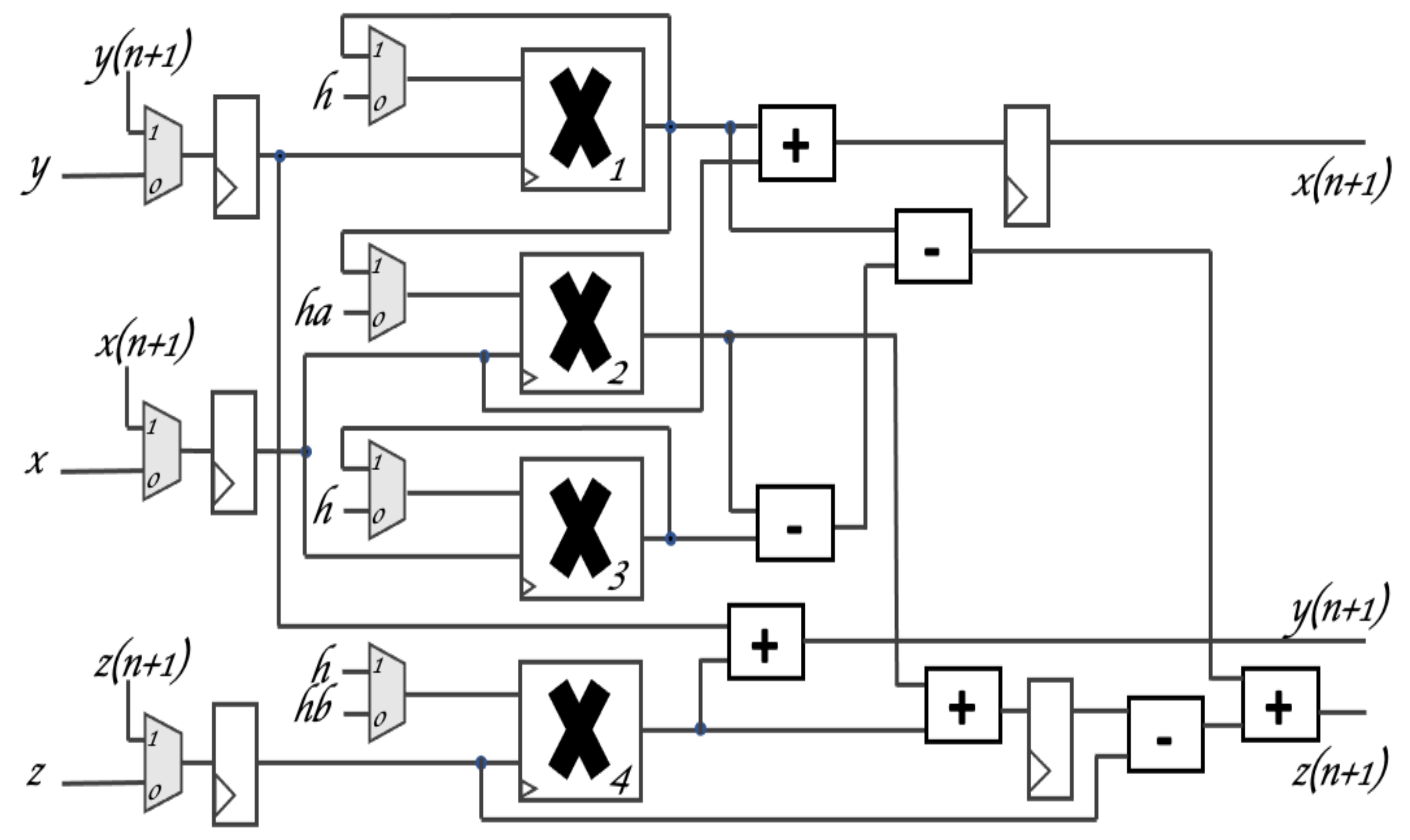
6. FPGA Implementation of the New Jerk System
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reis, E.V.; Savi, M.A. Spatiotemporal chaos in a conservative Duffing-type system. Chaos Solitons Fractals 2022, 165, 112776. [Google Scholar] [CrossRef]
- Cai, C.; Shen, Y.; Wen, S. Primary and super-harmonic simultaneous resonance of van der Pol oscillator. Int. J. Non-Linear Mech. 2022, 147, 104237. [Google Scholar] [CrossRef]
- Madiot, G.; Correia, F.; Barbay, S.; Braive, R. Random number generation with a chaotic electromechanical resonator. Nanotechnology 2022, 33, 475204. [Google Scholar] [CrossRef]
- Balamurali, R.; Telem, A.N.K.; Kengne, J.; Rajagopal, K.; Hermann-Dior, M.E. On the mechanism of multiscroll chaos generation in coupled non-oscillatory Rayleigh-Duffing oscillators. Phys. Scr. 2022, 97, 105207. [Google Scholar] [CrossRef]
- Liu, H. Audio block encryption using 3D chaotic system with adaptive parameter perturbation. Multimed. Tools Appl. 2023, 82, 27973–27987. [Google Scholar] [CrossRef]
- Dongmo, E.D.; Ramadoss, J.; Tchamda, A.R.; Sone, M.E.; Rajagopal, K. FPGA implementation, controls and synchronization of autonomous Josephson junction jerk oscillator. Phys. Scr. 2023, 98, 035224. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Madian, A.H.; Radwan, A.G.; Said, L.A. An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics 2023, 12, 1219. [Google Scholar] [CrossRef]
- Dridi, F.; El Assad, S.; Youssef, W.E.H.; Machhout, M. Design, Hardware Implementation on FPGA and Performance Analysis of Three Chaos-Based Stream Ciphers. Fractal Fract. 2023, 7, 197. [Google Scholar] [CrossRef]
- Sun, J.Y.; Cai, H.; Wang, G.; Gao, Z.B.; Zhang, H. FPGA image encryption-steganography using a novel chaotic system with line equilibria. Digit. Signal Process. 2023, 134, 103889. [Google Scholar]
- Sprott, J.C. Some simple chaotic jerk functions. Am. J. Phys. 1997, 65, 537–543. [Google Scholar] [CrossRef]
- Sun, K.H.; Sprott, J.C. A simple jerk system with piecewise exponential nonlinearity. Int. J. Nonlinear Sci. Numer. Simul. 2000, 10, 1443–1450. [Google Scholar] [CrossRef]
- Liu, M.; Sang, B.; Wang, N.; Ahmad, I. Chaotic dynamics by some quadratic jerk systems. Axioms 2021, 10, 227. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N.; Pham, V.T. Analysis, adaptive control and anti-synchronization of a six-term novel jerk chaotic system with two exponential nonlinearities and its circuit simulation. J. Eng. Sci. Technol. Rev. 2021, 8, 24–36. [Google Scholar] [CrossRef]
- Rajagopal, K.; Pham, V.T.; Tahir, F.R.; Akgul, A.; Abdolmohammadi, H.R.; Jafari, S. A chaotic jerk system with non-hyperbolic equilibrium: Dynamics, effect of time delay and circuit realisation. Pramana J. Phys. 2018, 90, 52. [Google Scholar] [CrossRef]
- Ramakrishnan, B.; Tamba, V.K.; Natiq, H.; Tsafack, A.S.K.; Karthikeyan, A. Dynamical analysis of autonomous Josephson junction jerk oscillator with cosine interference term embedded in FPGA and investigation of its collective behavior in a network. Eur. Phys. J. B 2022, 95, 145. [Google Scholar] [CrossRef]
- Tagne, S.; Bodo, B.; Eyebe, G.F.V.A.; Fouda, J.S.A.E. PIC micro-controller based synchronization of two fractional order jerk systems. Sci. Rep. 2022, 12, 14281. [Google Scholar] [CrossRef]
- Wang, Q.; Tian, Z.; Wu, X.; Tan, W. Coexistence of multiple attractors in a novel simple jerk chaotic circuit with CFOAs implementation. Front. Phys. 2022, 10, 835188. [Google Scholar] [CrossRef]
- Wei, M.; Han, X.; Ma, X.; Zou, Y.; Bi, Q. Bursting patterns with complex structures in a parametrically and externally excited Jerk circuit system. Eur. Phys. J. Spec. Top. 2022, 231, 2265–2275. [Google Scholar] [CrossRef]
- Kamdem Tchiedjo, S.; Kamdjeu Kengne, L.; Kengne, J.; Djuidje Kenmoe, G. Dynamical behaviors of a chaotic jerk circuit based on a novel memristive diode emulator with a smooth symmetry control. Eur. Phys. J. Plus 2022, 137, 940. [Google Scholar] [CrossRef]
- Kengne, L.K.; Muni, S.S.; Chedjou, J.C.; Kyandoghere, K. Various coexisting attractors, asymmetry analysis and multistability control in a 3D memristive jerk system. Eur. Phys. J. Plus 2022, 137, 848. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Feudjio, C.; Signing, V.F.; Koumetio, B.N.; Tsafack, N.; Awrejcewicz, J. Circuit and microcontroller validation of the extreme multistable dynamics of a memristive Jerk system: Application to image encryption. Eur. Phys. J. Plus 2022, 137, 619. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Cruz-Hernández, C.; Martínez-Clark, R. A new simple chaotic LLorenz-type system and its digital realization using a TFT touch-screen display embedded system. Complexity 2017, 2017, 6820492. [Google Scholar] [CrossRef]
- Gupta, A.; Dubey, B. Bifurcation and chaos in a delayed eco-epidemic model induced by prey configuration. Chaos Solitons Fractals 2022, 165, 112785. [Google Scholar] [CrossRef]
- Xing, J.; Yang, Z.; Ren, Y. Analysis of bifurcation and chaotic behavior for the flexspline of an electromagnetic harmonic drive system with movable teeth transmission. Appl. Math. Model. 2022, 112, 467–485. [Google Scholar] [CrossRef]
- Yan, H.; Qiao, Y.; Ren, Z.; Duan, L.; Miao, J. Master–slave synchronization of fractional-order memristive MAM neural networks with parameter disturbances and mixed delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 120, 107152. [Google Scholar] [CrossRef]
- Kumar, S.; Prasad, R.P.; Nishad, C.; Tiwary, A.K.; Khan, F. Analysis and chaos synchronization of Genesio–Tesi system applying sliding mode control techniques. Int. J. Dyn. Control 2023, 11, 656–665. [Google Scholar] [CrossRef]
- Dousseh, Y.P.; Monwanou, A.V.; Koukpémèdji, A.A.; Miwadinou, C.H.; Chabi Orou, J.B. Dynamics analysis, adaptive control, synchronization and anti-synchronization of a novel modified chaotic financial system. Int. J. Dyn. Control 2023, 11, 862–876. [Google Scholar] [CrossRef]
- Benkouider, K.; Vaidyanathan, S.; Sambas, A.; Tlelo-Cuautle, E.; Abd El-Latif, A.A.; Abd-El-Atty, B.; Bermudez-Marquez, C.F.; Sulaiman, I.M.; Awwal, A.M.; Kumam, P. A New 5-D Multistable Hyperchaotic System With Three Positive Lyapunov Exponents: Bifurcation Analysis, Circuit Design, FPGA Realization and Image Encryption. IEEE Access 2022, 10, 90111–90132. [Google Scholar] [CrossRef]
- Valencia-Ponce, M.A.; Castañeda-Aviña, P.R.; Tlelo-Cuautle, E.; Carbajal-Gómez, V.H.; González-Díaz, V.R.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.C. CMOS OTA-based filters for designing fractional-order chaotic oscillators. Fractal Fract. 2021, 5, 122. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T. Backstepping Control of Nonlinear Dynamical Systems; Academic Press: New York, NY, USA, 2021. [Google Scholar]
- Dong, H.; Cao, J.; Liu, H. Observers-based event-triggered adaptive fuzzy backstepping synchronization of uncertain fractional order chaotic systems. Chaos 2023, 33, A366. [Google Scholar] [CrossRef]
- Yan, S.; Wang, J.; Wang, E.; Wang, Q.; Sun, X.; Li, L. A four-dimensional chaotic system with coexisting attractors and its backstepping control and synchronization. Integration 2023, 91, 67–78. [Google Scholar] [CrossRef]
- He, J.; Qiu, W.; Cai, J. Synchronization of hyperchaotic systems based on intermittent control and its application in secure communication. J. Adv. Comput. Intell. Intell. Inform. 2023, 27, 292–303. [Google Scholar] [CrossRef]
- Gong, X.; Wang, H.; Ji, Y.; Zhang, Y. Optical chaos generation and synchronization in secure communication with electro-optic coupling mutual injection. Opt. Commun. 2022, 521, 128565. [Google Scholar] [CrossRef]



| Resources | Used | Util |
|---|---|---|
| Slice | 134 | 1.01% |
| LUTs | 304 | 0.57% |
| FFs | 292 | 0.21% |
| DSPs | 10 | 3.18% |
| Frequency Max | 111 MHz | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaidyanathan, S.; Tlelo-Cuautle, E.; Benkouider, K.; Sambas, A.; Ovilla-Martínez, B. FPGA-Based Implementation of a New 3-D Multistable Chaotic Jerk System with Two Unstable Balance Points. Technologies 2023, 11, 92. https://doi.org/10.3390/technologies11040092
Vaidyanathan S, Tlelo-Cuautle E, Benkouider K, Sambas A, Ovilla-Martínez B. FPGA-Based Implementation of a New 3-D Multistable Chaotic Jerk System with Two Unstable Balance Points. Technologies. 2023; 11(4):92. https://doi.org/10.3390/technologies11040092
Chicago/Turabian StyleVaidyanathan, Sundarapandian, Esteban Tlelo-Cuautle, Khaled Benkouider, Aceng Sambas, and Brisbane Ovilla-Martínez. 2023. "FPGA-Based Implementation of a New 3-D Multistable Chaotic Jerk System with Two Unstable Balance Points" Technologies 11, no. 4: 92. https://doi.org/10.3390/technologies11040092
APA StyleVaidyanathan, S., Tlelo-Cuautle, E., Benkouider, K., Sambas, A., & Ovilla-Martínez, B. (2023). FPGA-Based Implementation of a New 3-D Multistable Chaotic Jerk System with Two Unstable Balance Points. Technologies, 11(4), 92. https://doi.org/10.3390/technologies11040092