Abstract
We propose a comprehensive approach for the analysis of real economy and government sector risk transmission to the banking system and apply it in ten Euro-Area countries from 2005 to 2017. A flexible methodology is developed to model banks’ assets according to the risk-adjusted balance sheet of the counterparts. The use of distance to distress as a popular risk metric shows that Contingent Claims Analysis underestimates banks risk in stable periods and overstates it during crisis. Furthermore, the approach succeeds in detecting spillovers from households, non-financial corporations and sovereign sectors: for the countries examined the main source of instability comes from the Non-Financial Corporation sector and its increased assets volatility.
JEL Classification:
G1; G2; G13; G32; G33; H63
1. Introduction
The 2008 financial crisis, together with the subsequent sovereign debt crisis, showed the key role of banks in the world’s economy and the relevance of sector interconnections in risk transmission. Indeed, the deep network of links between real economy and financial institutions has been the new frontier of research, given its central importance in terms of economic and financial stability. In this paper we present a new comprehensive approach for measuring banking sector risks. This methodology exploits the results from previous works on sectors’ risk analysis and combines them with the scope of becoming a useful tool to predict credit institution’s vulnerability. This approach uses Contingent Claims Analysis (CCA) to infer the market value of banks’ assets, accounting for the banks’ portfolio structure mainly composed by credits to other sectors. This evaluation leads to the calculation of banks’ risk indicators according to credit institution liabilities. Hence the banking sector balance sheet and the associated risk measures become a function of the debtors’ equity and volatility of equity which can be easily stressed for policy analysis. The methodology does not apply CCA on the banking balance sheet because it rejects the common assumption that the bank assets follow a log-normal distribution.
CCA has its roots in option pricing theory Black and Scholes (1973), Merton et al. (1973) and it has the main objective of producing risk indicators (such as Distance-to-Default (), Probability of Default (), Expected Loss (), etc.) in order to highlight the vulnerabilities of the entity under investigation. The main feature of CCA is the production of risk-adjusted balance sheets by combining data from static accounting balance sheets with market-based information on the price and the volatility of the equity and the consideration that equity is a contingent claim on the assets. This procedure, in turn, leads to the calculation of risk indicators able to capture the non-linear risks in a forward-looking perspective. Moreover, these indicators can also be used in conjunction with more conventional measures of risks such as Value-At-Risk. CCA is extremely flexible and can be applied at micro and macro level, with various objectives ranging from the estimation of the default risk of a specific firm up to the computation of the interlinks across sectors within the economy and be used as a policy tool to inspect the risks’ transmission.
From a macro perspective, the Non-financial corporations (NFC) sector is the most straightforward step to expand CCA analysis from firm-level to aggregate level. For instance, Gapen et al. (2004) apply CCA to corporate sector’s aggregated balance sheets and address the risk of spillovers towards the financial and public sectors. Gapen et al. (2008) implement CCA to sovereigns balance sheet and show that the Merton approach overcomes the traditional purely accounting-based measures of risk of emerging countries government (GVT) sector. In the same manner Brière et al. (2016) focus on Asia emerging countries governments and Keller et al. (2007) on Turkey GVT sector, assessing the role of rising market volatility and of policy adjustments in scenarios valuation. The use of CCA on sovereigns can also be found in Bodie and Briere (2013), where the authors investigate Chile public sector, with particular attention to guarantees to private corporations. They find that this analysis can be extremely useful in terms of sovereign wealth management, especially with respect to sovereign wealth funds and foreign exchange reserves. In addition, from an investor perspective, Gray et al. (2007) explore through CCA credit risk deriving from sovereign debts. Nevertheless, as presented in Gray et al. (2013), the application of CCA to the GVT sector is not straightforward when it comes to non-emerging markets, leading to models which rely on sovereign CDS. Recently the households (HH) sector has been modeled according to Merton’s theory too. Lai (2016) underlines how credit risk measure variations correspond to economic growth in Singapore by evaluating balance sheet data and implied households market data and detects that the usual CCA conclusion of assets volatility as risk driver holds for this sector as well.
With respect to the banking or credit institutions sector (CI)1, CCA is commonly applied to reveal the mechanisms of risk transmission within the sector and the implications for financial stability. The development of a “Systemic CCA” (Gray and Jobst 2010, 2011) is meant to pursue the objective of taking a closer look to spillovers between the financial and government sectors. Romero et al. (2013), focusing on the Colombian financial system, consider the joint distribution of expected losses and the cost of an implicit bailout for the government. The lack of precise cross-country/sector balance sheet data has been a major obstacle in the analysis of how real economy losses are transmitted to the financial sector, often requiring the application of statistical approaches to estimate the links among sectors in the economy. Castrén and Kavonius (2009) adopt the maximum entropy methodology to overcome the missing information on cross-border exposures, and Gray et al. (2013) define sector-specific risk indicators and combine them with a Global VAR approach to capture macroeconomic risk. Moreover, attention is devoted to sectoral DtDs and light have been shed on how contingent claim analysis measures and . Chan-Lau and Sy (2007) highlight the importance of setting a specific default threshold, especially for banks, since they are required to maintain capital and reserves for regulatory purposes. Jessen and Lando (2015) describe the strong robustness of this measure with respect to misspecification and Chen and So (2014) analyze the comparatively effectiveness of over in predicting defaults. Finally, Antunes and Silva (2010), studying Portuguese banks, also stressed the importance of in assessing risk, even though they notice the role played by lack of economic fundamentals in the common CCA approach for the banks.
The approach presented in this paper tries to get an overview of each sector risk to describe how real economy losses are transmitted to the financial sector. The final scope of the employed methodologies is to build an aggregate-level indicator which does not only capture instantaneous spillovers between sectors, but also provides a forward-looking signal of financial stability. This paper contributes to the current status of the literature by exploiting the most recent micro-level theoretical findings on banks’ risk evaluation and developing them on an empirical macro level. For each sector, the most realistic model to calculate risk is employed, according to sector-specific assumptions. This is the reason behind the partial rejection of CCA, since it has been proved not to be able to suit every situation. In addition, to assess risk is chosen over . After recognizing that CCA can be very useful for stress-testing in the banking sector (Gray et al. 2014) because the non-linearities associated with risk can be detected from a macro perspective through a few market-based variables in a “top-down” approach, stylized risk-adjusted balance sheets at sector level are constructed and stressed. The resulting distance to distress for the banking sector is therefore a balance sheet and market-based indicator of financial instability. Notably, given the forward-looking nature of CCA applied on debtors, the computed measure acts also as an early-warning indicator. The methodology is applied to the banking sector of ten Euro-Area (EA) countries and the behavior of the for these countries is examined on the time span 2005–2017, allowing the inclusion of the 2008 and 2010–2014 crises. Furthermore, with the static shock of the debtors’ input parameters, the sensitivities of the banking sector risk parameters are assessed and useful results for the transmission of risks from the real economy and the government to the banking system are extracted.
Finally, this risk measure for the banking sector takes a different and to some extent complementary perspective with respect to the work on systemic risk indexes CISS (Hollo et al. 2012): this latter composite indicator indeed aims at real time monitoring of rising stress from market data and at revealing changing of stress regimes. Our attempt, on the other hand is more focused on defining a methodology which incorporates market data in a broader macroprudential context, exploiting sectors’ balance sheet information. In this way the current debtors’ vulnerability is taken into account and the forward-looking nature of the measure can detect the system’s reaction to future instability through stress testing.
The paper is organized as follows: in Section 2 the approach is explained, Section 3 presents the data used for the ten EA countries and the procedure followed to compute the banking sector assets and distress thresholds. Results, comparisons to the standard CCA and the effects of the static shocks are shown in Section 4. Conclusions and future directions are in Section 5.
2. Methodology
The methodology follows two separate directions, according to the assumptions made for the specific sectors to be analyzed:
- CCA for Households (HH) and Non-Financial Corporations (NFC) sectors and CDS valuation for the Government (GVT) sector.
- a new approach based on sectors balance sheet interconnections is adopted to detect the banking sector proximity to distress.
2.1. The Standard CCA Approach
CCA uses balance sheet and market data and by exploiting option pricing theory provides risk-adjusted balance sheets that can reveal firm’s risks. The non-linear nature of this approach, makes the key risk metrics indicators, and , forward looking, in contrast with the historical metrics produced by adopting only balance sheet data with the usual accounting lags (Gapen et al. 2004). Here we must note that powerful statistical methodologies for default predictions such as the one presented in Duan et al. (2012) could be also be used but in this paper the main focus is to capture the defaults through the non-linearities of the option theory. CCA employs the concept of distress barrier (B): it is defined as a certain amount of debt assumed to be the lower bound for the assets, such that if they fall below it, the firm (or sector) is in distress (or even default—depending on the severity of the threshold2), because the promised amount (B) cannot be repaid. According to the mainstream empirical methodology on this field, specifically carried on by Moody’s with the KMV model (Crosbie and Bohn 2003; Gray and Malone 2008), the general rule is to employ the sum of the short-term debt () and a fraction of the long-term debt () as distress barrier (B):
The distress barrier will be calibrated according to each specific sector and therefore the used to determine the barrier will conform to the particular features of the sector. CCA methodology focuses on the nature of risky debt and on its default likelihood. A given risky debt is composed by a default-free portion minus an expected loss, which is modeled here as an implicit put option on the assets of the balance sheet with the distress barrier as strike price. This is so because debt holders can be considered to be writers to the equity holders of a put option and they have to pay the difference between the assets and the default-free debt whenever the assets are lower than the distress barrier. This can be written as:
where is the value of risky debt at time t, B is the distress barrier, T is the maturity, r is the risk-free rate and is the implicit put option at time t. The risky debt is equal to the default-free debt minus a guarantee against default, which in the previous Equation (2) is exactly a put option with exercise price equal to B.
The assets are usually assumed to follow a stochastic process as:
where and are the instantaneous drift and the volatility of the assets respectively, represents the random component of the process modeled as a standard Brownian motion. In discrete time setting the random part has a normal distribution (with zero mean and variance equal to the square root of the time step ) and in a continuous context the equation above is referred to as a geometric Brownian motion, where is a Wiener-process with .
The value of the assets at time t is:
Given the value of the distress barrier at time t, , a firm is in distress if the assets are below this threshold. The probability of this event is:
where is the standard cumulative normal distribution function. The quantity is called Distance to Default () and it depends on the drift and the volatility of the assets. The Probability of Default () calculated with this procedure is the so-called “actual” probability of default, which is outside of the common CCA/Merton Model (Gray et al. 2007). The “risk-neutral” is obtained by replacing in the above formulas the growth rate of the asset with the risk-free rate r.
Normally the risk-free rate is lower than the asset drift rate , resulting in lower actual than risk-free default probabilities. Throughout the analysis, consistent to “risk-neutral” measures (Gray et al. 2007) the need for the estimation of asset drift is spared. This is sufficient for our needs since the primary focus is on the comparison of s either among the different sectors or through time.
The equity value can be described as a junior claim on the assets, and hence as a call option on them. The assets are the sum of equity and debt, and the value of the risky debt is:
where is the market value of equity at time t and is the market value of the assets. For the sake of simplicity, we assume (the case where is handled with a simple time shift). As E is a call option on the assets, we can write (Black and Scholes 1973):
and
where
To find the market value of the debt, we rely on the market value of the assets and on their volatility. Although we cannot directly observe these two values, we can retrieve from the market equity and and A and are calculated by applying Itô’s lemma on E:
We get:
This last equation, together with (7), defines a system of two equations and two unknowns (A and ) which allows the obtaining of the implicit market value of the assets and their volatility. From a practical perspective, the above two by two non-linear system is highly sensitive to the initial condition of E and 3. A and are then used to calculate two risk-measures: the distance to default/distress () and the probability of default/distress (). The is defined as:
or more naively as
is a measure that expresses the number of standard deviations the expected value of the assets is away from the threshold given by the distress barrier and the associated is .
2.2. The Application of CCA Approach to NFC and HH Sectors
The analysis starts focusing on the NFC and HH sectors, applying to each of them CCA and trying to fit the model in the best way according to the available data for each of sector. Since the interest is on the whole sector and not on a specific entity in it, the methodology is calibrated taking into account the specific characteristics of the sector and the quality of the aggregate data available.
2.2.1. Non-Financial Corporations
To analyze the NFC sector the data are aggregated from the listed non-financial corporations.
We use:
The practice of treating the whole sector as if it were one big entity follows from Gray and Malone (2008) and therefore, for each point in time, the risk metrics are produced for the whole sector.
2.2.2. Households
It is challenging to apply CCA on the HH sector and extract credible results, mainly because the households do not issue equity. Although it is possible to construct stylized balance sheets, this has limited practical application due to the difficulty to quantify consistently the various items of these balance sheets. Moreover, since there is no empirical evidence of households defaults on a massive scale per country, understandably higher s and lower s than those of the other sectors are expected. Following Castrén and Kavonius (2009) we use:
- the net financial worth of the aggregated households balance sheet as E;
- the volatility of the ten years government bond as 6;
- the whole liabilities of households as B.
2.3. The Government Sector
The GVT sector require us to move in a slightly different direction. It does not issue any equity and, even trying to construct a sovereign balance sheet this leads to the practical challenge of a market value of debt greater than the distress barrier7. Following the same methodology as Gray et al. (2013) we rely on the concept of expected loss ratio, which is the expected loss value per unit of default-free debt:
For the debt valuation the market traded sovereign CDS is used. The CDS spread s8 depends on the expected loss ratio and the time horizon, therefore we can write:
Solving for the risky debt, we obtain:
The risk-neutral probability of distress given a CDS spread s is computed through the formula (Hull 2003)9:
where R is the recovery rate10. Since we are working in the risk-neutral environment, it is possible to move back to the distance to distress. Indeed the is calculated as the inverse of the cumulative normal distribution of the :
2.4. The Comprehensive Approach for the Banking Sector
For the banking sector, following Nagel and Purnanandam (2019), we abandon the usual CCA since its assumptions are not valid anymore. Indeed, as the authors stress considering the typical asset portfolio of the banks, it is mostly composed by debt claims (such as mortgages or bonds) which is not consistent with the Merton’s assumption of log-normally distributed assets because this part of the banking sector assets is not uncapped but it is limited to the full repayment of the borrowers. To overcome this problem, in contrast with the theoretical modeling of these relations, our analysis takes a different and more intuitive perspective: we consider macro-level data on balance sheet and we quantify the exposures with respect to each relevant counterparty. The analysis focuses on the three main borrower sectors highlighted previously: government (GVT), non-financial corporations (NFC) and households (HH). In the previous sections we calculated the value of the risky debt for these agents employing each time a reasonable but still ad hoc value for the distress barrier. Since now we are interested in the actual ability of a sector to repay its whole debt, we assume that B is equal to the sum of the liabilities.
First we define for a sector i
which is the ratio between the value of the risky debt evaluated using the total debt and the total debt itself.
Then we focus on the different assets which compose the bank portfolio. According to the data available, for each EU country (the reference country), we distinguish, depending if the issuer is from this country (area D), from another EU country (area ), from a non-Euro area (area ) or the asset has no issuer (area K), four main categories of banks assets (exposures):
- assets with a domestic counterpart (issuer) ();
- assets with counterpart (issuer) from the Euro Area (except the reference country)();
- assets with non-Euro counterpart (issuer) ();
- other assets without a counterpart (for instance gold) (K)11.
For each bank asset12, (excluding K) the following identity holds:
where are the distress barrier and market value of debt of counterpart sector i in j area respectively. This identity shows the double way we are proceeding: for each counterpart area j and sector i the left side is equal to the market value of its total risky debt multiplied by the percentage the banks hold of the total debt issued. The right hand side expresses the product between the total book value of banks assets with counterpart sector i in area j and the value of the risky debt per unit of the total debt issued by counterpart sector i in area j. This methodology assumes that the risk within a sector propagates equally to its whole debt, and therefore each part of it is a scaled version of the total without distinguishing among the possible different types of issued debt.
The stochasticity of debts value, which we assume are modeled according to CCA (as aforementioned in the previous subsections), is then integrated in the static banks’ asset side. We can now compute the total market value of the assets of the banking sector as:
This last equation shows that the level of risk in banks’ assets depends on counterparties’ stability and that the stress transmission follows a non-linear path due to the nature of vulnerability assessment of debtors.
2.5. Sensitivity Analysis
Based on (22), we compute the market value of the assets of the banking sector, exploiting the Merton-style analysis employed on the other sectors as a function of the observed observable market variables E and . The solution of equation system (7) and (11), although non-analytical, gives the value of asset A and volatility of asset as a function of the observable market variables E and :
The partial sensitivities of the market value of debt D with respect E and due to chain rule and its gradient are:
The gradient shows us how a shock of one of the market observables affects the risky debt.
For the calculation of a contemporaneous shock, we calculate the Hessian matrix of D ().
The total variation of D is calculated as:
where
The leading assumption along this sensitivity analysis is that the sector-specific instantaneous shocks are independent of the other’s sectors situation. From (22) and (29), given sector i and counterpart j, we compute:
which is the variation of the market value of the banking sector assets. The results of this section will be used for the shocks performed in Section 4.3. The simulations13 for the effect on the partial sensitivities of debt in respect to equity and volatility of equity exist in Figure 1. Figure 1a presents the effects of a 10% negative shock in the equity value and Figure 1b for a 10% shock in . As the two figures show, an increase in the market value of equity (or a leverage decrease) has a positive effect on D; hence the higher is E, the higher is the market value of the debt and, in turn, the lower the risk that the sector falls below the distress barrier. On the contrary, a growing is reflected in a lower D and so in greater risk. Comparing Figure 1a,b we can spot on the z-axis that the magnitude on the variation of D due the volatility shock is around 10 times higher than due to the equity shock. Therefore, a shift of volatility is, in consistence with option theory, extremely more effective than a shift in the equity.
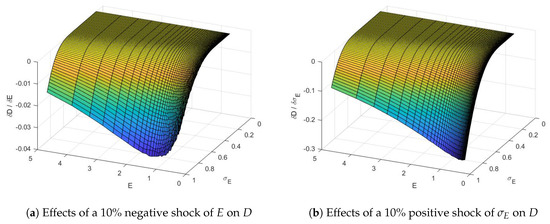
Figure 1.
Effect on the Sensitivities of D. The left and right panels show the impact of a shock in equity and volatility of euqity (respectively) on the market value of the debt. The shock is applied on different touples of euqity and volatility of equity (from 0 to 5 for E and from 0 to 1 for ).
3. Data
The analysis developed in this paper covers the period 2005–201714 with a quarterly frequency for ten Euro countries: Austria (AT), Belgium (BE), Germany (DE), Spain (ES), France (FR), Ireland (IE), Italy (IT), Netherlands (NL), Portugal (PT), Slovenia (SL). Since CCA requires the use of both aggregated balance sheet data and market data for the sectors, a major issue was to find data sources for the market value of equity and equity volatility, which had to be not only representative of each sector but also suitable for the analysis performed. The data for the non-financial listed companies are taken from Bloomberg15 as total value of equity of the sector, the sum of their market capitalization is used, while the sum of current liabilities and half of long-term liabilities is taken for the computation of the distress barrier. As value for we consider the weighted average of the 90-days volatilities of each firm16. For the HH we use the Quarterly Sectoral Accounts data (QSA)17 from the ECB Statistical Data Warehouse (SDW). For HH equity E, the aggregated net financial wealth is used and as a proxy for HH equity volatility we use the 10-year sovereign bond volatility in each country18. For the HH distress barrier, we use the aggregated liabilities in the QSA database. As explained in Section 2, for the GVT sector the valuation is through CDS and, from SDW, we get the 1-year sovereign CDS spreads for each country. For the banking sector, we use the Balance Sheet Items database (BSI) from SDW for Monetary Financial Institutions (MFI). We collect the data to reconstruct the aforementioned four macro-classes of banks exposures, although for two categories of items19 we miss part of the specific counterparts. Specifically, we lack of information on the counterparts different from GVT, HH and NFC for the domestic area, for the EA we know only the sectoral counterparts and not the country-specific and, lastly, for EX we miss both i and j. We denote the unknown counterpart by u. Therefore, given the set of sector counterparts, in order to calculate the market value of these items of the banks’ assets for a reference country 20, the approach is:
- when it comes to evaluate the domestic area (D), we consider as of the unknown counterpart the simple mean of the risky debt of the sectors in S of c21:
- when it comes to evaluate the Euro Area (EA), we consider as the simple mean of the risky debt of the sectors of all the countries, except the domestic one:
- when it comes to evaluate the Extra Euro area (EX), we consider as the simple mean of the risky debt of the sectors of all the countries:
The assumption behind the above is that the average cross-sector risk is representative of the whole country (D) and for the EA it is natural to rely on the same principle, since we have the data of most of the euro-area countries. With a slightly stronger assumption the cross-sector and cross-country risk can be extended to the rest of the world (EX), with the country set being representative of an overall global environment. When we evaluate the market value of debt securities, HH is excluded as a counterpart sector, because households do not issue debt securities. As distress barrier for banks the whole debt is used (Nagel and Purnanandam 2019) and by employing the BSI database it is computed as the difference between the aggregate total liabilities and the aggregate capital and reserves. To calculate the distance to distress of the banking sector, the market volatility of the assets is still needed, which is not observable though. Therefore we assume that this value is the volatility of the portfolio of the assets of the banks: hence we compute it starting from the single volatilities of the components of . To do so, we use:
This is the spot market volatility of a general risky debt and we calculate it for each exposure, assuming that the correlation of A and E () is the historical one computed from the sample. For cases that fall in (32), (33) or (34), in which there are no specific counterparts, the is computed as the mean of the volatilities of the respective . For K, its volatility is computed using a five-period rolling window. After computing the asset volatilities and the cross asset correlations, the portfolio volatility is calculated22. The 1-year interbank deposit rate for each country is used as a proxy for the risk-free rate r23.
4. Results
With the approach presented in Section 2.4, the results in Nagel and Purnanandam (2019) are extended from a micro to a macro level. Our methodology aims at measuring the distance to distress of the banking sector of 10 euro-area countries without taking into account the somewhat non-realistic assumption of log-normality of banks assets returns. As mentioned before, the is the metric we decided to employ in our analysis, contrary to the probability of default that the general CCA environment suggests. There are two main reasons behind this choice. The first comes from the need to use a measure which gives a direct picture on what the risk status of one sector is, once the ad hoc distress barrier is defined. Indeed, although B is empirically defined as the point below which one sector is experiencing stress, the definition of “stress” itself is a shaded concept presumably implying default. But the amount chosen for the barrier is arbitrary, in the sense that it comes from empirical analysis, even though there is not enough information about what the true stress value for a whole sector is. Therefore, when we refer to distress, we are implying a situation that is likely to cause default for a certain sector. Furthermore, the choice of B for each sector depends largely on the particular characteristics of the sector the literature is rich enough of suggestions which claim to reflect the empirical evidence (Chan-Lau and Sy 2007; Crosbie and Bohn 2003). The second reason is that since for the banks we are rejecting the usual log-normal hypothesis on the assets returns, we depart from the full Merton practice. This implies that if we were using the Standard Normal distribution to map the to , we would have biased results for the credit institutions sector. Also, it has been shown (see for instance Bharath and Shumway 2008) that this mapping produces distorted default probabilities due to the thin tails of the normal distribution usually assumed. That is why the Moody’s KMV model, in order to find the expected default frequencies (EDFTM), uses empirical data (for instance, historical defaults) to create a reliable map to the real s (Crosbie and Bohn 2003) in its effort to get fatter tails. In addition, since is a strictly monotonic increasing function, it preserves the ranking provided by the distance to default and therefore does not return any new information to the comparative analysis (Jessen and Lando 2015). For these reasons, we devote our full attention to the distance to default as a risk metric. This section is divided as follows: first we show the results of our methodology comparing, for each country, the s of the four sectors. Then, we compare our findings with the ones obtained through the usual CCA applied to the banking sector. Finally, we present a static stress exercise to give a hint of how a sudden shock hitting GTV, NFC and HH affect the banking sector.
4.1. A Comparison of Sectoral Distance to Distress
The time span we selected for the analysis contains two main events that affected all the countries with different magnitudes: the 2007–2008 world financial collapse and the subsequent 2011–2013 European sovereign debt crisis. The analysis is focused solely on the banking sector across the selected countries. As Figure 2 shows, the banking sector for each country in the sample presents the same general trend, i.e., a substantial common decrease of during the 2008 crisis followed by a slow recovery over the next years and a decrease (albeit smaller) during the 2011–2013 sovereign debt crisis. Although the time series for each country shows a similar behavior, the magnitude differs from country to country. This in general can be attributed to country-specific reasons and not to the choice of B which, accounting for the total debt, is not prone to arbitrary choices able to affect the results.
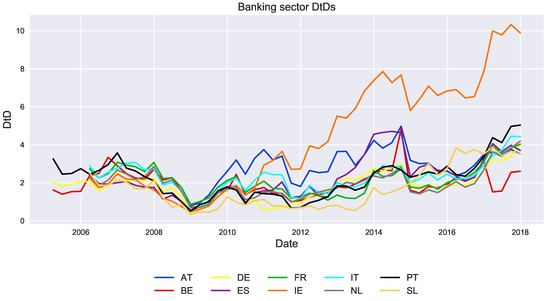
Figure 2.
Banking sectors s. The chart shows the level of aggregate banks’ in the analysed countries (AT, BE, DE, ES, FR, IE, IT, NL, PT, SL) from 2005 to end 2017. The y-axis expresses this measure in standard deviations.
Sectoral comparison for the selected countries exist in Figure 3. Portugal (Figure 3i) is used as representative country for the analysis mainly because it was the country in the sample most hardly hit by the two crises24. As predicted, the households sector is the one with the lowest risk. Moreover, there is a strong relation between NFCs and banking sector. Indeed25, the Portuguese banks are mostly exposed to the domestic area and, in particular, to non-financial corporations and households. This is also the reason the higher risk faced by the GVT sector was not completely transmitted to the banks, even though the drop in the government was massive from 2010 to 2014.
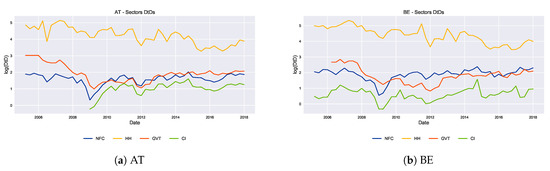

Figure 3.
Sectors . The panels show the level of for each sector considered in the analysis for each country (NFCs in blue, HH in yellow, GVT in red and CI in green). The y-axis expresses the measure in standard deviations (log-scale).
The overall picture clearly presents the banking sector as the one which faces the highest risk through time and moves according to the exposures in its aggregated balance sheet. As expected, NFC and GVT sector move independently, spreading their shocks to the credit institutions. These patterns are similar to the rest of the countries i.e., there is a strong correlation between NFC risk and bank risk across all the reference areas and for each point in time. Households sector remains always the less risky and thus a safe counterpart for the credit institutions. Between 2008 and 2009 the aggregate banking sector appeared to be the riskiest and mostly damaged by the crush of the non-financial corporations. Overall, Portuguese, Slovenian and German banks are the ones that suffered the most, while Austrian and Irish banks, after the huge drop around 2009, recovered and stabilized to higher values of 26.
4.2. The Alternative versus the CCA Approach
We address the risk of the banking sector mainly through the links to the debtors’ sectors rather than with a sole market-based contingent claim analysis. The banking risk is reflected by its exposures to counterparts’ ability to repay. The higher the , the safer is for the credit institution to select its lending strategy and to buy debt securities from the other sectors. To apply a comparison with the mainstream technique of CCA, market capitalization equity volatility and liabilities for listed banks were used27 for the selected countries. We proceed in the same manner we did for the NFC sector, except for the distress barrier which, as with the non-CCA methodology, is set to the full value of the liabilities. The results are shown in Figure 4.
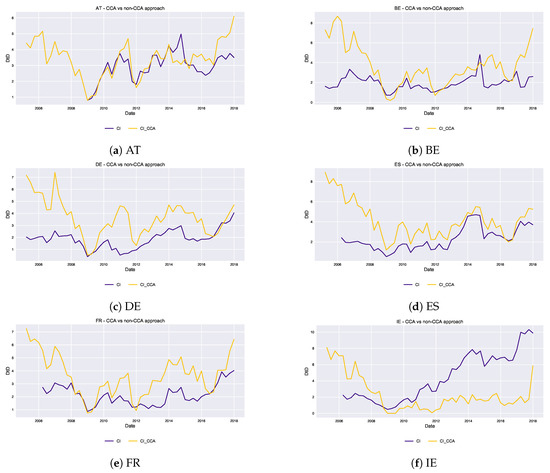
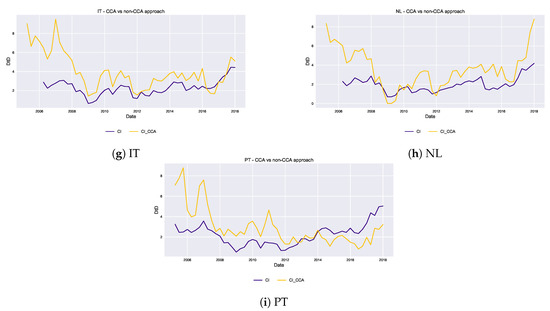
Figure 4.
Banking sector s comparison between CCA and non-CCA approach. The panels show the level of for the CI sector of each country given the two possible approaches to compute it: the yellow line refers to the usual use of CCA while the blue line refers to the new methodology proposed in the paper. The y-axis expresses the measure in standard deviations.—For Slovenia, the comparison was not possible due to lack of market data for the banks.
Mainly for Belgium and France (Figure 4b,e), during the crisis period the CCA overestimates the risk (predicting a lower ). On the other hand, in calmer times CCA strongly underestimates the risk. The same findings holds, albeit to a minor extent, for the rest of the countries. Indeed, in CCA practice low equity volatility infers a low asset volatility which, always according to the Merton model, is assumed constant. This does not take consider the effects on the assets volatility of a drop in A. Therefore, observing a low value of banks equity volatility would tempt us to assume that the assets are high, resulting in a high . This does not take into account the state of the rest of the counterparts which, if in distress and with a high assets volatility, would transmit their stress to their lender. Furthermore, CCA results are excessively responsive to jumps in equity volatility, not properly accounting for the underlying market values of the assets in the portfolio of the banks. Indeed, the high sensitivity of distance to default to leads to the overstatement of risk after bad shocks in banks observed market value.
The new methodology is also useful from another perspective. As it is less affected by a sudden rise in equity volatility, it produces more stable time series, while the series produced by the Merton model are considerably more volatile through time, implying a lack of predictive power.
Finally, in line with what we saw in the previous subsections, the sovereign crisis appears to hit stronger the banks in 2010 and 2012 using the CCA environment. This pattern can be observed for the remaining countries. It confirms again that a large drop in financial markets, as the one caused by the tumble of government bonds in the recent sovereign debt crisis, propagates and affects banks’ market value of equity and , and finally is translated to a massive drop in distances to distress through an underestimation of the market value of bank assets.
4.3. Effects of a Shock
The alternative approach to the mainstream Merton analysis for the banking sector is helpful in disentangling the risk sources among the several borrowers of the credit institutions. As we saw in Section 4.1, the banking sector suffered mostly during the 2008 crisis, with the worst negative peaks of in the late 2008 and early 2009. According to the data on banks’ balance sheets, the sovereign debt crisis was less severe for the banks because of the limited exposures to the government sector. The overall major risk source for the credit institutions was the exposure to the NFC domestic sector, and we expect a shock on this sector to have the biggest impact on the banking sector risks. The propagation of a shock on each sector allow us to see how the banking sector is affected through time.
We define a shock in a borrower’s ability to repay the debts, whenever it suffers a drop in its market value of equity or an increase in the respective volatility for NFC and HH or an increase in CDS spread for GVT. We impose a shock of 20% drop in E, contemporary 20% positive jump in for the NFC and HH and 200 basis point increase for GVT CDS spread (in the same reference area we are looking into) and we inspect the elasticity of the of the banking sector. The results exist in Figure 5. As we observed in Section 2, the resulting changes in the distance to distress do not follow a linear pattern, and are larger for high initial values of and low initial values of E. In general, for all countries the impact on the banking of the HH shock is the smallest. For most of the countries, for different periods, the sector shocks affect differently the banking s. Clear patterns of major relevance of the NFC sector are in Austria, Spain, Ireland, Italy and Portugal, whereas in Belgium the GVT shock affects the most the banking . The country with smoothest and most stable sector shock pattern is Austria with Italy and Portugal to follow. Moreover, in 2009 the NFC shock was particularly harsh on Slovenia (around −17%), Ireland (−16%), Portugal (around −13%) and Netherlands(around −14%); on the other hand, Germany suffered the least (−4%). Also in Belgium the impact of the GVT shock was very high (almost −15.5%), it decreased in the following years and stabilized around −10% in 2016 and 2017. Lastly, for the period 2012–2014, the government shock did not have a dramatic impact on banks s. The only countries with larger GVT impacts than those of NFC are France (although small in absolute numbers) and Belgium. Furthermore, we can see that besides the common general trend of sectors’ distress propagation, for each country every sector shows a different point in time at which it predominantly affects the banking sector. For instance in Portugal, government shock has its maximum of about −7.5% impact on credit institutions around 2012, in the middle of the sovereign bond crisis. On the other hand HH sector had its worst shock of almost −4% in late 2006 and has presented several spikes during the government crisis.
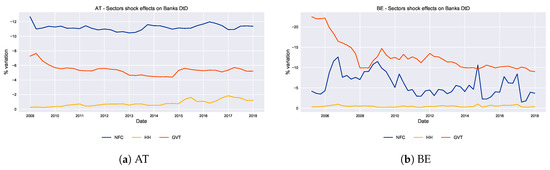
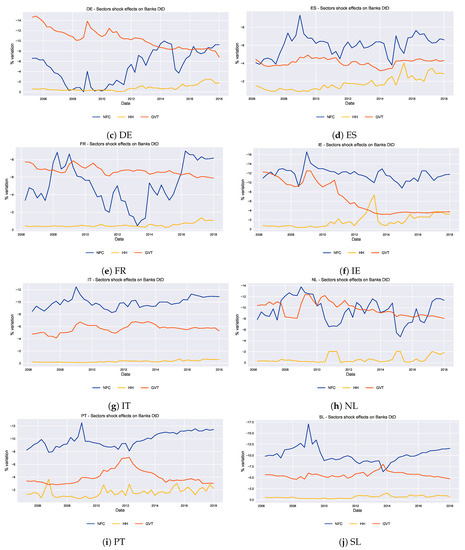
Figure 5.
Sectors Shocks to banks . The panels present the variation in given a shock in one of the analysed counterparty sectors (HH, NFC, GVT). For the first two sectors we employed a 20% shock on E and (negative to the former, positive to the latter). For the government sector we employ a 200 basis points positive shock on the CDS spead. The shock is separately applied on each sector and for each point in time (each quarter from beginning 2005 to end 2017). The blue line represents the shock from NFC, the yellow line the impact of a variation in HH and, lastly, the red line represents the impact of a shock in GVT CDS spreads.
5. Conclusions and Future Directions
CCA has become the mainstream methodology for describing firms’ risk, starting from observable data in the market and inferring the value of the assets and the associated risk indicators. More recently this approach has been extended on a macro level, in the attempt of describing whole sectors’ stability, according to their aggregated balance sheets. Nevertheless, Nagel and Purnanandam (2019) showed that the Merton model fails in correctly assessing banks’ risk, overestimates the default probabilities during crisis and understates them in normal periods. This is mainly due to the fact it assumes log-normally distributed assets returns, which is incorrect for most of banks assets whose value is capped to the full repayment of the borrowers.
The approach in this paper tries to remedy to this, and at the same time to exploit the advantages of CCA in order to correctly capture the banking sector risks which are linked to borrowers’ ability to repay. The debtor are mainly classified at the asset side of banks as non-financial corporations, households and sovereigns. The first two were modeled, at a sector level, through the CCA approach. Government sector required a different approach, since the associated put on its assets would be zero or negative in a Merton environment, given the significant drop of interest rates in recent years. Therefore, we relied on sovereigns CDS evaluation, to define their debt market value and to capture the non-linear part of the government’s risk. The market value of these sectors’ liabilities was then used to rebuild the credit institutions assets side, at an aggregate level. The market values of the banks’ assets obtained allowed us to calculate the distance to distress of the credit institution as for the other sectors, granting us a metric for the risk comparison among each country considered.
The resulting stress indicator fits our purposes: we obtain a measure able to capture the real time market environment and suitable to assess future risks. The former feature derives from the application of CCA-like analysis on banks’ counterparties, returning their debts valued at current market levels. The latter is determined by the one-year ahead perspective of the counterparties’ evaluation. This last characteristic accommodates also the possibility to add an exogenous shock to the input variables to perform a stress test aimed at foreseeing the likely developments of the banking sector given the employed scenario. Therefore, the advantage of this measure consists of two main pillars: ability to reflect market valued banks credits and flexibility for simulation purposes. We are convinced that it can be a useful instrument for macroprudential policy analysis. On top of micro-founded granular monitoring, the overall banks’ DtD allows a broad expansion of the regulator perspective, using this as an early warning for systemic risk.
We analyzed ten Euro-area countries to highlight the features of our model. First, the pattern of credit institution s were similar across the countries, showing that the years of crises (2008 year of sub-prime crisis and 2011–2013 years of sovereign crisis) were the riskiest. The country-specific analysis presented the same trends of the macro sectors: banks are the most vulnerable, absorbing others risk. NFC sector strongly drive credit institutions trends, as well as the government, even though sovereign debt is held in lower amounts by the banks. Households appear as the safest borrowers. Comparing CCA to this approach on the banking sector we showed how a Merton-style analysis leads to an overstatement of the risk during crisis and an underestimation in normal market periods, ending in a highly volatile time series. These results are consistent with the previous findings in the literature and are confirmed across all the countries under examination. Finally, the stress of banks portfolio was performed by statically shocking the market inputs of our model for the borrower sectors. We found that each stressed sector hit in a different way the banking sector, according to its inner risk and to the specific point in time, during which that sector suffered its major distress. Again the results for the countries were similar, showing the NFC as the sector that can affect most the credit institutions, mainly because of the great exposures of the banks to the real economy firms.
Although the approach presented in this paper seems very promising in identifying credit institutions’ risk due to its tractability and flexibility, future work might include the effect of correlation and causality between country/sectors variables, both on a book level and from a market perspective. Moreover, analyzing together inputs patterns could lead to reduce even further the variables to be shocked, describing more precisely the adverse macro scenarios. Finally, the research has been limited to EA countries due to the lack of detailed information on banks’ balance sheet composition for the other EU countries. Including these other countries (or possibly non-EU countries) would have required stronger assumptions on banks exposures and more biased results.
Author Contributions
All authors have equally contributed to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Antunes, António, and Nuno Silva. 2010. An application of contingent claim analysis to the portuguese banking system. Financial Stability Report 141: 603–26. [Google Scholar]
- Bharath, Sreedhar T., and Tyler Shumway. 2008. Forecasting default with the merton distance to default model. The Review of Financial Studies 21: 1339–69. [Google Scholar] [CrossRef]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bodie, Zvi, and Marie Briere. 2013. Sovereign Wealth and Risk Management: A Framework for Optimal Asset Allocation of Sovereign Wealth. Boston U. School of Management Research Paper (2011-8). Available online: https://ssrn.com/abstract=1460692 (accessed on 15 October 2019).
- Brière, Marie, Benno Ferrarini, and Arief Ramayandi. 2016. Contingent Claims Analysis of Sovereign Debt Sustainability in Asian Emerging Markets. Asian Development Bank Economics Working Paper Series No. 486. Available online: https://ssrn.com/abstract=2811537 (accessed on 15 June 2019).
- Castrén, Olli, and Ilja Kristian Kavonius. 2009. Balance Sheet Interlinkages and Macro-Financial Risk Analysis in the Euro Area. ECB Working Paper. Available online: https://www.ecb.europa.eu/pub/pdf/scpwps/ecbwp1124.pdf (accessed on 12 June 2018).
- Chan-Lau, Jorge A., and Amadou N. R. Sy. 2007. Distance-to-default in banking: A bridge too far? Journal of Banking Regulation 9: 14–24. [Google Scholar] [CrossRef]
- Chen, Wei-ling, and Leh-chyan So. 2014. Validation of the merton distance to the default model under ambiguity. Journal of Risk and Financial Management 7: 13–27. [Google Scholar] [CrossRef]
- Crosbie, Peter, and Jeff Bohn. 2003. Modeling Default Risk. Singapore: World Scientific. [Google Scholar]
- Duan, Jin-Chuan, Jie Sun, and Tao Wang. 2012. Multiperiod corporate default prediction—A forward intensity approach. Journal of Econometrics 170: 191–209. [Google Scholar] [CrossRef]
- Duffie, Darrell. 1999. Credit swap valuation. Financial Analysts Journal 55: 73–87. [Google Scholar] [CrossRef]
- Gapen, Michael, Dale Gray, Cheng Hoon Lim, and Yingbin Xiao. 2008. Measuring and analyzing sovereign risk with contingent claims. IMF Staff Papers 55: 109–48. [Google Scholar] [CrossRef]
- Gapen, Michael T., Dale F. Gray, Cheng Hoon Lim, and Yingbin Xiao. 2004. The contingent claims approach to corporate vulnerability analysis: Estimating default risk and economywide risk transfer. In Corporate Restructuring: Lessons from Experience. Washington: The World Bank Group, pp. 261–300. [Google Scholar]
- Gray, Dale, Marco Gross, Jonas Paredes, and Matthias Sydow. 2013. Modeling Banking, Sovereign, and Macro Risk in a CCA Global VAR. Number 13-218. Washington: International Monetary Fund. [Google Scholar]
- Gray, Dale, and A. Jobst. 2010. Systemic cca—A model approach to systemic risk. In Deutsche Bundesbank/Technische Universität Dresden Conference: Beyond the Financial Crisis: Systemic Risk, Spillovers and Regulation. Dresden: Citeseer. [Google Scholar]
- Gray, Dale, and Samuel Malone. 2008. Macrofinancial Risk Analysis. Hoboken: John Wiley & Sons, vol. 433. [Google Scholar]
- Gray, Dale F., and Andreas A. Jobst. 2011. Modelling systemic financial sector and sovereign risk. Sveriges Riksbank Economic Review 2: 106. [Google Scholar]
- Gray, Dale F., Andreas A. Jobst, Cheng Hoon Lim, and Yingbin Xiao. 2014. Introduction to the contingent claims analysis approach for stress testing. In A Guide to IMF Stress Testing: Methods and Models. Washington: International Monetary Fund, p. 333. [Google Scholar]
- Gray, Dale F., Robert C. Merton, and Zvi Bodie. 2007. Contingent claims approach to measuring and managing sovereign credit risk. Journal of Investment Management 5: 5. [Google Scholar]
- Gray, Dale F., Robert C. Merton, and Zvi Bodie. 2007. New Framework for Measuring and Managing Macrofinancial Risk and Financial Stability. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Hollo, Daniel, Manfred Kremer, and Marco Lo Duca. 2012. CISS—A Composite Indicator of Systemic Stress in the Financial System. ECB Working Paper. Available online: https://ideas.repec.org/p/ecb/ecbwps/20121426.html (accessed on 30 October 2020).
- Hull, John C. 2003. Options Futures and other Derivatives. New Delhi: Pearson Education India. [Google Scholar]
- Izzi, Luisa, Gianluca Oricchio, and Laura Vitale. 2012. Cds-implied edf credit measures and fair-value spreads. In Basel III Credit Rating Systems. Berlin/Heidelberg: Springer, pp. 257–301. [Google Scholar]
- Jessen, Cathrine, and David Lando. 2015. Robustness of distance-to-default. Journal of Banking & Finance 50: 493–505. [Google Scholar]
- Keller, Christian, Peter Kunzel, and Marcos Souto. 2007. Measuring Sovereign Risk in Turkey: An Application of the Contingent Claims Approach. Number 7-233. Washington: International Monetary Fund. [Google Scholar]
- Lai, Wan-Ni. 2016. Evaluating the sovereign and credit risk in singapore: A continent claims approach. Research in International Business and Finance 37: 435–47. [Google Scholar] [CrossRef]
- Merton, Robert C. 1973. Theory of rational option pricing. The Bell Journal of Economics and Management Science 4: 141–83. [Google Scholar] [CrossRef]
- Nagel, Stefan, and Amiyatosh Purnanandam. 2019. Bank Risk Dynamics and Distance to Default. Technical Report. Cambridge: National Bureau of Economic Research. [Google Scholar]
- O’Kane, Dominic, and Stuart Turnbull. 2003. Valuation of credit default swaps. Lehman Brothers Quantitative Credit Research Quarterly 2003: Q1–Q2. [Google Scholar]
- Romero, Laura Capera, Mariana Laverde Quintero, and Miguel A. Mosquera. 2013. Measuring systemic risk in the colombian financial system: A systemic contingent claims approach. Journal of Risk Management in Financial Institutions 6: 253–79. [Google Scholar]
- Singh, Manmohan, and Mohsan Bilal. 2012. CDS Spreads in European Periphery: Some Technical Issues to Consider. Number 12-77. Washington: International Monetary Fund. [Google Scholar]
| 1. | In this paper, the terms “banking sector”, “credit institutions sector” and “financial sector” are used interchangeably although understandably the financial sector is more broad since it includes financial companies that do not provide credit. |
| 2. | Although for banks actual default depends also on the regulatory environment which seems to be more protective the recent years due to the central role of banks for the economy. |
| 3. | Simulations have shown that when the put is at the money then the system is unstable and even small differences in the initial conditions produce large output deviations. |
| 4. | To define a representative volatility for the whole sector two methodologies were employed. The first one is the average of each corporation volatility weighted according to its market capitalization relevance on the aggregated one, ignoring equity correlations. The second one enriches the weighted average with the correlations. The results show that the second methodology, producing a lower volatility, leads to higher values. In the results section we chose to show the s obtained through the latter approach, since it seems more reasonable to assume that the volatility of the whole sector is softened by the negative correlations of the firms in it. Nevertheless, the application of both the methodologies reveal similar final results. |
| 5. | The mainstream empirical practice is followed and is set to 0.5. |
| 6. | Instead of using a mixture of resale price index volatility and private residential index volatility as in Lai (2016), the volatility of ten-year government bond is used as a proxy for the HH equity volatility. This was chosen because it was felt that the ten-year yield volatility represents a better proxy for the future HH volatility. We follow Castrén and Kavonius (2009), and we consider two main justifications for this assumption. First, European banks’ market portfolio is composed by 25% of domestic bonds, which therefore represent a crucial component of banks’ profitability. Hence, higher volatility in sovereign debt securities leads to increasing risk on credit institutions’ asset side, which is in turn transmitted to loan rates (directly hitting households’ assets). Secondly, 10-year government bonds mirror structural features of each economy, as expected inflation and growth, being a gauge of country soundness. Therefore, we can assume that the market perceived level of uncertainty of households’ assets is significantly represented by the volatility of long-term sovereign securities. |
| 7. | Given that the level of global interest rates is extremely low (sometimes near zero for the time period we analyze), this leads to a zero or negative put which, in turn, results in either no solution or an instable solution for our system of equations. |
| 8. | is in basis points so s is defined as . |
| 9. | See also Duffie (1999); O’Kane and Turnbull (2003), and Izzi et al. (2012) in support of the claim that the analysis of the CDS relies on a risk-neutral world which is, hence, comparable to the one seen for the other sectors. |
| 10. | Throughout the paper, the recovery rate for the government sector debt is assumed to be 40%. We rely on the empirical evidence presented in Singh and Bilal (2012). |
| 11. | We assume that for K the book value and the market value coincide. |
| 12. | denote a quantity from counterpart sector i in j area and if superscript exist denotes the total quantity of this. |
| 13. | The shocks were under the assumption of 1% risk-free rate. |
| 14. | The methodology can be applied to the most recent available data. |
| 15. | Bloomberg L.P. |
| 16. | The weights are chosen with respect to each firm market capitalization contribution to the total E. |
| 17. | This database contains the aggregated balance sheet data of macro sectors for the EU countries. |
| 18. | Where ten-year sovereign bond volatility is not available, the volatility of the ICE 10-year sovereign bond index is used. |
| 19. | Loans (l) and debt securities (ds). |
| 20. | Where is the country set. |
| 21. | Subscripts and superscripts in A should be self-explanatory. For instance denotes a non-Euro loan in country c issued by an unknown counterpart u. |
| 22. | The weights are the market value contributions of each asset to . |
| 23. | To measure the annual risk-free return, we use a 1 year rate. Furthermore, we rely on the interbank deposit rate as monetary authorities are assumed to act as lender of last resort to support these exposures, supporting the assumption of risk-freeness of the rate. |
| 24. | To visually distinguish the different sectors in these graphs we opted for a log-scale, since the extremely high levels of households’ would otherwise make the comparison hard. Sectors where are considered to be in high stress. |
| 25. | Countries data can be provided by the authors upon request. |
| 26. | Irish banks suffered extremely from the global financial crush mainly due to heavy exposure to the EA and to the rest of the world. |
| 27. | Bloomberg L.P. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).