Abstract
Oil, also called black gold, is considered as the commodity which has the greatest impact on the world’s economy, and it has been studied in terms of its relationship and effects on macroeconomic variables such as Gross Domestic Product (GDP), inflation, trade balance, exchange rate and some others. Likewise, the relationship of oil with the financial market has been deepened and is very interesting in the case of emergent economies such as Brazil, Russia, India and China (BRIC) countries. There are many studies and approaches to this topic, but few of them focus on seeking investment opportunities through the diversification of these variables and therefore creating efficient portfolios using other distribution from the norm. This research proposes the construction of diversified portfolios with the returns of the indexes and oil mixes of the BRIC countries modeled under a Normal Inverse Gaussian (NIG) distribution, which is a notable member of the Generalized Hyperbolic (GH) family, and analyzing the effect on investment, by the inclusion of each variable into the portfolio. An important property of the GH family is that the correlations matrix of the returns is obtained from estimation of the parameters of empirical distribution through maximum likelihood. The results show in an optimal configuration, that each instrument of India, China and Brazil, contributes to the portfolio efficiency, in contrast to the index and oil mix of Russia, that do not contribute significantly.
Keywords:
multivariate NIG distribution; portfolio optimization; BRIC economies; stock indexes; oil prices; JEL Classification:
G11G15
1. Introduction
There are currently numerous investigations dealing with the relationship between the oil price and economic variables, including: Hamilton (1983, 2003); Davis and Haltiwanger (2001); Lee et al. (2001); Lee and Ni (2002); Hooker (2002); Brown and Yücel (2002); Akram (2004); Jones et al. (2004); Hamilton and Herrera (2004); Cunado and Perez de Gracia (2005); Lardic and Mignon (2006); Chen and Chen (2007); Huang and Guo (2007) and Nandha and Hammoudeh (2007) among others. Hamilton’s seminal work in 1983, where it is argued that most financial crises in the United States are preceded by a significant increase in the price of oil, establishes a line of research that continues to this day to be very fruitful.
Due to the appearance and evolution of oil financial instruments such as futures and derivatives in the last decades of this past century, the commodity adopted financial characteristics that led to the study of its links with the financial market (Alquist and Gervais 2013; Ma et al. 2019; Zhang and Wang 2015).
There are several works with various methodologies that have studied, and continue to study, the interaction of oil and financial markets. Lin and Su (2020) pointed to some subdivisions in this topic, including the spillover effect of crude oil price and the stock market (Du and He 2015; Ji et al. 2020; Wen et al. 2019a); the connections between oil price and stocks from the industry level or national level (Badeeb and Lean 2018; Pal and Mitra 2019) and the influence of structural oil shocks on stock markets (Apergis and Miller 2009; Bastianin et al. 2016; Kang et al. 2015).
In Wen et al. (2019b) stocks and emerging markets from Brazil, Chile, Mexico, Russia, South Africa, India, South Korea, Thailand, China and Malaysia show a positive relationship with the oil market. The dependence between oil and stock markets is influenced by variables in each emergent economy but finding that uncertainty of American economy reinforces this link, and an American strengthened economy provokes a weaker relationship.
There is also research on the subject of oil-stock oriented to Brazil, Russia, India and China (BRIC) emerging economies. Naming just some of them, Tiwari et al. (2019); Fang and You (2014).
Ansari and Sensarma (2019) studied the impact of the Federal Fund Rate (as monetary policy of USA), gold price and Brent crude oil price on the leading stock indices of BRICS markets as a set (with a vector auto regression), finding no sensitivity of BRICS to the Federal Rate Fund (except in the case of India) and no sensitivity of India´s index to oil and gold.
A special case to name is the Chinese economy. It had a structural change after the reform of March 2013 in the relationship between the stock market in this country and the international oil market. The important changes suffered in the management of the refined oil price provoked a different dynamic (in mean and volatility) of both markets as is shown in Bouri et al. (2017b). For the case of the Indian, in a novelty approach, Bouri et al. (2017a) demonstrated the existence of a nonlinear dynamic of the volatility (implied) among the markets of gold, crude oil and the stock market. A causal relationship from these two commodities to the Indian stock market is shown but not the inverse.
Interestingly, Wang et al. (2020) showed that stock markets of the BRICS are strongly related to oil market (WTI) under severe circumstances using extreme Granger analysis. In an important finding Bouri et al. (2018) demonstrated a heterogeneity in the response of the risk of BRICS economies with respect to the oil implicit volatility. Positive movements in the volatility of oil have a more important impact on the exporters of this group, Russian and Brazil economies. On the contrary, negative movements have a more important impact on the importers China and India.
The original term BRIC composed by the first letter of the four countries: Brazil, Russia, India and China, was coined by the English economist Jim O’Neill to designate emerging economies that, according to O’Neill’s forecasts, would exceed in 2050 the World’s main economies. The power of these countries lies both on the size of its GDP, population and territory, as well as in the wealth of its natural and energy resources, its sustained growth and in the volume of its foreign trade (O’Neill 2001).
According to the International Monetary Fund, the Nominal GDP in 2018 of the four countries represented in the BRIC, near to 24% of world GDP, 95.7% of the GDP of the United States of America (International Monetary Fund 2020); and according to the World Bank, the block has more than 40% of the world’s population and together more than 25% of the planet’s surface, according to data from the Central Intelligence Agency (CIA) of the United States (Central Intelligence Agency 2020a, 2020b, 2020c, 2020d).
Therefore, the objective of this research focuses on the study of the relationship between the economies of the BRIC block, specifically on the movement of stock indexes and crude oil mixes in those countries, in order to find investment opportunities through the Markowitz theory (Markowitz 1952), building a portfolio with main indexes and crude oil mixes of the BRIC countries.
Multivariate Normal Inverse Gaussian (MNIG) Distribution
The GH family distributions, specifically the NIG distribution has been a notable option to model the distribution of return of numerous financial instruments, such as commodities, equities, options and so on. Nevertheless, empirical studies frequently focus on univariate cases. In this paper we have extended previous works (Núñez et al. 2018; Sánchez-Ruenes et al. 2020) to model returns of BRIC Indexes and Crude Oil prices using an MNIG distribution.
In the paper of 1977, Barndorff-Nielsen proposed the family of the GH distributions, which is considered in the literature as a seminal paper (Barndorff-Nielsen 1977). The NIG distribution type resulted in a convenient alternative for modeling financial series due its properties of capturing some stylized features, like semi-heavy tails, asymmetry and high volatility, present in financial data. This kind of distribution is the only member of GH family that is closed under convolution, guaranteeing the conservation of the same NIG distribution even the logarithmic increments for the exponential process (Barndorff-Nielsen 1998).
On the other hand, the MNIG distribution is a mean-variance mixture combination of a Gaussian distribution with an inverse Gaussian distribution (Oigard and Hanssen 2002).
The Multivariate Normal (MNormal) distribution is defined as X = (X1, …, Xd)t if X = μ + AZ, where Z = (Z1, …, Zk)t is an independent identically distributed vector of random variables with univariate Standard Normal distribution, A∈Rd×k and μ∈Rd. With this specification, we can express the multivariate distribution with the next density (Mardia et al. 1979):
where Σ is a semidefinite positive and non-singular matrix representing the covariance. Once the parameters were determined, Press et al. (1992) proposed an algorithm to simulate random vectors that follows the same distribution by employing the Cholesky decomposition of Σ.
If we consider a random vector, expressed as X = μ + √W AZ where W ≥ 0 is a random variable scalar. Assuming W has a Generalize Inverse Gaussian (GIG) distribution with density
where Kλ is the Bessel function of third kind defined as:
then, the variance mixture of distributions has the joint density of:
which is a special case of the GH case of:
With this expression, particular cases may be extended, for the purpose of this paper, the MNIG distribution is obtained when λ = −0.5 which becomes close to the Hyperbolic distribution but with heavier tails (McNeil et al. 2005).
Although there are several parameterizations for the GH distributions, we selected the one corresponding to that allows a faster convergence when fitting the empirical data (Weibel et al. 2020). To realize this, we will use the following transformation:
Set
It should be mentioned that the applications and the potential of the family of the Generalized Hyperbolic are vast. Andresen et al. (2010) present a discrete random-field model for forward prices driven by the MNIG distribution. Likewise, O’Hagan et al. (2016) establish that a combination of MNIG distributions is a great alternative to a mixture of Gaussian distributions as a tool to develop a model of clustering.
On the other hand, Eberlein and Prause (2001) confirmed that the GH family allows a better description of the returns of financial assets. In particular, these authors derive a formula for valuing options for models that include the GH using the Esscher transformation as a possibility to determine prices in an incomplete market.
2. Methodology
In this research we worked with daily data obtained from Bloomberg of market indexes of BRIC economies: IBOV from Brazil, RTSI from Russia, NIFTY from India and SHCOMP from China. We also studied the main crude oil mixes in those countries, except in India, owing to the unavailability of data. The oil mixes included in this study were: Marlim from Brazil, Urals from Russia and Daqing from China, and the data were obtained from Platts.
The period of time selected for the stock and oil prices series was from 2004 to 2019, owing to include structural oil price breakpoints and important events for the oil market in the current millennium such as the beginning of the oil price surge until the financial crisis in 2005 and the oil price rebound in 2012 until 2014. The bubble periods identified by Perifanis (2019) are included in the studying intervals as well. Finally, the decline in oil prices since 2014 was considered due to oversupply and demand decrease in oil markets, besides Saudi Arabia’s decision to maintain its oil production levels.
We applied the Augmented Dickey–Fuller test with Schwarz information criterion and the Phillips–Perron test with the Bartlett kernel spectral estimation method to find out the unit root of the variables. Then, we re-evaluated the stationarity using the logarithmic returns of the series and we obtained for every series a p-value less than 0.0001, that means the null hypothesis is rejected, that is, the series are stationary. Table 1 presents the descriptive statistics for those series.

Table 1.
Descriptive statistics for logarithmic returns of Brazil, Russia, India and China (BRIC) indexes and oil mixes. High kurtosis values appeared in every data series distribution. Source: own elaboration with data from Bloomberg.
Taking into account the stylized facts, mainly the presence of high levels of kurtosis, this could lead intuitively to the empirical adjustment of a distribution with semi-heavy tails. In this case, the proposal is the NIG distribution, as it has praiseworthy properties for financial analysis (Barndorff-Nielsen 1997).
In previous research (Núñez et al. 2018), the returns of BRIC indexes: IBOV, RTSI, NIFTY and SHCOMP, adjusted significantly in a univariate approach to NIG distribution, even during periods of economic crisis. In this study, we first verified if NIG distribution also fits the series of crude oil returns: MARLIM, URALS and DAQING. The results confirm that NIG distribution reasonably adjusted to the empirical data in a univariate case for those crude oil mixes. However, the world is connected through different variables, including the financial variables, so it makes sense to look for a multivariate distribution.
For this research, we created some vectors of dimension four, five and six with returns of BRIC indexes and crude oil mixes, and then we confirmed their adjustment to a MNIG distribution using a goodness-of-fit test through Cramer criteria with significance levels of 0.95 and 0.99 (Baringhaus and Franz 2004). See Table 2. The parameters of the MNIG distributions that adjust the suggested vectors are presented in Appendix A.

Table 2.
p-Values for every proposed vector using the Cramer test considering a Multivariate Normal Inverse Gaussian (MNIG) distribution. In all cases the p-values are not statistically significant and indicate strong evidence for the null hypothesis. Elaborated by authors with data from Bloomberg.
For every proposed vector, we did not reject the null hypothesis for NIG distribution—H0: the empirical data follow a MNIG distribution. We used R software to obtain these results, as well as the later ones.
3. Results
The results from the previous tests indicate that the logarithmic returns from the oil prices and indexes altogether adjust statistically, to an MNIG distribution.
We observed the strongest correlation between the oil mix and stock index of Russia. We could intuit, excluding Russia, that it is possible to create a diversified portfolio, and we proved it through an empirical study.
In this regard, we created a portfolio for every vector, according to the theory of Markowitz (1952), finding the optimal weights (ω’s), as seen in Table 3, for each investment instrument, in our case market indexes and commodities, in order to obtain a higher return with a lower risk.

Table 3.
Asset weights obtained for suggested portfolios 1 to 6 considering the 1st and 2nd moments of the adjusted MNIG distribution. From these weights, the expected returns and the standard deviation of each portfolio were calculated. Elaborated by authors with data from Bloomberg.
Therefore, we employed the relationship between the return–standard deviation to show the efficiency of every portfolio, obtaining the following ratios (Table 4):

Table 4.
Return–standard deviation relationship for portfolios 1 to 6 using the particular variance-covariance matrix of the adjusted MNIG and MNormal distribution. Elaborated by authors with data from Bloomberg.
It should be noted that the variance–covariance matrix plays a fundamental role in portfolio optimization theory (Markowitz 1952) and in the case of the family of GH distributions, it is calculated with the skewness (γ) and dispersion (Σ) parameters, through the variance equation according to McNeil et al. (2005). In Appendix B, we present the variance–covariance matrices obtained through the maximum likelihood criterion with a MNIG distribution for each portfolio.
Using those matrices, we obtained the following curves as a result of the optimization of the return–standard deviation relationship for those portfolios and we compared them with those obtained using the empirical sample variance–covariance matrix (see Figure 1).
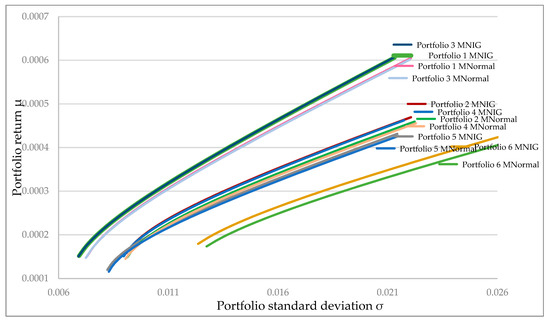
Figure 1.
Efficient frontier curves for portfolios (described in Table 3) considering the MNIG and Empirical sample (MNormal) variance–covariance matrix. Elaborated by authors with data from Bloomberg.
In all cases, we observed that the curves of the MNIG portfolios exceed those in which the MNormal variance–covariance matrices were considered. The difference between both groups of portfolios is attributed to the better fit of MNIG distribution on the logarithmic returns of the asset series. The variance–covariance matrices estimated through the multivariate distribution better represent the return behavior than the traditional covariance matrix.
Regarding the efficient frontier curves for portfolios obtained using the MNIG distribution, the curves of portfolio 1 (oil mixes from China, Russia and Brazil; and indexes from China, Brazil and India) and portfolio 3 (oil mixes from China and Brazil and indexes of China, Brazil and India); as well as portfolio 2 (oil mixes and indexes from China, Russia and Brazil) and portfolio 4 (oil mixes and indexes from China and Brazil) would be almost overlapping, with a difference of less than 0.14% and 0.8%, respectively. Comparing the curves of portfolios 1 and 3, we observe that the inclusion of the Russian mix does not represent a significant increase in the efficiency of the portfolio. Similarly, if we compare curves 2 and 4, we also find that, incorporating the Russian mix and index, it does not have a significant impact on portfolio efficiency.
On the other hand, the curves of portfolios 1 and 3 are above the pair of curves 2 and 4, revealing that the incorporation of the Hindu index contributes more than 32.6% to the efficiency of the portfolio. However, the increase greater than 6.7% in the curves of portfolios 2 and 4 with respect to curve 5, responds to the inclusion of the Brazilian mix and index. Finally, the growth of more than 23.8% in the efficiency of portfolio 5 compared to 6, is due to the exchange of instruments from Brazil for those from China.
In this sense, the instruments that had the greatest impact on portfolio efficiency (highest return with the lowest risk) are, in this order: NIFTY index (India); Daqing mix and the SHCOMP index (China); and Marlim mix and IBOV index (Brazil). On the opposite side, the contribution of the Urals mix and RTSI index (Russia) represents less than 1% in the return–standard deviation ratio of the portfolio.
4. Conclusions
In the present work, a multivariate approach for portfolio construction is employed using the market indexes IBOV, RTSI, NIFTY and SHCOMP, and crude oil mixes of Marlim, Urals and Daqing. Employing a Multivariate Normal Inverse Gaussian test for the logarithmic returns it was possible to determine that Normal Inverse Gaussian assumptions hold even in the multivariate case fitting the empirical data appropriately. In order to make efficient portfolios using MNIG distributions, the Markowitz theory was employed for some combinations of the oil mixes and market indexes of BRIC. The results show an insignificant diversification effect of including Russia’s index and/or oil mix in the Portfolio. From an investment optimization perspective, the results of this work show the possibility to diversify with market indexes and oil mixes of India, China and Brazil, even in periods including extreme and crisis events, showing that the greatest impact on portfolio efficiency is due to the Hindu index and the Chinese mix and index.
Focusing on an industrial context, as in the case of risk management, the estimation of risk measures, such as VaR and CVaR, requires a more precise approximation of the values, leading to better estimates and allowing more accurate decisions. This can be achieved through the method presented in this article, due to the fact that the MNIG distribution better models the stylized facts of the financial series, with no large computational power requirement, and is accessible to the managers, policymakers and investors.
Author Contributions
Conceptualization, J.A.N.-M. and E.S.-R.; methodology, J.A.N.-M.; software, E.S.-R.; validation, J.A.N.-M.; formal analysis, J.A.N.-M. and E.S.-R.; writing—original draft preparation, E.S.-R.; writing—review and editing, J.A.N.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Parameters of Multivariate Normal Inverse Gaussian (MNIG) distribution for proposed vectors.

Table A1.
MNIG Shape parameter for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
Table A1.
MNIG Shape parameter for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
| (Shape Parameter) |
|---|
| 0.9539552 |

Table A2.
MNIG Location parameter for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
Table A2.
MNIG Location parameter for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
| μ (Location Parameter) | |||||
|---|---|---|---|---|---|
| Daqing | Urals | Marlim | SHCOMP | IBOV | NIFTY |
| 0.001879721 | 0.001595145 | 0.001626657 | 0.001476737 | 0.001679586 | 0.001929382 |

Table A3.
MNIG Dispersion parameter for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
Table A3.
MNIG Dispersion parameter for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
| Σ (Dispersion Parameter) | ||||||
|---|---|---|---|---|---|---|
| Daqing | Urals | Marlim | SHCOMP | IBOV | NIFTY | |
| Daqing | 5.871779 × 10−4 | 2.712689 × 10−4 | 1.309442 × 10−4 | 5.422485 × 10−5 | 6.821899 × 10−5 | 4.617644 × 10−5 |
| Urals | 2.712689 × 10−4 | 5.949218 × 10−4 | 4.288536 × 10−4 | 4.788936 × 10−5 | 1.563676 × 10−4 | 7.103873 × 10−5 |
| Marlim | 1.309442 × 10−4 | 4.288536 × 10−4 | 7.116214 × 10−4 | 5.093432 × 10−5 | 2.259380 × 10−4 | 7.561874 × 10−5 |
| SHCOMP | 5.422485 × 10−5 | 4.788936 × 10−5 | 5.093432 × 10−5 | 3.316850 × 10−4 | 7.773826 × 10−5 | 7.598589 × 10−5 |
| IBOV | 6.821899 × 10−5 | 1.563676 × 10−4 | 2.259380 × 10−4 | 7.773826 × 10−5 | 7.406710 × 10−4 | 1.347001 × 10−4 |
| NIFTY | 4.617644 × 10−5 | 7.103873 × 10−5 | 7.561874 × 10−5 | 7.598589 × 10−5 | 1.347001 × 10−4 | 3.245957 × 10−4 |

Table A4.
MNIG Skewness parameter γ for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
Table A4.
MNIG Skewness parameter γ for Vector 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY.
| (Skewness Parameter) | |||||
|---|---|---|---|---|---|
| Daqing | Urals | Marlim | SHCOMP | IBOV | NIFTY |
| −0.001627277 | −0.001301048 | −0.001322349 | −0.001166164 | −0.001325997 | −0.001475250 |

Table A5.
MNIG Shape parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
Table A5.
MNIG Shape parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
| (Shape Parameter) |
|---|
| 0.9329531 |

Table A6.
MNIG Location parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
Table A6.
MNIG Location parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
| (Location Parameter) | |||||
|---|---|---|---|---|---|
| Daqing | Urals | Marlim | SHCOMP | RTSI | IBOV |
| 0.002233566 | 0.001820986 | 0.001726932 | 0.001666436 | 0.002339706 | 0.001424282 |

Table A7.
MNIG Dispersion parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
Table A7.
MNIG Dispersion parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
| (Dispersion Parameter) | ||||||
|---|---|---|---|---|---|---|
| Daqing | Urals | Marlim | SHCOMP | RTSI | IBOV | |
| Daqing | 5.873262 × 10−4 | 2.711392 × 10−4 | 1.324914 × 10−4 | 5.300234 × 10−5 | 1.496152 × 10−4 | 6.690959 × 10−5 |
| Urals | 2.711392 × 10−4 | 5.945670 × 10−4 | 4.274482 × 10−4 | 4.606771 × 10−5 | 2.085086 × 10−4 | 1.575886 × 10−4 |
| Marlim | 1.324914 × 10−4 | 4.274482 × 10−4 | 7.133162 × 10−4 | 4.995115 × 10−5 | 1.913549 × 10−4 | 2.280843 × 10−4 |
| SHCOMP | 5.300234 × 10−5 | 4.606771 × 10−5 | 4.995115 × 10−5 | 3.350986 × 10−4 | 8.076749 × 10−5 | 7.668110 × 10−5 |
| RTSI | 1.496152 × 10−4 | 2.085086 × 10−4 | 1.913549 × 10−4 | 8.076749 × 10−5 | 4.841467 × 10−4 | 2.336435 × 10−4 |
| IBOV | 6.690959 × 10−5 | 1.575886 × 10−4 | 2.280843 × 10−4 | 7.668110 × 10−5 | 2.336435 × 10−4 | 7.442306 × 10−4 |

Table A8.
MNIG Skewness parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
Table A8.
MNIG Skewness parameter for Vector 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV.
| (Skewness Parameter) | |||||
|---|---|---|---|---|---|
| Daqing | Urals | Marlim | SHCOMP | RTSI | IBOV |
| −0.001980172 | −0.001526153 | −0.001421928 | −0.001355208 | −0.002084975 | −0.001070141 |

Table A9.
MNIG Shape parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
Table A9.
MNIG Shape parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
| (Shape Parameter) |
|---|
| 0.878861 |

Table A10.
MNIG Location parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
Table A10.
MNIG Location parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
| (Location Parameter) | ||||
|---|---|---|---|---|
| Daqing | Marlim | SHCOMP | IBOV | NIFTY |
| 0.001674036 | 0.001738409 | 0.001599045 | 0.001764533 | 0.002011464 |

Table A11.
MNIG Dispersion parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
Table A11.
MNIG Dispersion parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
| (Dispersion Parameter) | |||||
|---|---|---|---|---|---|
| Daqing | Marlim | SHCOMP | IBOV | NIFTY | |
| Daqing | 6.073313 × 10−4 | 1.305301 × 10−4 | 5.362729 × 10−5 | 6.796856 × 10−5 | 4.580358 × 10−5 |
| Marlim | 1.305301 × 10−4 | 7.325409 × 10−4 | 5.049618 × 10−5 | 2.278790 × 10−4 | 7.484912 × 10−5 |
| SHCOMP | 5.362729 × 10−5 | 5.049618 × 10−5 | 3.300815 × 10−4 | 7.684276 × 10−5 | 7.592939 × 10−5 |
| IBOV | 6.796856 × 10−5 | 2.278790 × 10−4 | 7.684276 × 10−5 | 7.428642 × 10−4 | 1.334200 × 10−4 |
| NIFTY | 4.580358 × 10−5 | 7.484912 × 10−5 | 7.592939 × 10−5 | 1.334200 × 10−4 | 3.233551 × 10−4 |

Table A12.
MNIG Skewness parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
Table A12.
MNIG Skewness parameter for Vector 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY.
| (Skewness Parameter) | ||||
|---|---|---|---|---|
| Daqing | Marlim | SHCOMP | IBOV | NIFTY |
| −0.001420577 | −0.001433104 | −0.001287578 | −0.001409962 | −0.001556247 |

Table A13.
MNIG Shape parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
Table A13.
MNIG Shape parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
| (Shape Parameter) |
|---|
| 0.821983 |

Table A14.
MNIG Location parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
Table A14.
MNIG Location parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
| (Location Parameter) | |||
|---|---|---|---|
| Daqing | Marlim | SHCOMP | IBOV |
| 0.001724782 | 0.001827421 | 0.001652227 | 0.001572860 |

Table A15.
MNIG Dispersion parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
Table A15.
MNIG Dispersion parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
| (Dispersion Parameter) | ||||
|---|---|---|---|---|
| Daqing | Marlim | SHCOMP | IBOV | |
| Daqing | 6.037915 × 10−4 | 1.330179 × 10−4 | 5.284570 × 10−5 | 6.921679 × 10−5 |
| Marlim | 1.330179 × 10−4 | 7.310414 × 10−4 | 5.031627 × 10−5 | 2.346953 × 10−4 |
| SHCOMP | 5.284570 × 10−5 | 5.031627 × 10−5 | 3.279021 × 10−4 | 7.639908 × 10−5 |
| IBOV | 6.921679 × 10−5 | 2.346953 × 10−4 | 7.639908 × 10−5 | 7.536017 × 10−4 |

Table A16.
MNIG Skewness parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
Table A16.
MNIG Skewness parameter for Vector 4: Daqing, Marlim, SHCOMP, IBOV.
| (Skewness Parameter) | |||
|---|---|---|---|
| Daqing | Marlim | SHCOMP | IBOV |
| −0.001471361 | −0.001522132 | −0.001340790 | −0.001218463 |

Table A17.
MNIG Shape parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
Table A17.
MNIG Shape parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
| (Shape Parameter) |
|---|
| 0.7936773 |

Table A18.
MNIG Location parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
Table A18.
MNIG Location parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
| (Location Parameter) | |||
|---|---|---|---|
| Daqing | Urals | SHCOMP | RTSI |
| 0.001836324 | 0.001395869 | 0.001723940 | 0.001924799 |

Table A19.
MNIG Dispersion parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
Table A19.
MNIG Dispersion parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
| (Dispersion Parameter) | ||||
|---|---|---|---|---|
| Daqing | Urals | SHCOMP | RTSI | |
| Daqing | 6.035950 × 10−4 | 2.811235 × 10−4 | 5.510528 × 10−5 | 0.0001540243 |
| Urals | 2.811235 × 10−4 | 6.138225 × 10−4 | 4.647012 × 10−5 | 0.0002135782 |
| SHCOMP | 5.510528 × 10−5 | 4.647012 × 10−5 | 3.343305 × 10−4 | 0.0000807863 |
| RTSI | 1.540243 × 10−4 | 2.135782 × 10−4 | 8.078630 × 10−5 | 0.0004928031 |

Table A20.
MNIG Skewness parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
Table A20.
MNIG Skewness parameter for Vector 5: Daqing, Urals, SHCOMP, RTSI.
| (Skewness Parameter) | |||
|---|---|---|---|
| Daqing | Urals | SHCOMP | RTSI |
| −0.001582824 | −0.001101023 | −0.001412450 | −0.001669955 |

Table A21.
MNIG Shape parameter for Vector 6: Urals, Marlim, RTSI, IBOV.
Table A21.
MNIG Shape parameter for Vector 6: Urals, Marlim, RTSI, IBOV.
| (Shape Parameter) |
|---|
| 0.8879731 |

Table A22.
MNIG Location parameter for Vector 6: Urals, Marlim, RTSI, IBOV.
Table A22.
MNIG Location parameter for Vector 6: Urals, Marlim, RTSI, IBOV.
| (Location Parameter) | |||
|---|---|---|---|
| Urals | Marlim | RTSI | IBOV |
| 0.001780400 | 0.002149520 | 0.002453884 | 0.001978662 |

Table A23.
MNIG Dispersion parameter for Vector 6: Urals, Marlim, RTSI, IBOV.
Table A23.
MNIG Dispersion parameter for Vector 6: Urals, Marlim, RTSI, IBOV.
| (Dispersion Parameter) | ||||
|---|---|---|---|---|
| Urals | Marlim | RTSI | IBOV | |
| Urals | 0.0006007258 | 0.0004371611 | 0.0002083842 | 0.0001569735 |
| Marlim | 0.0004371611 | 0.0007264886 | 0.0001957445 | 0.0002273840 |
| RTSI | 0.0002083842 | 0.0001957445 | 0.0004714375 | 0.0002300495 |
| IBOV | 0.0001569735 | 0.0002273840 | 0.0002300495 | 0.0007288311 |

Table A24.
MNIG Skewness parameter γ for Vector 6: Urals, Marlim, RTSI, IBOV.
Table A24.
MNIG Skewness parameter γ for Vector 6: Urals, Marlim, RTSI, IBOV.
| (Skewness Parameter) | |||
|---|---|---|---|
| Urals | Marlim | RTSI | IBOV |
| −0.001485447 | −0.00184417 | −0.002198906 | −0.001624147 |
Appendix B

Table A25.
Maximum Likelihood Variance-Covariance Matrices for portfolio 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY. Elaborated by authors with data from Bloomberg.
Table A25.
Maximum Likelihood Variance-Covariance Matrices for portfolio 1: Daqing, Urals, Marlim, SHCOMP, IBOV, NIFTY. Elaborated by authors with data from Bloomberg.
| Variance-Covariance Matrix Portfolio 1 | Daqing | Urals | Marlim | SHCOMP | IBOV | NIFTY |
|---|---|---|---|---|---|---|
| Daqing | 5.90 × 10−4 | 2.73 × 10−4 | 1.33 × 10−4 | 5.62 × 10−5 | 7.05 × 10−5 | 4.87 × 10−5 |
| Urals | 2.73 × 10−4 | 5.97 × 10−4 | 4.31 × 10−4 | 4.95 × 10−5 | 1.58 × 10−4 | 7.31 × 10−5 |
| Marlim | 1.33 × 10−4 | 4.31 × 10−4 | 7.13 × 10−4 | 5.26 × 10−5 | 2.28 × 10−4 | 7.77 × 10−5 |
| SHCOMP | 5.62 × 10−5 | 4.95 × 10−5 | 5.26 × 10−5 | 3.33 × 10−4 | 7.94 × 10−5 | 7.78 × 10−5 |
| IBOV | 7.05 × 10−5 | 1.58 × 10−4 | 2.28 × 10−4 | 7.94 × 10−5 | 7.43 × 10−4 | 1.37 × 10−4 |
| NIFTY | 4.87 × 10−5 | 7.31 × 10−5 | 7.77 × 10−5 | 7.78 × 10−5 | 1.37 × 10−4 | 3.27 × 10−4 |

Table A26.
Maximum Likelihood Variance–Covariance Matrices for portfolio 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV. Elaborated by authors with data from Bloomberg.
Table A26.
Maximum Likelihood Variance–Covariance Matrices for portfolio 2: Daqing, Urals, Marlim, SHCOMP, RTSI, IBOV. Elaborated by authors with data from Bloomberg.
| Variance−Covariance Matrix Portfolio 2 | Daqing | Urals | Marlim | SHCOMP | RTSI | IBOV |
|---|---|---|---|---|---|---|
| Daqing | 5.92 × 10−4 | 2.74 × 10−4 | 1.36 × 10−4 | 5.59 × 10−5 | 1.54 × 10−4 | 6.92 × 10−5 |
| Urals | 2.74 × 10−4 | 5.97 × 10−4 | 4.30 × 10−4 | 4.83 × 10−5 | 2.12 × 10−4 | 1.59 × 10−4 |
| Marlim | 1.36 × 10−4 | 4.30 × 10−4 | 7.15 × 10−4 | 5.20 × 10−5 | 1.95 × 10−4 | 2.30 × 10−4 |
| SHCOMP | 5.59 × 10−5 | 4.83 × 10−5 | 5.20 × 10−5 | 3.37 × 10−4 | 8.38 × 10−5 | 7.82 × 10−5 |
| RTSI | 1.54 × 10−4 | 2.12 × 10−4 | 1.95 × 10−4 | 8.38 × 10−5 | 4.89 × 10−4 | 2.36 × 10−4 |
| IBOV | 6.92 × 10−5 | 1.59 × 10−4 | 2.30 × 10−4 | 7.82 × 10−5 | 2.36 × 10−4 | 7.45 × 10−4 |

Table A27.
Maximum Likelihood Variance–Covariance Matrices for portfolio 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY. Elaborated by authors with data from Bloomberg.
Table A27.
Maximum Likelihood Variance–Covariance Matrices for portfolio 3: Daqing, Marlim, SHCOMP, IBOV, NIFTY. Elaborated by authors with data from Bloomberg.
| Variance−Covariance Matrix Portfolio 3 | Daqing | Marlim | SHCOMP | IBOV | NIFTY |
|---|---|---|---|---|---|
| Daqing | 6.10 × 10−4 | 1.33 × 10−4 | 5.57 × 10−5 | 7.02 × 10−5 | 4.83 × 10−5 |
| Marlim | 1.33 × 10−4 | 7.35 × 10−4 | 5.26 × 10−5 | 2.30 × 10−4 | 7.74 × 10−5 |
| SHCOMP | 5.57 × 10−5 | 5.26 × 10−5 | 3.32 × 10−4 | 7.89 × 10−5 | 7.82 × 10−5 |
| IBOV | 7.02 × 10−5 | 2.30 × 10−4 | 7.89 × 10−5 | 7.45 × 10−4 | 1.36 × 10−4 |
| NIFTY | 4.83 × 10−5 | 7.74 × 10−5 | 7.82 × 10−5 | 1.36 × 10−4 | 3.26 × 10−4 |

Table A28.
Maximum Likelihood Variance–Covariance Matrices for portfolio 4: Daqing, Marlim, IBOV, SHCOMP. Elaborated by authors with data from Bloomberg.
Table A28.
Maximum Likelihood Variance–Covariance Matrices for portfolio 4: Daqing, Marlim, IBOV, SHCOMP. Elaborated by authors with data from Bloomberg.
| Variance−Covariance Matrix Portfolio 4 | Daqing | Marlim | IBOV | SHCOMP |
|---|---|---|---|---|
| Daqing | 6.06 × 10−4 | 1.36 × 10−4 | 7.14 × 10−5 | 5.52 × 10−5 |
| Marlim | 1.36 × 10−4 | 7.34 × 10−4 | 2.37 × 10−4 | 5.28 × 10−5 |
| IBOV | 7.14 × 10−5 | 2.37 × 10−4 | 7.55 × 10−4 | 7.84 × 10−5 |
| SHCOMP | 5.52 × 10−5 | 5.28 × 10−5 | 7.84 × 10−5 | 3.30 × 10−4 |

Table A29.
Maximum Likelihood Variance–Covariance Matrices for portfolio 5: Daqing, Urals, SHCOMP, RTSI. Elaborated by authors with data from Bloomberg.
Table A29.
Maximum Likelihood Variance–Covariance Matrices for portfolio 5: Daqing, Urals, SHCOMP, RTSI. Elaborated by authors with data from Bloomberg.
| Variance−Covariance Matrix Portfolio 5 | Daqing | Urals | SHCOMP | RTSI |
|---|---|---|---|---|
| Daqing | 6.07 × 10−4 | 2.83 × 10−4 | 5.79 × 10−5 | 1.57 × 10−4 |
| Urals | 2.83 × 10−4 | 6.15 × 10−4 | 4.84 × 10−5 | 2.16 × 10−4 |
| SHCOMP | 5.79 × 10−5 | 4.84 × 10−5 | 3.37 × 10−4 | 8.38 × 10−5 |
| RTSI | 1.57 × 10−4 | 2.16 × 10−4 | 8.38 × 10−5 | 4.96 × 10−4 |

Table A30.
Maximum Likelihood Variance–Covariance Matrices for portfolio 6: Urals, Marlim, RTSI, IBOV. Elaborated by authors with data from Bloomberg.
Table A30.
Maximum Likelihood Variance–Covariance Matrices for portfolio 6: Urals, Marlim, RTSI, IBOV. Elaborated by authors with data from Bloomberg.
| Variance−Covariance Matrix Portfolio 6 | Urals | Marlim | RTSI | IBOV |
|---|---|---|---|---|
| Urals | 6.03 × 10−4 | 4.40 × 10−4 | 2.12 × 10−4 | 1.60 × 10−4 |
| Marlim | 4.40 × 10−4 | 7.30 × 10−4 | 2.00 × 10−4 | 2.31 × 10−4 |
| RTSI | 2.12 × 10−4 | 2.00 × 10−4 | 4.77 × 10−4 | 2.34 × 10−4 |
| IBOV | 1.60 × 10−4 | 2.31 × 10−4 | 2.34 × 10−4 | 7.32 × 10−4 |
References
- Akram, Qaisar Farooq. 2004. Oil prices and exchange rates: Norwegian evidence. The Econometrics Journal 7: 476–504. [Google Scholar] [CrossRef]
- Alquist, Ron, and Olivier Gervais. 2013. The Role of Financial Speculation in Driving the Price of Crude Oil. The Energy Journal 34: 35–54. [Google Scholar] [CrossRef]
- Andresen, Arne, Steen Koekebakker, and Sjur Westgaard. 2010. Modeling electricity forward prices using the multivariate normal inverse Gaussian distribution. The Journal of Energy Markets 3: 3–25. [Google Scholar] [CrossRef][Green Version]
- Ansari, Md Gyasuddin, and Rudra Sensarma. 2019. US monetary policy, oil and gold prices: Which has a greater impact on BRICS stock markets? Economic Analysis and Policy 64: 130–51. [Google Scholar] [CrossRef]
- Apergis, Nicholas, and Stephen M. Miller. 2009. Do structural oil-market shocks affect stock prices? Energy Economics 31: 569–75. [Google Scholar] [CrossRef]
- Badeeb, Ramez Abubakr, and Hooi Hooi Lean. 2018. Asymmetric impact of oil price on Islamic sectoral stocks. Energy Economics 71: 128–39. [Google Scholar] [CrossRef]
- Baringhaus, Ludwig, and Carsten Franz. 2004. On a new multivariate two-sample test. Journal of Multivariate Analysis 88: 190–206. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole Eiler. 1977. Exponentially decreasing distributions for the logarithm of particle size. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 353: 401–19. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole Eiler. 1997. Normal Inverse Gaussian Distributions and Stochastic Volatility Modelling. Scandinavian Journal of Statistics 24: 1–13. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole Eiler. 1998. Processes of normal inverse Gaussian type. Finance and Stochastics 2: 41–68. [Google Scholar] [CrossRef]
- Bastianin, Andrea, Francesca Conti, and Matteo Manera. 2016. The Impacts of Oil Price Shocks on Stock Market Volatility: Evidence from the G7 Countries. Energy Policy 98: 160–69. [Google Scholar] [CrossRef]
- Bouri, Elie, Anshul Jain, Pratap Chandra Biswal, and David Roubaud. 2017a. Cointegration and nonlinear causality amongst gold, oil, and the Indian stock market: Evidence from implied volatility indices. Resources Policy 52: 201–206. [Google Scholar] [CrossRef]
- Bouri, Elie, Qian Chen, Donald Lien, and Xin Lv. 2017b. Causality between oil prices and the stock market in China: The relevance of the reformed oil product pricing mechanism. IREF 48: 34–48. [Google Scholar] [CrossRef]
- Bouri, Elie, Syed Jawad Hussain Shahzad, Naveed Raza, and David Roubaud. 2018. Oil volatility and sovereign risk of BRICS. Energy Economics 70: 258–69. [Google Scholar] [CrossRef]
- Brown, Stephen Paul Adolph, and Mine Kuban Yücel. 2002. Energy prices and aggregate economic activity: An interpretative survey. QREF 42: 193–208. [Google Scholar] [CrossRef]
- Central Intelligence Agency. 2020a. Brazil. In The World Factbook. Available online: https://www.cia.gov/library/publications/resources/the-world-factbook/geos/br.html (accessed on 24 July 2020).
- Central Intelligence Agency. 2020b. Russia. In The World Factbook. Available online: https://www.cia.gov/library/publications/resources/the-world-factbook/geos/rs.html (accessed on 24 July 2020).
- Central Intelligence Agency. 2020c. China. In The World Factbook. Available online: https://www.cia.gov/library/publications/resources/the-world-factbook/geos/ch.html (accessed on 24 July 2020).
- Central Intelligence Agency. 2020d. India. In The World Factbook. Available online: https://www.cia.gov/library/publications/resources/the-world-factbook/geos/in.html (accessed on 24 July 2020).
- Chen, Shiu-Sheng, and Hung-Chyn Chen. 2007. Oil prices and real exchange rates. Energy Economics 29: 390–404. [Google Scholar] [CrossRef]
- Cunado, Juncal, and Fernando Perez de Gracia. 2005. Oil prices, economic activity and inflation: Evidence for some Asian countries. QREF 45: 65–83. [Google Scholar] [CrossRef]
- Davis, Steven J., and John Haltiwanger. 2001. Sectoral job creation and destruction responses to oil price changes. Journal of Monetary Economics 48: 465–512. [Google Scholar] [CrossRef]
- Du, Limin, and Yanan He. 2015. Extreme risk spillovers between crude oil and stock markets. Energy Economics 51: 455–65. [Google Scholar] [CrossRef]
- Eberlein, Ernst, and Karsten Prause. 2001. The generalized hyperbolic model: Financial derivatives and risk measures. In Mathematical Finance—Bachelier Congress. Edited by Hélyette Geman, Dilip Madan, Stanley Pliska and Ton Vorst. Berlin: Springer, pp. 245–67. [Google Scholar]
- Fang, Chung-Rou, and Shih-Yi You. 2014. The impact of oil price shocks on the large emerging countries’ stock prices: Evidence from China, India and Russia. IREF 29: 330–38. [Google Scholar] [CrossRef]
- Hamilton, James Douglas. 1983. Oil and the Macroeconomy since World War II. Journal of Political Economy 91: 228–48. [Google Scholar] [CrossRef]
- Hamilton, James Douglas. 2003. What is an oil shock? Journal of Econometrics 113: 363–98. [Google Scholar] [CrossRef]
- Hamilton, James Douglas, and Ana Maria Herrera. 2004. Oil Shocks and Aggregate Macroeconomic Behavior: The Role of Monetary Policy: A Comment. JMCB 36: 265–86. [Google Scholar] [CrossRef]
- Hooker, Mark A. 2002. Are Oil Shocks Inflationary? Asymmetric and Nonlinear Specifications versus Changes in Regime. JMCB 34: 540–61. [Google Scholar] [CrossRef]
- Huang, Ying, and Feng Guo. 2007. The role of oil price shocks on China’s real exchange rate. China Economic Review 18: 403–16. [Google Scholar] [CrossRef]
- International Monetary Fund. 2020. World Economic Outlook. Washington, D.C.: International Monetary Fund. Available online: https://www.imf.org/external/pubs/ft/weo/2020/01/weodata/weoselgr.aspx (accessed on 24 July 2020).
- Ji, Qiang, Bing-Yue Liu, Wan-Li Zhao, and Ying Fan. 2020. Modelling dynamic dependence and risk spillover between all oil price shocks and stock market returns in the BRICS. IRFA 68: 101238. [Google Scholar] [CrossRef]
- Jones, Donald Wallace, Paul N. Leiby, and Inja K. Paik. 2004. Oil Price Shocks and the Macroeconomy: What Has Been Learned Since 1996. The Energy Journal 25: 1–32. [Google Scholar] [CrossRef]
- Kang, Wensheng, Ronald A. Ratti, and Kyung Hwan Yoon. 2015. Time-varying effect of oil market shocks on the stock market. JBF 61: S150–S63. [Google Scholar] [CrossRef]
- Lardic, Sandrine, and Valerie Mignon. 2006. The impact of oil prices on GDP in European countries: An empirical investigation based on asymmetric cointegration. Energy Policy 34: 3910–15. [Google Scholar] [CrossRef]
- Lee, Kiseok, and Shawn Ni. 2002. On the dynamic effects of oil price shocks: A study using industry level data. Journal of Monetary Economics 49: 823–52. [Google Scholar] [CrossRef]
- Lee, Byung Rhae, Kiseok Lee, and Ronald A. Ratti. 2001. Monetary policy, oil price shocks, and the Japanese economy. Japan and the World Economy 13: 321–49. [Google Scholar] [CrossRef]
- Lin, Boqiang, and Tong Su. 2020. Mapping the oil price-stock market nexus researches: A scientometric review. IREF 67: 133–47. [Google Scholar] [CrossRef]
- Ma, Yan-ran, Qiang Ji, and Jiaofeng Pan. 2019. Oil financialization and volatility forecast: Evidence from multidimensional predictors. Journal of Forecasting 38: 564–81. [Google Scholar] [CrossRef]
- Mardia, Kantilal Vardichand, John T. Kent, and John M. Bibby. 1979. Multivariate Analysis. Cambridge: Academic Press. [Google Scholar]
- Markowitz, Harry Max. 1952. Portfolio Selection. The Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- McNeil, Alexander John, Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management: Concepts, Techniques, and Tools. Princeton: Princeton University Press. [Google Scholar]
- Nandha, Mohan, and Shawkat Hammoudeh. 2007. Systematic risk, and oil price and exchange rate sensitivities in Asia-Pacific stock markets. RIBAF 21: 326–41. [Google Scholar] [CrossRef]
- Núñez, José Antonio, Mario Iván Contreras-Valdez, Alfredo Ramírez-García, and Eduardo Sánchez-Ruenes. 2018. Underlying Assets Distribution in Derivatives: The BRIC Case. Theoretical Economics Letters 8: 502–13. [Google Scholar] [CrossRef]
- O’Hagan, Adrian, Thomas Brendan Murphy, Isobel Claire Gormley, Paul D. McNicholas, and Dimitris Karlis. 2016. Clustering with the multivariate normal inverse Gaussian distribution. Computational Statistics and Data Analysis 93: 18–30. [Google Scholar] [CrossRef]
- O’Neill, Jim. 2001. Building Better Global Economic BRICs. Global Economics. Goldman Sachs 66: 1–16. [Google Scholar]
- Oigard, Tor Arne, and Alfred Hanssen. 2002. The multivariate normal inverse Gaussian heavy-tailed distribution; simulation and estimation. Paper presented at 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, May 13–17. [Google Scholar]
- Pal, Debdatta, and Subrata Kumar Mitra. 2019. Oil price and automobile stock return co-movement: A wavelet coherence analysis. Economic Modelling 76: 172–81. [Google Scholar] [CrossRef]
- Perifanis, Theodosios. 2019. Detecting West Texas Intermediate (WTI) Prices’ Bubble Periods. Energies 12: 2649. [Google Scholar] [CrossRef]
- Press, William Henry, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery. 1992. Numerical Recipes in C. Cambridge: Cambridge University Press. [Google Scholar]
- Sánchez-Ruenes, Eduardo, José Antonio Núñez, and Martha Beatriz Mota. 2020. VaR and CVaR estimates in BRIC’s Oil Sector: A Normal Inverse Gaussian Distribution Approach. Economía: teoría y práctica 52: 207–36. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Nader Trabelsi, Faisal Alqahtani, and Shawkat Hammoudeh. 2019. Analysing systemic risk and time-frequency quantile dependence between crude oil prices and BRICS equity markets indices: A new look. Energy Economics 83: 445–66. [Google Scholar] [CrossRef]
- Wang, Lu, Feng Ma, Tianjiao Niu, and Chengting He. 2020. Crude oil and BRICS stock markets under extreme shocks: New evidence. Economic Modelling 86: 54–68. [Google Scholar] [CrossRef]
- Weibel, Marc, Wolfgang Breymann, and David Lüthi. 2020. ghyp: A package on generalized hyperbolic distributions. Manual for the R package GHYP 1: 1–27. [Google Scholar]
- Wen, Danyan, Gang-Jin Wang, Chaoqun Ma, and Yudong Wang. 2019a. Risk spillovers between oil and stock markets: A VAR for VaR analysis. Energy Economics 80: 524–35. [Google Scholar] [CrossRef]
- Wen, Xiaoqian, Elie Bouri, and Hua Cheng. 2019b. The crude oil-stock market dependence and its determinants: Evidence from emerging economies. Emerging Markets Finance and Trade 55: 2254–74. [Google Scholar] [CrossRef]
- Zhang, Yue-Jun, and Jing Wang. 2015. Exploring the WTI crude oil price bubble process using the Markov regime switching model. Physica A: Statistical Mechanics and its Applications 421: 377–87. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).