A Quasi-Closed-Form Solution for the Valuation of American Put Options
Abstract
1. Introduction
2. The American Put Option Valuation Model
2.1. Analytical Solution for the Value of an American Put Option
- for
- is a parameter with for m − i ≤ 0 and i = 1,2,3.
- is a parameter with .
2.2. The Application of the Richardson Extrapolation in the Valuation Model of an American Put Option
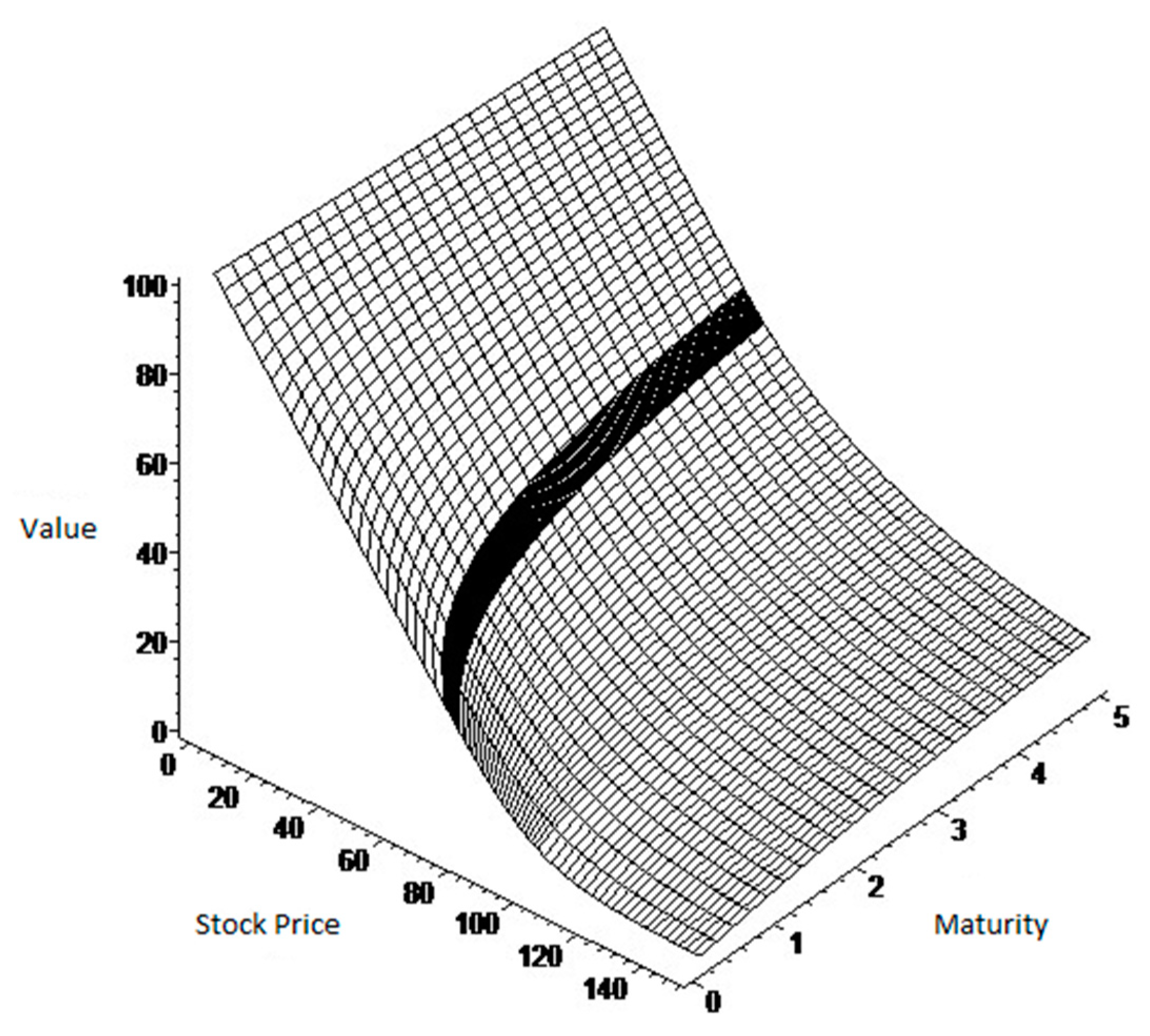
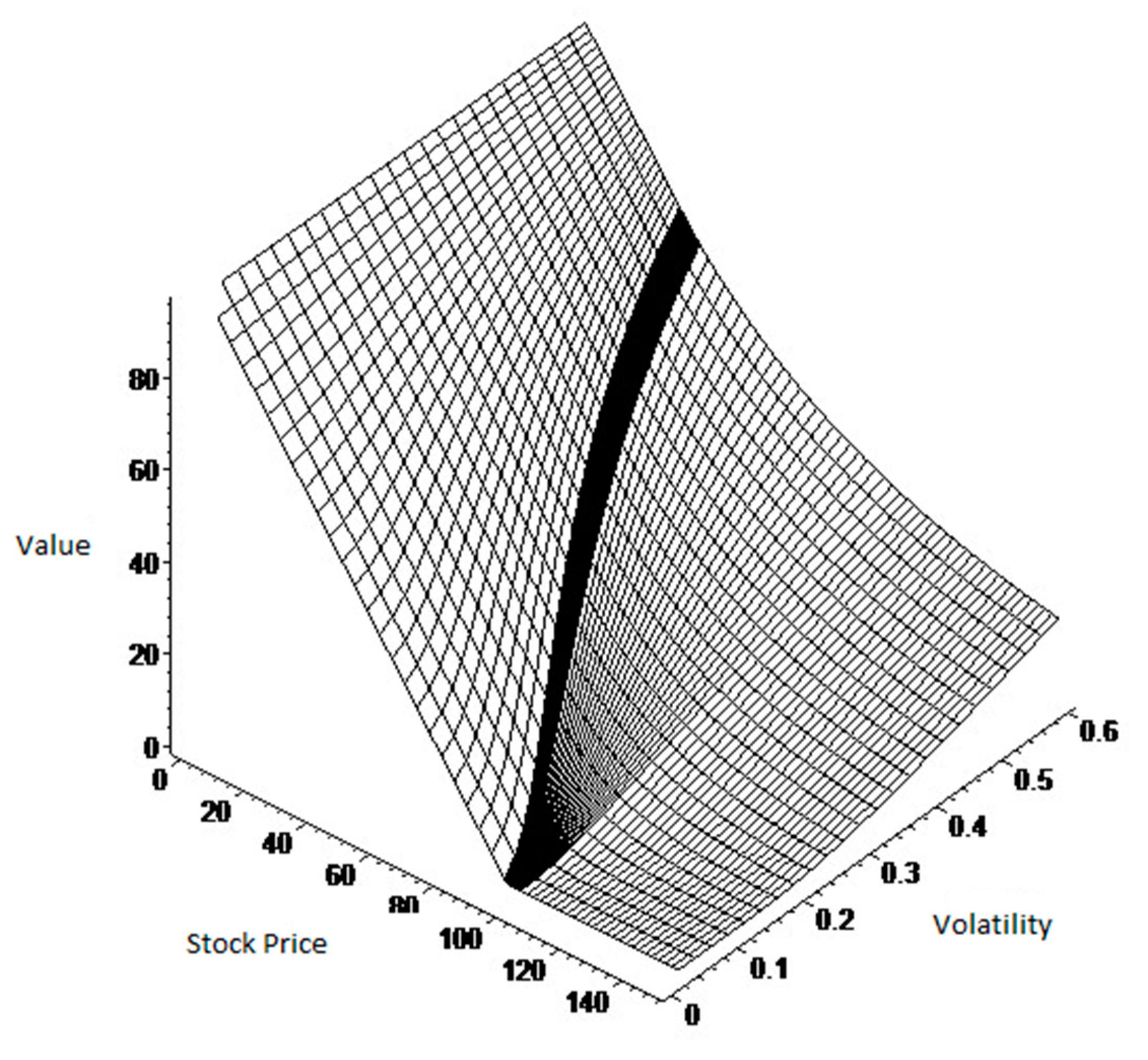
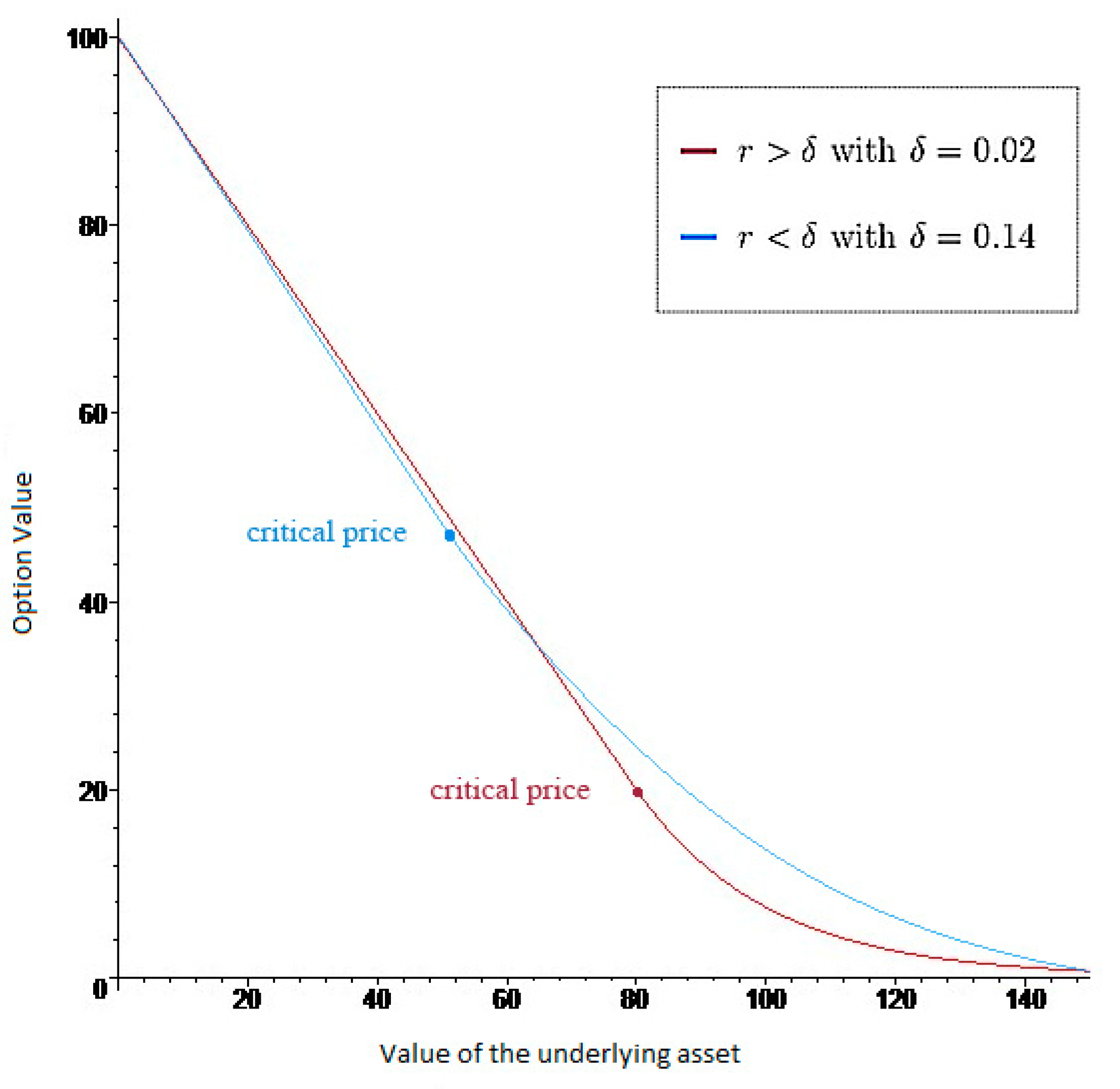
3. Results of the American Put Option Valuation Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aitsahlia, Farid, and Peter Carr. 1997. American options: A comparison of numerical methods. In Numerical Methods in Finance. Edited by Leonard Christopher Gordon Rogers and Denis Talay. Cambridge: Cambridge University Press, pp. 67–87. [Google Scholar]
- Ballestra, Luca Vincenzo. 2018. Fast and accurate calculation of American option prices. Decisions in Economics and Finance 41: 399–426. [Google Scholar] [CrossRef]
- Bjerksund, Petter, and Gunnar Stensland. 1993. Closed-form approximation of American options. Scandinavian Journal of Management 9: 87–99. [Google Scholar] [CrossRef]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–59. [Google Scholar] [CrossRef]
- Bunch, David, and Herb Johnson. 1992. A simple and numerically efficient valuation method for American puts using a modified Geske-Johnson approach. Journal of Finance 47: 809–816. [Google Scholar]
- Bunch, David, and Herb Johnson. 2000. The American put option and its critical stock price. Journal of Finance 55: 2333–56. [Google Scholar] [CrossRef]
- Carr, Peter. 1998. Randomization and the American put. The Review of Financial Studies 11: 597–626. [Google Scholar] [CrossRef]
- Carr, Peter, and Dmitri Faguet. 1996. Valuing Finite-Lived Options as Perpetual. SSRN Electronic Journal. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=706 (accessed on 6 October 2020).
- Carr, Peter, Robert Jarrow, and Ravi Myneny. 1992. Alternative characterizations of American put options. Mathematical Finance 2: 87–106. [Google Scholar] [CrossRef]
- Fabozzi, Frank J., Tommaso Paletta, Silvia Stanescu, and Radu Tunaru. 2016. An improved method for pricing and hedging long dated American options. European Journal of Operational Research 254: 656–66. [Google Scholar] [CrossRef][Green Version]
- Fatone, Lorella, Francesca Mariani, Maria Cristina Recchioni, and Francesco Zirilli. 2015. The Barone-Adesi Whaley formula to price American options revisited. Applied Mathematics 6: 382–402. [Google Scholar] [CrossRef]
- Geske, Robert, and Herb E. Johnson. 1984. The American put valued analytically. Journal of Finance 39: 1511–24. [Google Scholar] [CrossRef]
- Ho, Thomas S., Richard Christopher Stapleton, and Marti Gurunath Subrahmanyam. 1994. A Simple technique for the valuation and hedging of American options. Journal of Derivatives 2: 52–66. [Google Scholar] [CrossRef]
- Huang, Jing-zhi, Marti Gurunath Subrahmanyam, and G. George Yu. 1996. Pricing and hedging American options: A recursive integration method. The Review of Financial Studies 9: 277–300. [Google Scholar] [CrossRef]
- Ingersoll, Jonathan E., Jr. 1998. Approximating American options and other financial contracts using barrier derivatives. Journal of Computational Finance 2: 85–112. [Google Scholar] [CrossRef]
- Jacka, Saul D. 1991. Optimal stopping and the American put. Mathematical Finance 1: 1–14. [Google Scholar] [CrossRef]
- Ju, Nengjiu. 1998. Pricing an American option by approximating its early exercise boundary as a multipiece exponential function. Review of Financial Studies 11: 627–46. [Google Scholar] [CrossRef]
- Kim, In Joon. 1990. The analytic valuation of American puts. Review of Financial Studies 3: 547–72. [Google Scholar] [CrossRef]
- Lee, Jongwoo, and Dean Paxson. 2003. Confined exponential approximations for the valuation of American options. The European Journal of Finance 9: 1–26. [Google Scholar] [CrossRef]
- Leipold, Markus, and Nikola Vasiljevic. 2017. Pricing and disentanglement of American puts in the hyper-exponential jump-diffusion model. Journal of Banking and Finance 77: 78–94. [Google Scholar] [CrossRef]
- Li, Minqiang. 2010. Analytical approximations for the critical stock prices of American options: A performance comparison. Review of Derivatives Research 13: 75–99. [Google Scholar] [CrossRef]
- Meyer, Gunter H., and John van der Hoek. 1997. The valuation of American options with the method of lines. In Advances in Futures and Options Research. Edited by Phelim Boyle, George Pennacchi and Peter Ritchken. Bingley: Emerald Group Publishing Limited, pp. 265–85. [Google Scholar]
- Roll, Richard. 1977. An analytic valuation formula for unprotected American call options on stocks with known dividends. Journal of Financial Economics 5: 251–58. [Google Scholar] [CrossRef]
- Zhao, Jing, and Hoi Ying Wong. 2012. A closed-form solution to American options under general diffusion processes. Quantitative Finance 12: 725–37. [Google Scholar] [CrossRef]
- Zhu, Song-Ping. 2006a. An exact and explicit solution for the valuation of American put options. Quantitative Finance 6: 229–42. [Google Scholar] [CrossRef]
- Zhu, Song-Ping. 2006b. A new analytical-approximation formula for the optimal exercise boundary of American put options. International Journal of Theoretical and Applied Finance 9: 1141–77. [Google Scholar] [CrossRef]
- Zhu, Song-Ping, Xin-Jiang He, and Xiaoping Lu. 2018. A new integral equation formulation for American put options. Quantitative Finance 18: 483–90. [Google Scholar] [CrossRef]
| (1) (S; δ) | (2) TRUE | (3) RAN4 | (4) EXP3 | (5) QD+ | (6) QD* | (7) PA | (8) MLE (n = 4) |
|---|---|---|---|---|---|---|---|
| (80;0.12) | 25.658 | 25.654 | 25.657 | 25.753 | 25.715 | 25.648 | 25.654 |
| (90;0.12) | 20.083 | 20.084 | 20.082 | 20.202 | 20.176 | 20.079 | 20.084 |
| (100;0.12) | 15.498 | 15.498 | 15.497 | 15.618 | 15.601 | 15.509 | 15.498 |
| (110;0.12) | 11.803 | 11.805 | 11.802 | 11.912 | 11.900 | 11.834 | 11.805 |
| (120;0.12) | 8.886 | 8.885 | 8.885 | 8.978 | 8.970 | 8.941 | 8.885 |
| (80;0.08) | 22.205 | 22.197 | 22.208 | 22.162 | 22.149 | 22.196 | 22.197 |
| (90;0.08) | 16.207 | 16.197 | 16.211 | 16.181 | 16.17 | 16.194 | 16.197 |
| (100;0.08) | 11.704 | 11.688 | 11.707 | 11.708 | 11.7 | 11.692 | 11.688 |
| (110;0.08) | 8.367 | 8.354 | 8.37 | 8.395 | 8.39 | 8.36 | 8.354 |
| (120;0.08) | 5.93 | 5.918 | 5.932 | 5.971 | 5.967 | 5.929 | 5.918 |
| (80;0.04) | 20.35 | 20.35 | 20.351 | 20.334 | 20.337 | 20.342 | 20.35 |
| (90;0.04) | 13.497 | 13.496 | 13.5 | 13.465 | 13.471 | 13.473 | 13.496 |
| (100;0.04) | 8.944 | 8.936 | 8.947 | 8.926 | 8.931 | 8.912 | 8.936 |
| (110;0.04) | 5.912 | 5.902 | 5.915 | 5.916 | 5.92 | 5.876 | 5.902 |
| (120;0.04) | 3.898 | 3.887 | 3.9 | 3.92 | 3.922 | 3.86 | 3.887 |
| (80;0.00) | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| (90;0.00) | 11.697 | 11.701 | 11.699 | 11.703 | 11.709 | 11.701 | 11.701 |
| (100;0.00) | 6.932 | 6.932 | 6.935 | 6.95 | 6.958 | 6.914 | 6.932 |
| (110;0.00) | 4.155 | 4.153 | 4.157 | 4.185 | 4.191 | 4.132 | 4.153 |
| (120;0.00) | 2.51 | 2.507 | 2.512 | 2.548 | 2.551 | 2.484 | 2.507 |
| - | 0.00105 | 0.00032 | 0.00590 | 0.00587 | 0.00413 | 0.00105 |
| (1) (S,τ,σ,r,δ) | (2) BENCH | (3) BJST | (4) IB | (5) CEAM | (6) MLE (n = 4) |
|---|---|---|---|---|---|
| (80;3.0;0.40;0.06;0.02) | 29.26 | 29.1 | 29.1 | 29.33 | 29.24 |
| (85;3.0;0.40;0.06;0.02) | 26.92 | 26.77 | 26.77 | 26.94 | 26.9 |
| (90;3.0;0.40;0.06;0.02) | 24.8 | 24.65 | 24.65 | 24.82 | 24.77 |
| (95;3.0;0.40;0.06;0.02) | 22.88 | 22.73 | 22.73 | 22.89 | 22.85 |
| (100;3.0;0.40;0.06;0.02) | 21.13 | 20.98 | 20.98 | 21.11 | 21.1 |
| (105;3.0;0.40;0.06;0.02) | 19.54 | 19.4 | 19.39 | 19.49 | 19.5 |
| (110;3.0;0.40;0.06;0.02) | 18.08 | 17.95 | 17.94 | 18.03 | 18.05 |
| (115;3.0;0.40;0.06;0.02) | 16.76 | 16.63 | 16.62 | 16.71 | 16.72 |
| (120;3.0;0.40;0.06;0.02) | 15.54 | 15.42 | 15.4 | 15.5 | 15.51 |
| (100;3.0;0.40;0.02;0.02) | 25.89 | 25.78 | 25.82 | 25.89 | 25.86 |
| (100;3.0;0.40;0.04;0.02) | 23.3 | 23.17 | 23.17 | 23.3 | 23.26 |
| (100;3.0;0.40;0.06;0.02) | 21.13 | 20.98 | 20.99 | 21.11 | 21.1 |
| (100;3.0;0.40;0.08;0.02) | 19.27 | 19.13 | 19.14 | 19.25 | 19.25 |
| (100;3.0;0.40;0.10;0.02) | 17.66 | 17.54 | 17.55 | 17.63 | 17.65 |
| (100;3.0;0.30;0.06;0.02) | 15.17 | 15.04 | 15.06 | 15.19 | 15.15 |
| (100;3.0;0.35;0.06;0.02) | 18.16 | 18.02 | 18.03 | 18.19 | 18.13 |
| (100;3.0;0.40;0.06;0.02) | 21.13 | 20.98 | 20.99 | 21.11 | 21.1 |
| (100;3.0;0.45;0.06;0.02) | 24.07 | 23.91 | 23.91 | 24.06 | 24.03 |
| (100;3.0;0.50;0.06;0.02) | 26.98 | 26.8 | 26.81 | 27.03 | 26.93 |
| (100;0.5;0.40;0.06;0.02) | 10.27 | 10.21 | 10.23 | 10.26 | 10.26 |
| (100;1.0;0.40;0.06;0.02) | 13.88 | 13.78 | 13.8 | 13.81 | 13.85 |
| (100;1.5;0.40;0.06;0.02) | 16.37 | 16.25 | 16.26 | 16.35 | 16.34 |
| (100;2.0;0.40;0.06;0.02) | 18.28 | 18.15 | 18.16 | 18.26 | 18.25 |
| (100;2.5;0.40;0.06;0.02) | 19.83 | 19.69 | 19.7 | 19.81 | 19.8 |
| (100;3.0;0.40;0.06;0.02) | 21.13 | 20.98 | 20.99 | 21.11 | 21.1 |
| (100;3.5;0.40;0.06;0.02) | 22.24 | 22.08 | 22.08 | 22.22 | 22.2 |
| (100;4.0;0.40;0.06;0.02) | 23.19 | 23.03 | 23.04 | 23.23 | 23.16 |
| (100;4.5;0.40;0.06;0.02) | 24.02 | 23.87 | 23.87 | 24.06 | 23.99 |
| (100;5.0;0.40;0.06;0.02) | 24.76 | 24.61 | 24.61 | 24.85 | 24.73 |
| (100;5.5;0.40;0.06;0.02) | 25.41 | 25.26 | 25.26 | 25.5 | 25.39 |
| (100;3.0;0.40;0.06;0.00) | 19.85 | 19.69 | 19.71 | 19.85 | 19.83 |
| (100;3.0;0.40;0.06;0.02) | 21.13 | 20.98 | 20.99 | 21.11 | 21.1 |
| (100;3.0;0.40;0.06;0.04) | 22.49 | 22.36 | 22.36 | 22.47 | 22.45 |
| - | 0.0069 | 0.0064 | 0.0019 | 0.0015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viegas, C.; Azevedo-Pereira, J. A Quasi-Closed-Form Solution for the Valuation of American Put Options. Int. J. Financial Stud. 2020, 8, 62. https://doi.org/10.3390/ijfs8040062
Viegas C, Azevedo-Pereira J. A Quasi-Closed-Form Solution for the Valuation of American Put Options. International Journal of Financial Studies. 2020; 8(4):62. https://doi.org/10.3390/ijfs8040062
Chicago/Turabian StyleViegas, Cristina, and José Azevedo-Pereira. 2020. "A Quasi-Closed-Form Solution for the Valuation of American Put Options" International Journal of Financial Studies 8, no. 4: 62. https://doi.org/10.3390/ijfs8040062
APA StyleViegas, C., & Azevedo-Pereira, J. (2020). A Quasi-Closed-Form Solution for the Valuation of American Put Options. International Journal of Financial Studies, 8(4), 62. https://doi.org/10.3390/ijfs8040062





