1. Introduction
Spillover effect refers to the impact that unrelated events in one nation can have on the economies of other nations. Spillover impact may be caused by stock market downturns such as the global financial crisis in 2008, or macro events like the Covid-19 outbreak in 2019. The internationalization of the Chinese economy affects the global structure of markets, resources, capital and finance, prices and consumer demand, supply and value chains, and production networks, and economic governance and organization (
Huang and Young 2013). To understand how the Chinese stock market interacts with US markets’ industrial metals and energy markets, this study examines information transmission as a function of daily return and volatility spillovers. Return and volatility spillovers are the most extensive channel for spreading out the news generated in one market to the other ones, which makes the financial markets inherit international risk factors as their own local risks. However,
Hou and Li (
2016) claim that the pattern of informational linkages observed in developed financial markets may not be relevant for Chinese stock markets due to their unique features and relatively short transaction history, though their data set covered the period between May 2010 and July 2013, which was before Trump’s presidency period and the Chinese stock market crash. China’s slump was the major topic of discussions at the International Monetary Fund annual meeting of finance ministers and central bankers in October 2015. The main concern was whether China’s economic downturn would trigger a new financial crisis or not. The turbulence in Chinese markets started with the burst of the bubble on 12 June 2015 and continued till February 2016. Shares on the Shanghai Stock Exchange lost a third of their value within one month of this incident. Aftershocks occurred between 27 July and 24 August, “Black Monday”. By 8–9 July 2015, the Shanghai stock market had fallen 30% and 1400 companies filed for a trading halt to prevent further losses. The values of Chinese stock markets continued to drop despite efforts by the government to reduce the fall. This fall trend was the largest fall since 2007. By the end of December 2015, China’s stock market had recovered and outperformed the S&P for 2015. By the end of 2015, the Shanghai Composite Index was up 12.6%. In January 2016, the Chinese stock market experienced a steep sell-off and trading was halted, and this instability continued till 2017 with other fluctuations and new shocks. After this last turbulence, the Shanghai Composite Index has been stable, however its value is still 50% less than before the bubble popped as of January 2017. After 2015, Chinese markets became more and more interconnected with developed markets which also made Trump fuel trade wars and the “digital cold war” era via Twitter against China.
Given the trade war tensions and concerns about economic growth, the industrial metals market was challenged by increasing macro risks and slowdown in demand growth. Being the global factory of the world economy, the significance of Chinese industrial metals demand relative to global demand is very crucial for market prices and it has been a key driver of growth in the past. Besides its consumption potential of industrial metals, another important input for China is oil.
According to the Global Risk Report from the 2020 World Economic Forum, the shift from oil to gas, electrification, renewables, nuclear, and hydrogen will require new strong technological developments and reforms. Demand for energy is continuing to increase and much of it is still sourced with fossil fuels. Global energy demand rose 2.3% in 2018 and 70% of the rise was constituted by China, the US, and India. As the climate change crisis worsens, more politicians will start to highlight the importance of the transition to clean energy. In this context, the role of rare earths increases in renewable energy developments. For example, when combined with iron and boron, neodymium
1 makes strong magnets that are important both for generators in wind turbines and motors in electrical vehicles. Neodymium is very much controlled by a single country since about 85% of the world’s neodymium comes out of a few mines in China. Moreover, China has the highest reserves of rare earth
2 minerals at 44 million MT. The country was also the world’s leading rare earths producer in 2018 by a long shot, putting out 120,000 MT
3. China’s dominance in both rare earth elements production and reserves has caused problems in the past in 2010, when the country cut exports. The government in Beijing further increased its control by forcing smaller, independent miners to merge into state-owned corporations or face closure. At the end of 2010, China announced that the first round of export quotas in 2011 for rare earths would be 14,446 tons, which was a 35% decrease from the previous first round of quotas in 2010. This resulted in a rush to secure the supply of the minerals elsewhere. Although that situation has since been resolved, the current trade war between the US and China has raised doubts again about the country’s position.
High volatility periods in the crude oil market and rare earths market is not welcomed by investors. Rare earths are a commodity that requires a high amount of R&D investment sourced by either government or private investors. In this context, studying the volatility spillover between rare earth, crude oil, industrial metals, and stock markets creates great value where China is the key element with its unique position both as a consumer of raw materials and producer of goods. Consequently, with its hybrid role, China’s stock markets affect US stock markets more as an outcome of this global cycle. These linkages are expected to increase significantly as China opens up its financial markets to the rest of the world; investors are increasingly looking for investment opportunities abroad as domestic returns are expected to decline following lower expectations about the growth of the Chinese economy in the future (
Vergeron 2015).
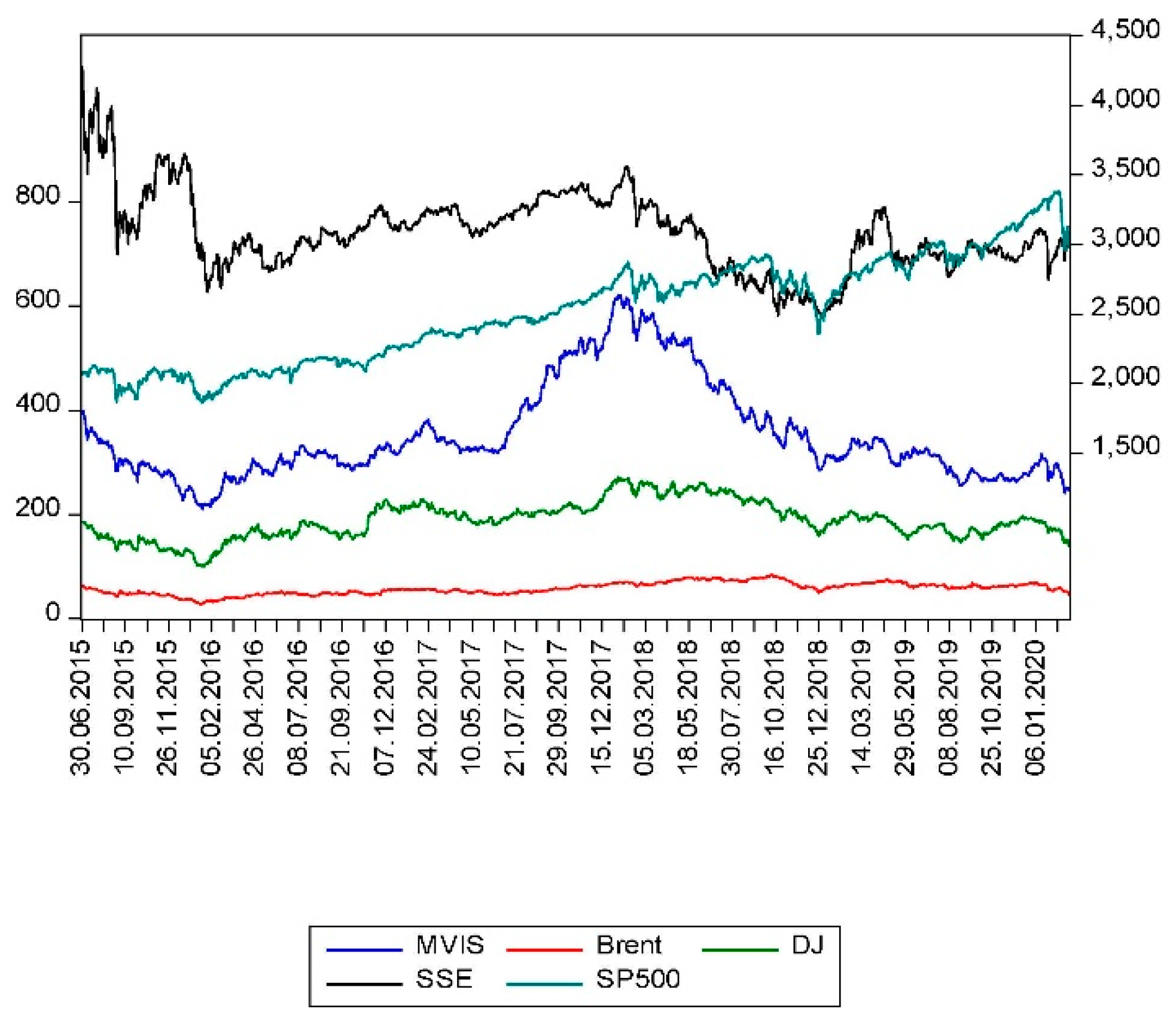
Figure 1 shows the time series of the daily returns of the markets. The time-varying and volatility clustering characteristics can be observed in
Figure 1. These clusters will be analyzed in detail as regards the following sessions based on the spillover effects of the selected assets.
2. Literature Review
For the world economy, China is the key element with its unique position both as a consumer of raw materials and producer of goods. This hybrid role enables China’s stock markets to affect US stock markets incrementally. In this context, studying the volatility spillover between interconnected markets such as rare earth, crude oil, industrial metals, and stock markets provides valuable insight for any type of investor. Dornbusch, Park, and Claessens (
Dornbusch et al. 2000) split the reasons for contagion into two categories such as fundamental-based contagion and non-fundamental-based contagion. Fundamental-based contagion refers to contagion spillovers that are source by real linkages and financial linkages. Non-fundamental-based contagion refers to contagion spillovers that are not subject to changes in macroeconomic dynamics or fundamentals. This type of spillover is mostly caused by the behavior of investors who are relocating their international assets under certain risk policies. Fundamental-based contagion works through the trade linkages between the source country and the affected countries. When a country is in a crisis, its trading partner may experience declining asset prices or sudden capital outflow. The expectation is for worsening exports and thus the trade account is a trigger point in this situation, because in today’s globalized economy the US and China have strong trade linkages both as partners and rivals. In this context, non-fundamental-based contagion explains the existing financial links between countries which are a result of the economic integration of a country into the world market. This channel is especially relevant for China as the country is increasingly getting more integrated into the world economy by liberalizing its capital account and increasing its foreign direct investments (
Vergeron 2015;
Arsnalalp et al. 2016).
Regardless of its effects, whether positive or negative, financial contagion is undesirable since it refers to the situation in which excess volatility is transferred from one country to another during a crisis period. The information linkage and spillover effects between stock markets have a wide range of research interest in literature (
Hamao et al. 1990;
Koutmos and Booth 1995;
Chen et al. 2020;
Kao et al. 2015;
Otsubo 2014;
Reboredo 2015;
Xu et al. 2019;
Uddin et al. 2020). In recent years, emerging markets, with greater return opportunities for especially institutional investors, have become very important in the global stock market. This created a greater information flow from developed stock markets to developing stock markets. There is a considerable amount of research in the literature proving the linkage between US and Taiwan markets (
Chan et al. 2008), Singapore and Taiwan markets (
Roope and Zurbruegg 2002), and Japan and other Asian markets (
Miyakoshi 2003).
There is a growing interest among researchers in the importance of rare earths to clean energy.
Habib and Wenzel (
2014) examined the dependency of emerging renewable energy technologies, especially wind turbines and electric vehicles, along with other background end uses on two key Rare Earth Elements (REEs), i.e., neodymium (Nd) and dysprosium (Dy). This study revealed that a business as usual development (BAUD) projected primary supply is unable to meet the forecasted demand of Nd and Dy in all the four modeled demand scenarios by 2050. Other important studies, such as
Stegen (
2015),
Zhou et al. (
2017), and
Zhang et al. (
2017) focus on the economy–politics of rare earths rather than their role as a financial instrument. Previous empirical research has focused on the price behavior of different REs and its impact on clean energy companies and other economic variables. In this context,
Apergis and Apergis (
2017) examined the long-run relationship between rare earth prices and renewable energy consumption. Other studies covered specific rare earth price features, such as
Proelss et al. (
2019), who studied the price volatility of the four largest rare earth element oxides (cerium, lanthanum, neodymium, and yttrium) and concluded that volatility is highly persistent over time and contains useful information for managing uncertainty for rare earth companies. For price forecasting, Riesgo
García et al. (
2018) show that several short-term RE oxide prices can be forecasted using transgenic time series models. There are just a few articles concerning the financial performances and dynamic correlations between rare earths and stock markets.
Reboredo and Ugolini (
2020) examined price transmission between rare earth stocks and the base metals, gold, clean energy, oil, and global MSCI stock markets using a Markov switching vector autoregressive model.
The trio of energy markets, China, and the USA is the landmark of the so-called trade wars in the last couple of years, which is the main catalyzer of contagion. Our research contributes to the extant rare earth literature by examining volatility transmission effects across markets for rare earth, Chinese and US financial markets. We compute price spillovers between rare earth and financial markets using VAR–VECH–TARCH models. Our empirical results on volatility spillovers between rare earth and financial markets provide new insights for investors in the new cold war era between China and the US.
3. Methodology
Usually, financial data suggest that some time periods are riskier than others. The goal of such models is to provide a volatility measure that can be used in financial decision making with risk analysis, portfolio selection, and derivative pricing (
Engle 1982;
Engle and Ng 1993). An important characteristic of such asset prices is that “bad” news has a more persistent impact on volatility than “good” news has. Most of the stocks have a strong negative correlation between the current return and future volatility. This is called “leverage effect”, which refers to the well-established relationship between stock returns and both implied and realized volatility. A standard explanation ties the phenomenon to the effect a change in market valuation of a firm’s equity has on the degree of leverage in its capital structure, with an increase in leverage producing an increase in stock volatility (
Figlewski and Wang 2000). Glosten, Jaganathan, and Runkle (
Glosten et al. 1993) showed how to allow the effects of good and bad news to have different effects on volatility. In a sense,
ԑt−1 = 0 is a threshold such that shocks greater than the threshold have different effects than shocks below the threshold. Consider the threshold–GARCH (TARCH) process:
where
dt−1 is a dummy variable that is equal to one if
ԑt−1 < 0 and is equal to zero if
ԑt−1 ≥ 0. The intuition behind the TARCH model is that positive values of
ԑt−1 are associated with a zero value of
dt−1. Hence if
ԑt−1 ≥ 0, the effect of
ԑt−1 shocks on
ht is
when
ԑt−1 < 0,
dt−1 = 1, and the effect of an
ԑt−1 shock on
ht is
. If
λ1 > 0, negative shocks will have larger effects on volatility than positive shocks.
VAR–VECH–TARCH Model
This method is extended from VAR–GARCH, which is proposed by
Ling and McAleer (
2003). An examination of the conditional returns and conditional volatility can be conducted with meaningful estimated parameters via this structure. This method is composed of two parts, namely the VAR model and asymmetric VECH–TARCH model, which are used to explore the joint evolution of conditional returns and volatility spillovers between different financial markets. First, the VAR model extends the univariate autoregressive (AR) to vector autoregressive (VAR) by internalizing the related variables into endogenous variables to examine the contagion and spillover effect between major financial markets.
The basic mathematical expression of the VAR model is as follows:
where
Rt refers to the value of endogenous variables vector at time
t,
C is the constant vector, matrix
A is the estimated coefficients and
k is the lag operator. Residual vector
is assumed to be normally distributed with a zero mean and constant variance where the market information available at time
t−1 denoted as
dt−1. The lag order of (
k) VAR structure is decided via AIC criterion, FPE criterion and LR.
In this approach we incorporate a three-dimensional model to examine the news spillover between different markets. Suppose that our model structure is as follows:
Equation (3) specifies the relation between the residual term
ԑi.t and the conditional variance
, which is normally distributed with a zero mean and constant variance.
α,
β are the coefficients.
Hi,t represents the conditional variance–covariance matrix,
C represents the lower triangular matrix,
A and
B are square arrays. If
CTC is positive, then it is almost positive.
where
h11,t,
h22,t,
h33,t in the matrix
Ht represent the conditional variances. Matrix
A is the ARCH coefficients of the model,
a11,
a22,
a33 represent the ARCH effect while Matrix
B is the GARCH coefficients of the model,
b11,
b22,
b33 are the GARCH effect.
In consideration of the asymmetric effect, diagonal VECH is:
where the conditional variance–covariance equation of a bivariate (VECH) TARCH model has the following form:
where the last term on the RHS of Equation (7) depicts the asymmetries. In this context, the diagonal bivariate
VECH model is as follows:
The coefficient
a11 refers to the ARCH process in the residuals from asset
i which depicts the fluctuations of the assets reflecting the impact of external shocks on fluctuations. The ARCH effects measure the short-term persistence while the GARCH effect measures the long-term persistence. The
coefficient represents the ARCH process in the second asset residuals and the parameters between asset
i and asset
j. The calculation of the time-varying beta coefficient is done as
where the symbol ^ indicates the estimated values of conditional variance.
4. Data
Chinese stock markets, US stock markets, and energy (both conventional and new) markets are three dimensions of our models. China is the key element in all models with its expanding hybrid role in the global economy both as a producer and a consumer. In this context, the data we use incorporate five variables which are utilized for three different model systems: MVIS Global Rare Earth/Strategic Metals Index
4 (MVIS), Dow Jones Industrial Metals and Mining Index (DJI), Brent crude oil futures (Brent), S&P 500 Index (SP500), and The SSE Composite Index (SSE) for the period between 30 June 2015 and 6 March 2020.
Next, the return of each market is calculated as follows:
where RMVIS, RDJ, RBrent, RSP500, and RSSE refers to the return series of related variables.
Table 1 exhibits the descriptive statistics for the returns. The mean values are close to zero for all the returns. The statistics of each return differ from each other, but in common the skewness of each return is not equal to zero and neither is the kurtosis, indicating that each return has typical characteristics of leptokurtosis and fat-tail. It is well known that leptokurtosis and fat-tail are the typical characteristics of financial time series.
The J–B statistic of each return is significant from zero, which means none of the returns obeys the normal distribution. Further, the stationarity of the variables has been examined using the Augmented Dickey–Fuller (ADF) unit root test. The null hypothesis of the unit root is rejected for all return series, indicating that variables are stationary.
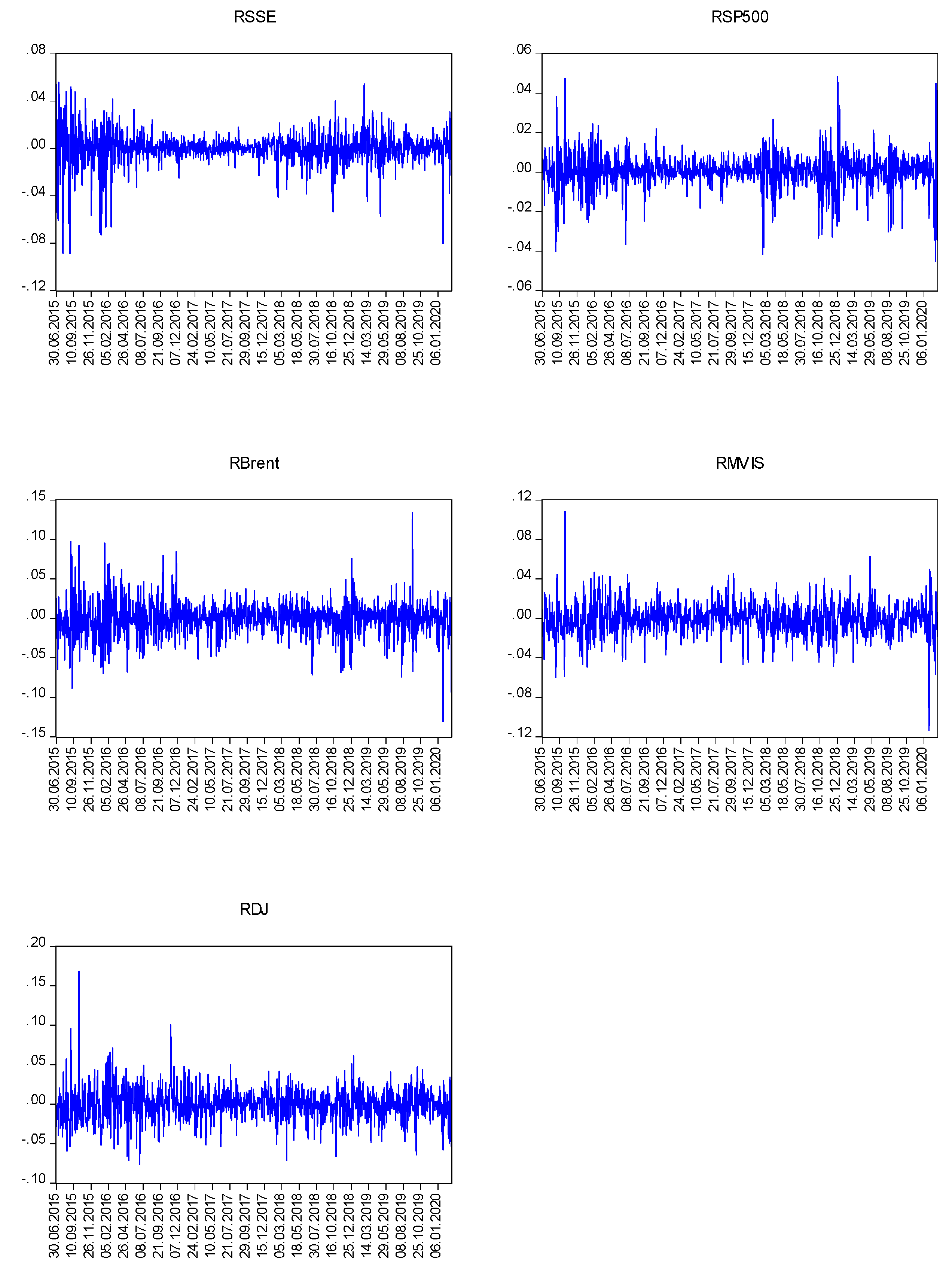
Figure 2 exhibits the return series. The negative return in 2015 shows the Chinese market bubble burst while the Dow Jones and S&P 500 experienced temporary jumps in the same period. The volatility in Brent returns is due to the global economy facing one of the largest oil price declines in modern history between mid-2014 and early 2016. Booming US shale oil production played a significant role in this price plunge period. Only for rare earth fund, we can say that it moves constantly in a relatively stable tunnel.
5. Empirical Results
We constructed three different model systems with three different VAR system specifications which are as follows:
VAR System Specification for Model 1: This model system represents the relationship between Chinese stock markets, crude oil, and industrial metals, and mining products are analyzed. The own conditional ARCH effects ( are significant at the %1 level for RSSE and at the %5 level for RBrent while not significant for RDJI even at a 10% level. These results indicate that Chinese stock markets and crude oil markets are influenced by the volatility of their own markets while industrial metals and mining products markets are not. Besides, there is no significant volatility spillover over effect among the markets in the short term since are not statistically significant even at 10% level. Moreover, the own conditional GARCH effects ( in matrix B are all significant at %1 level for all related markets in Model 1. Consequently, for the long-term volatility spillovers, the volatility spillover between Chinese stock markets, crude oil, and industrial metals and mining products are all significant at 5% level that are . As a result, we can conclude that a volatility spillover between the mentioned markets strongly exists in the long term, which is consistent with the economy theory that the impact of a shock in financial markets is reflected in the real economy with a lagged effect. Finally, the D matrix refers to the asymmetric coefficients of all markets that are positive and significant at 1% level. Positive coefficients mean that good news increases the volatility for all markets in Model 1. The coefficients of are all positive, which indicates that good news from Chinese stock markets to both crude oil and industrial metals and mining products market increases the volatility. Moreover, good news from crude oil markets to industrial metal and mining products increases the volatility as well. Last but not least, asymmetric volatility exists for all mentioned markets and between each other as well.
VAR System Specification for Model 2: In Model 2, the relationship between US stock markets, crude oil, and industrial metals and mining products is analyzed. The own conditional ARCH effects ( are significant at the %1 level for RDJI and at the %5 level for RBrent while not significant for RSP500 even at the 10% level. These results indicate that crude oil markets and industrial metal and mining products are influenced by the volatility of their own markets while US stock markets are not, which is an interesting result. Besides, there is no significant volatility spillover over effect among the markets in the short term since are not statistically significant even at the 10% level. Moreover, the own conditional GARCH effects ( in matrix B are all significant at %1 level for all related markets in Model 2. Consequently, for the long-term volatility spillovers, the volatility spillover between US stock markets, crude oil, and industrial metals and mining products are all significant at 1% level that are . As a result, we can conclude that volatility spillover between mentioned markets strongly exists in the long term. Finally, the D matrix referring to the asymmetric coefficients of all markets is positive and significant at 1% level. Positive coefficients mean that good news increases the volatility for all markets in Model 2. The coefficients of are all positive, which indicates that good news from US stock markets to both crude oil and industrial metals and mining products markets increases the volatility. Moreover, good news from crude oil markets to industrial metal and mining products increases the volatility as well. Last but not least, asymmetric volatility exists for all mentioned markets and between each other as well.
VAR System Specification Model 3: In Model 3, the relationship between US stock markets, the Chinese stock market and rare earth markets is analyzed. The own conditional ARCH effects ( are significant at the %1 level for RMVIS and RSSE while also significant at the %5 level for RSP500. These results indicate that all mentioned markets in Model 3 structure are influenced by the volatility of their own markets. Besides, there are also significant volatility spillover over effects among the rare earth and Chinese stock markets in the short term since is statistically significant at 1% level. Moreover, the own conditional GARCH effects ( in matrix B are all significant at %1 level for all related markets in Model 3. Consequently, for the long-term volatility spillovers, the volatility spillovers between US stock markets, Chinese stock markets, and rare earth markets are all significant at 1% level that are . As a result, we can conclude that a volatility spillover between the mentioned markets strongly exists in the long term. Finally, the D matrix referring to the asymmetric coefficients of all markets is positive and significant at 1% level. Positive coefficients mean that good news increases the volatility for all markets in Model 3. However, cross-asymmetry is valid for only the rare earths market and Chinese stock markets, which is consistent with China’s dominancy in the rare earth market. The coefficients of are positive and significant at 1% level which indicates that good news from the rare earth market to Chinese stock market increases the volatility.
Cross-market spillovers in
Table 2 show that there is a risk transmission channel between the industrial metals, rare earths, Chinese and US stock markets due to China’s strengthening position in the global economy. In Model 1 and Model 2, the return linkage between crude oil and industrial metals and mining products decreased significantly from the second half of 2016 to the beginning of 2017. Chinese industrial metal demand has been a key driver of growth in the past, which is a significant indicator for the health of global economic growth. Infrastructure investment is the key driving force for industrial metals demand and China was expected to invest heavily in railways and metro lines
5, which can explain the increasing correlation between RSSE and RDJI in the second half of 2018 and 2019.
The VAR–VECH–TARHC models illustrate spillover asymmetry for all three models. The covariance and correlation graphs also support these results, exhibiting both correlation and covariance plunges between Chinese stock markets, US stock markets and eventually energy markets.
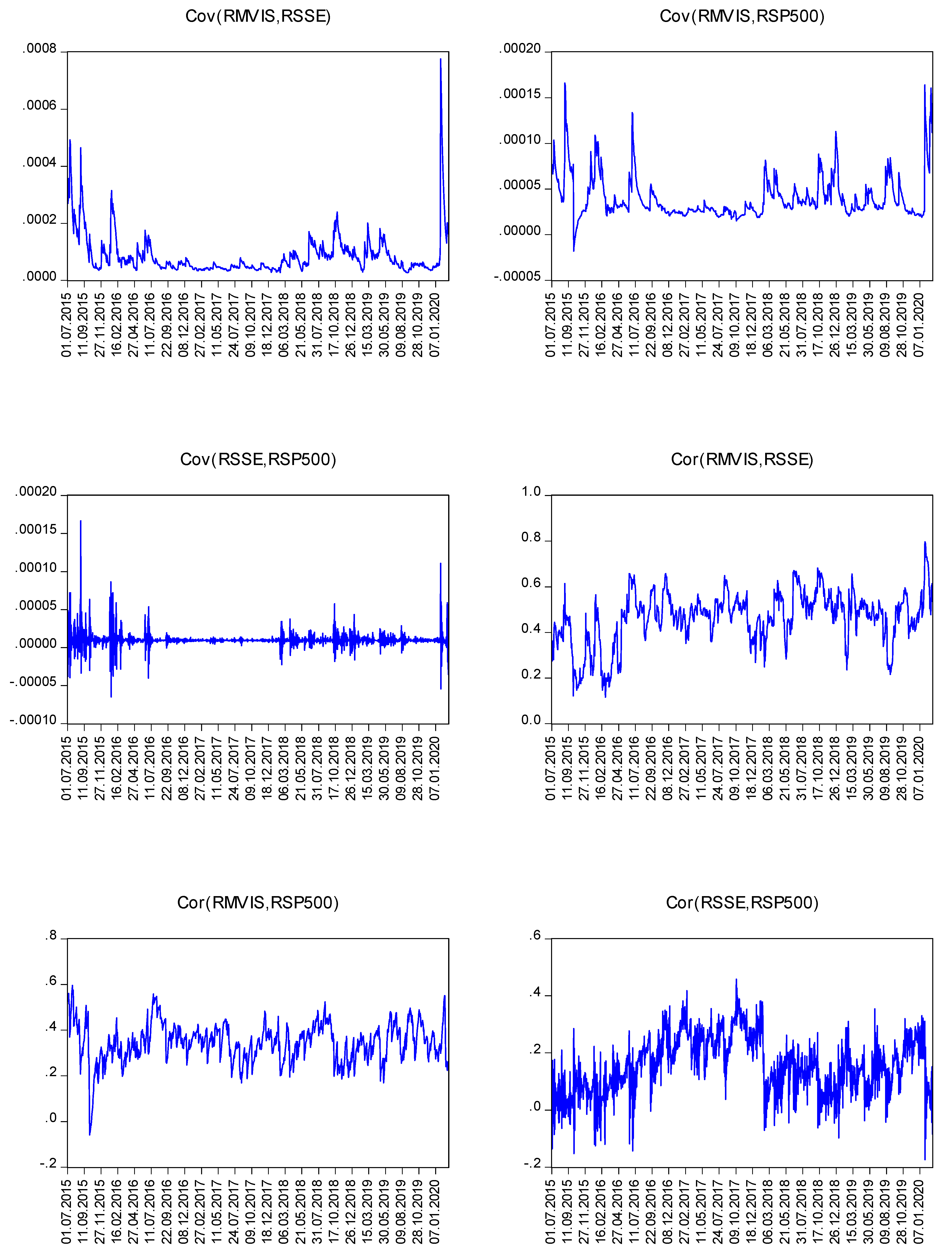
In
Figure 3,
Figure 4 and
Figure 5 we can see the covariance and correlation coefficients of related markets for three different models. Considering Model 1, between the second half of 2015 and second half of 2016, the correlation coefficient fluctuation range between related markets was relatively large, between 0.1 and 0.6, which indicates the unstable relationship fueled by Chinese stock market turbulence. Based on our VAR–VECH–TARCH models, we can also claim that the large correlation coefficients for the related markets in Model 2 and Model 3 indicate the contagion effect of the Chinese stock market meltdown.
6. Conclusions
For the world economy, China is the key element with its unique position both as a consumer of raw materials and producer of goods. This hybrid role enables China’s stock markets to affect US stock markets incrementally. In this context, studying the volatility spillover between interconnected markets such as rare earth, crude oil, industrial metals, and stock markets provides valuable insight for any type of investor. These linkages are expected to increase significantly; as China opens up its financial markets to the rest of the world, investors are increasingly looking for investment opportunities abroad as domestic returns are expected to decline following lower expectations about the growth of the Chinese economy in the future.
Rising tensions between the United States and China have sparked concerns that China could use its dominant position as a supplier of rare earths for leverage in the trade war between the two global economic powers. China supplied 80% of the rare earths which are used in rechargeable batteries for electric and hybrid cars, advanced ceramics, computers, DVD players, wind turbines, catalysts in cars and oil refineries, monitors, televisions, lighting, lasers, fiber optics, superconductors and glass polishing, imported by the United States from 2014 to 2017. According to the model systems in our analysis, bilateral spillover exists between US and Chinese stock markets. The conflict between China and the US spreads from trade to technology to supply chains, touching every aspect of bilateral relations. The conflict risks massive spillover costs to the global economy. In order to understand how the Chinese stock market interacts with US industrial metals and energy markets, this study examined information transmission as a function of daily return and volatility spillovers. Return and volatility spillovers are the most extensive channel for spreading out the news generated in one market to the other ones, which makes the financial markets inherit international risk factors as their local risks. Our empirical evidence for the period 30 June 2015 to 6 March 2020 indicates that cross-market spillovers show that there is a risk transmission channel between the industrial metals, rare earth, Chinese, and US stock markets due to China’s strengthening position in the global economy. Financial contagion may lead to undesirable outcomes for the affected countries since it might have a negative effect on the international portfolio optimization of investors in both the affected countries and the source country. If there is indeed financial contagion from one country or region to another, investors may want to reconsider their optimal portfolio selection (
Roy and Roy 2017). Especially for foreign investors, the Chinese stock market is too regulated, which leads to a relatively small share of foreign investors in China’s financial markets. The low level of market participation by foreign investors in the markets weakens the ability of these investors to understand the potential causes of a crisis in Chinese financial markets. This imperfect information causes different expectations among investors, who may falsely believe that a crisis in one country can lead to a crisis in another country even if the fundamentals of that country give no reason for such a market crash. Future research might focus on contagion at a more micro level and examine the effects for specific sectors or channels by using a different method than cross-market correlation analysis, such as a Markov switching vector autoregressive model that accounts for different volatility regimes. Company-level analysis, which may focus on the dynamic correlation between rare earth prices and the stock prices of companies involved in rare earth mining and industrial metals, can also be a more specific research area, especially for portfolio managers and financial investors.